Algoritmo de algas artificiais (AAA)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

As algas, um dos organismos mais antigos do planeta, desempenham um papel essencial nos ecossistemas aquáticos. Existem mais de 45 mil espécies de algas, que podem variar significativamente em cor, forma, tamanho e habitat. Elas sustentam a vida no ambiente aquático, servindo de base alimentar para diversas espécies animais. Além disso, produzem oxigênio por meio da fotossíntese, o que as torna fundamentais para a manutenção da vida no planeta. Esses organismos podem ser unicelulares ou multicelulares e frequentemente formam colônias que operam de maneira integrada.

As algas unicelulares se dividem por mitose, gerando novas células que permanecem conectadas e formam colônias. Já as algas multicelulares se reproduzem por esporos, que se dispersam na água e dão origem a novos organismos, criando também colônias. Esses organismos fascinantes demonstram como processos biológicos podem ser utilizados para desenvolver soluções inovadoras na modelagem matemática e na otimização.

O algoritmo de algas artificiais (Artificial Algae Algorithm, AAA), proposto por Uymaz, Tezel e Yel em 2015, combina fenômenos biológicos naturais com elegância matemática. Inspirado no fascinante mundo das microalgas, esse algoritmo de otimização meta-heurístico utiliza comportamentos coloniais e capacidades adaptativas desses organismos para criar um modelo algorítmico de otimização. A inspiração veio da habilidade das microalgas de se mover em direção à luz, adaptar-se a condições ambientais variáveis e se reproduzir por mitose para aprimorar a fotossíntese.

O algoritmo inclui três processos principais: movimento espiral, evolução e adaptação. O movimento espiral modela o deslocamento tridimensional das algas em uma solução nutritiva, de modo que elas encontrem condições ideais para o crescimento. O processo evolutivo garante a reprodução das colônias de algas nas condições mais favoráveis, promovendo seu desenvolvimento e melhorando as soluções. O processo de adaptação ajuda colônias menos bem-sucedidas a se assemelharem à maior colônia, garantindo sua sobrevivência e crescimento contínuo.

Implementação do algoritmo

O algoritmo de algas artificiais (AAA) foi desenvolvido para modelar matematicamente propriedades das algas, como seu movimento espiral, processo de adaptação e evolução. Cada colônia de algas representa uma possível solução candidata para o problema de otimização (e cada célula da colônia corresponde a uma coordenada individual), e essas colônias se agrupam para formar uma população de algas. Cada colônia é caracterizada por seu tamanho, que reflete a qualidade da solução que representa.

No processo evolutivo, as colônias de algas que alcançam condições ambientais mais favoráveis crescem e se desenvolvem. Já as que não encontram tais condições não se desenvolvem e morrem. Após a conclusão do movimento espiral, as colônias de algas são classificadas de acordo com seu tamanho. Uma célula aleatoriamente escolhida da maior colônia é copiada para a mesma posição da colônia menor, concluindo o processo evolutivo.

As colônias de algas se movimentam em espiral na água para alcançar melhores condições ambientais. A energia utilizada por elas é proporcional ao tamanho da colônia. Durante o deslocamento, elas perdem energia, mas, se encontrarem um ambiente mais favorável, recuperam metade dela. A energia da colônia está diretamente relacionada à concentração de nutrientes; portanto, quanto maior a concentração de nutrientes, maior a frequência do movimento da colônia.

A força de atrito é outro fator importante que afeta a movimentação na água. Colônias com menor área superficial possuem maior amplitude de movimento, pois apresentam menor resistência ao atrito. Colônias que alcançam melhores condições ambientais apresentam maior área de atrito devido ao seu tamanho, o que reduz sua velocidade. Esse fenômeno ajuda a explorar melhor a vizinhança da solução encontrada e aprimorar a capacidade de busca local.

O processo de adaptação ocorre quando colônias de algas que não atingiram um desenvolvimento suficiente durante o movimento espiral tentam se assemelhar à colônia maior. A colônia com o maior nível de "fome" é a que passa por esse processo. No início da otimização, todas as colônias começam com um nível de fome igual a zero. Durante o movimento espiral, o nível de fome das colônias que não encontraram uma solução melhor aumenta em uma unidade. Após o movimento espiral e o processo evolutivo, a colônia com o maior nível de fome entra no período de adaptação. No entanto, a adaptação não ocorre a cada iteração. Primeiro, é gerado um valor aleatório entre 0 e 1. Se esse valor for menor que o parâmetro de adaptação, o processo de adaptação é iniciado.

Após a análise do modelo apresentado das propriedades das algas, passamos à escrita do pseudocódigo do AAA:

Inicialização:
    Criar uma população de agentes
    Para cada agente:
        Inicializar uma posição aleatória no espaço de busca
        Inicializar parâmetros (tamanho, energia, fome, etc.)

Laço principal:
    Enquanto o critério de parada não for atingido:
        Para cada agente:
            Executar o movimento
            Avaliar a função de aptidão
        
        Atualizar a melhor solução encontrada
        
        Para cada agente:
            Atualizar energia
            Atualizar tamanho
            Atualizar fome
        
        Executar o processo evolutivo
        Executar o processo de adaptação

Função Movimento:
    Para cada agente:
        Selecionar outro agente usando seleção por torneio
        Para cada coordenada:
            Atualizar a posição do agente utilizando a fórmula trigonométrica espiral de movimento
            Aplicar o coeficiente de atrito

Função ProcessoEvolução:
    Encontrar o agente com o menor tamanho
    Substituir suas coordenadas pelas coordenadas de um agente selecionado aleatoriamente

Função ProcessoAdaptação:
    Encontrar o agente com o maior nível de fome
    Com uma determinada probabilidade:
        Encontrar o agente com o maior tamanho
        Atualizar as coordenadas do agente faminto aproximando-as das coordenadas
        do maior agente
        Reinicializar os parâmetros do agente faminto

Função CálculoEnergia:
    Calcular a energia com base no tamanho da colônia, concentração de nutrientes
    e velocidade de crescimento atual

Função SeleçãoPorTorneio:
    Selecionar dois agentes aleatórios
    Retornar o agente com o melhor valor da função de aptidão

Agora, listamos as fórmulas utilizadas no algoritmo. As fórmulas 1-5 estão diretamente relacionadas à implementação da lógica central do algoritmo.

1. Inicialização da população: população = [[x1_1, x1_2, ..., x1_D], [x2_1, x2_2, ..., x2_D], [xN_1, xN_2, ..., xN_D]], onde xj_i — i-ésima célula j-ésima colônia de algas, D — dimensionalidade da colônia, N — tamanho da população.

2. Movimento espiral: x'i_j = xi_j + α * cos (θ) * τ (Xi) * p; y'i_j = yi_j + α * sin (θ) * τ (Xi) * p; z'i_j = zi_j + r * v, onde (x'i_j, y'i_j, z'i_j) são as novas coordenadas i-ésima colônia, α, θ ∈ [0, 2π], p ∈ [-1, 1], r ∈ [-1, 1], v ∈ [-1, 1], τ(Xi) — área de atrito da i-ésima colônia.

3. Processo evolutivo: biggest = max(Gi), m = célula escolhida aleatoriamente, smallest.xm = biggest.xm

4. Processo de adaptação: starving = max(Ai); starving.x = starving.x + (biggest.x - starving.x) * rand

5. Modelo de crescimento de Monod para algas: μt = μtmax * St / (St + Kt), onde μt representa a taxa de crescimento das algas no momento t, μtmax  — taxa máxima de crescimento, St — tamanho da colônia no momento t, Kt — constante de meia-saturação.

6. Área de atrito: τ(Xi) = 2π * (3√(3*Gi) / (4π))², onde τ(Xi) — área de atrito da i-ésima colônia, Gi — tamanho da i-ésima colônia.

7. Seleção da colônia para movimento espiral: a seleção por torneio é utilizada para escolher a colônia que se moverá. Isso será discutido em mais detalhes abaixo.

8. Escolha aleatória de dimensões para o movimento espiral: p, r, v  — índices de dimensões escolhidos aleatoriamente, distintos entre si.

9. Seleção da colônia vizinha para o movimento espiral: Xj — colônia selecionada pelo método de torneio, em direção à qual a colônia Xi se moverá.

10. Valor inicial da fome de todas as colônias: Ai = 0 para todos i.

11. Aumento da fome das colônias que não melhoraram a solução: Ai = Ai + 1 se a colônia não encontrou uma solução melhor.

12. Seleção da colônia com maior nível de fome: starving = max(Ai.)

13. Probabilidade de execução do processo de adaptação: rand < Ap, onde Ap — parâmetro de adaptação.

As fórmulas 6-13 descrevem detalhes adicionais da implementação do algoritmo, incluindo o cálculo da área de atrito, a escolha das colônias para movimentação, o gerenciamento da fome das colônias e a probabilidade de execução do processo de adaptação.

O modelo de Monod, também conhecido como modelo de crescimento de Monod, é amplamente utilizado para descrever o crescimento e o comportamento de populações em sistemas biológicos. Ele se baseia nos estudos de Jacques Monod, bioquímico francês que investigou a cinética de crescimento de microrganismos. A taxa de crescimento da população depende da concentração dos nutrientes. Em baixas concentrações, a taxa de crescimento é proporcional à concentração do substrato, enquanto em altas concentrações, a taxa atinge um máximo. Em algoritmos de otimização, o modelo de Monod é utilizado para modelar o crescimento e a adaptação das populações em algoritmos evolutivos. Durante o processo de otimização, os parâmetros da população variam de acordo com os recursos disponíveis, possibilitando uma modelagem mais precisa dos processos biológicos reais.

Gostaria de chamar a atenção para a seleção por torneio utilizada para escolher a colônia. Esse método não havia sido empregado anteriormente em algoritmos deste tipo. ara visualizar melhor a distribuição das probabilidades de seleção dos indivíduos na população usando esse método, escreveremos um script e imprimiremos os resultados. O trecho de código destacado em azul participa diretamente da formação da distribuição durante a seleção.

input int      PopSize = 50;
input int      Count   = 1000000;
input int      BarWidth = 50; // Histogram width in characters

void OnStart()
{
  int pop[];
  ArrayResize(pop, PopSize);

  for(int i = 0; i < PopSize; i++) pop[i] = PopSize - i;

  Print("Original population:");
  ArrayPrint(pop);

  int tur[];
  ArrayResize(tur, PopSize);
  ArrayInitialize(tur, 0);

  int ind1 = 0, ind2 = 0;

  for(int i = 0; i < Count; i++)
  {
    ind1 = MathRand() % PopSize;
    ind2 = MathRand() % PopSize;

    if(pop[ind1] > pop[ind2]) tur[ind1]++;
    else                      tur[ind2]++;
  }

  Print("Probability distribution (in %):");

  double maxPercentage = 0;
  double percentages[];
  ArrayResize(percentages, PopSize);

  for(int i = 0; i < PopSize; i++)
  {
    percentages[i] = (double)tur[i] / Count * 100;
    if(percentages[i] > maxPercentage) maxPercentage = percentages[i];
  }

  for(int i = 0; i < PopSize; i++)
  {
    int barLength = (int)((percentages[i] / maxPercentage) * BarWidth);
    string bar = "";
    for(int j = 0; j < barLength; j++) bar += "|";

    PrintFormat("%2d: %5.2f%% %s", i, percentages[i], bar);
  }
}

Abaixo está o resultado da execução do script para visualizar a distribuição das probabilidades de seleção de cada indivíduo na população:

População inicial:
20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1
Distribuição de probabilidades (em porcentagem):
 0:  9.76% ||||||||||||||||||||||||||||||||||||||||||||||||||
 1:  9.24% |||||||||||||||||||||||||||||||||||||||||||||||
 2:  8.74% ||||||||||||||||||||||||||||||||||||||||||||
 3:  8.22% ||||||||||||||||||||||||||||||||||||||||||
 4:  7.77% |||||||||||||||||||||||||||||||||||||||
 5:  7.27% |||||||||||||||||||||||||||||||||||||
 6:  6.74% ||||||||||||||||||||||||||||||||||
 7:  6.26% ||||||||||||||||||||||||||||||||
 8:  5.78% |||||||||||||||||||||||||||||
 9:  5.25% ||||||||||||||||||||||||||
10:  4.75% ||||||||||||||||||||||||
11:  4.22% |||||||||||||||||||||
12:  3.73% |||||||||||||||||||
13:  3.25% ||||||||||||||||
14:  2.75% ||||||||||||||
15:  2.25% |||||||||||
16:  1.75% ||||||||
17:  1.25% ||||||
18:  0.77% |||
19:  0.25% |

A distribuição das probabilidades diminui linearmente, permitindo que colônias com maior potencial para boas soluções tenham mais chances de serem selecionadas, ao mesmo tempo em que opções menos eficientes ainda possuem alguma probabilidade de serem escolhidas. Essa abordagem de seleção não depende dos valores absolutos da aptidão dos indivíduos, garantindo uma ampla diversidade de soluções.

Em artigos anteriores, já analisamos fórmulas para modificar a distribuição de probabilidades na seleção, possibilitando tanto uma diminuição linear quanto não linear das probabilidades, mas com menor custo computacional (para a seleção por torneio, é necessário chamar a função MathRand() duas vezes).

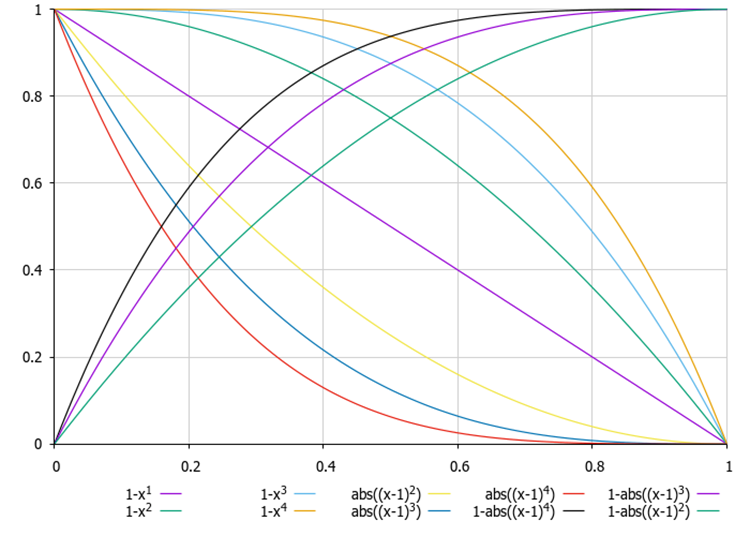
Figura 1. Exemplos de fórmulas para alterar a forma da distribuição de probabilidade, em que x é um número aleatório uniformemente distribuído no intervalo [0,0, 1,0]

Agora que examinamos detalhadamente todos os aspectos do algoritmo, podemos começar a escrever o código.

Descreveremos a estrutura "S_AAA_Agent", que será utilizada para modelar uma colônia de algas (agente) dentro do algoritmo. A estrutura contém quatro campos:

• energy — representa o nível de energia do agente.
• hunger — usado para rastrear o nível de fome do agente.
• size — indica o tamanho do agente (crescimento, comprimento da alga).
  
• friction — coeficiente de atrito, que influencia o movimento do agente.

O método Init inicializa os membros da estrutura com valores padrão. 

Dessa forma, a estrutura "S_AAA_Agent" representa um modelo simples de agente com características básicas.

//——————————————————————————————————————————————————————————————————————————————
struct S_AAA_Agent
{
  double energy;
  int    hunger;
  double size;
  double friction;

  void Init ()
  {
    energy   = 1.0;
    hunger   = 0;
    size     = 1.0;
    friction = 0.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Agora, escreveremos a definição da classe "C_AO_AAA", que herdará da classe base "C_AO". Isso significa que a nova classe manterá todos os membros e métodos da classe base, podendo estendê-los ou sobrescrevê-los.

1. No construtor da classe, os valores de vários parâmetros relacionados ao algoritmo são definidos e inicializados:

• popSize — tamanho da população.
• adaptationProbability — probabilidade de adaptação.
• energyLoss — perda de energia.
• maxGrowthRate — taxa máxima de crescimento.
• halfSaturationConstant — constante de meia-saturação.

Todos esses parâmetros são armazenados no array "params".

2. O método "SetParams" atualiza os valores dos parâmetros do algoritmo a partir do array "params".

3. Métodos:

• O método Init() é responsável pela inicialização e recebe arrays com os valores mínimos e máximos dos parâmetros, além dos passos e do número de épocas.
• O método Moving() gerencia o deslocamento ou atualização do estado dos agentes.
• O método Revision() é utilizado para revisar ou avaliar o estado dos agentes.
• Os métodos privados EvolutionProcess (), AdaptationProcess (), CalculateEnergy () e TournamentSelection () são responsáveis pelo processo evolutivo, processo de adaptação, cálculo da energia das algas e seleção por torneio, respectivamente.
  

Campos da classe:

• adaptationProbability, energyLoss, maxGrowthRate, halfSaturationConstant — variáveis que armazenam os valores dos parâmetros.
• S_AAA_Agent agent[] — array de agentes.
  
• fMin, fMax — usados para armazenar os valores de aptidão (tamanho das algas) da população.

A classe C_AO_AAA fornece uma estrutura que facilita o gerenciamento dos parâmetros e do estado dos agentes, permitindo sua integração a um sistema maior baseado na herança da classe C_AO.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAA : public C_AO
{
  public: //--------------------------------------------------------------------

  ~C_AO_AAA () { }

  C_AO_AAA ()
  {
    ao_name = "AAA";
    ao_desc = "Algae Adaptive Algorithm";
    ao_link = "https://www.mql5.com/en/articles/15565";

    popSize                = 200;
    adaptationProbability  = 0.2;
    energyLoss             = 0.05;
    maxGrowthRate          = 0.1;
    halfSaturationConstant = 1.0;

    ArrayResize (params, 5);

    params [0].name = "popSize";                params [0].val = popSize;
    params [1].name = "adaptationProbability";  params [1].val = adaptationProbability;
    params [2].name = "energyLoss";             params [2].val = energyLoss;
    params [3].name = "maxGrowthRate";          params [3].val = maxGrowthRate;
    params [4].name = "halfSaturationConstant"; params [4].val = halfSaturationConstant;
  }

  void SetParams ()
  {
    popSize                = (int)params [0].val;
    adaptationProbability  = params      [1].val;
    energyLoss             = params      [2].val;
    maxGrowthRate          = params      [3].val;
    halfSaturationConstant = params      [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double adaptationProbability;
  double energyLoss;
  double maxGrowthRate;
  double halfSaturationConstant;

  S_AAA_Agent agent [];

  private: //-------------------------------------------------------------------
  void   EvolutionProcess    ();
  void   AdaptationProcess   ();
  double CalculateEnergy     (int index);
  int    TournamentSelection ();
  double fMin, fMax;
};
//——————————————————————————————————————————————————————————————————————————————

Agora, analisemos detalhadamente o método Init da classe C_AO_AAA:

• rangeMinP — array contendo os valores mínimos de cada parâmetro.
• rangeMaxP — array contendo os valores máximos de cada parâmetro.
• rangeStepP — array contendo os incrementos para cada parâmetro.
• epochsP — número de épocas (por padrão, 0).

Campos do método:

1. O método StandardInit realiza a inicialização padrão utilizando os parâmetros fornecidos. 

2. O tamanho do array agent é ajustado para o valor de popSize, preparando a estrutura para armazenar os agentes.

3. São definidos os valores mínimo e máximo das funções utilizadas no processo.

4. Um laço percorre cada agente, inicializando-o com o método Init.

5. Um laço interno inicializa as coordenadas de cada agente:

• Primeiro, a coordenada c é atribuída aleatoriamente dentro do intervalo de rangeMin[c] a rangeMax[c], utilizando o método RNDfromCI.
• Em seguida, essa coordenada é ajustada pelo método SeInDiSp, que normaliza os valores.

Se todas as operações forem concluídas com sucesso, o método retorna true. Dessa forma, o método Init inicializa o array de agentes com os intervalos e incrementos especificados para suas coordenadas. Ele inclui uma inicialização padrão, a definição dos limites das funções e a atribuição aleatória de valores às coordenadas.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  ArrayResize (agent, popSize);

  fMin = -DBL_MAX;
  fMax =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init ();

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Agora, analisemos o código do método Moving da classe C_AO_AAA. Sua estrutura e funcionalidade geral são as seguintes:

1. Se a variável revision for false, ela é definida como true, e a função encerra sua execução. Isso significa que a lógica principal do método Moving não é executada na primeira iteração.

2. Um laço percorre todos os elementos da população popSize.

3. A seleção por torneio ocorre na função TournamentSelection, que retorna o índice de um dos agentes (algas) para uso posterior.

4. O laço interno percorre cada coordenada (dimensão do espaço, definida pela variável "coords").

5. Três valores aleatórios são gerados: "α" e "β" (ângulos) e "ρ" (um valor no intervalo de -1 a 1), utilizando o método "u.RNDfromCI".

6. Dependendo do valor da variável "variant" (que varia de 0 a 2), as coordenadas "a[i].c[c]" são atualizadas:

• Se "variant" for 0, o cosseno do ângulo "α" é utilizado.
• Se "variant" for 1, o seno do ângulo "β" é utilizado.
• Se "variant" for 2, o valor "ρ" é utilizado.

O uso da variável "variant" permite simular o movimento espiral tridimensional das algas em um espaço multidimensional. A atualização da coordenada leva em consideração o atrito, que é definido como "agent[i].friction".

7. As coordenadas "a[i].c[c]" são restringidas utilizando a função "u.SeInDiSp", que garante que os valores permaneçam dentro do intervalo especificado e respeitem os incrementos definidos.

A função "Moving" implementa o processo de movimentação usando variações aleatórias nas coordenadas dos agentes, considerando tanto o estado atual deles quanto o estado de outros agentes. O uso de atrito e valores aleatórios cria uma dinâmica que imita a forma como os agentes se comportam dentro do espaço de busca. O código inclui mecanismos para evitar que as coordenadas ultrapassem os limites estabelecidos, o que é essencial para garantir valores aceitáveis.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int variant = 0;

    int j = TournamentSelection ();

    for (int c = 0; c < coords; c++)
    {
      double α = u.RNDfromCI (0.0, 2 * M_PI);
      double β = u.RNDfromCI (0.0, 2 * M_PI);
      double ρ = u.RNDfromCI (-1.0, 1.0);

      if (variant == 0) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathCos (α);
      if (variant == 1) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathSin (β);
      if (variant == 2) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * ρ;

      variant++;

      if (variant > 2) variant = 0;

      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Após o método "Moving", passamos ao método "Revision" da classe "C_AO_AAA". Esse método é responsável por atualizar o estado dos agentes na população, considerando suas características e interações. Sua estrutura geral é a seguinte:

1. A variável "ind" é inicializada com o valor "-1". Ela será usada para armazenar o índice do agente com o melhor valor da função de aptidão.

2. Um laço percorre todos os agentes da população "popSize". Dentro do laço, se o valor da função "a[i].f" for maior que o valor máximo atual "fB", então: 

• O valor máximo "fB" é atualizado.
• O índice do agente com o melhor valor da função de aptidão é armazenado na variável "ind".
• O tamanho do agente "agent[i].size" é atualizado de acordo com seu valor da função de aptidão "a[i].f".
• Os valores mínimos "fMin" e máximos "fMax" da função de aptidão são atualizados para o agente atual.

3. Se um agente com o valor máximo da função de aptidão "f" foi encontrado, suas coordenadas são copiadas para o array "cB" usando a função "ArrayCopy".

4. Atualização da energia e outros parâmetros dos agentes:

• A energia do agente é calculada usando a função "CalculateEnergy".
• O atrito é calculado e normalizado com base nos valores "fMin" e "fMax".
• A energia do agente é reduzida pelo valor de "energyLoss".
• Se a nova energia for maior que a atual, a energia aumenta em metade do valor perdido e o nível de fome do agente é redefinido. Caso contrário, o nível de fome aumenta.
• O coeficiente de crescimento é calculado com base no tamanho atual do agente e em sua saciedade, e o tamanho do agente é atualizado.

5. Chamada dos processos: No final da função, os métodos "EvolutionProcess" e "AdaptationProcess" são chamados para continuar a evolução e adaptação dos agentes com base em seu estado atual.

No geral, a função "Revision" é responsável por atualizar o estado dos agentes na população com base em suas características e interações. Ela inclui a análise, a atualização e a chamada de processos adicionais, permitindo a modelagem da dinâmica populacional.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;

      ind = i;
    }

    agent [i].size = a [i].f;

    if (a [i].f < fMin) fMin = a [i].f;
    if (a [i].f > fMax) fMax = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].energy   = CalculateEnergy (i);

    agent [i].friction = u.Scale (a [i].f, fMin, fMax, 0.1, 1.0, false);

    agent [i].energy -= energyLoss;

    double newEnergy = CalculateEnergy (i);

    if (newEnergy > agent [i].energy)
    {
      agent [i].energy += energyLoss / 2;
      agent [i].hunger = 0;
    }
    else
    {
      agent [i].hunger++;
    }

    double growthRate = maxGrowthRate * agent [i].size / (agent [i].size + halfSaturationConstant);

    agent [i].size *= (1 + growthRate);
  }

  //----------------------------------------------------------------------------
  EvolutionProcess  ();
  AdaptationProcess ();
}
//——————————————————————————————————————————————————————————————————————————————

Agora descreveremos a função "EvolutionProcess()", que é responsável pelo processo evolutivo dos agentes na população. O principal objetivo dessa função é encontrar o agente menos adaptado (a alga mais baixa) e substituir suas coordenadas pelas de outros agentes mais adaptados selecionados aleatoriamente (algas mais altas).

1. Busca pelo agente menos adaptado:

• A variável "smallestIndex" é inicializada para armazenar o índice do agente menos adaptado. Inicialmente, é definida como "0".
• Um laço percorre todos os agentes (a partir do primeiro) e compara sua aptidão. Se a aptidão do agente atual for menor que a do agente no índice "smallestIndex", o "smallestIndex" é atualizado.

2. Cópia das coordenadas:

• A variável "m" é inicializada para armazenar um índice aleatório de um agente.
• Um laço percorre todas as coordenadas de "0" até "coords".
• Dentro do laço, o método "u.RNDminusOne(popSize)" é chamado para gerar um índice aleatório "m" no intervalo de "0" a "popSize - 1".
• As coordenadas do agente menos adaptado no índice "smallestIndex" são então substituídas pelas coordenadas de um agente aleatório no índice "m".

A função "EvolutionProcess" implementa um mecanismo evolutivo simples, no qual o agente menos adaptado da população adquire as coordenadas de um agente escolhido aleatoriamente. Essa operação faz parte do mecanismo de adaptação, permitindo que os agentes melhorem suas características ao herdar coordenadas de outros agentes bem-sucedidos. Além disso, essa estratégia desempenha um papel fundamental na recombinação de soluções dentro do algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::EvolutionProcess ()
{
  int smallestIndex = 0;

  for (int i = 1; i < popSize; i++)
  {
    if (agent [i].size < agent [smallestIndex].size) smallestIndex = i;
  }

  int m = 0;

  for (int c = 0; c < coords; c++)
  {
    m = u.RNDminusOne (popSize);

    a [smallestIndex].c [c] = a [m].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora, analisaremos detalhadamente o código da função "AdaptationProcess()", que gerencia o processo de adaptação dos agentes na população com base em seus níveis de fome e tamanho. O principal objetivo dessa função é modificar as coordenadas do agente mais faminto, caso uma condição de probabilidade de adaptação específica seja atendida.

1. Identificação do agente mais faminto (alga):

• A variável "starvingIndex" é inicializada para armazenar o índice do agente mais faminto. Inicialmente, é definida como "0".
• Um laço percorre todos os agentes (a partir do primeiro) e compara seus níveis de fome Se o nível de fome do agente atual for maior que o do agente no índice "starvingIndex", o valor deste é atualizado.

2. Verificação da probabilidade de adaptação:

• O método "u.RNDprobab()" gera um número aleatório (probabilidade). Se esse número for menor que a probabilidade de adaptação definida em "adaptationProbability", o próximo bloco de código será executado.

3. Busca pelo agente mais alto (alga maior):

• Semelhante ao primeiro passo, aqui o índice do agente mais alto na população é identificado. Inicialmente, "biggestIndex" é definido como "0".
• Um laço percorre todos os agentes e atualiza "biggestIndex" sempre que encontra um agente maior.

4. Adaptação das coordenadas:

• Um laço percorre todas as coordenadas.
• As coordenadas do agente no índice "starvingIndex" são atualizadas com a adição de um valor calculado como a diferença entre as coordenadas do agente mais alto e as do agente mais faminto, multiplicada por uma probabilidade aleatória.
• Depois disso, as coordenadas são normalizadas utilizando o método "u.SeInDiSp()", que verifica e ajusta os valores dentro dos limites especificados "rangeMin", "rangeMax" e "rangeStep".

5. Atualização do estado do agente:

• O tamanho do agente é atualizado com base no valor de aptidão "f" armazenado no array "a".
• O nível de fome "hunger" é redefinido para "0", indicando que o agente agora está saciado.
• A energia do agente "energy" é definida para "1.0", que é o valor máximo.

A função "AdaptationProcess" implementa um mecanismo de adaptação que permite ao agente mais faminto melhorar suas coordenadas ao herdá-las do agente mais alto, desde que a condição probabilística seja atendida. Esse processo faz parte de um sistema que simula a seleção natural, no qual os agentes se ajustam ao ambiente para aumentar suas chances de sobrevivência.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::AdaptationProcess ()
{
  int starvingIndex = 0;

  for (int i = 1; i < popSize; i++) if (agent [i].hunger > agent [starvingIndex].hunger) starvingIndex = i;
  
  if (u.RNDprobab () < adaptationProbability)
  {
    int biggestIndex = 0;

    for (int i = 1; i < popSize; i++) if (agent [i].size > agent [biggestIndex].size) biggestIndex = i;

    for (int j = 0; j < coords; j++)
    {
      a [starvingIndex].c [j] += (a [biggestIndex].c [j] - a [starvingIndex].c [j]) * u.RNDprobab ();

      a [starvingIndex].c [j] = u.SeInDiSp (a [starvingIndex].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }

    agent [starvingIndex].size   = a [starvingIndex].f;
    agent [starvingIndex].hunger = 0;
    agent [starvingIndex].energy = 1.0;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora, analisaremos o código da função "CalculateEnergy", responsável por calcular a energia de um agente com base em suas características, como o tamanho da colônia, o nível de energia e a concentração de nutrientes. Essa função retorna um valor de energia, que será utilizado em outras partes do algoritmo.

1. Inicialização de variáveis:

• colony_size — obtém a altura da alga usando o índice "index".
• max_growth_rate — definido como a taxa máxima de crescimento.
• half_saturation_constant — definido como metade da constante de saturação.

2. Normalização da função de aptidão: o valor normalizado da concentração de nutrientes é calculado como a razão entre a diferença do valor "f" (extraído do array "a") e o valor mínimo "fMin", em relação ao intervalo entre "fMax" e "fMin". A adição de "1e-10" evita a ocorrência de divisões por zero.

3. Obtenção da velocidade de crescimento atual: o valor "current_growth_rate" é obtido a partir do valor atual de energia do agente, que também pode ser interpretado como sua velocidade de crescimento.

4. Cálculo da taxa de crescimento: o valor "growth_rate" é determinado com base na taxa máxima de crescimento, na concentração normalizada de nutrientes e na velocidade de crescimento atual. A fórmula considera o efeito da saturação, no qual a taxa de crescimento diminui à medida que a velocidade de crescimento atual aumenta.

5. Cálculo da energia: o valor "energy" é obtido como a diferença entre "growth_rate" e as perdas de energia definidas por "energyLoss". Esse valor representa a quantidade de energia que o agente recebe após as perdas serem consideradas.

6. Prevenção de valores negativos: se o valor calculado da energia for negativo, ele será definido como "0" para evitar valores inválidos.

7. Retorno do valor calculado: a função devolve o valor final da energia do agente.

A função "CalculateEnergy" modela o processo pelo qual um agente recebe energia, considerando sua taxa de crescimento, o tamanho da colônia e a concentração de nutrientes. Além disso, ela incorpora perdas de energia para garantir um comportamento mais realista durante a simulação. 

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AAA::CalculateEnergy (int index)
{
  double colony_size              = agent [index].size;
  double max_growth_rate          = maxGrowthRate;
  double half_saturation_constant = halfSaturationConstant;

  // Use the normalized value of the fitness function
  double nutrient_concentration = (a [index].f - fMin) / (fMax - fMin + 1e-10);

  double current_growth_rate = agent [index].energy;

  double growth_rate = max_growth_rate * nutrient_concentration / (half_saturation_constant + current_growth_rate) * colony_size;

  double energy = growth_rate - energyLoss;

  if (energy < 0) energy = 0;

  return energy;
}
//——————————————————————————————————————————————————————————————————————————————

O último método implementado no algoritmo é o mecanismo de seleção por torneio. O método "TournamentSelection" escolhe um dos dois candidatos da população com base em seus valores de aptidão, retornando o índice do candidato com o melhor valor. A seleção por torneio garante um processo seletivo equilibrado, cujo comportamento probabilístico foi analisado previamente.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AAA::TournamentSelection ()
{
  int candidate1 = u.RNDminusOne (popSize);
  int candidate2 = u.RNDminusOne (popSize);

  return (a [candidate1].f > a [candidate2].f) ? candidate1 : candidate2;
}
//——————————————————————————————————————————————————————————————————————————————

Resultados dos testes

Impressão do desempenho do algoritmo AAA em funções de teste:

AAA|Algae Adaptive Algorithm|200.0|0.2|0.05|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.5000717048088521
25 Hilly's; Func runs: 10000; result: 0.3203956013467087
500 Hilly's; Func runs: 10000; result: 0.25525273777603685
=============================
5 Forest's; Func runs: 10000; result: 0.37021025883379577
25 Forest's; Func runs: 10000; result: 0.2228350161785575
500 Forest's; Func runs: 10000; result: 0.16784823154308887
=============================
5 Megacity's; Func runs: 10000; result: 0.2784615384615384
25 Megacity's; Func runs: 10000; result: 0.14800000000000005
500 Megacity's; Func runs: 10000; result: 0.097553846153847
=============================
All score: 2.36063 (26.23%)

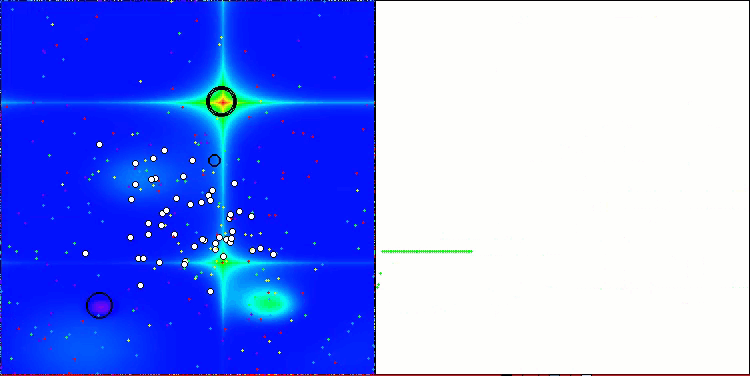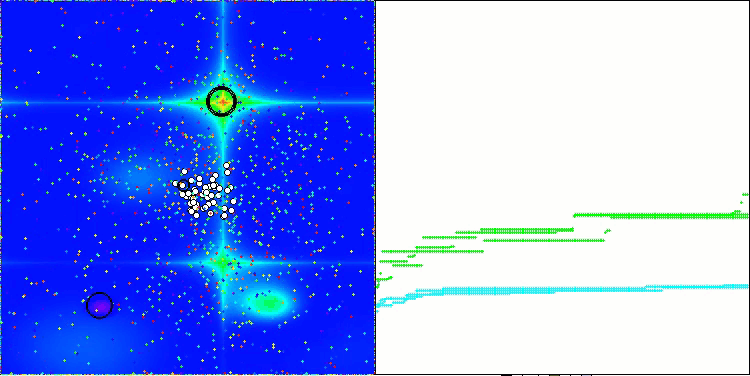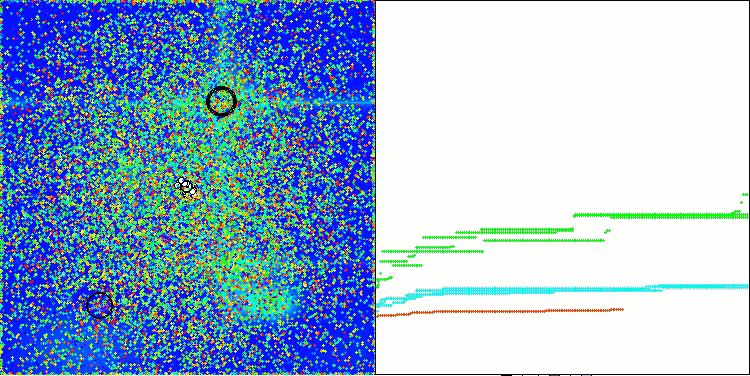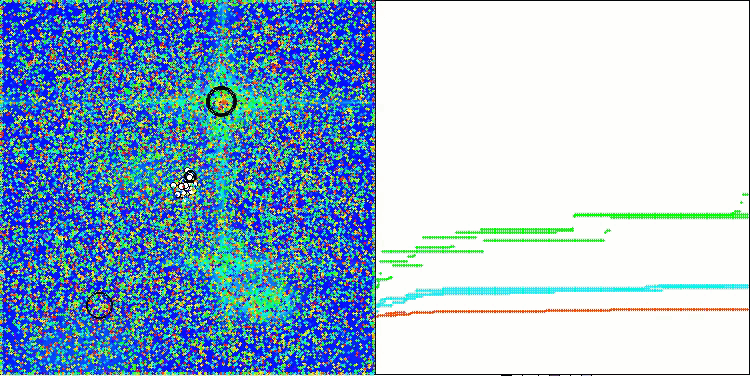
Tanto na saída impressa quanto na visualização do funcionamento do algoritmo, observa-se uma fraca convergência, o que é confirmado pelos resultados dos testes. Infelizmente, as expectativas de alto desempenho não foram atendidas. Apesar de contar com uma estratégia de busca complexa, o algoritmo tem dificuldade em localizar o ótimo global de maneira eficiente, o que torna desafiador identificar as causas exatas de sua baixa eficácia. No entanto, apesar dessas limitações, o algoritmo possui algumas vantagens, que serão discutidas a seguir.

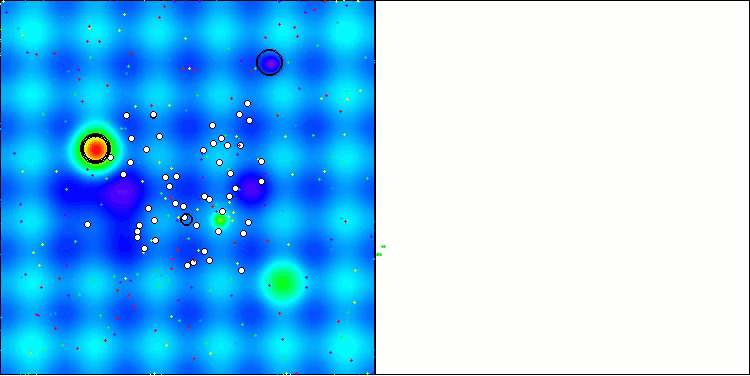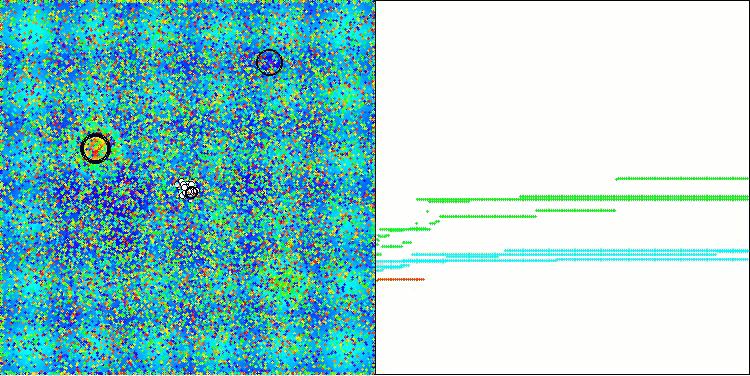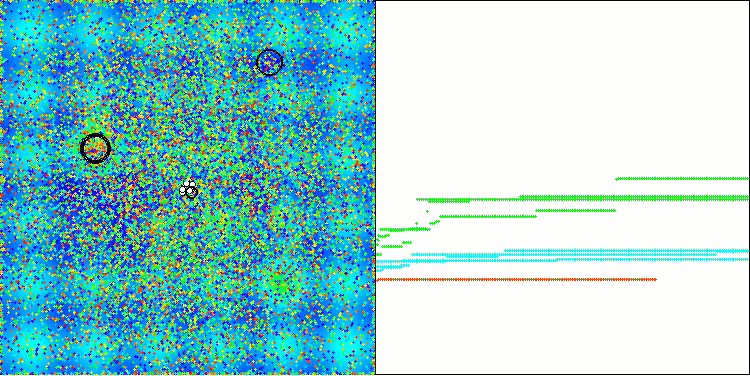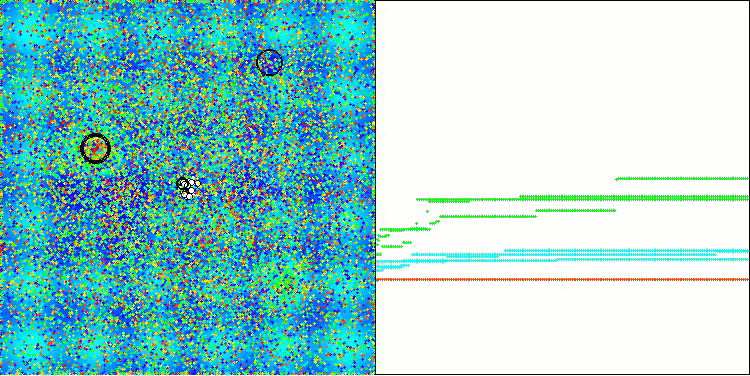
AAA na função de teste Hilly

AAA na função de teste Forest

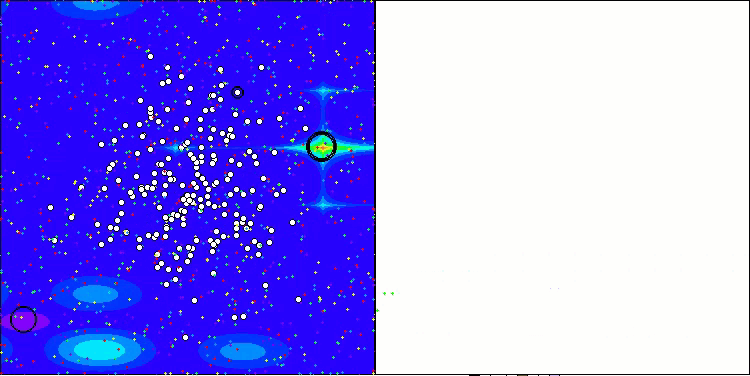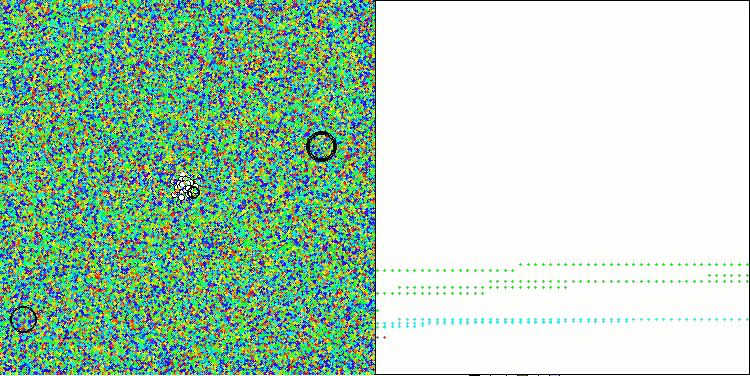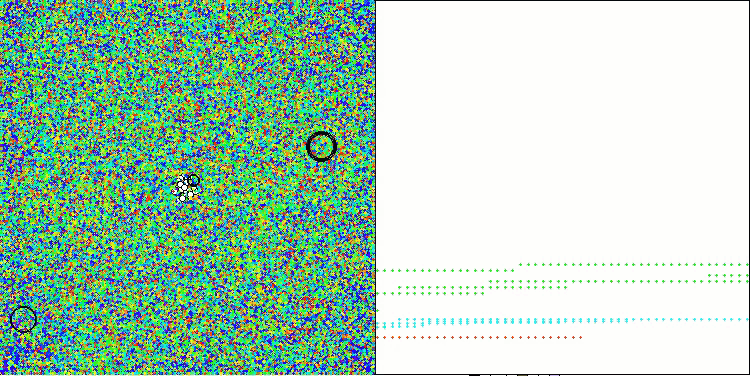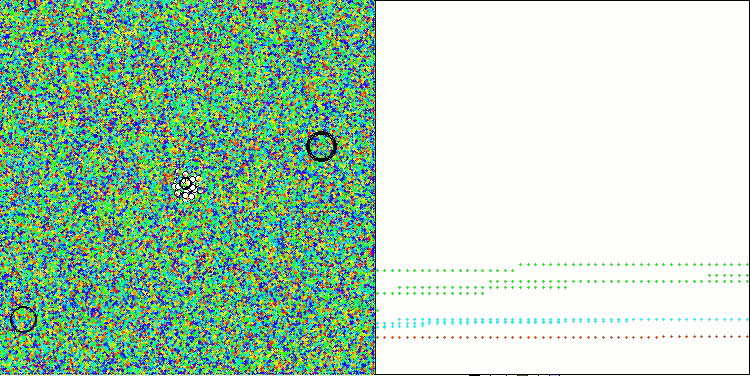
AAA na função de teste Megacity

Nos testes realizados, o algoritmo obteve a 36ª posição na tabela de classificação.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
18	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
19	WOAm	whale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
20	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
21	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
22	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
23	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
24	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
25	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
26	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
27	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
28	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
29	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
30	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
31	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
32	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
33	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
34	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
35	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
36	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
37	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
38	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
39	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
40	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
41	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
42	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
43	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
44	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
45	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32

Considerações finais

Com base nos resultados obtidos pelo algoritmo em funções de teste com diferentes dimensões, podemos tirar as seguintes conclusões: A saída do algoritmo indica uma fraca convergência. Fiquei um pouco decepcionado com o seu desempenho: apesar da aplicação de diversos métodos e de uma lógica escalonada complexa, eu esperava que ele apresentasse pelo menos bons resultados e se posicionasse na parte superior da tabela, em vez de figurar entre os últimos colocados. Talvez seja necessário dedicar mais atenção à análise dos métodos empregados, pois a quantidade de técnicas aplicadas nem sempre garante um aumento na qualidade dos resultados. Aqueles que desejam explorar melhorias já podem começar a experimentar. Se o algoritmo apresentar melhores resultados, por favor, compartilhem. Aguardo os comentários sobre o artigo com interesse.

Entre os aspectos positivos do algoritmo, destacam-se os bons resultados obtidos nas funções Forest e Megacity com 1000 variáveis, superando concorrentes diretos. Isso indica um potencial promissor para a escalabilidade do algoritmo em problemas com extremos "agudos" e em problemas discretos.

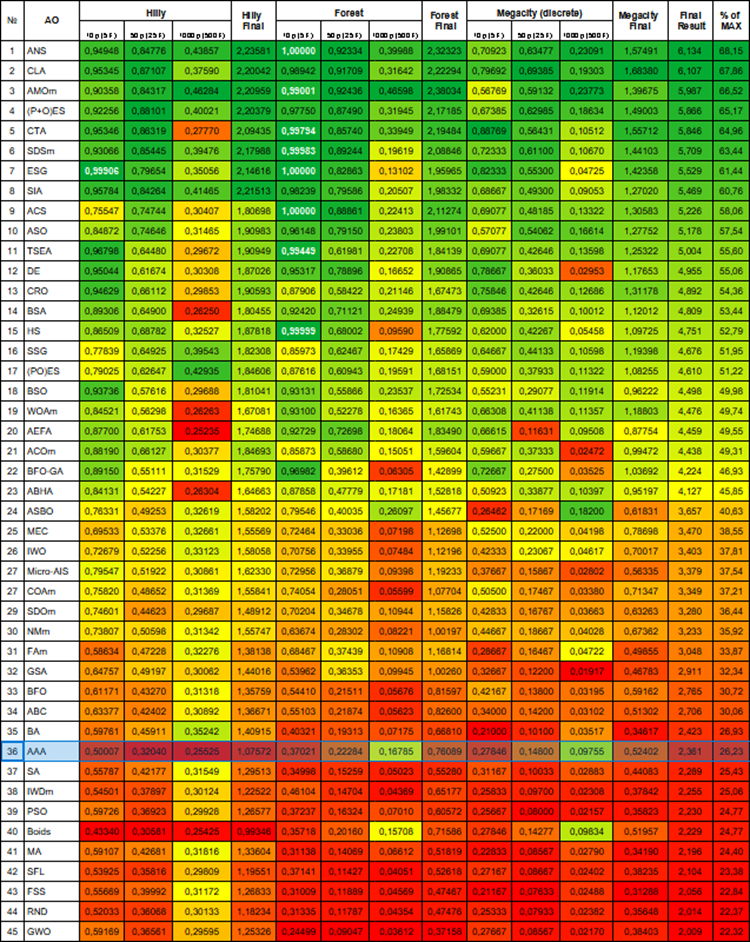
Figura 1. Graduação de cores dos algoritmos para os respectivos testes. Resultados iguais ou superiores a 0.99 estão destacados em branco.

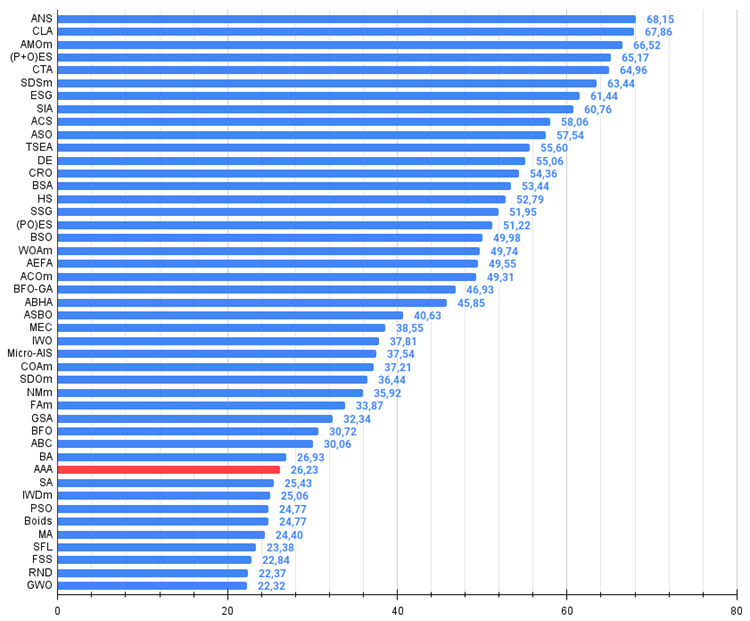
Figura 2. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível, e o arquivo contém um script para cálculo da tabela de classificação)

Prós e contras do algoritmo AAA:

Prós:

1. Ideia promissora e abordagens inovadoras.

Contras:

1. Grande número de parâmetros (dificultando a configuração do algoritmo).
   
2. Fraca convergência.
3. Implementação difícil de depurar.

O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355