取引におけるニューラルネットワーク：状態空間モデル

MetaTrader 5 — トレーディングシステム | 26 3月 2025, 11:03

139

Dmitriy Gizlyk

はじめに

近年、大規模モデルを新しいタスクに適応させるというパラダイムがますます普及しています。これらのモデルは、テキスト、画像、音声、時系列データなど、幅広いドメインの任意の生データを含む大規模なデータセットで事前学習されています。

この概念自体は特定のアーキテクチャに依存しませんが、ほとんどのモデルは単一のアーキテクチャ、すなわちTransformerとそのコア層である自己アテンション(Self-Attention)に基づいています。自己アテンションの効率性は、コンテキストウィンドウ内で情報を密に伝播させることで、複雑なデータのモデリングを可能にする能力に起因します。しかし、この特性には本質的な制約があります。すなわち、有限のウィンドウを超えたモデリングができないこと、およびウィンドウ長に対して計算コストが二次的に増大することです。

シーケンスモデリングのタスクにおいて、これに対する代替手法の一つとして、状態空間モデル（State Space Models、SSM）に基づく構造化シーケンスモデルの利用が挙げられます。これらのモデルは、再帰型ニューラルネットワーク(RNN)と畳み込みニューラルネットワーク(CNN)の組み合わせとして解釈でき、シーケンス長に対して線形または準線形の計算スケーリングを実現することで、高い計算効率を持ちます。さらに、特定のデータモダリティにおいて長距離依存関係をモデル化するための固有のメカニズムを備えています。

時系列予測において状態空間モデルを活用するためのアルゴリズムの一つとして、論文「Mamba:Linear-Time Sequence Modeling with Selective State Spaces」で紹介された手法があります。この論文では、新たなクラスの選択的状態空間モデルを提案しています。

著者らは、既存のモデルの主要な課題として、入力データに基づいて情報を適切にフィルタリングする能力、すなわち特定の入力データに焦点を当てるか、それを無視するかを制御する能力に着目しました。そして、SSMのパラメータを入力データに依存させるシンプルな選択メカニズムを開発し、無関係な情報を除外しながら、関連する情報を無期限に保持できるようにしました。

また、著者はSSMのアーキテクチャ設計とMLPを単一のブロックに統合することで、従来のディープシーケンスモデルのアーキテクチャを簡素化し、選択的状態空間を組み込んだシンプルかつ均質なアーキテクチャ「Mamba」を実現しました。

選択的SSM、およびその延長であるMambaアーキテクチャは、汎用的なシーケンスベースのモデルの基盤として適した特性を持つ、完全な再帰モデルです。

高品質：選択メカニズムにより、高密度なモダリティにおいても高いパフォーマンスを実現。
高速な学習と推論：学習時の計算とメモリ使用量はシーケンス長に対して線形にスケールし、推論時の自己回帰モデルの展開では、以前の要素をキャッシュする必要がないため、ステップごとに一定時間で処理可能。
長期的な文脈の活用：高い品質と計算効率の組み合わせにより、長いシーケンスを扱うタスクのパフォーマンスが向上。

1. Mambaアルゴリズム

Mambaの著者は、シーケンスモデリングにおける根本的な課題は、コンテキストをより小さな状態に圧縮することだと主張しています。この観点から、一般的なシーケンスモデルのトレードオフを考えることができます。例えば、アテンション機構は、コンテキストを明示的に圧縮しないため、一見効率的でありながら、実際には非効率的でもあります。これは、自己回帰推論においてコンテキスト全体（すなわち、Key-Valueキャッシュ）を明示的に保存する必要があるため、線形時間の推論と二次時間のTransformer訓練が遅くなることからも明らかです。

一方、再帰型モデルは有限の状態を維持するため、推論は一定時間で実行でき、訓練は線形時間でおこなえます。しかし、その効率性は、有限の状態がコンテキストをどの程度適切に圧縮できるかに依存します。

この原理を説明するために、著者は以下の2つの合成タスクの解決に焦点を当てています。

選択的コピータスク。関連するトークンを記憶し、無関係なトークンを除外するためには、コンテンツを認識した推論が必要になります。
誘導ヘッドタスク。コンテキスト学習におけるLLMの能力の多くを説明するタスクです。このタスクを解決するには、適切なコンテキストにおいて正しい出力をいつ取得すべきかを判断するコンテキスト依存の推論が求められます。

これらのタスクは、LTIモデルの欠点を浮き彫りにします。再帰的アプローチの観点から見ると、固定された動的特性により、コンテキストから適切な情報を選択したり、入力データに基づいてシーケンスを通じて伝播する隠れ状態に影響を与えたりすることが困難になります。一方、畳み込みの観点から見ると、グローバルな畳み込みは時間の認識のみを必要とするため、単純なコピータスクは解決できます。しかし、コンテンツの認識がないため、選択的コピーのタスクには対応できません。具体的には、入力と出力の間の距離が変動するため、静的な畳み込みカーネルでは適切にモデル化できないのです。

このように、シーケンスモデルにおける効率性のトレードオフは、状態をどれだけ適切に圧縮できるかによって決まります。そして、著者は、シーケンスモデルの設計における基本原則として、選択性（すなわち、連続する状態内で入力データに焦点を当てたり、無視したりするコンテキスト依存の能力）が重要であると提案しています。選択メカニズムは、シーケンス次元に沿って情報がどのように伝播・相互作用するかを制御します。

選択メカニズムをモデルに組み込む方法の1つは、シーケンスの相互作用に影響を与えるパラメータを入力データに依存させることです。ポイントとなるのは、いくつかのパラメータΔ B、Cを入力データの関数として定義し、それに応じてテンソルの形状を変更することです。具体的には、これらのパラメータには長さの次元Lが導入されます。つまり、モデルが時間不変から時間変動へと移行することを意味します。

著者は以下の定義を採用しています。

SB(x) = LinearN(x)
SC(x) = LinearN(x)
SΔ(x) = BroadcastD(Linear1(x))
τΔ = SoftPlus

SΔとτΔの選択は、RNNゲーティングメカニズムとの関連性を考慮したものです。

また、著者は、選択的SSMを最新のハードウェア(GPU)上で効率的にすることを目指しています。一般的に、SSMのような再帰型モデルは、効率と速度のバランスを取る必要があります。隠れ状態の次元が大きいほど効率は向上しますが、処理速度は低下します。そのため、Mambaの設計における課題は、モデルの速度やメモリ消費を犠牲にせず、隠れ状態の次元を最大化することでした。

選択メカニズムは、LTIモデルの制約を克服しますが、SSMには計算上の課題が残ります。これを解決するために、著者はカーネル融合、並列スキャン、再計算という3つの古典的な技法を採用しました。彼らは以下の2つの重要な観察をおこなっています。

単純な再帰計算はO(BLDN)FLOPを要する一方、畳み込み計算はO(BLDlog(L))FLOPを必要とします。前者の方が定数係数が小さいため、長いシーケンスやそれほど大きくない状態次元Nにおいては、再帰モードの方がFLOP数を抑えられます。
主な課題は、逐次処理の性質と高いメモリ使用量です。後者に関しては、畳み込みモードと同様に、完全な状態hの計算を回避することを試みます。

重要なアイデアは、最新のアクセラレータ(GPU)を活用して、メモリ階層のより効率的なレベルでhを計算することです。スキャンを含め、ほとんどの操作はメモリ帯域幅に依存します。そのため、著者はカーネル融合を用いてメモリI/O操作を削減し、標準的な実装と比較して大幅に高速化しています。

さらに、メモリ使用量を削減するため、古典的な再計算手法を慎重に適用しています。具体的には、中間状態を保存せず、入力処理の際に逆順で再計算する手法を採用しています。

選択的SSMは、ニューラルネットワークに柔軟に組み込むことができる自律的なシーケンス変換として機能します。

選択メカニズムは、他のパラメータに異なる方法で適用したり、さまざまな変換を通じて応用することが可能な、より広範な概念です。

選択性により、関連する入力データ内に混在する不要なノイズトークンを除去できます。例えば、選択的コピー問題は、特に離散データにおいて一般的に見られる課題です。これは、モデルが特定の入力データXtを機械的に除外できるために生じる特性です。

経験的観察によると、多くのシーケンスモデルは長いコンテキストでも性能が向上しないことが分かっています。その理由は、多くのモデルが不要なコンテキストを適切に無視できないためです。

一方、選択モデルは不要な履歴をリセットできるため、コンテキストが長くなるにつれて性能が単調に向上します。

この手法のオリジナルの視覚化を以下に示します。

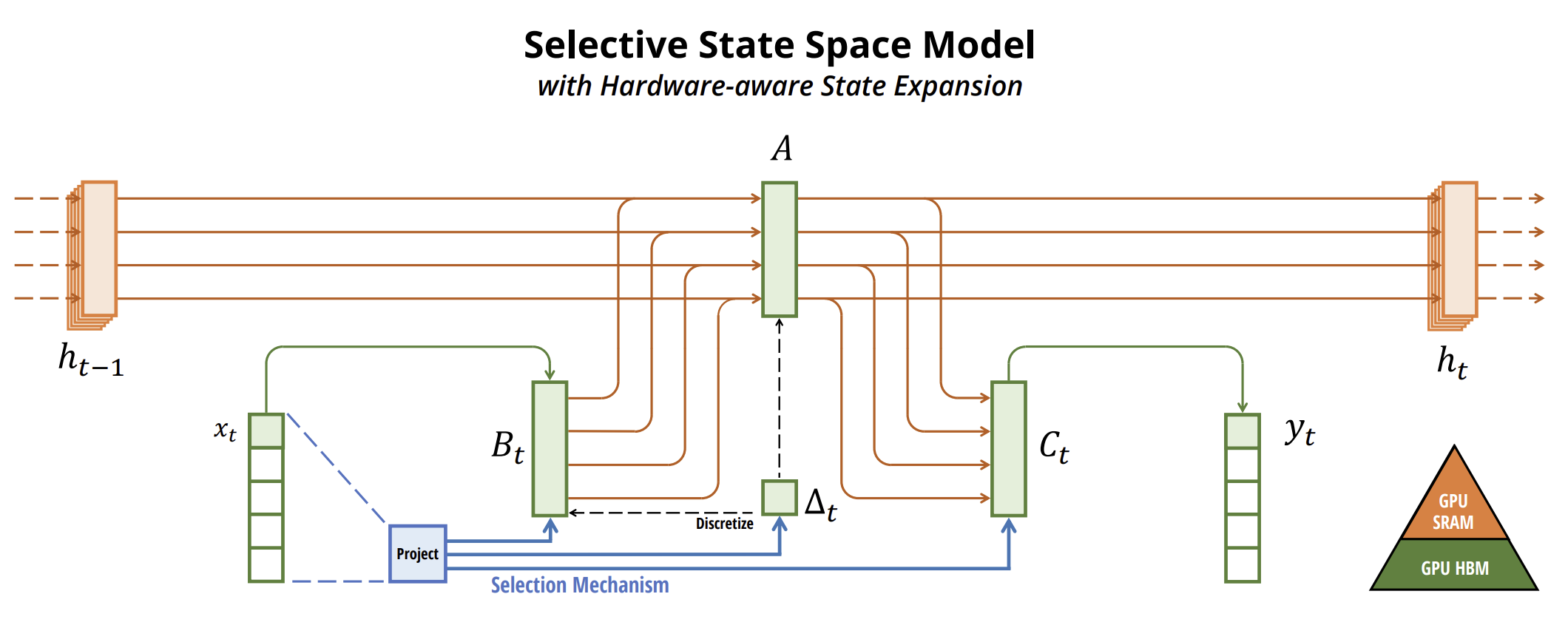
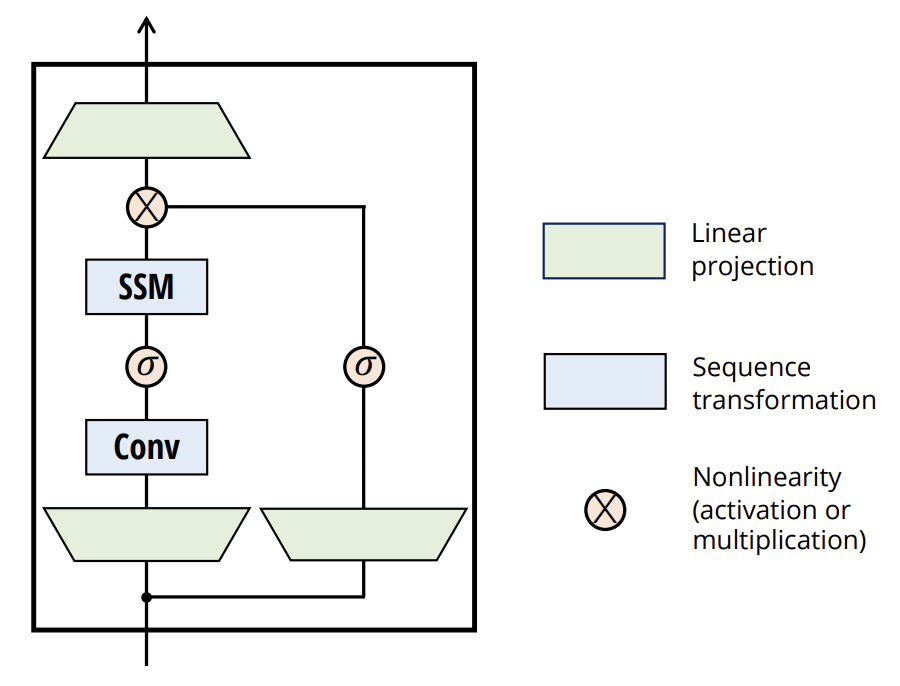
2. MQL5での実装

Mamba法の理論的側面を確認した後、MQL5を使用して提案されたアプローチの実際の実装に移ります。この作業は2段階に分かれています。まず、包括的なMamba法のネストされた層の1つとして機能するSSMアルゴリズムを実装するクラスを構築します。次に、トップレベルのアルゴリズムプロセスを構築します。

2.1 SSMの実装

SSMを構築するためのアルゴリズムは数多く存在します。この実験では、元のMamba実装から少し逸脱して、最も単純な状態空間選択モデルの1つを作成しました。これはCNeuronSSMOCLクラスで実装されました。親オブジェクトとして、完全接続ニューラル層の基本クラスCNeuronBaseOCLを使用します。以下に新しいクラスの構造を示します。

class CNeuronSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint              iWindowHidden;
   CNeuronBaseOCL    cHiddenStates;
   CNeuronConvOCL    cA;
   CNeuronConvOCL    cB;
   CNeuronBaseOCL    cAB;
   CNeuronConvOCL    cC;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronSSMOCL(void)  {};
                    ~CNeuronSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

提示された構造では、1つの要素(iWindowHidden)の非表示状態の次元を定義する1つの定数の宣言と、5つの内部ニューラル層が確認できます。その機能性については、実装時に見ていくことにしましょう。

私たちのクラス内のオーバーライド可能なメソッドのセットは非常に標準的です。そして、その機能的な目的についてはすでにお分かりだと思います。

クラスのすべての内部オブジェクトは静的に宣言されているため、クラスのコンストラクターとデストラクターを空のままにすることができます。宣言および継承されたすべてのオブジェクトの初期化は、Initメソッドで実行されます。このメソッドのパラメータでは、ユーザーが作成したいオブジェクトを明確に判断できる定数を受け取ります。

bool CNeuronSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window, uint window_key, uint units_count, 
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

ここには3つのパラメータがあります。

window：シーケンス内の1つの要素のベクトルサイズ
window_key：シーケンス内の1つの要素の内部表現のベクトルのサイズ
unit_count：分析対象のシーケンスのサイズ

すでに述べたように、この実験では簡略化されたSSMアルゴリズムを使用しています。特に、マルチモーダルシーケンスを独立したチャネルに分割する機能は実装されていません。

メソッド本体内では、継承されたオブジェクトと変数の初期化がすでに含まれている親クラスから同じ名前のメソッドをすぐに呼び出し、外部プログラムから受信したパラメータの最小限かつ必要な検証を実行します。

親クラスメソッドが正常に実行されたら、このクラスで宣言されたオブジェクトの初期化に進みます。まず、隠し状態を保存する内部層を初期化します。

   if(!cHiddenStates.Init(0, 0, OpenCL, window_key * units_count, optimization, iBatch))
      return false;
   cHiddenStates.SetActivationFunction(None);
   iWindowHidden = window_key;

また、単一のシーケンス要素の内部状態ベクトルのサイズをローカル変数にすぐに保存します。

検証を実行せずにこのパラメータ値を意図的に保存することに注意することが重要です。ここでの考え方は、サイズがこのパラメータによって決定される内部層を最初に意識的に初期化することです。ユーザーが誤った値を指定すると、クラスの初期化段階自体でエラーが発生します。したがって、内部層を慎重に初期化すると、暗黙的にパラメータ検証が実行されます。これにより、この段階では追加のチェックが不要になります。

また、cHiddenStatesオブジェクトは一時的なデータ保存にのみ使用され、その中の活性化関数は明示的に無効にされていることにも注意してください。

次に、入力データが結果にどのように影響するかを制御する2つのデータ投影層を初期化します。まず、隠し状態投影層を初期化します。

   if(!cA.Init(0, 1, OpenCL, iWindowHidden, iWindowHidden, iWindowHidden, units_count, 1, optimization, iBatch))
      return false;
   cA.SetActivationFunction(SIGMOID);

ここでは、畳み込み層を使用します。これにより、各シーケンス要素の隠し状態の独立した投影を実行できます。各要素が最終結果に与える影響を調整するために、この層の活性化関数としてシグモイドを使用します。ご存知のとおり、シグモイド関数は値を[0,1]の範囲にマッピングします。「0」の場合、要素は全体の結果に影響を与えません。

次に、同様の方法で入力データ投影層を初期化します。

   if(!cB.Init(0, 2, OpenCL, window, window, iWindowHidden, units_count, 1, optimization, iBatch))
      return false;
   cB.SetActivationFunction(SIGMOID);

入力テンソルの次元が異なっていても、両方の投影層は隠し状態のサイズに一致するテンソルを返すことに注意してください。これは、データウィンドウのサイズと、オブジェクトを初期化するときのステップから明らかです。

入力データと隠れ状態が結果に与える影響を計算するには、加重合計を使用します。操作数を最適化して削減するために、このステップをターゲット結果ディメンションへの投影と組み合わせることにしました。したがって、最初に、シーケンス要素の次元に沿ってデータを共通テンソルに連結します。

   if(!cAB.Init(0, 3, OpenCL, 2 * iWindowHidden * units_count, optimization, iBatch))
      return false;
   cAB.SetActivationFunction(None);

次に、別の内部畳み込み層を適用します。

   if(!cC.Init(0, 4, OpenCL, 2*iWindowHidden, 2*iWindowHidden, window, units_count, 1, optimization, iBatch))
      return false;
   cC.SetActivationFunction(None);

最後に、初期化メソッドの最後で、クラスの結果バッファーと勾配バッファーへのポインターをリダイレクトして、内部結果投影層の同等のバッファーを指すようにします。この簡単なステップにより、前方パスと後方パスの両方で不要なデータのコピーを回避できます。

   SetActivationFunction(None);
   if(!SetOutput(cC.getOutput()) || !SetGradient(cC.getGradient()))
      return false;
//---
   return true;
  }

当然、実行されたすべての操作の成功も監視し、メソッドの最後に、呼び出し元のプログラムに成功を示すブール値を返します。

クラスの初期化が完了したら、フィードフォワードパスアルゴリズムの構築に進みます。ご存知のとおり、この機能はオーバーライドされたfeedForwardメソッドで実装されています。ここではすべてが非常に簡単です。

bool CNeuronSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cA.FeedForward(cHiddenStates.AsObject()))
      return false;
   if(!cB.FeedForward(NeuronOCL))
      return false;

メソッドパラメータには、入力データを提供する前のニューラル層オブジェクトへのポインタが含まれます。

メソッド内では、互換性のある形式への2つの投影(入力データと隠し状態)がすぐに実行されます。これは、対応する内部畳み込み層のフォワードパス方式を使用しておこなわれます。

取得された投影は、シーケンス要素の次元に沿って単一のテンソルに連結されます。

   if(!Concat(cA.getOutput(), cB.getOutput(), cAB.getOutput(), iWindowHidden, iWindowHidden, 
                                                               cA.Neurons() / iWindowHidden))
      return false;

最後に、連結された層を必要な結果ディメンションに投影します。

   if(!cC.FeedForward(cAB.AsObject()))
      return false;

ここで注意すべき点が2つあります。まず、結果を現在の層の結果バッファにコピーしません。データバッファポインタをリダイレクトするため、この操作は必要ありません。

次に、非表示の状態を更新していないことに気づいたかもしれません。したがって、この時点では、フォワードパスメソッドは不完全なように見えます。しかし、問題は、バックプロパゲーションの目的のために、現在の隠し状態が依然として必要になるという事実にあります。したがって、隠し状態は現在の層のアルゴリズム内でのみ使用されるため、バックプロパゲーションパス中に隠し状態を更新することは理にかなっています。

しかし欠点もあります。モデルの推論（デプロイメント）中は、バックプロパゲーション法を使用しません。隠し状態の更新をバックプロパゲーションパスまで延期すると、推論中に更新されることがなくなり、アルゴリズム全体のロジックに違反することになります。

したがって、モデルの現在の動作モードをチェックし、推論中にのみ隠し状態を更新します。これを実現するには、以前の隠し状態と入力データの投影を合計して正規化します。

   if(!bTrain)
      if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true))
      return false;
//---
   return true;
  }

これで、フォワードパスメソッドが完了し、呼び出し元のプログラムに操作成功のブールステータスが返されます。

フィードフォワードパスを実装した後、バックプロパゲーションパスメソッドに進みます。いつものように、2つのメソッドをオーバーライドします。

calcInputGradients：誤差勾配分布用
updateInputWeights：モデルパラメータの更新用

誤差勾配分散アルゴリズムは、フィードフォワードパスを逆の順序でミラーリングします。このメソッドは添付のコードで提供されているので、自分で調べてみることをお勧めします。ただし、パラメータの更新方法には特別な注意が必要です。モデルの訓練の一部として、隠し状態の更新プロセスを組み込んだためです。

bool CNeuronSSMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cA.UpdateInputWeights(cHiddenStates.AsObject()))
      return false;
   if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true))
      return false;

ここでは、まず内部の隠れ状態投影層のパラメータを調整します。その後でのみ、隠し状態自体を更新します。

このメソッドは訓練中にのみ呼び出されるため、ここではモデルの動作モードをチェックしないことに注意してください。

次に、学習可能なパラメータを持つ残りの内部オブジェクトの対応するパラメータ更新メソッドを呼び出します。

   if(!cB.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cC.UpdateInputWeights(cAB.AsObject()))
      return false;
//---
   return true;
  }

すべての操作が完了すると、メソッドは呼び出し元のプログラムにブール値のステータスを返します。

これで、SSM実装クラスメソッドの説明は終了です。これらすべてのメソッドの完全なコードは添付ファイルにあります。

2.2 Mamba法クラス

SSM層のクラスを実装しました。ここで、Mamba法のトップレベルアルゴリズムの構築に進むことができます。この手法を実装するには、クラスCNeuronMambaOCLを作成します。このクラスは、前のクラスと同様に、全結合層クラスCNeuronBaseOCLから基本機能を継承します。以下に新しいクラスの構造を示します。

class CNeuronMambaOCL   :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL    cXProject;
   CNeuronConvOCL    cZProject;
   CNeuronConvOCL    cInsideConv;
   CNeuronSSMOCL     cSSM;
   CNeuronBaseOCL    cZSSM;
   CNeuronConvOCL    cOutProject;
   CBufferFloat      Temp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronMambaOCL(void) {};
                    ~CNeuronMambaOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMambaOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

ここでは、オーバーライド可能なメソッドの一般的なセットと、内部ニューラルネットワーク層の宣言を確認できます。これらの機能については、クラスメソッドの実装中に検討します。

同時に、定数を格納するために宣言された内部変数はありません。実装フェーズ中に定数を保存せずに済むようにした決定について説明します。

通常どおり、すべての内部オブジェクトは静的に宣言されます。したがって、クラスのコンストラクタとデストラクタは両方とも空のままです。オブジェクトの初期化はInitメソッドで実行されます。

bool CNeuronMambaOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint window, uint window_key, uint units_count, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

このメソッドのパラメータのリストは、前述のCNeuronSSMOCLクラスの同じ名前のメソッドに似ています。これらが同様の機能を持っていることは容易に推測できます。

メソッド本体では、まず継承されたオブジェクトと変数を処理する親クラスの初期化メソッドを呼び出します。

Mamba法の理論的な説明から思い出せるように、ここでの入力データは2つの並列ストリームに従います。両方のストリームに対して、畳み込み層を使用して実行されるデータ投影を実行します。

   if(!cXProject.Init(0, 0, OpenCL, window, window, window_key + 2, units_count, 1, optimization, iBatch))
      return false;
   cXProject.SetActivationFunction(None);
   if(!cZProject.Init(0, 1, OpenCL, window, window, window_key, units_count, 1, optimization, iBatch))
      return false;
   cZProject.SetActivationFunction(SIGMOID);

最初のストリームでは、畳み込み層とSSMブロックを使用します。2番目では、活性化関数を適用し、その後、データはマージ段階に進みます。したがって、両方のストリームの出力は、同等のサイズのテンソルである必要があります。これを実現するために、最初のストリームの投影サイズをわずかに増やし、畳み込み中のデータ圧縮によって補正します。

活性化関数は2番目のストリームの投影にのみ使用されることに注意してください。

次のステップは畳み込み層の初期化です。

   if(!cInsideConv.Init(0, 2, OpenCL, 3, 1, 1, window_key, units_count, optimization, iBatch))
      return false;
   cInsideConv.SetActivationFunction(SIGMOID);

ここでは、個々のシーケンス要素内で独立した畳み込みを実行します。したがって、隠れ状態テンソルのサイズを畳み込み要素の数として指定します。シーケンス要素の数も独立変数として追加します。

畳み込みウィンドウのサイズとストライドは、最初のデータストリームの増加した投影サイズと一致します。

この時点で、両方のストリーム間でデータの比較可能性を確保するために、活性化関数も追加します。

次は状態選択を実行するSSMブロックです。

   if(!cSSM.Init(0, 3, OpenCL, window_key, window_key, units_count, optimization, iBatch))
      return false;

アルゴリズムを完成させ、2つのデータストリームのマージに非線形性を導入するために、出力を統合されたテンソルに連結します。

   if(!cZSSM.Init(0, 4, OpenCL, 2 * window_key * units_count, optimization, iBatch))
      return false;
   cZSSM.SetActivationFunction(None);

次に、別の畳み込み層を使用して、結果のデータを各シーケンス要素内の必要なサイズに投影します。

   if(!cOutProject.Init(0, 5, OpenCL, 2*window_key, 2*window_key, window, units_count, 1, optimization, iBatch))
      return false;
   cOutProject.SetActivationFunction(None);

さらに、中間結果を保存するためのバッファを割り当てます。

   if(!Temp.BufferInit(window * units_count, 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;

そして、これらのバッファを参照するためにポインタスワッピングを実行します。

   if(!SetOutput(cOutProject.getOutput()))
      return false;
   if(!SetGradient(cOutProject.getGradient()))
      return false;
   SetActivationFunction(None);
//---
   return true;
  }

最後に、メソッドは実行された操作のブール結果を呼び出し元プログラムに返します。

クラス初期化メソッドを完了したら、feedForwardメソッドでフィードフォワードアルゴリズムを実装します。このアルゴリズムの一部は、初期化メソッドの作成時にすでに説明されています。それでは、コードでの実装を見てみましょう。

bool CNeuronMambaOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cXProject.FeedForward(NeuronOCL))
      return false;
   if(!cZProject.FeedForward(NeuronOCL))
      return false;

このメソッドは、バッファに入力データが含まれる前の層のオブジェクトへのポインターを受け取ります。メソッド本体内で、投影畳み込み層のフォワードパスメソッドを呼び出して、入力データを直ちに投影します。

この時点で、2番目の情報ストリームの操作が完了します。ただし、メインのデータストリームを処理する必要があります。ここでは、データの畳み込みから始めます。

   if(!cInsideConv.FeedForward(cXProject.AsObject()))
      return false;

その後、状態選択を実行します。

   if(!cSSM.FeedForward(cInsideConv.AsObject()))
      return false;

両方のストリームの操作が完了したら、結果を統合されたテンソルにマージします。

   if(!Concat(cSSM.getOutput(), cZProject.getOutput(), cZSSM.getOutput(), 1, 1, cSSM.Neurons()))
      return false;

個々のシーケンス要素の内部状態の次元を保存しなかったことに注意することが重要です。それは問題ではありません。両方の情報ストリームからのテンソルは同じ次元であることがわかっています。したがって、全体の構造を崩すことなく、各テンソルから1つの要素を順番に組み合わせることができます。

最後に、データを目的の出力次元に投影します。

   if(!cOutProject.FeedForward(cZSSM.AsObject()))
      return false;
//---
   return true;
  }

メソッドは、操作が成功したことを示すブール値の結果を呼び出し元プログラムに返すことで終了します。

ご覧のとおり、フィードフォワードパスアルゴリズムは特に複雑ではありません。バックプロパゲーションパス方式にも同じことが当てはまります。したがって、本稿ではそれらのアルゴリズムについて詳しく検討することはしません。このクラスとそのすべてのメソッドの完全なコードは添付ファイルに含まれています。

2.3 モデルアーキテクチャ

前のセクションでは、Mambaの著者によって提案されたアプローチの解釈を実装しました。しかし、おこなわれた作業は結果を生み出さなければいけません。実装されたアルゴリズムの効率を評価するには、それらをモデルに統合する必要があります。新しく作成された層を環境状態エンコーダーモデルに追加することはすでにご想像のとおりでしょう。結局のところ、これは将来の価格変動を予測する枠組みの中で訓練するモデルです。

このモデルのアーキテクチャは、CreateEncoderDescriptionsメソッドで説明されています。

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

このメソッドは動的配列へのポインターを受け取り、そこに作成中のモデルのアーキテクチャ記述を書き込みます。

メソッド本体では、受信したポインタの関連性をチェックし、必要に応じてオブジェクトの新しいインスタンスを作成します。この準備ステップの後、モデルアーキテクチャの説明に進みます。

最初の層は、生データをモデルに入力するためのものです。いつものように、十分なサイズの全結合層を使用します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

通常、端末から受信した形式で「生の」初期データをモデルに入力します。当然、これらの入力は異なる分布に属します。正規化され比較可能な値を使用すると、どのモデルの効率も大幅に向上することが分かっています。したがって、多様な入力データを比較可能なスケールにするために、バッチ正規化層を使用します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、3つの同一のMamba層のブロックを作成します。このため、ブロックに対して単一のアーキテクチャ記述を定義し、それを必要な回数配列に追加します。

   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMambaOCL;
   descr.window = BarDescr;                                       //window
   descr.window_out = 4 * BarDescr;                               //Inside Dimension
   prev_count = descr.count = HistoryBars;                        //Units
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   for(int i = 2; i <= 4; i++)
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

分析されたデータウィンドウのサイズは、単一のシーケンス要素を記述する要素の数に対応し、内部表現のサイズは4倍大きくなることに注意してください。これは、Mamba法で拡張投影を実行するという著者の推奨に従います。

シーケンス要素の数は、分析された履歴の深さに対応します。

クラスの実装中に述べたように、このバージョンでは個別の情報チャネルを割り当てませんでした。ただし、私たちのアルゴリズムは独立したシーケンス要素を処理します。独立したチャネルを分析する必要がある場合は、データを事前に転置し、それに応じて層パラメータを調整できます。しかし、これは別の実験のテーマです。

ただし、独立したチャネル全体のシーケンスを予測します。したがって、Mambaブロックの後にデータを転置します。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、2つの畳み込み層を適用して、独立したチャネルの次の値を予測します。

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = prev_count;
   descr.window_out = 4 * NForecast;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = 4 * NForecast;
   descr.window_out = NForecast;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

その後、予測値を元の表現に戻します。

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

さらに、正規化中に取得された元のデータ分布の統計特性を追加します。

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

モデルの最終ステップは、周波数領域で結果を調整することです。

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ActorモデルとCriticモデルのアーキテクチャは変更されません。また、環境と対話するためのプログラムを変更する必要はありませんでした。ただし、モデル訓練プログラムにいくつかのターゲットを絞った変更を導入する必要がありました。これは、SSMブロック内の隠し状態を使用するには、再帰モデルの特徴に従って入力データのシーケンスを調整する必要があるためです。このような調整は、時間の経過とともに情報が蓄積される、隠れた状態を持つモデルが使用される場合は常に標準です。添付ファイルでそれらを研究することをお勧めします。この記事の作成に使用されたすべてのプログラムとクラスの完全なコードがそこに含まれています。これで実装の説明は終了し、実際の履歴データでの実際のテストに移ります。

3. テスト

私たちの作業は完了に近づいており、モデルの訓練と達成された結果のテストという最終段階に移行しています。モデルは、2023年のH1時間枠の過去のEURUSDデータに基づいて訓練されます。すべてのインジケーターのパラメータはデフォルトに設定されています。

最初の段階では、環境状態エンコーダーを訓練して、指定された期間内の将来の価格変動を予測します。このモデルは、Actorの行動を完全に無視して、過去の価格データのみを分析します。これにより、以前に収集したデータセットを更新することなく、包括的なモデル訓練を実行できるようになります。ただし、過去の訓練期間が変更または延長された場合は、このような更新が必要になることがあります。

最初の観察結果は、モデルがコンパクトかつ高速であることが判明したということです。訓練プロセスは比較的安定しており、堅牢でした。モデルは興味深い結果を示しました。

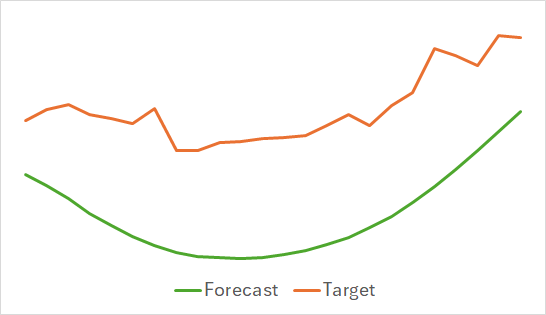
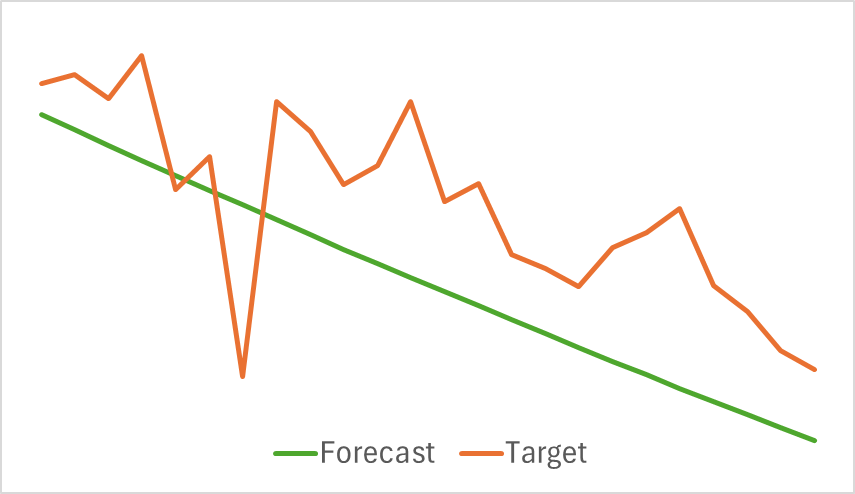
上記のグラフは、今後24時間の予測価格変動を示しています。特に、最初のグラフでは予測線がトレンドの変化をスムーズに示しているのに対し、2番目のグラフでは予測線が進行中のトレンドをほぼ直線的に反映しています。

第2段階では、反復的なActor方策の訓練を実行しました。Critic値関数も訓練しました。批評家の役割は、Actorが方策の効率性を改善できるように導くことです。

前述したように、2番目の訓練フェーズは反復的です。つまり、訓練全体を通じて、現在のActor方策に関連するデータが含まれるように訓練データセットを定期的に更新します。適切なモデル訓練を行うには、最新の訓練セットを維持することが重要です。

しかし、訓練プロセス中に、預金増加傾向が明確に定義された方策を達成できませんでした。モデルは2024年1月の過去のテストデータで利益を生み出すことに成功しましたが、一貫した傾向は観察されませんでした。

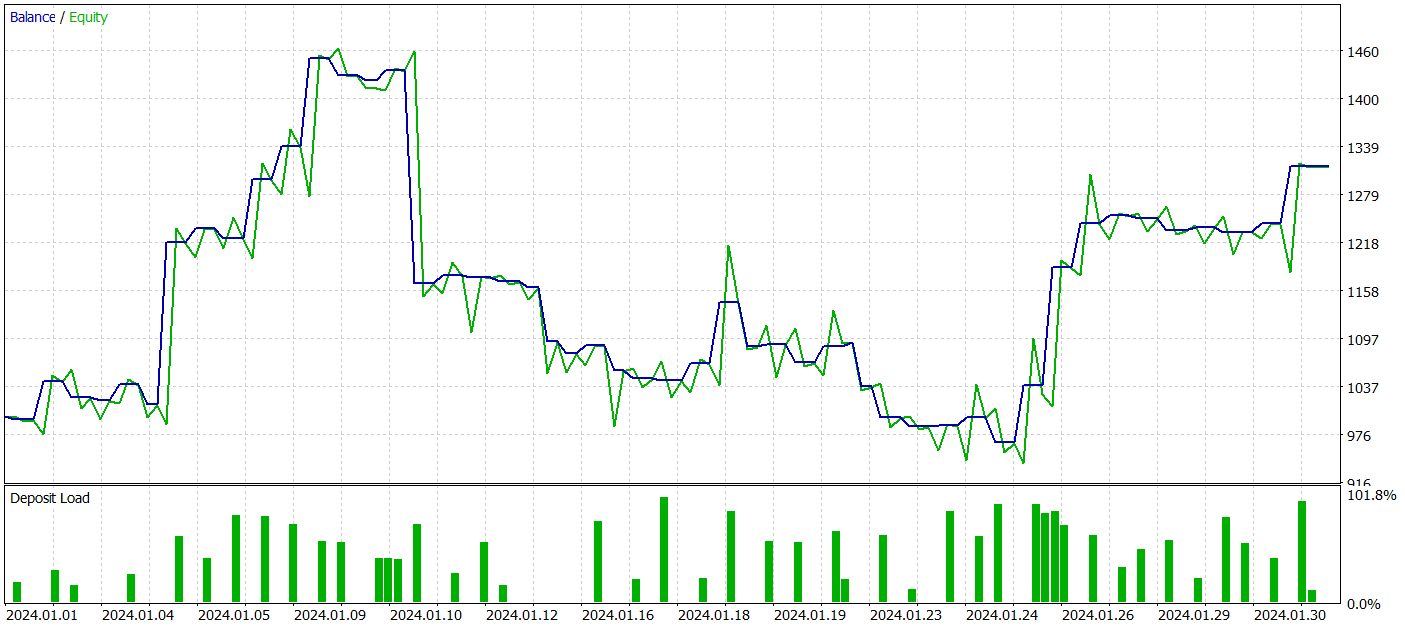
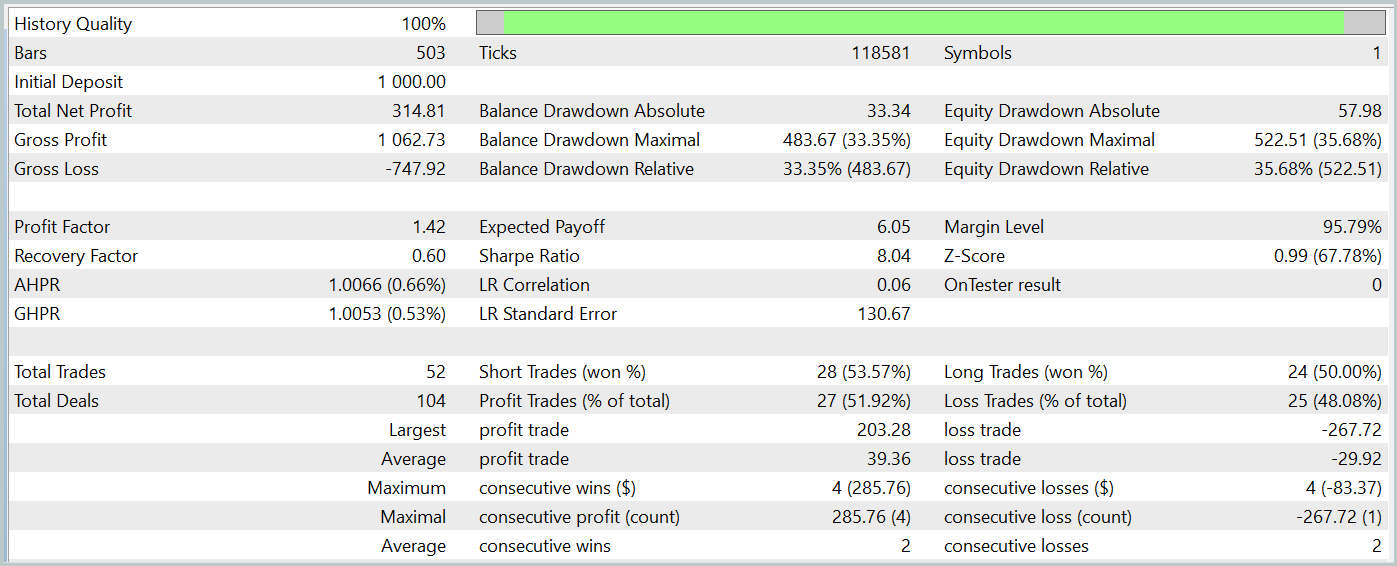
テスト期間中、モデルは52件の取引を実行し、そのうち27件（約52%）が利益で終了しました。平均利益は取引あたりの平均損失を上回りました(39.36対-29.82)。それにもかかわらず、最大損失は最大利益より30%大きくなっていました。さらに、株式の35%以上の下落も観測されました。明らかに、このモデルはさらに改良する必要があります。

時間別、日別の損益の内訳も興味深いです。

金曜日は利益が著しく増加し、水曜日は損失が出ています。利益の出る取引と損失の出る取引が集中する特定の日中の期間もあります。これにはさらなる分析が必要です。特に、ポジションの平均保有時間は1時間強、最大2時間でした。

結論

この記事では、Transformerなどの従来のアーキテクチャに代わる効率的な代替手段を提供する新しい時系列予測方法Mambaについて説明しました。サンプル状態空間モデル(SSM)を統合することにより、Mambaは高いスループットとシーケンス長の線形スケーリングを実現します。

記事の実践部分では、MQL5を使用して提案されたアプローチのビジョンを実装しました。実際のデータでモデルを訓練したところ、さまざまな結果が得られました。

参照文献

記事で使用されているプログラム

#	ファイル名	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコーダー訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15546

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1613.29 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

リプレイシステムの開発（第60回）：サービスの再生(I)

これまで長い間インジケーターだけに取り組んできましたが、今度はサービスを再び稼働させて、提供されたデータに基づいてチャートがどのように構築されるかを確認するときが来ました。しかし、すべてがそれほど単純ではないので、先に何が待ち受けているのかを理解するために注意深くならなければなりません。

人工藻類アルゴリズム(AAA)

本稿では、微細藻類に特徴的な生物学的プロセスに基づく人工藻類アルゴリズム(AAA)について考察します。このアルゴリズムには、螺旋運動、進化過程、適応過程が含まれており、最適化問題を解くことができます。この記事では、AAAが機能する原理と、数学的モデリングにおけるその可能性について詳しく分析し、自然とアルゴリズムによる解とのつながりを強調しています。

初級から中級へ：値渡しまたは参照渡し

この記事では、値渡しと参照渡しの違いを実際の例を通じて理解します。これは単純で一般的な概念であり、特に問題を引き起こすようには思えませんが、多くの経験豊富なプログラマーでさえ、この小さな違いのためにコードの作成中に思わぬ失敗をすることがあります。値渡しまたは参照渡しをいつ、どのように、なぜ使用するかを知ることは、プログラマーとしての私たちの生活に大きな違いをもたらします。ここで提示されるコンテンツは、教育目的のみを目的としています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。

ウィリアム・ギャンの手法（第2回）：ギャンスクエアインジケーターの作成

ギャンのSquare of 9に基づいて、時間と価格を2乗したインジケーターを作成します。コードを準備し、プラットフォームで異なる時間間隔でインジケーターをテストします。