古典的な戦略を再構築する（第7回）：USDJPYにおける外国為替市場とソブリン債務分析

MetaTrader 5 — 例 | 8 11月 2024, 08:13

136

人工知能は、現代の投資家のための新しい取引戦略を生み出す可能性を秘めています。自分の資本をどの戦略に託すかを決める前に、投資家がそれぞれの戦略を慎重に評価するのに十分な時間を持つ可能性は低いでしょう。本連載では、どの戦略があなたの特定の投資家プロファイルに最も適しているかについて、十分な情報に基づいた決定を下すために必要な情報を提供することを目的としています。

取引戦略の概要

固定利付証券は、投資家がポートフォリオを安全に分散できる投資商品であり、満期まで固定または変動利回りを提供するものです。満期時には投資元本が返済され、それ以降の支払いはおこなわれません。代表的な固定収入証券には、債券や預金証書など、さまざまな種類があります。

債券は最も人気のある固定収入証券のひとつであり、本稿の主な焦点でもあります。債券は企業または政府によって発行され、特に国債は世界で最も安全な投資先の1つとされています。投資家が特定の政府債券を購入したい場合、その国の通貨で購入する必要があります。特定の政府債券への国際的な需要が高まると、投資家は自国通貨をその国の通貨に両替する必要があるため、2つの通貨間の為替レートに対する市場の評価が影響を受けることもあります。

債券のパフォーマンスは利回りで測定され、利回りと債券需要には逆相関の関係があります。つまり、特定の債券の需要が減少すると利回りが上昇し、それが需要を押し上げる要因となります。通貨市場で成功を収めるトレーダーの中には、このファンダメンタル分析を取引戦略に取り入れる人もいます。2か国の中長期国債の利回りを為替レートと比較することで、トレーダーはそれぞれの経済状況について洞察を得ることができます。

一般に、高い金利を提供する債券は投資家に人気があり、そのため、発行国の通貨も時間とともに上昇する傾向があります。一方、低い金利で債券を発行する国の通貨は、時間の経過とともに価値が下落する傾向があります。

方法論の概要

戦略を評価するために、USDJPY為替レートの終値を予測するさまざまなモデルを訓練しました。モデルには以下の3種類の予測子セットが使用されました。

USDJPY市場から取得された通常の始値、高値、安値、終値、ティックボリューム(OHLCV)データ
日本国債10年物と米国国債10年物のOHLCVデータ
上記の両方のデータ

目的は、未知のデータに対して最も低いRMSE（平均二乗誤差平方根）を持つモデルを特定することです。日本と米国の国債価格とUSDJPYの相関係数は-0.85と非常に強力でしたが、最初の予測子セットを使って訓練したモデルが最も低いテスト誤差率を示しました。

最も優れたモデルとして線形回帰(LR)モデルが特定されましたが、パラメータ調整の余地がなかったため、候補ソリューションとして線形サポートベクトル回帰(LSVR)を採用しました。LSVRモデルは、訓練セットへの過剰適合を避けつつ、ハイパーパラメータのチューニングをおこなうことに成功し、カスタマイズされたLSVRモデルは、より単純なLRモデルが達成したベンチマークパフォーマンスを検証データ上で上回りました。モデルの訓練と比較には、時系列データの特性に合わせ、ランダムシャッフルを行わずに時系列交差検証を使用しました。

モデルの調整後、最終モデルをONNX形式でエクスポートし、カスタマイズしたエキスパートアドバイザー(EA)に統合しました。

データの取得

では始めましょう。まず、必要なライブラリをインポートします。

#Import the libraries we need
import pandas as pd
import numpy as np
import MetaTrader5 as mt5
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import sklearn
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split

使用しているライブラリのバージョンは次のとおりです。

#Show library versions
print(f"Pandas version: {pd.__version__}")
print(f"Numpy version: {np.__version__}")
print(f"MetaTrader 5 version: {mt5.__version__}")
print(f"Matplotlib version: {matplotlib.__version__}")
print(f"Seaborn version: {sns.__version__}")
print(f"Scikit-learn version: {sklearn.__version__}")

Pandasバージョン：1.5.3

Numpyバージョン：1.24.4

MetaTrader 5バージョン：5.0.45

Matplotlibバージョン：3.7.1

Seabornバージョン：0.13.0

Scikit-learnバージョン：1.2.2

端末を初期化します。

#Initialize the terminal
mt5.initialize()

True

どのくらい先の将来を予測したいかを定義します。

#Define how far ahead into the future we should forecast
look_ahead = 20

MetaTrader 5端末から必要な時系列データを取得します。

#Fetch historical market data 
usa_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("UST10Y_U4",mt5.TIMEFRAME_M1,0,100000))
jpn_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("JGB10Y_U4",mt5.TIMEFRAME_M1,0,100000))
usd_jpy      = pd.DataFrame(mt5.copy_rates_from_pos("USDJPY",mt5.TIMEFRAME_M1,0,100000))

データフレームの時間列をフォーマットします。

#Convert the time from seconds
usa_10y_bond["time"] = pd.to_datetime(usa_10y_bond["time"],unit="s")
jpn_10y_bond["time"] = pd.to_datetime(jpn_10y_bond["time"],unit="s")
usd_jpy["time"] = pd.to_datetime(usd_jpy["time"],unit="s")

時間列をインデックスとして設定します。これにより、3つのデータフレームを 1つに結合しやすくなります。

#Prepare to merge the data
usa_10y_bond.set_index("time",inplace=True)
jpn_10y_bond.set_index("time",inplace=True)
usd_jpy.set_index("time",inplace=True)

データフレームを結合します。

#Merge the data
merged_data = usa_10y_bond.merge(jpn_10y_bond,how="inner",left_index=True,right_index=True,suffixes=(" usa"," japan"))
merged_data = merged_data.merge(usd_jpy,left_index=True,right_index=True)

探索的データ分析

プロット目的で使用するデータフレームのコピーを作成します。

data_visualization = merged_data

可視化データのインデックスをリセットします。

#Reset the index
data_visualization.reset_index(inplace=True)

すべての列の値が1から始まるようにスケーリングします。

#Let's scale the data so all the first values in the column are one
for i in np.arange(1,data_visualization.shape[1]):
    data_visualization.iloc[:,i] = data_visualization.iloc[:,i] / data_visualization.iloc[0,i]

3つの時系列をプロットして、観察可能な関係があるかどうかを確認してみましょう。

#Let's create a plot
plt.figure(figsize=(10, 5))
plt.plot(data_visualization.loc[:,"open usa"])
plt.plot(data_visualization.loc[:,"open japan"])
plt.plot(data_visualization.loc[:,"open"])
plt.legend(["USA 10Y T-Note","JGB 10Y Bond","USDJPY Fx Rate"])

市場データ

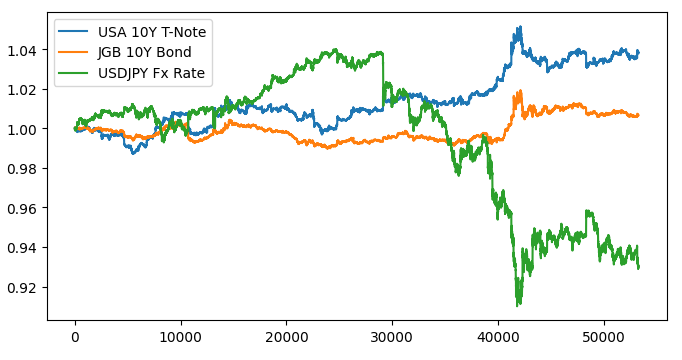
図1：市場データの可視化

3つの市場を重ね合わせると、識別できる関係はないようです。米国債と日本国債のスプレッドをグラフ化して、グラフを読みやすくしてみましょう。そうすれば、USDJPY為替レートと米国と日本の10年債スプレッドのみを考慮する必要があります。言い換えれば、上でプロットした3つの曲線は、わずか2つの曲線で完全に表すことができます。

まず、債券間のスプレッドを計算する必要があります。

#Let's create a new feature to show the spread between the securities
data_visualization["spread"] = data_visualization["open usa"] - data_visualization["open japan"]

チャートの左側には、USDJPY為替レートのサンプルが表示されています。為替レートが1を超えると、ドルは円よりもパフォーマンスが良くなり、為替レートが1を下回ると、その逆のことが当てはまります。さらに、スプレッドが0を超えると、米国債のパフォーマンスは日本債よりも良くなり、スプレッドが0を下回ると逆のことが当てはまります。したがって、スプレッドが0を下回る場合には、日本国債が市場で優勢となり、為替レートも円に有利に傾くことが期待されます。しかし、実際のプロットを視覚的に確認すると、この想定が必ずしも成立しないことが明らかです。

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,2,sharex=True,sharey=False,figsize=(8,4))
columns = ["open","spread"]

for i,ax in enumerate(axs.flat):
    ax.plot(data_visualization.loc[:,columns[i]])
    ax.set_title(columns[i])

為替レートにおけるスプレッドの可視化

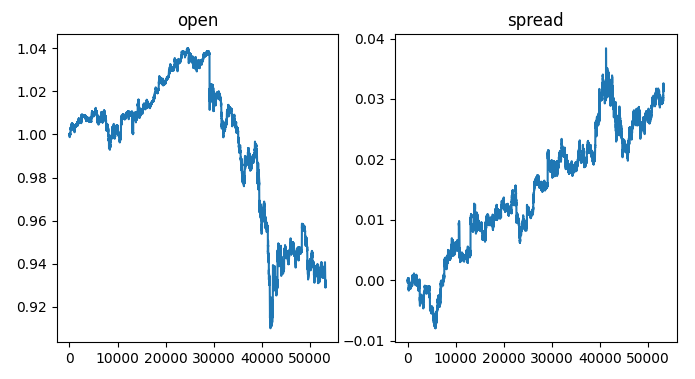
図2：為替レートにおける債券スプレッドの可視化

それでは、データにラベルを付けてみましょう。

#Label the data
merged_data["target"] = merged_data["close"].shift(-look_ahead)
merged_data["binary target"] = np.nan
merged_data.loc[merged_data["close"] > merged_data["target"],"binary target"] = 0
merged_data.loc[merged_data["close"] < merged_data["target"],"binary target"] = 1
merged_data.dropna(inplace=True)
merged_data.reset_index(inplace=True)
merged_data

ラベル付けされたデータ

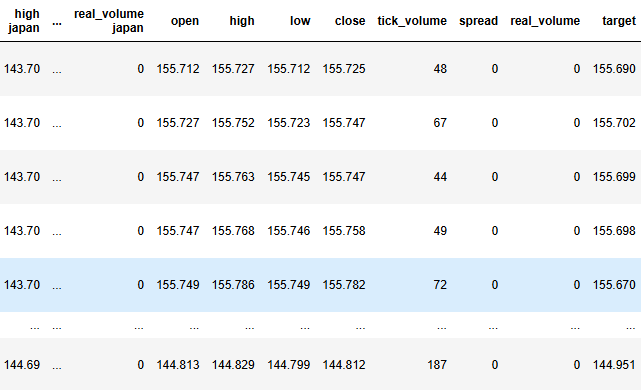
図3：データフレームの現在の状態

ここで、ターゲットと入力を定義します。

#Define the predictors and target
target = "target"
ohlc_predictors = ['open', 'high', 'low', 'close','tick_volume']
bonds_predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan']
predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan','open', 'high', 'low', 'close','tick_volume']

データセット内の相関レベルを分析します。

#Analyze correlation levels
plt.subplots(figsize=(8,6))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True)

相関行列

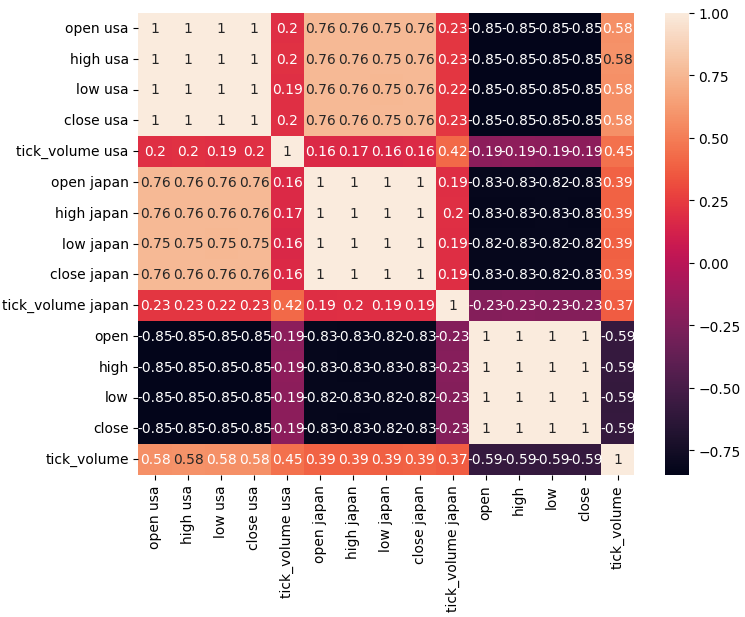
図4：相関行列

ご覧のとおり、米国債と日本国債の間には0.76という強い相関関係があります。さらに、米国債と日本国債はどちらも、USDJPY為替レートと強い負の相関関係にあります。

散布図を使用すると、変数間の関係を2次元で可視化できます。債券市場から収集したデータを使用して散布図を作成しましょう。まず、米国債の始値とUSDJPY為替レートの始値の散布図を作成します。

散布図 1

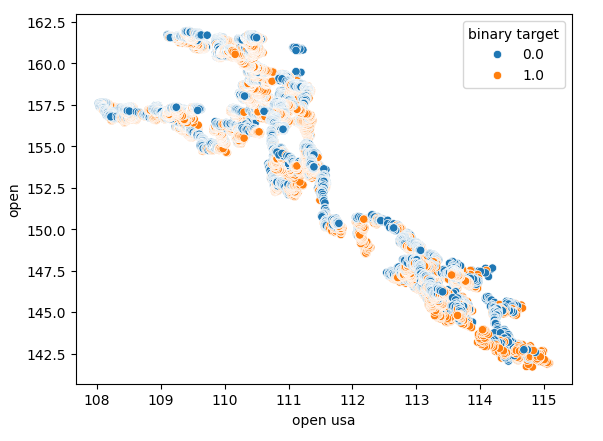
図5：米国債券始値とUSDJPY始値の散布図

ご覧のとおり、散布図では明確なパターンや依存関係は示されていません。債券市場で起こっている変化に関係なく、為替レートは上昇したり下落したりする可能性があるようです。

また、x軸に日本国債の始値、y軸にUSDJPY為替レートの始値を使用して、別の散布図も作成しました。残念ながら、データにはまだ目に見える関係性はありませんでした。

散布図 2

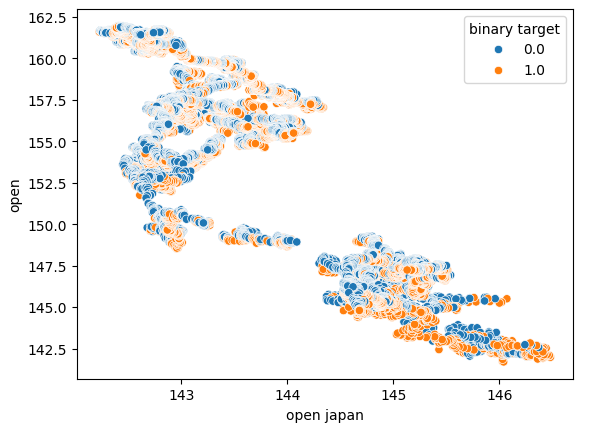
図6：日本国債の始値とUSDJPYの始値の散布図

さらに、各軸に日本国債と米国債の始値を用いて、別の散布図を作成しました。X軸には日本国債の始値、Y軸には米国債の始値を配置しています。しかし、この散布図には目立ったパターンは見られませんでした。これは、他に考慮すべき変数が存在し、それらがデータに影響を与えている可能性を示唆していると考えられます。

散布図3

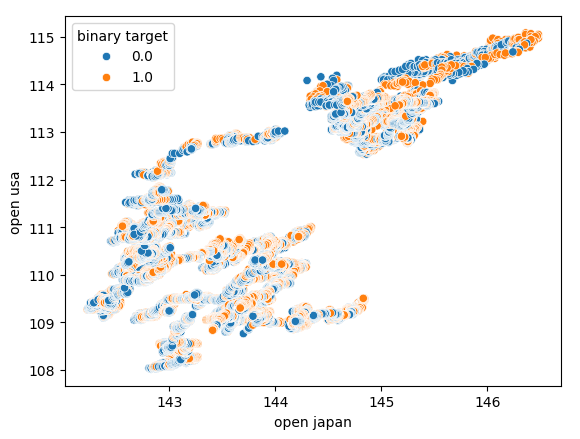
図7：日本国債の始値と米国債の始値の散布図

米国債市場のティックボリュームとUSDJPY為替レートの終値との間に関係があるかどうかも確認してみましょう。残念ながら、散布図では明確な区別がないため、同じティックボリュームの読み取りで価格が上昇したり下落したりする例が多数見られます。

散布図4

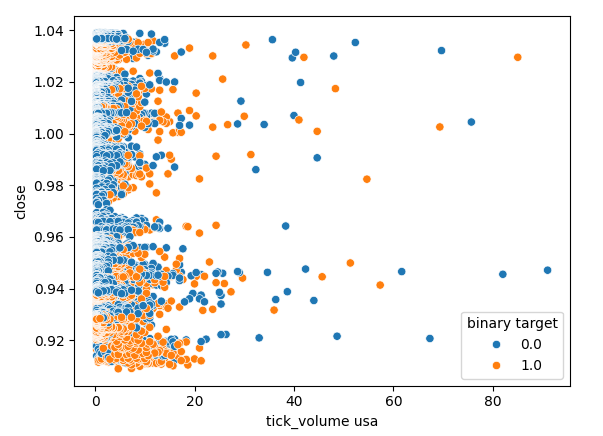
図8：USDJPY終値と米国債ティックボリュームの散布図

データのモデリング

これでデータのモデリングを開始する準備が整いました。まずはデータセットのスケーリングと標準化から始めます。これにより、機械学習モデルが効果的に学習できるようになります。

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

次に、データセットを2つに分割します。一方の半分はモデルの訓練と最適化に使用され、もう一方の半分はモデルの検証と過剰適合のテストに使用されます。

#Partition the data
train_X , test_X, train_y, test_y = train_test_split(scaled_data,merged_data.loc[:,target],shuffle=False,test_size=0.5)

さまざまなモデルを効果的にテストするために、モデルをリストに保存して、それらをループし、それぞれのパフォーマンスを順番に交差検証できるようにします。また、3つのデータフレームを作成する必要があります。

最初のデータフレームには、USDJPY市場からの通常のOHLCVデータのみを使用する場合の誤差レベルが格納されます。
2番目のデータフレームには、両方の債券市場からのOHCLVデータのみに依存した場合の誤差レベルが格納されます。
そして最後のデータフレームには、利用可能なすべてのデータを組み込んだときの誤差レベルが格納されます。

#Model selection
from sklearn.linear_model import LinearRegression , Lasso , SGDRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import GradientBoostingRegressor , RandomForestRegressor , BaggingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error 
from sklearn.model_selection import TimeSeriesSplit

#Define the columns
columns = [
    "Linear Model",
    "Lasso",
    "SGD",
    "Linear SV",
    "Gradient Boost",
    "Random Forest",
    "Bagging",
    "K Neighbors",
    "Neural Network"
]

#Define the models
models = [
    LinearRegression(),
    Lasso(),
    SGDRegressor(),
    LinearSVR(),
    GradientBoostingRegressor(),
    RandomForestRegressor(),
    BaggingRegressor(),
    KNeighborsRegressor(),
    MLPRegressor(hidden_layer_sizes=(100,40,20,10),shuffle=False)
]

#Create 2 dataframes to store our error on the training and test sets respectively
ohlc_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
ohlc_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

ここで、各モデルを交差検証します。外側のループは利用可能な各モデルを反復処理し、内側のループは各モデルを交差検証し、それぞれの訓練およびテストの誤差レベルを保存します。訓練セットのみでモデルを交差検証していることに注意してください。

#Now perform cross validation
for j in np.arange(0,len(models)):
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],predictors],train_y.loc[train[0]:train[-1]])
        all_training_loss.iloc[i,j] = mean_squared_error(train_y.loc[train[0]:train[-1]],model.predict(train_X.loc[train[0]:train[-1],predictors]))
        all_validation_loss.iloc[i,j] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],predictors]))

ここで、USDJPY市場の通常のOHLCVデータを使用した場合の誤差レベルを観察してみましょう。ご覧のとおり、この特定の設定では、線形モデルのパフォーマンスと線形サポートベクトル回帰が著しく良好に機能しました。

#Our results using the OHLC data
ohlc_validation_loss

OHLCV誤差レベル

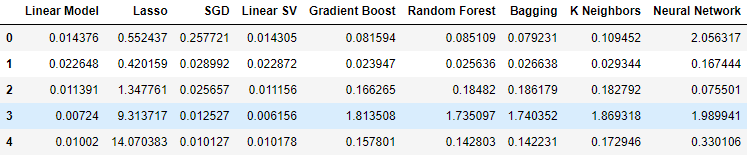
図9：OHLCV誤差レベル

結果を可視化してみましょう。まず、5段階の交差検証手順における各モデルのパフォーマンスの折れ線グラフから始めます。

#Visualizing the results of using the OHLC predictors
plt.plot(ohlc_validation_loss)
plt.legend(columns)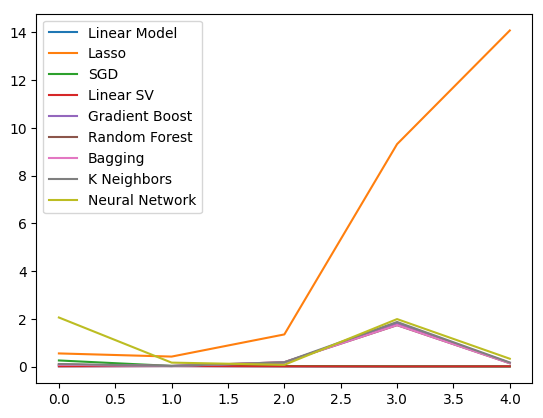

OHLCV誤差値

図10：OHLCV誤差値の折れ線グラフ

ラッソ回帰は最もパフォーマンスの低いモデルであり、検証誤差率が他のモデルと比較して大幅に高いことが明らかです。ただし、どのモデルが最も低い誤差率を達成しているかは一見して分かりにくいですが、ボックスプロットを用いることでこの疑問に答えることができます。

ボックスプロットは、特定のタスクにおいてどのモデルが良好に機能しているかを迅速に把握するのに役立ちます。下のグラフから、線形回帰モデルが平均誤差レベルで最も低く、さらに安定していることが示され、外れ値も最小限に抑えられていることがわかります。

#Visualizing the results of using the OHLC predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(ohlc_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

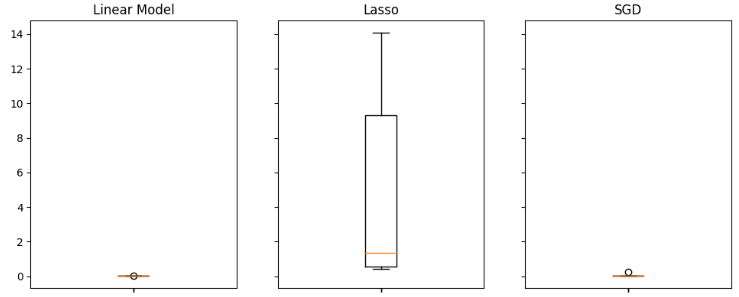
図11：通常のUSDJPY OHLCVを使用した場合の誤差レベルの一部

国債関連のデータを使用したところ、パフォーマンスレベルが全体的に低下しました。ただし、線形サポートベクトル回帰（線形SVR）はこのデータを非常にうまく処理できるようです。

#Our results using the bonds data
bonds_validation_loss

債券データを使用した場合の誤差結果

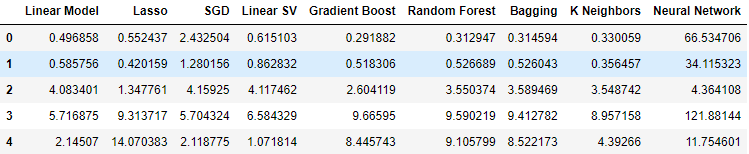
図12：債券データを使用する際の誤差レベル

結果を可視化してみましょう。

#Visualizing the results of using the bonds predictors
plt.plot(bonds_validation_loss)
plt.legend(columns)

債券データ使用時の誤差レベル

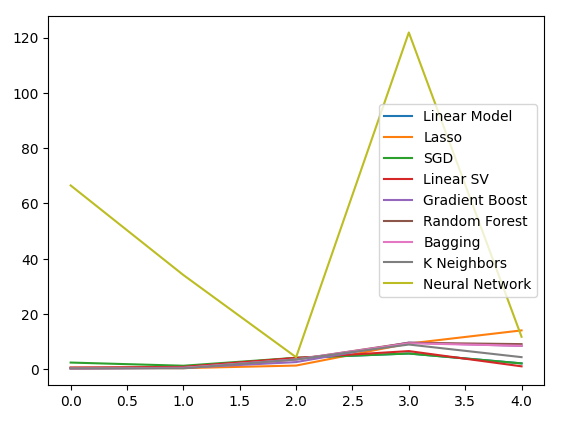
図13：債券データを使用してUSDJPY為替レートを予測した際の検証誤差

ボックスプロットを使用して誤差レベルを評価することもできます。

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(bonds_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

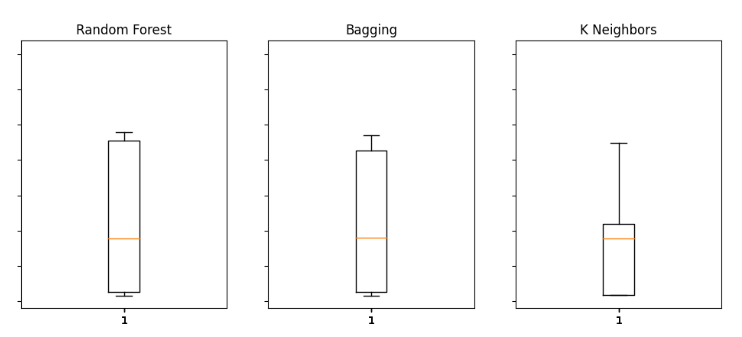債券データ使用時の誤差レベル図 14：債券市場のOHLCVデータを使用してUSDJPYの将来の終値を予測した際の誤差レベルの一部

最後に、利用可能なすべてのデータを組み込むと、前のステップと比較して誤差レベルは改善されましたが、USDJPY市場の市場相場のみを使用した誤差レベルと比較すると満足できるものではありませんでした。

#Our results using all the data we have
all_validation_loss

保有するすべてのデータを使用した場合の誤差レベル

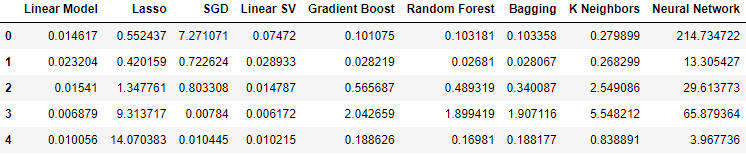
図15：すべての保有データを使用した場合の誤差レベル

パフォーマンスを可視化してみましょう。

#Visualizing the results of using the bonds predictors
plt.plot(all_validation_loss)
plt.legend(columns)

すべての保有データを使用してUSDJPYの終値を予測した場合の誤差レベル

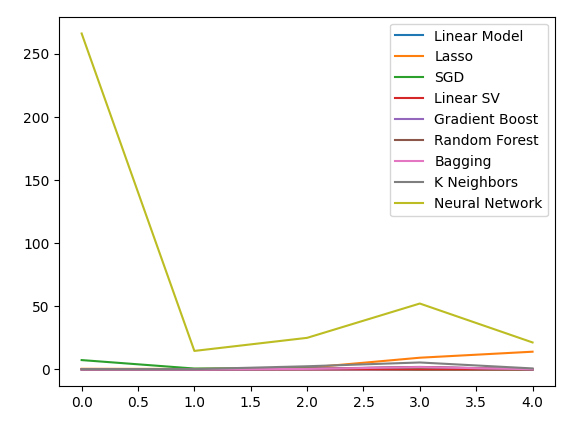
図16：すべての保有データを使用してUSDJPYの終値を予測した場合の誤差レベル

ここでは、線形回帰モデルが最善の選択肢であることが明らかです。しかし、このモデルには調整可能なハイパーパラメータがないため、次に優れた選択肢である線形SVRを採用し、訓練セットへの過剰適合を避けつつ、線形回帰モデルを上回るパフォーマンスが得られるように調整していきます。モデルを最適化する前に、モデルにとって重要な特徴量を評価しましょう。戦略が有効であれば、特徴量除去アルゴリズムによって列が保持されると予想されます。そうでない場合、債券データが破棄されると、戦略を見直す理由が生じる可能性があります。

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(all_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

すべての保有データを使用した場合の誤差レベル

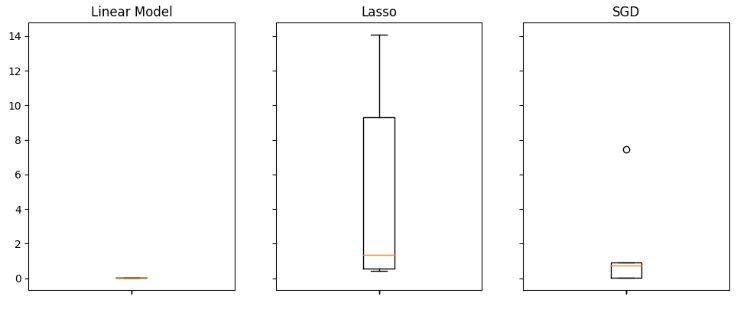
図17：すべての保有データを使用した場合、線形モデルは最高のパフォーマンスを発揮した

特徴量の選択

まず、Shapley (SHAP)値を計算することから始めましょう。SHAP値は、各入力がモデルの予測に与える影響を、ベースライン値と比較する形で示すことを目的としたメトリックです。たとえば、ドライバーがスピード違反の切符を切られる可能性を予測するモデルを考えてみましょう。このモデルが合理的な予測を行えるかどうかを評価するために、「ドライバーの血中アルコール濃度が高いという事実をモデルはどのように解釈するのか」といった質問を投げかけることができます。

モデルは当然、飲酒運転をした場合にはスピード違反切符を切られる可能性が高くなると予測するでしょう。SHAP値はこのような質問に答えるのに役立ちます。具体的には、「ドライバーの血中アルコール濃度が法定限度を超えているという事実をモデルはどのように解釈するのか」といった質問に対し、ベースライン値を含めて考慮することで、より明確な回答を導き出します。

法的制限を考慮することで、ベースラインを定義しました。そのため、運転者の血中アルコール濃度が法定限度を下回る場合と上回る場合のモデルの予測値の差を計算することで、SHAP値を求めます。

SHAPライブラリをインポートします。

#Feature selection
import shap

次に、モデルを訓練します。

#The SVR performed quite well, let's inspect it further
model = LinearSVR()
model.fit(train_X,train_y)

SHAPのエクスプレイナーを適合させます。

#Calculate SHAP Values
explainer = shap.Explainer(model.predict,test_X)
shap_values = explainer(test_X)

SHAPプロットを見てみましょう。

shap.plots.beeswarm(shap_values)

SHAP値

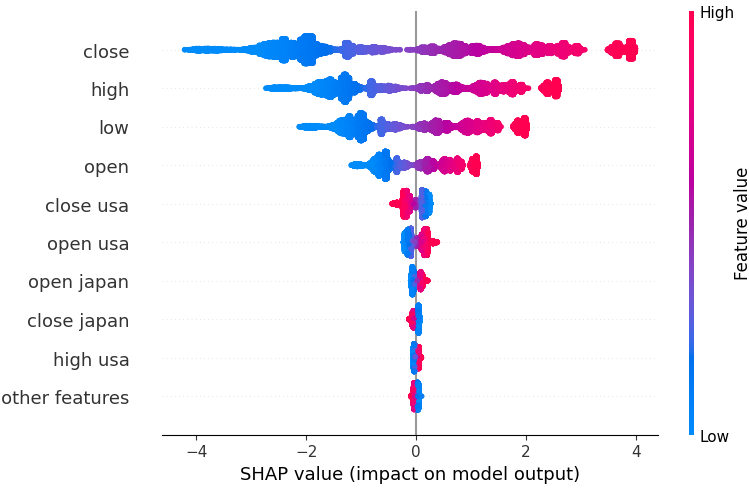
図18：線形SVRモデルからのSHAP値

特徴量は、最も重要なものから順に並べられています。このSHAPの解釈によれば、USDJPYの終値が最も重要な特徴であると考えられます。また、国債に関連するデータが通貨ペアの価格データに続いて位置していることも確認できます。これは戦略を支持する良い証拠であり、SHAP値によれば債券データはUSDJPY市場のティックボリュームよりも重要であると示唆されています。

ただし、すべてのモデルの解釈は鵜呑みにしてはいけません。誤差を免れることはできません。

後方選択も考えてみましょう。後方選択アルゴリズムは、完全なモデルを適合することから始まり、テスト誤差が改善されなくなるまで特徴量を順番に排除します。

mlxtendライブラリをインポートします。

#Let's also perform backward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

モデルを初期化します。

#Reinitialize the model
model = LinearSVR()

特徴量選択器オブジェクトを作成します。

#Prepare the feature selector
sfs = SFS(model,
         k_features=(1,train_X.shape[1]),
         forward=False,
          n_jobs = -1,
          scoring="neg_mean_squared_error",
          cv=5)

特徴量選択器を適合させます。

#Fit the feature selector
sfs_results = sfs.fit(train_X,train_y)

選択された特徴量を見てみましょう。

#The best features we identified
sfs_results.k_feature_names_

('open usa',

'high usa',

'tick_volume usa',

'open japan',

'low japan',

'close',

'tick_volume')

後方除去法アルゴリズムでは、SHAP値よりも債券市場データを重視しました。したがって、債券データとUSDJPYペアの将来の為替レートの間には信頼できる関係がある可能性があると合理的に結論付けることができます。

結果をプロットしましょう。

#Prepare the plot
fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev")
plt.title("Backward Selection on our Linear SVR")
plt.grid()

後方除去法の結果

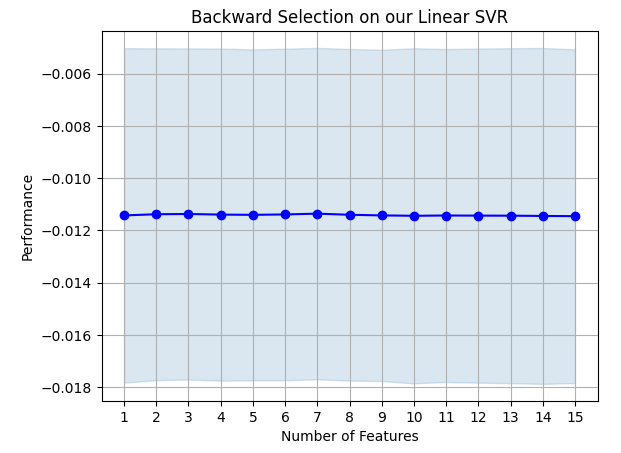
図19：後方消去法の結果

モデルの誤差率は大きく変動していないため、データが限られた状況でもモデルが安定している可能性を示唆しています。アルゴリズムによって選択された特徴量のいずれかを削除しても誤差率がこれ以上改善されなくなるまで、アルゴリズムは特徴量を1つずつ削除し続けることに注意してください。

ハイパーパラメータの調整

次に、線形回帰を上回るパフォーマンスが得られるようにモデルを最適化します。

まず、必要なライブラリをインポートします。

#Parameter tuning 
from sklearn.model_selection import RandomizedSearchCV

モデルを初期化します。

#Reinitialize the model
model = LinearSVR()

チューナーオブジェクトを定義します。

tuner = RandomizedSearchCV(model,
                          {
                              "epsilon":[0,0.001,0.01,0.1,25,50,100],
                              "tol": [0.1,0.01,0.001,0.0001,0.00001],
                              "C" : [1,5,10,50,100,1000,10000,100000],
                              "loss":["epsilon_insensitive", "squared_epsilon_insensitive"],
                              "fit_intercept": [False,True]
                          },
                           n_jobs=-1,
                           n_iter=100,
                           scoring="neg_mean_squared_error"
                          )

モデルを調整します。

tuner_results = tuner.fit(train_X,train_y)

興味深いことに、最適なパラメータはデフォルト設定とほぼ同じです。しかし、パフォーマンスの違いを観察してみましょう。

tuner_results.best_params_

{'tol':0.0001,

'loss': 'epsilon_insensitive',

'fit_intercept':True,

'epsilon':0,

'C':1}

過剰適合のテスト

ここで、訓練セットが過剰適合しているかどうかをテストしてみましょう。モデルをインスタンス化します。

#Testing for overfitting
baseline_model = LinearRegression()
default_model =  LinearSVR()
customized_model = LinearSVR(tol=0.0001,loss='epsilon_insensitive',fit_intercept=True,epsilon=0,C=1)

それでは、3つのモデルすべてを適合させてみましょう。

#Fit the models
baseline_model.fit(train_X,train_y)
default_model.fit(train_X,train_y)
customized_model.fit(train_X,train_y)

各モデルのパフォーマンスを交差検証する準備をしています。

#Create a list of models
models = [
    baseline_model,
    default_model,
    customized_model
]

columns = [
    "Linear Regression",
    "Default Linear SVR",
    "Customized Linear SVR"
]

We need to reset the index of our datasets.
#Let's assess our new accuracy levels
test_y = test_y.reset_index()
test_X.reset_index(inplace=True)

時系列分割オブジェクトを再定義し、検証誤差を格納するデータフレームを作成します。

#Create our time-series test object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
overfitting_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Cross-validate each model.
for j in np.arange(0,len(columns)):
    model = models[j]
    for i , (train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],predictors],test_y.loc[train[0]:train[-1],"target"])
        overfitting_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"target"],model.predict(test_X.loc[test[0]:test[-1],predictors]))

結果を見てみましょう。

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,3,sharex=True,sharey=True,figsize=(8,4))

for i,ax in enumerate(axs.flat):
    ax.boxplot(overfitting_error.iloc[:,i])
    ax.set_title(columns[i])

目に見えないデータに対する誤差レベル

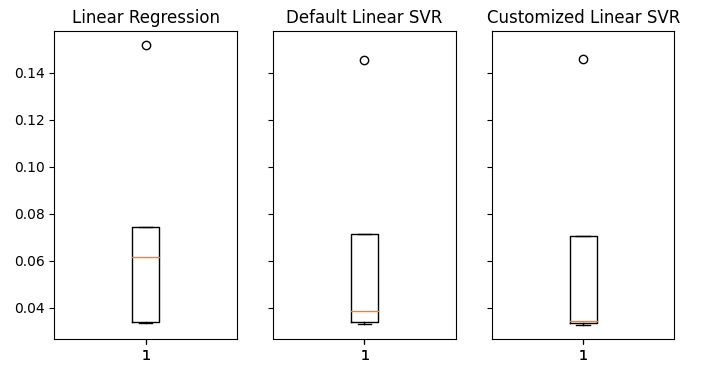
図20：目に見えないデータに対する誤差レベル

検証では、LinearSVRモデルが平均誤差が最も低かったことがはっきりとわかります。したがって、線形モデルによって設定されたベンチマークを上回るパフォーマンスを達成することができました。さらに、訓練セットに過剰適合することなく、デフォルトの誤差率を上回るパフォーマンスも達成しました。

ONNXへのエクスポート

次に、モデルを ONNX形式にエクスポートして、MQL5プログラムに簡単に統合できるように準備します。

先に進む前に、まず MQL5で再現できる形式でデータを標準化する必要があります。これを実現するには、各列の値から列の平均を減算し、その後各列をその標準偏差で割ります。

端末のファイルパスにあるCSVファイルにそれぞれの値を書き出してみましょう。

#Create scaling factors
scaling_factors = pd.DataFrame(index=("mean","standard deviation"),columns=predictors)

#Write our the values
for i in np.arange(0,scaling_factors.shape[1]):
    scaling_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
    scaling_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std()
    merged_data.loc[:,predictors[i]] = ((merged_data.loc[:,predictors[i]] - scaling_factors.iloc[0,i]) / scaling_factors.iloc[1,i])

scaling_factors

スケーリング係数

図21：スケーリング係数

ここでCSVファイルを保存します。

#Save the scaling factors
scaling_factors.to_csv("C:\\Enter \\Your\\Path\\Here\\MetaQuotes\\Terminal\\D0E82094358C8CF3394F550E51FF075\\MQL5\\Files\\usdjpy scaling factors.csv")

利用可能なすべてのデータでモデルを訓練してみましょう。

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,"target"])

必要なライブラリをインポートします。

#Let's import the libraries we need
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import netron
import onnx

ONNXモデルの入力タイプと形状を定義します。

#Define the initial input types
initial_types = [('float_input',FloatTensorType([1,len(predictors)]))]

ONNXモデルを作成します。

#Create an ONNX representation of the model
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

ONNXモデルを .onnx拡張子を持つファイルに保存します。

#Save the ONNX model
onnx_name = "USDJPY M1 FLOAT.onnx"
onnx.save(onnx_model,onnx_name)

netronでモデルを可視化してみましょう。

#Visualize the model
netron.start(onnx_name)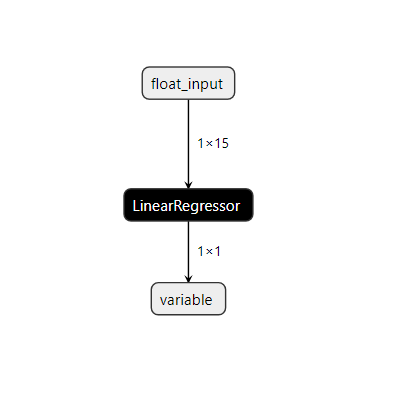

LinearSVRモデル

図22：線形SVRモデルの可視化

ONNXモデルメタデータ

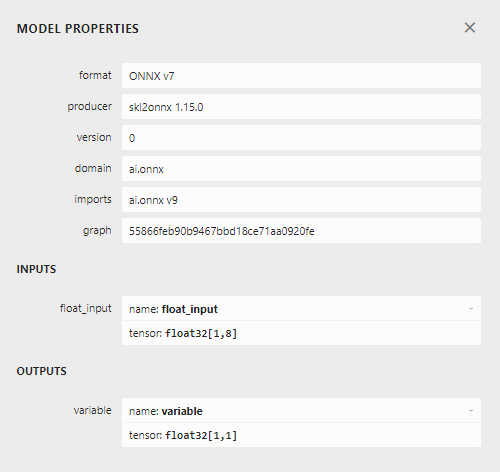
図23：ONNXモデルの入力と出力の形状

モデルの入力と出力の形状は、仕様と一致しています。EAの構築を進めましょう。

MQL5での実装

まず、プログラムにコンパイルされるリソースとして ONNXモデルが必要になります。

//+------------------------------------------------------------------+
//|                                                 USDJPY Bonds.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/ja/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource "\\Files\\USDJPY M1 FLOAT.onnx" as const uchar onnx_model_buffer[];

ここで、プログラム全体で必要ないくつかのグローバル変数を定義しましょう。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
float mean_values[15],std_values[15];
vector model_output = vector::Zeros(1);
int state = 0;
int prediction = 0;

取引ライブラリをインポートすると、ポジションを簡単に開いて管理できるようになります。

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

ここで、EAのヘルパー関数を定義します。ONNXモデルを読み込み、その入力と出力の形状を定義する関数が必要です。手順のどの時点でも失敗した場合、関数は初期化手順を中断するフラグを返します。

//+------------------------------------------------------------------+
//| Load our onnx file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT);

//--- Set the input shape
   ulong input_shape [] = {1,15};

//--- Check if the input shape is valid
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model));
      return(false);
     }

//--- Set the output shape
   ulong output_shape [] = {1,1};

//--- Check if the output shape is valid
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model));
      return(false);
     }
//--- Everything went fine
   return(true);
  }

また、スケーリング値を含む CSVファイルを読み取り、それを後ほど予測関数で使用するために配列に保存する関数も必要です。最初の行には列タイトルのみが含まれていることに注意してください。2行目の最初のエントリはインデックスラベルであり、2行目の2番目のエントリは最初の列の平均です。したがって、関数は現在のループ反復を確認して、それがどこにあり、どの値が重要であるかを追跡します。

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
void load_scaling_factors(void)
    {
//--- Read in the file
   string file_name = "usdjpy scaling factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). 

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file
      
      int counter = 0;
      string value = "";
      
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end 
       {
       
         if (counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read
           break; //stop the reading progress
         
         value = FileReadString(result);
         Print("Trying to read string: ",value," count value: ",counter);
         
         //--- Check where we are
         if((counter >= 17) && (counter < 32))
            {
               mean_values[counter - 17] = (float) value;
            }   
         //--- Check where we are
         if((counter >= 33) && (counter < 48))
            {
               std_values[counter - 33] = (float) value;
            }   
         //--- Reading a new row
         if(FileIsLineEnding(result))
           { 
             Print("row++");
           }
         
         counter++;
       }
      //---Close the file
      ArrayPrint(mean_values);
      ArrayPrint(std_values);
      FileClose(result);
     }
//--- We failed to find the file
else 
   {
      Print("Failed to find the file");
   }

  }

この関数は、モデルから予測を取得する前に、モデルの入力値を取得し、標準化します。その後、モデルの予測はバイナリ状態として保存されます。1は強気の予測、2は弱気のポジションです。これは、モデルがいつ反転を予測しているかを識別するのに役立ちます。

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void model_predict(void)
   {
     //--- Fetch input values
      string symbols[3] = {"UST10Y_U4","JGB10Y_U4","USDJPY"};
      vectorf model_inputs = {iOpen(symbols[0],PERIOD_CURRENT,0),iHigh(symbols[0],PERIOD_CURRENT,0),iLow(symbols[0],PERIOD_CURRENT,0),iClose(symbols[0],PERIOD_CURRENT,0),iTickVolume(symbols[0],PERIOD_CURRENT,0),
                      iOpen(symbols[1],PERIOD_CURRENT,0),iHigh(symbols[1],PERIOD_CURRENT,0),iLow(symbols[1],PERIOD_CURRENT,0),iClose(symbols[1],PERIOD_CURRENT,0),iTickVolume(symbols[1],PERIOD_CURRENT,0),
                      iOpen(symbols[2],PERIOD_CURRENT,0),iHigh(symbols[2],PERIOD_CURRENT,0),iLow(symbols[2],PERIOD_CURRENT,0),iClose(symbols[2],PERIOD_CURRENT,0),iTickVolume(symbols[2],PERIOD_CURRENT,0)
                     };
     //--- Normalize and scale our inputs
     for(int i=0;i < 15;i++)
         {
            model_inputs[i] = ((model_inputs[i] - mean_values[i])/std_values[i]);
         }
     //--- Show the inputs
     Print("Model inputs: ",model_inputs);
     //--- Fetch a forecast from our model
     OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
     //--- Give the user feedback
     Comment("Model forecast: ",model_output[0]);
     
     //--- Store the prediction
     if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 1;
         }
     else if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 2;
         }       
   }

初期化プロシージャでは、スケーリング値を読み取り、最後にモデルが機能するかどうかをテストする前に、まず ONNXファイルを正常に読み込む必要があります。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Load the ONNX file
   if(!load_onnx_file())
     {
      //--- We failed to load our onnx model
      return(INIT_FAILED);
     }
     
//--- Load scaling factors
load_scaling_factors();

//--- Test if our ONNX model works
model_predict();

//--- Everything worked out
   return(INIT_SUCCEEDED);
   
  }

プログラムが使用されなくなったときは、不要になったリソースを解放する必要があります。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we used for our onnx model
   OnnxRelease(onnx_model);
//--- Release the expert advisor
   ExpertRemove();
  }

最後に、価格レベルに変化があるたびに、まずモデルから予測を取得します。ポジションがない場合は、モデルの予測に従い、現在のポジションを表すフラグを保存します。それ以外の場合、すでにポジションがある場合は、モデルの予測がポジションと一致しているかどうかを確認し、一致していない場合はポジションをクローズします。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
      //--- Obtain a forecast from our model
      model_predict();
      
      //--- Check if we have any positions
      if(PositionsTotal() == 0)
         {
            //--- Reset the state of our system
            state = 0;
            
            //--- Check for an entry
            if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Buy(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_ASK),SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,"USDJPY Bonds AI");
                  state = 1;
               }
            
             if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Sell(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_BID),SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,"USDJPY Bonds AI");
                  state = 2;
               }
         }
         
      //--- Check for reversals
      if(state != prediction)
         {
            Alert("Reversal detected by the AI system!");
            Trade.PositionClose("USDJPY");
         }
  }
//+------------------------------------------------------------------+

プログラムの動作

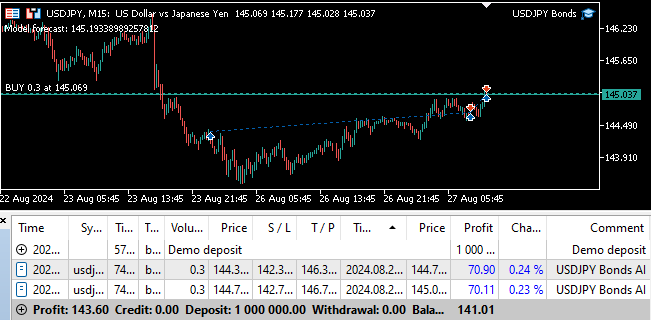
図24：プログラムのフォワードテスト

AIモデルが逆転を検出

図25：EAは反転を検出すると自動的にポジションをクローズできる

結論

この記事では、AIを活用して従来の取引戦略を強化する方法について説明しました。私たちの戦略がその複雑さに見合う効果を持っているかについては議論の余地がありますが、より単純なモデルを採用すれば精度が低下していた可能性も考えられます。したがって、特徴量を変換して関係性をさらに明確にしない限り、市場の通常の見積もりに基づくシンプルな戦略を使用する方が合理的であると結論付けることができます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15719

添付されたファイル |

ZIPをダウンロード

USDJPY_M1_FLOAT.onnx (0.33 KB)

USDJPY_Sovereign_Debt.ipynb (1264.27 KB)

USDJPY_Bonds.mq5 (8.22 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

知っておくべきMQL5ウィザードのテクニック（第36回）：マルコフ連鎖を用いたQ学習

強化学習は、教師あり学習、教師なし学習と並んで、機械学習における3つの主要な考え方の1つです。そのため、最適制御、つまり目的関数に最も適した長期的な方針を学習することに関心があります。このような背景から、ウィザードが作成したEAのMLPの学習プロセスにおいて、MLPがどのような役割を果たす可能性があるのかを探ります。

ニュース取引が簡単に（第2回）：リスク管理

この記事では、以前のコードと新しいコードに継承を導入します。効率性を高めるために新しいデータベース設計が実装されます。さらに、取引量計算に取り組むためのリスク管理クラスも作成されます。

人工協調探索(ACS)アルゴリズム

人工協調探索(ACS)は、バイナリ行列と、相互主義的関係と協調に基づく複数の動的な個体群を用いて、最適解を迅速かつ正確に探索する革新的な手法です。捕食者と被食者に対するACS独自のアプローチにより、数値最適化問題で優れた結果を出すことができます。

チャート上で取引を視覚化する（第1回）：分析期間の選択

ここでは、取引エントリを分析するために取引の印刷画面のアンロードを簡素化するスクリプトをゼロから開発します。単一の取引に関するすべての必要な情報は、異なる時間枠を描画する機能を備えた1つのチャートに便利に表示されます。