MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語
preview
Introducción a las curvas ROC (Receiver Operating Characteristic)

Introducción a las curvas ROC (Receiver Operating Characteristic)

MetaTrader 5 — Ejemplos |
22 0
Francis Dube
Francis Dube

Introducción

El gráfico ROC sirve como método para visualizar, organizar y seleccionar clasificadores en función de su rendimiento. Con origen en la teoría de la detección de señales, los gráficos ROC se han empleado para ilustrar la relación entre las tasas de verdaderos positivos y las tasas de falsos positivos de los clasificadores. Más allá de su utilidad general como método de representación gráfica del rendimiento, las curvas ROC presentan propiedades que las hacen especialmente valiosas en ámbitos caracterizados por distribuciones de clases sesgadas y costes de error de clasificación dispares. Lo cual es especialmente relevante para los clasificadores aplicados a conjuntos de datos de series temporales financieras.

Aunque el marco conceptual de los gráficos ROC es sencillo, su aplicación práctica revela complejidades que merecen una cuidadosa consideración. Además, existen conceptos erróneos comunes y posibles dificultades en su uso empírico. El objetivo de este artículo es ofrecer una introducción básica a las curvas ROC y servir como guía práctica para su aplicación en la evaluación del rendimiento de los clasificadores.


Clasificación binaria

Muchas aplicaciones del mundo real implican problemas de clasificación binaria, en los que las instancias pertenecen a una de dos clases mutuamente excluyentes y colectivamente exhaustivas. Un ejemplo frecuente de este escenario se da cuando se define una única clase objetivo y cada instancia se clasifica como miembro de esta clase o como su complemento. Consideremos, por ejemplo, la clasificación de señales de radar, en la que un contorno detectado en una pantalla se clasifica como un tanque (la clase objetivo) o como un objeto que no es un tanque. Del mismo modo, una transacción con tarjeta de crédito puede clasificarse como fraudulenta (la clase objetivo) o legítima.

¿Objetivo o no?

Esta formulación específica del problema de clasificación binaria, caracterizada por la identificación de una única clase objetivo, constituye la base para el análisis posterior. En lugar de asignar explícitamente las instancias a una de las dos clases distintas, el enfoque adoptado aquí se centra en determinar si una instancia pertenece a la clase objetivo designada. Aunque la terminología empleada, que hace referencia al «objetivo» y su complemento, puede evocar connotaciones militares, el concepto es ampliamente aplicable. La clase objetivo puede representar diversas entidades, como un tumor maligno, una operación financiera exitosa o, como se ha mencionado anteriormente, una transacción fraudulenta con tarjeta de crédito. La característica esencial es la dualidad de la clase de interés principal y todas las demás posibilidades.


La matriz de confusión

Para un clasificador determinado aplicado a un conjunto de datos de prueba, son posibles cuatro resultados distintos. Si una instancia perteneciente a la clase positiva se clasifica como positiva, se designa como verdadero positivo (True Positive, TP). Por el contrario, si se clasifica como negativo, se designa como falso negativo (False Negative, FN). Del mismo modo, si una instancia perteneciente a la clase negativa se clasifica como negativa, se designa como verdadera negativa (True Negative, TN); si se clasifica como positiva, se designa como falsa positiva (False Positive, FP). Estos cuatro valores conforman una matriz de confusión dos por dos, también conocida como tabla de contingencia.

Matriz de confusión

Esta matriz resume la distribución de casos en estos cuatro resultados y sirve como base fundamental para numerosas métricas de rendimiento comúnmente utilizadas, entre las que se incluyen:

  • Tasa de acierto, sensibilidad o recuperación: La proporción de instancias objetivo clasificadas correctamente como objetivos, calculada como TP / (TP + FN).
  • Tasa de falsas alarmas (tasa de error de tipo I): La proporción de casos no objetivo clasificados incorrectamente como objetivos, calculada como FP / (TN + FP).
  • Tasa de error (tasa de error de tipo II): La proporción de instancias objetivo clasificadas incorrectamente como no objetivo, calculada como FN / (TP + FN).
  • Especificidad: La proporción de casos no objetivo clasificados correctamente como no objetivo, calculada como TN / (TN + FP).

Wikipedia tiene un gráfico útil que muestra una lista extensa de métricas de rendimiento derivadas de una matriz de confusión.

Tabla de confusión


Curvas ROC

El funcionamiento interno de la mayoría de los modelos de clasificación binaria consiste en realizar una predicción numérica y, posteriormente, compararla con un umbral predeterminado. Si la predicción iguala o supera este umbral, la instancia se clasifica como objetivo; de lo contrario, se clasifica como no objetivo. Es evidente que el valor umbral influye en todas las medidas de rendimiento mencionadas anteriormente. Establecer el umbral en o por debajo del mínimo posible da como resultado que todos los casos se clasifiquen como objetivos, lo que produce una tasa de aciertos perfecta, pero una tasa de falsas alarmas correspondientemente deficiente.

Mecanismo de decisión

Por el contrario, establecer el umbral por encima de la predicción máxima posible hace que todas las instancias se clasifiquen como no objetivo, lo que da como resultado una tasa de aciertos cero y una tasa de falsas alarmas perfectamente nula. El valor umbral óptimo se encuentra entre estos extremos. Al variar sistemáticamente el umbral en todo su rango, tanto la tasa de aciertos como la tasa de falsas alarmas recorren sus respectivos rangos de 0 a 1, mejorando una métrica a expensas de la otra. La curva generada al trazar estas dos tasas una contra otra (con el umbral actuando como parámetro latente) se denomina curva característica operativa del receptor.
La curva ROC se representa convencionalmente con la tasa de falsas alarmas en el eje horizontal y la tasa de aciertos en el eje vertical. Consideremos un modelo de clasificación que genera predicciones numéricas aleatorias, sin correlación con la clase real de un caso.

Rendimiento aleatorio

En tal escenario, la tasa de aciertos y la tasa de falsas alarmas serán, en promedio, equivalentes en todos los umbrales, lo que dará como resultado una curva ROC que se aproxima a una línea diagonal que se extiende desde la esquina inferior izquierda hasta la esquina superior derecha del gráfico. Por ejemplo, si un clasificador asigna aleatoriamente una instancia a la clase positiva con una probabilidad del 50 %, se espera que clasifique correctamente el 50 % de las instancias positivas y negativas, lo que da como resultado el punto de coordenadas (0,5, 0,5) dentro del espacio ROC.

Del mismo modo, si el clasificador asigna una instancia a la clase positiva con una probabilidad del 90 %, se prevé que clasifique correctamente el 90 % de las instancias positivas; sin embargo, la tasa de falsos positivos aumentará concomitantemente al 90 %, lo que dará como resultado el punto de coordenadas (0,9, 0,9). Por consiguiente, un clasificador aleatorio generará un punto ROC que atraviesa la diagonal, cuya posición viene determinada por la frecuencia con la que predice la clase positiva. Para lograr un rendimiento superior al de las conjeturas aleatorias, tal y como indica una ubicación dentro de la región triangular superior del espacio ROC, el clasificador debe aprovechar los patrones informativos presentes en los datos.

Rendimiento perfecto

Por el contrario, un modelo perfecto, caracterizado por la existencia de un umbral que separa con precisión los objetivos (predicciones iguales o superiores al umbral) de los no objetivos (predicciones por debajo del umbral), presenta una curva ROC distinta. A medida que el umbral paramétrico pasa de su mínimo al óptimo, la tasa de falsas alarmas disminuye de 1 a 0, mientras que la tasa de aciertos se mantiene constante en 1. Los aumentos posteriores en el umbral paramétrico provocan que la tasa de aciertos disminuya de 1 a 0, mientras que la tasa de falsas alarmas se mantiene en 0. Esto da como resultado una curva ROC que forma una trayectoria desde la esquina superior derecha hasta la esquina superior izquierda y, a continuación, hasta la esquina inferior izquierda.

Rendimiento intermedio

Los modelos de rendimiento intermedio, que muestran una precisión entre estos extremos, producirán curvas ROC situadas entre la diagonal y la esquina superior izquierda. El grado en que la curva se desvía de la diagonal hacia la esquina superior izquierda indica el rendimiento del modelo. En términos generales, un punto en un gráfico ROC se considera superior a otro si tiene una tasa de verdaderos positivos más alta, una tasa de falsos positivos más baja, o ambas cosas. Los clasificadores situados en el lado izquierdo de un gráfico ROC, próximos a la abscisa, pueden caracterizarse como conservadores.

Estos clasificadores tienden a emitir clasificaciones positivas solo cuando se les presentan pruebas sustanciales, lo que da lugar a una baja tasa de falsos positivos, pero a menudo va acompañado de una disminución de la tasa de verdaderos positivos. Por el contrario, los clasificadores situados en la parte superior derecha del gráfico ROC, caracterizados por ser menos conservadores, tienden a emitir clasificaciones positivas incluso con pruebas mínimas, lo que da lugar a una alta tasa de verdaderos positivos, pero a menudo acompañada de una elevada tasa de falsos positivos. En numerosos ámbitos del mundo real, donde predominan los casos negativos, el rendimiento de los clasificadores en la región izquierda del gráfico ROC cobra cada vez más relevancia.
Los clasificadores que se encuentran en la región triangular inferior derecha del espacio ROC muestran un rendimiento inferior al de las conjeturas aleatorias. Por consiguiente, esta región suele carecer de puntos de datos en los gráficos ROC. La negación de un clasificador, definida como la inversión de sus decisiones de clasificación para todos los casos, da como resultado que sus clasificaciones verdaderas positivas se conviertan en errores falsos negativos y sus clasificaciones falsas positivas se conviertan en clasificaciones verdaderas negativas. Por lo tanto, cualquier clasificador que produzca un punto dentro del triángulo inferior derecho puede transformarse, mediante negación, para producir un punto correspondiente dentro del triángulo superior izquierdo. Un clasificador situado a lo largo de la diagonal puede caracterizarse por no poseer información discernible sobre la pertenencia a una clase. Por el contrario, un clasificador situado por debajo de la diagonal puede interpretarse como poseedor de patrones informativos, aunque los aplique de manera errónea.


ROC: Métricas de rendimiento

Si bien la inspección visual de un gráfico de la curva ROC puede ofrecer información preliminar, se logra una comprensión más completa del rendimiento del modelo mediante el análisis de medidas de rendimiento relevantes. Antes de realizar un análisis detallado, es necesario aclarar los constructos de datos que caracterizan una curva ROC. Para facilitar la comprensión, se proporciona un ejemplo ilustrativo.

La siguiente tabla presenta una muestra hipotética de métricas de rendimiento ROC derivadas de un modelo de clasificación. Este ejemplo utiliza el conjunto de datos iris, accesible a través de la biblioteca Sklearn Python. Siguiendo el paradigma objetivo/no objetivo, el objetivo de la clasificación se limitó a la identificación de una variante singular del iris. Concretamente, si se designa a setosa como objetivo, todas las demás variantes se clasifican como no objetivos. De acuerdo con las metodologías de clasificación convencionales, el modelo se entrenó para generar un resultado de 0 para los no objetivos y 1 para los objetivos. Las etiquetas de muestra se transformaron en consecuencia. Cabe destacar que también son viables otros sistemas de etiquetado alternativos.

Para cada valor umbral dentro del rango de umbrales de decisión, se genera una matriz de confusión para calcular la tasa de verdaderos positivos y la tasa de falsos positivos. Estos cálculos utilizan la probabilidad de salida o el valor de la función de decisión del modelo de predicción entrenado, con el umbral correspondiente que determina la pertenencia a la clase. La tabla aquí presentada se generó utilizando el script ROC_curves_table_demo.mq5.

KG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH
NF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195
DI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708
OI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556
GI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334
GH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221
RH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211
IK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935
CK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736
NK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715
EJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645
DJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552
HJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534
NM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417
GM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155
CL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943
LL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699
NL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593
KO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660
CN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489
OQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420
NQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619
GQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375
PP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087
OP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257
RP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124
RS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349
KS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523
JR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147
HE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841
QE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488
DE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058
MG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819
JG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744
EG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683
LF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635
CF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589
KF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494
NH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416
PH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347
LH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244
KK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238
HK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225
LK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213
PJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192
CJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189
EM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177
IM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157
HM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132
EL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127
DL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119
KL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104
DO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102
RO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085
DN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069
HN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062
HQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052
DQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048
FQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044
MP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028
LP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026
NS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015
ES      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012
MS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007
QR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004
CR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002

Un examen de los datos tabulados de la curva ROC revela una tendencia discernible: Tanto el TPR como el FPR muestran una disminución de 1 a 0 a medida que aumenta el umbral de decisión. Dada la capacidad predictiva inherente al modelo, la FPR muestra una reducción más rápida que la TPR. Cabe destacar que el FPR alcanza el valor cero, mientras que el TPR mantiene un valor de 1. Por consiguiente, a menos que los costes relativos de los errores de tipo I y tipo II sean sustancialmente dispares, se espera que el umbral óptimo se sitúe dentro del intervalo definido por estos extremos. También es importante observar que la tabla incluye la especificidad, que es equivalente a la tasa de verdaderos negativos (True Negative Rate, TNR) y representa el complemento de la FPR (False Positive Rate).
En numerosos casos, la determinación del umbral óptimo puede lograrse mediante la inspección directa de las columnas «True Positive Rate» y «False Positive Rate». La interpretabilidad de este proceso se ve mejorada por la inclusión de tamaños de muestra objetivo y no objetivo. Cuando los costes asociados a los errores de tipo I y tipo II son aproximadamente equivalentes, el error medio sirve como una métrica de rendimiento escalar adecuada. Esta métrica, indicada como M_E en la tabla, se calcula como la media aritmética de la tasa de falsas alarmas y la tasa de fallos.

Sin embargo, en situaciones en las que los costes de estos tipos de errores difieren significativamente, la métrica de error medio pierde relevancia. La precisión, en particular, es un indicador de rendimiento crítico en diversas aplicaciones. Por lo general, la precisión de la detección del objetivo es de interés primordial. En determinados contextos, la precisión de la identificación de elementos no objetivo también puede ser pertinente. Para el objetivo de la detección precisa de objetivos, la columna denominada PREC proporciona información pertinente. Por el contrario, la columna denominada NPREC es relevante para la identificación precisa de los no objetivos.

La tabla presenta métricas de rendimiento adicionales, incluyendo la precisión (Accuracy, ACC) y la precisión equilibrada (Balanced Accuracy, B_ACC). La precisión se define como la proporción de casos clasificados correctamente, incluyendo tanto los verdaderos positivos como los verdaderos negativos, dentro del conjunto de datos total. La precisión equilibrada (Balanced Accuracy, B_ACC), calculada como la media aritmética de la sensibilidad y la especificidad, se emplea para mitigar el impacto del desequilibrio de clases, una condición caracterizada por una disparidad significativa en los tamaños de las muestras de las clases objetivo y no objetivo. Antes de abordar el área bajo la curva ROC, conviene examinar los procedimientos computacionales utilizados para generar la tabla de métricas ROC mencionada anteriormente. En concreto, se analizará el código responsable del cálculo de estas métricas relacionadas con ROC.
El código relevante está encapsulado en el archivo de encabezado roc_curves.mqh, que define una serie de funciones y la estructura de datos conf_stats. La estructura conf_stats sirve como contenedor para el almacenamiento de diversos parámetros derivados de la matriz de confusión.

//+------------------------------------------------------------------+
//|  confusion matrix stats                                          |
//+------------------------------------------------------------------+
struct conf_stats
  {
   double              tn;                //true negatives
   double              tp;                //true positives
   double              fn;                //false negatives
   double              fp;                //false positives
   double              num_targets;       //number of actual positive labels(target)
   double              num_non_targets;   //number of acutal negative labels(non targets)
   double            tp_rate;             //true positives rate - hit rate -  recall - sensitivity
   double            fp_rate;             //false positives rate - fall out - type 1 error
   double            fn_rate;             //false negatives rate - miss rate - type 2 error
   double            tn_rate;             //true negatives rate - specificity
   double            precision;           //precision - positive predictve value
   double            null_precision;      //null precision - false discovery rate
   double            prevalence;          //prevalence
   double            lr_plus;             //positive likelihood ratio
   double            lr_neg;              //negative likelihood ratio
   double            for_rate;            //false omission rate
   double            npv;                 //negative predictive value
   double            acc;                 //accuracy
   double            b_acc;               //balanced accuracy
   double            f1_score;            //f1 score
   double            mean_error;          //mean error
  };

La estructura conf_stats funciona como el parámetro principal dentro de la función roc_stats(), facilitando el almacenamiento de los resultados de la evaluación derivados de la matriz de confusión. Esta evaluación se lleva a cabo sobre un conjunto de datos que comprende etiquetas verdaderas, predicciones correspondientes y un umbral designado. Las etiquetas verdaderas se proporcionan como un vector, denominado «targets», que sirve como segundo parámetro. El tercer argumento, probas, representa el vector de probabilidades previstas o variables de decisión. 

//+------------------------------------------------------------------+
//| defines                                                          |
//+------------------------------------------------------------------+
bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0)
  {
   vector all_labels = np::unique(targets);

   if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return false;
     }
//---
   cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0;
//---
   for(ulong i = 0; i<targets.Size(); i++)
     {
      if(probas[i]>=threshold && long(targets[i]) == target_label)
         cmat.tp++;
      else
         if(probas[i]>=threshold && long(targets[i]) == non_target_label)
            cmat.fp++;
         else
            if(probas[i]<threshold && long(targets[i]) == target_label)
               cmat.fn++;
            else
               cmat.tn++;
     }
//---
   cmat.num_targets = cmat.tp+cmat.fn;
   cmat.num_non_targets = cmat.fp+cmat.tn;
//---
   cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na");
   cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na");
   cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na");
   cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na");
   cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na");
   cmat.null_precision = 1.0 - cmat.precision;
   cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na");
   cmat.npv = 1.0 - cmat.for_rate;
   cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na");
   cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na");
   cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0);
   cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na");
   cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0);
//---
   return true;
//---
  }

El parámetro umbral define el valor crítico utilizado para delimitar la pertenencia a una clase. Los dos últimos parámetros permiten especificar explícitamente las etiquetas de destino y no destino, respectivamente. La función devuelve un valor booleano, indicando una ejecución correcta con verdadero y la ocurrencia de un error con falso.

//+------------------------------------------------------------------+
//| roc table                                                        |
//+------------------------------------------------------------------+
matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0)
  {
   matrix roctable(probas.Rows(),10);

   conf_stats mts;

   vector probs = probas.Col(target_probs_col);

   if(!np::quickSort(probs,false,0,probs.Size()-1))
      return matrix::Zeros(1,1);

   for(ulong i = 0; i<roctable.Rows(); i++)
     {
      if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label))
         return matrix::Zeros(1,1);
      roctable[i][0] = mts.tp_rate;
      roctable[i][1] = mts.fp_rate;
      roctable[i][2] = mts.fn_rate;
      roctable[i][3] = mts.tn_rate;
      roctable[i][4] = mts.precision;
      roctable[i][5] = mts.null_precision;
      roctable[i][6] = mts.mean_error;
      roctable[i][7] = mts.acc;
      roctable[i][8] = mts.b_acc;
      roctable[i][9] = probs[i];
     }
//---
   return roctable;
  }

La función roc_table() genera una matriz que encapsula los datos de la curva ROC. Los parámetros de entrada incluyen un vector de etiquetas de clase verdaderas, una matriz de probabilidades previstas o variables de decisión, y un entero largo sin signo que especifica el índice de columna para la determinación de la pertenencia a una clase en matrices de varias columnas. Los dos últimos parámetros definen las etiquetas objetivo y no objetivo. En caso de error, la función devuelve una matriz 1x1 de ceros. Es imprescindible señalar que tanto roc_stats() como roc_table() están diseñadas específicamente para modelos de clasificación binaria. El incumplimiento de este requisito dará lugar a un mensaje de error.

//+------------------------------------------------------------------+
//| roc curve table display                                          |
//+------------------------------------------------------------------+
string roc_table_display(matrix &out)
  {
   string output,temp;

   if(out.Rows()>=10)
     {
      output = "TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH";
      for(ulong i = 0; i<out.Rows(); i++)
        {
         temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf",
                             out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]);
         StringAdd(output,temp);
        }
     }
   return output;
  }

La función roc_table_display() acepta un único parámetro matricial, idealmente el resultado de una invocación previa de roc_table(), y formatea los datos en una representación tabular en forma de cadena (string).


Área bajo una curva ROC

El área bajo la curva ROC (Area Under the ROC Curve, AUC) proporciona una métrica concisa y de valor único para el rendimiento del clasificador, abordando el exceso de detalle de la curva ROC completa. Mientras que la curva ROC representa visualmente la relación entre las tasas de verdaderos y falsos positivos, el AUC cuantifica la capacidad general del modelo para distinguir entre clases. Un modelo inútil, representado por una línea diagonal en el gráfico ROC, arroja un AUC de 0,5, lo que indica un rendimiento aleatorio. Por el contrario, un modelo perfecto, con una curva ROC que se ajusta a la esquina superior izquierda, alcanza un AUC de 1,0. Por lo tanto, un AUC más alto significa un mejor rendimiento del modelo. El cálculo del AUC implica determinar el área bajo la curva ROC y, debido a la variación estadística inherente a los conjuntos de datos de prueba, normalmente basta con una simple suma para obtener una estimación precisa, sin necesidad de realizar complejas integraciones numéricas.
El AUC tiene una interpretación estadística significativa: representa la probabilidad de que un clasificador asigne una clasificación más alta a una instancia positiva seleccionada al azar en comparación con una instancia negativa seleccionada al azar. Esta característica establece una equivalencia entre el AUC y la prueba de suma de rangos de Wilcoxon, también conocida como prueba U de Mann-Whitney.

La prueba de suma de rangos de Wilcoxon, un método estadístico no paramétrico, evalúa la diferencia entre dos grupos independientes sin suponer normalidad. Funciona clasificando todas las observaciones y comparando las sumas de rangos entre los grupos, evaluando así las diferencias en las medianas.

Además, el AUC está intrínsecamente vinculado al coeficiente de Gini. Concretamente, el coeficiente de Gini se calcula como el doble del área entre la línea diagonal del azar y la curva ROC. El coeficiente de Gini, una medida de la desigualdad distributiva, cuantifica el grado de dispersión dentro de una distribución, y oscila entre 0 (igualdad perfecta) y 1 (desigualdad máxima). En el contexto de la distribución de los ingresos, refleja la disparidad en los niveles de ingresos. Gráficamente, el coeficiente de Gini se define como la relación entre el área entre la curva de Lorenz y la línea de igualdad perfecta y el área bajo la línea de igualdad perfecta.
La función roc_auc(), definida en roc_curves.mqh, calcula el AUC para un problema de clasificación binaria, con la opción de limitar el cálculo a un FPR máximo específico. Toma como entrada las etiquetas de clase reales y las probabilidades previstas, junto con una etiqueta de destino opcional y un FPR máximo. Si el FPR máximo es 1,0, calcula el AUC estándar. De lo contrario, calcula la curva ROC, encuentra el punto de la curva correspondiente al FPR máximo utilizando searchsorted, interpola el TPR en ese punto y, a continuación, calcula el AUC parcial hasta ese FPR máximo utilizando la regla trapezoidal. Por último, normaliza este AUC parcial a una puntuación entre 0,5 y 1,0, lo que proporciona una medida eficaz del rendimiento del clasificador dentro del rango de FPR especificado.

//+------------------------------------------------------------------+
//|  area under the curve                                            |
//+------------------------------------------------------------------+
double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0)
  {
   vector all_labels = np::unique(true_classes);

   if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   if(max_fpr == 1.0)
     {
      vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
      return auc[0];
     }

   matrix tpr,fpr,threshs;

   if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs))
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   vector xp(1);
   xp[0] = max_fpr;
   vector stop;

   if(!np::searchsorted(fpr.Row(0),xp,true,stop))
     {
      Print(__FUNCTION__, " ", __LINE__, " searchsorted failed ");
      return EMPTY_VALUE;
     }

   vector xpts(2);
   vector ypts(2);

   xpts[0] = fpr[0][long(stop[0])-1];
   xpts[1] = fpr[0][long(stop[0])];
   ypts[0] = tpr[0][long(stop[0])-1];
   ypts[1] = tpr[0][long(stop[0])];

   vector vtpr = tpr.Row(0);
   vtpr = np::sliceVector(vtpr,0,long(stop[0]));
   vector vfpr = fpr.Row(0);
   vfpr = np::sliceVector(vfpr,0,long(stop[0]));

   if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1))
     {
      Print(__FUNCTION__, " ", __LINE__, " error  ", GetLastError());
      return EMPTY_VALUE;
     }

   vfpr[vfpr.Size()-1] = max_fpr;

   vector yint = np::interp(xp,xpts,ypts);


   vtpr[vtpr.Size()-1] = yint[0];

   double direction = 1.0;

   vector dx = np::diff(vfpr);

   if(dx[dx.ArgMin()]<0.0)
      direction = -1.0;

   double partial_auc = direction*np::trapezoid(vtpr,vfpr);

   if(partial_auc == EMPTY_VALUE)
     {
      Print(__FUNCTION__, " ", __LINE__, " trapz failed ");
      return EMPTY_VALUE;
     }

   double minarea = 0.5*(max_fpr*max_fpr);
   double maxarea = max_fpr;

   return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea));
  }

El parámetro max_fpr facilita el cálculo del área parcial bajo la curva ROC (AUC), lo que permite evaluar el rendimiento del clasificador dentro de un rango definido de valores FPR. Esta funcionalidad es especialmente relevante en escenarios en los que se hace hincapié en el rendimiento con umbrales de FPR más bajos. Además, resulta ventajoso al analizar conjuntos de datos desequilibrados, en los que la curva ROC puede verse influida de manera desproporcionada por una cantidad considerable de negativos verdaderos. El empleo de este parámetro permite realizar una evaluación centrada en la región pertinente de la curva.

Si bien las curvas ROC (Receiver Operating Characteristic) proporcionan un marco útil para la evaluación de clasificadores, su aplicación para determinar la superioridad definitiva de un clasificador requiere una consideración cuidadosa, especialmente cuando se incorpora el coste de la clasificación errónea. Aunque el AUC ofrece una métrica para evaluar la calidad del clasificador, las evaluaciones comparativas del rendimiento requieren un enfoque más matizado. Para abordar adecuadamente las consideraciones de coste, es necesario volver a la matriz de confusión fundamental.
Los paradigmas de clasificación convencionales suelen dar prioridad a la maximización de la precisión, asumiendo implícitamente que todos los errores de clasificación tienen un coste uniforme. Por el contrario, la clasificación sensible al coste reconoce los costes diferenciales asociados a los distintos tipos de errores, con el objetivo de minimizar el coste agregado de los errores en lugar de optimizar únicamente la precisión. Por ejemplo, en un clasificador diseñado para identificar acciones de inversión prometedoras, el coste de una oportunidad perdida (falso negativo) puede considerarse menos importante que el coste de un falso positivo. La asignación de costes a cada tipo de clasificación errónea da como resultado una matriz de costes. Esta matriz articula los costes asociados a diversos resultados de predicción, especificando las sanciones o pérdidas incurridas por predicciones incorrectas, como falsos positivos y falsos negativos, e incluyendo potencialmente los costes de las predicciones correctas. A continuación se muestra una matriz de confusión hipotética, acompañada de su matriz de costes correspondiente.

Matriz de costes

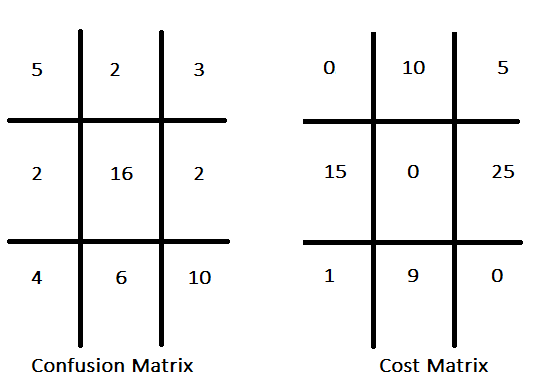
La matriz de costes suele presentar valores nulos a lo largo de su diagonal, lo que significa un coste cero asociado a las predicciones correctas, una convención que, aunque es habitual, no es obligatoria. Dada una estructura de costes definida para todos los tipos de clasificación errónea, la información contenida en la matriz de confusión puede agregarse en una métrica de rendimiento única. Un enfoque rudimentario consiste en multiplicar la frecuencia de cada tipo de clasificación errónea por su coste correspondiente y, a continuación, sumar estos productos. Sin embargo, la eficacia de esta métrica depende de que las proporciones de clases del conjunto de datos reflejen con precisión las que se encuentran en las aplicaciones del mundo real.
Una medida más sólida del rendimiento sensible al coste es el coste esperado por muestra. Esta métrica se obtiene normalizando los recuentos de muestras de la matriz de confusión por sus respectivos totales de fila, lo que da como resultado las probabilidades condicionales de las clases clasificadas dadas las clases verdaderas. A continuación, estas probabilidades se multiplican por sus costes correspondientes de la matriz de costes, y los productos se suman en cada fila, lo que da como resultado el coste esperado para un miembro de cada clase. Posteriormente, estos costes específicos de cada clase se ponderan según las proporciones esperadas de muestras en cada clase y se suman, lo que da como resultado el coste total esperado por muestra. Para estimar las proporciones de clase esperadas en escenarios reales es necesario comprender a fondo la distribución subyacente de los datos dentro del entorno de implementación. Las metodologías para esta estimación incluyen:

  • Análisis de datos históricos, en el que se examinan los registros existentes para proporcionar estimaciones fiables de las proporciones de las clases. Por ejemplo, en el diagnóstico médico, los historiales de los pacientes pueden arrojar luz sobre la prevalencia de las enfermedades.
  • Consulta con expertos en la materia, cuyos conocimientos especializados pueden refinar o validar las estimaciones obtenidas por otros medios.
  • Aplicación de técnicas de muestreo representativas cuando sea viable recopilar nuevos datos, garantizando que la muestra refleje con precisión la distribución real, especialmente en conjuntos de datos desequilibrados. El muestreo estratificado puede garantizar aún más una representación adecuada de todas las clases, incluso en casos de distribución desigual.

Las proporciones esperadas de muestras dentro de una clase son formalmente equivalentes a las probabilidades a priori. En el contexto específico de la clasificación binaria, sea
q denota la probabilidad a priori de que una muestra pertenezca a la clase objetivo. Además, defina p1 como la probabilidad de un error de tipo I (falso positivo), donde c1 representa su coste asociado, y p2 como la probabilidad de un error de tipo II (falso negativo), donde c2 representa su coste asociado. En numerosas aplicaciones, q se puede determinar mediante métodos teóricos o empíricos, y los costes c1 y c2 se conocen con precisión o con una aproximación razonable. Por consiguiente, estas tres cantidades pueden tratarse como parámetros fijos. Las probabilidades de error p1 y p2 están determinadas por el umbral de clasificación. El coste previsto se expresa mediante la siguiente ecuación.

Fórmula de costes

Reorganizando esta ecuación se obtiene:

Fórmula de coste reorganizada

Demostrar una relación lineal entre p1 y p2 para cualquier coste esperado dado. Cuando esta relación lineal se representa gráficamente en la curva ROC, su pendiente viene determinada por la probabilidad a priori q y la relación de costes c2/c1. La variación del coste previsto genera una familia de líneas paralelas, en la que las líneas situadas más abajo y a la derecha indican costes más elevados. La intersección de esta línea con la curva ROC en dos puntos indica dos umbrales que producen costes equivalentes, aunque subóptimos. Las líneas situadas completamente por encima y a la izquierda de la curva ROC representan un rendimiento inalcanzable para el modelo. La línea tangente a la curva ROC representa el coste óptimo alcanzable.
Este análisis subraya que el AUC no proporciona necesariamente una medida definitiva del rendimiento práctico de un modelo de clasificación. Si bien el AUC es una métrica de calidad válida en términos generales, su utilidad se ve reducida cuando se tienen en cuenta los costes operativos, ya que puede dar lugar a conclusiones erróneas en aplicaciones sensibles al coste.


Problemas de decisión con más de dos clases

Ampliar el marco de la curva ROC a la clasificación multiclase requiere la adopción de estrategias de adaptación específicas. Se emplean principalmente dos metodologías: el enfoque «uno contra el resto» (OvR), también conocido como «uno contra todos» (OvA), y el enfoque «uno contra uno» (OvO). La estrategia OvR transforma el problema multiclase en múltiples tareas de clasificación binaria al tratar cada clase como la clase positiva frente al conjunto de clases restantes, lo que da como resultado n curvas ROC para n clases. Por el contrario, el método OvO construye problemas de clasificación binaria para todos los pares de clases posibles, lo que da como resultado n(n-1)/2 curvas ROC.

Para agregar las métricas de rendimiento derivadas de estas clasificaciones binarias, se utilizan técnicas de promediado. El micropromedio calcula el TPR y el FPR globales teniendo en cuenta todas las instancias de todas las clases, asignando así el mismo peso a cada instancia. Por otro lado, el promedio macro calcula el TPR y el FPR para cada clase de forma independiente y luego los promedia, asignando así el mismo peso a cada clase, un método especialmente útil cuando el rendimiento específico de cada clase es primordial. Por consiguiente, la interpretación de las curvas ROC multiclase depende de la estrategia de descomposición elegida (OvR u OvO) y del método de promediado (micro o macro), ya que estas elecciones influyen significativamente en la evaluación del rendimiento resultante.


Funciones integradas de MQL5 para curvas ROC y AUC

En MQL5, el cálculo de las curvas ROC (Receiver Operating Characteristic) y el área bajo la curva (AUC) se facilita mediante una funcionalidad específica.

El método vectorial ReceiverOperatingCharacteristic() se emplea para generar los valores necesarios para la visualización de la curva ROC. Este método opera sobre un vector que representa las etiquetas de clase verdaderas. El primer argumento es una matriz de probabilidades o valores de decisión, estructurada con columnas que corresponden al número de clases. El segundo argumento, una variable de la enumeración ENUM_AVERAGE_MODE, especifica la metodología de cálculo del promedio. Cabe destacar que esta función solo admite AVERAGE_NONE, AVERAGE_BINARY y AVERAGE_MICRO. Tras la ejecución satisfactoria, la tasa de falsos positivos (FPR), la tasa de verdaderos positivos (TPR) y los umbrales asociados se escriben en las matrices designadas, los tres últimos parámetros. El método devuelve un valor booleano que indica si la ejecución se ha realizado correctamente.

El cálculo del AUC se realiza mediante el método vectorial ClassificationScore(). Al igual que el método ROC, se invoca sobre el vector de etiquetas de clase verdaderas y requiere una matriz de probabilidades previstas o valores de decisión.. El segundo parámetro, una enumeración ENUM_CLASSIFICATION_METRIC, debe establecerse en CLASSIFICATION_ROC_AUC para especificar el cálculo del AUC. A diferencia del método ROC, esta función admite todos los valores de ENUM_AVERAGE_MODE. El método devuelve un vector de áreas calculadas, cuya cardinalidad depende del modo de promedio y del número de clases presentes en el conjunto de datos.
Para dilucidar el impacto de los distintos modos de promedio, se desarrolló el script ROC_Demo.mq5. Este script utiliza el conjunto de datos Iris y un modelo de regresión logística para abordar problemas de clasificación binaria o multiclase configurables por el usuario. A continuación se proporciona el código completo del script.

//+------------------------------------------------------------------+
//|                                                     ROC_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<logistic.mqh>
#include<ErrorDescription.mqh>
#include<Generic/SortedSet.mqh>
//---
enum CLASSIFICATION_TYPE
  {
   BINARY_CLASS = 0,//binary classification problem
   MULITI_CLASS//multiclass classification problem
  };
//--- input parameters
input double   Train_Test_Split = 0.5;
input int      Random_Seed = 125;
input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS;
input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj());
//---
   matrix data = np::readcsv("iris.csv");
   data = np::sliceMatrixCols(data,1);
//---
   if(classification_problem == BINARY_CLASS)
      data = np::sliceMatrixRows(data,0,100);
//---
   ulong rindices[],trainset[],testset[];
   np::arange(rindices,int(data.Rows()));
//---
//---
   if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset))
     {
      Print(__LINE__, "  error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   CSortedSet<ulong> test_set(rindices);
//---
   test_set.ExceptWith(trainset);
//---
   test_set.CopyTo(testset);
//---
   matrix testdata = np::selectMatrixRows(data,testset);
   matrix test_predictors = np::sliceMatrixCols(testdata,0,4);
   vector test_targets = testdata.Col(4);
   matrix traindata = np::selectMatrixRows(data,trainset);
   matrix train_preditors = np::sliceMatrixCols(traindata,0,4);
   vector train_targets = traindata.Col(4);
//---
   logistic::Clogit logit;
//--
   if(!logit.fit(train_preditors,train_targets))
     {
      Print(" error training logistic model ");
      return;
     }
//---
   matrix y_probas = logit.probas(test_predictors);
   vector y_preds = logit.predict(test_predictors);
//---
   vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode);
//---
   if(auc.Size()>0)
      Print(" AUC ", auc);
   else
      Print(" AUC error ", ErrorDescription(GetLastError()));
//---
   matrix fpr,tpr,threshs;
   if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs))
     {
      Print(" ROC error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   string legend;
   for(ulong i = 0; i<auc.Size(); i++)
     {
      string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]);
      StringAdd(legend,temp);
     }

   CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500);
   if(CheckPointer(roc)!=POINTER_INVALID)
     {
      Sleep(7000);
      roc.Destroy();
      delete roc;
      ChartRedraw();
     }
  }
//+------------------------------------------------------------------+

Inicialmente, se examina un problema de clasificación binaria, con el modo de promedio establecido en AVERAGE_BINARY. Este modo calcula la curva ROC y el AUC bajo el supuesto de que la clase objetivo está etiquetada como 1, adhiriéndose al paradigma fundamental objetivo/no objetivo inherente a la generación de la curva ROC. El resultado obtenido tras la ejecución del script con estas configuraciones demuestra que el vector del valor AUC contiene un único elemento. Además, las matrices FPR, TPR y de umbral comprenden cada una una sola fila.

Salida del script de demostración ROC de clasificación binaria

MK      0       12:45:28.930    ROC_Demo (Crash 1000 Index,M5)   AUC [1]

Para examinar la curva ROC y el AUC asociado para clases objetivo distintas de la etiqueta 1, el modo de promedio debe establecerse en AVERAGE_NONE. En este modo, las funciones ReceiverOperatingCharacteristic() y ClassificationScore() evalúan cada clase de forma independiente como objetivo, proporcionando los resultados correspondientes. Al ejecutar el script con AVERAGE_NONE y un problema de clasificación binaria, se obtiene el siguiente resultado. En este caso, el gráfico ROC muestra dos curvas, que representan los gráficos de las filas respectivas en las matrices FPR y TPR. También se calculan dos valores AUC.

Demostración ROC de clasificación binaria: Sin promediado

CK      0       16:42:43.249    ROC_Demo (Crash 1000 Index,M5)   AUC [1,1]

Los resultados se presentan en correspondencia con el orden de las etiquetas de clase. Por ejemplo, en el problema de clasificación binaria descrito en el script mencionado anteriormente, donde las etiquetas son 0 y 1, las primeras filas de las matrices TPR, FPR y umbral representan los valores de la curva ROC cuando la etiqueta 0 se considera la clase objetivo, mientras que las segundas filas se refieren a la etiqueta 1 como objetivo. Esta convención de ordenación también se aplica a los valores AUC. Cabe señalar que este formato de resultados es coherente en todas las estadísticas ROC calculadas a partir de conjuntos de datos multiclase. En escenarios de clasificación binaria, el uso de opciones de promedio distintas de AVERAGE_NONE y AVERAGE_BINARY invoca métodos computacionales que se corresponden con el manejo de conjuntos de datos multiclase. Por el contrario, en la clasificación multiclase, AVERAGE_BINARY provoca un error. Sin embargo, AVERAGE_MICRO, AVERAGE_MACRO y AVERAGE_WEIGHTED producen un único valor AUC agregado.

Demostración ROC multiclase: Sin promediar

LL      0       17:27:13.673    ROC_Demo (Crash 1000 Index,M5)   AUC [1,0.9965694682675815,0.9969135802469137]

El modo de promedio AVERAGE_MICRO calcula las curvas ROC y el AUC de forma global tratando cada elemento de la matriz de clases verdaderas codificadas como «one-hot» como una etiqueta distinta. Este enfoque transforma el problema multiclase en un problema de clasificación binaria mediante la codificación inicial «one-hot» de las etiquetas de clase verdaderas, generando una matriz con columnas correspondientes al número de clases. Esta matriz, junto con la matriz de valores de decisión previstos o probabilidades, se aplana entonces en una estructura de una sola columna. Los cálculos posteriores de la curva ROC y el AUC se realizan en estos contenedores aplanados. Esta metodología genera métricas de rendimiento exhaustivas que abarcan todas las clases, asignando la misma ponderación a cada instancia. Esto resulta especialmente ventajoso en situaciones con un desequilibrio significativo entre clases, ya que mitiga el sesgo hacia la clase mayoritaria. Los resultados empíricos del script de demostración ilustran este comportamiento.

Demostración ROC multiclase: Micropromedio

RG      0       17:26:51.955    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9984000000000001]

El modo de promediado AVERAGE_MACRO adopta una estrategia distinta para abordar el desequilibrio de clases. Cada clase se evalúa de forma independiente, calculando el AUC en función de sus respectivas probabilidades de clase. El AUC final se obtiene entonces como la media aritmética de estos valores AUC individuales. Cabe destacar que la documentación de MQL5 indica que AVERAGE_MACRO no es compatible con el método ReceiverOperatingCharacteristic(). El método ClassificationScore() implementa la técnica OvR para el cálculo del AUC en conjuntos de datos multiclase. La ejecución del script con AVERAGE_MACRO confirma el cálculo correcto del AUC, mientras que la generación de la curva ROC falla como se esperaba.

ER      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   AUC [0.997827682838166]
NF      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

El modo de promedio AVERAGE_WEIGHTED funciona de manera análoga a AVERAGE_MACRO, excepto por el paso final de agregación. En lugar de una simple media aritmética, se calcula una media ponderada, en la que las ponderaciones se determinan mediante la distribución de clases de las etiquetas de clase verdaderas. Este enfoque arroja un valor AUC final que tiene en cuenta las clases dominantes dentro del conjunto de datos. Al igual que AVERAGE_MACRO, ReceiverOperatingCharacteristic() no admite AVERAGE_WEIGHTED. La salida del script ejemplifica este comportamiento.

IN      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9978825995807129]
HO      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function


Conclusión

Las curvas ROC son herramientas eficaces para la visualización y evaluación de clasificadores. Ofrecen una evaluación más completa del rendimiento de la clasificación en comparación con métricas escalares como la precisión, la tasa de error o el coste del error. Al desvincular el rendimiento del clasificador del sesgo de clase y los costes de error, ofrecen ventajas sobre otras metodologías de evaluación alternativas, incluidas las curvas de precisión y recuperación. Sin embargo, al igual que con cualquier métrica de evaluación, la aplicación juiciosa de los gráficos ROC requiere un conocimiento profundo de sus características y limitaciones inherentes. Se prevé que este artículo contribuya a ampliar los conocimientos generales sobre las curvas ROC y fomente la adopción de prácticas de evaluación mejoradas dentro de la comunidad.


Nombre del archivo 
Descripción del archivo
MQL5/Scripts/ROC_Demo.mq5 El script utilizado muestra las funciones integradas de MQL5 relacionadas con las curvas ROC.
MQL5/Scripts/ ROC_curves_table_demo.mq5 Script que muestra la generación de diversas métricas de rendimiento basadas en ROC.
MQL5/Include/logisitc.mqh
Archivo de encabezado que contiene la definición de la clase Clogit que implementa la regresión logística.
MQL5/Include/roc_curves.mqh
Encabezado de funciones personalizadas que implementan diversas utilidades para la evaluación del rendimiento de la clasificación binaria.
MQL5/Include/np.mqh
Archivo de cabecera de diversas funciones de utilidad para vectores y matrices.
MQL5/Files/iris.csv Archivo CSV del conjunto de datos sobre el iris.

Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/17390

Archivos adjuntos |
Descargar ZIP
iris.csv (3.29 KB)
np.mqh (90.9 KB)
logistic.mqh (16.16 KB)
roc_curves.mqh (8.92 KB)
ROC_curves_table_demo.mq5 (2.81 KB)
ROC_Demo.mq5 (3.56 KB)
Mql5.zip (22.86 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Análisis de múltiples símbolos con Python y MQL5 (Parte 3): Tipos de cambio triangulares Análisis de múltiples símbolos con Python y MQL5 (Parte 3): Tipos de cambio triangulares
Los operadores suelen enfrentarse a pérdidas por señales falsas, mientras que esperar a la confirmación puede llevar a perder oportunidades. Este artículo presenta una estrategia comercial triangular que utiliza el precio de la plata en dólares (XAGUSD) y euros (XAGEUR), junto con el tipo de cambio EURUSD, para filtrar el ruido. Al aprovechar las relaciones entre mercados, los operadores pueden descubrir el sentimiento oculto y perfeccionar sus entradas en tiempo real.
Aplicación de la teoría de juegos a algoritmos comerciales Aplicación de la teoría de juegos a algoritmos comerciales
Hoy crearemos un asesor comercial adaptativo de autoaprendizaje basado en DQN de aprendizaje automático, con inferencia causal multivariante, que negociará con éxito simultáneamente en 7 pares de divisas, con agentes de diferentes pares intercambiando información entre sí.
Particularidades del trabajo con números del tipo double en MQL4 Particularidades del trabajo con números del tipo double en MQL4
En estos apuntes hemos reunido consejos para resolver los errores más frecuentes al trabajar con números del tipo double en los programas en MQL4.
Arbitraje de swaps en Forex: Reunimos un portafolio sintético y creamos un flujo de swaps estable Arbitraje de swaps en Forex: Reunimos un portafolio sintético y creamos un flujo de swaps estable
¿Quiere saber cómo aprovechar los spreads de los tipos de interés? En este artículo, veremos cómo usar el arbitraje de swaps en Forex para generar unos ingresos constantes cada noche construyendo un portafolio resistente a las fluctuaciones del mercado.