Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)

Introducción

El espacio geométrico hiperbólico es capaz de representar estructuras discretas arborescentes o jerárquicas que encuentran aplicación en diversos problemas de aprendizaje de grafos. También tiene un potencial considerable para resolver el problema de la anisotropía estructural de espacios no euclidianos en procesos de difusión latente de grafos. La geometría hiperbólica combina las medidas angulares y radiales de las coordenadas polares, ofreciendo a las medidas geométricas una semántica física y una interpretabilidad.

Y en este contexto, el framework HypDiff supone un método mejorado para crear ruido gaussiano hiperbólico que resuelva el problema del fallo aditivo de las distribuciones gaussianas en el espacio hiperbólico. Para preservar la estructura local de los grafos, los autores del framework introdujeron restricciones geométricas de similitud angular aplicadas en el proceso de difusión anisotrópica.

A continuación le mostramos la visualización del framework realizada por el autor.

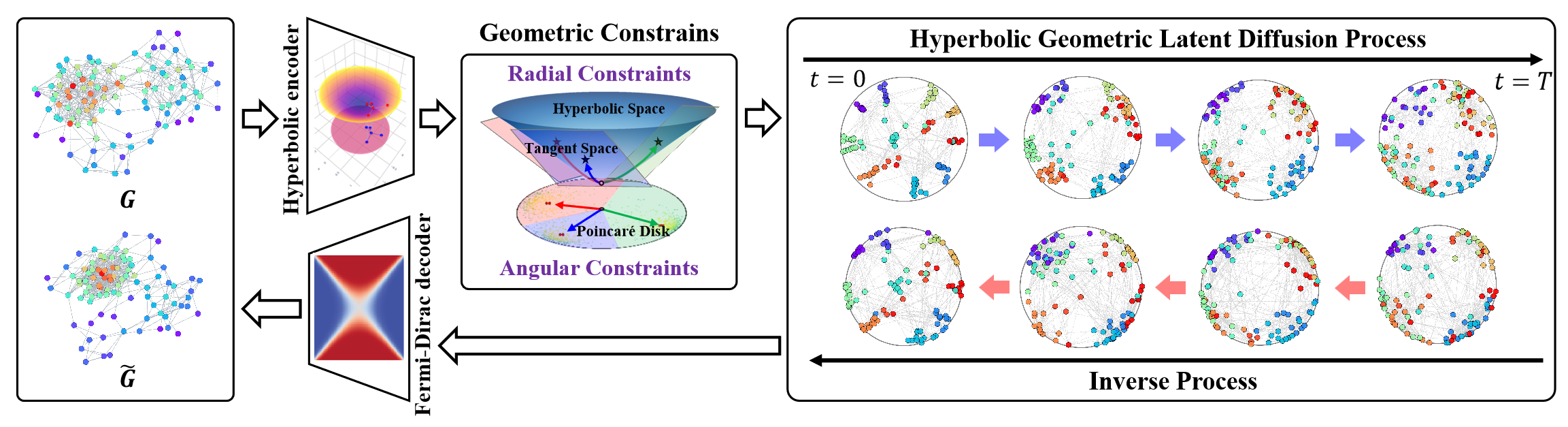
En el artículo anterior, comenzamos a trabajar en la implementación de los enfoques propuestos mediante MQL5. Sin embargo, el volumen de trabajo resultó demasiado grande, por lo que solo pudimos analizar los bloques de implementación en el lado del programa OpenCL. En este artículo continuaremos el trabajo iniciado, y llevaremos la aplicación del framework HypDiff a su conclusión lógica. No obstante, en nuestra implementación, nos desviaremos en ciertos momentos respecto al algoritmo del autor. Discutiremos dichas desviaciones durante la construcción del algoritmo.

1. Proyección de los datos en un espacio hiperbólico

Comenzaremos nuestro trabajo en el lado del programa OpenCL construyendo los kernels de pasada directa e inversa de la proyección de los datos de origen en el espacio hiperbólico (HyperProjection y HyperProjectionGrad respectivamente). También comenzaremos la implementación de los enfoques del framework HypDiff en el lado del programa principal mediante la construcción de algoritmos para esta funcionalidad. Para ello, crearemos una nueva clase CNeuronHyperProjection, cuya estructura le mostramos a continuación.

class CNeuronHyperProjection   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronHyperProjection(void) : iWindow(-1), iUnits(-1) {};
                    ~CNeuronHyperProjection(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperProjection;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
  };

En la estructura presentada, vemos la declaración de dos variables internas que sirven para registrar las constantes que definen la arquitectura del objeto, así como el conjunto ya familiar de métodos redefinidos. Pero tenga en cuenta que el método updateInputWeights para actualizar los parámetros del modelo está representado por un "stub" positivo. Y esto no es casualidad. Al fin y al cabo, los kernels de pasada directa e inversa de proyección de datos que implementamos ejecutan un algoritmo prescrito explícitamente y carente de parámetros entrenables. Sin embargo, la presencia de un método de actualización de parámetros resultará necesaria para que nuestro modelo funcione correctamente. Y nos veremos obligados a redefinir el método especificado con un retorno constante de un resultado positivo.

La ausencia de declaraciones de nuevos objetos internos nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de los objetos heredados y de las variables internas declaradas se realizará en el método Init.

El algoritmo del método de inicialización es bastante simple. En los parámetros del método, como es habitual, obtendremos las constantes básicas que nos permiten identificar unívocamente la arquitectura del objeto creado.

bool CNeuronHyperProjection::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                  uint window, uint units_count, 
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + 1)*units_count, optimization_type, batch))
      return false;
   iWindow = window;
   iUnits = units_count;
//---
   return true;
  }

Y en el cuerpo del método llamaremos directamente al método homónimo de la clase padre, transmitiéndole la parte necesaria de los parámetros recibidos. Como sabe, el cuerpo de la clase padre ya implementa los algoritmos para controlar los parámetros recibidos y la inicialización de los objetos heredados. Y solo necesitaremos comprobar el resultado lógico de la ejecución del método de la clase padre. Después guardaremos las constantes de arquitectura de objetos obtenidas del programa externo en las variables internas.

Y ya está. No hemos declarado ningún nuevo objeto interno, y los heredados se inicializarán en el método de la clase padre. Todo lo que tendremos que hacer es devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.

Le sugiero que se familiarice por su cuenta con los métodos de pasada directa e inversa de esta clase. Estos no son más que "envoltorios" para llamar a los correspondientes kernels de los programas OpenCL. Ya hemos descrito estos métodos muchas veces en nuestra serie de artículos, así que la aplicación de sus algoritmos no le planteará ninguna duda. Encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.

2. Proyección sobre planos tangentes

Tras proyectar los datos de origen en el espacio hiperbólico, el framework HypDiff prevé la construcción del Codificador de generación de incorporaciones de nodos hiperbólicos. Tenemos previsto abarcar esta funcionalidad con las herramientas ya disponibles en nuestra biblioteca. Las incorporaciones resultantes se proyectarán en planos tangentes correspondientes a los k centroides. Ya implementamos los algoritmos de proyección sobre tangentes y distribución de gradiente inverso en el lado del programa OpenCL en los kernels LogMap y LogMapGrad, respectivamente. Pero la cuestión de los centroides sigue abierta.

Aquí hay que decir que los autores del framework HypDiff determinaron los centroides a partir de la muestra de entrenamiento en la fase de preparación de datos. Desgraciadamente, este planteamiento resulta inaceptable para nosotros. Y no se trata solo de que el proceso requiera mucho trabajo. Este enfoque no resulta adecuado para analizar en un mercado dinámico de instrumentos financieros. Después de todo, en el framework del análisis técnico del movimiento de los precios a veces se presta más atención a los patrones formados que a los valores específicos del valor del instrumento. Y diferentes centroides pueden ser relevantes para situaciones de mercado similares registradas en distintos intervalos de tiempo. De esto podemos concluir que necesitaremos un modelo dinámico de adaptación o generación para los centroides y sus parámetros. En nuestra aplicación, hemos decidido crear un modelo de generación de centroides basado en la incorporación de los datos de origen. Así que hemos decidido combinar los procesos de generación de centroides y proyección de datos sobre los planos tangentes correspondientes dentro de la clase CNeuronHyperboloids. Resumiremos su estructura a continuación.

class CNeuronHyperboloids  :  public CNeuronBaseOCL
  {
protected:
   uint              iWindows;
   uint              iUnits;
   uint              iCentroids;
   //---
   CLayer            cHyperCentroids;
   CLayer            cHyperCurvatures;
   //---
   int               iProducts;
   int               iDistances;
   int               iNormes;
   //---
   virtual bool      LogMap(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                            CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   virtual bool      LogMapGrad(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                                CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronHyperboloids(void) : iWindows(0), iUnits(0), iCentroids(0), 
                                                 iProducts(-1), iDistances(-1), iNormes(-1) {};
                    ~CNeuronHyperboloids(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperboloids;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual void      TrainMode(bool flag);
  };

En la estructura presentada de la nueva clase podemos notar la declaración de 2 arrays dinámicos y 6 variables divididas en 2 grupos.

Los arrays dinámicos están diseñados para registrar los punteros a los objetos de las capas neuronales de los dos modelos anidados. Sí, en nuestra implementación hemos decidido dividir la funcionalidad de generación de parámetros del centroide en 2 modelos. El primer modelo se encargará de generar las coordenadas del centroide en el espacio hiperbólico. Y el segundo devolverá los parámetros de curvatura espacial en los puntos correspondientes.

La división de las variables internas en 2 grupos también tiene una explicación lógica. En un grupo hemos combinado los parámetros de arquitectura del objeto creado que recibiremos de un programa externo. Mientras que el segundo bloque contendrá las variables necesarias para escribir los punteros a los búferes para escribir los valores intermedios que crearemos solo en el contexto de OpenCL sin copiar los datos a la RAM del dispositivo.

Declararemos todos los objetos internos estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos. La inicialización de todos los objetos heredados y declarados se realizará en el método Init.

bool CNeuronHyperboloids::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                               uint window, uint units_count, uint centroids,
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window*units_count*centroids, optimization_type, batch))
      return false;

En los parámetros del método, como es habitual, obtendremos una serie de constantes que nos permitirán interpretar sin ambigüedades la arquitectura del objeto creado. En este caso serán:

• units_count – número de elementos de la secuencia analizada;
• window – tamaño del vector de incorporación de un elemento de la secuencia analizada;
• centroids – número de centroides que genera el modelo para el análisis exhaustivo de los datos de origen.

En el cuerpo del método llamaremos al método homónimo de la clase padre para inicializar los objetos y variables heredados. Y aquí cabe destacar que, a diferencia del algoritmo HypDiff del autor, en nuestra implementación no separaremos los elementos de la secuencia original según su pertenencia a uno u otro centroide. En su lugar, para proporcionar al modelo toda la información posible, generaremos proyecciones de la secuencia completa sobre todos los planos tangentes, lo que naturalmente aumentará el volumen del tensor resultante de forma proporcional al número de centroides generados. Por consiguiente, al llamar al método de inicialización de la clase padre, especificaremos el producto de las tres constantes recibidas del programa externo como el tamaño de la capa a crear.

Y tras ejecutar con éxito las operaciones del método de la clase padre, que conoceremos por el resultado lógico de su funcionamiento, guardaremos las constantes obtenidas en las variables internas.

   iWindows = window;
   iUnits = units_count;
   iCentroids = centroids;

En el siguiente paso, prepararemos nuestros arrays dinámicos para registrar los punteros a los objetos de los modelos de generación de parámetros de centroides.

   cHyperCentroids.Clear();
   cHyperCurvatures.Clear();
   cHyperCentroids.SetOpenCL(OpenCL);
   cHyperCurvatures.SetOpenCL(OpenCL);

Y pasaremos al trabajo directo de inicialización de los objetos modelo. En primer lugar, inicializaremos el modelo de generación de coordenadas del centroide.

Aquí partiremos de siguiente base: construiremos un modelo lineal que, tras analizar el conjunto de datos inicial, retornará un paquete de coordenadas para los centroides reales. Sin embargo, el uso de capas totalmente conectadas para este fin provocará la creación de un gran número de parámetros entrenados y un mayor número de cálculos. El uso de capas de convolución nos permitirá reducir tanto el número de parámetros a entrenar como el volumen de los cálculos. En este punto, la aplicación de capas de convolución dentro de secuencias unitarias separadas parece bastante lógica. Para aplicar dicho enfoque, necesitaremos transponer previamente los datos de origen obtenidos,

   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 0, OpenCL, iUnits, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction(None);

y luego añadir una capa de convolución de reducción de la dimensionalidad de las secuencias unitarias.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 1, OpenCL, iUnits, iUnits, iCentroids, iWindows, 1, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);

Aquí utilizaremos un conjunto de parámetros para todas las secuencias unitarias, mientras que en la salida de la capa, utilizaremos la tangente hiperbólica como función de activación para crear no linealidad.

A continuación, añadiremos otra capa de convolución sin función de activación, pero esta vez contendrá parámetros entrenables ya separados para cada secuencia unitaria.

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 2, OpenCL, iCentroids, iCentroids, iCentroids, 1, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Así, las dos capas de convolución sucesivas nos permitirán crear un MLP único para cada fila unitaria de la secuencia original. Cada MLP de este tipo nos dará una coordenada para el número requerido de centroides. En otras palabras, así crearemos un MLP para cada dimensión del espacio de coordenadas, que en conjunto generará para nosotros las coordenadas de un número determinado de centroides.

Y ahora solo nos quedará devolver a la representación original las coordenadas del centroide obtenidas. Para ello, añadiremos otra capa de transposición de datos.

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 3, OpenCL, iWindows, iCentroids, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

A continuación crearemos los objetos del segundo modelo, que nos darán los parámetros de curvatura del espacio hiperbólico en los puntos centroides. Luego determinaremos los parámetros de curvatura basándonos en las coordenadas del centroide generadas. Y aquí resultará bastante lógico que el parámetro de curvatura dependa solo de coordenadas específicas. En efecto, supondremos que la representación del espacio hiperbólico utilizada por el modelo se adquirirá durante el entrenamiento y se reflejará en sus parámetros entrenados. Por lo tanto, ya no utilizaremos capas de transposición en el modelo de parametrización de la curvatura. Simplemente crearemos un MLP único para cada centroide partiendo de 2 capas de convolución consecutivas.

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 4, OpenCL, iWindows, iWindows, iWindows, iCentroids, 1, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 5, OpenCL, iWindows, iWindows, 1, 1, iCentroids, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Aquí también utilizaremos una tangente hiperbólica para crear no linealidad entre las capas del modelo.

En este paso, finalizaremos la inicialización de los objetos de modelo para generar los parámetros del centroide. Y solo nos quedará preparar los objetos necesarios para ofrecer servicio a los kernels de proyección de datos sobre planos tangentes y las distribuciones de los gradientes de error. Aquí quiero recordarle que mientras construíamos los algoritmos de los kernels anteriores, hablamos de crear búferes de almacenamiento temporal para los resultados de las operaciones intermedias. Se trata de 3 búferes de datos, cada uno de los cuales contendrá un elemento para los pares "Centroide - Elemento de secuencia".

El búfer de datos solo se utilizará para transferir la información del kernel de pasada directa al kernel de distribución del gradiente de error. Esto significa que su creación solo se justificará en el contexto OpenCL. En otras palabras, la creación de los búferes especificados en la RAM del dispositivo y las operaciones de copiado de datos entre la memoria contextual OpenCL y la memoria principal serán innecesarias. Tampoco será necesario registrar estos datos al guardar los parámetros del modelo, ya que se actualizarán en cada pasada directa. Por lo tanto, en el lado del programa principal, solo crearemos las variables necesarias para almacenar los punteros a los búferes de datos especificados.

Pero todavía tendremos que crearlos en el lado del contexto OpenCL. Para ello, primero determinaremos el tamaño necesario de los búferes de datos. Como ya hemos dicho, los 3 búferes tendrán el mismo tamaño.

   uint size = iCentroids * iUnits * sizeof(float);
   iProducts = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iProducts < 0)
      return false;
   iDistances = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iDistances < 0)
      return false;
   iNormes = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iNormes < 0)
      return false;
//---
   return true;
  }

A continuación, crearemos los búferes de datos en la memoria del contexto OpenCL guardando los punteros obtenidos en las variables correspondientes. Al mismo tiempo, no nos olvidaremos de comprobar la validez del puntero obtenido.

Y después de inicializar todos los objetos, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

El siguiente paso en nuestro trabajo consistirá en construir los algoritmos de pasada directa para nuestra clase CNeuronHyperboloids. Aquí debemos decir que los métodos LogMap y LogMapGrad suponen envoltorios para llamar a los kernels homónimos. Y dejaremos que el lector los estudie por su cuenta.

Vamos a analizar el método feedForward. En los parámetros de este método, obtendremos el puntero del objeto de capa neuronal que contiene el tensor de datos de origen.

bool CNeuronHyperboloids::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *prev = NeuronOCL;
   CNeuronBaseOCL *centroids = NULL;
   CNeuronBaseOCL *curvatures = NULL;

Y en el cuerpo del método haremos primero un pequeño trabajo preparatorio: declararemos las variables locales para almacenar temporalmente los punteros a los objetos de las capas de neuronas internas. A uno de ellos le transmitiremos el puntero obtenido al objeto de datos fuente. Dejaremos los otros dos vacíos por ahora.

Tenga en cuenta que en esta fase no comprobaremos la relevancia del puntero resultante al objeto de datos fuente. No tenemos previsto acceder directamente a los búferes de este objeto dentro de las operaciones del método actual. Por lo tanto, dicho control sería innecesario.

A continuación, tendremos que generar las coordenadas del centroide para el conjunto actual de datos de entrada. Para ello, organizaremos un ciclo de enumeración de objetos del modelo interno correspondiente.

//--- Centroids
   for(int i = 0; i < cHyperCentroids.Total(); i++)
     {
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.FeedForward(prev))
         return false;
      prev = centroids;
     }

En el cuerpo del ciclo, tomaremos uno a uno los punteros a los objetos de la capa neuronal y comprobaremos si son válidos. Después llamaremos al método homónimo de pasada directa del objeto extraído transmitiéndole como dato inicial el puntero de la variable local correspondiente. Una vez que el método de pasada directa de la capa interna tenga éxito, se convertirá en la fuente de datos de entrada para la capa posterior del modelo. Por lo tanto, escribiremos su puntero en la variable local de los datos de origen.

Tenga en cuenta que inicialmente se escribía en la variable local el puntero al objeto de datos fuente recibido del programa externo. Por lo tanto, en la primera iteración de nuestro ciclo, lo hemos utilizado como datos de entrada. Y esto significa que la comprobación de la relevancia del puntero al objeto recibido del programa externo se realizaba como parte de la ejecución de las operaciones del método de pasada directa de la capa del modelo interno. De este modo, se cumplirán todos los puntos de control y se respetará el flujo de información del objeto de datos de origen.

Organizaremos un ciclo similar para determinar los parámetros de curvatura del hiperespacio en los puntos centroides. Y aquí cabe destacar que una vez finalizadas las iteraciones del ciclo anterior, las variables locales prev y centroids contendrán un puntero al mismo objeto de la última capa del modelo de generación de coordenadas centroides. Y puesto que planeamos determinar los parámetros de curvatura usando coordenadas centroides, podemos seguir trabajando con seguridad con la variable prev.

//--- Curvatures
   for(int i = 0; i < cHyperCurvatures.Total(); i++)
     {
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.FeedForward(prev))
         return false;
      prev = curvatures;
     }

Y tras obtener con éxito todos los parámetros necesarios de los centroides, podremos realizar la proyección de los datos iniciales sobre los planos tangentes correspondientes. Para ello, llamaremos al método de envoltorio del kernel LogMap creado en el artículo anterior.

   if(!LogMap(NeuronOCL, centroids, curvatures, AsObject()))
      return false;
//---
   return true;
  }

Tenga en cuenta que, como objeto de destino del resultado, transmitiremos el puntero al objeto actual. Esto nos permitirá almacenar los resultados de las operaciones en los búferes de las interfaces de nuestra clase, a los que accederán las siguientes capas neuronales de nuestro modelo.

Todo lo que deberemos hacer es retornar el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método de pasada directa.

Después de construir los métodos de pasada directa, pasaremos a trabajar en los algoritmos de pasada inversa. Y aquí le propongo considerar el algoritmo del método de distribución del gradiente de error calcInputGradients, mientras que el método de actualización de los parámetros del modelo updateInputWeights se dejará para el estudio independiente por parte del lector.

Como es habitual, en los parámetros del método calcInputGradients de distribución del gradiente de error obtendremos el puntero al objeto de la capa anterior, en cuyo búfer tendremos que pasar el gradiente de error según la influencia de los datos iniciales en el resultado final del modelo.

bool CNeuronHyperboloids::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Y esta vez comprobaremos directamente si el puntero obtenido es correcto. Al fin y al cabo, si obtenemos un puntero incorrecto, todas las operaciones posteriores carecerán inmediatamente de sentido.

Asimismo, al igual que ocurre con la pasada directa, declararemos las variables locales para almacenar temporalmente los punteros a los objetos internos del modelo. Solo que esta vez, extraeremos directamente los punteros a las últimas capas de los modelos internos.  

   CObject *next = NULL;
   CNeuronBaseOCL *centroids = cHyperCentroids[-1];
   CNeuronBaseOCL *curvatures = cHyperCurvatures[-1];

A continuación, llamaremos al método de envoltorio del kernel de distribución del gradiente mediante las operaciones de proyección de los datos de origen en planos tangentes.

   if(!LogMapGrad(prevLayer, centroids, curvatures, AsObject()))
      return false;

Y luego distribuiremos el gradiente de error sobre el modelo interno de determinación de la curvatura del hiperespacio en los puntos centroides, creando un ciclo de pasada inversa de las capas neuronales del modelo.

//--- Curvatures
   for(int i = cHyperCurvatures.Total() - 2; i >= 0; i--)
     {
      next = curvatures;
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.calcHiddenGradients(next))
         return false;
     }

Y después deberemos transferir el gradiente de error del modelo de determinación de la curvatura al modelo de generación de coordenadas centroides. Pero aquí observamos que el búfer de la última capa del modelo de generación de coordenadas centroides ya tiene un gradiente de error procedente de las operaciones de proyección de datos sobre planos tangentes. Y resultará deseable que mantengamos los valores existentes. Como es habitual, en estos casos recurriremos a la sustitución de los punteros por búferes de datos. Primero almacenaremos en una variable local el puntero actual al búfer de gradiente de error de la última capa del modelo de generación de coordenadas centroides y, de ser necesario, ajustaremos los valores según la derivada de la función de activación de la capa neuronal.

   CBufferFloat *temp = centroids.getGradient();
   if(centroids.Activation()!=None)
      if(!DeActivation(centroids.getOutput(),temp,temp,centroids.Activation()))
        return false;
   if(!centroids.SetGradient(centroids.getPrevOutput(), false) ||
      !centroids.calcHiddenGradients(curvatures.AsObject()) ||
      !SumAndNormilize(temp, centroids.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !centroids.SetGradient(temp, false)
     )
      return false;

A continuación, lo sustituiremos temporalmente por un búfer no utilizado del tamaño correspondiente. Luego llamaremos al método de distribución del gradiente de error a la última capa del modelo de generación de coordenadas centroides, transmitiéndole como objeto posterior la primera capa del modelo de determinación de la curvatura del hiperespacio en los puntos centroides. Después sumaremos los valores de los dos búferes de datos y retornaremos sus punteros a su estado inicial. No se olvide de controlar el proceso de cada operación descrita.

Ahora que ya tenemos el gradiente de error total en el búfer de la última capa del modelo de determinación de las coordenadas del centroide, podremos organizar un ciclo de pasada inversa de las capas neuronales del modelo. Dentro de este ciclo, organizaremos las distribuciones del gradiente de error entre las capas del modelo según su contribución al resultado final.

//--- Centroids
   for(int i = cHyperCentroids.Total() - 2; i >= 0; i--)
     {
      next = centroids;
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.calcHiddenGradients(next))
         return false;
     }

Después, todo lo que deberemos hacer es pasar el gradiente de error a la capa de datos de origen. Pero aquí de nuevo nos enfrentaremos al problema de preservar el gradiente de error previamente acumulado. Y repetiremos el truco antes descrito de sustituir los búferes de datos, solo que esta vez para el objeto de datos de origen.

   temp = prevLayer.getGradient();
   if(prevLayer.Activation()!=None)
      if(!DeActivation(prevLayer.getOutput(),temp,temp,prevLayer.Activation()))
        return false;
   if(!prevLayer.SetGradient(prevLayer.getPrevOutput(), false) ||
      !prevLayer.calcHiddenGradients(centroids.AsObject()) ||
      !SumAndNormilize(temp, prevLayer.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !prevLayer.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

Todo lo que tendremos que hacer es devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.

Con esto concluiremos nuestra revisión de los algoritmos para construir los métodos de nuestra clase CNeuronHyperboloids. Podrá leer el código completo de esta clase y todos sus métodos por sí mismo en el archivo adjunto.

3. Creación del framework HypDiff

Ya hemos completado nuestro trabajo de construcción de los nuevos bloques individuales del framework HypDiff y hemos llegado al momento en que deberemos construir un objeto único para la implementación de nivel superior del framework. Para ello, crearemos una nueva clase CNeuronHypDiff, cuya estructura se muestra a continuación.

class CNeuronHypDiff :  public CNeuronRMAT
  {
public:
                     CNeuronHypDiff(void) {};
                    ~CNeuronHypDiff(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint centroids,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronHypDiff; }
   //---
   virtual uint      GetWindow(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetWindow() - 1);
     }
   virtual uint      GetUnits(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetUnits());
     }
  };

Como podemos ver en la estructura de la nueva clase presentada anteriormente, heredaremos la funcionalidad principal del objeto CNeuronRMAT. El objeto especificado tendrá la funcionalidad necesaria para organizar el trabajo de un pequeño modelo lineal, lo cual bastará para implementar el framework HypDiff. Por lo tanto, en esta etapa solo tendremos que redefinir el método de inicialización de objetos especificando en él la arquitectura correcta del modelo anidado. Y todos los demás procesos ya serán cubiertos por los métodos de la clase padre.

En los parámetros del método de inicialización del objeto obtendremos las constantes básicas que nos permitirán interpretar sin ambigüedades la arquitectura del objeto a crear.

bool CNeuronHypDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint units_count, 
                          uint heads, uint layers, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Y en el cuerpo del método llamaremos inmediatamente al método homónimo del objeto básico de capas neuronales dentro del cual se implementará la inicialización de las interfaces principales. En esta etapa, no utilizaremos intencionalmente el método de inicialización de la clase padre directa, ya que la arquitectura del modelo interno a crear es muy diferente.

A continuación, prepararemos el array dinámico heredado para el almacenamiento de los punteros a los objetos internos.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   int layer = 0;

Y pasaremos al proceso real de construcción de la arquitectura interna del framework HypDiff.

Los datos de origen introducidos en el modelo se proyectarán primero en un espacio hiperbólico. Para ello, añadiremos un objeto sobre la clase CNeuronHyperProjection creada.

//--- Projection
   CNeuronHyperProjection *lorenz = new CNeuronHyperProjection();
   if(!lorenz ||
      !lorenz.Init(0, layer, OpenCL, window, units_count, optimization, iBatch) ||
      !cLayers.Add(lorenz))
     {
      delete lorenz;
      return false;
     }
   layer++;

Además, el framework HypDiff proporcionará un codificador hiperbólico diseñado para generar las incorporaciones de los nodos del grafo analizado. Los autores del framework utilizaron aquí modelos neuronales de grafos junto con capas convolucionales. En nuestra aplicación, sustituiremos las redes neuronales de grafos por un Transformer con codificación relativa.

//--- Encoder
   CNeuronRMAT *rmat = new CNeuronRMAT();
   if(!rmat ||
      !rmat.Init(0, layer, OpenCL, window + 1, window_key, units_count, heads, layers, optimization, iBatch) ||
      !cLayers.Add(rmat))
     {
      delete rmat;
      return false;
     }
   layer++;
//---
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, window + 1, window + 1, 2 * window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 2 * window, 2 * window, 3, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;

Aquí deberemos prestar atención a que, en lo sucesivo, al proyectar las incorporaciones recibidas sobre planos tangentes, aumentaremos fuertemente el volumen de la información procesada, realizando proyecciones sobre todos los planos tangentes del volumen completo de información. Y para compensar ligeramente el impacto negativo de este enfoque, comprimiremos el tamaño de incorporación de cada nodo.

Las incorporaciones resultantes de los datos de origen tendremos que proyectarlas sobre los planos tangentes de los centroides. Ya hemos organizado la funcionalidad para generar centroides y proyectar los datos de origen sobre las tangentes correspondientes en la clase CNeuronHyperboloids. Ahora todo lo que tendremos que hacer es añadir una instancia de dicho objeto a nuestro modelo lineal.

//--- LogMap projecction
   CNeuronHyperboloids *logmap = new CNeuronHyperboloids();
   if(!logmap ||
      !logmap.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(logmap))
     {
      delete logmap;
      return false;
     }
   layer++;

Como salida, obtendremos las proyecciones de los datos de origen en varios planos. Y ahora podremos aplicarles el algoritmo de difusión dirigida desarrollado originalmente para los modelos euclidianos. En nuestra implementación utilizaremos el objeto CNeuronDiffusion.

//--- Diffusion model
  CNeuronDiffusion *diff = new CNeuronDiffusion();
  if(!diff ||
     !diff.Init(0, layer, OpenCL, 3, window_key, heads, units_count*centroids, 2, layers, optimization, iBatch) ||
     !cLayers.Add(diff))
    {
     delete diff;
     return false;
    }
  layer++;

En este punto conviene señalar que no hemos combinado en una única entidad las distintas proyecciones de un mismo elemento de la secuencia. En cambio, en nuestra aplicación, el modelo de difusión dirigida tratará cada proyección como un objeto independiente. De este modo, proponemos que el modelo aprenda a comparar proyecciones individuales de una misma secuencia y forme a partir de ellas una visión tridimensional de los datos analizados.

Otro punto implícito que debemos mencionar es el ruido añadido. No vamos a complicar el modelo en un intento de comparar el ruido de diferentes proyecciones de un único elemento de secuencia. Al fin y al cabo, el propio proceso de adición de ruido implica "desenfocar" los datos de origen en alguna vecindad de los mismos. Y la diferente adición de ruido en las distintas proyecciones hará que este "desenfoque" sea volumétrico.

En la salida del modelo de difusión, esperamos obtener una representación limpia de ruido de los datos de origen en diferentes proyecciones. Y aquí es donde empezarán nuestras desviaciones más drásticas respecto al framework del autor. Los autores de HypDiff realizaron una proyección inversa de los datos en el espacio hiperbólico y obtuvieron la representación original del grafo usando un descodificador Fermi-Dirac. Nuestro objetivo, en cambio, será obtener una representación latente informativa de los datos de origen para luego introducirla en el modelo del Actor y entrenar una política rentable para el comportamiento de nuestro agente. Por lo tanto, usaremos la capa de agrupación basada en la dependencia para obtener una visión global de cada elemento de la secuencia.

//--- Pooling
   CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling();
   if(!pooling ||
      !pooling.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(pooling))
     {
      delete pooling;
      return false;
     }
   layer++;

Y luego redimensionaremos el tensor resultante al nivel de los datos de origen.

//--- Resize to source size
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 3, 3, window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }

Ahora tendremos que sustituir los punteros de los búferes de datos de la interfaz por los búferes correspondientes de la última capa de nuestro modelo. Y finalizar el método de inicialización de nuestra clase.

//---
   if(!SetOutput(conv.getOutput(), true) ||
      !SetGradient(conv.getGradient(), true))
      return false;
//---
   return true;
  }

Con esto completaremos nuestro trabajo de implementación de nuestra propia visión de los enfoques del framework HypDiff usando MQL5. Encontrará el código completo de todas las clases presentadas y sus métodos en el archivo adjunto al artículo. También encontrará el código de los programas de interacción con el entorno y del entrenamiento de modelos, que se han mantenido sin cambios respecto a trabajos anteriores.

Ahora diremos unas cuantas palabras sobre la arquitectura de los modelos entrenados. La arquitectura de los modelos del Actor y el Crítico permanecerá inalterada. No obstante, hemos introducido pequeñas modificaciones en el modelo del Codificador del entorno. Los datos introducidos en la entrada del modelo, como antes, se someterán a un procesamiento primario en la capa de normalización por lotes.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, se transferirán directamente a nuestro modelo hiperbólico de difusión latente.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronHypDiff;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=10;                                        // centroids
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

El algoritmo del modelo hiperbólico de difusión latente descrito anteriormente supone un proceso bastante complejo. Por lo tanto, excluiremos el procesamiento posterior de los datos. Así, solo utilizaremos una capa completamente conectada para llevar los datos al tamaño de tensor requerido, que se suministrará a la entrada del modelo del Actor.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Con esto concluiremos nuestro trabajo de aplicación de los planteamientos del framework HypDiff y pasaremos a la fase más emocionante: la evaluación práctica de los resultados realizada con datos históricos reales.

4. Simulación

Ya hemos implementado el framework HypDiff usando MQL5, así que ahora pasaremos a la etapa final: el entrenamiento del modelo y la evaluación de la política obtenida de comportamiento del Actor. Seguiremos el algoritmo de aprendizaje descrito en trabajos anteriores y entrenaremos tres modelos simultáneamente: El Codificador del estado de la cuenta, el Actor y el Crítico. El Codificador analizará la situación del mercado. El Actor tomará decisiones comerciales basadas en las políticas estudiadas. Y el Crítico evaluará las acciones del Actor y señalará las direcciones para ajustar sus políticas.

El entrenamiento se realizará con datos históricos reales para todo el año 2023, con el instrumento financiero EURUSD, marco temporal H1. Los parámetros de todos los indicadores analizados se han usado por defecto.

El proceso de entrenamiento será iterativo e implicará la actualización periódica de la muestra de entrenamiento.

Asimismo, se utilizarán los datos históricos reales del primer trimestre de 2024 para comprobar la eficacia de la política entrenada. Ahora le presentamos los resultados de las pruebas.

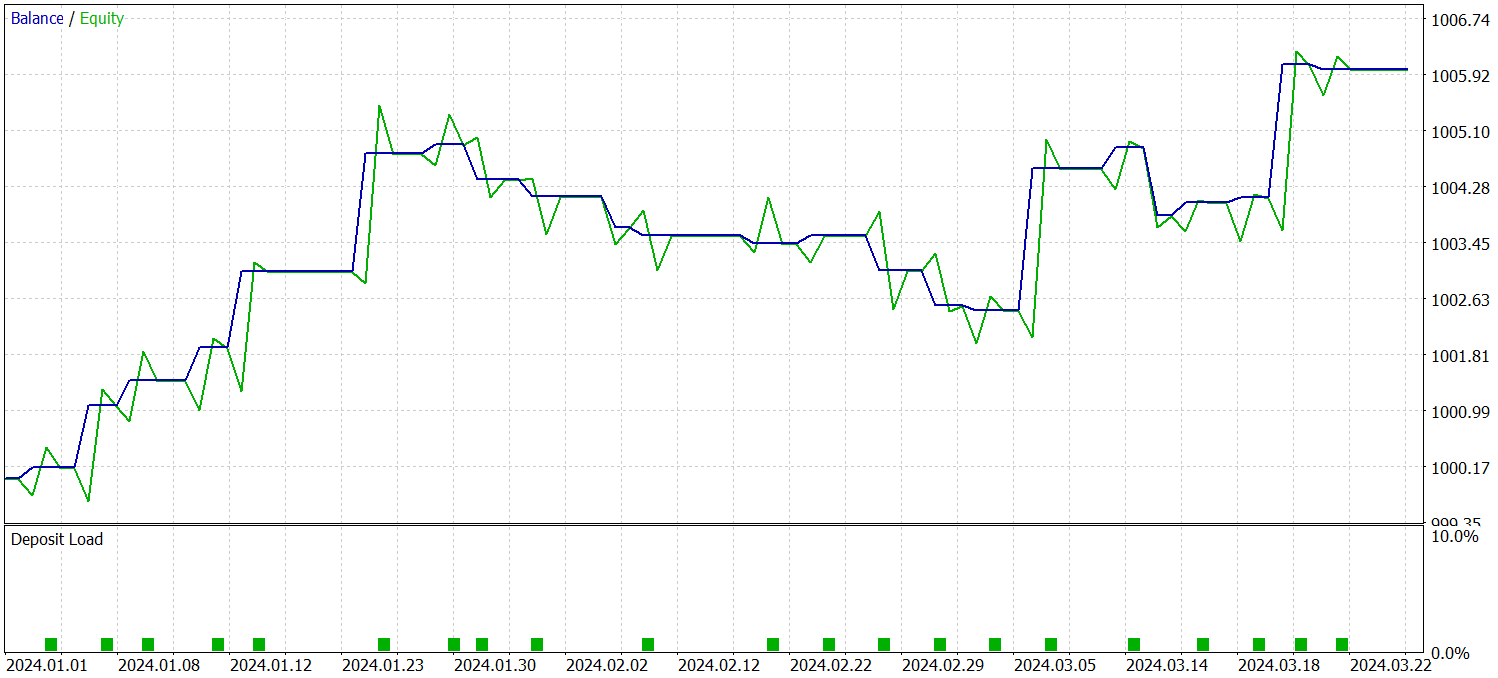
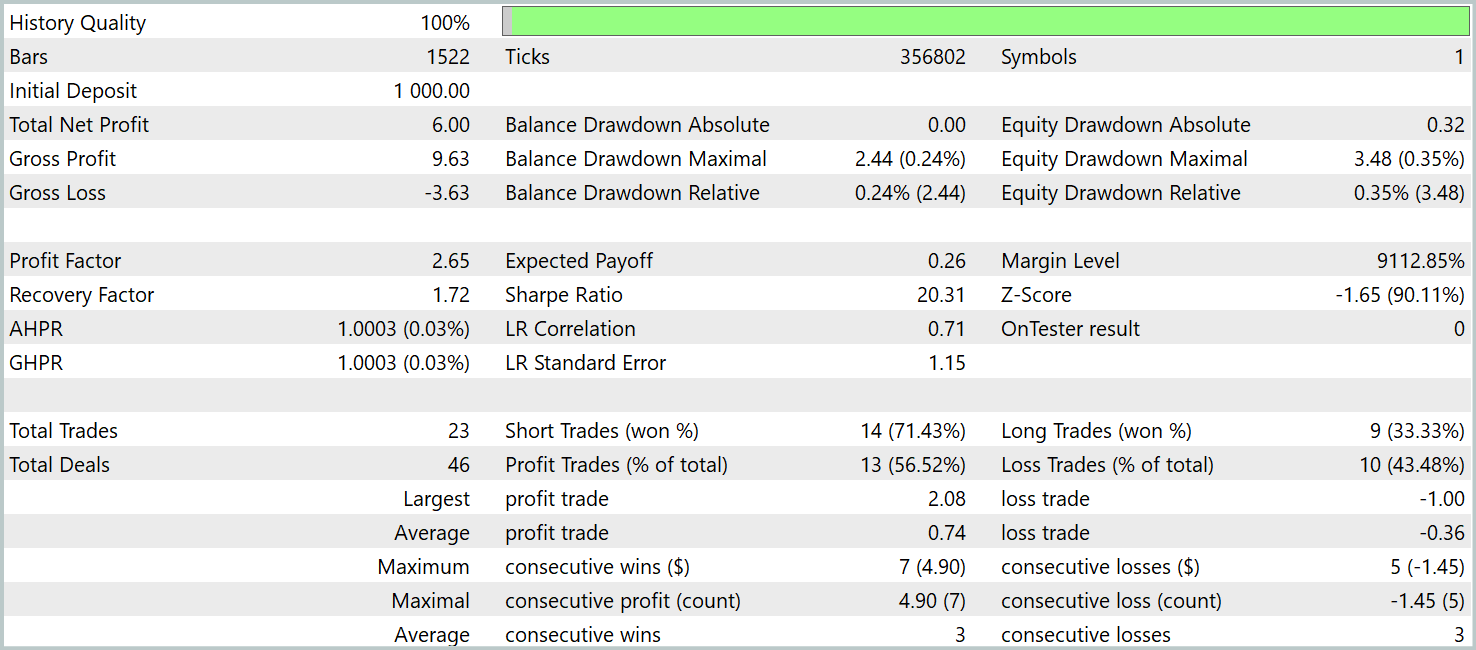
Como se desprende de los datos presentados, el modelo ha sido capaz de obtener beneficios durante el periodo de prueba. Solo se han realizado 23 transacciones en 3 meses, lo que sin duda resulta insuficiente. Más del 56% se han cerrado con beneficios. Al mismo tiempo, tanto el máximo como la media de las transacciones rentables son 2 veces superiores al mismo indicador de las transacciones deficitarias.

Mucho más interesante, sin embargo, resulta la observación detallada de las transacciones. De 3 meses de pruebas, el modelo solo ha sido capaz de obtener beneficios en 2 de ellos. El mes de febrero ha resultado un completo fracaso. Al mismo tiempo, de las 8 transacciones realizadas en enero de 2024, solo la última no ha sido rentable, lo cual confirma considerablemente la anterior teoría de que la representatividad de la muestra de entrenamiento disminuye al cabo de un año tras el primer mes de funcionamiento del modelo.

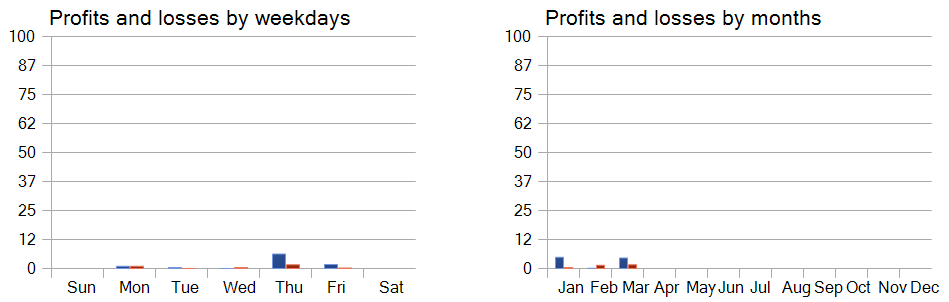
Asimismo, el análisis de la rentabilidad de las transacciones comerciales por días de la semana nos permite concluir que el modelo prioriza claramente el jueves y el viernes.

Conclusión

La aplicación de la geometría hiperbólica ayuda a superar los problemas derivados del conflicto entre la naturaleza discreta de los datos de grafos y el modelo de difusión continua. El framework HypDiff ofrece un método mejorado para generar ruido gaussiano hiperbólico que aborda el problema de los fallos aditivos de las distribuciones gaussianas en el espacio hiperbólico. Así, para preservar la estructura local durante la difusión anisotrópica, se introducen restricciones geométricas en la similitud angular.

En la parte práctica de nuestro trabajo, hemos implementado nuestra propia visión de los enfoques propuestos mediante MQL5. Además, hemos entrenado los modelos con los métodos propuestos a partir de datos históricos reales, y hemos probado la política entrenada de comportamiento del Actor fuera de la muestra de entrenamiento. Los resultados obtenidos muestran el potencial de los planteamientos propuestos e indican posibles formas de mejorar el rendimiento del modelo.

Enlaces

• Hyperbolic Geometric Latent Diffusion Model for Graph Generation
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL