Reimaginando las estrategias clásicas en MQL5 (Parte IX): Análisis de múltiples marcos temporales (II)
183
0
Hay muchos marcos temporales que los traders pueden utilizar. Para un nuevo miembro de la comunidad, o cualquiera que esté aprendiendo a comerciar, la elección puede ser difícil. Incluso los traders experimentados con frecuencia debaten y comparten diferentes puntos de vista, tratando de establecer qué marco de tiempo es óptimo. Intentaremos responder a esta pregunta de forma objetiva, definiendo el marco temporal óptimo como aquel que minimiza los niveles de error de nuestro modelo de IA.
En la discusión de hoy, prestaremos atención a la distribución de los residuos de nuestro modelo en 11 marcos de tiempo, observamos 2 regiones de bajo error en los marcos de tiempo mensual y horario. Sin embargo, no existe un patrón obvio en la distribución de los niveles de error del modelo; parece alcanzar un máximo y un mínimo en el marco horario. Antes de que podamos responder definitivamente a la vieja pregunta "¿Cuál es el mejor marco temporal para utilizar?", debemos estar razonablemente seguros de que la distribución de los residuos no cambia si cambiamos de mercado. Además, en el futuro deberíamos considerar una búsqueda exhaustiva en todos los marcos temporales disponibles.
Descripción general de la metodología de negociación
Si bien el patrón creado por las velas de precios puede parecer muy diferente en todos los períodos de tiempo, solo se ofrece un precio en cada una de ellas en cualquier momento. Los traders a menudo analizan diferentes períodos de tiempo a la vez para obtener información sobre el estado actual del mercado. Si la tendencia se debilita, probablemente veremos acciones de precios contradictorias en marcos de tiempo inferiores al que usamos para abrir nuestra operación. Además, estos signos de debilidad siempre serán visibles primero en el marco temporal inferior, antes de volverse perceptibles en los marcos temporales superiores.
En general, la mayoría de las estrategias que incluyen análisis de múltiples marcos temporales buscan comprender el sentimiento del mercado a partir de marcos temporales más altos. Algunos traders exitosos buscan la formación de patrones de acción de precios bien conocidos en marcos temporales más altos, como patrones de velas envolventes alcistas. Tradicionalmente, la presencia o ausencia de estos patrones de velas servía como señal para los traders que buscaban configuraciones de alta probabilidad. Queríamos aprender algorítmicamente qué marco de tiempo nos da niveles de error confiables al pronosticar el par EURUSD.
En cierto nivel, todos generalmente apreciamos la intuición de que cuanto más lejos en el futuro intentamos predecir, más difícil se vuelve la tarea. Los resultados de nuestro análisis de hoy desafían esa creencia en un nivel fundamental. Antes de que puedas entender por qué digo esto, o si estas conclusiones son acertadas, debemos analizar primero la metodología empleada.
Descripción general de la metodología
Para que nuestra prueba fuera justa, tuvimos que obtener la misma cantidad de datos de cada período de tiempo. El factor limitante en este paso fue el número de barras disponibles en el marco temporal mensual. Tan solo 400 barras de datos mensuales se componen de aproximadamente 33 años. Sólo hay un puñado de mercados tan antiguos, lo que puede sesgar nuestra comprensión del mejor marco temporal entre todos los mercados posibles. Sin embargo, para el alcance de nuestra discusión, el par EURUSD tiene amplios conjuntos de datos en los que podemos confiar.
Obtuvimos 400 filas de cotizaciones de precios mensuales del terminal MetaTrader 5. Luego obtuvimos 400 filas correspondientes al valor futuro del par EURUSD. Este proceso de dos pasos se repitió durante los 10 períodos de tiempo restantes. Para este análisis, seleccioné:
- Semanalmente
- A diario
- H12
- H8
- H4
- H1
- M30
- M15
- M5
- M1
Debo admitir que esperaba observar fuertes niveles de correlación, especialmente entre períodos de tiempo que periódicamente están cerca uno del otro. Sin embargo, sólo se encontraron niveles moderados de correlación en toda la muestra. Los únicos pares de correlaciones interesantes que podrían merecer un análisis más profundo fueron:
- Precio actual del H4 y precio futuro del H8
- Precio actual del M1 y precio futuro del H4
- Precio actual del M1 y precio futuro del M5
Recordemos que nuestros datos de entrada tenían 22 columnas, naturalmente la matriz de correlación que obtuvimos fue grande y no se mostrará en su totalidad en nuestra discusión. A partir de los datos que tenemos hasta el momento, pudimos crear 11 conjuntos de entradas para probar. Después de modelar nuestros datos, observamos que nuestros modelos funcionaron mejor en los marcos temporales mensuales y horarios. Este resultado fue bastante contra-intuitivo. Nuestro objetivo era avanzar 20 pasos en el tiempo hacia el futuro. 20 meses en el futuro es un período de 1 año y 8 meses. Nuestro modelo podría predecir los cambios de precio a lo largo de un año con mayor precisión que si lo hiciera en un período de 20 minutos.
Intrigados por los dos marcos temporales de bajo error, transformamos los datos de precios en retornos periódicos y posteriormente realizamos pruebas de causalidad de Granger sobre los retornos. Observamos valores "p" significativos que nos sugieren que los rendimientos horarios causaron en Granger los rendimientos mensuales. Esta prueba demuestra que podemos modelar los rendimientos mensuales utilizando los rendimientos horarios con un modelo de regresión automática vectorial (Vector Auto Regression, VAR).
Utilizamos una biblioteca de deformación de series temporales para alinear y encontrar similitudes entre los datos mensuales y horarios. Nuestro algoritmo fue capaz de encontrar muchos puntos de similitud entre los datos. Esto nos dio confianza en nuestro proceso de selección y procedimos a ajustar con éxito los parámetros de nuestro modelo mensual y exportar nuestro modelo al formato ONNX.
Por último, implementé un Asesor Experto que hace predicciones en niveles de precios anticipados en el marco de tiempo mensual y luego ejecuta sus operaciones en el marco de tiempo horario. El sistema puede alternar entre cerrar sus posiciones basándose en reversiones previstas por IA o utilizar promedios móviles. Utilizamos análisis técnico para cronometrar nuestras entradas de posiciones.
Obteniendo los datos que necesitamos
Comencemos importando primero la biblioteca MetaTrader 5 y algunas otras bibliotecas que necesitamos.
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns import MetaTrader5 as mt5 from sklearn.model_selection import cross_val_score,train_test_split,TimeSeriesSplit from sklearn.metrics import mean_squared_error import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression
Ahora probemos si podemos llegar a la Terminal.
#Initialize the terminal
mt5.initialize()Definamos los marcos temporales que nos gustaría probar.
#Declare the time-frames we are interested in
time_frames = [mt5.TIMEFRAME_MN1,
mt5.TIMEFRAME_W1,
mt5.TIMEFRAME_D1,
mt5.TIMEFRAME_H12,
mt5.TIMEFRAME_H8,
mt5.TIMEFRAME_H4,
mt5.TIMEFRAME_H1,
mt5.TIMEFRAME_M30,
mt5.TIMEFRAME_M15,
mt5.TIMEFRAME_M5,
mt5.TIMEFRAME_M1
]¿Cuántas barras de datos debemos obtener?
#How many bars should we fetch fetch = 400
Pronostiquemos veinte pasos hacia el futuro.
#How far into the future should we forecast? look_ahead = 20
Define las columnas de nuestro marco de datos.
#Create our dataframe inputs = ["MN","W","D","H12","H8","H4","H1","M30","M15","M5","M1"] target = [] for i in np.arange(0,len(inputs)): target.append(inputs[i] + " Target")
Crea el marco de datos que contiene nuestros precios.
columns = inputs + target
prices = pd.DataFrame(columns=columns,index=np.arange(0,fetch))
Figura 1: Algunas de las entradas en nuestro marco de datos.
Figura 2: Algunos de los objetivos en nuestro marco de datos.
Necesitamos un marco de datos para almacenar nuestros niveles de error.
#The columns for our error levels data frame. error_columns = [] for i in np.arange(0,len(inputs)): error_columns.append(inputs[i]) #Create a dataframe to store our error levels error_levels = pd.DataFrame(columns=error_columns,index=[0]) test_error_levels = pd.DataFrame(columns=error_columns,index=[0])
Obtenga los datos de precios que necesitamos.
for i in np.arange(0,len(time_frames)): print(i) prices.iloc[:,i] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],look_ahead,fetch)).loc[:,"close"] prices.iloc[:,i+10] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],0,fetch)).loc[:,"close"]
Análisis exploratorio de datos
Analicemos los niveles de correlación en nuestro marco de datos. Observe los fuertes niveles de correlación entre los marcos de tiempo H12 y H8. ¿Qué otros niveles de correlación le llaman la atención?
fig, ax = plt.subplots(figsize=(15,15)) sns.heatmap(prices.corr(),annot=True,ax=ax)
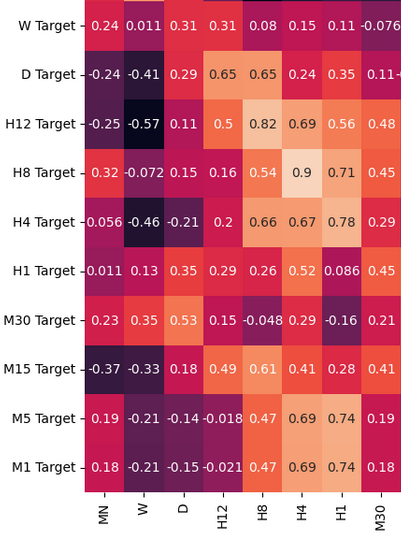
Figura 3: Algunos de los valores de la matriz de correlación que obtuvimos.
Al realizar un diagrama de dispersión de los precios de cierre mensuales y semanales se observó una tendencia poco clara. En su mayor parte, parece que los datos tienen una tendencia general alcista.
sns.scatterplot(data=prices,x="MN Close",y="W Close")
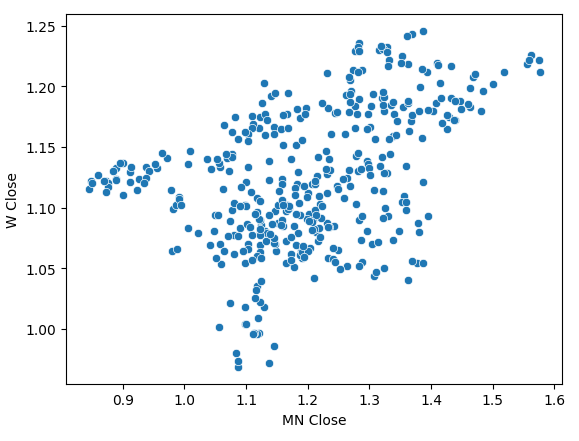
Figura 4: Un diagrama de dispersión de nuestros precios de cierre mensuales y semanales.
Transformamos nuestros datos de precios en retornos periódicos y realizamos nuevamente el diagrama de dispersión. Esta vez aparece una tendencia general: parece que nuestros retornos se agrupan alrededor de 0.
sns.scatterplot(data=prices.pct_change(),x="MN Close",y="W Close")
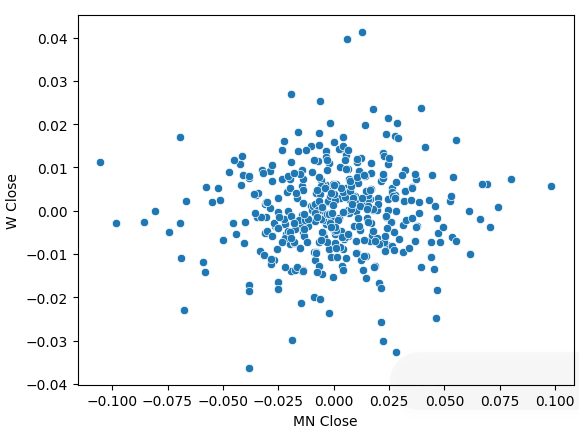
Figura 5: Un diagrama de dispersión de nuestros retornos en diferentes períodos de tiempo.
Cuando realizamos diagramas de caja de nuestros rendimientos en diferentes períodos de tiempo, podemos observar otra tendencia. La variación en nuestros retornos disminuye a medida que nos alejamos del marco temporal mensual hacia marcos temporales más bajos. Asimismo, el rendimiento promedio en todos los períodos de tiempo es cercano a 0. Esto también puede interpretarse como que si estamos tratando de maximizar los retornos de una cartera, deberíamos considerar marcos temporales más altos.
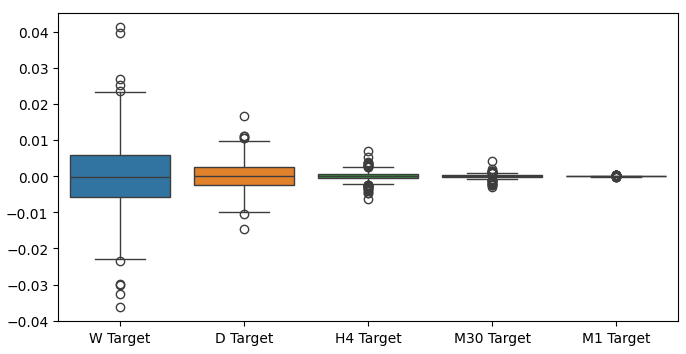
Figura 6: Un diagrama de caja de nuestros rendimientos en diferentes períodos de tiempo.
Preparación para modelar los datos
Ahora hagamos los preparativos necesarios para comenzar a modelar los datos. Primero, necesitamos hacer divisiones de entrenamiento y prueba de nuestros datos.
#Create train test splits X_train_mn,X_test_mn,y_train_mn,y_test_mn = train_test_split(prices.loc[:,["MN"]],prices.loc[:,"MN Target"],test_size=0.5,shuffle=False) X_train_w,X_test_w,y_train_w,y_test_w = train_test_split(prices.loc[:,["W"]],prices.loc[:,"W Target"],test_size=0.5,shuffle=False) X_train_d,X_test_d,y_train_d,y_test_d = train_test_split(prices.loc[:,["D"]],prices.loc[:,"D Target"],test_size=0.5,shuffle=False) X_train_h12,X_test_h12,y_train_h12,y_test_h12 = train_test_split(prices.loc[:,["H12"]],prices.loc[:,"H12 Target"],test_size=0.5,shuffle=False) X_train_h8,X_test_h8,y_train_h8,y_test_h8 = train_test_split(prices.loc[:,["H8"]],prices.loc[:,"H8 Target"],test_size=0.5,shuffle=False) X_train_h4,X_test_h4,y_train_h4,y_test_h4 = train_test_split(prices.loc[:,["H4"]],prices.loc[:,"H4 Target"],test_size=0.5,shuffle=False) X_train_h1,X_test_h1,y_train_h1,y_test_h1 = train_test_split(prices.loc[:,["H1"]],prices.loc[:,"H1 Target"],test_size=0.5,shuffle=False) X_train_m30,X_test_m30,y_train_m30,y_test_m30 = train_test_split(prices.loc[:,["M30"]],prices.loc[:,"M30 Target"],test_size=0.5,shuffle=False) X_train_m15,X_test_m15,y_train_m15,y_test_m15 = train_test_split(prices.loc[:,["M15"]],prices.loc[:,"M15 Target"],test_size=0.5,shuffle=False) X_train_m5,X_test_m5,y_train_m5,y_test_m5 = train_test_split(prices.loc[:,["M5"]],prices.loc[:,"M5 Target"],test_size=0.5,shuffle=False) X_train_m1,X_test_m1,y_train_m1,y_test_m1 = train_test_split(prices.loc[:,["M1"]],prices.loc[:,"M1 Target"],test_size=0.5,shuffle=False)
Ahora almacene estas divisiones en listas.
train_X = [ X_train_mn, X_train_w, X_train_d, X_train_h12, X_train_h8, X_train_h4, X_train_h1, X_train_m30, X_train_m15, X_train_m5, X_train_m1 ] test_X = [ X_test_mn, X_test_w, X_test_d, X_test_h12, X_test_h8, X_test_h4, X_test_h1, X_test_m30, X_test_m15, X_test_m5, X_test_m1 ]
Repita el procedimiento anterior para los valores objetivo.
train_y = [ y_train_mn, y_train_w, y_train_d, y_train_h12, y_train_h8, y_train_h4, y_train_h1, y_train_m30, y_train_m15, y_train_m5, y_train_m1, ] test_y = [ y_test_mn, y_test_w, y_test_d, y_test_h12, y_test_h8, y_test_h4, y_test_h1, y_test_m30, y_test_m15, y_test_m5, y_test_m1, ]
Validar de forma cruzada cada modelo.
#Record our error for i in np.arange(0,len(train_X)): #Fit the model model = LinearRegression() cv_score = cross_val_score(model,train_X[i],train_y[i],cv=5) error_levels.iloc[0,i] = np.mean(cv_score * -1) #Record validation error model.fit(train_X[i],train_y[i]) test_error_levels.iloc[0,i] = mean_squared_error(test_y[i],model.predict(test_X[i]))
Nuestros respectivos niveles de error.
error_levels
| MN | W | D | H12 | H8 | H4 | H1 | M30 | M15 | M5 | M1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.719131 | 3.979435 | 3.897228 | 5.023601 | 5.218168 | 40.406227 | 0.196244 | 18.264356 | 3.680168 | 20.331821 | 3.540946 |
Visualicemos nuestra aproximación de la distribución de los residuos de nuestro modelo.
fig, ax = plt.subplots(figsize=(7,4)) sns.barplot(error_levels,ax=ax)
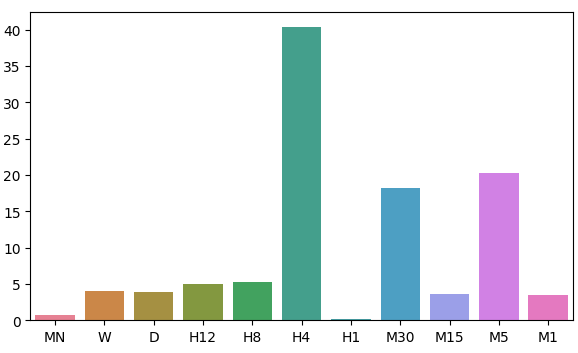
Figura 7: Visualización de los niveles de error de nuestro modelo.
Importancia de las características
Ahora que hemos identificado nuestros marcos temporales óptimos, intentemos detectar si puede haber alguna causalidad en juego entre los dos marcos temporales. En 1969, Sir Clive Granger propuso una prueba para determinar empíricamente si dos datos de series de tiempo se causaban mutuamente, incluso en casos en que los valores pasados de una serie de tiempo afectaban los valores futuros de esta última. En pocas palabras, la prueba de Granger se aprueba si podemos desfasar los valores de una serie temporal y utilizarla para predecir el valor futuro de la segunda sin una caída significativa en la varianza de nuestras predicciones.
Desde su creación, la prueba de Granger ha experimentado muchos cambios y mejoras. En la actualidad, su uso se extiende a todas las industrias, desde la neurociencia hasta las finanzas. El uso de la prueba ha estado en el centro de mucho debate en los círculos académicos durante más de medio siglo. La mayor parte del problema radica en los supuestos de linealidad que implica implícitamente la prueba de Granger. Por lo tanto, si existe una relación causal que no sea lineal, la prueba de Granger refutará su existencia. Además, en la práctica, la prueba suele limitarse a problemas bivariados. Es decir, rara vez utilizamos la prueba de Granger en problemas grandes con más de dos conjuntos de datos de series de tiempo.
Figura 8: El difunto economista británico Sir Clive Granger.
Para comenzar, primero importemos la biblioteca statsmodels y luego ejecutemos la prueba. La prueba se realiza sobre versiones rezagadas del H1 Close. La prueba se supera si obtenemos valores "p" < 0,05, lo que hicimos en el primer rezago. Todos los rezagos posteriores no pasaron la prueba y podemos rechazar que exista alguna causalidad más allá del primer rezago.
from statsmodels.tsa.stattools import grangercausalitytests result = grangercausalitytests(prices[['H1 Close','MN Close']].pct_change().dropna(), maxlag=4)
number of lags (no zero) 1
ssr based F test: F=4.4913 , p=0.0347 , df_denom=395, df_num=1
ssr based chi2 test: chi2=4.5254 , p=0.0334 , df=1
likelihood ratio test: chi2=4.4999 , p=0.0339 , df=1
parameter F test: F=4.4913 , p=0.0347 , df_denom=395, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=2.2706 , p=0.1046 , df_denom=392, df_num=2
ssr based chi2 test: chi2=4.5991 , p=0.1003 , df=2
likelihood ratio test: chi2=4.5727 , p=0.1016 , df=2
parameter F test: F=2.2706 , p=0.1046 , df_denom=392, df_num=2
La causalidad de Granger normalmente funciona en un solo sentido. Asegurémonos de ello comprobando la causalidad en la dirección opuesta. Ninguno de los valores "p" obtenidos fue significativo, lo que nos asegura que la causalidad efectivamente va en una dirección como esperábamos.
result = grangercausalitytests(prices[['MN Close','H1 Close']].pct_change().dropna(), maxlag=4)
Granger Causality
number of lags (no zero) 1
ssr based F test: F=0.0188 , p=0.8909 , df_denom=395, df_num=1
ssr based chi2 test: chi2=0.0190 , p=0.8905 , df=1
likelihood ratio test: chi2=0.0190 , p=0.8905 , df=1
parameter F test: F=0.0188 , p=0.8909 , df_denom=395, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
ssr based chi2 test: chi2=4.4930 , p=0.1058 , df=2
likelihood ratio test: chi2=4.4678 , p=0.1071 , df=2
parameter F test: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=1.7310 , p=0.1601 , df_denom=389, df_num=3
ssr based chi2 test: chi2=5.2863 , p=0.1520 , df=3
likelihood ratio test: chi2=5.2513 , p=0.1543 , df=3
parameter F test: F=1.7310 , p=0.1601 , df_denom=389, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=1.4694 , p=0.2108 , df_denom=386, df_num=4
ssr based chi2 test: chi2=6.0148 , p=0.1980 , df=4
likelihood ratio test: chi2=5.9694 , p=0.2014 , df=4
parameter F test: F=1.4694 , p=0.2108 , df_denom=386, df_num=4
La deformación dinámica de series de tiempo también nos permite encontrar similitudes entre dos conjuntos de datos de series de tiempo. El algoritmo también se puede utilizar para alinear series de diferentes longitudes. Empleamos el algoritmo para encontrar puntos de similitud entre los retornos mensuales y horarios de nuestros datos. El algoritmo realiza esta tarea minimizando una función de costo especializada que mide la diferencia entre dos series. Comenzaremos importando las librerías que necesitamos.
#Let's calculate the simillarities between our time series data from dtaidistance import dtw from dtaidistance import dtw_visualisation as dtwvis
Ahora busquemos similitudes entre los retornos.
series_1 = prices["MN Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 series_2 = prices["H1 Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 path = dtw.warping_path(series_1, series_2) dtwvis.plot_warping(series_1, series_2, path)
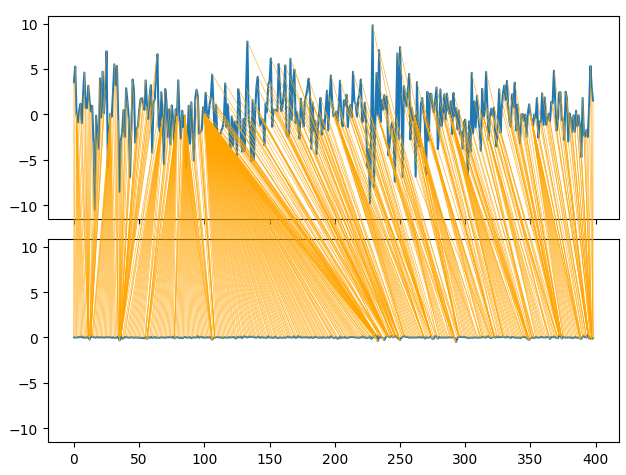
Figura 9: Visualización de las similitudes entre los retornos mensuales y horarios.
Ajuste de parámetros
Ajustemos ahora los parámetros de nuestra red neuronal profunda para superar el rendimiento de referencia establecido por nuestra regresión lineal. Tenga en cuenta que debido a la naturaleza de los procedimientos de optimización utilizados para entrenar DNN, los resultados obtenidos en esta sección del artículo pueden ser difíciles de reproducir. De hecho, ejecuté esta prueba 5 veces y no pudimos ejecutar el modelo lineal en 2 pruebas.
Importamos las bibliotecas que necesitamos e inicializamos el modelo.
#Let's try to outperform our linear regression model from sklearn.neural_network import MLPRegressor from sklearn.model_selection import RandomizedSearchCV #Let's tune our model model = MLPRegressor(max_iter=500)
Define el espacio de parámetros.
#Tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,0.000000001,0.000000000000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.000000001,0.000000000000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[1,0.1,0.0001,0.000001,100,10000,1000000,1000000000,100,1000],
"shuffle": [True,False],
"hidden_layer_sizes":[(1,4),(1,4,5),(1,8,10),(2,5),(8),(10,12),(5,10,4)]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)Coloque el afinador.
tuner.fit(X_train_mn,y_train_mn)
Los mejores parámetros que encontramos.
tuner.best_params_
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 1,
'learning_rate': 'adaptive',
'hidden_layer_sizes': (2, 5),
'alpha': 1e-05,
'activation': 'identity'}
Optimización más profunda
Realicemos una búsqueda más profunda de parámetros óptimos utilizando la biblioteca SciPy.
#Deeper optimization
from scipy.optimize import minimizeCrear estructuras de datos para registrar nuestro progreso.
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) optimization_progress = []
Definir la función objetivo a minimizar. Queremos minimizar el error cuadrático medio de nuestro modelo.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(X_train_mn)): #Train the model model.fit(X_train_mn.loc[train[0]:train[-1],:],y_train_mn.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(y_train_mn.loc[test[0]:test[-1]],model.predict(X_train_mn.loc[test[0]:test[-1],:])) #Record the progress made by the optimizer optimization_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Especifique el punto de inicio para el procedimiento de optimización y especifique límites grandes para que podamos aproximarnos a la optimización global.
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((0.000000001,10000000000),(0.0000000001,10000000000),(0.000000001,10000000000))
Optimizando nuestro modelo DNN.
#Searchin deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
Parece que hemos realizado la optimización con éxito.
result
success: True
status: 2
fun: 0.04257403904271943
x: [ 4.864e-05 1.122e-03 9.999e-01]
nit: 1
jac: [ 1.298e+04 1.806e+02 -3.371e+03]
nfev: 92
Almacene nuestros valores óptimos.
optima_y = result.fun
optima_x = optimization_progress.index(optima_y)
inputs = np.arange(0,len(optimization_progress))Visualice el progreso realizado por el procedimiento de optimización.
plt.scatter(inputs,optimization_progress) plt.plot(optima_x,optima_y,'s',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.title("Minimizing Training MSE")
Figura 10: Los resultados de nuestro procedimiento de optimización de TNC.
Prueba de sobreajuste
Veamos si realmente podemos superar nuestro modelo lineal predeterminado.
#Test for overfitting benchmark = LinearRegression() default_model = MLPRegressor(max_iter=200) random_search_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"], max_iter=200 ) lbfgs_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2], max_iter=200 )
Ajuste los modelos al conjunto de entrenamiento.
#Fit the models
benchmark.fit(X_train_mn,y_train_mn)
default_model.fit(X_train_mn,y_train_mn)
random_search_model.fit(X_train_mn,y_train_mn)
lbfgs_model.fit(X_train_mn,y_train_mn)Haga preparativos para registrar nuestras puntuaciones de validación cruzada.
#Record our cross val scores
models = [benchmark,
default_model,
random_search_model,
lbfgs_model
]
val_error = pd.DataFrame(columns=["Linear Reg","Default NN","Random Search NN","TNC NN"],index=[0])Validar de forma cruzada cada modelo.
for i in np.arange(0,len(models)): val_error.iloc[0,i] = np.mean(cross_val_score(models[i],X_test_mn,y_test_mn,cv=5,n_jobs=-1)) * -1
Nuestro error de validación muestra claramente que nuestra red neuronal optimizada para TNC fue la que tuvo mejor rendimiento.
val_error
| Linear Reg | Default NN | Random Search NN | TNC NN |
|---|---|---|---|
| 3.323741 | 3.987083 | 3.314776 | 3.283775 |
Exportación al formato ONNX
Ahora preparémonos para exportar nuestro modelo al formato ONNX. ONNX significa Open Neural Network Exchange y es un protocolo de código abierto para representar cualquier modelo de aprendizaje automático como un árbol de nodos que representan cálculos y el flujo de datos después de cada cálculo. ONNX nos permite construir y utilizar modelos de aprendizaje automático en diferentes lenguajes de programación, siempre que esos lenguajes implementen la especificación ONNX.
Importe la biblioteca ONNX para comenzar.
#Preparing to export to ONNX import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
Preparar el modelo.
#Fit the model on all the data we have model = MLPRegressor( solver= 'lbfgs', shuffle= True, activation= 'identity', learning_rate= 'adaptive', hidden_layer_sizes= (2, 5), alpha= 4.864e-05, tol= 1.122e-03, learning_rate_init= 9.999e-01, )
Ajuste el modelo a todos los datos que tenemos.
model.fit(prices[["MN Close"]],prices.loc[:,"MN Target"])
Define la forma de entrada de nuestro modelo.
#Define the input types for our ONNX model initial_types = [("float_input",FloatTensorType([1,1]))]
Cree la representación ONNX del modelo.
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Exportar el modelo al formato ONNX.
# Save the ONNX model onnx.save_model(onnx_model,"EURUSD MN1 AI.onnx")
Visualicemos ahora nuestro modelo en formato ONNX para asegurarnos de que nuestras entradas tengan el tamaño correcto.
import netron
netron.start("EURUSD MN1 AI.onnx")
Figura 11: Visualización de nuestro modelo DNN.
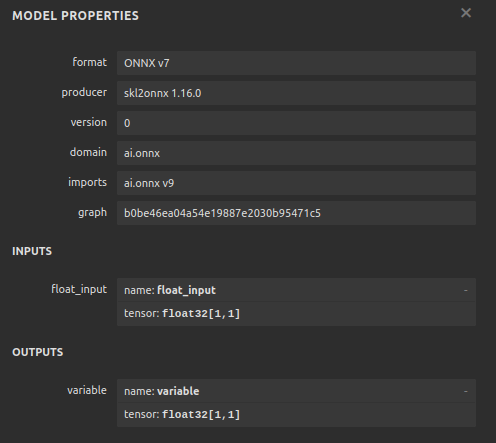
Figura 12: Forma de E/S de nuestro modelo.
Implementación en MQL5
Ahora queremos implementar nuestro algoritmo comercial en MQL5. Deseamos que nuestro algoritmo comercial pueda alternar entre cerrar sus posiciones utilizando promedios móviles simples y utilizar predicciones de IA. Además, queremos guiar nuestro modelo de IA utilizando análisis técnico. Para comenzar, primero importaremos el modelo ONNX que exportamos anteriormente.
//+------------------------------------------------------------------+ //| EURUSD MTF AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load the ONNX resources | //+------------------------------------------------------------------+ #resource "\\Files\\EURUSD MN1 AI.onnx" as const uchar onnx_buffer[];
Ahora definiremos nuestro enumerador personalizado para especificar cómo le gustaría al usuario cerrar posiciones.
//+-------------------------------------------------------------------+ //| Define our custom type | //+-------------------------------------------------------------------+ enum close_type { MA_CLOSE = 0, // Moving Averages Close AI_CLOSE = 1 // AI Auto Close };
Creemos entradas para que podamos cambiar la forma en que nuestra aplicación cierra sus posiciones para ver cuál es mejor.
//+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input close_type user_close_type = AI_CLOSE; // How should we close our positions?
Necesitamos importar la clase comercial.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
Cree variables globales que necesitaremos a lo largo de nuestro programa.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vectorf model_input = vectorf::Zeros(1); vectorf model_output = vectorf::Zeros(1); double bid,ask; int ma_hanlder; double ma_buffer[]; int bb_hanlder; double bb_mid_buffer[]; double bb_high_buffer[]; double bb_low_buffer[]; int rsi_hanlder; double rsi_buffer[]; int system_state = 0,model_state=0;
Cuando se carga nuestra aplicación, primero crearemos nuestro modelo ONNX a partir del búfer que creamos anteriormente. Luego asignaremos nuestros manejadores de indicadores técnicos.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load our ONNX function if(!load_onnx_model()) { return(INIT_FAILED); } //--- Load our technical indicators bb_hanlder = iBands("EURUSD",PERIOD_D1,30,0,1,PRICE_CLOSE); rsi_hanlder = iRSI("EURUSD",PERIOD_D1,14,PRICE_CLOSE); ma_hanlder = iMA("EURUSD",PERIOD_D1,20,0,MODE_EMA,PRICE_CLOSE); //--- return(INIT_SUCCEEDED); }
Si nuestro Asesor Experto es eliminado del gráfico, deberíamos liberar los recursos que ya no utilizamos.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we don't need release_resources(); }
Ahora, cada vez que recibamos precios actualizados, primero almacenaremos los nuevos datos técnicos, haremos una predicción a partir de nuestro modelo y luego mostraremos estadísticas importantes al usuario. Si no tenemos posiciones abiertas, seguiremos las predicciones de nuestro modelo. De lo contrario, seguiremos las entradas del usuario para determinar si debemos mantener nuestras posiciones abiertas o cerradas.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data update_market_data(); //--- Fetch a prediction from our model model_predict(); //--- Display stats display_stats(); //--- Find a position if(PositionsTotal() == 0) { if(model_state == 1) check_bullish_setup(); else if(model_state == -1) check_bearish_setup(); } //--- Manage the position we have else { //--- How should we close our positions? if(user_close_type == MA_CLOSE) { ma_close_positions(); } else { ai_close_positions(); } } } //+------------------------------------------------------------------+
Definamos ahora cómo debería nuestro sistema de IA cerrar sus operaciones. Si nuestro sistema de IA detecta que los niveles de precios cambiarán de una manera que contradice la afirmación de nuestra posición, cerraremos nuestras operaciones.
//+------------------------------------------------------------------+ //| Close whenever our AI detects a reversal | //+------------------------------------------------------------------+ void ai_close_positions(void) { if(system_state != model_state) { Alert("Reversal detected by our AI system,closing open positions"); Trade.PositionClose("EURUSD"); } }
Por otro lado, si confiamos en la media móvil para cerrar nuestras posiciones, entonces querremos cerrar cualquier operación de venta si el precio de cierre está por encima de la media móvil y viceversa para nuestras operaciones de venta.
//+------------------------------------------------------------------+ //| Close whenever price reverses the moving average | //+------------------------------------------------------------------+ void ma_close_positions(void) { //--- Is our buy position possibly weakening? if(system_state == 1) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) Trade.PositionClose("EURUSD"); } //--- Is our sell position possibly weakening? if(system_state == -1) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) Trade.PositionClose("EURUSD"); } }
Para abrir una operación, primero necesitaremos una ruptura de la Banda de Bollinger seguida de la confirmación del indicador RSI y, por último, también querríamos ver el promedio móvil en el lado derecho en relación con el precio.
//+------------------------------------------------------------------+ //| Check bearish setup | //+------------------------------------------------------------------+ void check_bearish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) < bb_low_buffer[0]) { if(50 > rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) { Trade.Sell(0.3,"EURUSD",bid,0,0,"EURUSD MTF AI"); system_state = -1; } } } } //+------------------------------------------------------------------+ //| Check bullish setup | //+------------------------------------------------------------------+ void check_bullish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) > bb_high_buffer[0]) { if(50 < rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) { Trade.Buy(0.3,"EURUSD",ask,0,0,"EURUSD MTF AI"); system_state = 1; } } } }
Esta función actualmente mostrará solo la predicción del modelo.
//+------------------------------------------------------------------+ //| Display account stats | //+------------------------------------------------------------------+ void display_stats(void) { Comment("Forecast: ",model_output[0]); }
Obtener una predicción de nuestro modelo y almacenarla utilizando un indicador binario.
//+------------------------------------------------------------------+ //| Fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get inputs model_input.CopyRates("EURUSD",PERIOD_MN1,COPY_RATES_CLOSE,0,1); //--- Fetch a prediction from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output); //--- Store the model's prediction as a flag if(model_output[0] > model_input[0]) { model_state = -1; } else if(model_output[0] < model_input[0]) { model_state = 1; } }
Especifiquemos ahora la función que liberará los recursos que no necesitamos.
//+------------------------------------------------------------------+ //| Release the resources we don't need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(onnx_model); IndicatorRelease(ma_hanlder); IndicatorRelease(rsi_hanlder); IndicatorRelease(bb_hanlder); ExpertRemove(); }
Cada vez que se cotice un nuevo precio, se llamará esta función para actualizar los datos de mercado que tenemos.
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update_market_data(void) { //--- Update all our technical data bid = SymbolInfoDouble("EURUSD",SYMBOL_BID); ask = SymbolInfoDouble("EURUSD",SYMBOL_ASK); CopyBuffer(ma_hanlder,0,0,1,ma_buffer); CopyBuffer(rsi_hanlder,0,0,1,rsi_buffer); CopyBuffer(bb_hanlder,0,0,1,bb_mid_buffer); CopyBuffer(bb_hanlder,1,0,1,bb_high_buffer); CopyBuffer(bb_hanlder,2,0,1,bb_low_buffer); }
Por último, definamos la función que creará nuestro modelo ONNX a partir del buffer que definimos anteriormente.
//+------------------------------------------------------------------+ //| Load our ONNX model | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from our buffer onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model if(onnx_model == INVALID_HANDLE) { //--- Give feedback Comment("Failed to create the ONNX model"); //--- We failed to create the model return(false); } //--- Specify the I/O shapes ulong input_shape[] = {1,1}; ulong output_shape[] = {1,1}; //--- Validate the I/O shapes if(!(OnnxSetInputShape(onnx_model,0,input_shape)) || !(OnnxSetOutputShape(onnx_model,0,output_shape))) { //--- Give feedback Comment("We failed to define the correct input shapes"); //--- We failed to define the correct I/O shape return(false); } return(true); } //+------------------------------------------------------------------+
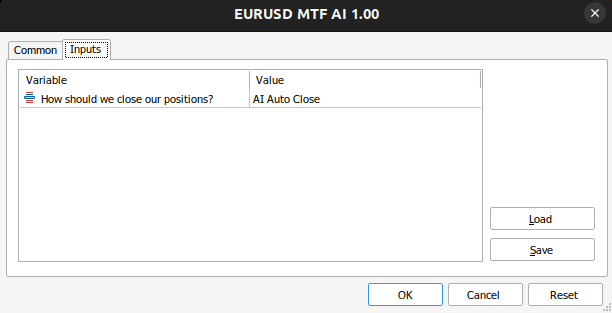
Figura 13: Aportaciones de nuestro asesor experto.
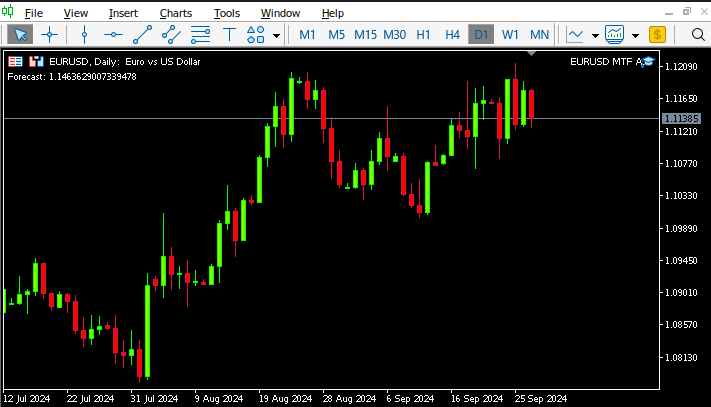
Figura 14: Nuestro asesor experto en acción.
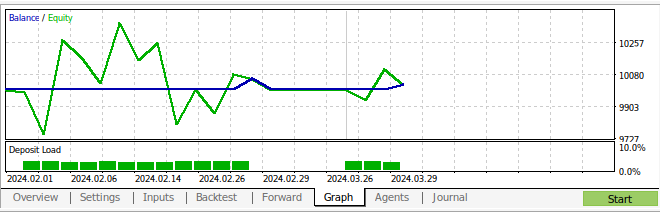
Figura 15: Los resultados de las pruebas retrospectivas de nuestra estrategia
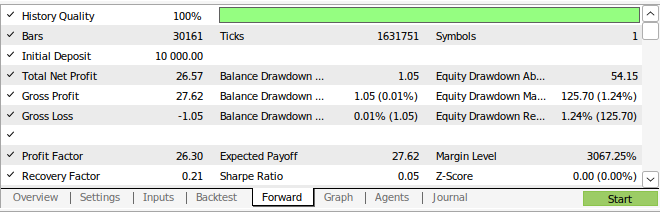
Figura 16: Resultados de las pruebas adelantadas (walk forward) de nuestra estrategia.
Conclusión
En este artículo, hemos demostrado que los marcos temporales mensuales y horarios parecen ser los más estables para predecir el par EURUSD. No podemos estar seguros de que esto sea válido para todos los mercados existentes. Del mismo modo, en el futuro también debemos considerar la búsqueda de más marcos temporales posibles para asegurarnos de que no estamos pasando por alto ningún marco temporal óptimo. Además, hay más ajustes que podemos hacer en nuestro enfoque para buscar métricas de menor error. Por ejemplo, podríamos tener curiosidad por saber si existe una combinación de marcos temporales que pudieran reducir aún más nuestros niveles de error.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15972
Algoritmo de búsqueda orbital atómica - Atomic Orbital Search (AOS)
Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
Simulador rápido de estrategias comerciales en Python usando Numba
Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte V): Modelos profundos de Markov
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso