Die Grenzen des maschinellen Lernens überwinden (Teil 1): Mangel an interoperablen Metriken
14
1
Bedauerlicherweise besteht die Gefahr, dass andere Instrumente, auf die wir uns bei unseren Handelsstrategien stützen, durch die blinde Befolgung der „Best Practices“ zum Schweigen gebracht werden, und die Praktiker sollten nicht glauben, dass dieses Problem nur für technische Indikatoren gilt.
In dieser Artikelserie werden wir uns mit kritischen Problemen befassen, denen algorithmische Händler tagtäglich ausgesetzt sind, und zwar durch genau die Richtlinien und Praktiken, die sie bei der Verwendung von Modellen des maschinellen Lernens schützen sollen. Kurz gesagt, wenn die Modelle für maschinelles Lernen, die täglich in der MQL5-Cloud eingesetzt werden, die in dieser Diskussion dargelegten Fakten noch vor den verantwortlichen Praktikern kennen, droht Ärger. Die Anleger können schnell feststellen, dass sie einem größeren Risiko ausgesetzt sind, als sie erwartet haben.
Um ehrlich zu sein, werden solche Probleme selbst in den weltweit führenden Büchern über statistisches Lernen nicht genügend betont. Der Gegenstand unserer Diskussion ist eine einfache Wahrheit, die jeder Praktiker in unserer Gemeinschaft kennen sollte:
„Es kann analytisch bewiesen werden, dass die erste Ableitung euklidischer Dispersionsmetriken wie RMSE, MAE oder MSE durch den Mittelwert des Ziels gelöst werden kann.“
Praktiker, die sich dieser Tatsache und ihrer Auswirkungen bereits bewusst sind, brauchen an dieser Stelle nicht weiterzulesen.
Aber gerade die Praktiker, die nicht verstehen, was das bedeutet, muss ich mit diesem Artikel dringend erreichen. Kurz gesagt, die Regressionsmetriken, die wir zur Erstellung unserer Modelle verwenden, eignen sich nicht zur Modellierung von Vermögenserträgen.
In diesem Artikel erfahren Sie, wie dies geschieht, welche Gefahren es für Sie birgt und welche Änderungen Sie vornehmen können, um dieses Prinzip als Kompass zu nutzen, um die Märkte herauszufiltern, wenn Sie die Wahl zwischen Hunderten von potenziellen Märkten haben, die Sie handeln könnten.
Praktiker, die einen tieferen Nachweis wünschen, finden Literatur von der Harvard University, in der die Grenzen von Metriken wie dem RMSE erörtert werden. Insbesondere bietet der Harvard-Artikel einen analytischen Beweis dafür, dass der Mittelwert der Stichprobe den RMSE minimiert. Der Leser findet den Artikel hier.
Andere Institutionen wie das Social Science Research Network (SSRN) führen ein Journal mit veröffentlichten und begutachteten Arbeiten aus verschiedenen Bereichen, darunter auch eine für unsere Diskussion nützliche Arbeit, in der alternative Verlustfunktionen als Ersatz für den RMSE bei der Bewertung von Vermögenswerten untersucht werden. In dem von mir für den Leser ausgewählten Beitrag werden andere Arbeiten auf diesem Gebiet besprochen und eine Zusammenfassung der aktuellen Literatur gegeben, bevor ein neuer Ansatz vorgestellt wird. Dieser Artikel ist für den Leser leicht zugänglich, er ist here.
Ein Gedankenexperiment (das sollte man wissen).
Stellen Sie sich vor, Sie nehmen an einem Lotterie-Wettbewerb teil. Sie und 99 andere Personen werden nach dem Zufallsprinzip ausgewählt, um um einen Jackpot von 1.000.000 Dollar zu spielen. Die Regeln sind einfach: Sie müssen die Körpergröße der anderen 99 Teilnehmer erraten. Der Gewinner ist die Person mit dem geringsten Gesamtfehler über alle 99 Tipps hinweg.
Jetzt kommt der Clou: Stellen Sie sich für dieses Beispiel vor, die durchschnittliche Körpergröße eines Menschen beträgt weltweit 1,1 Meter. Wenn Sie einfach 1,1 Meter für alle tippen, könnten Sie den Jackpot gewinnen, auch wenn jede einzelne Vorhersage technisch gesehen falsch ist. Warum? Denn in verrauschten, unsicheren Umgebungen führt das Erraten des Durchschnitts in der Regel zum kleinsten Gesamtfehler.
Die Parallele zum Handel
Dieses Gedankenexperiment sollte dem Leser verdeutlichen, wie die meisten Modelle des maschinellen Lernens für den Einsatz auf den Finanzmärkten ausgewählt werden.
Nehmen wir zum Beispiel an, Sie erstellen ein Modell zur Vorhersage der Rendite des S&P 500. Ein Modell, das immer den historischen Durchschnitt des Index vorhersagt, d. h. etwa 7 % pro Jahr, könnte komplexere Modelle übertreffen, wenn man sie anhand von Kennzahlen wie RMSE, MAE oder MSE beurteilt. Aber hier ist die Falle: Dieses Modell hat nichts Nützliches gelernt. Es hat sich lediglich um den statistischen Mittelwert herum gruppiert. Und schlimmer noch, die Metriken und Validierungsverfahren, auf die vertraut wurden, belohnten ihn dafür.
Anmerkung für Anfänger: RMSE (Root Mean Square Error) ist eine „Einheit“, die zur Beurteilung der Qualität von maschinellen Lernmodellen zur Vorhersage realer Werte verwendet wird.
Es bestraft große Abweichungen, ohne sich darum zu kümmern, warum das Modell den Fehler gemacht hat, aber bedenken Sie, dass einige dieser Abweichungen, für die das Modell bestraft wird, eigentlich Gewinne waren.
Ein Modell, das immer den Durchschnitt vorhersagt (auch wenn es den Markt nicht versteht), kann also auf dem Papier gut aussehen, wenn es mit dem RMSE beurteilt wird. Dies führt leider dazu, dass wir Modelle erstellen, die zwar mathematisch fundiert, aber praktisch nutzlos sind.
Was wirklich vor sich geht
Finanzdaten sind verrauscht. Wir können wichtige Variablen wie das tatsächliche globale Angebot und die Nachfrage, die Stimmung der Anleger oder die Tiefe der institutionellen Orderbücher nicht beobachten. Um den Fehler zu minimieren, wird Ihr Modell also das tun, was statistisch am logischsten ist: den Durchschnitt vorhersagen.
Und der Leser muss verstehen, dass dies mathematisch gesehen eine solide Praxis ist. Durch die Vorhersage des Mittelwerts werden die häufigsten Regressionsfehler minimiert. Aber beim Handel geht es nicht darum, statistische Fehler zu minimieren, sondern darum, unter Unsicherheit profitable Entscheidungen zu treffen. Und diese Unterscheidung ist wichtig. In unserer Gemeinschaft ist ein solches Verhalten mit einer Überanpassung vergleichbar, aber die Statistiker, die diese Modelle erstellt haben, haben die Dinge nicht so gesehen wie wir.
Es wäre naiv zu glauben, dass dieses Problem nur bei Regressionsmodellen auftritt. Bei Klassifizierungsaufgaben kann ein Modell Fehler minimieren, indem es einfach immer die häufigste Klasse in der Trainingsstichprobe vorhersagt. Und wenn die größte Klasse im Trainingssatz zufällig der größten Klasse in der gesamten Population entspricht, kann der Praktiker meiner Meinung nach schnell erkennen, wie ein Modell seine Fähigkeiten leicht vortäuschen kann.
Belohnungs-Hacking: Wenn Modelle durch Betrug gewinnen
Dieses Phänomen wird als „Reward Hacking“ bezeichnet: Ein Modell erreicht erwünschte Leistungen, indem es unerwünschtes Verhalten erlernt. Im Falle des Handels führt das Reward Hacking dazu, dass Praktiker ein Modell wählen, das geschickt erscheint, aber in Wirklichkeit spielt das Modell nur ein Spiel mit dem Durchschnitt, ein statistisches Kartenhaus. Man denkt, dass man etwas gelernt hat, aber in Wirklichkeit hat man das statistische Äquivalent zu der Aussage „jeder ist 1,1 Meter groß“ gemacht. Und die RMSE akzeptiert das jedes Mal, ohne zu fragen.
Echte Beweise
Da unsere Motivation nun klar ist, wollen wir uns von der Allegorie lösen und stattdessen reale Marktdaten betrachten. Mit Hilfe der MetaTrader 5 Python API habe ich auf 333 Märkte meines Brokers zugegriffen. Wir haben nach Märkten mit mindestens vier Jahren realer historischer Daten gefiltert. Durch diesen Filter wurde das Universum der Märkte auf 119 reduziert.
Anschließend haben wir für jeden Markt zwei Modelle erstellt:
- Kontrollmodell: Es sagt immer die durchschnittliche 10-Tage-Rendite voraus.
- Vorhersagemodell: Es versucht zu lernen und zukünftige Erträge vorherzusagen.
Unsere Ergebnisse
In 91,6 % der von uns getesteten Märkte gewann das Kontrollmodell. Das heißt, dass das Modell, das immer den historischen Durchschnitt der 10-Tage-Rendite vorhersagt, über 4 Jahre in 91 % der Fälle einen geringeren Fehler aufweist! Wie der Praktiker bald sehen wird, war die Verbesserung vernachlässigbar, selbst wenn wir tiefere neuronale Netze ausprobierten.
Sollte der Praktiker also die „Best Practices“ des maschinellen Lernens befolgen und immer das Modell wählen, das den geringsten Fehler produziert, was, wie Sie sich erinnern, bedeutet, dass das Modell immer die durchschnittliche Rendite vorhersagt?
Anmerkung für Anfänger: Das bedeutet nicht, dass maschinelles Lernen für Sie nicht funktionieren kann. Das bedeutet, dass Sie äußerst vorsichtig sein müssen, wie „gute Leistung“ in Ihrem Handelskontext definiert werden sollte. Wenn Sie nicht vorsichtig sind, können wir davon ausgehen, dass Sie unwissentlich ein Modell wählen, das für die Vorhersage der durchschnittlichen Marktrendite belohnt wird.
Und was nun?
Die Schlussfolgerung ist klar: Die von uns derzeit verwendeten Bewertungskennzahlen - RMSE, MSE, MAE - sind nicht für den Handel geeignet. Sie wurden in der Statistik, der Medizin und anderen Naturwissenschaften geboren, in denen die Vorhersage des Mittelwerts sinnvoll ist. Aber in unserer algorithmischen Handelsgemeinschaft kann die Vorhersage der durchschnittlichen Rendite manchmal sogar schlechter sein als gar keine Vorhersage, und manchmal ist es sicherer, überhaupt keine KI zu haben. Aber KI ohne Verständnis ist niemals sicher!
Wir brauchen Bewertungsrahmen, die nützliche Fähigkeiten belohnen, nicht statistische Kooperationsmetriken. Wir brauchen Metriken, die Gewinn und Verlust verstehen. Darüber hinaus brauchen wir Schulungsprotokolle, die geiziges Verhalten bestrafen, und Verfahren, die das Modell ermutigen, die Werte unserer Gemeinschaft widerzuspiegeln und gleichzeitig die Realitäten des Handels zu lernen. Und genau darum geht es in dieser Serie. Eine einzigartige Reihe von Problemen, die nicht direkt durch den Markt verursacht werden. Sie ergeben sich vielmehr aus den Werkzeugen, die wir einsetzen wollen, und werden selten in anderen Artikeln, akademischen Büchern über statistisches Lernen oder sogar in unseren eigenen Diskussionen in der Gemeinschaft diskutiert.
Praktiker müssen zu ihrer eigenen Sicherheit mit diesen Fakten vertraut sein. Bedauerlicherweise ist das grundlegende Wissen um diese Einschränkungen nicht bei allen Mitgliedern unserer Gemeinschaft vorhanden. Im Alltag werden sehr gefährliche statistische Praktiken bedenkenlos wiederholt.
Die ersten Schritte
Lassen Sie uns sehen, ob das, was wir bisher erörtert haben, etwas taugt. Laden Sie unsere Standardbibliotheken.
import pandas as pd import numpy as np import matplotlib.pyplot as plt import MetaTrader5 as mt5 import multiprocessing as mp
Legen wir fest, wie weit wir in die Zukunft vorausschauen wollen.
HORIZON = 10Laden Sie das MetaTrader 5-Terminal, damit wir echte Marktdaten abrufen können.
if(not mt5.initialize()): print("Failed to load MT5")
Hier finden Sie eine umfassende Liste aller verfügbaren Symbole.
symbols = mt5.symbols_get()
Extrahieren Sie einfach die Namen der Symbole.
symbols[0].name
symbol_names = []
for i in range(len(symbols)):
symbol_names.append(symbols[i].name)Nun wollen wir sehen, ob wir ein Modell übertreffen können, das immer den Mittelwert vorhersagt.
from sklearn.linear_model import Ridge from sklearn.model_selection import TimeSeriesSplit,cross_val_score
Erstellen wir einen Zeitreihen-Validierungssplitter.
tscv = TimeSeriesSplit(n_splits=5,gap=HORIZON)Wir benötigen eine Methode, die unsere Fehlerquote bei der Vorhersage der durchschnittlichen Marktrendite und unsere Fehlerquote bei der Vorhersage der zukünftigen Marktrendite angibt.
def null_test(name): data_amount = 365 * 4 f_data = pd.DataFrame(mt5.copy_rates_from_pos(name,mt5.TIMEFRAME_D1,0,data_amount)) if(f_data.shape[0] < data_amount): print(f"{symbol_names[i]} did not have enough data!") return(None) f_data['time'] =pd.to_datetime(f_data['time'],unit='s') f_data['target'] = f_data['close'].shift(-HORIZON) - f_data['close'] f_data.dropna(inplace=True) model = Ridge() res = [] res.append(np.mean(np.abs(cross_val_score(model,f_data.loc[:,['open']] * 0,f_data['target'],cv=tscv)))) res.append(np.mean(np.abs(cross_val_score(model,f_data.loc[:,['open','high','low','close']],f_data['target'],cv=tscv)))) return(res)
Nun werden wir den Test für alle uns zur Verfügung stehenden Märkte durchführen.
res = pd.DataFrame(columns=['Mean Forecast','Direct Forecast'],index=symbol_names) for i in range(len(symbol_names)): test_score = null_test(symbol_names[i]) if(test_score is None): print(f"{symbol_names[i]} does not have enough data!") res.iloc[i,:] = [np.nan,np.nan] continue res.iloc[i,0] = test_score[0] res.iloc[i,1] = test_score[1] print(f"{i/len(symbol_names)}% complete.") res['Score'] = ((res.iloc[:,1] / res.iloc[:,0])) res.to_csv("Deriv Null Model Test.csv")
0.06606606606606606% abgeschlossen.
0.06906906906906907% abgeschlossen.
0.07207207207207207% abgeschlossen.
...
GBPUSD RSI Trend Down Index hatte nicht genügend Daten!
GBPUSD RSI Trend Down Index hat nicht genügend Daten!
Wie viele der Märkte, die uns zur Verfügung standen, konnten wir analysieren?
#How many markets did we manage to investigate? test = pd.read_csv("Null Model Test.csv") print(f"{(test.dropna().shape[0] / test.shape[0]) * 100}% of Markets Were Evaluated")
35.73573573573574% der Märkte wurden ausgewertet
Wir werden nun unsere 119 Märkte auf der Grundlage eines jedem Markt zugeordneten Punktwerts gruppieren. Das Ergebnis ist das Verhältnis zwischen unserem Fehler bei der Vorhersage des Marktes und unserem Fehler bei der Vorhersage der durchschnittlichen Rendite. Werte kleiner als 1 sind beeindruckend, weil sie bedeuten, dass wir ein Modell, das immer die durchschnittliche Rendite vorhersagt, übertreffen. Andernfalls bestätigen Werte größer als 1 unsere Motivation für die Durchführung dieser Übung im Lichte dessen, was wir in der Einleitung dieses Artikels mitgeteilt haben.
Anmerkung für Anfänger: Die von uns kurz skizzierte Scoring-Methode ist im Bereich des maschinellen Lernens nichts Neues. Es handelt sich um eine Metrik, die gemeinhin als r-Quadrat bekannt ist. Sie gibt Aufschluss darüber, wie viel der Varianz in der Zielvorgabe wir mit unserem vorgeschlagenen Modell erklären können. Wir verwenden nicht die exakte r-Quadrat-Formel, die Sie vielleicht aus Ihrem Selbststudium kennen.
Lassen Sie uns zunächst alle Märkte gruppieren, bei denen wir eine Punktzahl von weniger als 1 erhalten haben.
res.loc[res['Score'] < 1]
| Name des Marktes | Mittlere Vorhersage | Direkte Vorhersage | Score |
|---|---|---|---|
| AUDCAD | 0.022793 | 0.018566 | 0.814532 |
| EURCAD | 0.037192 | 0.027209 | 0.731587 |
| NZDCAD | 0.019124 | 0.015117 | 0.790466 |
| USDCNH | 0.125586 | 0.112814 | 0.898297 |
Bei welchem Prozentsatz aller von uns getesteten Märkte haben wir ein Modell, das stets die durchschnittliche Marktrendite vorhersagt, über 4 Jahre hinweg übertroffen? Ungefähr 8%.
res.loc[res['Score'] < 1].shape[0] / res.shape[0]
0.08403361344537816
Das bedeutet also auch, dass wir über vier Jahre hinweg ein Modell, das stets die durchschnittliche Rendite für etwa 91,6 % aller von uns getesteten Märkte vorhersagt, nicht übertreffen konnten.
res.loc[res['Score'] > 1].shape[0] / res.shape[0]
0.9159663865546218
An dieser Stelle werden einige Leser vielleicht denken: „Der Autor hat einfache lineare Modelle verwendet, wenn wir uns Zeit nehmen und flexiblere Modelle entwickeln würden, könnten wir das Modell, das die durchschnittliche Rendite vorhersagt, immer übertreffen. Das kann nicht sein“. Das ist zum Teil richtig. Wir wollen ein tiefes Neuronales Netz auf dem EURUSD-Markt aufbauen, um das Modell zur Vorhersage der durchschnittlichen Marktrendite zu übertreffen.
Zunächst benötigen wir ein MQL5-Skript, um detaillierte Marktinformationen über den EURUSD-Wechselkurs zu erfassen. Wir werden die Zuwächse in jedem der vier Preisniveaus und auch ihre Zuwächse im Verhältnis zueinander aufzeichnen.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| System constants | //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| File name | //+------------------------------------------------------------------+ string file_name = Symbol() + " IID Candlestick Recognition.csv"; //+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input int size = 3000; input int HORIZON = 10; //+------------------------------------------------------------------+ //| Our script execution | //+------------------------------------------------------------------+ void OnStart() { //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i=size;i>=1;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close","Delta Open","Delta High","Delta Low","Delta Close","O - H","O - L","O - C","H - L","H - C","L - C"); } else { FileWrite(file_handle, iTime(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i), iClose(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iOpen(_Symbol,PERIOD_CURRENT,i + HORIZON), iHigh(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,i + HORIZON), iLow(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i + HORIZON), iClose(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i + HORIZON), iOpen(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| Undefine system constants | //+------------------------------------------------------------------+ #undef HORIZON
Ziehen Sie nun Ihr Skript per Drag & Drop auf das Chart, um historische Daten über den Markt abzurufen, und schon kann es losgehen.
#Read in market data HORIZON = 10 data = pd.read_csv('EURUSD IID Candlestick Recognition.csv') #Label the data data['Null'] = 0 data['Target'] = data['Close'].shift(-HORIZON) - data['Close'] #Drop the last HORIZON rows of data data = data.iloc[:-HORIZON,:] data
Leser, die glauben, dass tiefe neuronale Netze und ausgefeilte Modelle das Problem lösen, ein Modell zu übertreffen, das die durchschnittliche Marktrendite vorhersagt, werden schockiert sein, wenn sie lesen, was im Rest dieses Artikels folgt.
Ich empfehle Ihnen, dieses Experiment mit Ihrem Broker zu wiederholen, bevor Sie Ihre Modelle mit Ihrem Kapital einsetzen. Laden wir nun die Scikit-Learn-Tools, um zu vergleichen, wie gut unser tiefes neuronales Netzwerk im Vergleich zu unserem einfachen linearen Modell abschneidet.
#Load our models from sklearn.neural_network import MLPRegressor from sklearn.linear_model import Ridge from sklearn.model_selection import TimeSeriesSplit,train_test_split,cross_val_score
Teilen wir die Daten auf.
#Split the data into half train,test = train_test_split(data,test_size=0.5,shuffle=False)
Wir erstellen ein Zeitreihenvalidierungsobjekt
#Create a time series validation object tscv = TimeSeriesSplit(n_splits=5,gap=HORIZON)
und passen das Modell an, das immer die durchschnittliche Marktrendite vorhersagt. Der Fehler, der dadurch entsteht, dass immer der Mittelwert vorhergesagt wird, wird als „Gesamtsumme der Quadrate“ bezeichnet. Der TSS ist ein kritischer Fehler-Benchmark beim maschinellen Lernen, der uns sagt, wo Norden ist.
#Fit the model predicting the mean on the train set null_model = Ridge() null_model.fit(train[['Null']],train['Target']) tss = np.mean(np.abs(cross_val_score(null_model,test[['Null']],test['Target'],cv=tscv,scoring='neg_mean_absolute_error'))) tss
np.float64(0.011172426520738554)
Definieren wir unseren Input und unser Ziel.
X = data.iloc[:,4:-2].columns y = 'Target'
Passen wir unser tiefes neuronales Netz an. Ich möchte den Leser ermutigen, dieses neuronale Netz nach eigenem Ermessen anzupassen, um zu sehen, ob er das Zeug dazu hat, den Mittelwert zu übertreffen.
#Let us now try to outperform the null model model = MLPRegressor(activation='logistic',solver='lbfgs',random_state=0,shuffle=False,hidden_layer_sizes=(len(X),200,50),max_iter=1000,early_stopping=False) model.fit(train.loc[:,X],train['Target']) rss = np.mean(np.abs(cross_val_score(model,test.loc[:,X],test['Target'],cv=tscv,scoring='neg_mean_absolute_error'))) print(f"Test Passed: {rss < tss} || New R-Squared Metric {rss/tss}") res = [] res.append(rss) res.append(tss) sns.barplot(res,color='black') plt.axhline(tss,color='red',linestyle=':') plt.grid() plt.ylabel("RMSE") plt.xticks([0,1],['Deep Neural Network','Null Model']) plt.title("Our Deep Neural Network vs The Null Model") plt.show()
Nach vielen Konfigurationen, Anpassungen und Optimierungen war ich in der Lage, das Modell zur Vorhersage der durchschnittlichen Rendite mithilfe eines tiefen neuronalen Netzwerks zu besiegen. Aber sehen wir uns doch einmal genauer an, was hier passiert.
Abb. 1: Ein Modell zu übertreffen, das die durchschnittliche Marktrendite vorhersagt, ist eine große Herausforderung.
Veranschaulichen wir uns die Verbesserungen, die unser tiefes neuronales Netz erzielt. Zunächst werde ich ein Raster aufstellen, mit dem wir die Verteilung der Marktrenditen in der Testgruppe und die Verteilung der von unserem Modell vorhergesagten Renditen bewerten können. Wir speichern die Ergebnisse, die das Modell für die Testmenge vorhersagt.
predictions = model.predict(test.loc[:,X])
Zunächst markieren wir die durchschnittliche Marktrendite, die wir im Trainingsset beobachtet haben, als rote gestrichelte Linie in der Mitte des Charts.
plt.title("Visualizing Our Improvements")
plt.plot()
plt.grid()
plt.xlabel("Return")
plt.axvline(train['Target'].mean(),color='red',linestyle=':')
legend = ['Train Mean']
plt.legend(legend)
Abb. 2: Visualisierung der durchschnittlichen Marktrendite aus dem Trainingssatz
Überlagern wir nun die Vorhersage des Modells für die Testmenge mit dem durchschnittlichen Ergebnis der Trainingsmenge. Wie der Leser sehen kann, liegen die Vorhersagen des Modells um den Mittelwert der Trainingsmenge herum. Das Problem wird jedoch deutlich, wenn wir schließlich die tatsächliche Verteilung, der der Markt gefolgt ist, als schwarze Grafik darunter legen.
plt.title("Visualizing Our Improvements") plt.plot() plt.grid() plt.xlabel("Return") plt.axvline(train['Target'].mean(),color='red',linestyle=':') sns.histplot(predictions,color='blue') legend = ['Train Mean','Model Predictions'] plt.legend(legend)
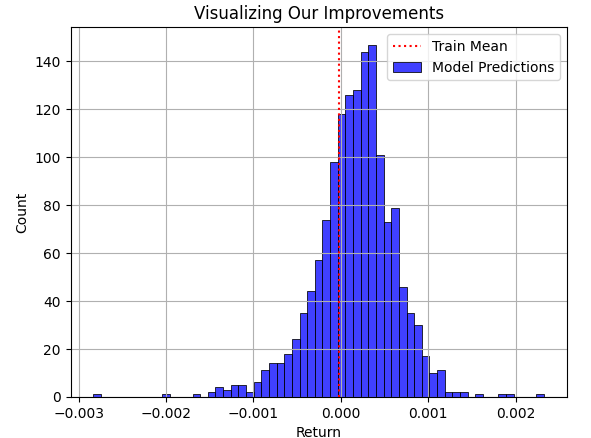
Abb. 3: Visualisierung der Vorhersagen unseres Modells in Bezug auf die durchschnittliche Rendite, die das Modell in der Trainingsgruppe beobachtet hat
Der blaue Bereich der Vorhersagen unseres Modells erschien in Abb. 3 vernünftig, aber wenn wir schließlich die tatsächliche Verteilung des Marktes in Abb. 4 betrachten, wird deutlich, dass dieses Modell für die gestellte Aufgabe nicht geeignet ist. Das Modell erfasst nicht die Breite der tatsächlichen Marktverteilung, in der sich einige der größten Gewinne und Verluste vor der Wahrnehmung des Modells verstecken. Bedauerlicherweise führt der RMSE die Praktiker häufig zu solchen Modellen, wenn die Metrik des RMSE vom zuständigen Praktiker nicht sorgfältig verstanden, beachtet und interpretiert wird. Die Verwendung eines solchen Modells im realen Handel wäre für Ihre Erfahrung im Live-Handel katastrophal.
plt.title("Visualizing Our Improvements") plt.plot() plt.grid() plt.xlabel("Return") plt.axvline(train['Target'].mean(),color='red',linestyle=':') sns.histplot(test['Target'],color='black') sns.histplot(predictions,color='blue') legend = ['Train Mean','Test Distribution','Model Prediction'] plt.legend(legend)
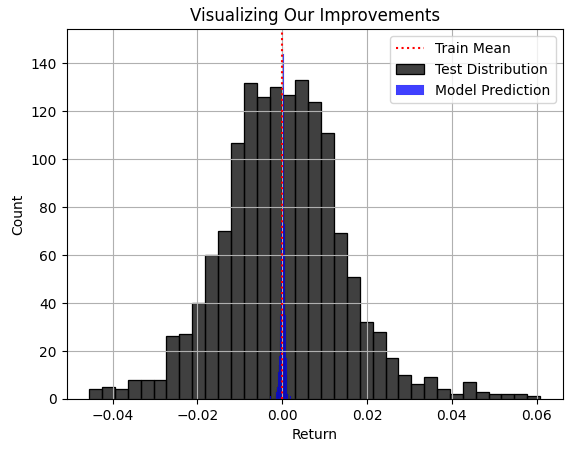
Abb. 4: Visualisierung der Verteilung der Vorhersagen unserer Modelle in Bezug auf die tatsächliche Verteilung des Marktes
Unser Lösungsvorschlag
An dieser Stelle haben wir dem Leser gezeigt, dass Kennzahlen wie der RMSE leicht optimiert werden können, indem immer die durchschnittliche Marktrendite vorhergesagt wird, und wir haben dargelegt, warum dies unattraktiv ist, weil der RMSE uns häufig mitteilen könnte, dass ein solch nutzloses Modell das beste ist, was wir tun können. Wir haben zum Ausdruck gebracht, dass es eindeutig einen Bedarf an Verfahren und neuen Techniken gibt, die explizit:
- das reale Marktverständnis testen,
- den Unterschied zwischen Gewinn und Verlust verstehen und
- lästige Umarmungen verhindern.
Ich möchte eine einzigartige Modellarchitektur vorschlagen, die für den Leser ein möglicher Lösungsvorschlag sein könnte. Ich bezeichne diese Strategie als „Dynamic Regime Switching Models“ (dynamische Regime-Umschaltung) oder kurz DRS. In einer separaten Diskussion über Setups mit hoher Wahrscheinlichkeit haben wir festgestellt, dass die Modellierung des durch eine Handelsstrategie erzielten Gewinns/Verlusts einfacher sein kann als der Versuch, den Markt direkt vorherzusagen. Leser, die diesen Artikel noch nicht gelesen haben, finden ihn hier verlinkt.
Wir werden diese Beobachtung nun in interessanter Weise ausnutzen. Wir werden zwei identische Modelle erstellen, um entgegengesetzte Versionen einer Handelsstrategie zu simulieren. Ein Modell geht immer davon aus, dass sich der Markt in einem trendfolgenden Zustand befindet, während das letzte Modell immer davon ausgeht, dass sich der Markt in einem Zustand der Umkehr zum Mittelwert befindet. Jedes Modell wird separat trainiert und hat keine Möglichkeit, seine Vorhersagen mit dem anderen Modell abzustimmen.
Der Leser sollte sich daran erinnern, dass die Hypothese des effizienten Marktes den Anlegern lehrt, dass der Anleger durch den Kauf und Verkauf der gleichen Menge desselben Vermögenswerts perfekt abgesichert ist, und wenn beide Positionen gleichzeitig eröffnet und geschlossen werden, beträgt der Gesamtgewinn 0, ohne Berücksichtigung etwaiger Transaktionsgebühren. Daher sollten wir davon ausgehen, dass unsere Modelle immer mit dieser Tatsache übereinstimmen sollten. In der Tat können wir prüfen, ob unsere Modelle mit dieser Wahrheit übereinstimmen; Modelle, die nicht mit dieser Wahrheit übereinstimmen, haben kein echtes Marktverständnis.
Daher können wir die Notwendigkeit, sich auf Messgrößen wie den RMSE zu verlassen, dadurch ersetzen, dass wir stattdessen prüfen, ob unser DVM-Modell ein Verständnis dieses Prinzips, das die Marktstruktur aufbaut, demonstriert. Hier kommt unser Test zum realen Marktverständnis ins Spiel. Wenn unsere beiden Modelle die Realitäten des Handels wirklich verstehen, dann sollte die Summe ihrer Prognosen immer 0 ergeben. Wir werden unsere Modelle an die Trainingsmenge anpassen und sie dann außerhalb der Stichprobe testen, um zu sehen, ob die Vorhersagen des Modells immer 0 ergeben, selbst wenn die Modelle unterbelastet sind.
Es sei daran erinnert, dass die Vorhersagen der Modelle in keiner Weise koordiniert werden. Die Modelle werden getrennt voneinander trainiert und kennen sich nicht gegenseitig. Wenn die Modelle also nicht wünschenswerte Fehlermetriken „hacken“, sondern wirklich die zugrunde liegende Struktur des Marktes lernen, dann werden sie beweisen, dass sie ihre Vorhersagen durch ethisches Verhalten erreicht haben, wenn beide Vorhersagen des Modells gleich 0 sind.
Nur eines dieser Modelle kann zu einem bestimmten Zeitpunkt eine positive Belohnung erwarten. Wenn die Summe der Vorhersagen unseres Modells nicht 0 ist, haben die Modelle möglicherweise unbeabsichtigt eine Tendenz gelernt, die gegen die Hypothese des effizienten Marktes verstößt. Andernfalls können wir im besten Fall dynamisch zwischen diesen beiden Marktzuständen hin- und herwechseln, und zwar mit einem Maß an Vertrauen, das wir in der Vergangenheit nicht kannten. Nur ein Modell sollte zu einem bestimmten Zeitpunkt eine positive Rendite erwarten, und unsere Handelsphilosophie besteht darin, dass wir glauben, dass dieses Modell dem verborgenen Zustand entspricht, in dem sich der Markt derzeit befindet. Und das könnte für uns möglicherweise mehr wert sein als niedrige RMSE-Werte.
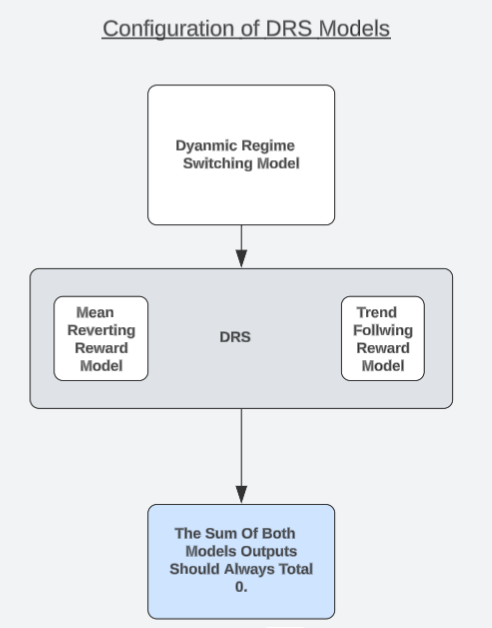
Abb. 5: Verstehen der allgemeinen Architektur unserer DRS-Modelle
Daten von unserem Terminal abrufen
Unsere Daten sollten so detailliert wie möglich sein, um die besten Ergebnisse zu erzielen. Daher verfolgen wir die aktuellen Werte unserer technischen Indikatoren und Kursniveaus sowie die Entwicklung dieser Marktdynamik zur gleichen Zeit.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //--- Define our moving average indicator #define MA_PERIOD 5 //--- Moving Average Period #define MA_TYPE MODE_SMA //--- Type of moving average we have #define HORIZON 10 //--- Our handlers for our indicators int ma_handle; //--- Data structures to store the readings from our indicators double ma_reading[]; //--- File name string file_name = Symbol() + " DRS Modelling.csv"; //--- Amount of data requested input int size = 3000; //+------------------------------------------------------------------+ //| Our script execution | //+------------------------------------------------------------------+ void OnStart() { int fetch = size + (HORIZON * 2); //---Setup our technical indicators ma_handle = iMA(_Symbol,PERIOD_CURRENT,MA_PERIOD,0,MA_TYPE,PRICE_CLOSE); //---Set the values as series CopyBuffer(ma_handle,0,0,fetch,ma_reading); ArraySetAsSeries(ma_reading,true); //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i=size;i>=1;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close","Delta O","Delta H","Delta Low","Delta Close","SMA 5","Delta SMA 5"); } else { FileWrite(file_handle, iTime(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i), iClose(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i) - iOpen(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iHigh(_Symbol,PERIOD_CURRENT,i) - iHigh(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iLow(_Symbol,PERIOD_CURRENT,i) - iLow(_Symbol,PERIOD_CURRENT,(i + HORIZON)), iClose(_Symbol,PERIOD_CURRENT,i) - iClose(_Symbol,PERIOD_CURRENT,(i + HORIZON)), ma_reading[i], ma_reading[i] - ma_reading[(i + HORIZON)] ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Die ersten Schritte
Um den Ball ins Rollen zu bringen, werden wir zunächst unsere Standardbibliotheken importieren.
#Load our libraries import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns
Jetzt können wir die Daten einlesen, die wir zuvor in die CSV-Datei geschrieben haben.
#Read in the data data = pd.read_csv("/content/drive/MyDrive/Colab Data/Financial Data/FX/EUR USD/DRS Modelling/EURUSD DRS Modelling.csv") data
Als wir unser MQL5-Skript erstellt haben, haben wir 10 Schritte in die Zukunft prognostiziert. Das müssen wir beibehalten.
#Recall that in our MQL5 Script our forecast horizon was 10 HORIZON = 10 #Calculate the returns generated by the market data['Return'] = data['Close'].shift(-HORIZON) - data['Close'] #Drop the last horizon rows data = data.iloc[:-HORIZON,:]
Kennzeichnen wir nun die Daten. Erinnern Sie sich daran, dass wir zwei Kennzeichnungen haben werden, von denen eines immer davon ausgeht, dass der Markt sich in einem Trend fortsetzen wird, und das andere davon, dass der Markt in einer Umkehr zum Mittelwert stecken bleibt.
#Now let us define the signals being generated by the moving average, in the DRS framework there are always at least n signals depending on the n states the market could be in #Our simple DRS model assumes only 2 states #First we will define the actions you should take assuming the market is in a trending state #Therefore if price crosses above the moving average, buy. Otherwise, sell. data['Trend Action'] = 0 data.loc[data['Close'] > data['SMA 5'], 'Trend Action'] = 1 data.loc[data['Close'] < data['SMA 5'], 'Trend Action'] = -1 #Now calculate the returns generated by the strategy data['Trend Profit'] = data['Trend Action'] * data['Return']
Nach der Kennzeichnung der trendfolgenden Aktionen fügen wir die Aktionen für die Umkehr zum Mittelwert ein.
#Now we will repeat the procedure assuming the market was mean reverting data['Mean Reverting Action'] = 0 data.loc[data['Close'] > data['SMA 5'], 'Mean Reverting Action'] = -1 data.loc[data['Close'] < data['SMA 5'], 'Mean Reverting Action'] = 1 #Now calculate the returns generated by the strategy data['Mean Reverting Profit'] = data['Mean Reverting Action'] * data['Return']
Durch diese Kennzeichnung der Daten hoffen wir, dass der Computer die Bedingungen erkennt, unter denen jede Strategie Geld verliert, und wann er auf die einzelnen Strategien hören sollte. Wenn wir den kumulativen Zielwert aufzeichnen, können wir deutlich sehen, dass der EURUSD-Markt über den ausgewählten Zeitraum in unseren Daten mehr Zeit damit verbracht hat, das Verhalten einer Umkehr zum Mittelwert zu zeigen, als einem Trend zu folgen. Es ist jedoch zu beachten, dass beide Linien plötzliche Erschütterungen aufweisen. Ich glaube, dass diese Schocks mit plötzlichen Regimewechseln auf dem Markt zusammenhängen können.
#If we plot our cumulative profit sums, we can see the profit and losses aren't evenly distributed between the two states plt.plot(data['Trend Profit'].cumsum(),color='black') plt.plot(data['Mean Reverting Profit'].cumsum(),color='red') #The mean reverting strategy appears to have been making outsized profits with respect to the trending stratetefgy #However, closer inspection reveals, that both strategies are profitable, but never at the same time! #The profit profiles of both strategies show abrupt shocks, when the opposite strategy become more profitable. plt.legend(['Trend Profit','Mean Reverting Profit']) plt.xlabel('Time') plt.ylabel('Profit/Loss') plt.title('A DRS Model Visualizes The Market As Being in 2 Possible States') plt.grid() plt.axhline(0,color='black',linestyle=':')
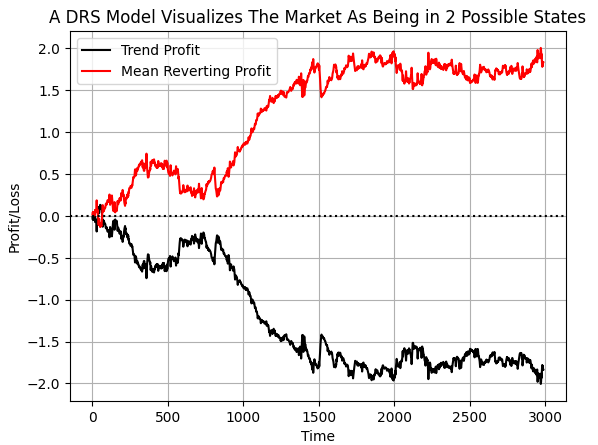
Abb. 6: Visualisierung der Verteilung des Gewinns auf 2 gegensätzliche Strategien
Definieren wir unseren Eingaben und das Ziel.
#Let's define the inputs and target X = data.iloc[:,1:-5].columns y = ['Trend Profit','Mean Reverting Profit']
Wir wählen unsere Tools für die Modellierung des Marktes
#Import the modelling tools from sklearn.model_selection import train_test_split,TimeSeriesSplit from sklearn.ensemble import RandomForestRegressor
und teilen die Daten zweimal. Wir haben also eine Trainingsmenge, eine Validierungsmenge und eine endgültige Testmenge.
#Split the data train , test = train_test_split(data,test_size=0.5,shuffle=False) f_train , f_validation = train_test_split(train,test_size=0.5,shuffle=False)
Jetzt bereiten wir unsere 2 Modelle vor. Es sei daran erinnert, dass beide Modelle eine zweifache Sicht auf die Welt vermitteln, aber in keiner Weise koordiniert werden sollten.
#The trend model trend_model = RandomForestRegressor() #The mean reverting model mean_model = RandomForestRegressor()
Passend zu unseren Modellen.
trend_model.fit(f_train.loc[:,X],f_train.loc[:,y[0]]) mean_model.fit(f_train.loc[:,X],f_train.loc[:,y[1]])
Prüfung der Gültigkeit unserer Modelle. Wir werden die Vorhersagen der beiden Modelle darüber aufzeichnen, welche Werte ihre Ziele in der Testmenge annehmen werden. Es sei daran erinnert, dass die Modelle nicht das gleiche Ziel lernen. Jedes Modell lernte unabhängig von den anderen Modellen sein eigenes Ziel und arbeitete daran, seinen Fehler zu reduzieren.
pred_1 = trend_model.predict(f_validation.loc[:,X]) pred_2 = mean_model.predict(f_validation.loc[:,X])
Der Inhalt des Validierungssatzes ist für unsere Modelle nicht geeignet. Wir führen im Wesentlichen Stresstests mit Daten durch, die sie noch nie zuvor gesehen haben, um zu sehen, ob sich unsere Modelle unter materiellem Stress ethisch korrekt verhalten.
Unser Test wird anhand der Summe der Vorhersagen beider Modelle durchgeführt. Wenn der Maximalwert der Summe der Vorhersagen des Modells gleich 0,0 ist, dann hat unser Modell den Test bestanden. Denn unser Modell stimmt im Wesentlichen mit der Hypothese des effizienten Marktes überein, die besagt, dass der Anleger, wenn er beide Modelle gleichzeitig verfolgt, nichts verdient. Wir beabsichtigen, jeweils nur 1 Modell zu verfolgen. Daher werden wir dynamisch zwischen den Regimen wechseln. Das heißt, dass unsere Strategie die Fähigkeit hat, die Strategie ohne menschliches Zutun zu ändern.
test_result = pred_1 + pred_2 print(f" Test Passed: {np.linalg.norm(test_result,ord=2) == 0.0}")
Das numpy-Paket enthält viele nützliche Bibliotheken, wie z. B. das Paket für lineare Algebra, das wir oben verwendet haben. Die von uns aufgerufene Funktion norm liefert einfach die Gesamtsumme des Inhalts eines Vektors oder den größten Wert in einem Vektor, je nachdem, wie die Methode aufgerufen wird. Dies ist logischerweise dasselbe wie die manuelle Überprüfung des Inhalts des Arrays, um sicherzustellen, dass alle Zahlen im Array 0 sind. Beachten Sie, dass ich die Ausgaben des Arrays abgeschnitten habe, aber der Leser kann sicher sein, dass sie alle 0 waren.
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
Wenn wir den tatsächlichen Gewinn der Trendfolgestrategie aufzeichnen und mit den Vorhersagen des Trendfolgemodells vergleichen, stellen wir fest, dass unser Modell, abgesehen von einigen massiven Schwankungen in der Rentabilität, wie z. B. während des 600- und 700-Tage-Intervalls, als der ERUUSD-Markt mit erheblicher Volatilität schwankte, in der Lage war, mit den anderen normal großen Gewinnen Schritt zu halten.
plt.plot(f_validation.loc[:,y[0]],color='black') plt.plot(pred_1,color='red',linestyle=':') plt.legend(['Actual Profit','Predicted Profit']) plt.grid() plt.ylabel('Loss / Profit') plt.xlabel('Out Of Sample Days') plt.title('Visualizing Our Model Performance Out Of Sample on the EURUSD 10 Day Return')
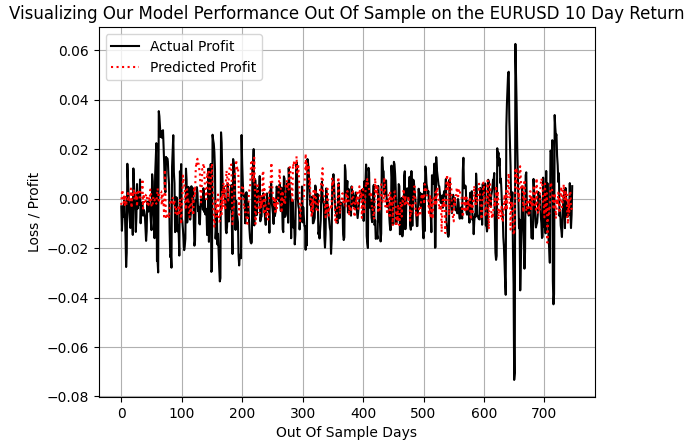
Abb. 7: Unser DRS-Modell konnte die tatsächliche Volatilität des Marktes nicht erfassen
Wir sind nun bereit, unsere maschinellen Lernmodelle in das ONNX-Format zu exportieren und unsere Handelsanwendungen in neue Richtungen zu lenken. ONNX steht für Open Neural Network Exchange und ermöglicht es uns, Modelle für maschinelles Lernen über eine Reihe von weit verbreiteten APIs zu erstellen und einzusetzen. Diese weit verbreitete Annahme ermöglicht es verschiedenen Programmiersprachen, mit demselben ONNX-Modell zu arbeiten. Und erinnern Sie sich: Jedes ONNX-Modell ist nur eine Darstellung Ihres maschinellen Lernmodells. Wenn Sie die Bibliotheken skl2onnx und ONNX noch nicht installiert haben, müssen sie zunächst installiert werden.
!pip install skl2onnx onnx
Nun laden wir die Bibliotheken, die Sie exportieren möchten.
import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
Wir definieren die E/A-Form Ihrer ONNX-Modelle.
eurusd_drs_shape = [("float_input",FloatTensorType([1,len(X)]))] eurusd_drs_output_shape = [("float_output",FloatTensorType([1,1]))]
Bereiten wir die ONNX-Prototypen für das DRS-Modell vor.
trend_drs_model_proto = convert_sklearn(trend_model,initial_types=eurusd_drs_shape,final_types=eurusd_drs_output_shape,target_opset=12) mean_drs_model_proto = convert_sklearn(mean_model,initial_types=eurusd_drs_shape,final_types=eurusd_drs_output_shape,target_opset=12)
Speichern wir die Modelle.
onnx.save(trend_drs_model_proto,"EURUSD RF D1 T LBFGSB DRS.onnx") onnx.save(mean_drs_model_proto,"EURUSD RF D1 M LBFGSB DRS.onnx")
Herzlichen Glückwunsch, wir haben eine erste DRS-Modellarchitektur gebaut. Nun wollen wir die Modelle einem Backtest unterziehen, um zu sehen, ob sie einen Unterschied machen und ob wir den RMSE aus unserem Entwurfsprozess sinnvoll ersetzen konnten.
Erste Schritte in MQL5
Zu Beginn werden wir zunächst Systemkonstanten definieren, die für unsere Handelsaktivitäten wichtig sind.
//+------------------------------------------------------------------+ //| EURUSD DRS.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| System constants | //+------------------------------------------------------------------+ #define HORIZON 10 #define MA_PERIOD 5 #define MA_SHIFT 0 #define MA_MODE MODE_SMA #define TRADING_VOLUME SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN)
Jetzt können wir unsere Systemressourcen laden.
//+------------------------------------------------------------------+ //| System dependencies | //+------------------------------------------------------------------+ #resource "\\Files\\DRS\\EURUSD RF D1 T DRS.onnx" as uchar onnx_proto[] //Our Trend Model #resource "\\Files\\DRS\\EURUSD RF D1 M DRS.onnx" as uchar onnx_proto_2[] //Our Mean Reverting Mode
Wir laden die Handelsbibliothek.
//+------------------------------------------------------------------+ //| System libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Wir benötigen auch Variablen für unsere technischen Indikatoren.
//+------------------------------------------------------------------+ //| Technical Indicators | //+------------------------------------------------------------------+ int ma_o_handle,ma_c_handle,atr_handle; double ma_o[],ma_c[],atr[]; double bid,ask; int holding_period;
Geben wir die globalen Variablen an.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model,onnx_model_2;
Wenn unsere Anwendung zum ersten Mal geladen wird, rufen wir eine Methode auf, die für das Laden unserer technischen Indikatoren und ONNX-Modelle verantwortlich ist.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if(!setup()) return(INIT_FAILED); //--- return(INIT_SUCCEEDED); }
Wenn wir die Anwendung nicht nutzen, sollten wir die nicht mehr benötigten Ressourcen bereinigen.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- release(); }
Wenn wir schließlich aktualisierte Kursniveaus erhalten, suchen wir entweder nach einer Handelsmöglichkeit oder verwalten die offenen Positionen, die wir haben.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- static datetime time_stamp; datetime current_time = iTime(Symbol(),PERIOD_D1,0); if(time_stamp != current_time) { time_stamp = current_time; update_variables(); if(PositionsTotal() == 0) { find_setup(); } else if(PositionsTotal() > 0) { manage_setup(); } } } //+------------------------------------------------------------------+
Dies ist die Implementierung der Funktion, die wir geschrieben haben, um das gesamte System einzurichten.
//+------------------------------------------------------------------+ //| Attempt To Setup Our System Variables | //+------------------------------------------------------------------+ bool setup(void) { atr_handle = iATR(Symbol(),PERIOD_CURRENT,14); ma_c_handle = iMA(Symbol(),PERIOD_CURRENT,MA_PERIOD,MA_SHIFT,MA_MODE,PRICE_CLOSE); ma_o_handle = iMA(Symbol(),PERIOD_CURRENT,MA_PERIOD,MA_SHIFT,MA_MODE,PRICE_OPEN); holding_period = 0; onnx_model = OnnxCreateFromBuffer(onnx_proto,ONNX_DEFAULT); onnx_model_2 = OnnxCreateFromBuffer(onnx_proto_2,ONNX_DEFAULT); if(onnx_model == INVALID_HANDLE) { Comment("Failed to load Trend DRS model"); return(false); } if(onnx_model_2 == INVALID_HANDLE) { Comment("Failed to load Mean Reverting DRS model"); return(false); } ulong input_shape[] = {1,10}; ulong output_shape[] = {1,1}; if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("Failed to set Trend DRS Model input shape"); return(false); } if(!OnnxSetInputShape(onnx_model_2,0,input_shape)) { Comment("Failed to set Mean Reverting DRS Model input shape"); return(false); } if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("Failed to set Trend DRS Model output shape"); return(false); } if(!OnnxSetOutputShape(onnx_model_2,0,output_shape)) { Comment("Failed to set Mean Reverting DRS Model output shape"); return(false); } return(true); }
Wenn wir das System deinitialisieren, werden wir die Indikatoren und ONNX-Modelle, die wir nicht mehr verwenden, manuell freigeben.
//+------------------------------------------------------------------+ //| Free up system resources | //+------------------------------------------------------------------+ void release(void) { IndicatorRelease(ma_c_handle); IndicatorRelease(ma_o_handle); OnnxRelease(onnx_model); OnnxRelease(onnx_model_2); }
Wir aktualisieren die Systemvariablen immer dann, wenn wir neue Preisinformationen haben.
//+------------------------------------------------------------------+ //| Update our system variables | //+------------------------------------------------------------------+ void update_variables(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); CopyBuffer(ma_c_handle,0,1,(HORIZON*2),ma_c); CopyBuffer(ma_o_handle,0,1,(HORIZON*2),ma_o); CopyBuffer(atr_handle,0,0,1,atr); ArraySetAsSeries(ma_c,true); ArraySetAsSeries(ma_o,true); }
Wir verwalten die offene Handelsgeschäfte, indem wir im Wesentlichen bis zu unserer 10-Tage-Rendite herunterzählen.
//+------------------------------------------------------------------+ //| Manage The Trade We Have Open | //+------------------------------------------------------------------+ void manage_setup(void) { if((PositionsTotal() > 0) && (holding_period < (HORIZON-1))) holding_period +=1; else if((PositionsTotal() > 0) && (holding_period == (HORIZON - 1))) Trade.PositionClose(Symbol()); }
Finden Sie ein Handels-Setup, indem Sie detaillierte Informationen über den aktuellen Marktzustand abrufen und diese in unser Modell einspeisen. Unsere Strategie stützt sich auf die Verwendung gleitender Durchschnitte als Indikatoren für die Anlegerstimmung. Wenn die gleitenden Durchschnitte Leerverkaufssignale geben, gehen wir davon aus, dass die meisten Anleger Leerverkäufe tätigen wollen, aber wir glauben, dass die Mehrheit auf dem Devisenmarkt dazu neigt, sich zu irren.
//+------------------------------------------------------------------+ //| Find A Trading Oppurtunity For Our Strategy | //+------------------------------------------------------------------+ void find_setup(void) { vectorf model_inputs = vectorf::Zeros(10); vectorf model_outputs = vectorf::Zeros(1); vectorf model_2_outputs = vectorf::Zeros(1); holding_period = 0; int i = 0; model_inputs[0] = (float) iOpen(Symbol(),PERIOD_CURRENT,0); model_inputs[1] = (float) iHigh(Symbol(),PERIOD_CURRENT,0); model_inputs[2] = (float) iLow(Symbol(),PERIOD_CURRENT,0); model_inputs[3] = (float) iClose(Symbol(),PERIOD_CURRENT,0); model_inputs[4] = (float)(iOpen(Symbol(),PERIOD_CURRENT,0) - iOpen(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[5] = (float)(iHigh(Symbol(),PERIOD_CURRENT,0) - iHigh(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[6] = (float)(iLow(Symbol(),PERIOD_CURRENT,0) - iLow(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[7] = (float)(iClose(Symbol(),PERIOD_CURRENT,0) - iClose(Symbol(),PERIOD_CURRENT,HORIZON)); model_inputs[8] = (float) ma_c[0]; model_inputs[9] = (float)(ma_c[0] - ma_c[HORIZON]); if(!OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_outputs)) { Comment("Failed to run the ONNX model correctly."); } if(!OnnxRun(onnx_model_2,ONNX_DEFAULT,model_inputs,model_2_outputs)) { Comment("Failed to run the ONNX model correctly."); } if(model_outputs[0] > 0) { if(ma_c[0] < ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) > ma_c[0]) Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0,""); } else if(ma_c[0] > ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) < ma_c[0]) Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0,""); } } else if(model_2_outputs[0] > 0) { if(ma_c[0] < ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) < ma_c[0]) Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0,""); } if(ma_c[0] > ma_o[0]) { if(iClose(Symbol(),PERIOD_CURRENT,0) > ma_c[0]) Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0,""); } } Comment("0: ",model_outputs[0],"1: ",model_2_outputs[0]); }
Undefinierte Systemkonstanten.
//+------------------------------------------------------------------+ //| Undefine system constants | //+------------------------------------------------------------------+ #undef HORIZON #undef MA_MODE #undef MA_PERIOD #undef MA_SHIFT #undef TRADING_VOLUME //+------------------------------------------------------------------+
Zunächst wählen wir die Daten für unsere Rückprüfungen aus. Erinnern Sie sich daran, dass wir immer Daten auswählen, die über die Trainingsmenge des Modells hinausgehen, um eine zuverlässige Vorstellung davon zu bekommen, wie gut das Modell in der Zukunft abschneiden wird.
Abb. 8: Vergewissern Sie sich, dass Sie Daten ausgewählt haben, die außerhalb der Trainingsmenge des Modells liegen.
Im Allgemeinen möchten wir unser Modell einem Stresstest unterziehen. Wählen Sie daher „Zufällige Verzögerung“ und „Jeder Tick basierend auf echten Ticks“, um unsere Strategie unter realistischen und schwierigen Marktbedingungen zu testen.
Abb. 9: Die Verwendung von „Jeder Tick basierend auf echten Ticks“ ist die realistischste Modellierungsoption, die wir für den Stresstest unserer DRS-Architektur wählen können.
Nachstehend finden Sie eine detaillierte Zusammenfassung der Ergebnisse unserer neuen DRS-Strategie. Es ist interessant festzustellen, dass es uns gelungen ist, den RMSE durch den DRS zu ersetzen und trotzdem eine rentable Strategie zu entwickeln, obwohl dies unser erster Versuch war, den RMSE in unserem Modellbildungsprozess auf formale Weise zu ersetzen.
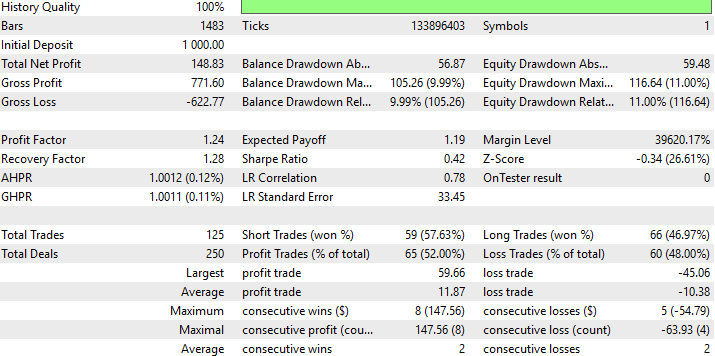
Abb. 10: Detaillierte Ergebnisse der Leistung unserer Strategie bei Daten, die sie zuvor nicht gesehen hatte
Wenn wir uns die von unserer Strategie erzeugte Aktienkurve ansehen, können wir die Probleme erkennen, die dadurch entstehen, dass unser DRS-Modell die Marktvolatilität nicht vorhersehen kann, wie wir bereits besprochen haben. Dies führt dazu, dass unsere Strategie zwischen profitablen und unprofitablen Perioden oszilliert. Unsere Strategie zeigt jedoch, dass wir in der Lage sind, uns zu erholen und auf dem richtigen Weg zu bleiben, und das ist es, was wir wollen.
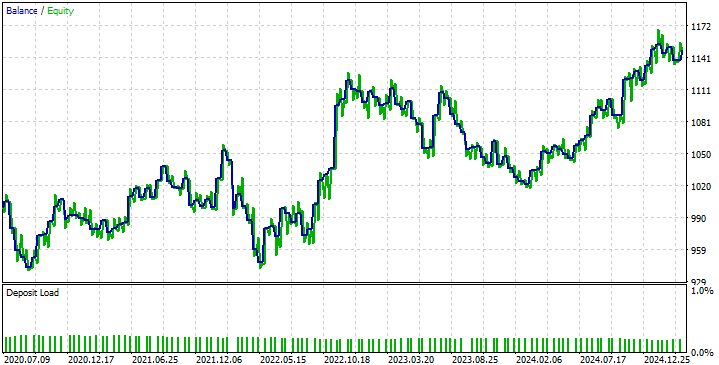
Abb. 11: Die Kapitalkurve, die durch unsere neue Handelsstrategie entsteht
Schlussfolgerung
Nach der Lektüre dieses Artikels gehen die Leser, die sich der Grenzen dieser Messgrößen nicht bewusst waren, gestärkt aus der Lektüre hervor. Die Grenzen Ihrer Werkzeuge zu kennen ist ebenso wichtig wie ihre Stärken. Die Optimierungsmethoden, die wir zur Entwicklung von KI verwenden, können bei besonders schwierigen Problemen „stecken bleiben“. Und wenn Praktiker diese Instrumente zur Modellierung der Renditen von Vermögenswerten einsetzen, sollten sie sich darüber im Klaren sein, dass ihre Modelle dazu neigen können, an der durchschnittlichen Rendite des Marktes hängen zu bleiben.
Der Leser hat auch umsetzbare Erkenntnisse gewonnen und versteht nun die Vorteile der Filterung von Märkten danach, wie gut sie ein Modell, das die durchschnittliche Rendite in diesem Markt vorhersagt, übertreffen können, da dies impliziert, dass der Markt Ineffizienzen aufweist, die der Praktiker ausnutzen sollte.
Durch die Filterung der Märkte auf der Grundlage der Frage, wie gut der Praktiker den Mittelwert übertreffen kann, hat der Leser gelernt, den RMSE nicht blindlings als eigenständige Kennzahl zu interpretieren, sondern den RMSE stets im Verhältnis zum TSS zu sehen. Der Leser hat ein praktisches Verständnis für die Einschränkungen, die diese Metriken für seine tägliche Arbeit mit sich bringen, was in der meisten Literatur zu diesem Thema oder in den hier verlinkten Forschungsarbeiten nicht der Fall ist.
Und schließlich, wenn der Leser beabsichtigt, ein maschinelles Lernmodell für den baldigen Handel mit seinem Privatkapital einzusetzen, sich aber dieser Einschränkungen nicht bewusst ist, dann würde ich den Leser warnen, zunächst die Übung zu wiederholen, die ich in diesem Artikel gezeigt habe, um sicher zu sein, dass er sich nicht stillschweigend in den Fuß schießt. Der RMSE ermöglicht es unseren Modellen, bei unseren Tests zu schummeln, aber ich bin zuversichtlich, dass die Leser, die bis hierher gelesen haben, sich nicht so leicht von den Grenzen der KI täuschen lassen.
| Dateiname | Beschreibung der Datei |
|---|---|
| DRS Models.mq5 | Das MQL5-Skript, das wir erstellt haben, um die detaillierten Marktdaten abzurufen, die wir für die Erstellung unseres DRS-Modells benötigten. |
| Dynamic_Regime_Switching_Models_(DRS_Modelling).ipynb | Das Jupyter-Notizbuch, das wir zur Entwicklung unseres DRS-Modells geschrieben haben. |
| EURUSD DRS.mq5 | Unser EURUSD-Expert Advisor, der unser DRS-Modell verwendet. |
| EURUSD RF D1 T DRS.onnx | Das trendfolgende DRS-Modell geht immer davon aus, dass sich der Markt im Trend befindet. |
| EURUSD RF D1 M DRS.onnx | Das Modell der Umkehr zum Mittelwert geht immer davon aus, dass sich der Markt im Zustand einer Umkehr zum Mittelwert befindet. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/17906
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
Optimierung und Optimierung des Roh-Codes zur Verbesserung der Backtest-Ergebnisse
Eine alternative Log-datei mit der Verwendung der HTML und CSS
Von der Grundstufe bis zur Mittelstufe: Template und Typename (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
"Unsere Strategie zeigt jedoch die Fähigkeit, sich zu erholen und auf Kurs zu bleiben, was genau das ist, was wir anstreben."
Ich habe immer gedacht, dass man danach streben sollte, dass eine Strategie Gewinne bringt :)