
Neuronale Netze im Handel: Einspeisung globaler Informationen in unabhängige Kanäle (InjectTST)
Einführung
In den letzten Jahren haben auf Transformer basierende Architekturen für multimodale Zeitreihenprognosen große Popularität erlangt und entwickeln sich zunehmend zu einem der am häufigsten verwendeten Modelle für die Zeitreihenanalyse. Modelle nutzen zunehmend unabhängige Kanalansätze, bei denen das Modell jede Kanalsequenz separat verarbeitet, ohne mit den anderen zu interagieren.
Die Kanalunabhängigkeit bietet zwei wesentliche Vorteile:
- Rauschunterdrückung: Unabhängige Modelle können sich auf die Vorhersage einzelner Kanäle konzentrieren, ohne durch Rauschen anderer Kanäle beeinflusst zu werden.
- Milderung der Verteilungsdrift: Kanalunabhängigkeit kann dazu beitragen, das Problem der Verteilungsdrift in Zeitreihen zu lösen.
Umgekehrt ist das Mischen von Kanälen bei der Bewältigung dieser Herausforderungen tendenziell weniger effektiv, was zu einer verringerten Modellleistung führen kann. Allerdings bietet das Mischen von Kanälen einzigartige Vorteile:
- Hohe Informationskapazität: Modelle, die Kanäle mischen, zeichnen sich durch die Erfassung von Abhängigkeiten zwischen Kanälen aus und bieten potenziell mehr Informationen für die Prognose zukünftiger Werte.
- Kanalspezifität: Durch die Optimierung mehrerer Kanäle innerhalb von Kanalmischungsmodellen kann das Modell die besonderen Merkmale jedes Kanals voll ausnutzen.
Da unabhängige Kanalansätze einzelne Kanäle über ein einheitliches Modell analysieren, kann das Modell außerdem nicht zwischen Kanälen unterscheiden, sondern konzentriert sich in erster Linie auf die gemeinsamen Muster mehrerer Kanäle. Dies führt zu einem Verlust der Kanalspezifität und kann sich negativ auf die multimodale Zeitreihenprognose auswirken.
Daher ist die Entwicklung eines effektiven Modells, das die Vorteile der Kanalunabhängigkeit und der Kanalmischung kombiniert und die Nutzung beider Ansätze (Rauschunterdrückung, Milderung der Verteilungsdrift, hohe Informationskapazität und Kanalspezifität) ermöglicht, der Schlüssel zur weiteren Verbesserung der Leistung multimodaler Zeitreihenprognosen.
Der Aufbau eines solchen Modells stellt jedoch eine komplexe Herausforderung dar. Erstens stehen unabhängige Kanalmodelle von Natur aus im Widerspruch zu Kanalabhängigkeiten. Durch die Feinabstimmung eines einheitlichen Modells für jeden Kanal können zwar die Kanalspezifitäten berücksichtigt werden, dies ist jedoch mit einem erheblichen Schulungsaufwand verbunden. Zweitens ist es mit den vorhandenen Methoden zur Rauschunterdrückung und Lösungen für die Verteilungsdrift noch nicht gelungen, die Kanalmischungsrahmen so robust zu machen wie unabhängige Kanalmodelle.
Eine mögliche Lösung für diese Herausforderungen wird in dem Artikel „InjectTST: A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting", das eine Methode zur Einspeisung globaler Informationen in die einzelnen Kanäle einer multimodalen Zeitreihe vorstellt (InjectTST). Die Autoren dieser Methode vermeiden die explizite Modellierung von Abhängigkeiten zwischen Kanälen zur Prognose multimodaler Zeitreihen. Stattdessen behalten sie die Struktur der Kanalunabhängigkeit als Grundlage bei, während sie selektiv globale Informationen (Kanalmischung) in jeden Kanal einfügen. Dies ermöglicht ein implizites Mischen von Kanälen.
Jeder einzelne Kanal kann selektiv nützliche globale Informationen empfangen und gleichzeitig Rauschen vermeiden, sodass sowohl eine hohe Informationskapazität als auch eine Rauschunterdrückung aufrechterhalten werden. Da die Kanalunabhängigkeit als Grundstruktur erhalten bleibt, kann auch die Verteilungsdrift gemildert werden.
Darüber hinaus integrieren die Autoren eine Kanalkennung in InjectTST, um das Problem der Kanalspezifität zu lösen.
1. Der Algorithmus von InjectTST
Um die Prognosen Y für einen gegebenen Horizont T zu erstellen, analysieren wir historische Werte einer multimodalen Zeitreihe X, die L Zeitschritte enthält, wobei jeder Zeitschritt als Vektor der Dimension M dargestellt wird.
Um diese Aufgabe unter Nutzung der Vorteile sowohl der Kanalunabhängigkeit als auch der Kanalmischung zu lösen, wird der komplexe mehrstufige Algorithmus InjectTST eingesetzt.
Der erste Schritt des Algorithmus umfasst die Segmentierung der Eingabedaten in unabhängige Kanalautobahnen. Anschließend wird eine lineare Projektion mit lernbarer Positionskodierung angewendet.
Die unabhängige Kanalplattform verarbeitet jeden Kanal mit einem gemeinsamen Modell. Infolgedessen kann das Modell nicht zwischen Kanälen unterscheiden und lernt in erster Linie die gemeinsamen Muster der Kanäle, wobei die Kanalspezifität fehlt. Um dieses Problem zu lösen, führen die Autoren von InjectTST einen Kanalbezeichner ein, der ein lernbarer Tensor ist.
Nach der linearen Projektion von Patches werden Tensoren mit Positionskodierung und Kanalkennungen hinzugefügt.
Diese aufbereiteten Daten werden dann zur Darstellung auf hoher Ebene in den Encoder des Transformers eingespeist.
Es ist wichtig zu beachten, dass der Transformer-Encoder in diesem Fall in unabhängigen Kanal-Highways arbeitet, was bedeutet, dass nur die Token der einzelnen Kanäle analysiert werden und kein Informationsaustausch zwischen den Kanälen stattfindet.
Die Kanalkennung stellt die charakteristischen Merkmale jedes Kanals dar, sodass das Modell zwischen ihnen unterscheiden und für jeden eine eindeutige Darstellung erhalten kann.
Gleichzeitig leitet die Kanalmischroute parallel zur unabhängigen Kanalautobahn die ursprüngliche Sequenz X durch ein globales Mischmodul, um globale Informationen zu erhalten. Das Hauptziel von InjectTST besteht darin, globale Informationen in jeden Kanal einzuspeisen, wodurch das Abrufen globaler Informationen zu einer kritischen Aufgabe wird. Die Autoren der Methode schlagen zwei Arten von globalen Mischmodulen vor, die als CaT (Channel as Token) und PaT (Patch as Token) bezeichnet werden.
Das CaT-Modul bildet jeden Kanal direkt in einen Token ab. Kurz gesagt wird eine lineare Projektion auf alle Werte innerhalb eines Kanals angewendet.
Das globale Mischmodul von PaT verarbeitet Patches als Eingabe. Zunächst werden Patches gruppiert, die den jeweiligen Zeitschritten der analysierten multimodalen Sequenz zugeordnet sind. Anschließend wird auf die gruppierten Patches eine lineare Projektion angewendet, die Informationen vor allem auf Patch-Ebene zusammenführt. Anschließend wird eine Positionskodierung hinzugefügt und die Daten werden zur weiteren Integration der Informationen über Patches und globale Informationen hinweg an den Encoder des Transformers übergeben.
Von den Autoren durchgeführte Experimente zeigen, dass PaT stabiler ist, während CaT bei bestimmten spezialisierten Datensätzen eine bessere Leistung zeigt.
Eine wesentliche Herausforderung der Methode InjectTST besteht in der Notwendigkeit, globale Informationen in jeden Kanal einzuspeisen, wobei die Zuverlässigkeit des Modells nur minimal beeinträchtigt werden darf. In einem einfachen Transformer ermöglicht eine Kreuzaufmerksamkeit (cross-attention), dass sich die Zielsequenz je nach Relevanz gezielt auf Kontextinformationen aus einer anderen Quelle konzentriert. Dieses Verständnis der Architektur der Kreuzaufmerksamkeit kann auch angewendet werden, um globale Informationen aus multimodalen Zeitreihen einzuspeisen. Daher können globale, über verschiedene Kanäle hinweg gemischte Informationen als Kontext behandelt werden. Die Autoren nutzen Kreuzaufmerksamkeit, um globale Informationen in jeden Kanal einzuspeisen.
Es ist erwähnenswert, dass die Autoren eine optionale Restverbindung für das kontextbezogene Aufmerksamkeitsmodul einführen. Normalerweise können Restverbindungen das Modell etwas instabil machen, bei bestimmten spezialisierten Datensätzen können sie jedoch die Leistung deutlich verbessern.
Im Allgemeinen werden globale Informationen als Schlüssel und Wert (Key und Value) in das kontextbezogene Aufmerksamkeitsmodul eingeführt, während kanalspezifische Informationen als Abfrage (Query) dargestellt werden.
Nach der Kreuzaufmerksamkeit werden die Daten mit globalen Informationen angereichert. Zur Generierung von Prognosewerten wird ein linearer Kopf hinzugefügt.
Die Autoren von InjectTST schlagen einen dreistufigen Trainingsprozess vor. In der Vortrainingsphase werden die ursprünglichen Zeitreihen zufällig maskiert und das Ziel besteht darin, die maskierten Teile vorherzusagen. In der Feinabstimmungsphase wird der vortrainierte Kopf von InjectTST durch einen Prognosekopf ersetzt und der Prognosekopf wird feinabgestimmt, während der Rest des Netzwerks eingefroren wird. Schließlich wird in der Feinabstimmungsphase das gesamte InjectTST-Netzwerk einer Feinabstimmung unterzogen.
Die originale Visualisierung der Methode wird unten angezeigt.
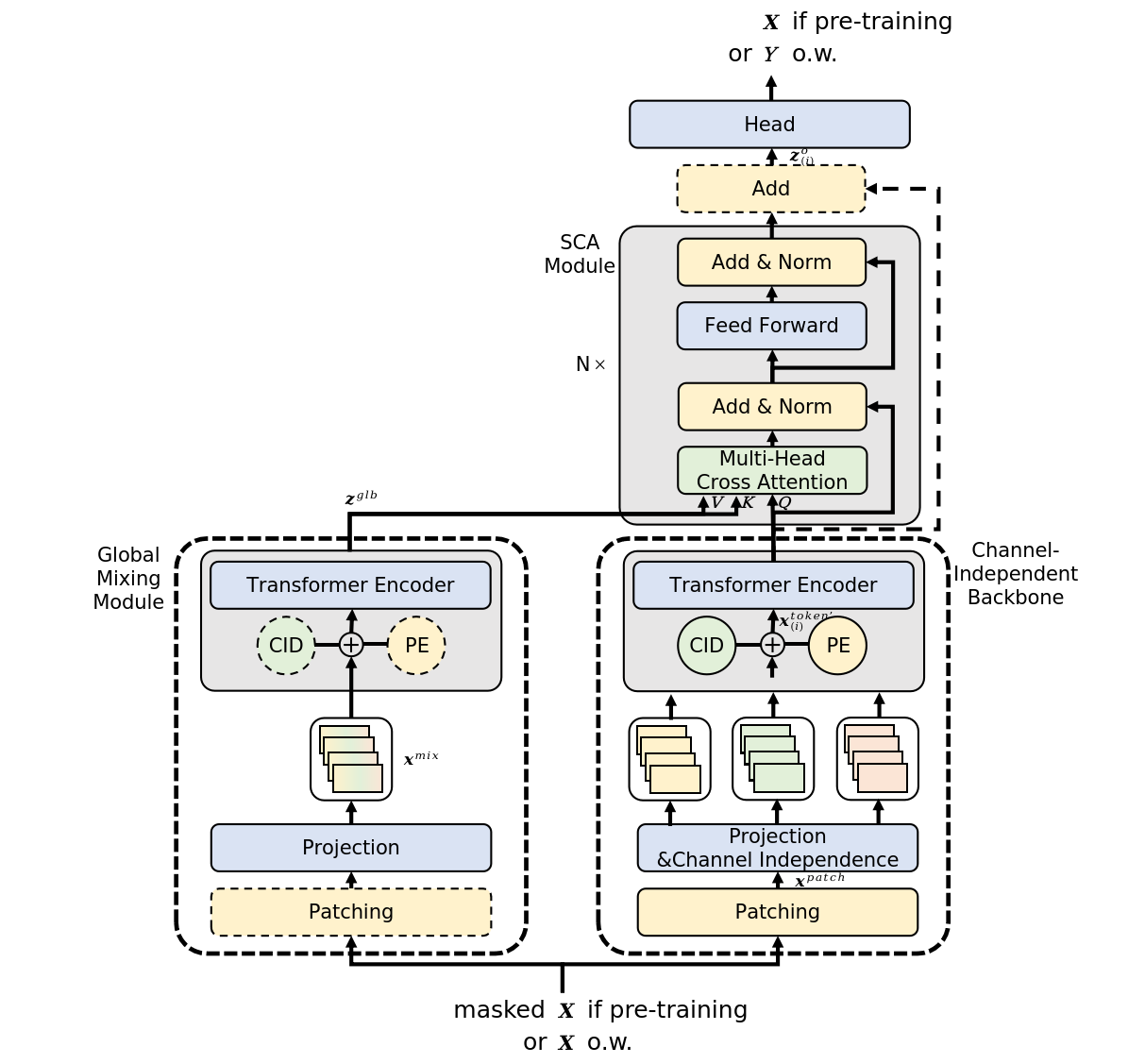
2. Implementierung in MQL5
Nachdem wir die theoretischen Aspekte der von InjectTST überprüft haben, fahren wir mit der praktischen Umsetzung unserer Interpretation der vorgeschlagenen Ansätze mithilfe von MQL5 fort.
Es ist wichtig zu beachten, dass die in diesem Artikel bereitgestellte Implementierung nicht die einzig richtige ist. Darüber hinaus spiegelt die vorgeschlagene Implementierung mein persönliches Verständnis der im Originalpapier vorgestellten Materialien wider und kann von der Vorstellung der Autoren hinsichtlich der vorgeschlagenen Ansätze abweichen. Gleiches gilt für die erzielten Ergebnisse.
Wenn wir mit der Arbeit an der Implementierung der vorgeschlagenen Ansätze beginnen, ist es wichtig hervorzuheben, dass wir zuvor mehrere auf Transformer basierende Modelle unter Verwendung des unabhängigen Kanalparadigmas untersucht haben. In diesen Modellen wurden Prognosen für unabhängige Kanäle durchgeführt und der Transformer- Block wurde verwendet, um Abhängigkeiten zwischen Kanälen zu untersuchen, was dem Ansatz von CaT des globalen Mischmoduls ähnelt.
Die Autoren der Methode verwenden jedoch eine Transformer-Architektur in unabhängigen Kanal-Highways und vermeiden so den Informationsfluss zwischen Kanälen in dieser Phase. Theoretisch könnten wir diesen Algorithmus implementieren, indem wir Daten in separaten Einheitssequenzen verarbeiten. Dieser Ansatz ist jedoch umfangreich und führt zu einer Zunahme der Anzahl sequentieller Operationen, die mit der Anzahl der in multimodalen Eingabedaten analysierten Variablen wächst.
Bei unserer Arbeit zielen wir darauf ab, so viele Operationen wie möglich in parallelen Threads auszuführen. Daher werden wir in dieser Implementierung eine neue Schicht erstellen, die eine unabhängige Analyse einzelner Kanäle ermöglicht.
2.1 Unabhängiger Kanalanalyseblock
Die Funktionsweise der unabhängigen Kanalanalyse ist in der Klasse CNeuronMVMHAttentionMLKV implementiert, die die grundlegende Funktionalität von einem anderen mehrschichtigen Multi-Head-Attention-Block CNeuronMLMHAttentionOCL erbt. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronMVMHAttentionMLKV : public CNeuronMLMHAttentionOCL { protected: uint iLayersToOneKV; ///< Number of inner layers to 1 KV uint iHeadsKV; ///< Number of heads KV uint iVariables; ///< Number of variables CCollection KV_Tensors; ///< The collection of tensors of Keys and Values CCollection K_Tensors; ///< The collection of tensors of Keys CCollection K_Weights; ///< The collection of Matrix of K weights to previous layer CCollection V_Tensors; ///< The collection of tensors of Values CCollection V_Weights; ///< The collection of Matrix of V weights to previous layer CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMVMHAttentionMLKV(void) {}; ~CNeuronMVMHAttentionMLKV(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMVMHAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
In dieser Klasse fügen wir 3 Variablen hinzu:
- iLayersToOneKV – die Anzahl der Schichten für einen Schlüssel-Wert-Tensor;
- iHeadsKV – die Anzahl der Aufmerksamkeitsköpfe (attention heads) im Schlüssel-Wert-Tensor;
- iVariablen – die Anzahl der univariaten Sequenzen in einer multimodalen Zeitreihe.
Darüber hinaus fügen wir 5 Datenpuffersammlungen hinzu, deren Zweck wir im Laufe der Implementierung kennenlernen werden. Alle internen Objekte werden statisch deklariert, sodass der Klassenkonstruktor und -destruktor „leer“ gelassen werden können. Die Initialisierung aller internen Variablen und Objekte wird in der Init-Methode durchgeführt.
bool CNeuronMVMHAttentionMLKV::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false;
In den Parametern dieser Methode erwarten wir die wichtigsten Konstanten, die es uns ermöglichen, die Architektur der initialisierten Klasse eindeutig zu identifizieren. Dazu gehören:
- window – die Größe des Vektors, der ein Element der Sequenz einer univariaten Zeitreihe darstellt;
- window_key – die Größe des Vektors der internen Darstellung der Schlüsselentität eines Elements der Sequenz einer univariaten Zeitreihe;
- heads – die Anzahl der Aufmerksamkeitsköpfe der Abfrageentität;
- heads_kv – die Anzahl der Aufmerksamkeitsköpfe im verketteten Schlüssel-Wert-Tensor;
- units_count – die Größe der analysierten Sequenz;
- layers – die Anzahl der verschachtelten Schichten im Block;
- layers_to_one_kv – die Anzahl der verschachtelten Schichten, die mit einem Schlüssel-Vakue-Tensor arbeiten;
- Variablen – die Anzahl der univariaten Sequenzen in einer multimodalen Zeitreihe.
Im Hauptteil der Methode rufen wir zunächst dieselbe Methode der Elternklasse auf, die die empfangenen Parameter kontrolliert und die geerbten Objekte initialisiert. Darüber hinaus implementiert diese Methode bereits die minimal notwendigen Kontrollen der vom Anrufer empfangenen Daten.
Nach erfolgreicher Ausführung der Methode der übergeordneten Klasse speichern wir die empfangenen Parameter in internen Variablen.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1); iVariables = variables;
Hier definieren wir die wichtigsten Konstanten, die die Architektur verschachtelter Objekte bestimmen.
uint num_q = iWindowKey * iHeads * iUnits * iVariables; //Size of Q tensor uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables; //Size of KV tensor uint q_weights = (iWindow * iHeads + 1) * iWindowKey; //Size of weights' matrix of Q tenzor uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey; //Size of weights' matrix of K/V tenzor uint scores = iUnits * iUnits * iHeads * iVariables; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits * iVariables; //Size of multi-heads self-attention uint out = iWindow * iUnits * iVariables; //Size of out tensore uint w0 = (iWindowKey * iHeads + 1) * iWindow; //Size W0 weights' matrix uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Hier ist es wichtig, kurz auf die Ansätze einzugehen, die wir für die Umsetzung im Rahmen dieses Kurses vorschlagen. Zunächst wurde entschieden, die neue Klasse zu erstellen, ohne OpenCL zu ändern. Mit anderen Worten: Trotz der neuen Anforderungen erstellen wir die Klasse vollständig unter Verwendung der vorhandenen Kernel.
Um dies zu erreichen, beginnen wir mit der Trennung der Generierung der Entitäten von Schlüssel und Wert. Zur Erinnerung: Früher wurden sie in einem einzigen Durchgang durch die Faltungsschicht generiert und für jedes Sequenzelement sequenziell in den Puffer geschrieben. Dieser Ansatz ist akzeptabel, wenn es darum geht, globale Aufmerksamkeit zu erzeugen. Wenn wir den Prozess jedoch innerhalb separater Kanäle organisieren, erhalten wir eine alternierende Schlüssel/Wert-Sequenz für einzelne Kanäle, die für die nachfolgende Analyse nicht ideal ist und nicht gut zum zuvor erstellten Algorithmus passt. Daher generieren wir diese Entitäten separat und verketten sie dann zu einem einzigen Tensor.
Es ist erwähnenswert, dass wir die Generierung von Entitäten in zwei Phasen unterteilt haben, deren Anzahl unabhängig von der Anzahl der analysierten Variablen oder Aufmerksamkeitsköpfe ist.
Der zweite Punkt ist, dass die Autoren der Methode InjectTST einen einzigen Transformer-Encoder für alle Kanäle verwenden. Ebenso verwenden wir einen einzigen Satz Gewichtsmatrizen für alle Kanäle. Dadurch bleibt die Größe der Gewichtsmatrizen unabhängig von der Kanalanzahl konstant.
Damit sind unsere Vorarbeiten abgeschlossen und wir fahren mit der Organisation einer Schleife fort, deren Anzahl an Iterationen der Anzahl der verschachtelten Schichten entspricht.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
Im Schleifenkörper organisieren wir eine verschachtelte Schleife, um Puffer der Ergebnisse von Zwischenoperationen und der entsprechenden Fehlergradienten zu erstellen.
for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Hier erstellen wir zuerst den Puffer des Tensors von Abfrage (Abfrage). Der Erstellungsalgorithmus ist für alle Puffer identisch. Zuerst erstellen wir eine neue Instanz des Pufferobjekts. Wir initialisieren es mit Nullwerten in einer bestimmten Größe. Anschließend erstellen wir eine Kopie des Puffers im Kontext von OpenCL und fügen der entsprechenden Sammlung einen Zeiger zum Puffer hinzu. Vergessen Sie nicht, die Vorgänge bei jedem Schritt zu kontrollieren.
Da wir vorhaben, für die Analyse in mehreren verschachtelten Schichten 1 Schlüssel-Wert-Tensor zu verwenden, erstellen wir die entsprechenden Puffer mit einer bestimmten Frequenz.
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(2 * num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
Beachten Sie, dass wir in dieser Phase drei Puffer erstellen: Schlüssel, Wert und verknüpfter Schlüssel-Wert.
Der nächste Schritt besteht darin, einen Puffer mit Aufmerksamkeitskoeffizienten zu erstellen.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
Darauf folgt der Puffer mit den Ergebnissen der mehrköpfigen Aufmerksamkeit.
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
Und dann gibt es noch die Komprimierungspuffer des Blocks für mehrfachen Aufmerksamkeitskopf und FeedForward (Vorwärtsdurchgang).
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Nachdem wir die Zwischenergebnispuffer und ihre Gradienten initialisiert haben, fahren wir mit der Initialisierung der Gewichtsmatrizen fort. Der Algorithmus für ihre Initialisierung ähnelt der Erstellung von Datenpuffern, nur dass die Matrix mit zufälligen Werten gefüllt wird.
Die erste generierte Matrix ist die Gewichtsmatrix der Entität der Abfrage.
//--- Initialize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Die Häufigkeit der Erstellung von Gewichtsmatrizen von Schlüssel und Wert ähnelt der Häufigkeit der Puffer der entsprechenden Einheiten.
//--- Initialize K weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; }
Fügen wir eine Komprimierungsmatrix von Aufmerksamkeitsköpfen hinzu.
//--- Initialize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Und der FeedForward-Block.
//--- Initialize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Danach erstellen wir eine weitere verschachtelte Schleife, in der wir Momentpuffer auf der Ebene der Gewichtungskoeffizienten hinzufügen. Die Anzahl der erstellten Puffer hängt von der Parameteraktualisierungsmethode ab.
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_1 : 4 * iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_2 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Am Ende der Initialisierungsmethode fügen wir einen Puffer hinzu, um temporäre Daten zu speichern und das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurückzugeben.
if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
Nachdem wir das Objekt initialisiert haben, fahren wir mit der Organisation der Vorwärtsdurchgangs-Algorithmen fort. Und hier sind noch ein paar Worte zur Verwendung zuvor erstellter Kernel erforderlich. Insbesondere zum Kernel der Vorwärtsdurchgangs der Kreuzaufmerksamkeits-Blocks MH2AttentionOut ist der Algorithmus zum Platzieren in der Ausführungswarteschlange in der Methode AttentionOut implementiert. Der Algorithmus zum Platzieren des Kernels in der Ausführungswarteschlange hat sich nicht geändert. Unsere Aufgabe besteht jedoch darin, die Analyse unabhängiger Kanäle mit diesem Algorithmus umzusetzen.
Sehen wir uns zunächst an, wie unser Kernel mit einzelnen Aufmerksamkeitsköpfen funktioniert. Sie werden unabhängig voneinander in separaten Streams verarbeitet. Ich denke, das ist genau das, was wir brauchen. Nehmen wir also an, dass die einzelnen Kanäle dieselben Aufmerksamkeitsköpfe sind.
bool CNeuronMVMHAttentionMLKV::AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) { if(!OpenCL) return false; //--- uint global_work_offset[3] = {0}; uint global_work_size[3] = {iUnits/*Q units*/, iUnits/*K units*/, iHeads * iVariables}; uint local_work_size[3] = {1, iUnits, 1};
Ansonsten bleibt der Algorithmus der Methode derselbe. Übergeben wir die erforderlichen Parameter an den Kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_q, q.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_kv, kv.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_score, scores.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_out, out.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_dimension, (int)iWindowKey)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Wir passen die Anzahl der Tensorköpfe von Schlüssel-Wert an.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_heads_kv, (int)(iHeadsKV * iVariables))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Dann stellen wir den Kernel in die Ausführungswarteschlange.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_mask, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_MH2AttentionOut, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Damit ist die Methode beendet. Dies ist jedoch nur ein Teil des Vorwärtsdurchgangs-Algorithmus. Wir werden den vollständigen Algorithmus in der Methode FeedForward erstellen.
bool CNeuronMVMHAttentionMLKV::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, das die Ausgangsdaten für unseren Algorithmus enthält. Als Ausgangsdaten erwarten wir einen dreidimensionalen Tensor – die Länge der Folge * der Anzahl der univariaten Folgen * Größe des analysierten Fensters eines Elements.
Im Hauptteil der Methode überprüfen wir die Relevanz des empfangenen Zeigers und organisieren einen Iterationszyklus durch die verschachtelten Schichten des Moduls.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
Hier deklarieren wir zunächst einen lokalen Zeiger auf den Quelldatenpuffer, in dem wir den erforderlichen Zeiger speichern. Anschließend extrahieren wir aus der Sammlung den Puffer der Entität von Abfrage, der der analysierten Schicht entspricht, und schreiben dort die auf Grundlage der Originaldaten generierten Daten hinein.
CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
Im nächsten Schritt prüfen wir, ob ein neuer Tensor Schlüssel-Wert generiert werden muss. Gegebenenfalls ermitteln wir zunächst den Ausgleich in den entsprechenden Inkassoverfahren.
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV;
Und wir extrahieren Zeiger zu den Puffern, die wir benötigen.
kv = KV_Tensors.At(i_kv * 2); CBufferFloat *k = K_Tensors.At(i_kv * 2); CBufferFloat *v = V_Tensors.At(i_kv * 2);
Danach generieren wir nacheinander die Entitäten von Schlüssel und Wert.
if(IsStopped() || !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, iWindow, iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, iWindow, iWindowKey * iHeadsKV, None)) return false;
Und wir verketten die erhaltenen Tensoren entlang der ersten Dimension (Elemente der Sequenz).
if(IsStopped() || !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits)) return false; }
Bitte beachten Sie, dass wir in dieser Version der Datenorganisation einen Datenpuffer erhalten, der als fünfdimensionaler Datentensor dargestellt werden kann: Units * [Schlüssel, Wert] * Variable * HeadsKV * Window_Key. Der Entitätstensor von Abfrage hat eine vergleichbare Dimension, nur, anstelle von [Schlüssel, Wert] haben wir [Abfrage] haben. Indem wir die Dimensionen der Variablen und der Köpfen in einer Dimension „Variable * Köpfe“ zusammenfassen, erhalten wir Tensordimensionen, die mit simplen mehrfachen Selbstaufmerksamkeitsköpfen vergleichbar sind.
Hier muss daran erinnert werden, dass wir auf der Kontextseite von OpenCL mit eindimensionalen Datenpuffern arbeiten. Das Aufteilen der Daten in einen mehrdimensionalen Tensor hat für das Verständnis der Datensequenz lediglich deklarativen Charakter. Im Allgemeinen verläuft die Datensequenz im Puffer von der letzten zur ersten Dimension.
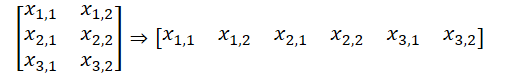
Dies ermöglicht uns, zuvor erstellte Kernel unseres OpenCL-Programms zur Analyse unabhängiger Kanäle zu verwenden. Wir erhalten Zeiger auf die erforderlichen Datenpuffer aus den Sammlungen und führen den Algorithmus des mehrfachen Selbstaufmerksamkeitskopfes aus. Wir haben die erforderliche Methode oben angepasst.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Anschließend formatieren wir die Ergebnisse der mehrköpfigen Aufmerksamkeit gedanklich in einen Tensor von [Einheiten * Variable] * Köpfe * Window_Key und projizieren die Daten auf die Dimension der Originaldaten.
//--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false; //--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
Danach summieren wir die erhaltenen Ergebnisse mit den Originaldaten und normalisieren die erhaltenen Werte.
Als Nächstes führen wir die Blockoperationen des Vorwärtsdurchganges im gleichen Stil aus und fahren mit der nächsten Iteration der Schleife fort.
//--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false; //--- Sum and normilize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- return true; }
Nachdem wir die Operationen aller verschachtelten Schichten innerhalb des Blocks erfolgreich abgeschlossen haben, schließen wir die Ausführung der Methode ab und geben ein logisches Ergebnis an das aufrufende Programm zurück, das den Abschlussstatus der Operationen angibt.
Normalerweise fahren wir nach der Implementierung der Methoden der Vorwärtsdurchgänge mit der Entwicklung der Algorithmen der Rückwärtsdurchgänge (backpropagation) fort. Heute möchte ich Sie einladen, die vorgeschlagene Implementierung, die Sie in den beigefügten Materialien finden, selbstständig zu analysieren. Bei der Implementierung der Methoden der Rückwärtsdurchgänge haben wir dieselben Ansätze verwendet, die zuvor für den Vorwärtsdurchgänge beschrieben wurden. Es ist wichtig zu beachten, dass die Rückwärtsdurchgänge strikt dem Algorithmus dees Vorwärtsdurchganges folgen, jedoch in umgekehrter Reihenfolge.
Darüber hinaus enthält der Anhang die Implementierung der Klasse CNeuronMVCrossAttentionMLKV, deren Algorithmen weitgehend denen der Klasse CNeuronMVMHAttentionMLKV entsprechen, mit der wichtigen Ergänzung von Mechanismen der Kreuzaufmerksamkeit.
Ich möchte Sie auch daran erinnern, dass die implementierten Klassen CNeuronMVMHAttentionMLKV und CNeuronMVCrossAttentionMLKV als Bausteine innerhalb des größeren Algorithmus von InjectTST dienen, dessen theoretische Aspekte wir zuvor untersucht haben. Der nächste Schritt unserer Arbeit wird die Entwicklung einer neuen Klasse sein, in der wir den vollständigen Algorithmus von InjectTST implementieren.
2.2 Implementierung von InjectTST
Wir werden InjectTST vollständig innerhalb der Klasse CNeuronInjectTST erstellen, die die Kernfunktionalität von der übergeordneten Klasse vollständig verbundener neuronaler Schichten, CNeuronBaseOCL, erbt. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronInjectTST : public CNeuronBaseOCL { protected: CNeuronPatching cPatching; CNeuronLearnabledPE cCIPosition; CNeuronLearnabledPE cCMPosition; CNeuronMVMHAttentionMLKV cChanelIndependentAttention; CNeuronMLMHAttentionMLKV cChanelMixAttention; CNeuronMVCrossAttentionMLKV cGlobalInjectionAttention; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronInjectTST(void) {}; ~CNeuronInjectTST(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronInjectTST; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual CBufferFloat *getWeights(void) override; };
In dieser Klasse sehen wir eine ziemlich große Anzahl interner Objekte, aber es gibt keine einzige Variable. Dies liegt daran, dass diese Klasse sozusagen eine „Großknotenassemblierung“ eines Algorithmus implementiert, dessen Hauptfunktionalität durch interne Objekte aufgebaut ist. Und alle Konstanten, die die Blockarchitektur definieren, werden nur in der Initialisierungsmethode der Klasse verwendet und in verschachtelten Objekten gespeichert. Die Funktionsweise dieser lernen wir im Laufe der Implementierung der Algorithmen kennen.
Alle internen Objekte der Klasse werden statisch deklariert, was es uns ermöglicht, den Klassenkonstruktor und -destruktor leer zu lassen. Und die Initialisierung aller verschachtelten und geerbten Objekte wird in der Methode Init durchgeführt.
bool CNeuronInjectTST::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false; SetActivationFunction(None);
Wie üblich erhalten wir in den Parametern dieser Methode die wichtigsten Konstanten, die die Architektur des erstellten Objekts bestimmen. Im Hauptteil der Methode rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf, die bereits grundlegende Steuerelemente für die empfangenen Parameter und die Initialisierung geerbter Objekte implementiert.
Als nächstes initialisieren wir die internen Objekte in dem Teil des Vorwärtsdurchlaufs von InjectTST. In der oben vom Autor vorgestellten Visualisierung der Methode ist leicht zu erkennen, dass die erhaltenen Ausgangsdaten in zwei Informationsflüssen verwendet werden: Blöcken unabhängiger Kanäle und globaler Mischung. In beiden Blöcken werden die Quelldaten zunächst segmentiert. Bei meiner Implementierung habe ich mich dazu entschieden, den Segmentierungsprozess nicht zu duplizieren, sondern ihn einmalig durchzuführen, bevor sich die Informationsflüsse verzweigen.
if(!cPatching.Init(0, 0, OpenCL, window, window, window, units_count, variables, optimization, iBatch)) return false; cPatching.SetActivationFunction(None);
Es sollte beachtet werden, dass ich in dieser Implementierung gleiche Parameter verwende: Segmentgröße, Segmentfensterschritt und Segmenteinbettungsgröße. Somit hat sich die Größe des Quelldatenpuffers vor und nach der Segmentierung nicht verändert. Allerdings hat sich die Reihenfolge der Daten im Puffer geändert. Der Datentensor aus den zwei Dimensionen L * V wurde in die drei Dimensionen L/p * V * p neu formatiert, wobei L die Länge der multimodalen Sequenz der Ausgangsdaten, V die Anzahl der analysierten Variablen und p die Segmentgröße ist.
Zu den Segment-Tokens im Block des unabhängigen Kanalstamms fügen die Autoren der Methode zwei trainierbare Tensoren hinzu: Positionscodierung und Kanalidentifikation. Die Summe zweier Zahlen ergibt eine Zahl. Deshalb habe ich mich bei meiner Implementierung für die Verwendung einer einzigen lernbaren Positionskodierungsschicht entschieden, die die Positionsbezeichnung jedes einzelnen Elements im Eingabetensor lernt.
if(!cCIPosition.Init(0, 1, OpenCL, window * units_count * variables, optimization, iBatch)) return false; cCIPosition.SetActivationFunction(None);
Im globalen Mischblock bietet der Algorithmus auch eine Positionscodierung. Wir initialisieren eine ähnliche Schicht für die zweite Informationsflussautobahn.
if(!cCMPosition.Init(0, 2, OpenCL, window * units_count * variables, optimization, iBatch)) return false; cCMPosition.SetActivationFunction(None);
Wir werden das unabhängige Kanal-Backbone unter Verwendung des oben besprochenen unabhängigen Kanal-Aufmerksamkeitsblocks CNeuronM V MHAttentionMLKV konstruieren.
if(!cChanelIndependentAttention.Init(0, 3, OpenCL, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, variables, optimization, iBatch)) return false; cChanelIndependentAttention.SetActivationFunction(None);
Und um den globalen Mischblock zu organisieren, verwenden wir den zuvor erstellten Aufmerksamkeitsblock CNeuronMLMHAttentionMLKV.
if(!cChanelMixAttention.Init(0, 4, OpenCL, window * variables, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, optimization, iBatch)) return false; cChanelMixAttention.SetActivationFunction(None);
Beachten Sie, dass in diesem Fall die Fenstergröße des analysierten Vektors eines Elements dem Produkt aus Segmentgröße und Anzahl der analysierten Variablen entspricht, was dem Kanalmischungsparadigma entspricht.
Die Einspeisung globaler Informationen in unabhängige Kanäle erfolgt innerhalb des Blocks der Kreuzaufmerksamkeit.
if(!cGlobalInjectionAttention.Init(0, 5, OpenCL, window, window_key, heads, window * variables, heads_kv, units_count, units_count, layers, layers_to_one_kv, variables, 1, optimization, iBatch)) return false; cGlobalInjectionAttention.SetActivationFunction(None);
Beachten Sie, dass wir in diesem Fall die Anzahl der Einheitszeilen im Kontext auf 1 setzen, da wir hier mit gemischten Kanälen arbeiten.
Am Ende der Initialisierungsmethode führen wir einen Datenpufferaustausch durch, wodurch wir unnötiges Kopieren zwischen den Puffern unserer Klasse und internen Objekten vermeiden können.
if(!SetOutput(cGlobalInjectionAttention.getOutput(), true) || !SetGradient(cGlobalInjectionAttention.getGradient(), true) ) return false;
Wir initialisieren einen Hilfspuffer zur Speicherung von Zwischendaten und geben das logische Ergebnis der Operationen an das aufrufende Programm zurück.
if(!cTemp.BufferInit(cPatching.Neurons(), 0) || !cTemp.BufferCreate(OpenCL) ) return false; //--- return true; }
Nachdem wir das Klassenobjekt initialisiert haben, fahren wir mit dem Erstellen des Algorithmus für den Vorwärtsdurchgang unserer Klasse fort. Wir haben bereits die wichtigsten Phasen des Algorithmus im Prozess der Implementierung der Initialisierungsmethode besprochen. Und jetzt müssen wir sie nur noch in der Methode feedForward beschreiben.
bool CNeuronInjectTST::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cPatching.FeedForward(NeuronOCL)) return false;
In den Methodenparametern erhalten wir einen Zeiger auf das Objekt der vorherigen Schicht, der uns die Originaldaten übergibt. Den erhaltenen Zeiger übergeben wir sofort an die gleichnamige Methode der verschachtelten Datensegmentierungsschicht.
Beachten Sie, dass wir in dieser Phase die Relevanz des erhaltenen Zeigers nicht überprüfen, da die erforderlichen Kontrollen in der Methode der Segmentierungsschicht implementiert sind und eine erneute Überprüfung unnötig wäre.
Der nächste Schritt besteht darin, den segmentierten Daten eine Positionskodierung hinzuzufügen.
if(!cCIPosition.FeedForward(cPatching.AsObject()) || !cCMPosition.FeedForward(cPatching.AsObject()) ) return false;
Danach leiten wir die Daten zunächst durch einen Block unabhängiger Kanäle.
if(!cChanelIndependentAttention.FeedForward(cCIPosition.AsObject())) return false;
Und dann durch den globalen Mischblock.
if(!cChanelMixAttention.FeedForward(cCMPosition.AsObject())) return false;
Bitte beachten Sie, dass es sich trotz der Ausführungsreihenfolge um zwei unabhängige Informationsströme handelt. Nur im kontextuellen Aufmerksamkeitsblock erfolgt die Einspeisung globaler Daten in unabhängige Kanäle.
if(!cGlobalInjectionAttention.FeedForward(cCIPosition.AsObject(), cCMPosition.getOutput())) return false; //--- return true; }
Wir haben den Entscheidungsprozess außerhalb der Klasse CNeuronInjectTST verlagert.
Wie Sie sehen, ist die Vorwärtsdurchgangs-Methode recht prägnant und lesbar. Mit anderen Worten, wie von einer Large-Node-Implementierung des Algorithmus erwartet. Die Rückwärtsdurchgangs-Methoden sind ähnlich aufgebaut. Sie können den Code selbst im Anhang finden. Der vollständige Code dieser Klasse und aller ihrer Methoden finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme.
2.3 Architektur der trainierbaren Modelle
Oben haben wir die grundlegenden Algorithmen von InjectTST mittels MQL5 implementiert und können nun die vorgeschlagenen Ansätze in unsere eigenen Modelle implementieren. Die von uns betrachtete Methode wurde zur Prognose von Zeitreihen vorgeschlagen. Und wir werden, ähnlich wie bei einer Reihe zuvor betrachteter Methoden zur Prognose von Zeitreihen, versuchen, die vorgeschlagenen Ansätze in das Modell des Encoders des Umgebungszustands (Environmental State Encoder) zu implementieren. Wie Sie wissen, wird die Beschreibung der Architektur dieses Modells in der Methode CreateEncoderDescriptions dargestellt.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
In den Parametern dieser Methode erhalten wir einen Zeiger auf ein dynamisches Array-Objekt zur Aufzeichnung der Modellarchitektur. Im Hauptteil der Methode überprüfen wir sofort die Relevanz des empfangenen Zeigers und erstellen bei Bedarf ein neues dynamisches Array-Objekt. Und dann beginnen wir, die Architektur des erstellten Modells zu beschreiben.
Die erste ist die grundlegende, vollständig verbundene Schicht, die zum Aufzeichnen der Originaldaten verwendet wird.
//--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Wie immer planen wir, das Modell mit Roheingabedaten zu füttern. Und sie werden einer Primärverarbeitung in der Batch-Datennormalisierungsschicht unterzogen, wo Informationen aus verschiedenen Verteilungen in eine vergleichbare Form gebracht werden.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Als nächstes kommt unsere neue Schicht unabhängiger Kanäle mit globaler Einspeisung.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronInjectTST; descr.window = PatchSize; //Patch window descr.window_out = 8; //Window Key
Um die Segmentgröße festzulegen, fügen wir die Konstante PatchSize hinzu. Wir berechnen die Größe der Sequenz basierend auf der Tiefe des analysierten Verlaufs und der Größe des Segments.
prev_count = descr.count = (HistoryBars + descr.window - 1) / descr.window; //Units
Die Anzahl der Aufmerksamkeitsköpfe für Abfrage, Schlüssel und Wert. Außerdem schreiben wir die Anzahl der einheitlichen Sequenzen in ein Array.
{
int temp[] =
{
4, //Heads
2, //Heads KV
BarDescr //Variables
};
ArrayCopy(descr.heads, temp);
}
Alle inneren Blöcke enthalten 4 gefaltete Schichten.
descr.layers = 4; //Layers
Und ein Schlüssel-Wert-Tensor ist für zwei verschachtelte Schichten relevant.
descr.step = 2; //Layers to 1 KV descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Als nächstes müssen wir einen Kopf hinzufügen, um nachfolgende Werte vorherzusagen. Wir erinnern uns, dass wir am Ausgang von InjectTST einen Tensor der Dimension L/p * V * p erhalten. Und um eine Prognose der Daten innerhalb unabhängiger Kanäle zu erstellen, müssen wir die Daten zunächst transponieren.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = prev_count; descr.window = PatchSize * BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Dann verwenden wir zweischichtiges MLP, um unabhängige Kanäle vorherzusagen.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = PatchSize * BarDescr; descr.window = prev_count; descr.window_out = NForecast; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = PatchSize * NForecast; descr.window_out = NForecast; descr.activation = TANH; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Dabei reduzieren wir die Dimensionalität der Daten auf Variablen * Prognose. Jetzt können wir die vorhergesagten Werte in die ursprüngliche Datendarstellung zurückführen.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Wir fügen statistische Indikatoren hinzu, die während der Normalisierung aus den Originaldaten entfernt wurden.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Darüber hinaus verwenden wir die Ansätze der Methode FreDF, um die vorhergesagten Werte univariater Reihen im Frequenzbereich auszurichten.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Ich verwende die Architekturen der Modelle von Akteur und Kritiker aus früheren Arbeiten. Deshalb werden wir jetzt nicht näher auf ihre Beschreibung eingehen.
Darüber hinaus haben wir in der neuen Encoder-Architektur weder die Quelldatenschicht noch die Ergebnisse zur Bestimmung des Kontostatus geändert. All dies ermöglicht es uns, alle zuvor erstellten Programme zur Interaktion mit der Umgebung und zum Trainieren von Modellen ohne Änderungen zu verwenden. Dementsprechend können wir die zuvor gesammelte Trainingsstichprobe für das anfängliche Training von Modellen verwenden.
Den vollständigen Code aller Klassen und ihrer Methoden sowie alle Programme, die bei der Erstellung des Artikels verwendet wurden, finden Sie im Anhang.
3. Tests
Oben haben wir die InjectTST -Methode mit MQL5 implementiert und ihre Anwendung im Environmental State Encoder- Modell demonstriert. Nun gehen wir dazu über, die Wirksamkeit des Modells anhand realer historischer Daten zu bewerten.
Wie zuvor trainieren wir zunächst den Encoder des Umgebungszustandes, um zukünftige Preisbewegungen über einen bestimmten Prognosezeitraum vorherzusagen. In diesem Experiment besteht der Trainingsdatensatz aus historischen Daten aus dem Jahr 2023 für das EURUSD-Instrument im H1-Zeitraum.
Der Encoder des Umgebungszustands analysiert nur historische Preisdaten, die nicht von den Aktionen des Agenten beeinflusst werden. Daher trainieren wir das Modell, bis wir zufriedenstellende Ergebnisse erzielen oder der Prognosefehler ein Plateau erreicht.
Nachfolgend finden Sie eine vergleichende Visualisierung der prognostizierten und tatsächlichen Preisbewegungsverläufe.
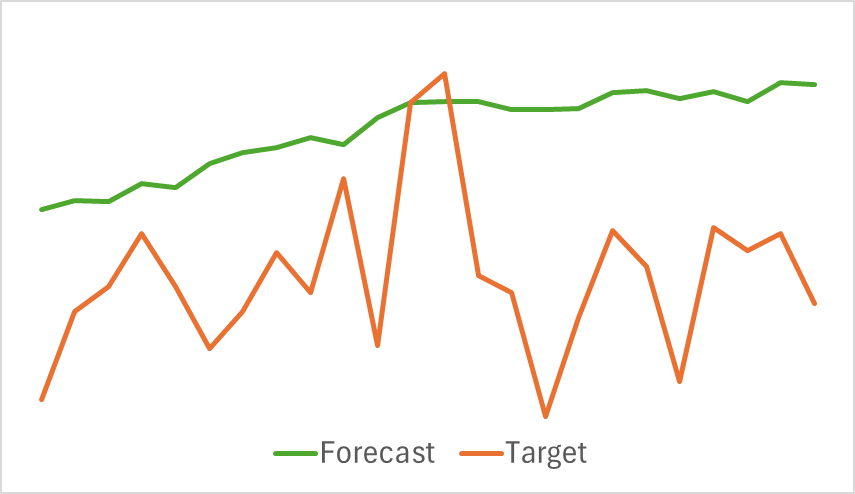
Wie in der Grafik zu sehen ist, ist die prognostizierte Flugbahn nach oben verschoben und weist weniger ausgeprägte Schwankungen auf. Die allgemeine Trendrichtung entspricht jedoch der Zielkurve. Obwohl dies im Vergleich zu zuvor untersuchten Modellen möglicherweise nicht die genaueste Prognose ist, fahren wir mit der zweiten Trainingsphase fort, um zu beurteilen, ob dieser Encoder dem Akteur bei der Entwicklung einer profitablen Strategie helfen kann.
Das Training der Modelle von Akteur und Kritiker erfolgt iterativ. Zunächst führen wir mehrere Epochen des Modelltrainings unter Verwendung des vorhandenen Trainingsdatensatzes durch. Anschließend aktualisieren wir während der Interaktion mit der Umgebung den Datensatz auf Grundlage der Belohnungen, die wir durch Aktionen im Rahmen der aktuellen Richtlinie des Akteurs erhalten haben. Dadurch können wir den Trainingssatz mit echten Aktionsbelohnungen aus der aktuellen Richtlinienverteilung des Akteurs anreichern. Diese Anreicherung des Trainingsdatensatzes mit realen Belohnungswerten ermöglicht eine bessere Optimierung der Belohnungsfunktion des Kritikers und eine präzisere Bewertung der Aktionen des Akteurs. Dies wiederum ermöglicht Anpassungen zur Verbesserung der Wirksamkeit der aktuellen Richtlinie. Die Iterationen werden fortgesetzt, bis das gewünschte Ergebnis erreicht ist.
Um die Wirksamkeit der Richtlinie des trainierten Akteurs zu beurteilen, führen wir einen Testlauf des Umgebungsinteraktionsberaters im Strategietester von MetaTrader 5 durch. Die Tests werden anhand historischer Daten ab Januar 2024 durchgeführt, während alle anderen Parameter unverändert bleiben. Die Ergebnisse des Testlaufs werden unten dargestellt.
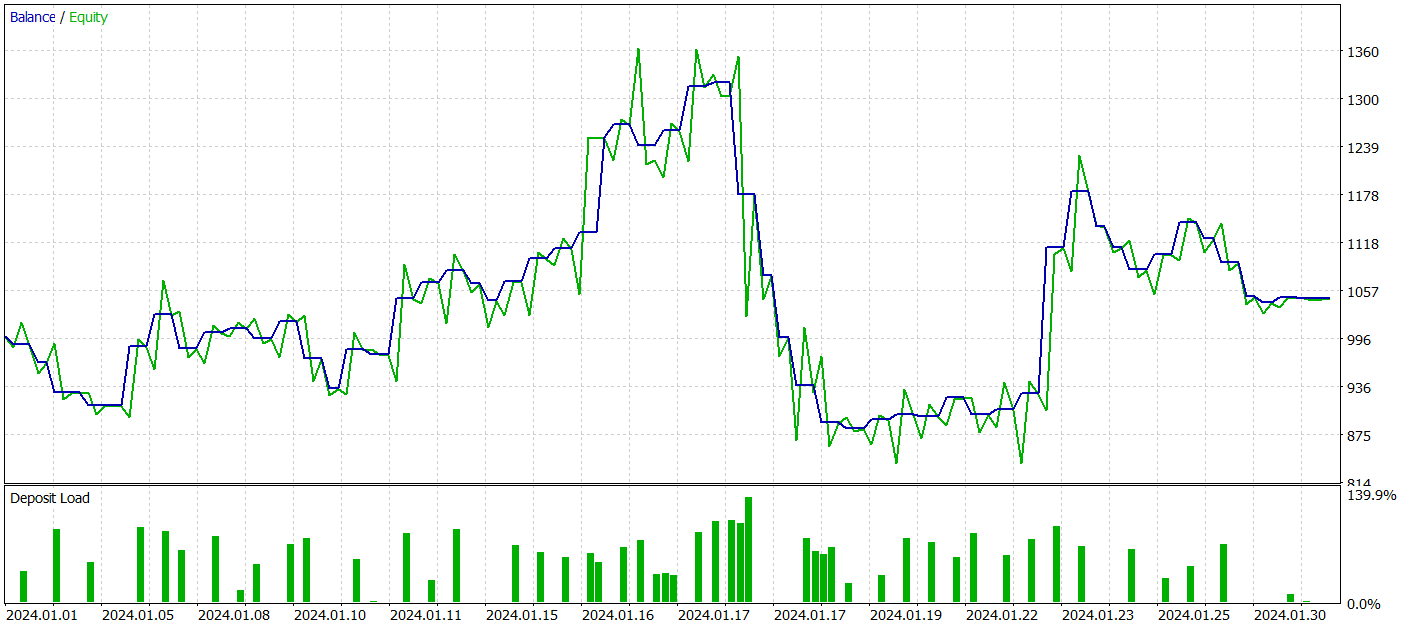
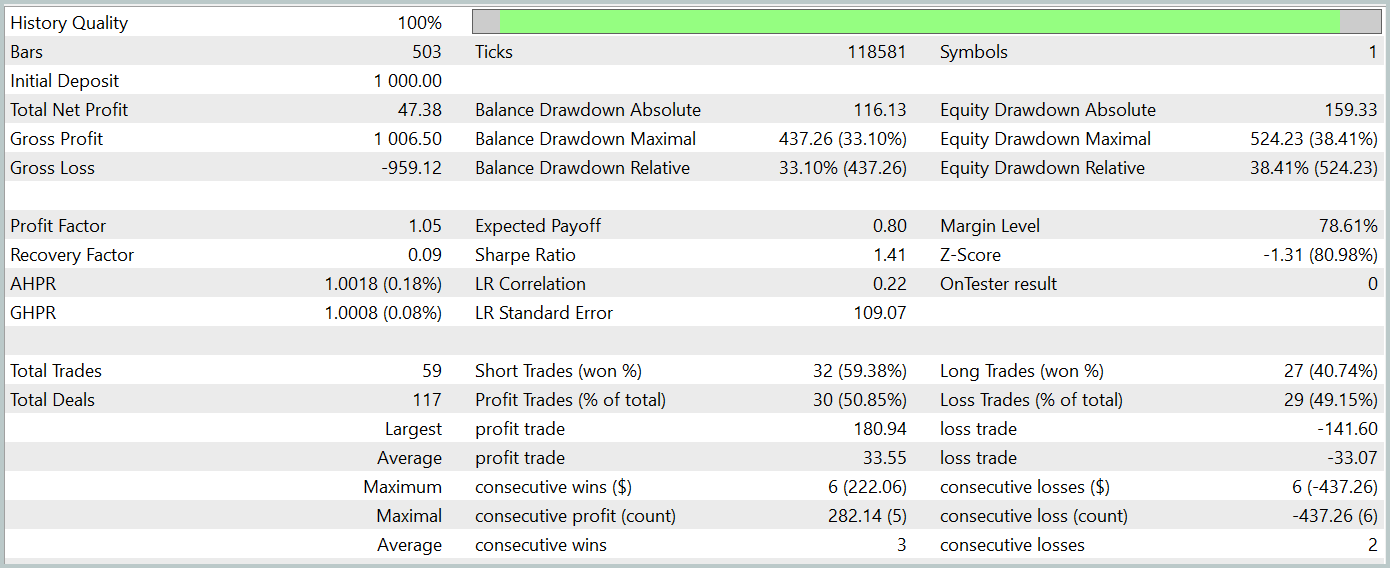
Während der Testphase erzielte das Modell einen kleinen Gewinn. Insgesamt wurden 59 Transaktionen ausgeführt, 30 davon endeten mit Gewinn. Das Maximum und der Durchschnitt der gewinnbringenden Handelsgeschäfte überstiegen ihre Entsprechungen mit Verlust. Daraus ergibt sich ein Profitfaktor von 1,05. Allerdings lässt die Saldenkurve einen deutlichen Aufwärtstrend vermissen und im Test konnte ein Drawdown von über 33% verzeichnet werden.
Schlussfolgerung
In diesem Artikel haben wir InjectTST untersucht, eine neuartige Methode zur Zeitreihenprognose, die darauf ausgelegt ist, langfristige Prognosen durch die Einspeisung globaler Informationen in unabhängige Datenkanäle zu verbessern.
Im praktischen Teil haben wir die vorgeschlagenen Ansätze in MQL5 implementiert und in das Environmental State Encoder-Modell integriert. Obwohl viel Arbeit geleistet wurde, blieben die Ergebnisse hinter unseren Erwartungen zurück.
Um die Gründe für die mangelhafte Leistung des Modells zu ermitteln, ist eine gründliche Analyse erforderlich. Eine mögliche Ursache könnte jedoch der direkte Ansatz beim Training des Umweltzustandsprognosemodells sein. Die Autoren von InjectTST empfahlen ursprünglich einen dreistufigen Trainingsprozess, der möglicherweise erforderlich ist, um bessere Ergebnisse zu erzielen.
Referenzen
- InjectTST: A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting
- Weitere Artikel aus dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Trainings-EA des Encoders |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15498
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Methoden von William Gann (Teil I): Erstellen des Gann Angles-Indikators
Methoden von William Gann (Teil I): Erstellen des Gann Angles-Indikators
 Neuronale Netze im Handel: Praktische Ergebnisse der Methode TEMPO
Neuronale Netze im Handel: Praktische Ergebnisse der Methode TEMPO
 Algorithmus einer Anarchischen Gesellschaftsoptimierung (ASO)
Algorithmus einer Anarchischen Gesellschaftsoptimierung (ASO)
 Algorithmus zur Optimierung der Migration der Tiere (AMO)
Algorithmus zur Optimierung der Migration der Tiere (AMO)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.