Neuronale Netze im Handel: Das „Dual-Attention-Based Trend Prediction Model“
Einführung
Der Preis eines Finanzinstruments stellt eine hochvolatile Zeitreihe dar, die von zahlreichen Faktoren beeinflusst wird, darunter Zinssätze, Inflation, Geldpolitik und Anlegerstimmung. Die Modellierung des Verhältnisses zwischen dem Preis eines Finanzinstruments und diesen Faktoren sowie die Vorhersage ihrer Dynamik ist eine große Herausforderung für Forscher und Anleger.
Die Vorhersage und Analyse von Finanzzeitreihen ist Gegenstand zahlreicher Forschungsarbeiten. Traditionelle statistische Methoden gehen oft davon aus, dass Zeitreihen durch lineare Prozesse erzeugt werden, was ihre Wirksamkeit bei nichtlinearen Prognosen einschränkt. Methoden des maschinellen Lernens und des Deep Learning haben sich bei der Modellierung von Finanzzeitreihen als erfolgreicher erwiesen, da sie in der Lage sind, nichtlineare Beziehungen zu erfassen. Viele Studien haben sich darauf konzentriert, Merkmale zu bestimmten Zeitpunkten zu extrahieren und sie für die Modellierung und Vorhersage zu verwenden. Bei solchen Ansätzen werden jedoch häufig Dateninteraktionen und die kurzfristige Kontinuität von Schwankungen übersehen.
Um diesen Einschränkungen zu begegnen, wurde die Studie „A Dual-Attention-Based Stock Price Trend Prediction Model With Dual Features“ (Ein auf zweifacher Aufmerksamkeit basierendes Aktienkurs-Trendprognosemodell mit zweifachen Merkmalen) schlägt eine Methode zur Extraktion von zwei Merkmalen vor. Bei dieser Methode werden sowohl einzelne Zeitpunkte als auch mehrere Zeitintervalle genutzt. Sie integriert kurzfristige Marktmerkmale mit langfristigen zeitlichen Merkmalen, um die Vorhersagegenauigkeit zu verbessern. Das vorgeschlagene Modell basiert auf einer Encoder-Decoder-Architektur und verwendet Aufmerksamkeitsmechanismen sowohl in der Encoder- als auch in der Decoder-Stufe, wodurch die Identifizierung der wichtigsten Merkmale in langen Zeitreihen ermöglicht wird.
In dieser Studie wird ein neues Trendprognosemodell (TPM) vorgestellt, das die Vorhersage von Aktienkurstrends durch die Verwendung von zwei Merkmalen und zwei Aufmerksamkeitsmechanismen ermöglicht. Das TPM zielt darauf ab, sowohl die Richtung als auch die Dauer von Aktienkursbewegungen vorherzusagen. Die wichtigsten Beiträge des vorgeschlagenen Ansatzes sind folgende:
- Eine neuartige Methode zur Extraktion von zwei Merkmalen auf der Grundlage verschiedener Zeitspannen, die wichtige Marktinformationen effektiv extrahiert und die Prognoseergebnisse optimiert. TPM verwendet eine stückweise, lineare Regression und ein neuronales Faltungsnetzwerk, um langfristige bzw. kurzfristige Marktmerkmale aus Finanzzeitreihen zu extrahieren. Die Darstellung von Marktinformationen durch duale Merkmale verbessert die Vorhersageleistung des Modells erheblich.
- Aktienkurs-Trendprognosemodell (TPM) unter Verwendung der Encoder-Decoder-Struktur und des Dual-Attention-Mechanismus. Durch Hinzufügen von Aufmerksamkeitsmechanismen sowohl in der Encoder- als auch in der Decoder-Stufe wählt TPM adaptiv die relevantesten kurzfristigen Marktmerkmale aus und kombiniert sie mit langfristigen zeitlichen Merkmalen, um die Vorhersagegenauigkeit zu verbessern.
1. TPM-Algorithmus
Bei der Analyse bestehender Zeitreihenprognoseverfahren kamen die Autoren von TPM zu folgenden Schlussfolgerungen:
- Univariaten Finanzzeitreihen mangelt es an ausreichenden Informationen für eine zuverlässige Vorhersage künftiger Kursbewegungen.
- Herkömmliche Methoden der Merkmalsextraktion sind nur begrenzt in der Lage, komplexe Marktverhaltensweisen zu erfassen.
- Die Zeitreihenanalyse mit einem einzigen neuronalen Netz ist unvollständig.
Die TPM-Methode geht auf diese Probleme ein, indem sie eine doppelte Merkmalsextraktion und einen doppelten Aufmerksamkeitsmechanismus einsetzt. Der vorgeschlagene Algorithmus besteht aus zwei Phasen. Zunächst wird die Methode der stückweisen, linearen Regression verwendet, um die Finanzzeitreihen zu segmentieren und historische langfristige zeitliche Merkmale auf der Grundlage von Teilsequenzen mit unterschiedlichen Zeitintervallen zu extrahieren. Kurzfristige räumliche Marktmerkmale werden aus einzelnen Zeitpunkten mit Hilfe eines neuronalen Faltungsnetzwerks extrahiert.
In der zweiten TPM-Phase werden dann die zuvor extrahierten dualen Merkmale durch das Trendprognosemodell auf der Grundlage von Dual-Attention-Mechanismen analysiert. Das vorgeschlagene Modell basiert auf der Encoder-Decoder-Architektur.
Der Encoder basiert auf einem rekurrenten LSTM-Block mit einem zusätzlichen Aufmerksamkeitsmechanismus, der dazu dient, die wichtigsten kurzfristigen Marktmerkmale adaptiv zu extrahieren.
Der Decoder besteht ebenfalls aus einem LSTM-Block und einem Aufmerksamkeitsmechanismus, der die relevantesten kombinierten Merkmale auswählt und dekodiert, um die Aktienkursentwicklung vorherzusagen.
Da die Informationen, die eine eindimensionale Finanzzeitreihe liefert, unzureichend sind, ist es schwierig, die Entwicklung der Aktienkurse auf der Grundlage solcher Daten zu modellieren und vorherzusagen. Die Autoren der TPM-Methode verwenden grundlegende Marktdaten für die Analyse, wie z. B. Eröffnungs- und Schlusskurse, Höchst- und Tiefstkurse sowie das Volumen, und wandeln diese in eine Reihe von technischen Indikatoren um.
Angesichts der kontinuierlichen Veränderungen in den Daten extrahiert TPM langfristige, zeitliche Merkmale mithilfe der stückweisen, linearen Regression (PLR). Die PLR-Methode glättet kurzfristiges Fluktuationsrauschen, reduziert die Dimensionalität der Daten und verbessert die Rechenleistung.
Die Segmentierung einer Zeitreihe hängt von der maximalen Fehlerschwelle δ ab. Am Beispiel der Daten des CSI 300 verwenden die Autoren der Methode PLR, um dessen historischen Schlusskurs zu segmentieren. Wenn δ gleich 2,0 ist, kann die Zeitreihe in 16 Teilsequenzen unterteilt werden. Wenn der Schwellenwert δ jedoch 4,0 beträgt, kann dieselbe Zeitreihe in nur 4 Teilsequenzen unterteilt werden. Je höher der Schwellenwert ist, desto mehr Datenschwankungen werden ignoriert und desto weniger Teilsequenzen werden gebildet. Der Schwellenwert beeinflusst die Zuverlässigkeit der Merkmale der historischen Zeitreihen. Jede Teilsequenz stellt eine Schwankung der Daten in einem bestimmten Zeitraum dar. Steigung sm und Dauer dm jeder Teilsequenz, die als langfristige zeitliche Merkmale für die Trendvorhersage erzeugt werden.
Unter Berücksichtigung der Interaktion verschiedener Daten zum gleichen Zeitpunkt werden kurzfristige räumliche Marktmerkmale jedes Zeitschritts mit Hilfe eines Faltungsneuronalen Netzes (CNN) extrahiert. Für die analysierten Finanzzeitreihen wird eine Marktmatrix erstellt. In der Marktmatrix steht jede Zeile für eine Dimension der analysierten Daten, und die Anzahl der Zeilen ist n. Dann steht jede Spalte für einen Zeitpunkt. Da CNN die Nachbarschaftsbeziehungen und die räumliche Lokalisierung der Originaldaten beibehält, kann es die nichtlineare Beziehung zwischen der Marktmatrix und dem Aktientrend erfassen. Daraus ergeben sich räumliche Merkmale für kurzfristige historische Zeitreihen.
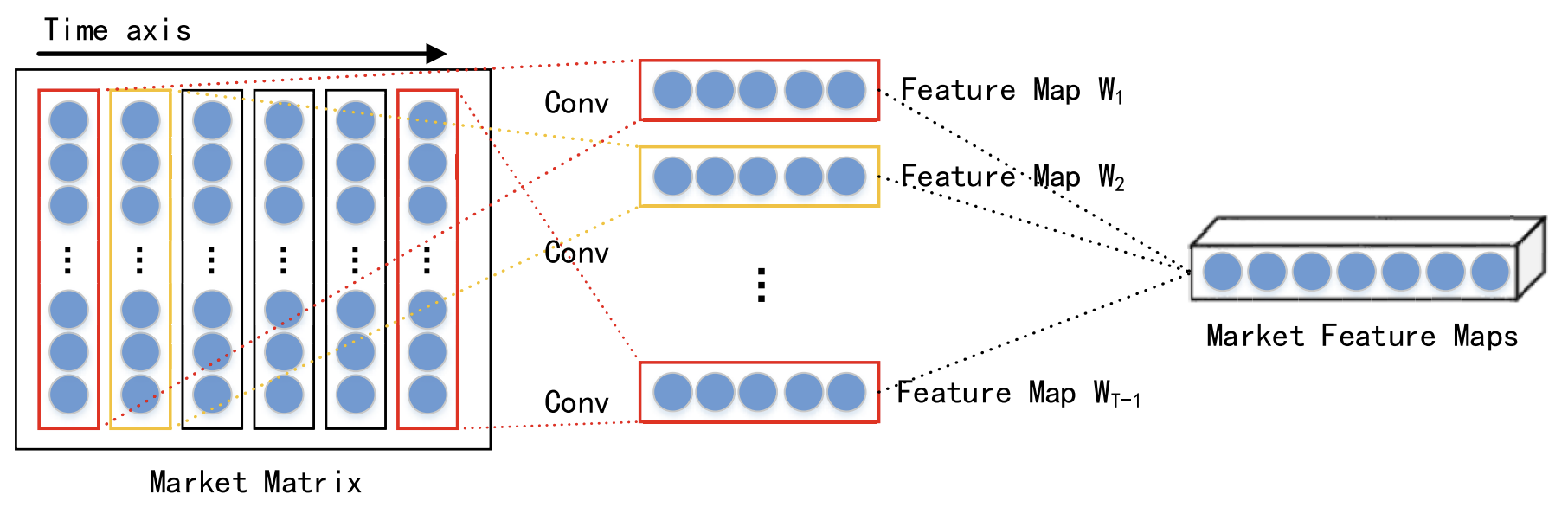
In ihrer Arbeit verwenden die Autoren Faltungsschichten mit unterschiedlichen Kernelgrößen, wie 1 × 3 bis 1 × 5, um abstrakte, mehrstufige räumliche Marktmerkmale zu extrahieren. Als nichtlineare Aktivierungsfunktion wird die ReLU-Funktion gewählt.
Nach den Faltungsschichten wird eine Max-Pooling-Schicht angewandt. Dadurch werden die Dimensionen der Merkmalskarten reduziert und eine Überanpassung verhindert.
Die Ergebnisse von mehreren Faltungsschichten und Max-Pooling-Schichten werden dann zur weiteren Verarbeitung an eine Projektionsschicht weitergeleitet.
Wie bereits erwähnt, werden die extrahierten Kurz- und Langzeitmerkmale innerhalb der Encoder-Decoder-Architektur verarbeitet. Bei dieser Struktur komprimiert der Encoder die Eingabedaten in einen Vektor fester Größe, und der Decoder verarbeitet diese Vektoren, um die endgültige Ausgabe zu erzeugen. Wenn die Eingabedaten jedoch sehr umfangreich sind, kann der Encoder Schwierigkeiten haben, alle relevanten Informationen effektiv zu erfassen, was zu einer Verschlechterung der Modellleistung führt. Der Aufmerksamkeitsmechanismus geht auf diese Einschränkung ein, indem er die verborgenen Zustände der betreffenden Neuronen entschlüsselt.
Es ist wichtig zu beachten, dass der Decoder mit einem Aufmerksamkeitsmechanismus nicht in der Lage ist, explizit die relevantesten Eingangsmerkmale auszuwählen. Um dieses Problem zu lösen, fügen die Autoren der TPM-Methode Aufmerksamkeitsmechanismen sowohl in der Encoder- als auch in der Decoderphase hinzu.
Die zweite Phase des TPM-Algorithmus basiert auf einem Mechanismus der doppelten Aufmerksamkeit. Die Encoder-Decoder-Struktur ist in zwei Stufen unterteilt. In der ersten Stufe analysiert der Encoder, der auf einem LSTM mit Aufmerksamkeitsmechanismus basiert, kurzfristige räumliche Marktmerkmale, die mit einem CNN extrahiert wurden. Die entsprechenden Kurzzeitmerkmale werden zu jedem Zeitpunkt adaptiv ausgewählt und in Vektoren kodiert.
In der zweiten Stufe werden die kodierten Vektoren und die mitPLR extrahierten langfristigen zeitlichen Merkmale einem LSTM-basierten Decoder zugeführt, der die entsprechenden Vektoren und Merkmale auf der Grundlage eines Aufmerksamkeitsmechanismus dekodiert, um den Börsentrend vorherzusagen. Durch den Mechanismus der doppelten Aufmerksamkeit identifiziert das TPM-Modell adaptiv die kritischsten räumlichen Markt- und zeitlichen Merkmale für die Modellierung und Prognose von Trends.
Zu jedem Zeitpunkt t lernt der Encoder die Beziehung zwischen dem Eingangsmerkmal Wt und dem verborgenen Zustand Ht:
![]()
wobei Ht der verborgene Zustand des Encoders zum Zeitpunkt t ist, fen(•) eine nichtlineare Funktion ist und ʘen die Encoder-Parameter bezeichnet.
Die Autoren der Methode verwenden LSTM als nichtlineare Funktion fen, um Zeitabhängigkeiten zu erfassen und einen Encoder der Kurzzeitmerkmale zu bilden. LSTM ist in der Lage, das dynamische zeitliche Verhalten von Zeitreihen effektiv zu modellieren und das Problem des verschwindenden oder explodierenden Gradienten bei RNN zu vermeiden.
Die Autoren der Methode führen einen Aufmerksamkeitsmechanismus in der Encoder-Stufe ein und teilen die Ausgangsmerkmale WMarket entsprechend ihrer Dimensionalität m auf. Der verborgene Zustand Ht-1 und der Zellzustand (Kontext) Ct-1, die im Zeitschritt t-1 berechnet wurden und der Dimensionalität der Eingangsmerkmale entsprechen, werden identifiziert und zur Aktualisierung der ursprünglichen Merkmale zum nächsten Zeitpunkt t verwendet.
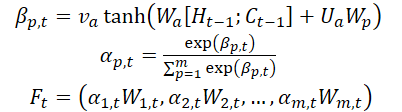
wobei va, Wa und Ua Parameter sind, und die Funktion SoftMax zur Berechnung der Wichtigkeit αm αm,t jeder Merkmalsdimension verwendet wird.
Alle Maße Wt werden zu Ft aktualisiert und in den Encoder eingespeist. Danach wird der verborgene Zustand des Zeitpunkts t aktualisiert.
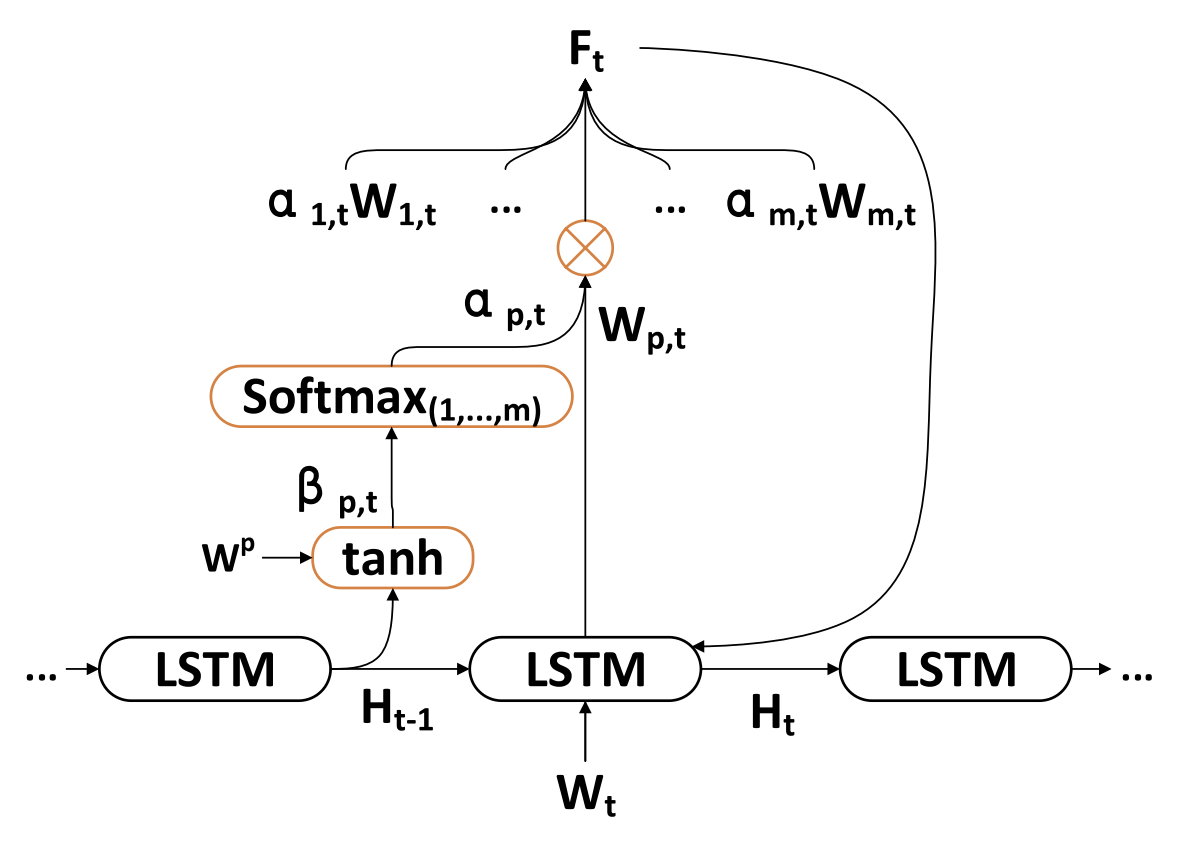
So können wir in jedem Zeitschritt t relevante Dimensionen von räumlichen Marktmerkmalen auswählen, die ursprünglichen Merkmale und den verborgenen Zustand des Encoders iterativ aktualisieren und den relevantesten Codierungsvektor für kurzfristige Merkmale erzeugen.
Der Decoder ist ein LSTM-Block, der für die Vorhersage von Börsentrends entwickelt wurde. Langfristige zeitliche Merkmale ZT-1 werden mit der PLR-Methode extrahiert.
In jedem Zeitschritt t lernt der Decoder die Beziehung zwischen dem Kodierungsvektor Wt, einem Langzeitmerkmal Lt und einem verborgenen Zustand Ht:
![]()
wobei H't der verborgene Zustand des Decoders zum Zeitpunkt t ist, fde(•) eine nichtlineare Funktion ist und ʘde die Decoderparameter bezeichnet.
Die Autoren von TPM verwenden LSTM als nichtlineare Funktion , um zeitliche Abhängigkeiten zu erfassen und einen Decoder der Langzeitmerkmale zu bilden. Das Berechnungsverfahren ist ähnlich wie bei der Encoder-Stufe.
Die Autoren von TPM führen einen Aufmerksamkeitsmechanismus in der Decoderstufe ein, um die zugehörigen verborgenen Zustände des Encoders aller Zeitpunkte zu erhalten.
Der Kontextvektor, der dem Decoder zugeführt wird, ergibt sich aus allen verborgenen Zuständen des Encoders.
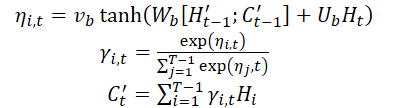
Sobald der Kontextvektor C't erhalten wurde, wird er mit den temporären Langzeitmerkmalen Lt kombiniert, um ein gemischtes Merkmal yt zu erzeugen:
![]()
Unter Verwendung der oben genannten Formeln wählt der Algorithmus in jedem Zeitschritt t die relevantesten verborgenen Zustände des Encoders aller Zeitpunkte und langfristigen zeitlichen Merkmale aus, um gemischte Merkmalsvektoren zu erzeugen.
Anschließend wird die nichtlineare Abbildungsfunktion F(•) zwischen Börsentrend und dualen Merkmalen untersucht. Schließlich wird eine lineare Funktion angewandt, um die Vorhersage des Börsentrends zum Zeitpunkt T zu erstellen.
Das Modell wurde mit der stochastischen Gradientenabstiegsmethode und einem Momentum-Optimierer trainiert. Die Größe der Trainingssatzes betrug 64 und die Lernrate 0,001.
Als Verlustfunktion wird eine quadratische Fehlerfunktion mit Regularisierungsterms verwendet.
Die Visualisierung der TPM-Methode durch den Autor wird im Folgenden dargestellt.
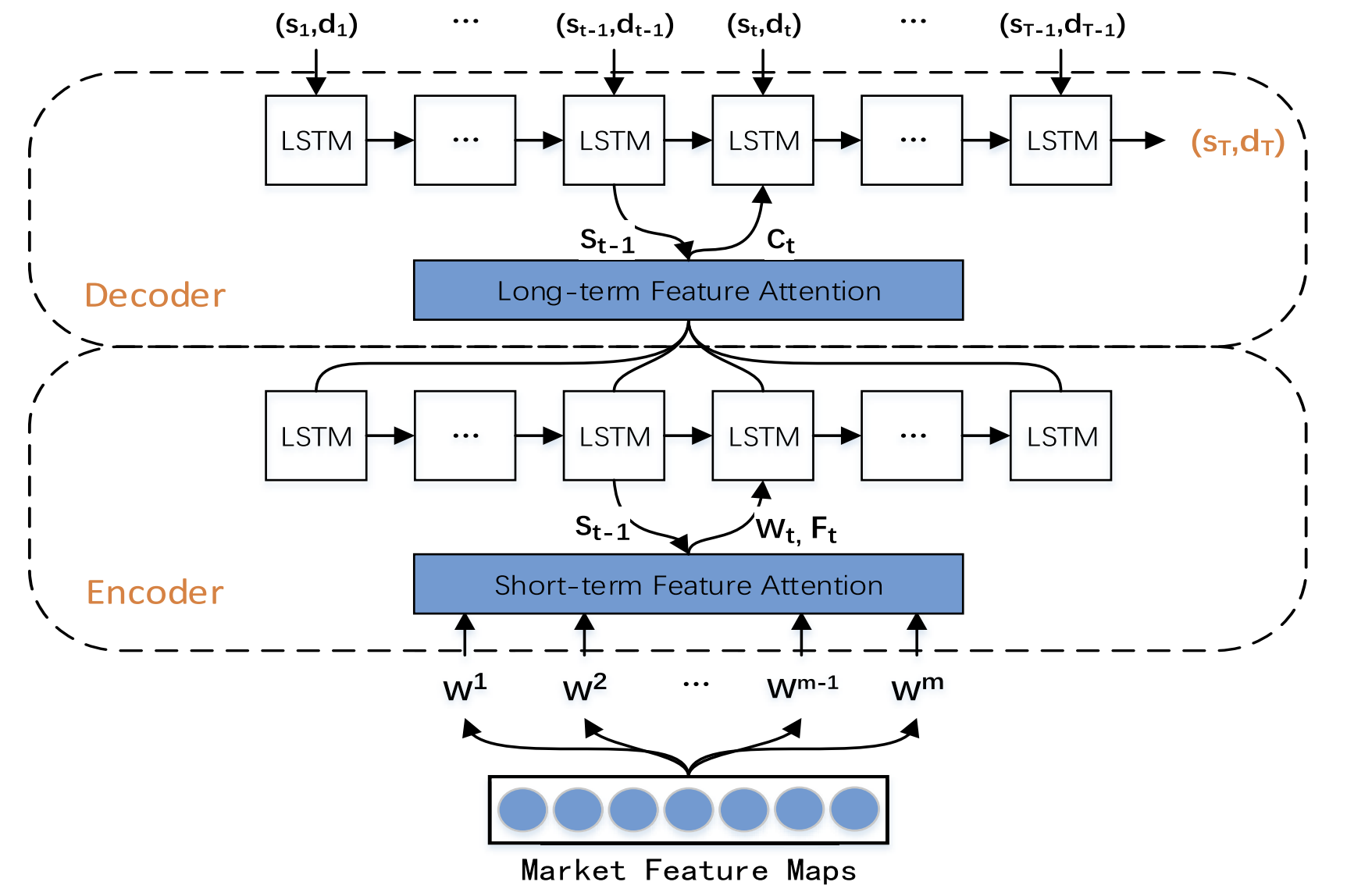
2. Implementierung in MQL5
Nachdem wir die theoretischen Aspekte der vorgeschlagenen TPM-Methode untersucht haben, gehen wir nun zur praktischen Umsetzung unseres Ansatzes über und stellen unsere Interpretation der vorgeschlagenen Ansätze vor. Wie üblich behalten wir den allgemeinen Rahmen der vorgeschlagenen Methodik bei, führen aber einige Abweichungen bei den Implementierungsdetails ein. Natürlich können sich diese Anpassungen unterschiedlich auf die endgültige Leistung des Modells auswirken.
Wir beginnen mit der Konstruktion des Encoders.
2.1 TPM-Encoder
Wir implementieren den Encoder für unser Modell in der Klasse CNeuronTPMEncoder, die die Grundfunktionalität von dem zuvor erstellten LSTM-Block CNeuronLSTMOCL erbt. Die Wahl dieser übergeordneten Klasse ist beabsichtigt. Wie Sie sich vielleicht erinnern, basiert der Encoder in der TPM-Methode auf einem LSTM-Block mit einem zusätzlichen Aufmerksamkeitsmechanismus.
Außerdem haben wir beschlossen, den Prozess der Merkmalsextraktion für Kurzzeitmerkmale direkt in den Encoder zu integrieren. Die Merkmalsextraktion wird unter Verwendung der zuvor entwickelten Datenpyramidenstruktur durchgeführt CSCM. Es gibt jedoch eine wichtige Nuance: Bisher wurde der CSCM-Block verwendet, um Merkmale aus univariaten Zeitreihen zu extrahieren. Nun müssen wir den Datenfluss leicht abändern, um Merkmale aus einzelnen Zeitpunkten zu extrahieren.
Die allgemeine Struktur des Encoders wird im Folgenden dargestellt.
class CNeuronTPMEncoder : public CNeuronLSTMOCL { protected: bool bTSinRow; //--- CNeuronCSCMOCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronTransposeOCL cTranspose; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPMEncoder(void){}; ~CNeuronTPMEncoder(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPMEncoder; } virtual void SetOpenCL(COpenCLMy *obj); };
Hier sehen wir den bekannten Satz überschriebener Methoden und mehrere verschachtelte Objekte, deren Zweck wir im Laufe der Implementierung klären werden.
Wie zuvor werden alle verschachtelten Objekte als statisch deklariert. Dieser Ansatz erlaubt es uns, sowohl den Konstruktor als auch den Destruktor der Klasse „leer“ zu lassen. Die eigentliche Initialisierung einer Instanz unserer neuen Klasse wird in der Methode Init durchgeführt.
bool CNeuronTPMEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(variables * lenth)) return false;
In den Parametern erhält diese Methode die Hauptparameter des erstellten Objekts. In diesem Fall gibt es 3 solcher Parameter:
- variables — die Anzahl der univariaten Sequenzen innerhalb der analysierten multimodalen Zeitreihe.
- lenth — die Größe der analysierten Sequenz (Tiefe der Historie).
- hidden_size — die Größe des versteckten Bereichs im LSTM-Block.
Außerdem haben wir das Flag ts_in_row hinzugefügt, das die Position der einzelnen univariaten Sequenzen in den Zeilen des Eingabedatentensensors angibt.
Im Methodenkörper rufen wir die gleichnamige Methode der Elternklasse auf, die einen erforderlichen Kontrollblock zur Überprüfung der Parameter der erstellten Ebene und zur Initialisierung der geerbten Objekte bereitstellt.
Hier geben wir auch die Größe des Eingabetensors der Elternklasse an, die gleich dem Produkt aus der Größe der univariaten Sequenz und der Anzahl solcher Sequenzen in den Eingabedaten ist.
Bitte beachten Sie, dass wir innerhalb des LSTM-Blocks vollständig verbundene Schichten verwendet haben, während der Eingabedatentensor in diesem Fall nicht relevant ist.
Der nächste Schritt ist die Initialisierung des Blocks für die kurzfristige Merkmalsextraktion.
uint windows[] = {variables, 6, 5, 4}; if(!cFeatureExtraction.Init(0, 0, OpenCL, windows, lenth, variables, ts_in_row, optimization, batch)) return false;
Zu diesem Zweck werden zunächst die Fenstergrößen der Faltungsmerkmalsextraktionsschichten festgelegt und die CSCM-Blockinitialisierungsmethode aufgerufen.
Bitte beachten Sie, dass wir beim Aufruf der CSCM-Blockinitialisierungsmethode die Parameter für die Größe und Anzahl der univariaten Sequenzen umgestellt haben. Dies ist darauf zurückzuführen, dass die Merkmale aus einzelnen Zeitschritten (Balken) extrahiert werden müssen und nicht aus univariaten Sequenzen, wie sie die Methode MSFformer.
Als Nächstes werden die verschachtelten Objekte des Aufmerksamkeitsblocks initialisiert. Hier erstellen wir zunächst eine Schicht, in deren Puffern wir den verborgenen Zustand und den Kontext des LSTM-Blocks aus dem vorherigen Schritt verketten.
if(!cMemAndHidden.Init(0, 1, OpenCL, hidden_size * 2, optimization, batch)) return false;
Zur Berechnung der Wichtigkeitskoeffizienten der einzelnen Merkmale verwenden wir eine Verkettungsschicht, deren Ergebnisse wir mit der SoftMax-Funktion normalisieren.
if(!cConcatenated.Init(0, 2, OpenCL, variables * lenth, variables * lenth, hidden_size * 2, optimization, batch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 3, OpenCL, variables * lenth, optimization, batch)) return false; cSoftMax.SetHeads(variables);
Beachten Sie, dass in diesem Stadium die Normalisierung der Daten in univariaten Sequenzen durchgeführt wird.
Als Nächstes fügen wir eine Ebene hinzu, um die Aufmerksamkeitsleistungen zu erfassen.
if(!cAttentionOut.Init(0, 4, OpenCL, variables * lenth, optimization, batch)) return false;
Falls erforderlich, initialisieren wir die Datenumsetzungsschicht.
bTSinRow = ts_in_row; if(!bTSinRow) { if(!cTranspose.Init(0, 5, OpenCL, variables, lenth, optimization, iBatch)) return false; }
Wir fügen auch einen Hilfspuffer für die Aufzeichnung von Zwischenwerten hinzu.
//--- if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Nach erfolgreicher Initialisierung aller verschachtelten Objekte übergeben wir das logische Ergebnis der durchgeführten Operationen an den Aufrufer und beenden die Methode.
Nachdem die Initialisierung des Objekts abgeschlossen ist, gehen wir dazu über, den Algorithmus des Vorwärtsdurchgangs für die neue Klasse zu konstruieren, den wir in der Methode feedForward implementieren.
bool CNeuronTPMEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
Wie üblich, erhalten wir in den Parametern dieser Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. In diesem Fall wird der empfangene Zeiger jedoch nicht überprüft, sondern an die Methode für den Vorwärtsdurchgang der inneren Kurzzeit-Merkmalextraktionsschicht weitergeleitet. Der Hauptteil der aufgerufenen Methode selbst implementiert die Kontrolle über den empfangenen Zeiger.
Der nächste Schritt besteht darin, den verborgenen Zustand und den Kontext unseres Objekts zu kombinieren, die aus dem vorangegangenen Vorwärtsdurchgang erhalten geblieben sind.
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false;
Damit sind unsere vorbereitenden Arbeiten abgeschlossen. Kommen wir nun zum Aufmerksamkeitsblock. In diesem Block berechnen wir die Wichtigkeitskoeffizienten der einzelnen Merkmale.
if(!cConcatenated.FeedForward(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false; int map = cSoftMax.getOutputIndex();
Falls erforderlich, transponieren wir den Tensor der Wichtigkeitskoeffizienten.
if(!bTSinRow) { if(!cTranspose.FeedForward(cSoftMax.AsObject())) return false; map = cTranspose.getOutputIndex(); }
Dann müssen wir die erhaltenen Koeffizienten Element für Element mit den entsprechenden Kurzzeitmerkmalen multiplizieren. Für die elementweise Multiplikation von 2 Tensoren verwenden wir den Vorwärtsdurchgangs-Kernel der Dropout Schicht.
Wir haben diesen Kernel erstellt, um die Eingabedaten mit der Neuronen-Ausschlussmaske zu multiplizieren. In diesem Fall verwenden wir Wichtigkeitskoeffizienten als Maske.
Definieren wir die Dimension des Aufgabenraums.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;
Übergabe der Parameter an den Kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, map)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Danach stellen wir sie in die Ausführungswarteschlange.
if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Nach der Ausführung des Kernels im AttentionOut-Schichtpuffer erhalten wir Kurzzeitmerkmale unter Berücksichtigung ihres Wichtigkeitskoeffizienten. Nun können wir die Grundfunktionalität des LSTM-Blocks für die Darstellung des Merkmalstensors am Ausgang unseres Encoders nutzen.
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttentionOut.AsObject())) return false; //--- return true; }
Vergessen Sie nicht, die Arbeitsabläufe in jeder Phase zu überwachen. Nach erfolgreicher Ausführung übergeben wir das logische Ergebnis der durchgeführten Operationen an den Aufrufer und beenden die Methode.
Nach der Implementierung des Vorwärtsdurchgangs geht man in der Regel dazu über, die Methoden der Rückwärtsdurchgänge (backpropagation) zu konstruieren. Dieser Klasse bildet da keine Ausnahme. Im nächsten Schritt implementieren wir die Fehlergradientenfortpflanzung auf alle verschachtelten Objekte und den Eingabedatentensor entsprechend ihrem Einfluss auf das Endergebnis des Modells. Wir implementieren die angegebene Funktionalität in der Methode calcInputGradients.
In den Parametern dieser Methode, die der oben beschriebenen Methode ähnlich ist, erhalten wir einen Zeiger auf das Objekt der vorherigen neuronalen Schicht.
bool CNeuronTPMEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird zunächst die Relevanz des empfangenen Zeigers geprüft.
Anschließend propagieren wir den Fehlergradienten mithilfe der vererbten Funktionalität durch den LSTM-Block-Algorithmus auf die Ausgangsebene unseres Aufmerksamkeitsblocks.
if(!CNeuronLSTMOCL::calcInputGradients(cAttentionOut.AsObject())) return false;
Danach verteilen wir den Fehlergradienten in 2 Richtungen: die Koeffizienten der Merkmalsbedeutung und die Merkmale selbst. Der Algorithmus für die Platzierung des Kernels in einer Warteschlange ist ähnlich wie der oben beschriebene.
//--- uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = cSoftMax.Neurons(); ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cTemp.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, (bTSinRow ? cSoftMax.getOutputIndex() : cTranspose.getOutputIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, (bTSinRow ? cSoftMax.getGradientIndex() : cTranspose.getGradientIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, NeuronOCL.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Hier sollten wir zwei Punkte beachten. Erstens hängt der Puffer für die Ausbreitung des Fehlergradienten für die Aufmerksamkeitskoeffizienten von der Notwendigkeit ab, die Transpositionsschicht für die Wichtigkeitskoeffizienten zu verwenden. Zweitens verwenden wir die kurzfristigen Merkmale selbst sowohl bei der Multiplikation mit den Wichtigkeitskoeffizienten als auch bei der Berechnung dieser Koeffizienten. Deshalb speichern wir in dieser Phase den Fehlergradienten der Kurzzeitmerkmale in einem temporären Datenpuffer.
Im nächsten Schritt transponieren wir, falls erforderlich, den Fehlergradienten der Wichtigkeitskoeffizienten der einzelnen Merkmale.
if(bTSinRow) { if(!cSoftMax.calcHiddenGradients(cTranspose.AsObject())) return false; }
Danach propagieren wir den Fehlergradienten durch den Aufmerksamkeitsblock-Algorithmus auf die Ebene der Kurzzeitmerkmale.
if(!cConcatenated.calcHiddenGradients((CObject*)cSoftMax.AsObject(),(CBufferFloat *)NULL,(CBufferFloat *)NULL) || !DeActivation(cConcatenated.getOutput(), cConcatenated.getGradient(), cConcatenated.getGradient(), cConcatenated.Activation())) return false; if(!cFeatureExtraction.calcHiddenGradients(cConcatenated.AsObject(), cMemAndHidden.getOutput(), cMemAndHidden.getGradient())) return false;
Dann summieren wir den Fehlergradienten auf der Ebene der Kurzzeitmerkmale aus 2 Informationssträngen.
if(!DeActivation(cFeatureExtraction.getOutput(), GetPointer(cTemp), GetPointer(cTemp), NeuronOCL.Activation()) || !SumAndNormilize(cFeatureExtraction.getGradient(), GetPointer(cTemp), cFeatureExtraction.getGradient(), 1, false)) return false;
Am Ende der Methode propagieren wir den Fehlergradienten bis zur Ebene der vorherigen Schicht und übergeben das logische Ergebnis der Operationen an den Aufrufer.
if(!NeuronOCL.calcHiddenGradients(cFeatureExtraction.AsObject())) return false; //--- return true; }
Nach der Verteilung des Fehlergradienten müssen wir nur noch die Modellparameter optimieren, um den Gesamtfehler zu minimieren. Wir implementieren diese Funktionalität in der Methode updateInputWeights, indem wir die gleichnamigen Methoden der verschachtelten Objekte aufrufen, die die trainierbaren Parameter enthalten.
bool CNeuronTPMEncoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronLSTMOCL::updateInputWeights(cAttentionOut.AsObject())) return false; if(!cFeatureExtraction.UpdateInputWeights(NeuronOCL)) return false; if(!cConcatenated.UpdateInputWeights(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; //--- return true; }
Damit ist die Beschreibung der Algorithmen zur Implementierung der Hauptfunktionen unseres Encoders abgeschlossen. Der vollständige Code für alle Methoden dieser Klasse ist im Anhang verfügbar, ebenso wie der vollständige Code für alle Programme, die bei der Erstellung dieses Artikels verwendet wurden.
2.2 TPM-Decoder
Nach der Implementierung der Algorithmen der TPM-Encoder gehen wir zum zweiten Schritt über - dem Aufbau des Decoders. Bei der Durchsicht der theoretischen Aspekte der TPM-Methode sind Ihnen wahrscheinlich bedeutende Ähnlichkeiten zwischen dem Encoder- und dem Decoder-Algorithmus aufgefallen. Doch selbst bei geringen Unterschieden müssen wir eine neue Klasse entwickeln.
Ähnlich wie der Encoder ist auch die neue Decoder-Klasse CNeuronTPMDecoder von der LSTM-Block-Klasse abgeleitet. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronTPM : public CNeuronLSTMOCL { protected: CNeuronTPMEncoder cEncoder; CNeuronPLROCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronConcatenate cAttAndFeature; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPM(void){}; ~CNeuronTPM(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPM; } virtual void SetOpenCL(COpenCLMy *obj); };
Die Ähnlichkeit mit der oben beschriebenen Klasse des Encoders ist leicht zu erkennen. Es wurden nur 2 verschachtelte Objekte hinzugefügt. Sie können auch die Änderung in der Art der Merkmalsextraktionsschicht feststellen: Im Decoder verwenden wir PLR, um langfristige Merkmale zu extrahieren.
Sie haben vielleicht bemerkt, dass die Klasse des Encoders eine Spezifikation der Eigentümerschaft enthält, die in der Klasse des Decoders nicht vorhanden ist. Für diese Unterscheidung gibt es einen Grund. Der Encoder und der Decoder arbeiten mit denselben Eingabedaten, extrahieren aber Merkmale auf unterschiedlichen Abstraktionsebenen. Um die Modellstruktur auf der oberen Ebene nicht zu sehr zu verkomplizieren, habe ich beschlossen, den Encoder und den Decoder zu einem einheitlichen Block zusammenzufassen. Die zuvor entwickelte Encoder-Klasse wurde als interne Schicht in die neue Klasse eingefügt, die den TPM-Algorithmus in einer einzigen Einheit vereint. Diese Entscheidung spiegelt sich in der Bezeichnung der neuen Klasse wider: CNeuronTPM.
Die Parameter der Initialisierungsmethode der neuen Klasse sind völlig identisch mit der oben beschriebenen Initialisierungsmethode für Encoder.
bool CNeuronTPM::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(hidden_size)) return false;
Im Hauptteil der Methode rufen wir auch die Initialisierungsmethode der übergeordneten Klasse auf. Allerdings entspricht die Größe seines Eingabedatentensensors bereits der Größe des verborgenen Zustands des Encoders. Dies liegt daran, dass der Decoder mit dem gewichteten Vektor der vom Encoder erhaltenen Merkmale gefüttert wird.
Wir initialisieren auch das Encoder-Objekt
if(!cEncoder.Init(0, 0, OpenCL, variables, lenth, hidden_size, ts_in_row, optimization, iBatch)) return false;
und die Merkmalsextraktionsschicht.
if(!cFeatureExtraction.Init(0, 1, OpenCL, variables, lenth, !ts_in_row, optimization, iBatch)) return false;
Der weitere Algorithmus zur Initialisierung der Aufmerksamkeitsblock-Objekte ähnelt ähnlichen Operationen bei der Initialisierung des Encoders, aber es gibt Unterschiede in den Größen der Eingabedatentensoren.
if(!cMemAndHidden.Init(0, 2, OpenCL, hidden_size * 2, optimization, iBatch)) return false; if(!cConcatenated.Init(0, 3, OpenCL, hidden_size, hidden_size, hidden_size * 2, optimization, iBatch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 4, OpenCL, hidden_size, optimization, iBatch)) return false; cSoftMax.SetHeads(1); if(!cAttentionOut.Init(0, 5, OpenCL, hidden_size, optimization, iBatch)) return false;
Wie bereits erwähnt, verwendet der LSTM-Block vollständig verbundene Schichten. Daher kann der vom Encoder erhaltene Tensor von Kurzzeitmerkmalen im Zusammenhang mit univariaten Sequenzen der analysierten multimodalen Eingangszeitreihen als „anonym“ betrachtet werden. Auf diese Weise können wir die Wichtigkeitskoeffizienten für den gesamten Tensor normalisieren. In diesem Stadium ist die Orientierung des Eingabetensors für uns nicht wichtig.
Fügen wir eine Projektionsschicht aus gewichteten Kurzzeit- und Langzeitmerkmalen der analysierten Zeitreihe hinzu, die wir in den LSTM-Block einspeisen werden.
if(!cAttAndFeature.Init(0, 6, OpenCL, hidden_size, hidden_size, variables * lenth, optimization, iBatch)) return false;
Am Ende der Initialisierungsoperationen der Klasse fügen wir einen Puffer hinzu, um temporäre Daten zu speichern.
if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Wir geben das logische Ergebnis der Initialisierung der verschachtelten Objekte an den Aufrufer zurück.
Nach der Initialisierung der verschachtelten Objekte geht es an die Implementierung des Feed-Forward-Algorithmus in der Methode feedForward. Ähnlich wie bei anderen gleichnamigen Methoden erhalten wir in den Parametern einen Zeiger auf das Objekt der vorherigen neuronalen Schicht.
bool CNeuronTPM::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Encoder if(!cEncoder.FeedForward(NeuronOCL)) return false;
Dann übergeben wir den empfangenen Zeiger an die Feed-Forward-Methode unseres Encoders.
Als Nächstes übergeben wir denselben Zeiger, um langfristige Merkmale der analysierten Zeitreihen zu extrahieren.
//--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
Die Funktionsweise des Aufmerksamkeitsblocks ist ähnlich wie die des oben beschriebenen Encoder-Blocks.
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false; //--- Attention if(!cConcatenated.FeedForward(cEncoder.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false;
Wir multiplizieren die Wichtigkeitskoeffizienten mit dem Vektor der Kurzzeitmerkmale des Encoders.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cEncoder.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cSoftMax.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Wir kombinieren den gewichteten Vektor der kurzfristigen Merkmale mit den langfristigen Merkmalen in einer Verkettungsschicht.
//--- Attention and Features if(!cAttAndFeature.FeedForward(cAttentionOut.AsObject(), cFeatureExtraction.getOutput())) return false;
Diese aufbereiteten Daten werden dann in den LSTM-Block eingespeist.
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttAndFeature.AsObject())) return false; //--- return true; }
Wir überprüfen das logische Ergebnis der Operationen und geben es an das aufrufende Programm zurück.
Als Nächstes würden wir normalerweise zur Konstruktion der Backpropagation-Methoden übergehen. Ich glaube jedoch, dass Sie die Ähnlichkeiten zwischen den Vorwärtspassmethoden von Encoder und Decoder bemerkt haben. Natürlich gibt es einige Nuancen. Ähnliche Nuancen gibt es auch bei den Backpropagation-Verfahren. Dennoch sind die Algorithmen insgesamt recht ähnlich. Ich möchte Sie daher ermutigen, sie in der beigefügten Anlage auf eigene Faust zu erkunden.
2.3 Architektur der trainierbaren Modelle
Wir haben die Umsetzung der TPM-Methode mit MQL5 untersucht. Diese Methode wurde entwickelt, um die Entwicklung der Aktienkurse vorherzusagen. Natürlich werden wir sie in unseren Umgebungszustand-Encoder integrieren, dessen Architektur in der Methode CreateEncoderDescriptions beschrieben wird.
In den Parametern erhält die Methode einen Zeiger auf ein dynamisches Array, in dem wir die eingebettete Modellarchitektur speichern werden.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Im Methodenrumpf wird die Relevanz des empfangenen Zeigers geprüft und gegebenenfalls eine neue Instanz des dynamischen Array-Objekts erstellt.
Wie üblich füttern wir das Modell mit Rohdaten, die den Zustand der Umwelt beschreiben. Zur Erfassung der Ausgangsdaten verwenden wir eine einfache, voll verknüpfte Schicht, deren Größe ausreichen sollte, um den analysierten Tensor zu schreiben.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die gewonnenen Ausgangsdaten werden in der Schicht der Stapelnormalisierung vorverarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die vorverarbeiteten Daten werden dann an unser TPM-Modul weitergeleitet.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTPM; descr.count = LatentCount; descr.window = BarDescr; descr.window_out = HistoryBars; descr.step = int(false); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die vom TPM-Modul erhaltenen Daten werden durch ein 3-Schichten-MLP propagiert, an dessen Ausgang wir die vorhergesagten Werte für die analysierten Zeitreihen erwarten.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = BarDescr * NForecast; descr.optimization = ADAM; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
Zu den Prognosewerten fügen wir statistische Variablen der ursprünglichen Zeitreihe hinzu, die zuvor in der Batch-Normalisierungsschicht entfernt wurden.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Dann gleichen wir die vorhergesagte Ausgabe mit der Frequenzdarstellung ab.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Die Modelle „Actor“ und „Critic“ (Akteur und Kritiker) wurden ohne Änderungen aus früheren Arbeiten übernommen. Sie finden sie in der Anlage.
2.4 EAs für das Modelltraining
Beim Training von Modellen sollten wir die Besonderheiten des Trainings von rekurrenten Modellen beachten. Wie Sie wissen, ist das Hauptmerkmal von rekurrenten Modellen ihre Empfindlichkeit gegenüber der Reihenfolge der Eingabedaten. Daher müssen wir beim Modelltraining Daten aus dem Trainingsdatensatz verwenden, die der historischen Abfolge folgen. Andererseits verringert dieser Ansatz die Trainingseffizienz der meisten Modelle, da er eine Überanpassung innerhalb kleiner Zeitintervalle fördert und eine Verallgemeinerung auf den gesamten Trainingszeitraum unmöglich macht.
Um die negativen Auswirkungen der genannten Faktoren zu minimieren, werden wir während des Trainingsprozesses nach dem Zufallsprinzip kleine Teilmengen aus dem Erfahrungswiedergabepuffer in Übereinstimmung mit der historischen Abfolge entnehmen. Dann werden wir ein neues Trainingspaket ausprobieren. Betrachten wir die Implementierung des vorgeschlagenen Ansatzes am Beispiel der Environment State Encoder Trainingsmethode. Die Expert Advisor-Datei „...\Experts\TPM\StudyEncoder.mq5“ ist ebenfalls unten angehängt.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Im Hauptteil der Methode erzeugen wir zunächst einen Vektor von Wahrscheinlichkeiten für die Auswahl von Durchgängen aus der Trainingsmenge, geordnet nach der Rentabilität der Durchgänge. Danach deklarieren wir die notwendigen lokalen Variablen.
vector<float> result, target, state; bool Stop = false;
Als Nächstes fügen wir eine Variable hinzu, die die Größe eines Teilmengen-Trainingsbatches angibt.
int Batch = 100;
Dann erstellen wir ein System von verschachtelten Schleifen. In der äußeren Schleife wird eine Trajektorie aus der Trainingsmenge und der Startzustand der Trainingsuntermenge auf der gesampelten Trajektorie ausgewählt.
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch) { int tr = SampleTrajectory(probability); int st = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(st <= 0) { iter -= Batch; continue; }
Wir löschen den verborgenen Zustand und die Kontextpuffer des LSTM-Blocks.
Encoder.Clear();
Danach führen wir eine verschachtelte Schleife aus, um die Zustände in ihrer historischen Abfolge ausgehend von dem ausgewählten Zustand der Umgebung zu durchlaufen.
for(int i = st; (i < MathMin(st + Batch, Buffer[tr].Total - NForecast) && !IsStopped() && !Stop); i++) { state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter += i - st - Batch; break; } bState.AssignArray(state);
Im Hauptteil der geschachtelten Schleife wird der analysierte Zustand der Umgebung in den Datenpuffer übertragen. Auf der Grundlage der gewonnenen Daten sagen wir die nächste Kursentwicklung voraus.
//--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Anschließend laden wir die Zielwerte der nächsten Trajektorie aus dem Erfahrungswiedergabepuffer.
//--- Collect target data if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!Result.Resize(BarDescr * NForecast)) continue;
Als Nächstes überprüfen wir die Genauigkeit unserer Prognosen. Während des Rückwärtsdurchgangs passen wir die Modellparameter so an, dass der Fehler bei der Vorhersage der nächsten Bewegung minimiert wird.
if(!Encoder.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Wir informieren den Nutzer über den Fortschritt des Lernprozesses und gehen zur nächsten Iteration des Schleifensystems über.
if(GetTickCount() - ticks > 500) { double percent = double(iter + i - st) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Nachdem alle Iterationen des Schleifensystems erfolgreich abgeschlossen wurden, löschen wir das Kommentarfeld in der Symboltabelle. Wir geben die Trainingsergebnisse in das Terminalprotokoll aus und initialisieren die Abschaltung des Expert Advisors.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
Ähnliche Änderungen wurden an dem Trainings-EA von Akteur und Kritiker vorgenommen. Obwohl diesen Modellen keine wiederkehrenden Blöcke hinzugefügt wurden, waren diese Änderungen notwendig, um das korrekte Funktionieren des Environmental State Encoders zu gewährleisten. Dies liegt daran, dass sowohl der Akteur als auch der Kritiker sie als Eingabedaten verwenden.
Im Anhang finden Sie den vollständigen Code des Modelltrainings EA. Der Anhang enthält auch den vollständigen Code aller in diesem Artikel verwendeten Programme, Klassen und Methoden.
3. Tests
In diesem Artikel untersuchten wir eine Methode zur Vorhersage künftiger Aktienkurse mit Hilfe von TPM und setzten unsere Interpretation der vorgeschlagenen Ansätze um. Nun ist es an der Zeit, die Ergebnisse unserer Arbeit anhand echter Daten zu testen. Wie üblich trainieren wir die vorgestellten Modelle auf historischen EURUSD-H1-Zeitrahmendaten für das Jahr 2023.
Wir beginnen mit dem Training des Environment Encoder-Modells, das historische Kursbewegungsdaten analysiert, ohne die Handlungen des Akteurs zu bewerten. Dieser Ansatz ermöglicht es uns, das Modell vollständig auf dem ursprünglichen Datensatz zu trainieren, ohne dass häufige Aktualisierungen erforderlich sind. Der Ausbildungsprozess verlief relativ schnell und zeigte gute Ergebnisse. In der nachstehenden Grafik werden die prognostizierten und die tatsächlichen Kursbewegungen verglichen.
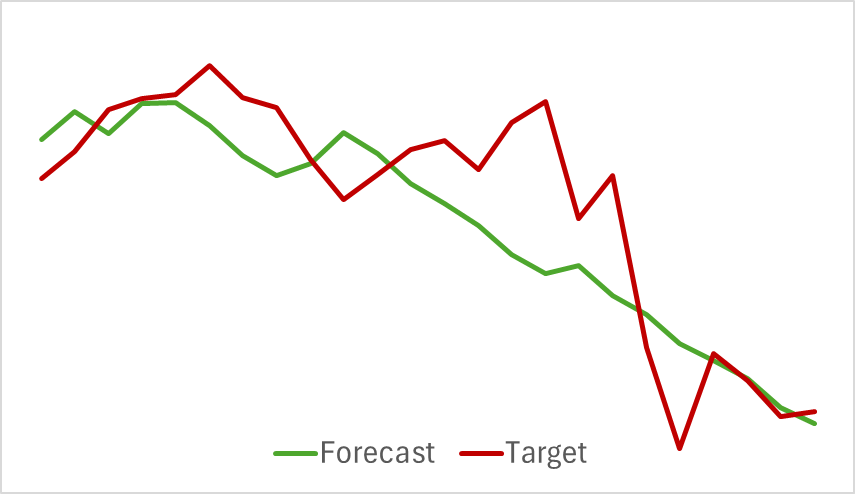
Das Chart zeigt eine enge Überschneidung der beiden Linien, wobei die vorhergesagte Flugbahn glatter erscheint. Dieser Glättungseffekt hat das Potenzial, die Stabilität des Akteurs-Trainings zu verbessern.
Wie Sie wissen, ist es unser oberstes Ziel, die Politik des Akteurs zu optimieren. Nachdem wir den Environment Encoder trainiert haben, gehen wir zur zweiten Stufe des Trainingsprozesses über - dem Training der Akteurspolitik. Dieser Prozess ist ein iterativer Prozess. Da sich die Aktionen des Akteurs verschieben und über die Grenzen der zuvor gesammelten Trainingsdaten hinausgehen können, müssen wir den Erfahrungswiedergabepuffer regelmäßig aktualisieren, indem wir ihn mit Zuständen und Belohnungen auffüllen, die den aktuellen politischen Aktionen des Akteurs näher kommen.
Nach mehreren abwechselnden Iterationen des Trainings der Modelle von Akteur und Kritiker sowie Aktualisierungen des Trainingsdatensatzes haben wir eine Strategie entwickelt, die in der Lage ist, mit den historischen Trainingsdaten Gewinne zu erzielen.
Um die Leistung des Modells außerhalb des Trainingsdatensatzes zu bewerten, testen wir es mit historischen Daten vom Januar 2024, wobei die anderen Bedingungen unverändert bleiben.
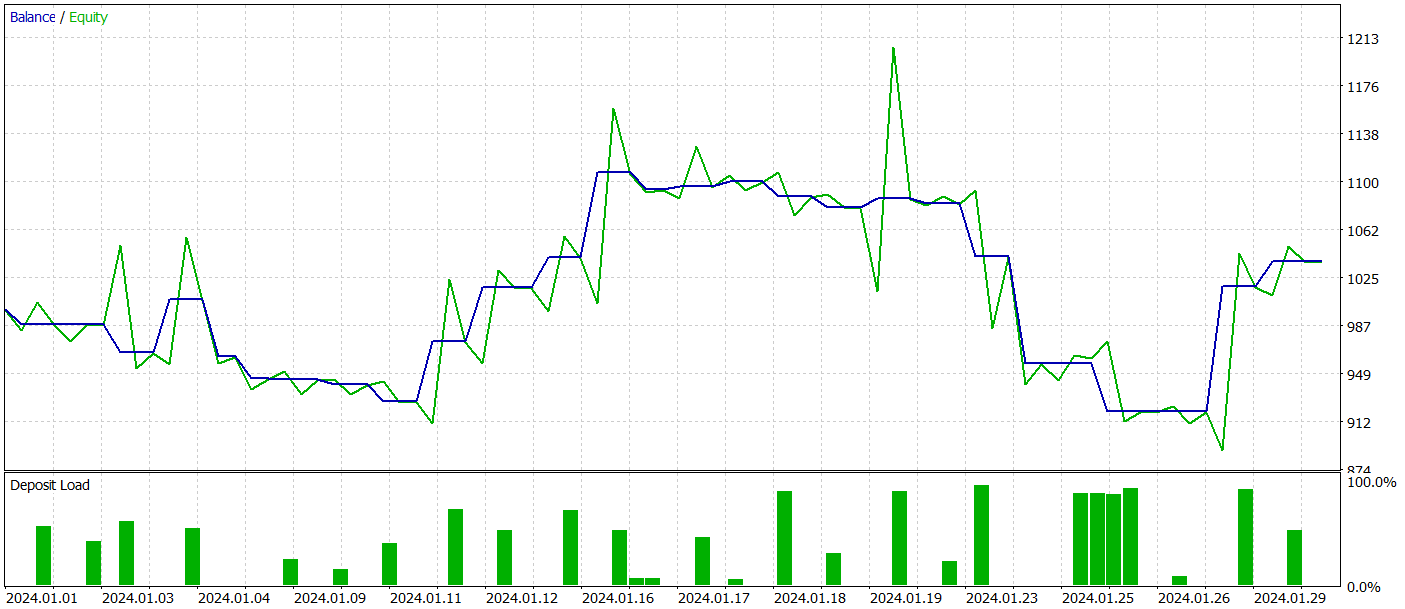
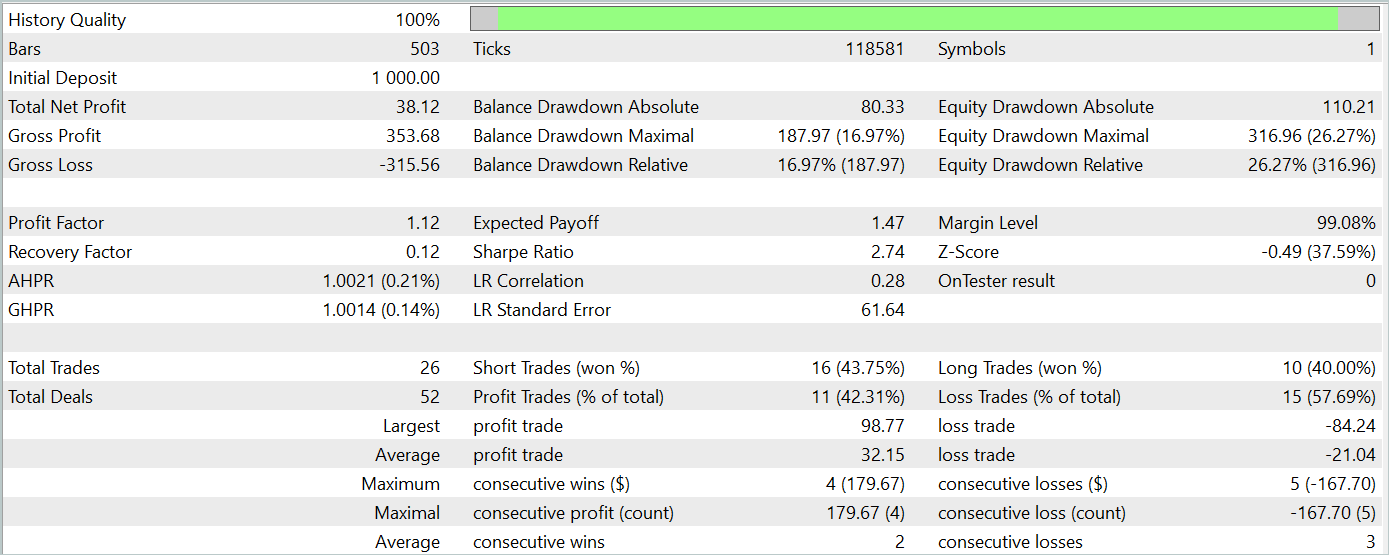
Während des Testzeitraums führte das Modell 26 Handelsgeschäfte aus, von denen nur 11 profitabel waren, d.h. etwas mehr als 42%. Allerdings übertrafen sowohl der maximale als auch der durchschnittliche Gewinn pro Handel die entsprechenden Verlustkennzahlen, sodass sich für den Testzeitraum ein Gesamtgewinn ergab. Der Gewinnfaktor für den Testzeitraum betrug 1,12.
Dennoch zeigt das Saldendiagramm einen deutlichen Rückgang zu Beginn der dritten Dekade des Monats. Dies gibt Anlass zur Sorge. Obwohl das Modell einen Gewinn abwirft, muss es noch weiter verfeinert werden.
Schlussfolgerung
In diesem Artikel haben wir eine faszinierende Methode zur Vorhersage von Kursentwicklungstrends mit Hilfe von TPM erforscht. Diese Methode kombiniert effektiv die Stärken von Faltungsmodellen für die Analyse kurzfristiger Abhängigkeiten und PLR für die Identifizierung langfristiger Trends.
Im praktischen Teil des Artikels haben wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umgesetzt, die Modelle trainiert und Tests durchgeführt. Die Ergebnisse zeigen, dass das trainierte Modell in der Lage war, auch bei Daten außerhalb des Trainingsdatensatzes Gewinne zu erzielen. Das Gleichgewichtsdiagramm wies jedoch nicht den gewünschten stetigen Aufwärtstrend auf und wies Rückschläge auf.
Insgesamt zeigt sich, dass die vorgeschlagene Methode zwar Potenzial hat, das von uns entwickelte Modell aber noch weiter verfeinert werden muss.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Trainings-EA des Modells |
| 4 | StudyEncoder.mq5 | EA | Trainings-EA des Encoders |
| 5 | Test.mq5 | EA | Modeltest-EA |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15255
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Räumlich-zeitliches neuronales Netz (STNN)
Neuronale Netze im Handel: Räumlich-zeitliches neuronales Netz (STNN)
 Neuronale Netze im Handel: Stückweise, lineare Darstellung von Zeitreihen
Neuronale Netze im Handel: Stückweise, lineare Darstellung von Zeitreihen
 Adaptive Social Behavior Optimization (ASBO): Das Verfahren von Schwefel und Box-Muller
Adaptive Social Behavior Optimization (ASBO): Das Verfahren von Schwefel und Box-Muller
 Algorithmus für künstliche elektrische Felder (AEFA)
Algorithmus für künstliche elektrische Felder (AEFA)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.