Algorithmen zur Optimierung mit Populationen: Binärer genetischer Algorithmus (BGA). Teil II
177
0
Inhalt
1. Einführung
2. Der Algorithmus
3. Testergebnisse
1. Einführung
Im vorangegangenen Artikel haben wir alle wichtigen grundlegenden Konzepte und Methoden kennengelernt, die nicht nur in genetischen Algorithmen, sondern auf die eine oder andere Weise in allen Populationsoptimierungsalgorithmen verwendet werden. Auf der Grundlage dieses Wissens können wir nun das Hauptthema des vorliegenden „zweibändigen Buches“ - den binären genetischen Algorithmus (BGA) - im Detail besprechen. Beginnen wir mit allgemeinen Informationen, gehen wir dann zum Code dieser bemerkenswerten Suchstrategie und schließlich zu den Testergebnissen über.
Ein genetischer Algorithmus (GA) bezieht sich auf evolutionäre Algorithmen, die verschiedene Ansätze wie genetische Algorithmen, genetische Programmierung, evolutionäre Strategien und andere umfassen. Sie basieren auf den Ideen der Evolution und der Vererbung, wobei Lösungen als Population dargestellt werden und genetische Operatoren (wie Crossover und Mutation) angewendet werden, um neue Generationen von Lösungen zu erzeugen.
Genetische Algorithmen nutzen die Prinzipien der natürlichen Selektion und der Genetik, um Optimierungsprobleme zu lösen. Der in dem Artikel besprochene binäre genetische Algorithmus (BGA) war der erste unter allen Arten genetischer Algorithmen. BGA gehört somit zur Klasse der evolutionären Algorithmen und ist eine spezifische Variante eines genetischen Algorithmus, der eine binäre Darstellung der Daten verwendet.
Die Arbeit an der Entwicklung genetischer Algorithmen begann in der Mitte des 20. Jahrhunderts. Einer der Begründer ist John Holland, der 1975 sein Buch „Adaptation in Natural and Artificial Systems“ (Anpassung in natürlichen und künstlichen Systemen) veröffentlichte, in dem er den genetischen Algorithmus als eine ganze Richtung zur Lösung von Optimierungsproblemen vorstellte.
Die Entwicklung des genetischen Binäralgorithmus wurde durch mehrere Faktoren und Ideen inspiriert. Die wichtigsten davon:
- Natürliche Selektion und Prinzipien der Evolution: Die BGA basiert auf den von Charles Darwin vorgeschlagenen Prinzipien der natürlichen Selektion und Evolution. Die Idee ist, dass es in einer Population eine Vielfalt von Lösungen gibt, und dass diejenigen, die besser an die Umwelt angepasst sind, eher überleben und ihre Eigenschaften an die nächste Generation weitergeben.
- Genetik und Vererbung: BGA verwendet auch genetische Begriffe wie Gen, Chromosom und Vererbung. Lösungen in BGA werden als binäre Zeichenketten dargestellt, wobei einzelne Bitgruppen bestimmte Gene darstellen und das Gen wiederum den zu optimierenden Parameter repräsentiert. Genetische Operatoren wie Crossover und Mutation werden auf binäre Zeichenketten angewendet, um neue Generationen von Lösungen zu erzeugen.
Insgesamt war die Entwicklung von BGA das Ergebnis einer Kombination von Ideen aus den Bereichen evolutionäre Algorithmen, Genetik und Optimierung. Er wurde entwickelt, um Optimierungsprobleme mit Hilfe der Prinzipien der natürlichen Selektion und der Genetik zu lösen, und seine Entwicklung dauert bis heute an. Es wurde eine große Anzahl von GA-Optionen geschaffen, und die Ideen und Ansätze genetischer Algorithmen werden weithin als Teil hybrider Algorithmen verwendet, darunter auch sehr komplexe Algorithmen.
Der binäre genetische Algorithmus (BGA) verwendet eine binäre Darstellung der Daten. Das bedeutet, dass jedes Individuum (Lösung) als eine Folge von Bits (0 und 1) dargestellt wird. Genetische Operatoren wie Crossover und Mutation werden auf Bit-Strings angewendet, um neue Generationen von Lösungen zu erzeugen.
Interessante Tatsache: Genetische Algorithmen, einschließlich BGA, können zur Schaffung und Verbesserung künstlicher Intelligenz eingesetzt werden. So können sie beispielsweise zur Entwicklung neuronaler Netze verwendet werden, was die Erstellung effizienterer Modelle für maschinelles Lernen ermöglicht.
Genetische Algorithmen im Allgemeinen und BGA im Besonderen sind ein leistungsfähiges Werkzeug für die Lösung komplexer Optimierungsprobleme, bei denen herkömmliche Methoden aufgrund des Fehlens einer analytischen Lösung möglicherweise nicht effektiv genug sind. Der MetaTrader 5 verwendet einen binären GA und daher ist es umso spannender, die Funktionsweise dieses bemerkenswerten Algorithmus zu studieren.
2. Der Algorithmus
Der binäre genetische Algorithmus umfasst die folgenden Schritte:
- Initialisierung der Population - Erstellen einer Anfangspopulation, die aus Chromosomen mit zufälligen binären Werten besteht.
- Bewertung der Fitness - Bewertung der Fitness jedes Individuums (Chromosoms) in der Tochterpopulation.
- Auswahl - Auswahl der Eltern zur Erzeugung von Nachkommen nach der Roulette-Rad-Methode.
- Crossover - die Elternchromosomen werden in Abschnitte unterteilt und es entstehen neue Tochterchromosomen mit Abschnitten beider Elternteile.
- Inversion - Spaltung des Chromosoms eines Tochterindividuums an einer zufällig ausgewählten Stelle und Vertauschung der resultierenden Abschnitte.
- Mutation - zufällige Veränderung von Bits in den Genen der Nachkommen mit einer bestimmten Mutationswahrscheinlichkeit.
- Bewertung der Fitness der Nachkommen - Bewertung der Fitness jedes neuen Nachkommens.
- Bildung einer neuen Population - Setzen Sie die Nachkommenpopulation an das Ende der Gesamtpopulation und sortieren Sie sie nach dem Fitnesswert.
- Abbruchkriterium - Wiederholen des Vorgangs ab Schritt 3, bis das Abbruchkriterium erreicht ist.
Wir werden den Abstand zwischen „max“ und „min“ der optimierten Parameter verwenden, um sicherzustellen, dass die BGA nur mit positiven Zahlen arbeitet, die Operationen mit binären Zeichenfolgen zu vereinfachen und die Geschwindigkeit der Berechnungen zu erhöhen. Die auf diese Weise erhaltenen positiven Abstandswerte werden in Form eines binären Gray-Codes dargestellt und nacheinander in ein gemeinsames Feld von Chromosomensymbolen eingefügt, wie in Abbildung 1 dargestellt. Bei der Crossover-Methode befinden sich die Chromosomenbruchpunkte an zufälligen Stellen auf dem Chromosom und nicht unbedingt an den Genverbindungspunkten. Haltepunkte können auch innerhalb des Genraums liegen.
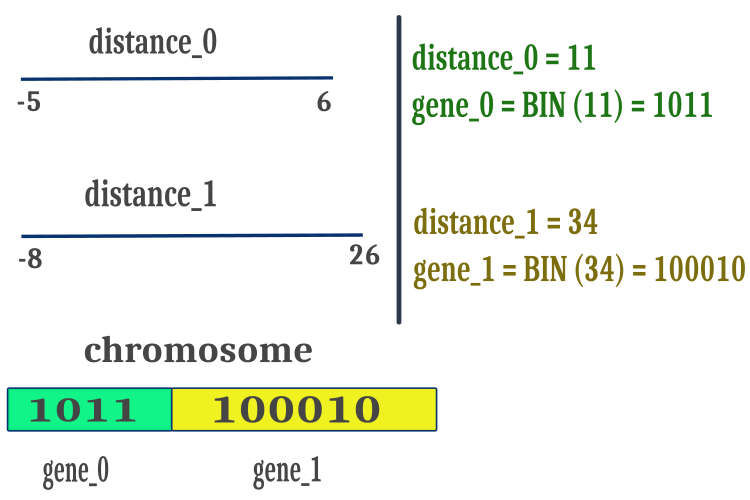
Abbildung 1. Platzierung der Merkmale eines Individuums (optimierte Parameter) im Chromosom
Es gibt eine beträchtliche Anzahl von externen Parametern für einen genetischen Algorithmus, sodass es sinnvoll ist, diese genauer zu betrachten. Die Standardeinstellungen stimmen fast vollständig mit den Empfehlungen vieler Autoren wissenschaftlicher Veröffentlichungen überein. Ich habe sie getestet und so ausgewählt, dass sie bei den meisten Aufgaben maximale Effizienz bieten. Eine Abweichung von diesen Parametern in irgendeine Richtung kann jedoch dazu führen, dass bei Tests mit 10 oder sogar 50 optimierten Parametern bei einzelnen Funktionen zwar eine 100%ige Konvergenz erreicht wird, gleichzeitig aber die Effizienz bei anderen Aufgaben deutlich sinkt. Daher sind die Standardeinstellungen in den meisten praktischen Fällen optimal.
- Population_P (Populationsgröße = 50) - die Anzahl der Nachfolger in jeder Generation der Population. Diese Populationsgröße wird in den meisten der in den Tests behandelten Algorithmen verwendet und bietet ein Gleichgewicht zwischen Lösungsvielfalt und Konvergenzgeschwindigkeit.
- ParentPopulation_P (Größe der Elternpopulation = 50) - die Anzahl der Elternteile, die für die Zucht und die Erzeugung der nächsten Generation ausgewählt wurden. Eine Verringerung des Wertes dieses Parameters verbessert die Konvergenz bei glatten Funktionen (erhöht die Genauigkeit), eine Erhöhung des Wertes verbessert die Konvergenz bei diskreten Funktionen (erhöht die Vielfalt des genetischen Materials).
- CrossoverProbab_P (Crossover-Wahrscheinlichkeit = 1,0) - die Wahrscheinlichkeit der Durchführung einer Crossover-Operation zwischen zwei ausgewählten Elternteilen. Eine hohe Crossover-Wahrscheinlichkeit erhöht die kombinatorischen Fähigkeiten des Algorithmus. Eine Verringerung des Wertes erhöht die Konvergenzgeschwindigkeit, erhöht aber auch die Wahrscheinlichkeit, dass man stecken bleibt.
- CrossoverPoints_P (Anzahl der Crossover-Punkte = 3) - die Anzahl der Punkte, an denen ein Crossover zwischen den beiden Elternchromosomen stattfindet. Eine Erhöhung der Punktezahl führt zu einer stärkeren Vermischung der Parameter untereinander und führt im Grenzfall zu einem zufälligen Verhalten des Algorithmus.
- MutationProbab_P (Mutationswahrscheinlichkeit = 0,001) - die Mutationswahrscheinlichkeit jedes Bits im Chromosomengenotyp. Die Mutation ermöglicht zufällige Veränderungen des genetischen Materials und fügt einer Population neue Lösungen hinzu. Eine geringe Wahrscheinlichkeit erhöht die Konvergenzrate des Algorithmus, verringert aber die Vielfalt, während eine zu hohe Wahrscheinlichkeit zum Verlust nützlicher Informationen führt.
- InversionProbab_P (Inversionswahrscheinlichkeit = 0,7) - die Wahrscheinlichkeit der Durchführung einer Inversionsoperation an einem Chromosom. Eine hohe Inversionswahrscheinlichkeit erhöht die Vielfalt des genetischen Materials, aber eine zu hohe Wahrscheinlichkeit führt zu einem zufälligen Verhalten des Algorithmus.
- DoubleDigitsInChromo_P (Anzahl der Dezimalstellen im Gen) - die Anzahl der Dezimalstellen der reellen Zahl (optimierter Parameter), die in binärer Form im Chromosom dargestellt wird. Eine Erhöhung des Wertes führt zu einer Erhöhung der Komplexität der Berechnungen und zu einer Erhöhung der Optimierungszeit (ohne die binäre Form direkt bei der Lösung des Problems zu verwenden, macht es keinen Sinn, mehr als 16 einzustellen - die Ausgabebits gehen bei der Umwandlung in einen „double“-Wert verloren).
Kommen wir nun zur Überprüfung des Codes.
Bei der Initialisierung von Agenten ist es notwendig, die Anzahl der Bits in der binären Darstellung des zu optimierenden Parameters zu bestimmen. Nehmen wir an, wir müssen fünf Dezimalstellen berücksichtigen, was einer bestimmten Länge des „Gray-Codes“ entspricht. Es können jedoch auch mehr als die erforderliche Anzahl in diesem Code verschlüsselt werden. Daher müssen wir die größte reelle Zahl bestimmen, die im Binärformat kodiert werden kann. In Zukunft können wir die kodierte Zahl auf den gewünschten Bereich des optimierten Ausgangsparameters skalieren. Für den Nachkommateil einer reellen Zahl wird eine bestimmte Anzahl von Stellen (in den Parametern angegeben) verwendet, für den ganzzahligen Teil so viele wie nötig in binärer Form.
Wenn der Eingangsparameter der Funktion digitsInGrayCode beispielsweise 3 ist, gibt die Funktion den maximalen Wert des Typs ulong unter Verwendung des Gray-Codes für 3 Bits zurück, d. h. 7 (111 im Binärformat).
Um die maximal mögliche Zahl zu ermitteln, die mit einer bestimmten Anzahl von Bits für den ganzzahligen und den Nachkommateil einer reellen Zahl kodiert werden kann, verwenden wir die Funktion GetMaxDecimalFromGray.
//—————————————————————————————————————————————————————————————————————————————— //Calculation of the maximum possible ulong number using the Gray code for a given number of bits ulong GetMaxDecimalFromGray (int digitsInGrayCode) { ulong maxValue = 1; for (int i = 1; i < digitsInGrayCode; i++) { maxValue <<= 1; maxValue |= 1; } return maxValue; } //——————————————————————————————————————————————————————————————————————————————
Zur Darstellung jedes Gens im Chromosom (die Position des Gens auf dem Chromosom) wird die Struktur S_BinaryGene verwendet, die Felder und Methoden für die Arbeit mit Genen im Binärformat enthält:
- „gene“ - Char.-Array, das ein Gen darstellt.
- „integPart“ - Char.-Array für den ganzzahligen Genanteil.
- „fractPart“ - Char.-Array für den Nachkommateil des Gens.
- „integGrayDigits“ - Anzahl der „Gray“-Stellen für den ganzzahligen Teil des Gens.
- „fractGrayDigits“ - Anzahl der „Gray“-Stellen für den Nachkommateil des Gens.
- „length“ - Gesamtlänge des Gens.
- „minDoubleRange“ - Mindestwert des reellen Zahlenbereichs.
- „maxDoubleRange“ - Höchstwert des reellen Zahlenbereichs.
- „maxDoubleNumber“ - größte reelle Zahl, die durch das Gen dargestellt werden kann.
- „doubleFract“ - Wert zur Umwandlung des Nachkommateils des Gens in eine reelle Zahl.
Methoden-Struktur:
- „Init“ - initialisiert die Felder der Struktur. Akzeptiert die Minimal- und Maximalwerte eines Bereichs von reellen Zahlen sowie die Anzahl der Stellen im Nachkommateil des Gens. Im Rahmen der Methode werden die Werte für die größten reellen Zahl der kodierenden Teile des Gens mit Hilfe des Gray-Codes berechnet.
- „ToDouble“ - wandelt das Gen in eine reelle Zahl um. Akzeptiert das Array „chromo“ (Chromosom) aus Gray-Code-Zeichen und den Genstartindex „indChr“. Die Methode liest einen Bereich eines Chromosoms, wandelt das gelesene Gen in einen Dezimalwert um und skaliert ihn dann auf einen bestimmten Bereich von reellen Zahlen.
- „Scale“ - skaliert den „In“-Eingangswert vom „InMIN“- und „InMAX“-Bereich auf den „OutMIN“- und „OutMAX“-Ausgangsbereich. Dies ist eine Hilfsmethode, die in „ToDouble“ verwendet wird.
//—————————————————————————————————————————————————————————————————————————————— struct S_BinaryGene { char gene []; char integPart []; char fractPart []; uint integGrayDigits; uint fractGrayDigits; uint length; double minDoubleRange; double maxDoubleRange; double maxDoubleNumber; double doubleFract; //---------------------------------------------------------------------------- void Init (double min, double max, int doubleDigitsInChromo) { doubleFract = pow (0.1, doubleDigitsInChromo); minDoubleRange = min; maxDoubleRange = max - min; ulong decInfr = 0; for (int i = 0; i < doubleDigitsInChromo; i++) { decInfr += 9 * (ulong)pow (10, i); } //---------------------------------------- DecimalToGray (decInfr, fractPart); ulong maxDecInFr = GetMaxDecimalFromGray (ArraySize (fractPart)); double maxDoubFr = maxDecInFr * doubleFract; //---------------------------------------- DecimalToGray ((ulong)maxDoubleRange, integPart); ulong maxDecInInteg = GetMaxDecimalFromGray (ArraySize (integPart)); double maxDoubInteg = (double)maxDecInInteg + maxDoubFr; maxDoubleNumber = maxDoubInteg; ArrayResize (gene, 0, 1000); integGrayDigits = ArraySize (integPart); fractGrayDigits = ArraySize (fractPart); length = integGrayDigits + fractGrayDigits; ArrayCopy (gene, integPart, 0, 0, WHOLE_ARRAY); ArrayCopy (gene, fractPart, ArraySize (gene), 0, WHOLE_ARRAY); } //---------------------------------------------------------------------------- double ToDouble (const char &chromo [], const int indChr) { double d; if(integGrayDigits > 0)d = (double)GrayToDecimal(chromo, indChr, indChr + integGrayDigits - 1); else d = 0.0; d +=(double)GrayToDecimal(chromo, indChr + integGrayDigits, indChr + integGrayDigits + fractGrayDigits - 1) * doubleFract; return minDoubleRange + Scale(d, 0.0, maxDoubleNumber, 0.0, maxDoubleRange); } //---------------------------------------------------------------------------- double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return OutMIN; if (In > InMAX) return OutMAX; return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } }; //——————————————————————————————————————————————————————————————————————————————
Zur Beschreibung des Agenten benötigen wir die Struktur S_Agent, die den Agenten repräsentiert und neben dem Chromosom die folgenden Daten enthält:
- „c“ - Array der Koordinatenwerte des Agenten als reelle Zahl.
- „f“ - Fitnesswert des Agenten.
- „genes“ - Array von „S_BinaryGene“-Strukturen, die die Position jedes Gens im Chromosom und die Regeln für die Umwandlung des Binärcodes in eine reelle Zahl beschreiben.
- „Chromosom“ - Array von Agentenchromosomen-Zeichen.
- „calculated“ - ein boolescher Wert, der angibt, ob die Werte des Agenten berechnet wurden (das Feld ist vorhanden, wird aber im Code nicht verwendet).
Methoden-Struktur:
- „Init“ - initialisiert die Felder der Struktur. Akzeptiert die Anzahl der „coords“-Koordinaten, „min“- und „max“-Arrays mit den Minimal- und Maximalwerten für jeden optimierten Parameter sowie doubleDigitsInChromo - die Anzahl der Stellen einer reellen Zahl im Nachkommateil des Gens. Die Methode erstellt und initialisiert Gene für jede Koordinate und setzt auch den anfänglichen Fitnesswert und das Flag „berechnet“.
- „ExtractGenes“ - extrahiert Genwerte aus einem Chromosom und speichert sie im Array „c“, verwendet die Methode „ToDouble“ aus der Struktur „S_BinaryGene“, um Gene aus einem Chromosom in reelle Zahlen umzuwandeln.
//—————————————————————————————————————————————————————————————————————————————— struct S_Agent { void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo) { ArrayResize(c, coords); f = -DBL_MAX; ArrayResize(genes, coords); ArrayResize(chromosome, 0, 1000); for(int i = 0; i < coords; i++) { genes [i].Init(min [i], max [i], doubleDigitsInChromo); ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY); } calculated = false; } void ExtractGenes () { uint pos = 0; for (int i = 0; i < ArraySize (genes); i++) { c [i] = genes [i].ToDouble (chromosome, pos); pos += genes [i].length; } } double c []; //coordinates double f; //fitness S_BinaryGene genes []; char chromosome []; bool calculated; }; //——————————————————————————————————————————————————————————————————————————————
Der folgende Code zeigt die Definition der Struktur S_Roulette, die das Roulette-Segment darstellt.
Felder strukturieren:
- „start“ - Startwert des Roulettesegments.
- „end“ - Endpunkt des Roulette-Segments.
//—————————————————————————————————————————————————————————————————————————————— struct S_Roulette { double start; double end; }; //——————————————————————————————————————————————————————————————————————————————
Deklaration der Klasse C_AO_BGA, die den genetischen Algorithmus implementiert:
- „cB“ - Array der besten Koordinatenwerte.
- „fB“ - Fitnesswert der besten Koordinaten.
- „a“ - Array von S_Agent-Strukturen, die Agenten darstellen.
- „rangeMax“ - Array der maximalen Suchbereichswerte.
- „rangeMin“ - Array der minimalen Suchbereichswerte.
- „rangeStep“ - Array von Werten, die den Suchschritt darstellen.
Methoden der Klasse:
- „Init“ - initialisiert das Klassenfeld und akzeptiert folgende Parameter: „coordsP“ Anzahl der Koordinaten, „popSizeP“ Populationsgröße, „parentPopSizeP“ Größe der Elternpopulation, „crossoverProbabP“ Kreuzungswahrscheinlichkeit, „crossoverPointsP“ Anzahl der Kreuzungspunkte, „mutationProbabP“ Mutationswahrscheinlichkeit, „inversionProbabP“ Inversionswahrscheinlichkeit, „doubleDigitsInChromoP“ Anzahl der Dezimalstellen im Gen. Die Methode initialisiert interne Variablen und Arrays, die für den Betrieb des genetischen Algorithmus erforderlich sind.
- „Moving“ - Hauptmethode des genetischen Algorithmus, führt Operationen an der Population durch, wie Crossover, Mutation, Inversion und Fitnessbewertung.
- „Revision“ - die Methode führt eine Populationsrevision durch, sortiert die Agenten und wählt die besten aus.
Die privaten Felder und Methoden der Klasse werden verwendet, um den genetischen Algorithmus intern zu implementieren, einschließlich Roulette-Operationen, Werteskalierung, Sortierung und anderer Operationen.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BGA { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Agent a []; //agent public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordsP, //coordinates number const int popSizeP, //population size const int parentPopSizeP, //parent population size const double crossoverProbabP, //crossover probability const int crossoverPointsP, //crossover points const double mutationProbabP, //mutation probability const double inversionProbabP, //inversion probability const int doubleDigitsInChromoP);//number of decimal places in the gene public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coords; //coordinates number private: int popSize; //population size private: int parentPopSize; //parent population size private: double crossoverProbab; //crossover probability private: int crossoverPoints; //crossover points private: double mutationProbab; //mutation probability private: double inversionProbab; //inversion probability private: int doubleDigitsInChromo; //number of decimal places in the gene private: bool revision; private: S_Agent parents []; //parents private: int ind []; //temporary array for sorting the population private: double val []; //temporary array for sorting the population private: S_Agent pTemp []; //temporary array for sorting the population private: char tempChrome []; //temporary chromosome for inversion surgery private: uint lengthChrome; //length of the chromosome (the length of the string of characters according to the Gray code) private: int pCount; //indices of chromosome break points private: uint poRND []; //temporal indices of chromosome break points private: uint points []; //final indices of chromosome break points private: S_Roulette roulette []; //roulette private: void PreCalcRoulette (); private: int SpinRoulette (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: void Sorting (S_Agent &p [], int size); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX); }; //——————————————————————————————————————————————————————————————————————————————
Der folgende Code stellt die Implementierung der Methode Init der Klasse C_AO_BGA dar. Diese Methode initialisiert die Klassenfelder und Arrays, die für das Funktionieren des genetischen Algorithmus erforderlich sind.
Eingaben zur Methode:
- „coordsP“ - Anzahl der Koordinaten.
- „popSizeP“ - Größe der Population.
- „parentPopSizeP“ - Größe der Elternpopulation.
- „crossoverProbabP“ - Crossover-Wahrscheinlichkeit.
- „crossoverPointsP“ - Anzahl der Crossover-Punkte.
- „mutationProbabP“ - Mutationswahrscheinlichkeit.
- „inversionProbabP“ - Inversionswahrscheinlichkeit.
- „doubleDigitsInChromoP“ - Anzahl der Dezimalstellen im Gen.
Die Init-Methode wird verwendet, um Klassenfelder und Arrays zu initialisieren, bevor der genetische Algorithmus ausgeführt wird. Es setzt die Werte von Klassenfeldern, prüft und passt die Werte einiger Parameter an und ändert auch die Größe von Arrays, indem es Speicher für sie zuweist.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BGA::Init (const int coordsP, //coordinates number const int popSizeP, //population size const int parentPopSizeP, //parent population size const double crossoverProbabP, //crossover probability const int crossoverPointsP, //crossover points const double mutationProbabP, //mutation probability const double inversionProbabP, //inversion probability const int doubleDigitsInChromoP) //number of decimal places in the gene { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coords = coordsP; popSize = popSizeP; parentPopSize = parentPopSizeP; crossoverProbab = crossoverProbabP; crossoverPoints = crossoverPointsP; pCount = crossoverPointsP; mutationProbab = mutationProbabP; inversionProbab = inversionProbabP; doubleDigitsInChromo = doubleDigitsInChromoP; if (crossoverPoints < 1) crossoverPoints = 1; if (pCount < 1) pCount = 1; ArrayResize (poRND, pCount); ArrayResize (points, pCount + 2); ArrayResize (ind, parentPopSize + popSize); ArrayResize (val, parentPopSize + popSize); ArrayResize (pTemp, parentPopSize + popSize); ArrayResize (a, popSize); ArrayResize (parents, parentPopSize + popSize); ArrayResize (roulette, parentPopSize); ArrayResize (rangeMax, coords); ArrayResize (rangeMin, coords); ArrayResize (rangeStep, coords); ArrayResize (cB, coords); } //——————————————————————————————————————————————————————————————————————————————
Alle grundlegenden Operationen für die Arbeit mit dem genetischen Material von Agenten werden mit der Methode Moving der Klasse C_AO_BGA durchgeführt. Die gleitende Methode führt einen Schritt des genetischen Algorithmus durch, der die Auswahl der Eltern, das Kreuzen, Invertieren und Mutieren von Chromosomen sowie die Anwendung von Operationen auf Gene und Koordinaten von Individuen umfasst.
Die Methode ist logischerweise in mehrere Teile gegliedert:
1. „if (!revision)“ - wenn „revision“ gleich „false“ ist, werden die Individuen der Population initialisiert:
- Die Methode Init wird aufgerufen, um das Individuum mit den angegebenen Parametern zu initialisieren.
- Ein Zufallschromosom wird erzeugt, indem jedes Gen mit einem Zufallswert von 0 oder 1 gefüllt wird.
- Die Methode ExtractGenes wird zur Extraktion von Genen aus dem Chromosom aufgerufen.
- Die Koordinaten des Individuums „c“ werden mit Hilfe der Funktion SeInDiSp auf einen Bereich reduziert.
- Der Fitnesswert eines jeden Individuums „f“ wird auf „-DBL_MAX“ gesetzt.
- „lengthChrome = ArraySize (a [0].chromosome)“ - Länge des Chromosoms eines Individuums (alle Individuen haben die gleiche Länge).
- „ArrayResize (tempChrome, lengthChrome)“ - ersetzt die Größe des temporären Arrays „tempChrome“ durch „lengthChrome“.
2. Für jedes Individuum der Population:
- Mit der Methode PreCalcRoulette wird eine vorläufige Berechnung des übergeordneten Auswahlrouletts durchgeführt.
- Das Elternteil wird nach der SpinRoulette-Methode ausgewählt.
- Das Chromosom des ausgewählten Elternteils wird in das Chromosom des aktuellen Individuums kopiert.
- Die Crossover-Operation wird mit der CrossoverProbab-Wahrscheinlichkeit durchgeführt.
- Das zweite Elternteil wird ausgewählt.
- Die Chromosomenbruchpunkte werden bestimmt.
- Die Chromosomen der beiden Elternteile werden gekreuzt.
- Die Inversionsoperation wird mit der Wahrscheinlichkeit inversionProbab durchgeführt.
- Es wird ein zufälliger Chromosomen-Bruchpunkt bestimmt.
- Teile des Chromosoms wechseln ihren Platz.
- Für jedes Chromosomengen wird eine Mutationsoperation mit der MutationsProbab-Wahrscheinlichkeit durchgeführt.
- Die Methode ExtractGenes wird zur Extraktion von Genen aus dem Chromosom aufgerufen.
- Die Koordinaten des Individuums „c“ werden mit Hilfe der Funktion SeInDiSp auf einen Bereich reduziert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BGA::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { a [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo); int r = 0; for (int len = 0; len < ArraySize (a [i].chromosome); len++) { r = MathRand (); //[0,32767] if (r > 16384) a [i].chromosome [len] = 1; else a [i].chromosome [len] = 0; } a [i].ExtractGenes (); for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].f = -DBL_MAX; a [i].calculated = true; } lengthChrome = ArraySize (a [0].chromosome); ArrayResize (tempChrome, lengthChrome); for (int i = 0; i < parentPopSize + popSize; i++) { parents [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo); parents [i].f = -DBL_MAX; } revision = true; return; } //---------------------------------------------------------------------------- int pos = 0; double r = 0; uint p1 = 0; uint p2 = 0; uint p3 = 0; uint temp = 0; for (int i = 0; i < popSize; i++) { PreCalcRoulette (); //selection, select and copy the parent to the child------------------------ pos = SpinRoulette (); ArrayCopy (a [i].chromosome, parents [pos].chromosome, 0, 0, WHOLE_ARRAY); //crossover----------------------------------------------------------------- r = RNDfromCI (0.0, 1.0); if (r < crossoverProbab) { //choose a second parent to breed with------------------------------------ pos = SpinRoulette (); //determination of chromosome break points-------------------------------- for (int p = 0; p < pCount; p++) { poRND [p] = (int)RNDfromCI (0.0, lengthChrome); if (poRND [p] >= lengthChrome) poRND [p] = lengthChrome - 1; } ArraySort (poRND); ArrayCopy (points, poRND, 1, 0, WHOLE_ARRAY); points [0] = 0; points [pCount + 1] = lengthChrome - 1; r = RNDfromCI (0.0, 1.0); int startPoint = r > 0.5 ? 0 : 1; for (int p = startPoint; p < pCount + 2; p += 2) { if (p < pCount + 1) { for (uint len = points [p]; len < points [p + 1]; len++) a [i].chromosome [len] = parents [pos].chromosome [len]; } } } //perform an inversion------------------------------------------------------ //(break the chromosome, swap the received parts, connect them together) r = RNDfromCI (0.0, 1.0); if (r < inversionProbab) { p1 = (int)RNDfromCI (0.0, lengthChrome); if (p1 >= lengthChrome) p1 = lengthChrome - 1; //copying the second part to the beginning of the temporary array for (uint len = p1; len < lengthChrome; len++) tempChrome [len - p1] = a [i].chromosome [len]; //copying the first part to the end of the temporary array for (uint len = 0; len < p1; len++) tempChrome [lengthChrome - p1 + len] = a [i].chromosome [len]; //copying a temporary array back for (uint len = 0; len < lengthChrome; len++) a [i].chromosome [len] = tempChrome [len]; } //perform mutation--------------------------------------------------------- for (uint len = 0; len < lengthChrome; len++) { r = RNDfromCI (0.0, 1.0); if (r < mutationProbab) a [i].chromosome [len] = a [i].chromosome [len] == 1 ? 0 : 1; } a [i].ExtractGenes (); for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].calculated = true; } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode führt eine Populationsrevision durch, sortiert die Individuen nach dem Wert ihrer Fitnessfunktion und aktualisiert die „fB“ Fitness der besten Lösung und die „cB“ Koordinaten der besten Lösung. Vor der Sortierung der Grundgesamtheit wird die Kindergrundgesamtheit an das Ende der Gesamtgrundgesamtheit kopiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BGA::Revision () { //---------------------------------------------------------------------------- for (int i = parentPopSize; i < parentPopSize + popSize; i++) { parents [i] = a [i - parentPopSize]; } Sorting (parents, parentPopSize + popSize); if (parents [0].f > fB) { fB = parents [0].f; ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY); } } //——————————————————————————————————————————————————————————————————————————————
Der vorläufige Roulette-Layoutcode stellt die Methode PreCalcRoulette dar. Bei dieser Methode werden im Vorfeld Werte für eine Roulette-Auswahl von Individuen auf der Grundlage ihrer Fitnessfunktion berechnet.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BGA::PreCalcRoulette () { roulette [0].start = parents [0].f; roulette [0].end = roulette [0].start + (parents [0].f - parents [parentPopSize - 1].f); for (int s = 1; s < parentPopSize; s++) { if (s != parentPopSize - 1) { roulette [s].start = roulette [s - 1].end; roulette [s].end = roulette [s].start + (parents [s].f - parents [parentPopSize - 1].f); } else { roulette [s].start = roulette [s - 1].end; roulette [s].end = roulette [s].start + (parents [s - 1].f - parents [s].f) * 0.1; } } } //——————————————————————————————————————————————————————————————————————————————
Die SpinRoulette-Methode stellt sicher, dass die Position des übergeordneten Individuums ausgewählt wird.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_BGA::SpinRoulette () { double r = RNDfromCI (roulette [0].start, roulette [parentPopSize - 1].end); for (int s = 0; s < parentPopSize; s++) { if (roulette [s].start <= r && r < roulette [s].end) return s; } return 0; } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Testergebnisse des BGA:
C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs: 10000; result: 0.9999191151339382
25 Hilly's; Func runs: 10000; result: 0.994841435673127
500 Hilly's; Func runs: 10000; result: 0.5048331764136147
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.9997457419655973
500 Forest's; Func runs: 10000; result: 0.32054251149158375
=============================
5 Megacity's; Func runs: 10000; result: 0.9066666666666668
25 Megacity's; Func runs: 10000; result: 0.9640000000000001
500 Megacity's; Func runs: 10000; result: 0.23034999999999997
=============================
All score: 6.92090 (76.90%)
Die Visualisierung der BGA-Optimierung zeigt deutlich die hohe Konvergenz des Algorithmus. Interessanterweise bleibt ein Teil der Population während des Optimierungsprozesses vom globalen Extremwert entfernt, was auf die Erkundung neuer unbekannter Regionen des Suchraums hinweist, wodurch die Vielfalt der Lösungen in der Population erhalten bleibt. Allerdings stößt der Algorithmus auf gewisse Schwierigkeiten, wenn er mit der diskreten Funktion Megacity arbeitet, was für die meisten Algorithmen problematisch ist. Trotz einiger Schwankungen in den Ergebnissen bei der Arbeit mit dieser komplexen Funktion schneidet BGA deutlich besser ab als andere Algorithmen.
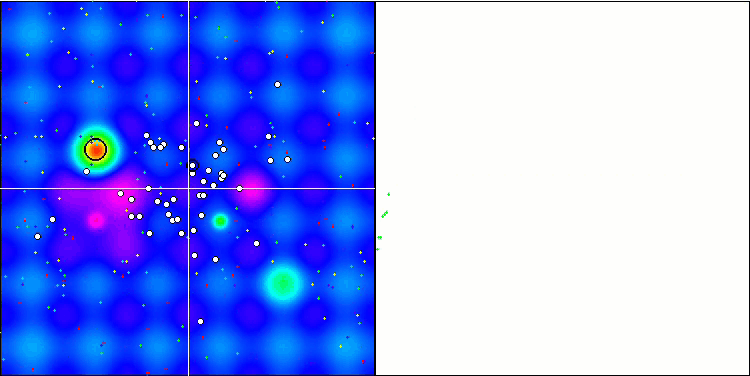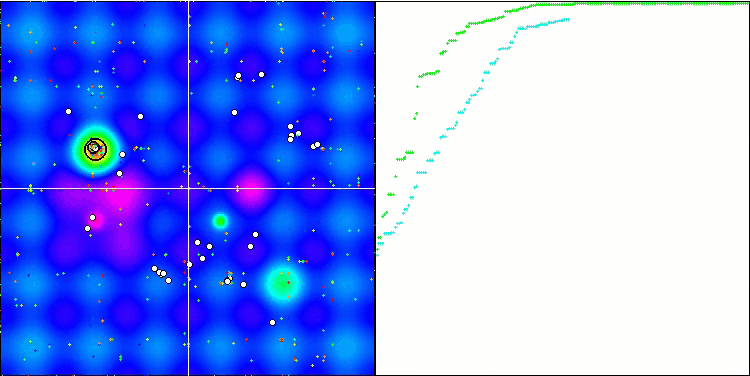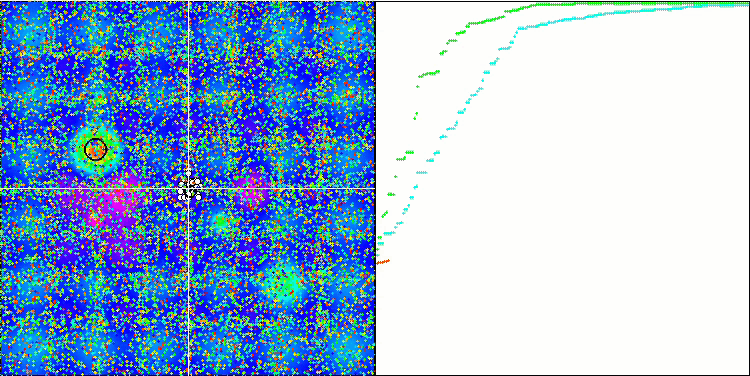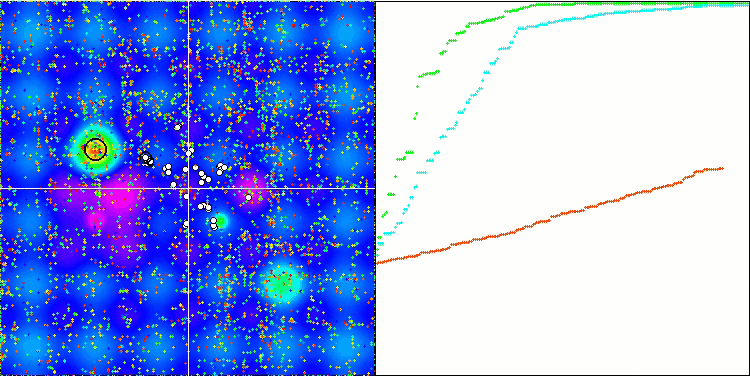
BGA mit der Testfunktion Hilly
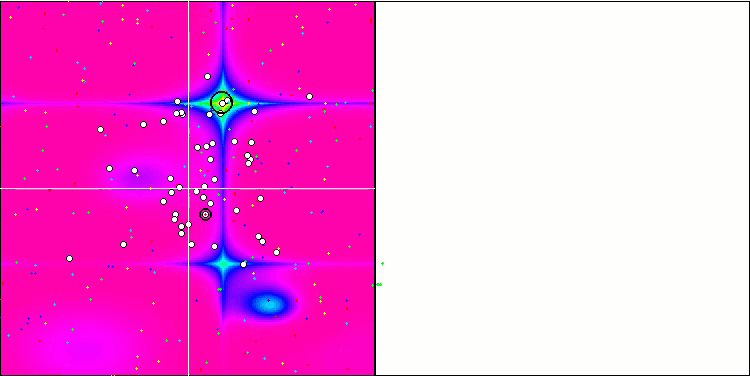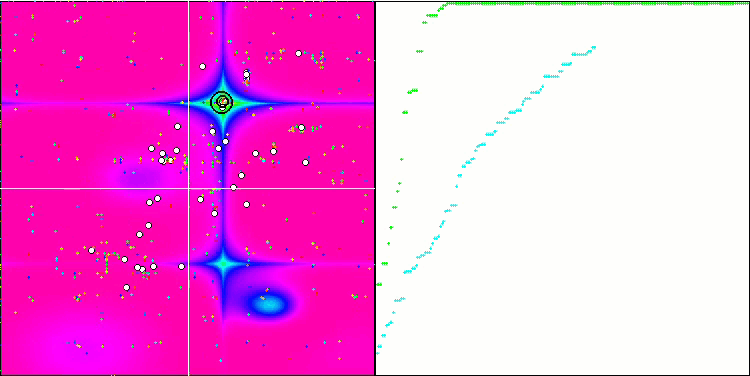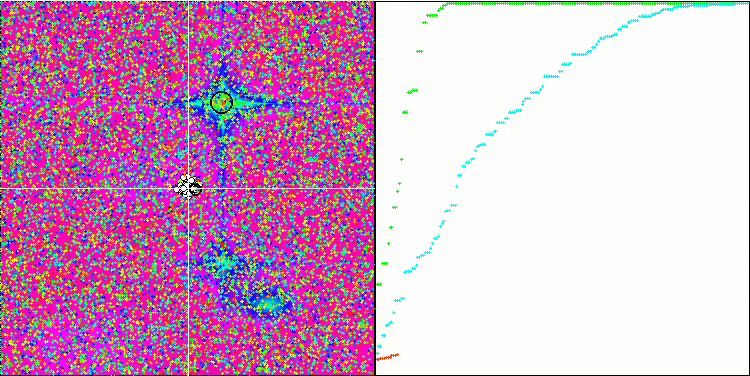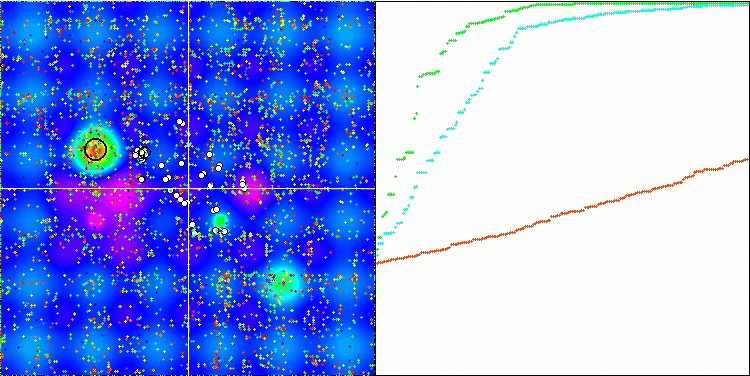
BGA mit der Testfunktion Forest
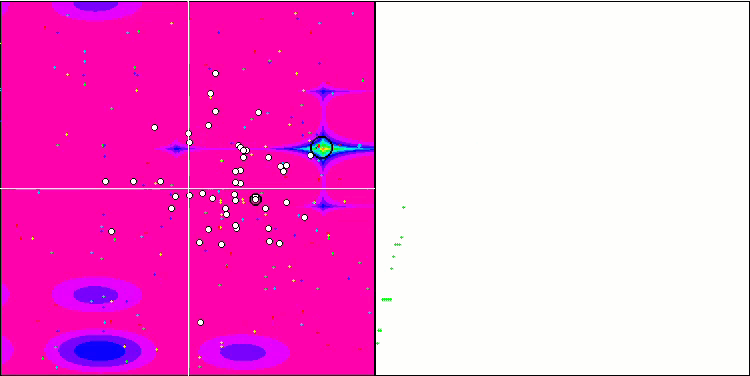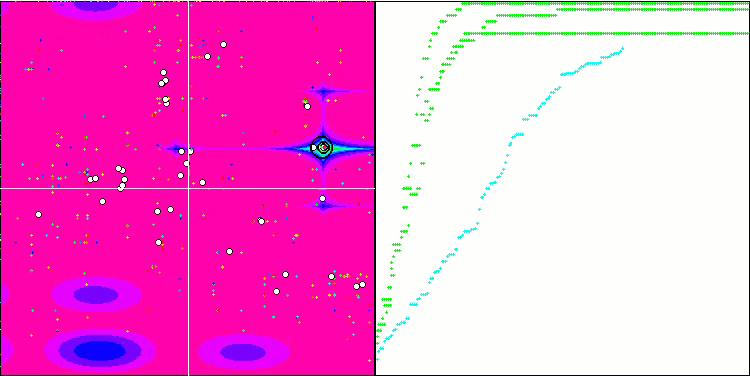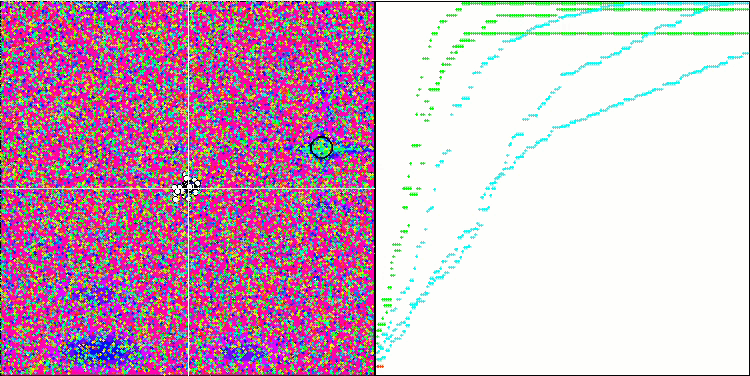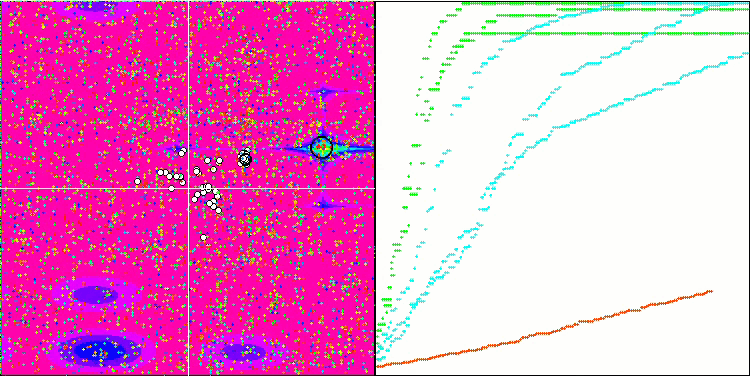
BGA mit der Testfunktion Megacity
BGA belegte den ersten Platz in der Tabelle und schnitt bei den meisten Tests für alle drei Testfunktionen am besten ab. BGA zeigte besonders beeindruckende Ergebnisse bei der diskreten Funktion Megacity und übertraf andere Algorithmen.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Zusammenfassung
In diesem Artikel haben wir die klassische Version von BGA untersucht, einen Spezialfall der allgemeinen Klasse der genetischen Algorithmen GA, und alle Schlussfolgerungen beziehen sich speziell auf diese Version. Trotz der seit langem bestehenden Idee, Lösungen in binärer Form darzustellen, ist der Ansatz des Binärcodes bis heute aktuell. Er kombiniert die unabhängigen räumlichen Dimensionen eines Optimierungsproblems zu einem einzigen Ganzen, indem er die Informationen in einem einzigen Chromosom kodiert, was bei der herkömmlichen Kodierung von reellwertigen Merkmalen nur schwer zu realisieren ist, wodurch sich dieser Algorithmus von anderen Optimierungsalgorithmen abhebt.
Obwohl mir die Mathematik und die Logik der BGA-Strategie völlig klar sind, bin ich immer noch fasziniert von dem, was mit dem Chromosom geschieht. Man kann es mit einem magischen Kaleidoskop vergleichen. Beim Drehen des Kaleidoskops verbinden sich die verschiedenen Formen und Farben zu einzigartigen Mustern und ergeben ein spektakuläres Bild. In ähnlicher Weise schneidet der Crossover-Operator in BGA das Chromosom nach dem Zufallsprinzip in mehrere Teile, einschließlich der internen Parameterbereiche. Diese Teile werden dann zusammengesetzt, so wie man die Teile eines Kaleidoskops mischt. So können wir die besten Eigenschaften verschiedener Lösungen kombinieren und eine neue, optimalere Kombination schaffen. Wie ein Kaleidoskop können die Ergebnisse der BGA-Kreuzung überraschend und unerwartet sein und einfache Chromosomen in echte „Diamanten“ optimaler Lösungen verwandeln.
Ich bin zuversichtlich, dass die Informationen in diesem zweiteiligen Artikel über die Methoden und Werkzeuge der genetischen Algorithmen Ihnen helfen werden, Ihr Wissen zu erweitern und neue Höhen in Ihrer Arbeit und Forschung zu erreichen. Die Kraft der Evolution manifestiert sich ständig in der Natur, der Technologie und dem menschlichen Geist, und BGA ist einer von vielen erstaunlichen Algorithmen, die uns helfen werden, neue Höhen und Errungenschaften zu erreichen.
BGA löst effektiv eine Vielzahl von Problemen, seien es glatte Oberflächen, diskrete Probleme oder sogar großräumige Probleme, einschließlich eines stochastischen Ansatzes, der neue Möglichkeiten eröffnet, wo analytische Lösungen begrenzt sind.
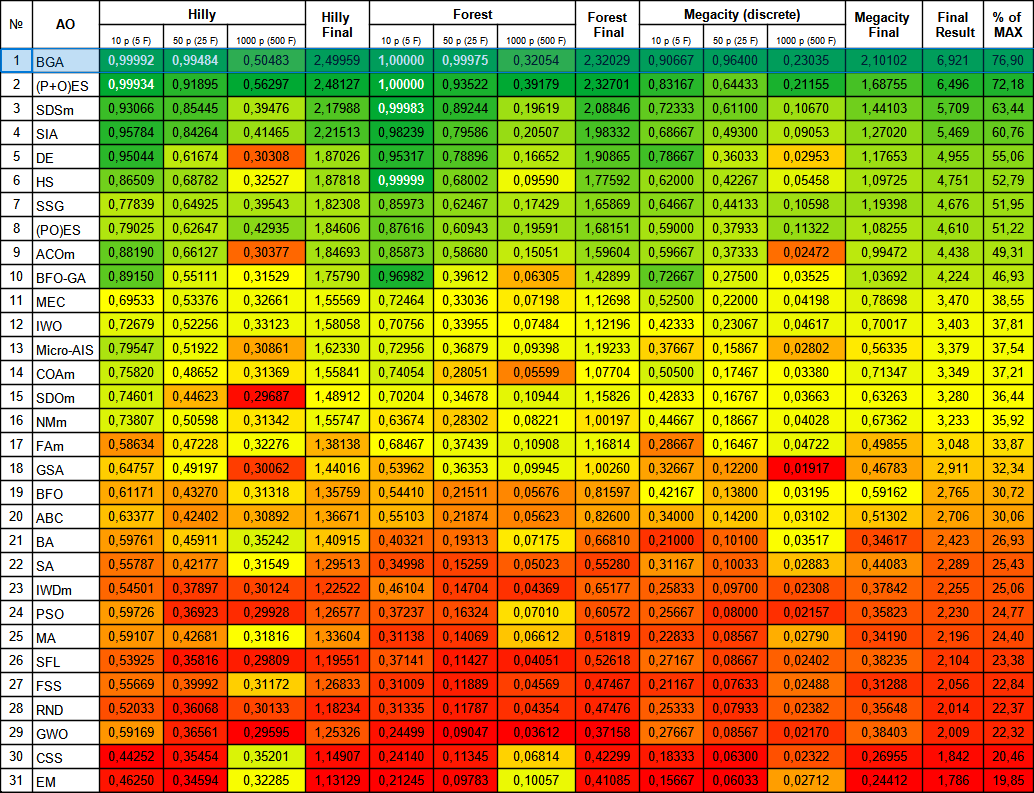
Bild 2. Farbliche Abstufung der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben
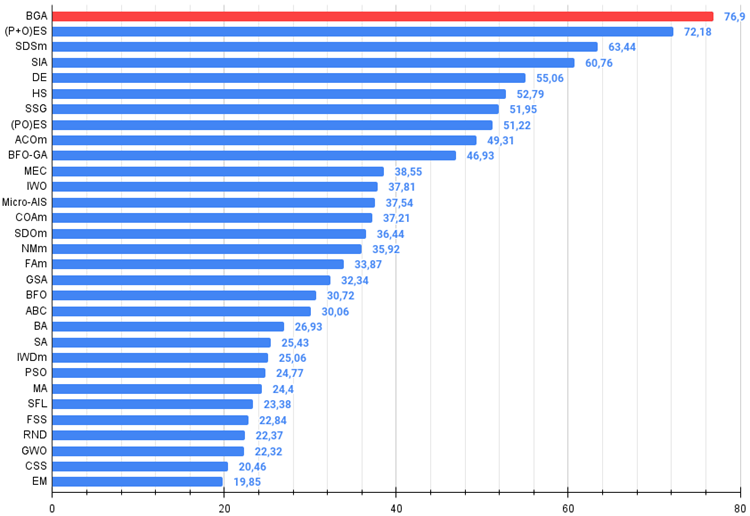
Abb. 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
Die Vor- und Nachteile des binären genetischen Algorithmus (BGA) gelten ausschließlich für die vorgestellte Implementierung:
Vorteile:
- Hohe Effizienz bei der Lösung einer Vielzahl von Problemen.
- Widerstandsfähigkeit gegen das Hängenbleiben.
- Vielversprechende Ergebnisse sowohl für glatte als auch für komplexe diskrete Funktionen.
- Hohe Konvergenz.
Nachteile
- Eine große Anzahl von externen Parametern.
- Eine recht komplexe Umsetzung.
- Hohe rechnerische Komplexität.
Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14040
DRAW_ARROW Zeichnungstyp in Multi-Symbol-Multi-Perioden-Indikatoren
Algorithmen zur Optimierung mit Populationen: Binärer genetischer Algorithmus (BGA). Teil I
Trailing-Stopp im Handel
Neuronale Netze leicht gemacht (Teil 71): Zielkonditionierte prädiktive Kodierung (Goal-Conditioned Predictive Coding, GCPC)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.