Neuronale Netze im Handel: Stückweise, lineare Darstellung von Zeitreihen

Einführung

Wenn wir über die Darstellung einer Zeitreihe sprechen, haben wir es meistens mit Daten zu tun, die eine Folge von Punkten sind, die in chronologischer Reihenfolge aufgezeichnet wurden. Mit der zunehmenden Menge an Ausgangsinformationen steigt jedoch auch die Komplexität ihrer Analyse, was die Effizienz der Nutzung der verfügbaren Informationen verringert. Dies ist besonders wichtig, wenn man auf den Finanzmärkten arbeitet, wo der zusätzliche Zeitaufwand für die Analyse von Informationen und die Entscheidungsfindung das Risiko von Gewinneinbußen und manchmal sogar von Verlusten erhöhen kann. Hier spielen die Vorteile der Reduzierung der Dimensionalität von Daten eine besondere Rolle, um die Effizienz und Effektivität ihrer intellektuellen Analyse zu erhöhen. Ein Ansatz zur Verringerung der Dimensionalität von Daten ist die stückweise, lineare Darstellung von Zeitreihen.

Die stückweise, lineare Darstellung von Zeitreihen ist eine Methode zur Annäherung einer Zeitreihe durch lineare Funktionen über kleine Intervalle. In diesem Artikel wird der Algorithmus der bidirektionalen, stückweisen, linearen Darstellung von Zeitreihen (BPLR) erörtert, der in dem Artikel „Bidirectional piecewise linear representation of time series with application to collective anomaly detection“ vorgestellt wurde. Diese Methode wurde vorgeschlagen, um Probleme im Zusammenhang mit der Suche nach Anomalien in Zeitreihen zu lösen.

Die Erkennung von Zeitreihenanomalien ist ein wichtiger Teilbereich des Time Series Data Mining. Ihr Zweck ist es, unerwartetes Verhalten im gesamten Datensatz zu erkennen. Da Anomalien oft durch unterschiedliche Mechanismen verursacht werden, gibt es keine spezifischen Kriterien für ihre Erkennung. In der Praxis erregen Daten, die das erwartete Verhalten zeigen, mehr Aufmerksamkeit, während anormale Daten oft als Rauschen wahrgenommen werden, das in der Regel ignoriert oder eliminiert wird. Anomalien können jedoch nützliche Informationen enthalten, sodass die Erkennung solcher Anomalien wichtig sein kann. Die genaue Erkennung von Anomalien kann dazu beitragen, unnötige nachteilige Auswirkungen in verschiedenen Bereichen wie Umwelt, Industrie, Finanzen und anderen zu mindern.

Anomalien in Zeitreihen lassen sich in die folgenden drei Kategorien einteilen:

1. Punktanomalien: Ein Datenpunkt wird als anomal im Verhältnis zu anderen Datenpunkten betrachtet. Diese Anomalien werden häufig durch Messfehler, Sensorausfälle, Dateneingabefehler oder andere außergewöhnliche Ereignisse verursacht;
2. Kontextabhängige Anomalien: Ein Datenpunkt wird in einem bestimmten Kontext als anomal betrachtet, in einem anderen jedoch nicht;
3. Kollektive Anomalien: eine Teilsequenz einer Zeitreihe, die ein anomales Verhalten aufweist. Dies ist eine recht schwierige Aufgabe, da solche Anomalien bei einer Einzelanalyse nicht als anomal angesehen werden können. Stattdessen ist es das kollektive Verhalten der Gruppe, das anomal ist.

Kollektive Anomalien können wertvolle Informationen über das zu analysierende System oder den Prozess liefern, da sie auf ein Problem auf Gruppenebene hinweisen können, das behoben werden muss. Die Erkennung kollektiver Anomalien kann daher in vielen Bereichen wie Cybersicherheit, Finanzen und Gesundheitswesen eine wichtige Aufgabe sein. Die Autoren der BPLR-Methode konzentrierten sich in ihrer Arbeit auf die Identifizierung kollektiver Anomalien.

Die hohe Dimensionalität von Zeitreihendaten erfordert erhebliche Rechenressourcen, wenn die Rohdaten für die Erkennung von Anomalien verwendet werden. Zur Verbesserung der Leistung bei der Erkennung von Anomalien umfasst ein typischer Ansatz jedoch zwei Phasen: zunächst die Dimensionenreduktion und dann die Verwendung eines Abstandsmaßes zur Durchführung der Aufgabe im transformierten Repräsentationsunterraum. Daher schlagen die Autoren der Methode einen neuen Algorithmus zur bidirektionalen, stückweisen, linearen Darstellung (BPLR) vor. Mit dieser Methode können die eingegebenen Zeitreihen in eine niedrigdimensionale Ausdrucksform umgewandelt werden, die für eine effiziente Analyse geeignet ist.

Das Papier schlägt auch einen neuen Algorithmus zur Messung der Ähnlichkeit vor, der auf der Idee der stückweisen Integration(PI) beruht. Es führt eine effiziente Berechnung von Ähnlichkeitsmaßen mit einem relativ geringen Rechenaufwand durch.

1. Der Algorithmus

Die Erkennung von Anomalien auf der Grundlage der vorgeschlagenen BPLR-Methode besteht aus zwei Stufen:

1. Darstellung von Zeitreihen
2. Messung der Ähnlichkeit

Bevor ich mit der Beschreibung des BPLR-Algorithmus fortfahre, möchte ich betonen, dass die Methode entwickelt wurde, um Probleme der Anomalieerkennung zu lösen. Es wird davon ausgegangen, dass die analysierte Zeitreihe eine gewisse Zyklizität aufweist, deren Ausmaß experimentell oder durch A-priori-Wissen ermittelt werden kann. Daher wird die gesamte Eingabezeitreihe in sich nicht überschneidende Teilsequenzen unterteilt, deren Größe dem erwarteten Zyklus der ursprünglichen Daten entspricht. Durch den Vergleich der erhaltenen Teilsequenzen versuchen die Autoren der Methode, anomale Bereiche zu finden. Anschließend wird ein Algorithmus zur Darstellung einer Teilfolge beschrieben, der für alle Elemente der analysierten Zeitreihe wiederholt wird.

Um eine Zeitreihe darzustellen, müssen wir in jeder Teilsequenz mehrere Gruppen von Segmentierungspunkten finden. Anschließend müssen wir die Eingabe-Teilsequenz in eine Reihe von linearen Segmenten umwandeln.

Um die wahrscheinlichsten Punkte für die Aufteilung der Teilsequenz in einzelne Segmente zu finden, ermitteln wir zunächst alle möglichen Trendwendepunkte (TTP). Die Autoren der Methode identifizieren 6 Varianten von Trendwendepunkten.

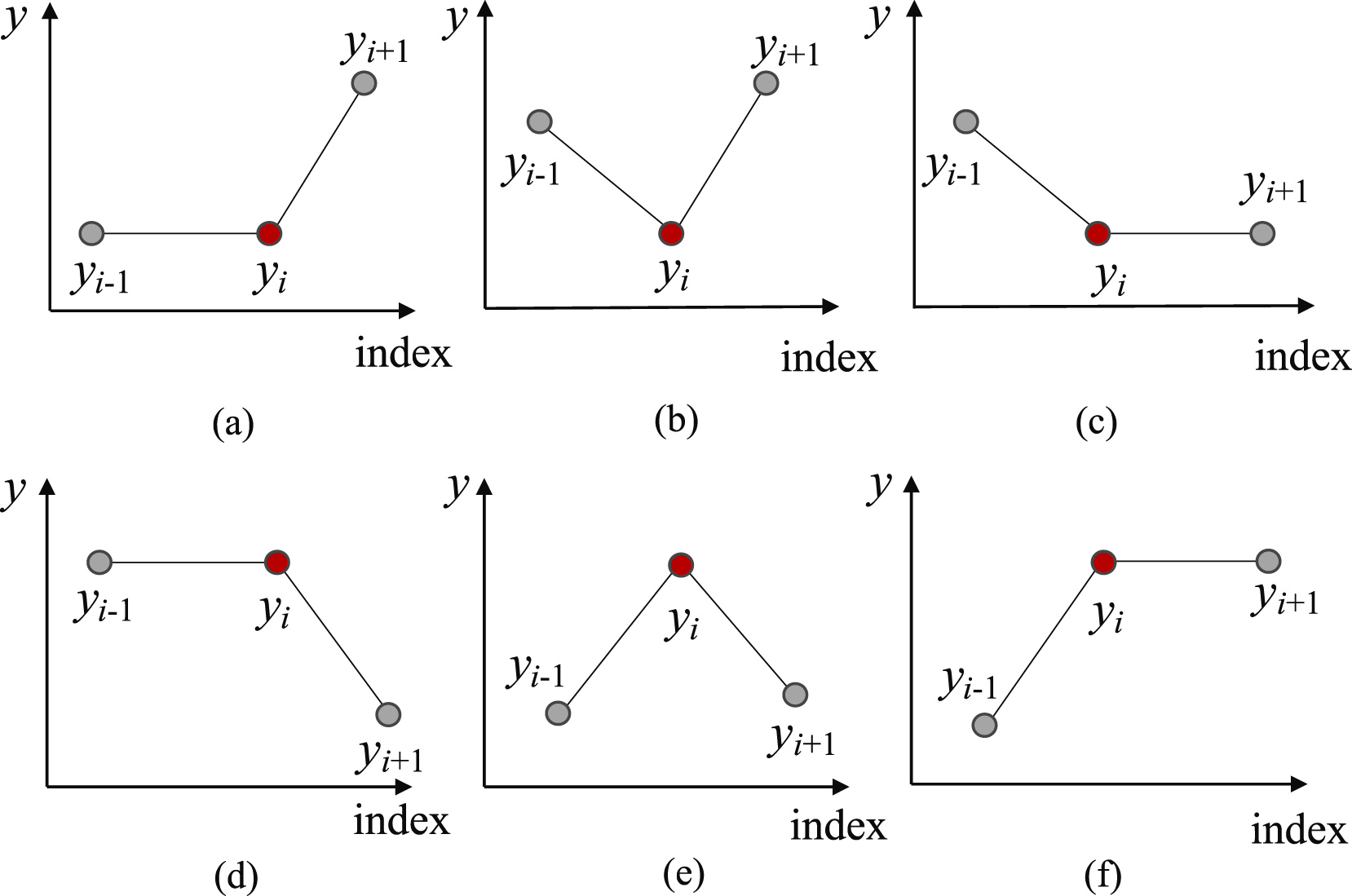
Das erste und das letzte Element der Teilsequenz werden automatisch als Trendwendepunkte betrachtet.

Der nächste Schritt besteht darin, die Bedeutung jeder gefundenen TTP zu bestimmen. Als Maß für die Wichtigkeit von TTP schlagen die Autoren der Methode vor, die Abweichung vom Mittelwert der Teilsequenz zu verwenden.

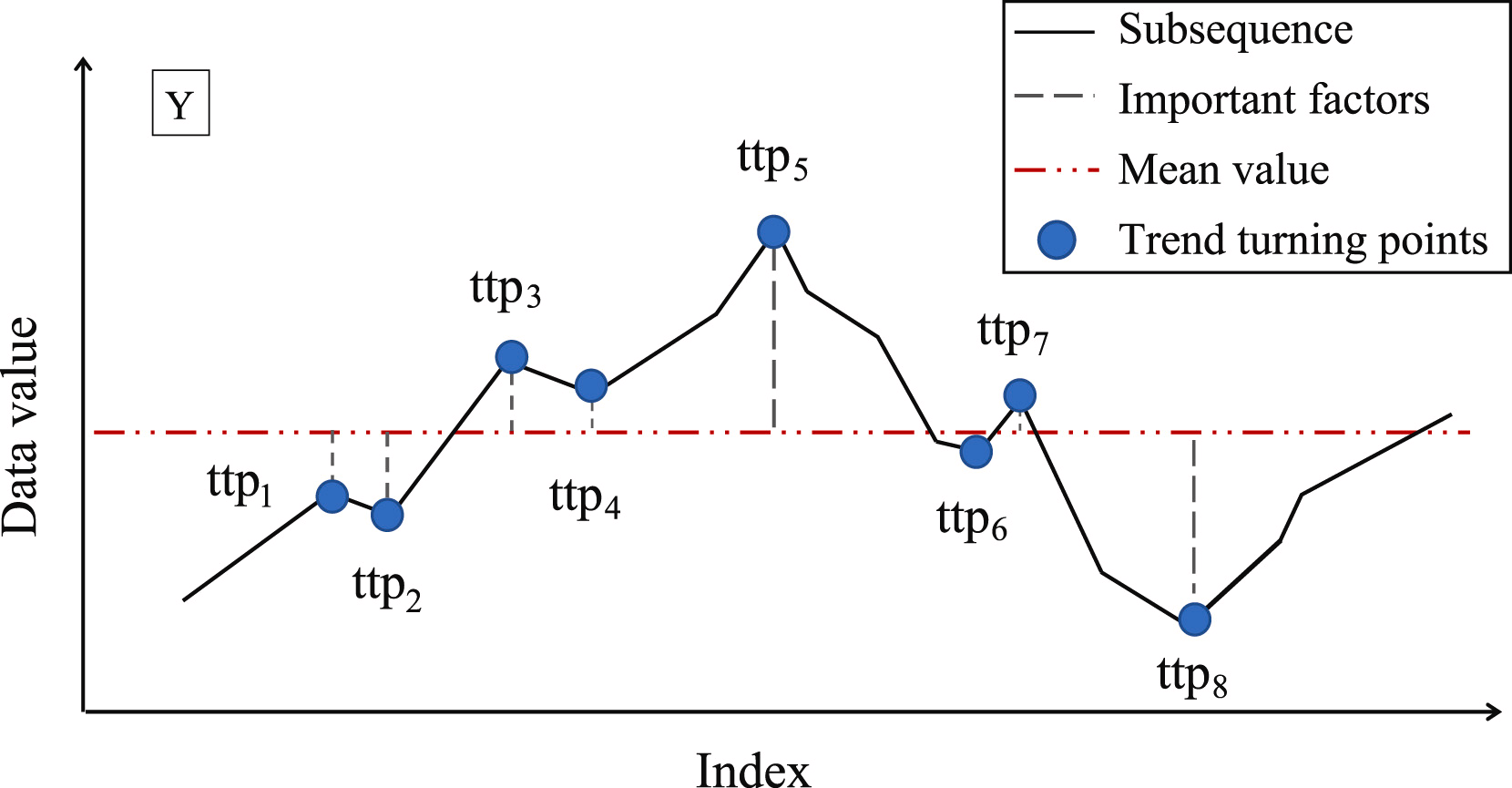
Die TTPs werden dann nach ihrer Wichtigkeit sortiert. Die Segmente werden iterativ bestimmt, beginnend mit TTP1, mit der höchsten Bedeutung in zwei Richtungen: vor und nach TTP1. In diesem Fall wird ein zusätzlicher Hyperparameter δß eingeführt, um die Qualität des Segments zu bestimmen. Der Hyperparameter definiert die maximal zulässige Abweichung der Sequenzpunkte von der Segmentlinie.

Um den Anfangspunkt des vorangegangenen Segments zu bestimmen, iterieren wir über die Elemente der Eingabesequenz in umgekehrter Reihenfolge ab dem aktuell analysierten TTP1, wobei alle Elemente zwischen TTP1 und dem Kandidaten für den Beginn des Segments nicht weiter als δß sind. Sobald ein Punkt jenseits dieser Schwelle gefunden wird, wird die Suche beendet und das Segment gespeichert. Wenn zuvor gefundene TTPs in den Erfassungsbereich des Segments fallen, werden sie gelöscht.

In ähnlicher Weise suchen wir das Ende des Segments in der Richtung nach TTP1. Da die Segmente in den Richtungen vor und nach dem Extremum gesucht werden, wurde die Methode als bidirektional bezeichnet.

Nachdem die Endpunkte der beiden Segmente bestimmt wurden, werden die Vorgänge mit dem nächstliegenden Extremum wiederholt. Die Iterationen werden beendet, wenn es keine unbearbeiteten Trendwendepunkte mehr im Array gibt.

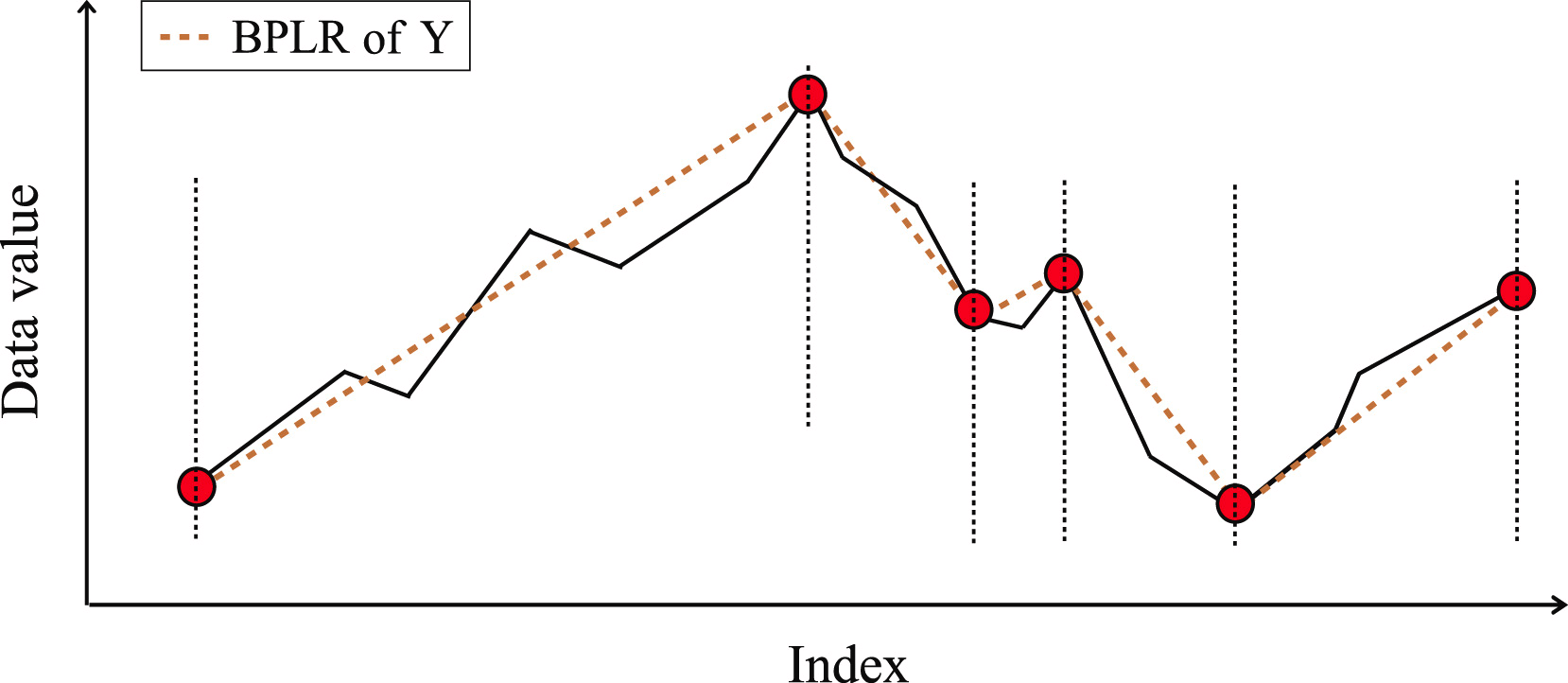
Die Ähnlichkeit zweier Teilsequenzen wird auf der Grundlage der Flächen der Formen bestimmt, die von den Segmenten der analysierten Sequenzen gebildet werden.

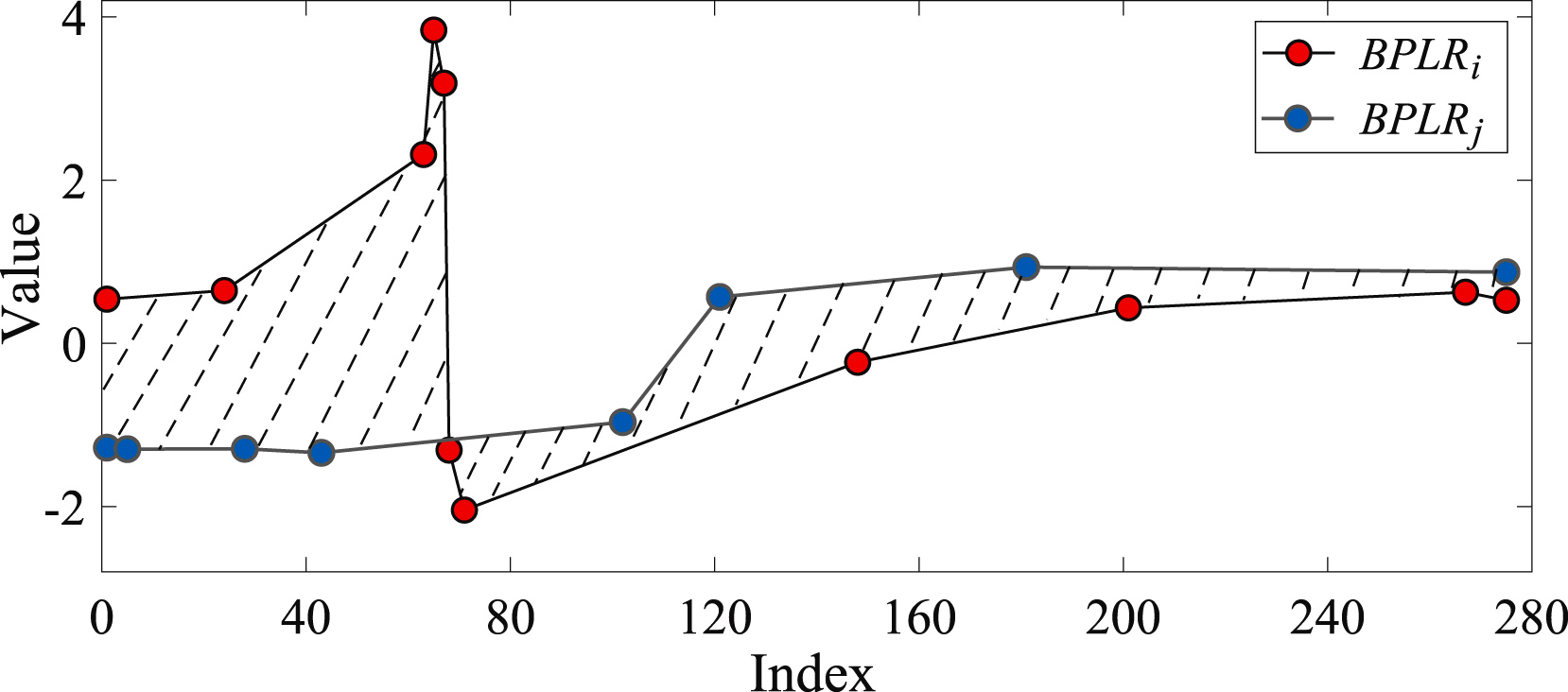
Um das Problem der Erkennung von Anomalien zu lösen, erstellen die Autoren der Methode eine Distanzmatrix Mdist. Dann berechnen sie für jede einzelne Teilsequenz die Gesamtabweichung von anderen Teilsequenzen der analysierten Zeitreihe Di. In der Praxis ist Di die Summe der Elemente der Matrix Mdist in der i-tenZeile. Eine Teilsequenz gilt als anomal, wenn ihre Gesamtabweichung vom entsprechenden Durchschnittswert der übrigen Teilsequenzen abweicht.

Die Autoren der Methode BPLR präsentieren in ihrem Beitrag die Ergebnisse von Experimenten mit synthetischen und realen Daten, die die Wirksamkeit der vorgeschlagenen Lösung belegen.

2. Implementierung in MQL5

Wir haben die theoretische Darstellung der Methode BPLR diskutiert, die darauf abzielt, anomale Teilsequenzen von Zeitreihen zu finden. Im praktischen Teil dieses Artikels werden wir unsere Vision der vorgeschlagenen Ansätze in MQL5 umsetzen. Bitte beachten Sie, dass wir die vorgeschlagenen Lösungen nur teilweise anwenden werden.

Im Rahmen unseres Anwendungsbereichs werden wir nicht nach Zeitreihenanomalien suchen. Die Finanzmärkte sind sehr dynamisch und vielschichtig, sodass zwischen zwei beliebigen disjunkten Teilsequenzen erhebliche Abweichungen zu erwarten sind.

Andererseits kann die alternative Darstellung der Zeitreihe als stückweise, lineare Folge recht nützlich sein. In den vorangegangenen Artikeln haben wir bereits über die Vorteile der Datensegmentierung gesprochen. Die Frage der Bestimmung der Segmentgröße blieb jedoch weiterhin sehr relevant. Zu diesem Zweck haben wir immer gleiche Segmentgrößen verwendet. Im Gegensatz dazu ermöglicht die stückweise, lineare Darstellungsmethode die Verwendung dynamischer Segmentgrößen, die von der analysierten Eingangszeitreihe abhängen, was bei der Extraktion von Merkmalen von Zeitreihen unterschiedlicher Größenordnungen hilfreich sein kann. Gleichzeitig hat die stückweise, lineare Darstellung unabhängig von der Segmentgröße eine feste Größe, was sie für die Analyse praktisch macht.

Ein weiterer bemerkenswerter Teil des Algorithmus ist die Darstellung der Segmente. Schon der Name „stückweise, lineare Darstellung“ weist auf die Darstellung eines Segments als lineare Funktion hin:

Daher geben wir die Richtung des Haupttrends im Zeitintervall des Segments ausdrücklich an. Darüber hinaus ist die Möglichkeit, Daten zu komprimieren, ein zusätzlicher Bonus, der dazu beiträgt, die Komplexität des Modells zu verringern.

Natürlich werden wir die analysierte Zeitreihe nicht in Teilsequenzen unterteilen. Wir werden den gesamten Satz von Ausgangsdaten als eine stückweise, lineare Folge darstellen. Unser Modell, das auf der Analyse der vorgelegten Daten beruht, muss Schlussfolgerungen ziehen und die „einzig richtige“ Lösung anbieten.

Beginnen wir mit der Erstellung eines Programms auf der OpenCL-Seite.

2.1 Implementierung auf der OpenCL-Seite

Wie Sie wissen, haben wir zur Optimierung der Modellschulung und der Betriebskosten den Großteil der Berechnungen in den Kontext von OpenCL-Geräten verlagert, wodurch wir die Berechnungen in einem mehrdimensionalen Raum organisieren konnten. Die derzeitige Umsetzung ist in dieser Hinsicht keine Ausnahme.

Um die Segmentierung der analysierten Zeitreihen durchzuführen, erstellen wir den PLR-Kernel.

__kernel void PLR(__global const float *inputs,
                  __global float *outputs,
                  __global int *isttp,
                  const int transpose,
                  const float min_step
                 )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

In den Parametern für den Kernel sollen Zeiger auf 3 Datenpuffer übergeben werden:

• Eingaben
• Ausgänge
• isttp – ein Servicepuffer zur Aufzeichnung von Trendwendepunkten

Darüber hinaus werden wir 2 Konstanten hinzufügen:

• transpose – das Flag, die anzeigt, dass die Ein– und Ausgänge transponiert werden müssen
• min_step – die Mindestabweichung der Teilsequenzelemente zur Registrierung einer TTP

Wir nennen den Kernel in einem 2-dimensionalen Aufgabenraum, entsprechend der Anzahl der Elemente in der analysierten Sequenz und der Anzahl der univariaten Sequenzen in der mehrdimensionalen Zeitreihe. Dementsprechend identifizieren wir im Kernelkörper sofort den aktuellen Fluss im Aufgabenraum und definieren dann die Konstanten für den Offset im Eingabepuffer.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);

Nach ein wenig Vorarbeit stellen wir das Vorhandensein eines TTP an der Position des analysierten Elements fest. Die Extrempunkte der analysierten Zeitreihe erhalten automatisch den Status eines Trendwendepunkts, da sie a priori die Extrempunkte des Segments sind.

   float value = inputs[shift_in];
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

In einigen Fällen suchen wir zunächst nach der geringsten Abweichung der Werte der analysierten Reihe vom erforderlichen Mindestwert vor dem aktuellen Element der Sequenz. Gleichzeitig speichern wir die Minimal- und Maximalwerte im iterierten Intervall.

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step && prev_pos > 0)
        {
         prev_pos--;
         prev = inputs[shift_in - (i - prev_pos) * step_in];
         if(prev >= max_v && (prev - min_v) < min_step)
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step)
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

Dann suchen wir auf ähnliche Weise das nächste Element mit der geringsten erforderlichen Abweichung.

      //---
      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step && next_pos < (lenth - 1))
        {
         next_pos++;
         next = inputs[shift_in + (next_pos - i) * step_in];
         if(next > max_v && (next - min_v) < min_step)
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step)
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

Wir prüfen, ob der aktuelle Wert ein Extremwert ist.

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

Dabei ist jedoch zu bedenken, dass bei der Suche nach Elementen mit der geringsten erforderlichen Abweichung ein Korridor von Werten aus mehreren Elementen der Sequenz gesammelt werden könnte, die ein bestimmtes Extremwertplateau bilden. Daher erhält ein Element nur dann ein TTP-Flag, wenn es ein Extremum in einem solchen Korridor ist.

Speichern wir das erhaltene Flag und löschen wir den Ausgabepuffer. Hier synchronisieren wir auch die Threads der lokalen Gruppe.

//---
   isttp[shift_in] = (int)bttp;
   outputs[shift_in] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

Wir müssen die Threads synchronisieren, um sicherzustellen, dass vor Beginn weiterer Operationen alle Threads der aktuellen univariaten Zeitreihe ihre Flags für das Vorhandensein einer TTP aufgezeichnet haben.

Weitere Operationen werden nur von Threads durchgeführt, in denen ein TTP definiert ist. Die verbleibenden Threads erfüllen die vorgegebenen Bedingungen nicht und werden praktisch beendet.

Hier berechnen wir zunächst die Position des aktuellen Extremums. Dazu zählen wir die Anzahl der positiven Flags für die aktuelle Position des Elements und speichern die Position des vorherigen TTP im Eingabepuffer in einer lokalen Variablen.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

Danach werden wir die Parameter der linearen Annäherung an den Trend des aktuellen Segments bestimmen.

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = inputs[prev_in + p * step_in];
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
      float intercept = (sum_y - slope * sum_x) / dist;

Speichern wir die erzielten Ergebnisse im Ausgabepuffer.

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
      outputs[shift_out] = slope;
      outputs[shift_out + 1 * step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

Hier charakterisieren wir jedes erhaltene Segment durch 3 Parameter:

• slope — Steigung der Trendlinie;
• intercept — die Verschiebung der Trendlinie im Eingabeunterraum;
• dist — Segmentlänge.

Vielleicht sollten noch ein paar Worte zur Darstellung der Segmentdauer (Länge) gesagt werden. Wie Sie vielleicht schon vermutet haben, ist die Angabe der Sequenzlänge als Ganzzahlwert in diesem Fall nicht das beste Ergebnis. Denn für den effizienten Betrieb des Modells ist ein normalisiertes Datenpräsentationsformat vorzuziehen. Daher habe ich beschlossen, die Segmentdauer als einen Bruchteil der Gesamtgröße der analysierten univariaten Zeitsequenz darzustellen. Dividieren wir also die Anzahl der Elemente in einem Segment durch die Anzahl der Elemente in der gesamten Sequenz der univariaten Zeitreihe. Um nicht in die „Falle“ der Integer-Operationen zu tappen, wandeln wir zunächst die Anzahl der Elemente im Segment von int in den Typ float um.

Außerdem werden wir für das letzte Segment einen eigenen Betriebszweig einrichten. Der Punkt ist, dass wir die Anzahl der Segmente, die sich zu einem bestimmten Zeitpunkt bilden werden, nicht kennen. Hypothetisch gesehen können wir bei erheblichen Schwankungen in den Elementen der Zeitreihe und dem Vorhandensein von Trendwendepunkten in jedem Element der Zeitreihe anstelle der Kompression dreimal so viele Werte erhalten. Natürlich ist ein solcher Fall unwahrscheinlich, aber es ist besser, einen Anstieg des Datenvolumens zu vermeiden. Gleichzeitig wollen wir aber auch keine Daten verlieren.

Daher gehen wir von einem A-priori-Wissen über die Darstellung von Zeitreihen in MQL5 aus und verstehen die Struktur der analysierten Daten: Die zeitlich jüngsten Daten stehen am Anfang unserer Zeitreihe. Deshalb schenken wir ihnen mehr Aufmerksamkeit. Die Daten am Ende des analysierten Zeitfensters liegen in der Vergangenheit und haben daher einen geringeren Einfluss auf spätere Ereignisse. Jedenfalls schließen wir einen solchen Einfluss nicht aus.

Daher verwenden wir zum Schreiben der Ergebnisse eine Datenpuffergröße, die der Größe des eingegebenen Zeitreihentensors entspricht. Dadurch können wir Segmente schreiben, die dreimal kleiner sind als die Sequenzlänge (3 Elemente für 1 Segment). Wir gehen davon aus, dass dieses Volumen mehr als ausreichend ist. Wir gehen jedoch auf Nummer sicher und fassen die Daten der letzten Segmente zu einem zusammen, um Datenverluste zu vermeiden, wenn es mehr Segmente gibt.

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = inputs[prev_in + p * step_in];
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
         float intercept = (sum_y - slope * sum_x) / dist;
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
         outputs[shift_out] = slope;
         outputs[shift_out + 1 * step_in] = intercept;
         outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
        }
     }
  }

In den meisten Fällen erwarten wir weniger Segmente, dann werden die letzten Elemente unseres Ergebnispuffers mit Nullwerten gefüllt sein.

An dieser Stelle sei darauf hingewiesen, dass der oben vorgestellte Algorithmus keine trainierbaren Parameter enthält und in der Phase der vorläufigen Aufbereitung der Ausgangsdaten verwendet werden kann. Dies impliziert nicht das Vorhandensein eines Prozesses für einen Rückwärtsdurchgang (backpropagation) und einer Fehlergradientenverteilung. In unserer Arbeit werden wir diesen Algorithmus jedoch in unsere Modelle integrieren. Infolgedessen müssen wir einen Algorithmus für den Rückwärtsdurchgang implementieren, um den Fehlergradienten von den nachfolgenden neuronalen Schichten auf die vorherigen zu übertragen. Da es keine lernbaren Parameter gibt, gibt es auch keine Optimierungsalgorithmen für sie.

Als Teil der Implementierung der Backpropagation-Algorithmen werden wir daher den Fehlergradienten-Verteilungskern PLRGradient erstellen.

__kernel void PLRGradient(__global float *inputs_gr,
                          __global const float *outputs,
                          __global const float *outputs_gr,
                          const int transpose
                         )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

In den Kernel-Parametern übergeben wir auch Zeiger auf 3 Datenpuffer. Diesmal haben wir jedoch 2 Puffer für Fehlergradienten (auf der Eingangs- und der Ausgangsebene) und einen Puffer mit den Ergebnissen der aktuellen Schicht für die Vorwärtsdurchgang. Darüber hinaus werden wir die Kernel-Parameter um das bereits bekannte Kennzeichen für die Datentransposition ergänzen. Dieses Flag wird bei der Bestimmung von Offsets in Datenpuffern verwendet.

Wir werden den Kernel in demselben 2-dimensionalen Aufgabenraum aufrufen. Die erste Dimension ist durch die Größe der Zeitreihenfolge begrenzt, die zweite durch die Anzahl der univariaten Zeitreihen in den multimodalen Quelldaten. Im Kernelkörper identifizieren wir zunächst den aktuellen Thread im Aufgabenraum in allen Dimensionen.

Als Nächstes definieren wir Konstanten für die Offsets in den Datenpuffern.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_out = ((bool)transpose ? v : (v * lenth));
   const int step_out = 3 * step_in;

Aber die Vorbereitungsarbeiten sind noch nicht abgeschlossen. Als Nächstes müssen wir das Segment finden, das das analysierte Eingabeelement enthält. Um sie zu finden, führen wir eine Schleife aus und geben im Schleifenkörper die Größen der Segmente an, beginnend mit dem ersten. Wir wiederholen die Schleifen, bis wir ein Segment finden, das das gewünschte Eingabedatenelement enthält.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(outputs[shift_out + pos * step_out + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Nach allen Iterationen der Schleife erhalten wir:

• pos — Index des Segments, das das gewünschte Element der Eingabedaten enthält
• prev_in — Offset im Eingangsdatenpuffer zum ersten Segmentelement
• dist — die Anzahl der Elemente im Segment

Zur Berechnung der Ableitungen erster Ordnung von Vorwärtsoperationen benötigen wir auch die Summe der Positionen der Segmentelemente und die Summe ihrer Quadratwerte.

//--- calc constants
   float sum_x = 0;
   float sum_xx = 0;
   for(int p = 0; p < dist; p++)
     {
      float x = (float)(p);
      sum_x += x;
      sum_xx += x * x;
     }

Damit sind die Vorarbeiten abgeschlossen und wir können zur Berechnung des Fehlergradienten übergehen. Zunächst extrahieren wir den Fehlergradienten für die Steigung und den Versatz.

//--- get output gradient
   float grad_slope = outputs_gr[shift_out + pos * step_out];
   float grad_intercept = outputs_gr[shift_out + pos * step_out + step_in];

Erinnern wir uns nun an die Formel, die wir im Vorwärtsdurchgang zur Berechnung der vertikalen Verschiebung der Trendlinie verwendet haben.

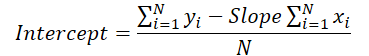
Der Wert der Geradensteigung wird zur Berechnung der Verschiebung verwendet. Daher ist es notwendig, den Neigungsfehlergradienten unter Berücksichtigung seines Einflusses auf die Verschiebungsanpassung anzupassen. Zu diesem Zweck wird die Ableitung der Verschiebungsfunktion nach der Steigung bestimmt.

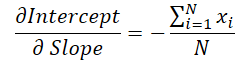
Wir multiplizieren den erhaltenen Wert mit dem Verschiebungsfehlergradienten und addieren das Ergebnis zum Neigungsfehlergradienten.

//--- calc gradient
   grad_slope -= sum_x / dist * grad_intercept;

Wenden wir uns nun der Formel zur Bestimmung der Steigung zu.

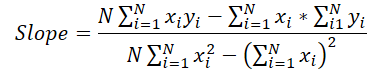
In diesem Fall ist der Nenner eine Konstante, die wir zur Anpassung des Steigungsfehlergradienten verwenden können.

   grad_slope /= fmax(dist * sum_xx - sum_x * sum_x, 1);

Und schließlich wollen wir uns den Einfluss der Eingabedaten in beiden Formeln ansehen:

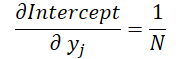
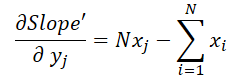
wobei 1 ≤ j ≤ N und

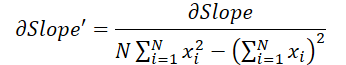
Mit diesen Formeln können wir den Fehlergradienten auf der Ebene der Eingabedaten bestimmen.

   float grad = grad_intercept / dist;
   grad += (dist * (i - prev_in) - sum_x) * grad_slope;
   if(isnan(grad) || isinf(grad))
      grad = 0;

Wir speichern das Ergebnis im entsprechenden Element des Gradientenpuffers der Eingabedaten.

//--- save result
   inputs_gr[shift_in] = grad;
  }

Damit ist unsere Arbeit an der Kontextseite von OpenCL abgeschlossen. Der vollständige Code von OpenCL ist im Anhang enthalten.

2.2 Implementierung der neuen Klasse

Nachdem wir die Operationen auf der Kontextseite OpenCL abgeschlossen haben, gehen wir zur Arbeit mit dem Hauptprogrammcode über. Hier werden wir eine neue Klasse, CNeuronPLROCL, erstellen, die es uns ermöglicht, den oben beschriebenen Algorithmus in unsere Modelle in Form einer regulären neuronalen Schicht zu implementieren.

Wie in den meisten, ähnlichen Fällen erbt das neue Objekt seine Hauptfunktionalität von unserer Basisklasse CNeuronBaseOCL für neuronale Schichten. Nachstehend finden Sie die Struktur der neuen Klasse.

class CNeuronPLROCL  :  public CNeuronBaseOCL
  {
protected:
   bool              bTranspose;
   int               icIsTTP;
   int               iVariables;
   int               iCount;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  { return true; }

public:
                     CNeuronPLROCL(void)  : bTranspose(false) {};
                    ~CNeuronPLROCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint units_count, bool transpose, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLROCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Die Struktur enthält die Neudefinition des Standardsatzes von Methoden mit mehreren zusätzlichen Variablen. Der Zweck der neuen Variablen lässt sich aus ihren Namen ableiten.

• bTranspose — Flag, die anzeigt, dass die Ein- und Ausgänge transponiert werden müssen
• iCount — die Größe der zu analysierenden Sequenz (Tiefe der Historie)
• iVariables — die Anzahl der analysierten Parameter einer multimodalen Zeitreihe (univariate Sequenzen)

Bitte beachten Sie, dass wir zwar einen Puffer für Hilfsdaten in den Kernelparametern des Vorwärtsdurchgangs haben, aber keinen zusätzlichen Puffer auf der Seite des Hauptprogramms erstellen. Hier speichern wir nur einen Zeiger darauf in der lokalen Variable icIsTTP.

Da wir keine internen Objekte haben, können wir den Konstruktor und Destruktor der Klasse leer lassen. Das Objekt wird in der Methode Init initialisiert.

bool CNeuronPLROCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window_in, uint units_count, bool transpose, 
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch))
      return false;

In den Parametern erhält die Methode die wichtigsten Konstanten zur Definition der Architektur des erstellten Objekts. Im Klassenkörper rufen wir zunächst die Methode der gleichnamigen Elternklasse auf, die bereits die notwendigen Kontrollen und die Initialisierung der geerbten Objekte und Variablen implementiert.

Dann speichern wir die Konfigurationsparameter des erstellten Objekts.

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

Am Ende der Methode erstellen wir einen Hilfsdatenpuffer auf der Kontextseite von OpenCL.

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;
//---
   return true;
  }

Nach der Initialisierung des Objekts wird in der Methode des Vorwärtsdurchgangs dessen Algorithmus konstruiert. Hier müssen wir nur den oben erstellten Kernel des Vorwärtsdurchgangs PLR aufrufen. Es ist jedoch notwendig, lokale Gruppen zu erstellen, um Threads innerhalb einzelner univariater Zeitreihen zu synchronisieren.

bool CNeuronPLROCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getOutput())
      return false;
//---
   uint global_work_offset[2] = {0};
   uint global_work_size[2] = {iCount, iVariables};
   uint local_work_size[2] = {iCount, 1};

Zu diesem Zweck definieren wir einen 2-dimensionalen globalen Aufgabenraum. Für die erste Dimension geben wir die Größe der zu analysierenden Sequenz an, für die zweite Dimension die Anzahl der univariaten Zeitreihen. Wir definieren auch die Größe der lokalen Gruppe in einem 2-dimensionalen Aufgabenraum. Die Größe der ersten Dimension entspricht dem globalen Wert, und für die zweite Dimension geben wir 1 an. So erhält jede lokale Gruppe ihre eigene univariate Sequenz.

Als Nächstes müssen wir dem Kernel nur noch die erforderlichen Parameter übergeben.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plt_isttp, icIsTTP))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_transpose, (int)bTranspose))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_step, (float)0.3))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Und wir stellen den Kernel in die Ausführungswarteschlange.

//---
   if(!OpenCL.Execute(def_k_PLR, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Vergessen Sie nicht, die Vorgänge in jeder Phase zu kontrollieren. Am Ende der Methode geben wir den logischen Wert der Methodenergebnisse an den Aufrufer zurück.

Der Algorithmus der Fehlergradientenverteilungsmethode calcInputGradients ist auf ähnliche Weise aufgebaut. Aber anders als bei der Methode des Vorwärtsdurchgangs werden hier keine lokalen Gruppen gebildet, und jeder Thread führt seine Operationen unabhängig aus. Den vollständigen Code aller im Artikel verwendeten Programme finden Sie in der Anlage unten.

Wie bereits erwähnt, enthält das von uns erstellte Objekt keine lernbaren Parameter. Daher wird die Parameteroptimierungsmethode updateInputWeights hier nur neu definiert, um die allgemeine Struktur der Objekte und ihre Kompatibilität bei der Implementierung zu erhalten. Diese Methode gibt immer true zurück.

Damit ist die Beschreibung der Algorithmen zur Implementierung der Methoden der neuen Klasse abgeschlossen. Den vollständigen Code der Klassenmethoden, einschließlich derer, die nicht in diesem Artikel beschrieben werden, finden Sie im Anhang.

2.3 Modellarchitektur

Wir haben einen der Algorithmen für die stückweise, lineare Darstellung von Zeitreihen implementiert und können ihn nun in die Architektur unserer Modelle aufnehmen.

Um die Effektivität der vorgeschlagenen Implementierung zu testen, haben wir eine neue Klasse in die Modellstruktur des Environmental State Encoders eingeführt. Ich muss sagen, dass wir die Modellarchitektur erheblich vereinfacht haben, um die Auswirkungen der nominalen Zerlegung der Zeitreihen auf einzelne lineare Trends zu bewerten.

Wie zuvor beschreiben wir die Architektur des Modells in der Methode CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

In Parametern erhält die Methode einen Zeiger auf ein dynamisches Array-Objekt zur Aufzeichnung der Architektur des Modells. Im Hauptteil der Methode wird zunächst die Relevanz des empfangenen Zeigers geprüft. Danach erstellen wir, falls erforderlich, eine neue Instanz des dynamischen Arrays.

Wie üblich füttern wir das Modell mit Informationen über den Zustand der Umwelt in einer bestimmten Tiefe der Vergangenheit, ohne dass die Daten vorverarbeitet werden.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Der stückweise, lineare Darstellungsalgorithmus funktioniert sowohl mit normalisierten als auch mit Rohdaten gleichermaßen gut. Aber es gibt ein paar Dinge zu beachten.

Erstens haben wir in unserer Implementierung den Parameter der minimal erforderlichen Abweichung der Zeitreihenwerte verwendet, um einen Trendwendepunkt zu registrieren. Dies erfordert natürlich eine sorgfältige Auswahl dieses Hyperparameters für die Analyse jeder einzelnen Zeitreihe. Die Verwendung des Algorithmus zur Analyse multimodaler Zeitreihen, bei denen die Werte univariater Sequenzen in verschiedenen Verteilungen liegen, erschwert diese Aufgabe erheblich. Außerdem ist es in den meisten Fällen nicht möglich, einen Hyperparameter für alle analysierten univariaten Sequenzen zu verwenden.

Zweitens werden die Ergebnisse von PLR in Modellen verwendet, deren Effizienz bei Verwendung normalisierter Quelldaten deutlich höher ist.

Natürlich können wir eine Normalisierung der Ergebnisse von PLR hinzufügen, bevor wir sie in das Modell einspeisen, aber selbst hier erschwert die dynamische Änderung der Segmentanzahl die Aufgabe.

Gleichzeitig vereinfacht die Normalisierung der Eingabedaten vor der Einspeisung in die stückweise, lineare Darstellungsschicht alle oben genannten Punkte erheblich. Indem wir alle univariaten Sequenzen auf eine einzige Verteilung normalisieren, können wir einen Hyperparameter zur Analyse multimodaler Zeitreihen verwenden. Die Normalisierung der Verteilung der Eingabedaten ermöglicht es uns außerdem, durchschnittliche Hyperparameter für völlig unterschiedliche Eingabesequenzen zu verwenden. 

Nachdem wir normalisierte Daten am Eingang der Schicht erhalten haben, haben wir normalisierte Sequenzen am Ausgang. Daher ist die nächste Schicht unseres Modells die Schicht der Stapelnormalisierung.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Um mit univariaten Sequenzen zu arbeiten, transponieren wir die Eingabedaten.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

In unserer Implementierung des Algorithmus von PLR könnte es natürlich effizienter sein, den Transpositionsparameter zu verwenden, anstatt eine Datenumsetzungsschicht zu nutzen. In diesem Fall verwenden wir jedoch aufgrund des weiteren Aufbaus der Modellarchitektur genau die Transposition.

Als Nächstes werden die vorbereiteten Daten in lineare Segmente aufgeteilt.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPLROCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = int(false);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir verwenden einen 3-Schicht-MLP für die Vorhersage einzelner univariater Sequenzen für einen bestimmten Planungshorizont.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   descr.window_out = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = LatentCount;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Beachten Sie, dass wir Faltungsschichten mit nicht überlappenden Fenstern verwenden, um eine bedingungsunabhängige Vorhersage einzelner univariater Sequenzwerte zu organisieren. Ich verwende die Definition der „bedingt unabhängigen Vorhersage“, weil dieselben Gewichtungsmatrizen verwendet werden, um die Vorhersagekurven aller univariaten Sequenzen zu konstruieren.

Wir transponieren die vorhergesagten Werte in eine Darstellung der Eingabedaten.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir fügen ihnen die statistischen Parameter der Verteilung hinzu, die bei der Normalisierung der ursprünglichen Daten eliminiert wurden.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Am Ausgang des Modells verwenden wir die Entwicklungen der Methode FreDF, um die einzelnen Schritte der von uns konstruierten prädiktiven univariaten Sequenzen der analysierten Zeitreihen zu koordinieren.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Wir haben also ein Modell des Environmental State Encoders entwickelt, das PLR und MLP für die Zeitreihenprognose vereint.

3. Tests

Im praktischen Teil dieses Artikels haben wir einen Algorithmus für die stückweise, lineare Darstellung (PLR) von Zeitreihen implementiert. Der vorgeschlagene Algorithmus enthält keine lernbaren Parameter. Vielmehr geht es darum, die analysierte Zeitreihe in eine alternative Darstellung zu transformieren. Wir haben auch ein recht vereinfachtes Zeitreihenvorhersagemodell vorgestellt, das die erstellte Schicht CNeuronPLROCL verwendet. Nun ist es an der Zeit, die Wirksamkeit dieser Ansätze zu bewerten.

Zum Trainieren des Environmental State Encoder-Modells für die Vorhersage der nachfolgenden Indikatoren der analysierten Zeitreihen verwenden wir den für den vorherigen Artikel gesammelten Trainingsdatensatz.

Wir trainieren Modelle mit realen historischen Daten des Instruments EURUSD mit dem Zeitrahmen H1, die für das gesamte Jahr 2023 gesammelt wurden. Während des Trainings des Environmental State Encoder arbeitet er nur mit historischen Daten von Kursbewegungen und analysierten Indikatoren. Daher trainieren wir das Modell so lange, bis wir das gewünschte Ergebnis erhalten, ohne den Trainingsdatensatz aktualisieren zu müssen.

Was die Modellschulung betrifft, so möchte ich auf die Stabilität des Prozesses hinweisen. Das Modell lernt recht schnell, ohne große Sprünge der Prognosefehler.

Das Ergebnis ist, dass wir trotz der relativen Einfachheit des Modells ein ziemlich gutes Ergebnis erzielt haben. Nachfolgend finden Sie zum Beispiel ein Vergleichsdiagramm der angestrebten und der prognostizierten Kursentwicklung.

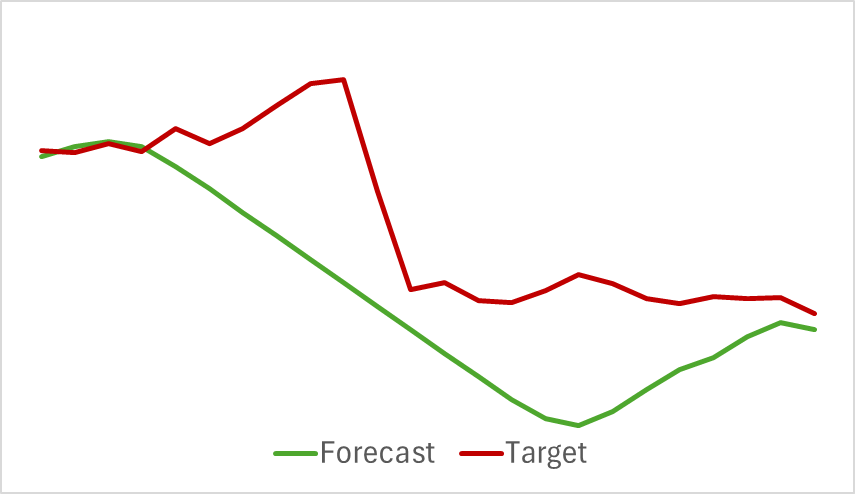
Das Diagramm zeigt, dass das Modell in der Lage war, die wichtigsten Trends der bevorstehenden Preisbewegung zu erfassen. Es ist bemerkenswert, dass bei einem Vorhersagehorizont von 24 Stunden die Werte am Anfang und am Ende der Vorhersagekurve recht nahe beieinander liegen. Lediglich die Preisbewegungsdynamik der prognostizierten Trajektorie ist zeitlich ausgedehnter.

Die Prognosen für die analysierten Indikatoren zeigen ebenfalls gute Ergebnisse. Nachfolgend finden Sie ein Diagramm mit den vorhergesagten RSI-Werten.

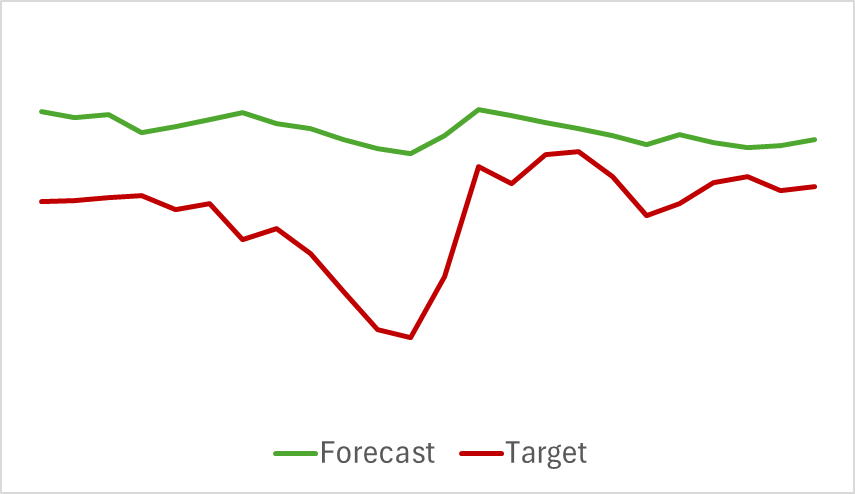
Die vorhergesagten Werte des Indikators sind etwas höher als die tatsächlichen Werte und haben eine geringere Amplitude, aber sie sind in Zeit und Richtung der Hauptimpulse konsistent.

Bitte beachten Sie, dass sich die dargestellten Prognosen für die Kursentwicklung und die Indikatorwerte auf denselben Zeitraum beziehen. Wenn Sie die beiden dargestellten Diagramme vergleichen, können Sie sehen, dass die Hauptdynamik der vorhergesagten und tatsächlichen Werte der Indikatoren zeitlich mit der Hauptdynamik der tatsächlichen Preisbewegung übereinstimmt.

Schlussfolgerung

In diesem Artikel haben wir Methoden für die alternative Darstellung von Zeitreihen in Form einer stückweisen, linearen Segmentierung erörtert. Im praktischen Teil des Artikels haben wir eine der Varianten der vorgeschlagenen Ansätze umgesetzt. Die Ergebnisse der durchgeführten Experimente zeigen das vorhandene Potenzial der betrachteten Ansätze.

Referenzen

Bidirectional piecewise linear representation of time series with application to collective anomaly detection

Andere Artikel aus dieser Reihe

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	EA	EA-Beispielsammlung
2	ResearchRealORL.mq5	EA	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	EA	Trainings-EA des Modells
4	StudyEncoder.mq5	EA	Trainings-EA des Encoders
5	Test.mq5	EA	Modeltest-EA
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL