
ALGLIB 库优化方法(第二部分)
内容
- 概述
- ALGLIB库的优化方法:
- ALGLIB方法中使用的函数表
- 测试方法
概述
在关于MetaTrader 5标准发行版中ALGLIB库优化算法的第一部分研究中,我们详细探究了以下算法:BLEIC(边界、线性等式-不等式约束)、L-BFGS(有限内存Broyden-Fletcher-Goldfarb-Shanno)和NS(盒式/线性/非线性——非光滑约束的非光滑非凸优化)。我们不仅研究了它们的理论基础,还讨论了如何将它们应用于优化问题的简单方法。
在本文中,我们将继续探索ALGLIB库中剩余的方法。特别关注在复杂的多维函数上测试它们,这将使我们能够形成对每种方法效率的全方位观点。最后,我们将对获得的结果进行全面分析,并提出选择特定类型任务的最优算法的实际建议。
BC(盒式约束优化)
盒式约束优化,该子程序最小化带有N个参数的F(x)函数,同时受到盒式约束(某些盒式约束实际上是等式)的限制。这种优化器使用一种与BLEIC(线性约束优化器)算法类似的算法,但由于只有盒式约束,这使得约束激活策略能够更快地执行。在大规模问题中,当解中存在多个活跃约束时,这种优化器可能比BLEIC更快。
让我更通俗地解释一下什么是盒式约束优化。这是一种优化算法,它搜索最优解,处理盒式约束(每个变量都必须在一定范围内),并且本质上是在所有变量都必须在给定范围内的情况下寻找函数的最小值。该算法的主要特点是它类似于BLEIC,但运行速度更快,并且专门针对范围约束进行了优化。
要求:起始点必须是可行的或接近可行区域,并且函数必须在整个可行区域内定义。
为了在ALGLIB库中使用BC方法和其他方法,我们需要连接文件(该库随MetaTrader 5终端提供,用户无需额外安装任何内容)。
#include <Math\Alglib\alglib.mqh> 让我们开发一个脚本——一个使用ALGLIB方法高效工作的示例。我将突出显示在使用ALGLIB方法时常用的主要步骤。相应的代码块也以适当的颜色突出显示。
1. 让我们定义问题的边界条件,例如适应度函数(目标函数)的启动次数、要优化的参数范围及其步长。对于ALGLIB方法,需要分配“x”优化参数的起始值(这些方法是确定性的,结果完全取决于初始值,因此我们将在问题参数范围内应用随机数生成),以及“s”比例(这些方法对参数之间的相对比例很敏感,在这种情况下我们将比例设置为“1”)。
2. 声明算法运行所需的必要对象。
3.设置算法的外部参数(设置项)。
4. 通过将待优化参数的范围和步长以及算法的外部参数传递给方法,来初始化算法。
5. 执行优化。
6. 获取优化结果以供进一步使用。
请记住,用户无法干预优化过程或在任何时候停止它。该方法会独立执行所有操作,在其过程中调用适应度函数。该算法可以调用适度性函数任意次数(尽管它是由用户指定的参数指导的)。用户可以通过向方法传递停止命令来控制允许调用的最大次数。
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinBCReport rep; // Set the parameters of the BC optimization algorithm------------------------------ double diffStep = 0.00001; double epsg = 1e-16; double epsf = 1e-16; CAlglib::MinBCCreateF (x, diffStep, fFunc.state); CAlglib::MinBCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinBCSetScale (fFunc.state, s); CAlglib::MinBCSetCond (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns); CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinBCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
由于该方法会自行调用适应度函数(而非通过用户程序调用),因此需要将适应度函数的调用封装在一个继承自ALGLIB中父类的类中(这些父类对于不同的方法而言是不同的)。将封装类声明为C_OptimizedFunction,并在该类中设置以下方法:
1. Func() 是一个虚方法,在派生类中会被重写。2. Init ()—— 初始化类参数。对于该方法而言:
- 初始化与函数运行次数和找到的最优函数值相关的变量。
- 预留c和cB数组用于存储坐标。
变量:
- state —— 在调用算法的静态方法和调用停止方法时,使用BC方法特有的CMinBCState类型对象。
- numberLaunches —— 当前运行次数(用于防止适应度函数不受控制或运行时间过长)。
- maxNumbLaunchesAllowed —— 允许的最大运行次数。
- fB —— 找到的适应度函数的最优值。
- c [] —— 当前坐标的数组。
- cB [] —— 用于存储最优搜索坐标的数组。
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_Func class C_OptimizedFunction : public CNDimensional_Func { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void Func (CRowDouble &x, double &func, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinBCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
C_OptimizedFunction类的Func方法旨在访问用户的适应度函数。它接受x向量作为参数(这是优化方法提出的问题的优化参数变体之一)、func参数用于接收返回的适应度函数的计算值,以及obj对象(其用途尚不明确,可能用于向该方法传递或从该方法接收额外信息)。该方法的主要阶段:
- numberLaunches计数器递增。其目的是跟踪Func方法的调用次数。
- 如果调用次数超过允许的maxNumbLaunchesAllowed值,函数将func值设置为DBL_MAX(“double”类型的最大值,ALGLIB方法旨在最小化函数,此值表示最差的可行解)。随后,调用MinBCRequestTermination函数,该函数用于向BC方法发出停止优化的信号。
- 接下来,在循环中将x向量中的值复制到c数组中。这是为了使用这些值传递给用户的适应度函数。
- 调用 ObjectiveFunction函数。针对c数组中的当前值计算目标函数值。计算结果保存在ffVal中,同时将func值设置为ffVal的相反数(我们要优化的是一个倒置的抛物面,需要对其进行最大化,而BC方法是对函数进行最小化,所以要对其值进行翻转)。
- 如果当前ffVal 值超过之前最优的fB值,则更新fB,并将cB数组复制为c的当前状态。这使我们能够跟踪适应度函数的最优获取值及其对应的参数,并在稍后必要时引用它们。
Func 函数实现了对自定义适应度函数的调用,并跟踪其调用次数,更新最优结果。如果调用次数超过设定的限制,它还会控制停止条件。
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { func = DBL_MAX; CAlglib::MinBCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); func = -ffVal; // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
在使用BC算法运行测试脚本对抛物面函数进行优化后,我们在输出中得到了以下结果:
遗憾的是,尽管我们使用了MinBCRequestTermination方法请求停止优化,但算法仍继续执行,并试图在超过10,000次运行的限制后继续访问适应度函数。
现在,我们尝试不对BC算法进行限制,让其自行运行。结果如下:
由此可见,BC算法能够在抛物面函数上实现完全收敛,但在这种情况下,我们无法提前估算出目标函数所需的运行次数。
在算法中,微分步长非常重要。例如,如果我们使用非常小的步长,例如1e-16而不是0.00001,那么算法会过早停止,基本上陷入停滞状态,结果如下:
NLC(基于预处理增广拉格朗日算法的非线性约束优化)
这种带有约束条件的非线性优化算法允许在考虑各种约束条件的情况下,最小化具有N个变量的复杂目标函数 F(x)。这些约束条件包括:变量边界约束(min <= x <= max)、线性不等式和等式约束、非线性等式约束 G(x) = 0以及非线性不等式约束 H(x) <= 0。
想象一下,您有一个想要达成的困难目标,但同时存在一些不能违反的限制条件。例如,您想要最大化销售利润,但同时不能超过一定的运营成本。ALGLIB算法能够帮助解决这类带约束的优化问题。以下是它的工作原理:
1. 您为算法设定了一个起始点——即关于如何达成目标的一个初步猜测。这个起始点必须满足所有约束条件。
2. 然后,算法从这个起始点开始,逐步缓慢移动,逐步接近最优解。在每一步,它都会解决一个辅助问题,以确定下一步的移动方向。
3. 为了加快这一过程,算法采用了一种称为“预处理”的特殊技术。这意味着它会根据任务的结构来调整其“步长”,以便更快地移动。
4. 最终,经过几次迭代后,算法会找到一个满足所有约束条件的同时最小化目标函数(例如,最小化运营成本)的解。
用户可以从ALGLIB中实现的三种不同求解器中选择,这些求解器适用于不同规模和复杂度的问题:
SQP(序列二次规划)适用于中等规模且目标函数较为复杂的问题。AUL((预处理增广拉格朗日方法)适用于大规模问题或目标函数计算成本较低(快速)的问题。SLP(序列线性规划)速度较慢,但在复杂情况下更为稳健。
对测试函数的实验表明,AUL求解器具有较高的效率,代码中其他求解器已被注释掉。
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinNLCReport rep; // Setting parameters of the NLC optimization algorithm----------------------------- double diffStep = 0.00001; double rho = 1000.0; int outerits = 5; CAlglib::MinNLCCreateF (x, diffStep, fFunc.state); CAlglib::MinNLCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinNLCSetScale (fFunc.state, s); CAlglib::MinNLCSetCond (fFunc.state, rangeStep, numbTestFuncRuns); //CAlglib::MinNLCSetAlgoSQP (fFunc.state); CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits); //CAlglib::MinNLCSetAlgoSLP (fFunc.state); CAlglib::MinNLCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinNLCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
在NLC(非线性约束优化)中,“状态”变量的类型被设置为CMinNLCState。
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinNLCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
使用MinNLCRequestTermination命令请求停止优化过程。
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); CAlglib::MinNLCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
在使用NLC算法运行测试脚本对抛物面函数进行优化后,我们在输出中得到以下结果:
NLC算法,最优结果:0.8858935739350294,函数调用次数:28007
在不限制目标函数调用次数的情况下,NLC算法能够完全收敛,但过程中会执行超过一百万次迭代:
NLC算法,最优结果:1.0,函数调用次数:1092273
当使用非常小的步长1e-16时,算法不会像BC方法那样过早停止,但显示的结果略逊于使用步长0.00001时的结果。
NLC算法,最优结果:0.8543715192632731,函数调用次数:20005
LM(莱文贝格-马夸尔特方法)
莱文贝格-马夸尔特方法(LM)是一种广泛用于解决非线性最小二乘问题的优化算法。该方法在曲线和曲面拟合问题中非常有效。
LM方法的基本思想结合了两种优化技术:梯度下降法和高斯-牛顿法。这使得算法能够适应目标函数的形状。其工作原理如下:
- 在每次迭代中,算法使用梯度下降和二阶近似相结合的方法来计算步长方向。
- 衰减比(λ)会自动调整,以控制步长和两种方法之间的平衡。
想象一下,您正在尝试在一片山区中找到最低点,但手头只有一张边缘模糊的地图。莱文贝格-马夸尔特方法就像一位聪明的导航员,它结合了两种寻找路径的方式:
1. 第一种方法(高斯-牛顿法)速度快,但风险高。这就像您沿着斜坡直线向下跑。当您接近目标时,这种方法效果很好,但如果地形复杂,您可能会摔倒。
2. 第二种方法(梯度下降法)速度慢,但可靠。这就像您小心翼翼地以小步幅向下走。虽然速度较慢,但更安全。即使在复杂地形上也能表现良好。
算法会在这两种方法之间智能切换。当路径清晰时,它使用快速方法;但当情况复杂时,它会切换到高度警戒模式。它会自动调整步长。
此外,该算法可能会陷入局部最小值。算法需要一个良好的初始近似值(您需要大致知道搜索范围),并且对于参数数量较多(超过 100 个)的问题效果不佳。
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; double rangeMin [], rangeMax [], rangeStep; ArrayResize (rangeMin, params); ArrayResize (rangeMax, params); for (int i = 0; i < params; i++) { rangeMin [i] = -10; rangeMax [i] = 10; } rangeStep = DBL_EPSILON; double x []; double s []; ArrayResize (x, params); ArrayResize (s, params); ArrayInitialize (s, 1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinLMReportShell rep; // Set the parameters of the LM optimization algorithm------------------------------ double diffStep = 1e-16;//0.00001; CAlglib::MinLMCreateV (1, x, diffStep, fFunc.state); CAlglib::MinLMSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinLMSetScale (fFunc.state, s); CAlglib::MinLMSetCond (fFunc.state, rangeStep, numbTestFuncRuns); CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj); CAlglib::MinLMResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
对于LM算法,其“状态”变量类型被设置为CMinLMStateShell。
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinLMStateShell state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
与之前的优化方法一样,我们对目标函数的调用次数进行了限制,但在LM方法中,并未提供停止命令。从逻辑上讲,我们本应期望存在MinLMRequestTermination函数(用于请求终止LM优化过程)。
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); //CAlglib::MinLMRequestTermination (state); // such method does not exist return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
在使用LM算法运行测试脚本以优化抛物面函数后,我们在打印输出中得到了以下结果:
LM,最优结果:0.6776047308612422,函数调用次数:4003
LM方法在目标函数的第4003次运行时停止,因此移除对迭代次数的限制将得到相同的结果,因为算法在达到10,000次迭代的“上限”之前就已经卡住了:
如果我们使用一个非常小的步长1e-16,算法甚至会更早地在目标函数的第2001次运行时提前停止:
LM,最优结果:0.6670839162547625,函数调用次数:2001
ALGLIB方法中使用的函数表
ALGLIB优化方法使用不同类型的变量作为初始值和边界约束,目标函数不同类型的父类以及优化所需的对象集合,以及需要调用的不同函数列表。这可能会使得直接编写使用这些方法的程序变得困难。
为了更容易理解和整理关于ALGLIB优化方法的知识,我准备了一个汇总表。它将帮助程序员快速地找到方向,并开始正确地优化他们的项目。
| 优化算法 | FF函数类型 | 变量类型 | 对象列表 | 调用方法列表 |
| BLEIC | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell | 1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination |
| LBFGS | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell | 1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination |
| NS | FVec | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState | 1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination |
| BC | Func | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState | 1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination |
| NLC | Fvec | CRowDouble | 1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState | 1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination |
| LM | FVec | double | 1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell | 1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist) |
测试方法
在研究完ALGLIB库的优化方法后,自然会提出一个问题:对于特定任务,应该选择这些方法中的哪一种?根据所选方法的不同,不同类型的优化问题解决的效率也有所不同。为了回答这个重要的问题,我们将使用已被证明与现实世界问题最为接近的复杂测试函数。这些函数代表了典型情况:平滑函数由Hilly测试函数表示,具有尖锐顶点(在整个定义域上并非处处可微)的平滑函数由Forest表示,而纯粹离散的函数则由Megacity表示。
测试将对每个测试函数进行50次重新运行,并将目标函数的调用次数限制为10,000次。我们将以BC方法为例,准备一个用于测试的基准脚本。这种方法将使我们能够获得更准确、更具代表性的结果,从而帮助我们为每个特定任务选择最合适的优化方法。
让我们实现FuncTests函数,该函数将使用相应的ALGLIB方法执行优化测试运行。该函数将使我们能够收集有关方法性能的数据,可视化它们的工作过程,并绘制收敛图。
让我们简要列出FuncTests函数的功能:
- 接受一个测试目标函数、测试次数、可视化颜色以及用于存储总体结果的变量。
- 如果启用了视频功能,它会绘制函数图像。
- 设置测试边界,并初始化用于存储结果的变量。
- 生成随机输入数据,并使用CAlglib库执行优化。
- 跟踪目标函数的调用次数和最优结果。
- 计算并显示平均结果。
- 根据当前测试更新总得分。
//—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, // Reference to the target function object const int funcCount, // Number of functions to test const color clrConv, // Visualization color double &allScore, // Total score of all tests double &allTests) // Total number of tests { if (funcCount <= 0) return; // If the number of functions = 0, exit the function allTests++; // Increase the total number of tests if (Video_P) // If visualization is enabled { ST.DrawFunctionGraph (f); // Draw the function graph ST.SendGraphToCanvas (); // Send the graph to the canvas ST.MaxMinDr (f); // Determine the maximum and minimum of the function ST.Update (); // Update the visualization } //---------------------------------------------------------------------------- C_AO_Utilities Ut; // Utilities for handling numbers int xConv = 0.0; // Variable for converting along the X axis int yConv = 0.0; // Variable for converting along the Y axis double aveResult = 0.0; // Average test result int aveRunsFF = 0; // Average number of function runs int params = funcCount * 2; // Number of parameters (2 for each function) int epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs //---------------------------------------------------------------------------- CRowDouble bndl; bndl.Resize (params); // Array for lower bounds CRowDouble bndu; bndu.Resize (params); // Array for upper bounds for (int i = 0; i < funcCount; i++) // Fill the boundaries for each function { bndu.Set (i * 2, f.GetMaxRangeX ()); // Set the upper boundary by X bndl.Set (i * 2, f.GetMinRangeX ()); // Set the lower boundary by X bndu.Set (i * 2 + 1, f.GetMaxRangeY ()); // Set the upper bound by Y bndl.Set (i * 2 + 1, f.GetMinRangeY ()); // Set the lower boundary by Y } CRowDouble x; x.Resize (params); // Array for parameter values CRowDouble s; s.Resize (params); // Array for scaling s.Fill (1); // Fill the array with ones for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests { for (int i = 0; i < funcCount; i++) // For each function { x.Set (i * 2, Ut.RNDfromCI (bndl [i * 2], bndu [i * 2])); // Generate random values by X x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y } //-------------------------------------------------------------------------- CObject obj; // Object for storing results C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function CNDimensional_Rep frep; // Representation of multidimensional space CMinBCState state; // State of the minimization method CMinBCReport rep; // Minimization report double epsg = 1e-16; // Parameter for gradient stop condition double epsf = 1e-16; // Parameter for the stop condition by function value CAlglib::MinBCCreateF (x, DiffStep_P, state); // Create minimization state CAlglib::MinBCSetBC (state, bndl, bndu); // Set the boundaries CAlglib::MinBCSetScale (state, s); // Set scaling CAlglib::MinBCSetCond (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P); // Set conditions CAlglib::MinBCOptimize (state, fFunc, frep, obj); // Optimization CAlglib::MinBCResults (state, x, rep); // Get results //-------------------------------------------------------------------------- aveRunsFF += fFunc.numberLaunches; // Sum up the number of function runs aveResult += -fFunc.bestMIN; // Sum up the best minimum found } aveRunsFF /= NumberRepetTest_P; // Calculate the average number of runs aveResult /= NumberRepetTest_P; // Calculate the average result double score = aveResult; // Estimate based on average result Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results allScore += score; // Update the overall score } //——————————————————————————————————————————————————————————————————————————————
让我们依次对ALGLIB库中所有考虑的优化方法运行测试基准。以下是各方法的测试结果打印输出,应按以下方式解读:
BLEIC|带等式和不等式约束的边界约束有限内存优化器|0.8| — 方法缩写、全称、微分步长(可选,其他方法参数)。
5 Hilly's — 多元问题中对应的测试目标函数的数量。
函数运行:2178(10000) — 目标函数的运行次数 — 即尝试调用目标函数方法的次数,以及指定的运行次数“上限”。
结果:0.38483704535107116 — 50 次测试运行的平均结果。
以下是BLEIC方法在测试目标函数上性能的打印输出:
BLEIC|带等式和不等式约束的边界约束有限内存优化器|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
总分:2.05290 (22.81%)
以下是L-BFGS方法在测试目标函数上性能的打印输出:
L-BFGS|用于大规模优化的有限内存BFGS方法|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); result: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); result: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); result: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); result: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); result: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); result: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); result: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); result: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); result: 0.09022461538461606
=============================
总分:1.84784 (20.53%)
以下是NS方法在测试目标函数上性能的打印输出:
NS|非光滑非凸优化|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
总分:2.09251 (23.25%)
以下是BC方法在测试目标函数上性能的打印输出:
BC|具有快速激活多个边界约束功能的盒式约束优化|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
总分:2.03457 (22.61%)
以下是NLC方法在测试目标函数上性能的打印输出:
NLC|采用预处理增广拉格朗日算法的非线性约束优化|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
总分: 2.04604 (22.73%)
以下是LM方法在测试目标函数上性能的打印输出:
LM|改进的Levenberg-Marquardt算法|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); result: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
总分:1.54204 (17.13%)
现在,我们可以清晰地分析算法在测试函数上的表现。大多数方法的特点是在目标函数运行次数达到我们设定的限制(在参数中我们指定了10,000次迭代限制)之前就提前终止了工作。例如,在具有1,000个参数的离散Megacity问题上,Levenberg-Marquardt(LM)方法平均在 2,081 次迭代时停止,而在具有10个参数的问题上,它仅在21次迭代时就停止了。与此同时,在平滑的Hilly函数上,该方法尝试在明显更多的迭代次数中寻找最小值。相比之下,其他方法对目标函数的调用次数超过了100万次。
以下是得分最高(NS方法)和得分最低(LM方法)的两种方法性能的可视化结果。
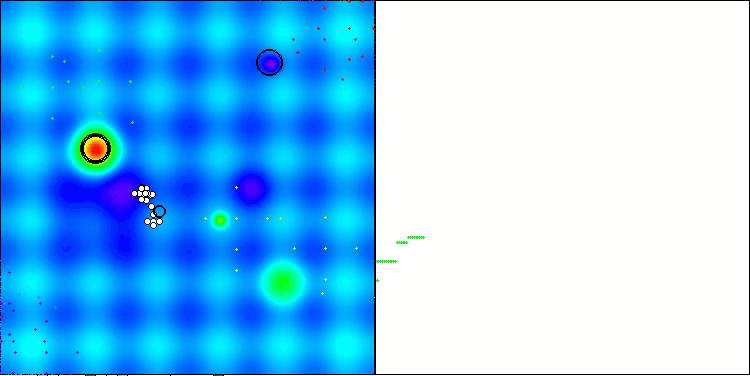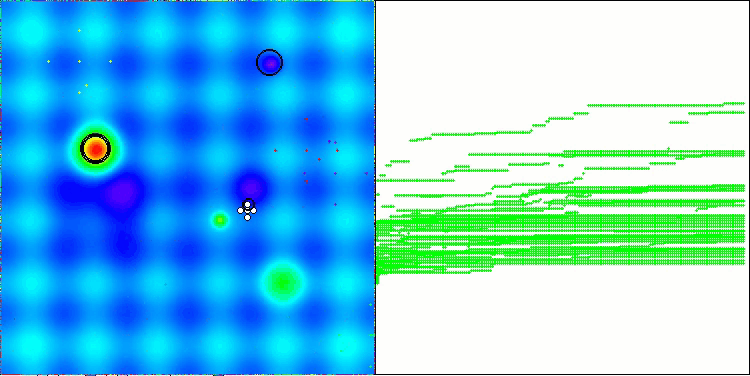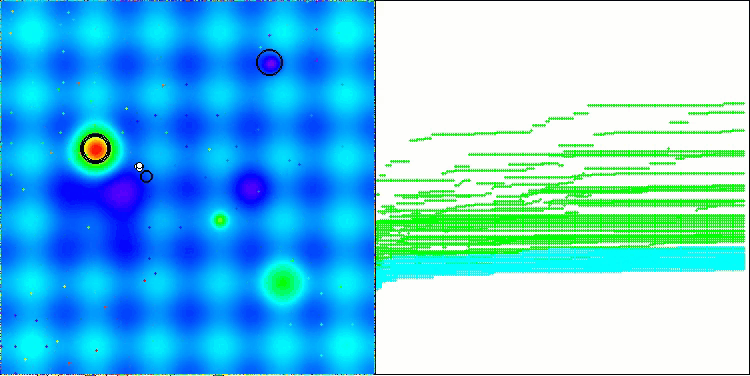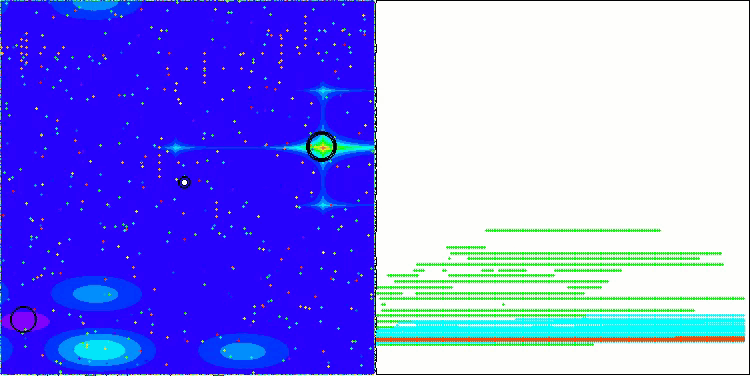
NS在Hilly测试函数上
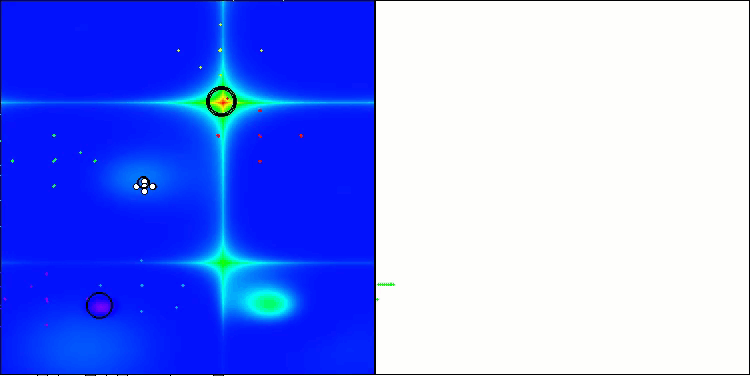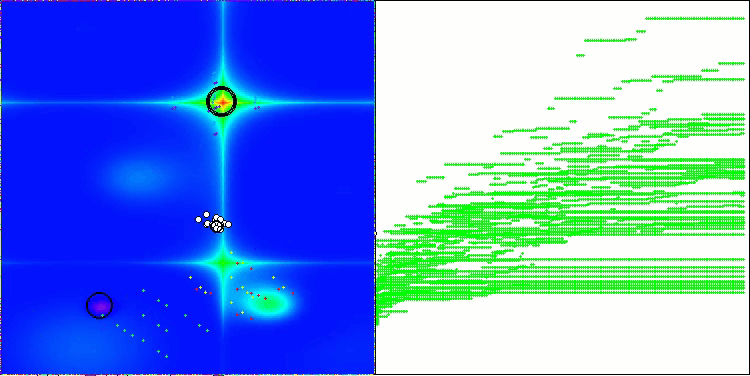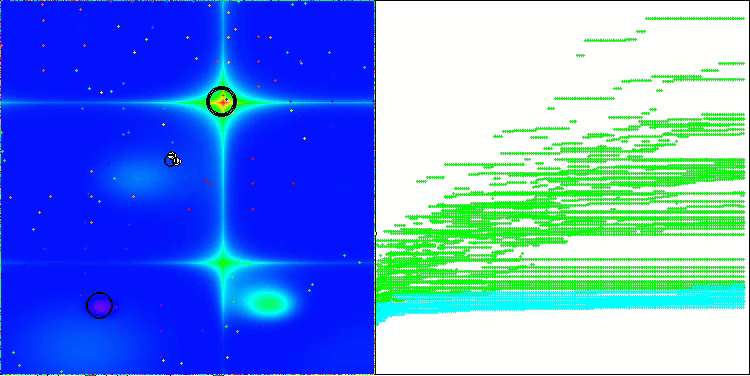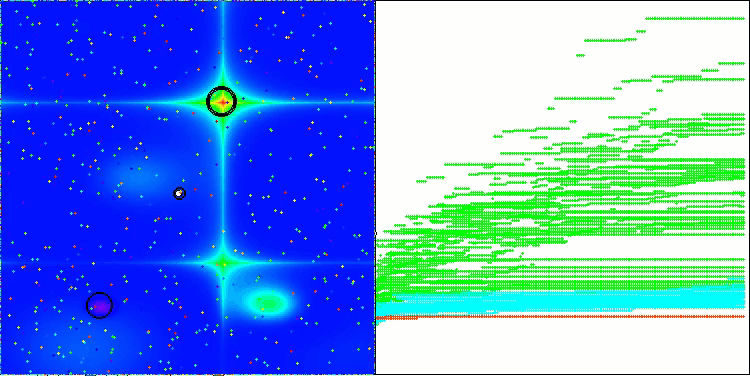
NS在Forest测试函数上
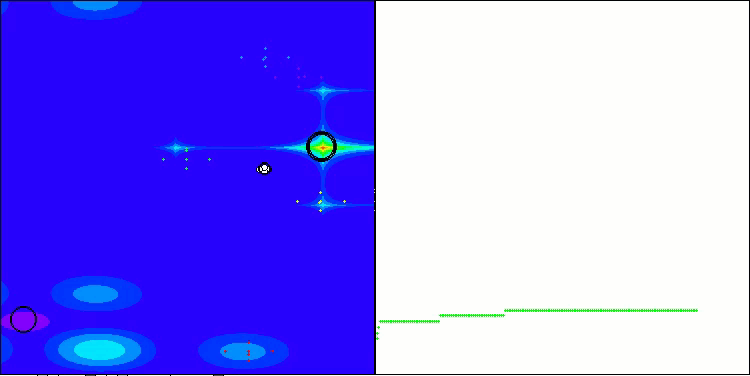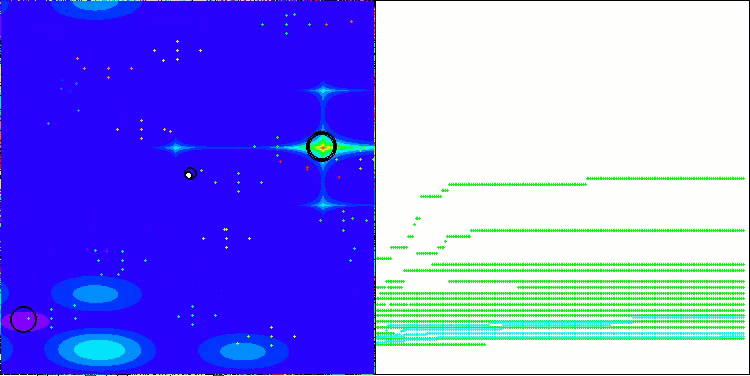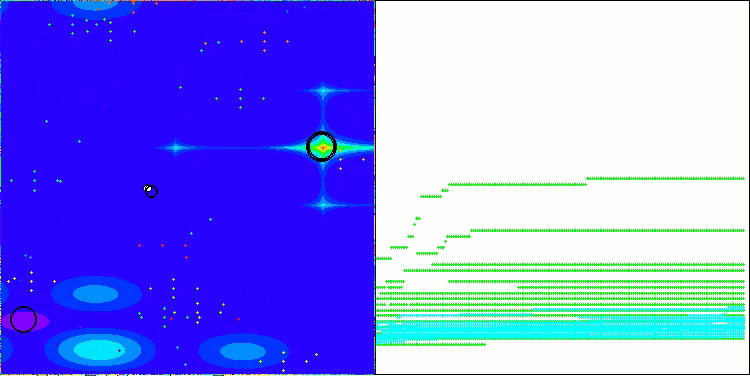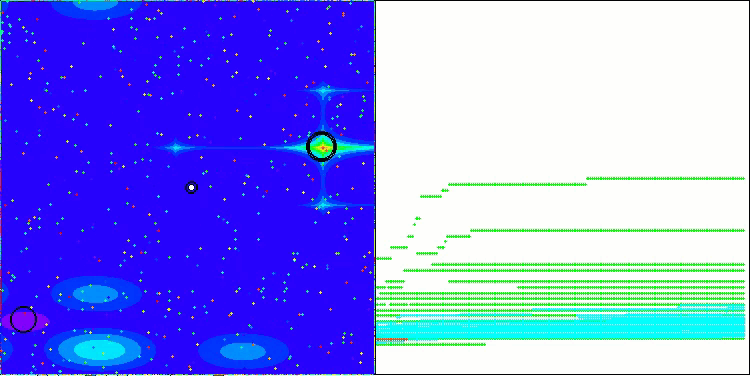
NS在Megacity测试函数上
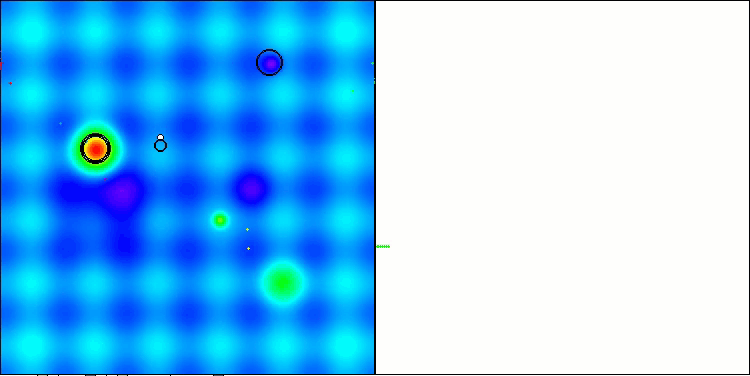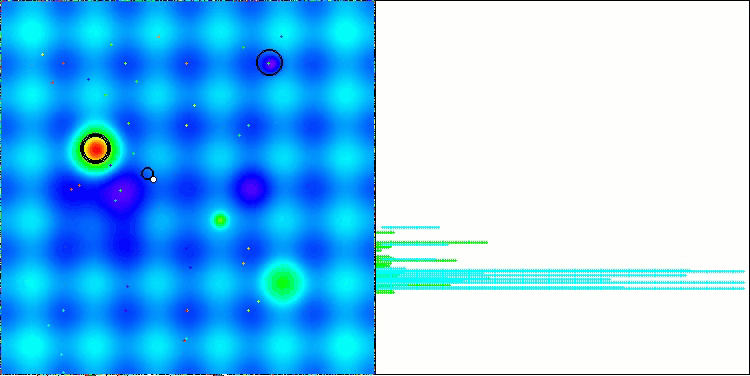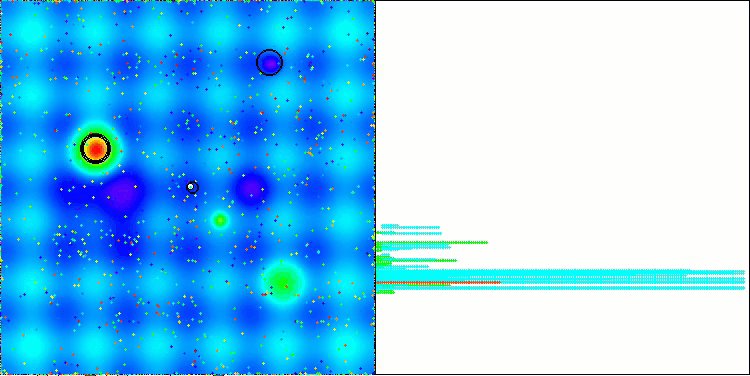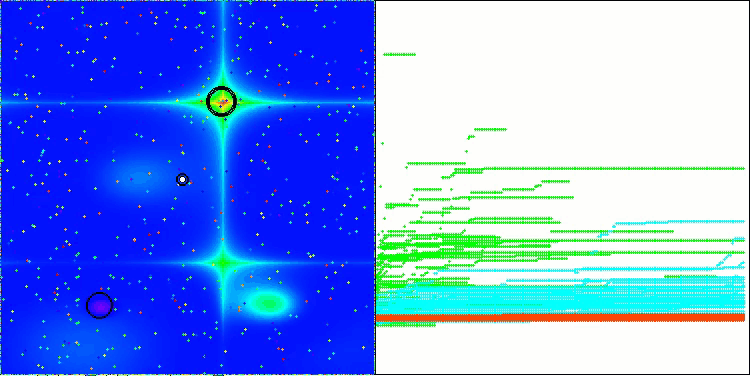
LM在Hilly测试函数上
LM在Forest测试函数上
LM在Megacity测试函数上
让我们将获得的结果汇总成一个表格。

算法在相应测试中的颜色渐变表示
总结
在两篇文章中,我们探讨了ALGLIB库中的优化方法,研究了如何将它们集成到用户程序中,以及与方法函数交互的特点。此外,我们还进行了测试,以识别算法的优缺点。我们的简要总结如下:
- 在低维度的平滑函数(Hilly)上,NLC方法表现出了最优结果,而在高维度上,LM方法则领先。
- 在具有尖锐极值(Forest)的低维度平滑函数上,NS方法展现出最优结果,而在高维度上,BC方法表现最优。
- 在小维度的离散Megacity问题上,NS方法领先,而在大维度上,BLEIC方法则位居第一。
各方法的结果差异并不显著,偏差都在其自身结果范围内,然而,NS方法可以被称为更通用的方法,尽管无法强制停止它。
随文章附带的代码包含了在项目中开始使用优化方法所需的条件,以及直观地查看和评估它们功能的内容。
文中所用的程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Simple test ALGLIB BLEIC.mq5 | 脚本 | 用于测试BLEIC算法的脚本 |
| 2 | Simple test ALGLIB LBFGS.mq5 | 脚本 | 用于测试L-BFGS算法的脚本 |
| 3 | Simple test ALGLIB NS.mq5 | 脚本 | 用于测试NS(非光滑非凸优化)算法工作的脚本 |
| 4 | Simple test ALGLIB BC.mq5 | 脚本 | Test script for working with BC |
| 5 | Simple test ALGLIB NLC.mq5 | 脚本 | 用于测试NLC算法的脚本 |
| 6 | Simple test ALGLIB LM.mq5 | 脚本 | 用于测试NLC算法的脚本 |
| 7 | Test_minBLEIC.mq5 | 脚本 | BLEIC测试台 |
| 8 | Test_minLBFGS.mq5 | 脚本 | L-BFGS测试台 |
| 9 | Test_minNS.mq5 | 脚本 | NS测试台 |
| 10 | Test_minBC.mq5 | 脚本 | BC测试台 |
| 11 | Test_minNLC.mq5 | 脚本 | NLC测试台 |
| 12 | Test_minLM.mq5 | 脚本 | LM测试台 |
| 13 | CalculationTestResults.mq5 | 脚本 | 用于计算比较表结果的脚本 |
| 14 | TestFunctions.mqh | 包含 | 测试函数库 |
| 15 | TestStandFunctions.mqh | 包含 | 测试台函数库 |
| 16 | Utilities.mqh | 包含 | 辅助函数库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/16164
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 交易中的神经网络:超点变换器(SPFormer)
交易中的神经网络:超点变换器(SPFormer)
 从基础到中级:按值传递还是按引用传递
从基础到中级:按值传递还是按引用传递
 开发回放系统(第 65 部分):玩转服务(六)
开发回放系统(第 65 部分):玩转服务(六)

1.
1.你可以质疑任何事情,但从完整的源代码和正确的可重复测试的角度出发,总是更有建设性。
2.如果你让 90 亿人随机地把手指伸进一张白纸上,函数的表面就隐藏在白纸后面,那么你就可以在二维巨城上得到一个最优结果(其中一个人最后肯定会非常接近全局,并会说他是成功解决了这个问题的人)。但是,我们需要找到最优解,而不是在 90 亿次尝试中随意捅一捅,而是在 10000 次尝试中使用一种策略。
在一系列独立测试中,平均结果越高(结果的稳定性、可重复性),在特定类型的问题上,所测试的方法与随机捅解相比就越高(在某些问题上,某些方法与随机捅解没有太大区别,而在另一些问题上,它们却非常有效)。
这就是测试和比较不同算法的意义所在。对于不同的算法,不是只用一个测试函数,而是用三个不同性质的测试函数作为基准,这样就能清楚地看到不同算法在不同任务中的适用性,以及它们在不同任务中的局限性和能力。这样就能以一种有意义的方式来解决优化问题。
今后,我更愿意回答有关文章内容和代码的具体问题。
我们采用局部优化方法,将其应用于全局问题,并与全局优化方法进行比较。这就是我要说的。
我说的是如何将这些方法用于全局优化。最简单的方法就是增加初始化的次数。
如果我没理解错的话,亚当等人是为了提高速度而不是质量。
如果以时间而不是迭代次数为限制,看看评分结果会很有趣。
如果我没理解错的话,亚当等人追求的是速度,而不是质量。
如果以时间而不是迭代次数为限制,看看评分结果会很有趣。
ADAM 系列算法(AdamW、RAdam、AdaBelief 等)以及 SGD、SGRAD 和其他算法(有很多)是作为经典梯度法的现代替代方法而开发的,旨在解决大维度问题,无需了解分析公式,通常用于训练神经网络(它们各有优缺点)。谷歌(2023 年)也推出了一些有趣的雄狮方法,还有其他一些最新方法。这个话题非常值得研究,尤其是在训练神经网络的背景下,在一些简单的例子(也可能是复杂的例子)上建立一个目标曲面并进行实验(解析其内部结构、深入研究各种方法的特性、仔细评估它们的能力--一切随心所欲)将会非常有用,而且信息量很大。
有了时间限制,就没有什么可约束的了。在这种情况下,我们如何比较算法呢?这就是为什么我们使用命中次数限制,并在此限制内比较效率的原因。
有了时间限制,就没有什么可绑定的了。在这种情况下,我们如何比较他们之间的算法?这就是为什么我们使用命中次数限制,并在此限制内比较效率的原因。
绑定作者的 PC。以 ANS 的 10000 次迭代时间为基础。
我在 fxsaber代码 上的结果:
PS 代码大小作为附加指标(算法实现的复杂程度)