在Python中使用Numba对交易策略进行快速测试

MetaTrader 5 — 测试者 | 11 八月 2025, 08:54

为何一个快速的定制化策略回测器至关重要

在开发基于机器学习的交易算法时，能够正确且快速地评估其在历史数据上的交易结果，这一点非常重要。如果我们只是在少数情况下使用回测器，例如在大型时间周期上或历史数据深度较小的情况下，那么 Python 回测器是完全适用的。然而，如果任务涉及多次测试和高频策略，那么像 Python 这样的解释型语言可能就太慢了。

假设我们对某些脚本的执行速度不满意，但又不想放弃我们熟悉的 Python 开发环境。这时，Numba 就派上了用场，它能将原生 Python 代码即时转换并编译成快速的机器码。这种代码的执行速度，其速度便可以与 C 语言和 FORTRAN 等编程语言的代码执行速度相媲美。

Numba 库简介

Numba是一个为 Python 编程语言设计的库，它通过使用 JIT（即时）编译将函数在字节码级别编译成机器码，旨在加速代码执行。这项技术可以显著提升计算性能，尤其是在那些频繁使用循环和复杂数学运算的科学计算应用中。该库支持 NumPy 数组的操作，并且还允许高效地进行并行计算和 GPU 计算。

使用 Numba 最常见的方式是将其一系列的装饰器应用于 Python 函数，以此告知 Numba 需要编译这些函数。当一个被 Numba 装饰的函数被调用时，它会被即时编译成机器码，从而使得全部或部分代码能够以原生机器码的速度运行。

目前支持以下架构：

操作系统：Windows (64 位)、OSX、Linux (64 位)。
架构：x86, x86_64, ppc64le, armv8l (aarch64), M1/Arm64。
GPU：Nvidia CUDA。
CPython
NumPy 1.22 - 1.26

值得注意的是，Numba 库不支持 Pandas 包，因此对 DataFrame 的操作将以常规速度（即未加速的速度）执行。

处理文章中的代码

为了让所有代码能立即正常运行，请采取以下预备步骤：

安装所有需要的库；

pip install numpy
pyp install pandas
pip install catboost
pip install scikit-learn
pip install scipy

下载 EURGBP_H1.csv 数据文件并将其放置在 Files 文件夹中；
下载所有 Python 脚本并将它们放在同一个文件夹中；
编辑 Tester_ML.py 的第一行代码，使其如下所示：from tester_lib import test_model；
在 Tester_ML.py 脚本中指定文件路径；
p = pd.read_csv('C:/Program Files/MetaTrader 5/MQL5/Files/'EURGBP_H1'.csv', sep='\s+').

如何使用 Numba 包？

总的来说，使用 Numba 包可以归结为安装它

pip install numba
conda install numba

并在我们想要加速的函数前应用装饰器，例如：

@jit(nopython=True)
def process_data(*args):
        ...

该装饰器有两种不同的调用方式。

nopython 模式
object 模式

第一种方式是编译被装饰的函数，使其运行时完全不涉及 Python 解释器。这是最快的方法，推荐使用。然而，Numba 有其局限性，例如它只能编译 Python 的内置操作和 Numpy 数组操作。如果一个函数包含了来自其他库（如 Pandas）的对象，Numba 将无法编译它，代码将由解释器执行。

Numba 可以使用 object 模式来规避对第三方库使用的限制。在此模式下，Numba 会将函数中的一切都视为 Python 对象来进行编译，实际上代码还是在解释器中运行。

@jit(forceobj=true, looplift=True)

与纯 object 模式相比，这可能会提高性能，因为 Numba 会尝试将循环编译成以机器码执行的函数，而其余代码则在解释器中运行。为了获得最佳性能，请完全避免使用 object 模式！

在可能的情况下，该包也支持并行计算（Parallel=True）。请注意，函数在第一次被调用时，会被编译成机器码，这需要一些时间。此后，该代码会被缓存，后续的调用就会更快。

加速交易标记函数的示例

在开始加速回测器之前，我们先尝试加速一些更简单的东西。一个绝佳的候选者就是交易标记函数。该函数接收一个包含价格的数据结构，并将交易标记为买入和卖出（0 和 1）。这类函数通常用于数据的预标记，以便后续训练分类器。

def get_labels(dataset, min = 1, max = 15) -> pd.DataFrame:
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'].iloc[i]
        future_pr = dataset['close'].iloc[i + rand]

        if (future_pr + hyper_params['markup']) < curr_pr:
            labels.append(1.0)
        elif (future_pr - hyper_params['markup']) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    return dataset

我们使用15年的欧元/英镑（EURGBP）分钟收盘价作为数据：

>>> pr = get_prices()
>>> pr
                       close
time                        
2010-01-04 00:00:00  0.88810
2010-01-04 00:01:00  0.88799
2010-01-04 00:02:00  0.88786
2010-01-04 00:03:00  0.88792
2010-01-04 00:04:00  0.88802
...                      ...
2024-10-09 19:03:00  0.83723
2024-10-09 19:04:00  0.83720
2024-10-09 19:05:00  0.83704
2024-10-09 19:06:00  0.83702
2024-10-09 19:07:00  0.83703

[5480021 rows x 1 columns]

该数据集包含超过五百万个观测值，这对于测试来说是相当充足的。

现在，让我们来测量一下该函数在我们的数据上的执行速度：

# get labels test
start_time = time.time()
pr = get_labels(pr)
pr['meta_labels'] = 1.0
end_time = time.time()
execution_time = end_time - start_time
print(f"Execution time: {execution_time:.4f} seconds")

执行时间为 74.1843 秒。

现在，让我们尝试使用 Numba 包来加速这个函数。我们可以看到，原始函数也使用了 Pandas 包，而我们知道这两个包是不兼容的。让我们将所有与 Pandas 相关的部分移到一个单独的函数中，并加速其余的代码。

@jit(nopython=True)
def get_labels_numba(close_prices, min_val, max_val, markup):
    labels = np.empty(len(close_prices) - max_val, dtype=np.float64)
    for i in range(len(close_prices) - max_val):
        rand = np.random.randint(min_val, max_val + 1)
        curr_pr = close_prices[i]
        future_pr = close_prices[i + rand]

        if (future_pr + markup) < curr_pr:
            labels[i] = 1.0
        elif (future_pr - markup) > curr_pr:
            labels[i] = 0.0
        else:
            labels[i] = 2.0

    return labels

def get_labels_fast(dataset, min_val=1, max_val=15):
    close_prices = dataset['close'].values
    markup = hyper_params['markup']

    labels = get_labels_numba(close_prices, min_val, max_val, markup)

    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)

    return dataset

第一个函数的前面有一个 @jit 装饰器的调用。这意味着这个函数将被编译成机器码。我们还在其内部摒弃了 Pandas，只使用列表、循环和 Numpy。

第二个函数则负责准备工作。它将 Pandas 数据结构转换为 Numpy 数组，然后将其传递给第一个函数。之后，它接收结果并再次返回一个 Pandas 数据结构。通过这种方式，标记的主要计算部分得到了加速。

现在，让我们来测量一下速度。计算时间已减少到 12 秒！对于这个函数，我们获得了超过 5 倍的加速。当然，这并非一个完全纯粹的测试，因为中间计算仍然使用了 Pandas 库，但在标签计算方面，我们确实实现了显著的加速。

针对机器学习任务，对策略测试器进行加速

我将策略回测器移到了一个独立的库中，可以在下方的附件中找到。它包含了用于比较的 tester 和 slow_tester 函数。

读者可能会反驳说，Python 中大部分的性能提升都来自于向量化。这话没错，但有时我们仍然不得不使用循环。例如，回测器中有一个相当复杂的循环，用于遍历整个历史数据，并在考虑止损和止盈的情况下累计总利润。要通过向量化来实现这一点，似乎并非易事。

下面展示了回测器循环的主体（即执行时间最长的部分），以供参考。

for i in range(dataset.shape[0]):
        line_f = len(report) if i <= forw else line_f
        line_b = len(report) if i <= backw else line_b
        
        pred = labels[i]
        pr = close[i]
        pred_meta = metalabels[i]  # 1 = allow trades

        if last_deal == 2 and pred_meta == 1:
            last_price = pr
            last_deal = 0 if pred < 0.5 else 1
            continue
        
        if last_deal == 0:
            if (-markup + (pr - last_price) >= take) or (-markup + (last_price - pr) >= stop):
                last_deal = 2
                profit = -markup + (pr - last_price)
                report.append(report[-1] + profit)
                chart.append(chart[-1] + profit)
                continue

        if last_deal == 1:
            if (-markup + (pr - last_price) >= stop) or (-markup + (last_price - pr) >= take):
                last_deal = 2
                profit = -markup + (last_price - pr)
                report.append(report[-1] + profit)
                chart.append(chart[-1] + (pr - last_price))
                continue
        
        # close deals by signals
        if last_deal == 0 and pred > 0.5 and pred_meta == 1:
            last_deal = 2
            profit = -markup + (pr - last_price)
            report.append(report[-1] + profit)
            chart.append(chart[-1] + profit)
            continue

        if last_deal == 1 and pred < 0.5 and pred_meta == 1:
            last_deal = 2
            profit = -markup + (last_price - pr)
            report.append(report[-1] + profit)
            chart.append(chart[-1] + (pr - last_price))
            continue

让我们用之前获取的数据来测试一下速度。首先，我们来看一下慢速回测器的速度：

# native python tester test
start_time = time.time()
tester_slow(pr, 
       hyper_params['stop_loss'], 
       hyper_params['take_profit'], 
       hyper_params['markup'],
       hyper_params['forward'],
       False)
end_time = time.time()
execution_time = end_time - start_time
print(f"Execution time: {execution_time:.4f} seconds")

执行时间为6.8639秒。

这看起来并不算很慢，甚至可以说，解释器执行代码的速度是相当快的。

让我们再次将这个回测器函数拆分成两个函数。一个将是辅助函数，另一个将执行主要的计算。

process_data 函数实现了回测器的主循环，这个循环需要被加速，因为 Python 中的循环是很慢的。与此同时，tester 函数本身首先为 process_data 函数准备数据，然后接收其结果并绘制图表。

@jit(nopython=True)
def process_data(close, labels, metalabels, stop, take, markup, forward, backward):
    last_deal = 2
    last_price = 0.0
    report = [0.0]
    chart = [0.0]
    line_f = 0
    line_b = 0

    for i in range(len(close)):
        line_f = len(report) if i <= forward else line_f
        line_b = len(report) if i <= backward else line_b
        
        pred = labels[i]
        pr = close[i]
        pred_meta = metalabels[i]  # 1 = allow trades

        if last_deal == 2 and pred_meta == 1:
            last_price = pr
            last_deal = 0 if pred < 0.5 else 1
            continue
        
        if last_deal == 0:
            if (-markup + (pr - last_price) >= take) or (-markup + (last_price - pr) >= stop):
                last_deal = 2
                profit = -markup + (pr - last_price)
                report.append(report[-1] + profit)
                chart.append(chart[-1] + profit)
                continue

        if last_deal == 1:
            if (-markup + (pr - last_price) >= stop) or (-markup + (last_price - pr) >= take):
                last_deal = 2
                profit = -markup + (last_price - pr)
                report.append(report[-1] + profit)
                chart.append(chart[-1] + (pr - last_price))
                continue
        
        # close deals by signals
        if last_deal == 0 and pred > 0.5 and pred_meta == 1:
            last_deal = 2
            profit = -markup + (pr - last_price)
            report.append(report[-1] + profit)
            chart.append(chart[-1] + profit)
            continue

        if last_deal == 1 and pred < 0.5 and pred_meta == 1:
            last_deal = 2
            profit = -markup + (last_price - pr)
            report.append(report[-1] + profit)
            chart.append(chart[-1] + (pr - last_price))
            continue

    return np.array(report), np.array(chart), line_f, line_b

def tester(*args):
    '''
    This is a fast strategy tester based on numba
    List of parameters:

    dataset: must contain first column as 'close' and last columns with "labels" and "meta_labels"

    stop: stop loss value

    take: take profit value

    forward: forward time interval

    backward: backward time interval

    markup: markup value

    plot: false/true
    '''
    dataset, stop, take, forward, backward, markup, plot = args

    forw = dataset.index.get_indexer([forward], method='nearest')[0]
    backw = dataset.index.get_indexer([backward], method='nearest')[0]

    close = dataset['close'].to_numpy()
    labels = dataset['labels'].to_numpy()
    metalabels = dataset['meta_labels'].to_numpy()
    
    report, chart, line_f, line_b = process_data(close, labels, metalabels, stop, take, markup, forw, backw)

    y = report.reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = 1 if lr.coef_[0][0] >= 0 else -1

    if plot:
        plt.plot(report)
        plt.plot(chart)
        plt.axvline(x=line_f, color='purple', ls=':', lw=1, label='OOS')
        plt.axvline(x=line_b, color='red', ls=':', lw=1, label='OOS2')
        plt.plot(lr.predict(X))
        plt.title("Strategy performance R^2 " + str(format(lr.score(X, y) * l, ".2f")))
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

现在，让我们来测试这个经过 Numba 加速的策略回测器：

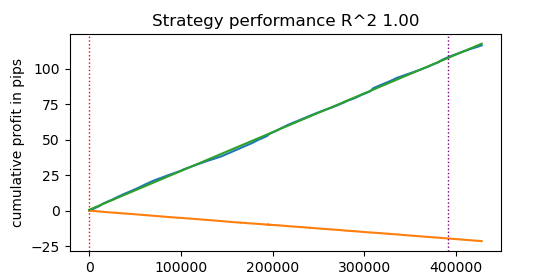
start_time = time.time()
tester(pr, 
       hyper_params['stop_loss'], 
       hyper_params['take_profit'], 
       hyper_params['forward'],
       hyper_params['backward'],
       hyper_params['markup'],
       False)
end_time = time.time()
execution_time = end_time - start_time
print(f"Execution time: {execution_time:.4f} seconds")

执行时间为0.1470秒。

速度提升接近50倍！执行超过400000笔交易。

试想一下，如果你每天花费1小时来测试你的算法，那么使用这个快速回测器，你将只需要1分钟。

在tick数据上进行测试

让我们来增加任务难度，从交易终端下载过去3年的Tick历史数据到一个 .csv 文件中。

为了正确读取文件，我们需要对报价加载函数稍作修改。我们将使用 Bid（买价）价格，而不是 Close（收盘价）。我们还需要移除那些具有相同索引（重复时间戳）的价格数据。

def get_prices() -> pd.DataFrame:
    p = pd.read_csv('files/'+hyper_params['symbol']+'.csv', sep='\s+')
    pFixed = pd.DataFrame(columns=['time', 'close'])
    pFixed['time'] = p['<DATE>'] + ' ' + p['<TIME>']
    pFixed['time'] = pd.to_datetime(pFixed['time'], format='mixed')
    pFixed['close'] = p['<BID>']
    pFixed.set_index('time', inplace=True)
    pFixed.index = pd.to_datetime(pFixed.index, unit='s')
    # Remove duplicate string by 'time' index
    pFixed = pFixed[~pFixed.index.duplicated(keep='first')]
    return pFixed.dropna()

结果是，我们得到了将近6200万条（tick）记录。回测器通过名为 “close” 的列来接收价格，因此我们需要将 “Bid” 重命名为 “Close”。

>>> pr
                           close
time                            
2022-01-03 00:05:01.753  0.84000
2022-01-03 00:05:04.032  0.83892
2022-01-03 00:05:05.849  0.83918
2022-01-03 00:05:07.280  0.83977
2022-01-03 00:05:07.984  0.83939
...                          ...
2024-11-08 23:58:53.491  0.82982
2024-11-08 23:58:53.734  0.82983
2024-11-08 23:58:55.474  0.82982
2024-11-08 23:58:57.040  0.82984
2024-11-08 23:58:57.337  0.82982

[61896607 rows x 1 columns]

让我们快速进行一次数据标记，并测量其执行时间。

# get labels test
start_time = time.time()
pr = get_labels_fast(pr)
pr['meta_labels'] = 1.0
end_time = time.time()
execution_time = end_time - start_time
print(f"Execution time: {execution_time:.4f} seconds")

标记过程耗时9.5秒。

现在让我们运行快速测试器。

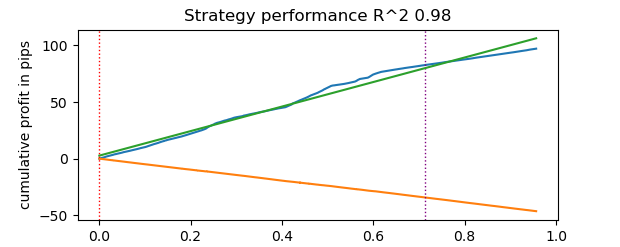
# numba tester test
start_time = time.time()
tester(pr, 
       hyper_params['stop_loss'], 
       hyper_params['take_profit'], 
       hyper_params['forward'],
       hyper_params['backward'],
       hyper_params['markup'],
       True)
end_time = time.time()
execution_time = end_time - start_time
print(f"Execution time: {execution_time:.4f} seconds")

测试耗时0.16秒。而慢速回测器完成同样的任务花费了5.5秒。

基于 Numba 的快速回测器完成任务的速度比纯 Python 回测器快了35倍。事实上，从观察者的角度来看，使用快速回测器时，测试是瞬间完成的；而使用慢速回测器则需要一些等待时间。尽管如此，我们还是要肯定慢速回测器的表现，它同样做得很好，并且即便在 Tick 数据上进行策略测试也相当适用。

总共有 1e6，即一百万笔交易。

关于将快速回测器用于机器学习任务的信息

如果你确实打算使用这个建议的回测器，那么以下信息可能会对你有用。

让我们为数据集添加特征，以便训练分类器。

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0
    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC-pFixedC.rolling(i).mean()
        count += 1
    return pFixed.dropna()

这些是基于价格与移动平均线之间差异的简单指标。

接下来，我们创建一个模型超参数的字典，它将用于训练和测试。我们将在生成新数据集时应用这些参数。

hyper_params = {
    'symbol': 'EURGBP_H1',
    'markup': 0.00010,
    'stop_loss': 0.01000,
    'take_profit': 0.01000,
    'backward': datetime(2010, 1, 1),
    'forward': datetime(2023, 1, 1),
    'periods': [i for i in range(50, 300, 50)],
}

# catboost learning
dataset = get_labels_fast(get_features(get_prices()))
dataset['meta_labels'] = 1.0
data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()

这里值得注意的一点是，回测器不仅接受 “labels”（标签）值，也接受 “meta_labels”（元标签）值。如果我们想为基于机器学习的交易系统使用过滤器，就可能需要它们。届时，值为1将允许交易，值为0将禁止交易。由于在这个演示示例中我们不会使用过滤器，我们将只创建一个额外的列，并用1填充它，以允许在任何时候进行交易。

dataset['meta_labels'] = 1.0

现在，我们可以在生成的数据集上训练 CatBoost 模型了，在此之前，我们已经从历史数据中移除了前向和后向测试数据，以确保模型不会在这些数据上进行训练。

data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()

X = data[data.columns[1:-2]]
y = data['labels']

train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True)

model = CatBoostClassifier(iterations=500,
                               thread_count=8,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=True,
                               use_best_model=True,
                               task_type='CPU')

model.fit(train_X, train_y, eval_set=(test_X, test_y),
            early_stopping_rounds=25, plot=False)

训练完成后，在整个数据集（包括测试数据）上测试该模型。test_model 函数与快速和慢速回测器本身的函数一同位于 tester_lib.py 文件中。它是一个快速回测器的包装器，其任务是获取已训练的机器学习模型的预测值（在我们的例子中是 CatBoost，但也可能是任何其他模型）。

def test_model(dataset: pd.DataFrame, 
               result: list, 
               stop: float, 
               take: float, 
               forward: float, 
               backward: float, 
               markup: float, 
               plt = False):
    
    ext_dataset = dataset.copy()
    X = ext_dataset[dataset.columns[1:-2]]

    ext_dataset['labels'] = result[0].predict_proba(X)[:,1]
    # ext_dataset['meta_labels'] = result[1].predict_proba(X)[:,1]
    ext_dataset['labels'] = ext_dataset['labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)
    # ext_dataset['meta_labels'] = ext_dataset['meta_labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)
    return tester(ext_dataset, stop, take, forward, backward, markup, plt)

上面的代码中有被注释掉的字符串，它们允许您获取负责指示是否交易的元标签。换句话说，第二个机器学习模型可以用于此目的。我们在本文中不使用它。

让我们直接开始测试。

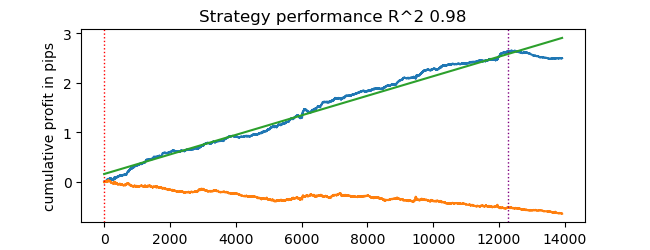
# test catboost model
test_model(dataset, 
           [model], 
           hyper_params['stop_loss'],
           hyper_params['take_profit'],
           hyper_params['forward'],
           hyper_params['backward'],
           hyper_params['markup'],
           True)

然后我们得到了结果。该模型已经过拟合，这可以从垂直线右侧的测试数据中看出。但这对我们来说并不重要，因为我们正在测试的是回测器本身。

由于该回测器本身就支持使用止损和止盈，而您可能希望对它们进行优化，那么我们就来使用优化功能吧，因为我们的回测器现在非常快！

使用机器学习优化交易系统参数

现在，让我们来看一下优化止损和止盈的可能性。事实上，也可以优化交易系统的其他参数，例如元标签，但这超出了本文的范畴，可以在下一篇文章中讨论。

我们实现了两种类型的优化：

参数网格搜索
使用 L-BFGS-B 方法进行优化

让我们首先简要地过一遍每种方法的代码。下面展示了 GRID_SEARCH 方法。

它接受以下参数：

用于测试的数据集
已训练的模型
包含上述算法超参数的字典
回测器对象

接下来，会创建将要进行迭代遍历的参数值范围，并在一个循环中对它们进行遍历。在每次迭代中，都会调用回测器，并选择那些对应于最大 R² 值的参数。

# stop loss / take profit grid search
def optimize_params_GRID_SEARCH(pr, model, hyper_params, test_model_func):
    best_r2 = -np.inf
    best_stop_loss = None
    best_take_profit = None

    # Ranges for stop_loss and take_profit
    stop_loss_range = np.arange(0.00100, 0.02001, 0.00100)
    take_profit_range = np.arange(0.00100, 0.02001, 0.00100)

    total_iterations = len(stop_loss_range) * len(take_profit_range)
    start_time = time.time()

    for stop_loss in stop_loss_range:
        for take_profit in take_profit_range:
            # Create a copy of hyper_params
            current_hyper_params = hyper_params.copy()
            current_hyper_params['stop_loss'] = stop_loss
            current_hyper_params['take_profit'] = take_profit

            r2 = test_model_func(pr,
                                 [model],
                                 current_hyper_params['stop_loss'],
                                 current_hyper_params['take_profit'],
                                 current_hyper_params['forward'],
                                 current_hyper_params['backward'],
                                 current_hyper_params['markup'],
                                 False)

            if r2 > best_r2:
                best_r2 = r2
                best_stop_loss = stop_loss
                best_take_profit = take_profit

    end_time = time.time()
    total_time = end_time - start_time
    average_time_per_iteration = total_time / total_iterations

    print(f"Total iterations: {total_iterations}")
    print(f"Average time per iteration: {average_time_per_iteration:.6f} seconds")
    print(f"Total time: {total_time:.6f} seconds")

    return best_stop_loss, best_take_profit, best_r2

现在我们来看一下 L-BFGS_B 方法的代码。更详细的信息请点击此处查看。

函数参数保持不变。但它创建了一个适应度函数，策略回测器通过该函数被调用。代码中指定了优化参数的边界，以及 L-BFGS_B 算法的初始化次数（参数集的随机点数）。需要随机初始化是为了防止优化算法陷入局部最小值。在此之后，会调用 minimize 函数，并将优化器自身的参数传递给它。

def optimize_params_L_BFGS_B(pr, model, hyper_params, test_model_func):
    def objective(x):
        current_hyper_params = hyper_params.copy()
        current_hyper_params['stop_loss'] = x[0]
        current_hyper_params['take_profit'] = x[1]
        
        r2 = test_model_func(pr,
                            [model],
                            current_hyper_params['stop_loss'],
                            current_hyper_params['take_profit'],
                            current_hyper_params['forward'],
                            current_hyper_params['backward'],
                            current_hyper_params['markup'],
                            False)
        return -r2

    bounds = ((0.001, 0.02), (0.001, 0.02))
    
    # Let's try some random starting points
    n_attempts = 50
    best_result = None
    best_fun = float('inf')
    
    start_time = time.time()
    for _ in range(n_attempts):
        # Random starting point
        x0 = np.random.uniform(0.001, 0.02, 2)
        
        result = minimize(
            objective,
            x0,
            method='L-BFGS-B',
            bounds=bounds,
            options={'ftol': 1e-5, 'disp': False, 'maxiter': 100}  # Increase accuracy and number of iterations
        )
        
        if result.fun < best_fun:
            best_fun = result.fun
            best_result = result
    # Get the end time and calculate the total time
    end_time = time.time()
    total_time = end_time - start_time
    print(f"Total time: {total_time:.6f} seconds")

    return best_result.x[0], best_result.x[1], -best_result.fun

现在我们可以运行这两种优化算法，并查看它们的执行时间和准确性。

# using
best_stop_loss, best_take_profit, best_r2 = optimize_params_GRID_SEARCH(dataset, model, hyper_params, test_model)
best_stop_loss, best_take_profit, best_r2 = optimize_params_L_BFGS_B(dataset, model, hyper_params, test_model)

网格搜索算法：

总迭代次数：400
单次迭代平均时间：0.031341 秒
总耗时：12.536394 秒

最佳参数：stop_loss=0.004, take_profit=0.002, R^2=0.9742298702323458

L-BFGS-B 算法：

Total time: 4.733158 seconds

Best parameters: stop_loss=0.0030492548809269732, take_profit=0.0016816794762543421, R^2=0.9733045271274298

With my standard settings, L-BFGS-B performed more than 2 times faster, showing results comparable to the grid search algorithm.

Thus, one can use both of these algorithms and choose the best one depending on the number and range of parameters to be optimized.

结论

This article demonstrates the possibility of accelerating the strategy tester, which can be used to quickly test machine learning-based strategies. Numba has been shown to provide the 50x speed boost. Testing becomes fast, allowing for multiple tests and even parameter optimization.

附件：

tester_lib.py - tester library
test tester.py - script for comparing slow (Python) and fast (Numba) testers
tester ticks.py - script for comparing testers on tick data
tester ML.py - script for classifier training and hyperparameter optimization

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14895

附加的文件 |

下载ZIP

tester_lib.py (6.86 KB)

test_tester.py (3.43 KB)

tester_ticks.py (3.38 KB)

tester_ML.py (6.67 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (53)

Maxim Dmitrievsky | 15 11月 2024 在 16:49

ys_mql5 #:

那么，固定值滑动窗口中的标准差会有一个非归一化的变化范围，这取决于波动率。据我所知，通常会使用 z 分数，因为它是一个归一化值。思考到此为止 )

明白了，我在所有可用历史数据中取最小值/最大值并设置为边界，然后在优化器的每次迭代中分成随机范围。你也可以使用 zscore。我想这种归一化可能对优化器更好（去掉小数点后有大量零的小数值），但我觉得不应该这样。

bestvishes | 16 11月 2024 在 05:29

你好，格言，我认为你是论坛上最聪明的人，希望在第二篇文章中看到详细的描述。谢谢。

Maxim Dmitrievsky | 17 11月 2024 在 07:37

bestvishes #:
你好，格言，我认为你是论坛上最聪明的人，我希望能在第二篇文章中看到详细的描述。谢谢。

谢谢您的夸奖，我会努力为您写一些有趣的东西。

pulsar86 | 21 11月 2024 在 10:30

def get_prices() -> pd.DataFrame：

尝试：

# 加载逗号分隔的 CSV 文件

p = pd.read_csv(f"files/{hyper_params['symbol']}.csv")

# 检查必填列

required_columns = ['time', 'close'] # 检查必填列

for col in required_columns：

if col not in p.columns：

raise KeyError(f"文件中缺少列'{col}'。")

# 将 "时间 "列转换为日期格式

p ['time'] = pd.to_datetime(p['time'], errors='coerce')

# 设置时间索引

p. set_index('time', inplace=True)

# 只保留 "关闭 "列，删除数据不正确的行

pFixed = p[[[close]].dropna()

返回 pFixed

except Exception as e：

print(f"处理数据时出错： {e}")

return pd.DataFrame() # 如果出现错误，返回空 DataFrame

Maxim Dmitrievsky | 6 12月 2024 在 01:20

我有一些时间，几乎在一个瓶子里完成了模型训练和超参数优化。

这样就可以同时训练许多模型，然后对它们进行优化，例如，选择具有最佳优化参数的最佳模型：

models = []
for i in range(20):
    print(f'Iteration: {i}')
    models.append(learnANDoptimize())

models.sort(key=lambda x: x[0][0]['score'])


index = -1
test_model(models[index][0][0]['dataframe'],
            [models[index][-1]],
            hyper_params['stop_loss'],
            hyper_params['take_profit'],
            hyper_params['forward'],
            hyper_params['backward'],
            hyper_params['markup'],
            True)