
您应当知道的 MQL5 向导技术(第 37 部分):配以线性和 Matérn 内核的高斯过程回归
概述
我们继续这些系列,通过研究 2 个高斯过程内核,实现以不同方式由向导组装智能系统的关键部件类。线性内核和 Matérn 内核。前者非常简单,您找不到它的维基百科页面,不过后者在这里有一个参考页面。
如果我们要回顾一下我们之前讲述的高斯过程内核(GPs)的内容,它们是非参数模型,能够映射数据集之间的复杂关系(通常以矢量形式),而无需对所涉及的数据集配对进行任何功能或预先了解。这令它们非常适合处理所涉及的数据集是非线性、甚至嘈杂的状况。此外,这种灵活性令它们对于经常波动的金融时间序列很理想,因为 GPs 往往会给出细致入微的输出。它们还提供预测估测值和置信区间。GPs 有助于判定两个数据集之间的相似性,并且由于在高斯过程回归中使用了多种类型的内核,故此辨别相应的内核、或注意所选内核的缺点始终是关键,尤其是在使用内核进行预测的实例之中。
下表总结了这些系列截至目前讲述过的内核、及其一些特征:
| 内核类型 | 理想的捕捉类型 | 解释 |
|---|---|---|
| 线性内核 | 趋势 | 捕获随时间变化的线性趋势;对于展现长期价格上涨或下跌的资产十分理想。简单且计算效率高,但要假设线性关系。 |
| 径向基函数(RBF)内核 | 趋势和波动性 | 捕捉价格逐渐变化的平稳、长期趋势最佳。它提供平滑的估测值,适用于连续形态。然而,它会在急剧转变、或极端波动时卡顿。 |
| Matérn 内核 | 趋势、波动性、周期 | 可以捕捉更粗糙、不太平滑的趋势,和波动性的突然变化。参数 ν 控制平滑度,故较低的 ν 捕获粗糙的波动性,而较高的 ν 捕捉平滑趋势。 |
根据所推断的时间序列,需要据其强度选择相应的内核。金融时间序列往往可以展现出区间性或周期性行为,而我们在下面讲述的诸如 Matérn 等内核,能帮助映射这些关系。甚至,正如我们在最初文章中看到的径向基函数那样,当交易者面临横盘、或反复拉扯的行情时,不确定性的量化可能是一个巨大的福音。如 RBF 这样的内核不仅提供点估测,而且还提供置信区间,在这些状况下可能是有益的。这是因为置信区间可以帮助筛选出微弱的信号,同时还可以高亮不确定环境中的主要转折点。
均值回归数据集也可由特殊内核处理,例如 Ornstein-Uhlenbeck,我们或许会在以后的文章中讲述。另一个有趣的层面,我们将来能够加以考察的是,GPs 允许内核综合,其中多个内核,如线性内核和 RBF 内核的堆叠,可用于针对数据集之间更复杂的关系进行建模。这可能包括短期价格行为形态,和长期趋势的配对,其中模型能够在最佳点上放置持仓离场,同时还可利用证券所能拥有的任何基层长期动作。
GPs 还有其它若干优点和用途,如处理和降低噪音,以及适应政权变化、等等。作为交易者,尽然,我们希望利用这些益处,如此我们来看一个非常基本的线性内核。
线性内核
线性内核的主要用途是在高斯过程中映射数据集之间的简单线性关系。例如,考虑一对非常简单的数据集,从中国将集装箱运到美国的成本,以及运输业 ETF BOAT的价格。在正常情况下,我们预计高昂的运输成本会反映出货运公司的定价能力,如此这般他们的收益和收入也会反映这一点,这将导致其股价升值。在这种境况下,希望随着时间的推移购买货运公司、甚至只是购买 ETF 的交易者,会有兴趣使用线性内核对他的预期股票价格和当前运输成本进行建模。
它相对简单、且不复杂,这令其在所有内核中需要最少的计算资源。在其公式中它还只需一个常量参数 c。该公式分享如下:
![]()
其中:
- x 和 x′是输入向量
- x⊤x′是转置向量 x 和 x′的点积
- c 是常数
仅需这样一个参数 c,令其在大型数据集上快速、且非常高效。它的作用主要有四个方面。首先,它有助于乖离调整,其意味着,如果数据集或标绘点没有穿过原点,常数会提供偏移量,从而平移超平面,并允许内核更好地表示基层模型。如果没有该常量,内核将假定所有数据点都以原点为中心。该常量本身不可优化,但可在预设的交叉验证步骤中进行调整。
其次,常数通过控制这个边际间隙,允许在两个数据集类之间实现更可定制的分离。当该内核与支持向量机搭配使用时,以及存在较大数据集不易线性分离的状况下,这一点尤其重要。第三,该常数实现了非线性同质性,这可能存在于某些数据集之中。没有该常量,若所有输入都按一个因子缩放,则内核的输出将按相同的因子缩放。现在,虽然一些数据集展现出这些特征,但并非所有数据集都如此。这就是为什么加上这个 c 常数之后会增加一些固有的乖离,并确保模型不会自动假设线性。
最后,有种论调说它为点积提供了数值稳定性,可能结果是非常小的述值,而这将令内核矩阵倾斜。在输入向量述值非常小的事件中,没有常数的点积亦非常小,这会影响优化过程。因此,常数为更好的优化提供了一些稳定性。
如今线性内核已在外推和趋势预测中发现了应用价值,正如我们将在下面看到的那样,它能做出超越观测数据的外推趋势。故此,特别诸如资产随时间推移的线性升值率存在问题的情况下,线性内核可能会有所帮助。此外,来自点积的特征加权,令线性核模型更易于解释。当某人得到一个输入数据向量时,可解释性很实用,他需要知道这个向量中每个输入数据点的相对重要性、或显要度。为了概括这一点,想象您有一个内核,您用它预测房产价格。该内核有一个大小为 4 的数据输入向量,其中包括:房屋的面积(以平方英尺为单位)、房屋中的卧室数量、其所在地区的收入中位数、以及建造年份。我们预测价格的内核将提供以下公式:
其中
- b 是我们加到向量点积的常数,上面已经高亮其作用(称为 c)
- w 1 到 w 4 是经由训练优化的权重
- x 1 到 x 4 是我们上面提到的数据输入
训练后,您将获得 w1 到 w4 的数值,配以这种简单的线性内核设置,权重越大,特征或数据点对物业的下一个价格就越重要。如果权重 w4 最小,亦如此,在于这意味着 x4(所购物业的年份)对下一个价格重要性最低。不过,在该设置中使用线性内核并非我们在此讲述的内容,而是将线性内核与高斯过程回归配合使用。意即,如果一个人需要推断特征重要性,他将无法像我们上面所示的那样简单地行事,因为上面的点积输出是一个标量,而在我们的应用程序中它是一个矩阵。可替代性,尽管,为了理解输入数据的相对重要性,其它选择包括自动相关性判定、敏感性分析(调整选定的输入,并观察它们对预测的影响)、和边际似然性 & 超参数(其中像批量归一化中的超参数量级可以推断输入数据的相对重要性)。
我们实现 MQL5 版本的线性内核,可在高斯过程回归中使用,如下所示:
//+------------------------------------------------------------------+ // Linear Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols) { matrix _linear, _c; _linear.Init(Rows.Size(), Cols.Size()); _c.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _linear[i][ii] = Rows[i] * Cols[ii]; } } _c.Fill(m_constant); _linear += _c; return(_linear); }
此处的输入是公式中已指示的 2 个向量,其中一个标记为 'Rows',意即该向量在应用于点积之前要转置。故此,线性内核尽管简单,但除了我们上面提到的好处之外,还可以作为模型与其它更复杂内核进行比较的基线,因为它们最容易设置和测试。从它们开始,可以逐渐弹性放大,具体取决于其它内核的额外复杂性是否有保障。这一点尤其重要,因为随着内核变得越来越复杂,计算成本亦飙升,这在应对非常大的数据集和内核时很严重。尽管线性内核可以捕获长期依赖关系,但与其它内核结合使用能定义更复杂的关系,并且当所比较数据集具有很强线性关系的情况下,它们可以充当一种正则化形式。
Matérn 内核
Matérn 内核也是高斯过程中常用的协方差函数,因为它拥有可调节的平滑度,以及捕获数据依赖关系的能力。它的平滑度由输入参数 ν(发音为 niǔ)控制。该参数能够调整其平滑度,以便在 ν 为 ½ 时将 Matérn 内核映射为锯齿状指数内核,当该参数趋于 ∞ 时,可将 Matérn 内核映射为径向基函数核。据第一原理,它的公式如下:
其中:
- ∥x−x′∥是两点之间的欧几里德距离
- ν 是平滑度控制参数
- l 是长度伸缩参数(类似于 RBF 内核中的那个)
- Γ(ν) 是伽马(Gamma)函数
- K ν 是第二种改编的贝塞尔(Bessel)函数
伽马函数和贝塞尔函数有点古怪,我们不会深入其中,不过出于我们的目的,我们将 ν 设置为 3/2,这令我们的内核几乎介于指数内核和径向基函数内核之间。当我们这般行事时,我们的 Matérn 内核公式简化为:
其中
- 表示类似于上面分享的第一个公式。
特殊情况:
- 当 ν=1/2 时,Matérn 内核变为指数内核。
- 对于 ν→∞,它变成 RBF 内核。
这个内核的平滑度对于 ν 参数非常敏感,通常它被赋值 1/2 或 3/2 或 5/2。这些参数值中的每一个,都意味着不同程度的平滑度,值越大,平滑度越高。
当 v 是 1/2 时,内核相当于前面提到的指数内核,这令它适合于针对急剧变化、或不连续性很常见的数据集进行建模。从交易者的角度来看,这通常指向证券或外汇对非常不稳定。该内核设置假定一个锯齿状过程,因此往往会产生不太平滑的结果,即是说它对即刻变化更敏锐。当 v 是 3/ 2 时,这是我们测试由向导组装的智能系统时采用的设置,其平滑度通常被评为中等。这是一种折衷,在于它能够处理轻度波动的数据、及轻度趋势的数据集。有论调称,这种设置令内核适合于判定时间序列中的转折点、或市场的波动点。5/2 和更高的设置令内核更适合趋势环境,尤其是当汇率有问题时。
故此,较小的 ν 值更适合于含噪声数据,或含有跳空或不连续性的数据集,而较高的 v 值则适用于更平缓、且变化平滑的数据集。旁注,可微性或内核函数可以微分的次数随着 v 参数的增加而增加。这反过来又与具有较高 v 参数值的计算资源相关,从而抬升更多的计算。我们实现 MQL5 版本的 Matérn 内核,如下所示:
//+------------------------------------------------------------------+ // Matern Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols) { matrix _matern; _matern.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next); } } return(_matern); }
因此,与线性内核相比,Matérn 内核更灵活,更适合捕获复杂的非线性数据关系。当为大量真实世界的现象和数据建模时,它显然比线性内核有优势,因为正如我们上面看到的,稍微优调/调整 v 参数令其不仅能够处理趋势性数据集,还能处理不稳定和不连续的数据。
信号类
我们创建了一个自定义信号类,将两个内核糅合到一起,作为信号类中的两个实现选项。我们的 GetOutput 函数也经重新编码,以便满足从智能系统的输入中选择内核的需求。新函数如下:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalGauss::GetOutput(double BasisMean, vector &Output) { ... matrix _k_s; matrix _k_ss; _k_s.Init(_next_time.Size(), _past_time.Size()); _k_ss.Init(_next_time.Size(), _next_time.Size()); if(m_kernel == KERNEL_LINEAR) { _k_s = Linear_Kernel(_next_time, _past_time); _k_ss = Linear_Kernel(_next_time, _next_time); } else if(m_kernel == KERNEL_MATERN) { _k_s = Matern_Kernel(_next_time, _past_time); _k_ss = Matern_Kernel(_next_time, _next_time); } ... }
一旦选择了适应的内核,插入下一个价格变化所涉及的步骤与我们在早前文章中讲述的步骤雷同。做多条件和做空条件处理也并无太大区别,为了完整起见,它们的代码在此分享:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalGauss::LongCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] > _o[0]) { result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalGauss::ShortCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] < _o[0]) { result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
链接文章中的条件基于预测价格变化是朝向正值亦或负值。然后将这些变化归一化为 0 到 100 整数范围,这是所有自定义信号类实例的预期结果。在此处和此处的单独文章中为新读者讲述了如何经由 MQL5 向导将该信号文件汇编到智能交易系统当中。
策略测试器报告
我们依据 GBPJPY 货币对, 2023 年的日线时间帧上优化了线性内核和 Matérn 内核。每个结果,都简单地展示了智能系统的可用性,但不以任何方式指代未来的性能,如下所示:
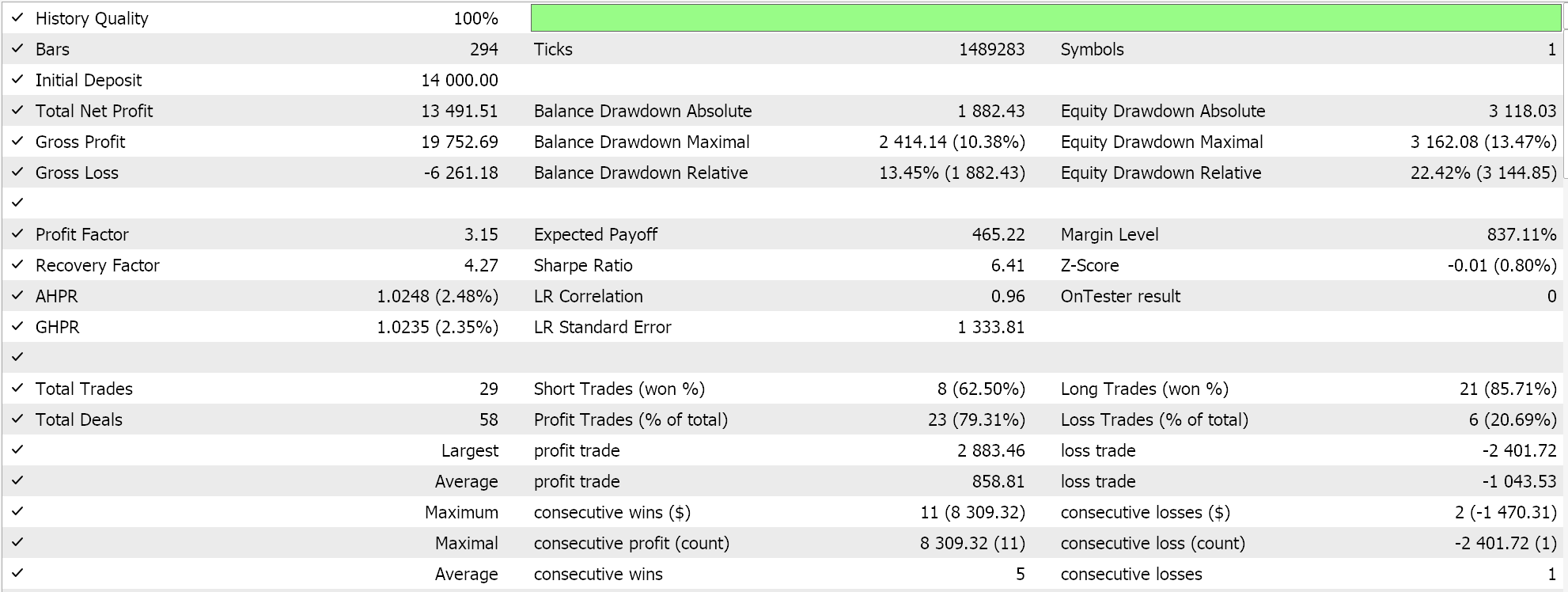
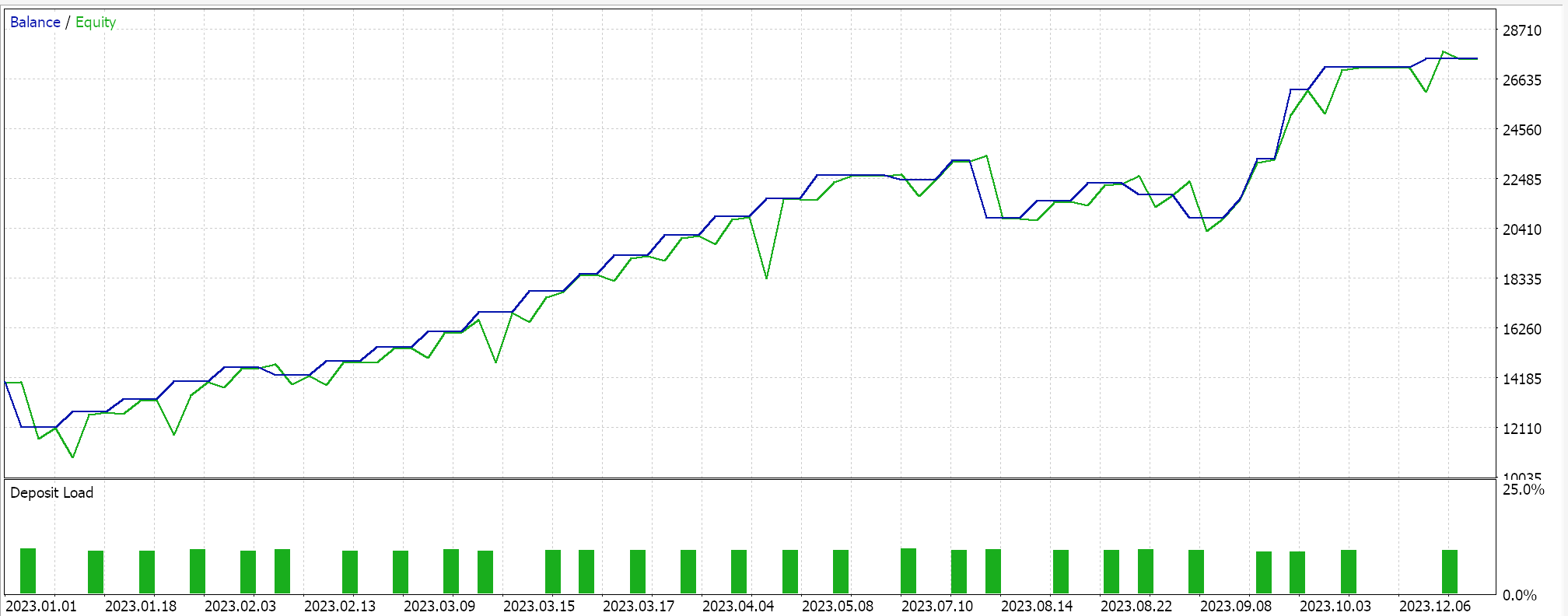
Matérn 内核的结果是:
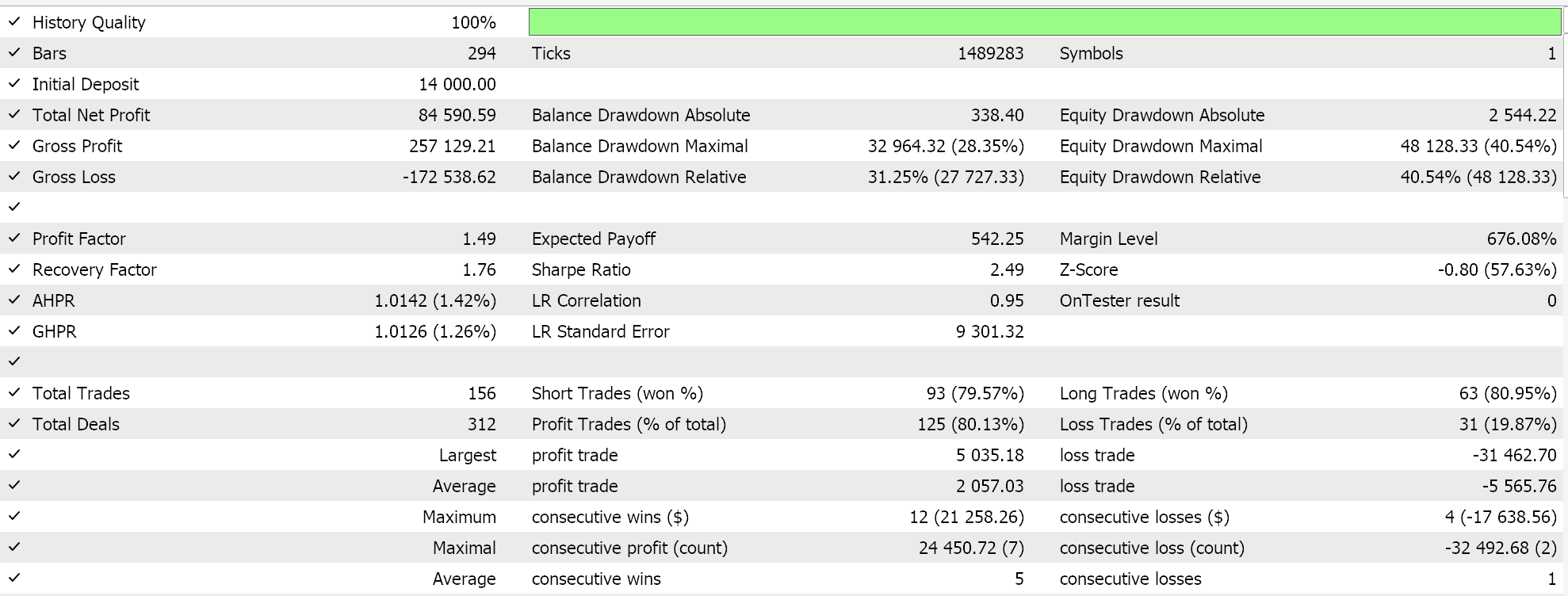
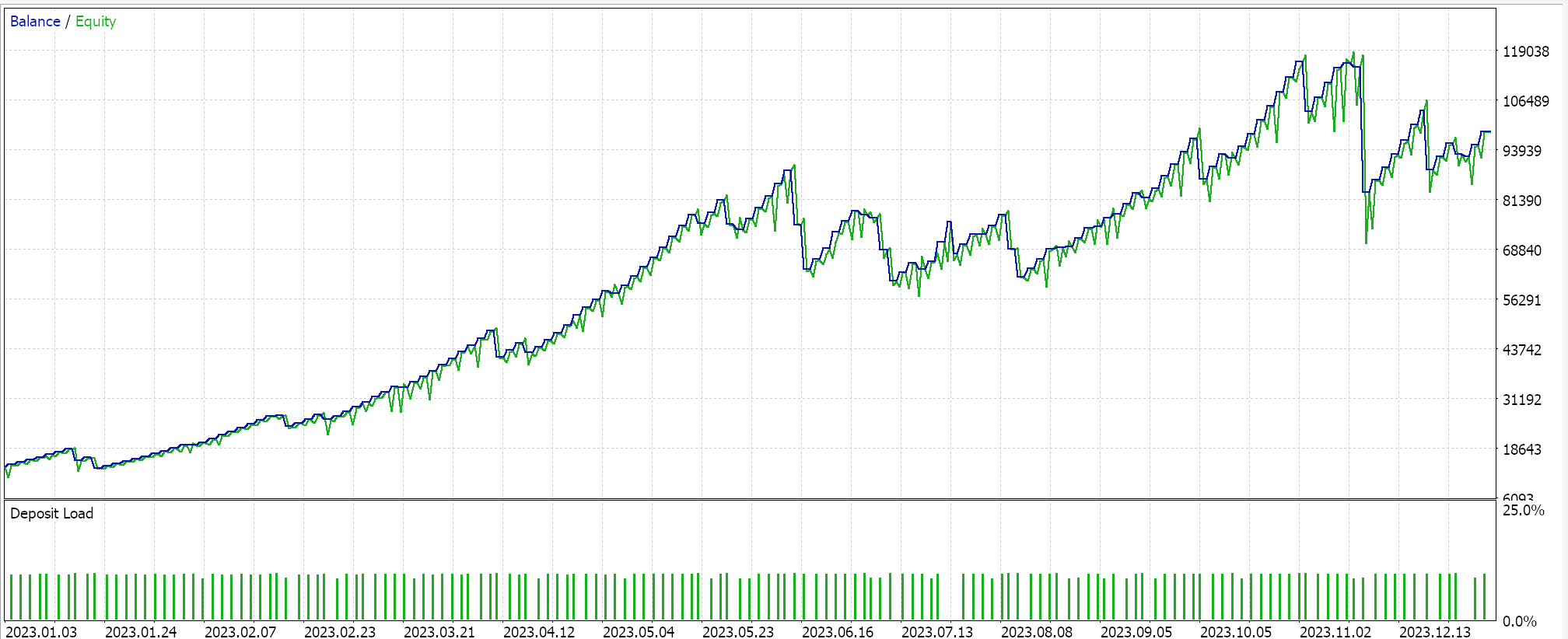
两个内核的一种替代实现,也能用于自定义资金管理类。这就像可在 MQL5 向导中组装信号一样,区别在于只能选择一个资金管理的自定义实例。若要像使用信号类一样使用高斯过程回归,理想情况下,我们应该有一个通用的锚点类,该类被自定义信号类和自定义资金管理类引用。这对于两个自定义类中执行非常相似任务的相同函数,最大限度地减少编码重复性。
然而,在资金管理类中,我们提供给高斯过程内核的数据类型有一些细微的变化。虽然我们将收盘价变化作为自定义信号类的输入数据集,但对于这个资金管理类,我们将 ATR 指标中的变化作为内核的输入。已训练的内核输出是 ATR 中的下一个变化。这个自定义类也是对常见的资金规模优化类的改编,对于那些可能不熟悉的人来说,它是为了在智能系统持续亏损时减少仓位规模而构建的。手数减少的比例与所承受的一连串亏损成正比。我们采用这个类,并进行一些修改,以便监管何时采取降低手数。
经过我的们修改,我们只在智能系统亏损并且预测值中 ATR 上升时降低手数。这些预测值的数量由参数 'm_next' 设置,如所链接的文章中所述,在这些系列中讲述了高斯过程回归。这些修改以及大多数优化持仓规模的原始代码分享如下:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneyGAUSS::Optimize(int Type, double lots) { double lot = lots; //--- calculate number of losses orders without a break if(m_decrease_factor > 0) { //--- select history for access HistorySelect(0, TimeCurrent()); //--- int orders = HistoryDealsTotal(); // total history deals int losses = 0; // number of consequent losing orders //-- int size = 0; matrix series; series.Init(fmin(m_series_size, orders), 2); series.Fill(0.0); //-- CDealInfo deal; //--- for(int i = orders - 1; i >= 0; i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket() == 0) { Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol() != m_symbol.Name()) continue; //--- check profit double profit = deal.Profit(); //-- series[size][0] = profit; size++; //-- if(size >= m_series_size) break; if(profit < 0.0) losses++; } //-- double _cond = 0.0; //-- vector _o; GetOutput(0.0, _o); //--- //decrease lots on rising ATR if(_o[_o.Size()-1] > _o[0]) lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2); } //--- normalize and check limits double stepvol = m_symbol.LotsStep(); lot = stepvol * NormalizeDouble(lot / stepvol, 0); //--- double minvol = m_symbol.LotsMin(); if(lot < minvol) lot = minvol; //--- double maxvol = m_symbol.LotsMax(); if(lot > maxvol) lot = maxvol; //--- return(lot); }
正如我们上面所演示的,在创建利用高斯过程内核的自定义尾随类时,也可以采用类似的方式。除了向量和矩阵数据类型提供的简单价格访问外,还有多种指标可供选择。
结束语
总而言之,我们继续深入研究高斯过程回归,研究了针对金融时间序列进行预测时,可以与这种回归形式一起使用的另一组内核。线性内核和 Matérn 内核几乎是相反的,不仅在它们适合的数据集类型上,还在于灵活性上。虽然线性内核只能处理给定类型的数据集,但用它进行起始建模通常是可行的,尤其是当所研究起始数据集样本可能很小的情况下。随着时间的推移,一旦数据集样本增加,数据变得更加复杂,甚至有噪声,那么像 Matérn 内核这样更健壮的内核不仅可以用于处理有噪声的数据、或间隙或中断,亦可处理可能非常平滑的数据集。这是因为其关键输入参数 v 的可调整性,令其能够根据数据集带来的挑战承担不同的角色,这就是为什么它可以说更适合大多数数据环境的原因。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15767
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 开发基于订单簿的交易系统(第一部分):指标
开发基于订单簿的交易系统(第一部分):指标
 非洲水牛优化(ABO)
非洲水牛优化(ABO)
 基于人工生态系统的优化(AEO)算法
基于人工生态系统的优化(AEO)算法
 在MQL5中创建交易管理员面板(第三部分):扩展内置类以进行主题管理(II)
在MQL5中创建交易管理员面板(第三部分):扩展内置类以进行主题管理(II)
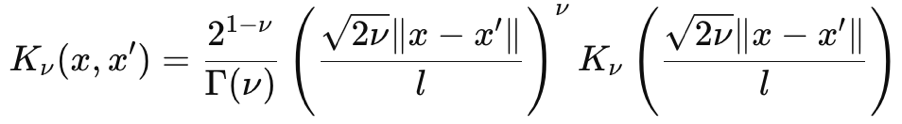
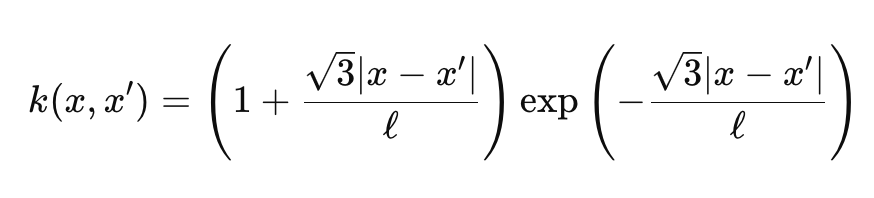
我遇到一个严重错误。
MoneyWZ_37.mqh 中的索引超出范围 (197,17)
相关行
series[size][0] = profit;
MoneyWZ_37.mqh 中的索引超出范围 (197,17)
与该行有关
series[size][0] = profit;
你好、
刚刚对所附代码进行了修改,并重新发送以供发布。