在Python和MQL5中应用局部特征选择

概述

在金融市场分析中，指标的有效性往往随着底层条件的变化而变化。例如，波动率的变动可能会使先前可靠的指标在市场环境变化时显示无效。这种变化性解释了交易者使用的指标种类繁多的原因，因为没有任何单一指标能够在所有市场条件下始终表现良好。从机器学习的角度来看，这需要一种灵活的特征选择技术来适应这种动态行为。

许多常见的特征选择算法优先选择在整个特征空间中表现出预测能力的特征。即使这些特征与目标变量之间的关系是非线性的，或者受到其他特征的影响，它们通常也会受到青睐。然而，这种全局偏差可能会引发问题，因为现代非线性模型能够从具备强局部预测能力的特征，或与目标变量在特征空间特定区域内呈现关系变化的特征中，挖掘出有价值的线索。

在本文中，我们探讨了Narges Armanfard、James P. Reilly和Majid Komeili在论文《数据分类的局部特征选择》中介绍的一种特征选择算法。该方法旨在识别通常被传统选择技术忽视的预测特征，因为它们的全局作用有限。我们将从算法的一般概述开始，然后通过Python实现以创建适合导出到MetaTrader 5的分类器模型。

局部特征选择

成功的机器学习依赖于选择有助于解决问题的信息性特征。在监督分类中，特征应该能够有效地区分数据类别。然而，识别这些信息性特征可能具有挑战性，因为非信息性特征可能会引入噪声并降低模型性能。因此，特征选择通常是构建预测模型关键的第一步。

与传统方法（寻求适用于所有数据的单一最优特征子集）不同，局部特征选择（LFS）为特定局部区域识别最优子集。这种适应性对于处理非平稳数据可能特别有效。此外，LFS结合了一个分类器，该分类器考虑了不同样本中使用的不同特征子集。它通过类别内的聚类实现这一目标，选择能够最小化类内距离同时最大化类间距离的特征。

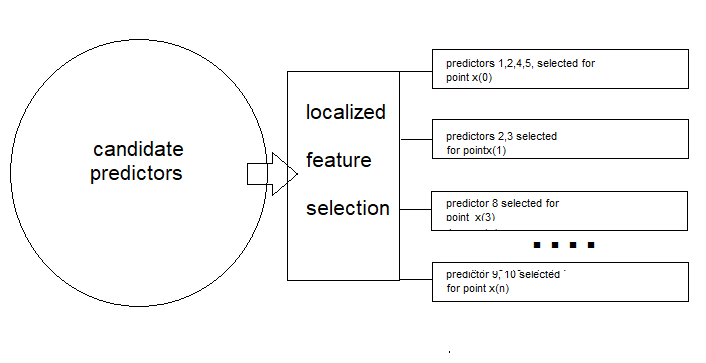
这种方法在重叠区域内识别局部最优的特征子空间，确保每个样本在多个特征空间中都有所体现。为了更好地理解这一概念，考虑一个电信公司试图预测客户流失的场景——即识别可能关闭账户的客户。公司收集了各种客户特征，包括：

• 客户在网时长：客户与公司合作了多长时间？
• 月账单金额：客户每月支付多少费用？
• 客户的体重和身高。
• 联系客服的次数：客户多久联系一次客服团队？

想象一下，选择两位与公司合作多年的忠诚客户。对于上述每个特征，这些忠诚客户之间可能几乎没有差异，因为他们属于同一个类别。现在，将这种情况与一个长期客户和一个注册后不久就取消订阅的客户之间的差异进行对比。尽管他们的体重和身高可能没有太大差异，但其他相关的预测因子可能会表现出显著的不同。

忠诚客户的在网时长显然会更长，他们可能更愿意选择价格更高的订阅套餐，并且在出现问题时更倾向于联系客服来解决，而不是因沮丧而取消服务。与此同时，像体重和身高这样的指标将接近人群平均水平，并不会明显有助于区分这些客户类型。

通过欧几里得距离分析成对的个体特征值，我们会发现最相关的预测因子将在客户之间展现出最大的类间距离，而最不相关的预测因子将展现出最小的类间距离。这使得有效预测因子的选择变得清晰：我们优先选择类内距离小且类间距离大的特征对。

尽管这种方法看起来很有效，但它在考虑数据的局部变化方面存在不足。为了解决这个问题，我们必须考虑预测能力在不同特征域中的差异。想象一个包含两个类别的数据集，其中一个类别被分为两个不同的子集。从这个数据集中绘制两个特征的散点图可以说明，第一个子集可能通过变量x1与类别1很好地分离，但通过x2则不行。相反，第二个子集可能通过x2很好地分离，但通过x1则不行。

如果我们只考虑类间分离，算法可能会错误地同时选择x1和x2，尽管在每个子集中只有一个真正有效。这是因为算法可能会优先考虑两个子集之间的整体较大距离，而不是每个子集内较小但更相关的距离。为了解决这个问题，引用的论文的作者引入了一种距离加权方案。通过为距离较近的样本对分配更高的权重，为距离较远的样本对分配更低的权重，算法可以减少类内异常值的影响。这同时考虑了类别成员关系和距离的全局分布。

总结而言，引用的论文中描述的局部特征选择（LFS）算法由两个主要部分组成。第一部分是特征选择过程，为每个样本选择一个特征子集。第二部分涉及一个局部机制，用于衡量测试样本与特定类别的相似性，这用于推理目的。

特征选择

在本节中，我们将逐步描述LFS方法采用的学习程序，并涉及到一些数学知识。我们从训练数据的预期结构开始。局部特征选择的实现是在一个包含N个训练样本的数据集上进行的，这些样本被分类为Z个类别标签，并且有M个特征或预测候选变量。

训练数据可以表示为一个矩阵X，其中行对应于样本，列代表不同的预测候选变量。因此，矩阵X有N行和M列。每个样本表示为X(i)，即矩阵中的第i行。类别标签存储在一个单独的列向量Y中，每个标签映射到矩阵中的一个对应样本（行）。

应用LFS方法的最终目标是确定每个训练样本X(i)的一个大小为M的二进制向量F(i)，以指示哪些候选预测变量对于确定相应的类别标签最为相关。矩阵F将与X具有相同的维度。

使用欧几里得距离，算法旨在最小化当前样本与其他具有相同类别标签的样本之间的平均距离，同时最大化当前样本与具有不同类别标签的样本之间的平均距离。此外，距离必须加权，以支持与当前样本处于同一邻域的样本，引入权重列向量W。由于权重（W）和二进制向量F(i)最初均不可取得，因此使用迭代程序来估算最优的W和F(i)向量。

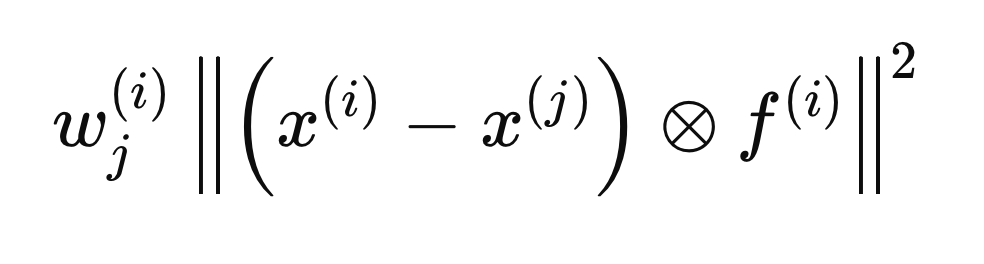
计算类内距离和类间距离

以下各节中描述的每个步骤都涉及对单个样本X(i)进行的计算，以确定最优的F(i)向量。该过程从将F的所有条目初始化为0并将初始权重设置为1开始。接下来，我们计算与X(i)相关的类内距离和类间距离。在距离计算中包含F(i)向量，确保只有认定为相关的变量（等于1的那些）被列入考虑。为了数学上的方便，将欧几里得距离平方，从而得到以下距离公式。

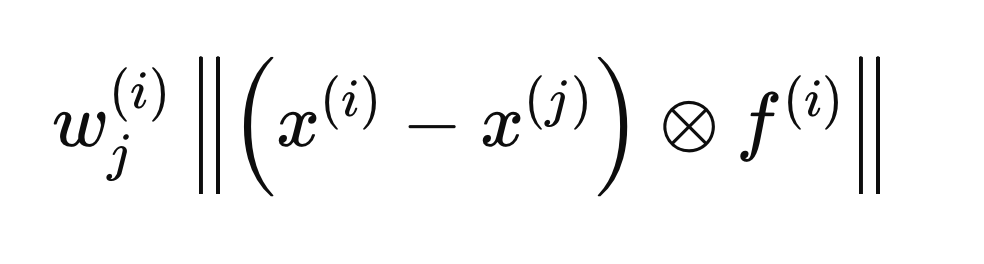
带有一个封闭“x”的圆圈表示逐元素乘法运算符。使用上述公式计算类内距离和类间距离，但使用了X的不同j元素（行）。类内距离是使用与X(i)具有相同类别标签的j元素计算得到的。

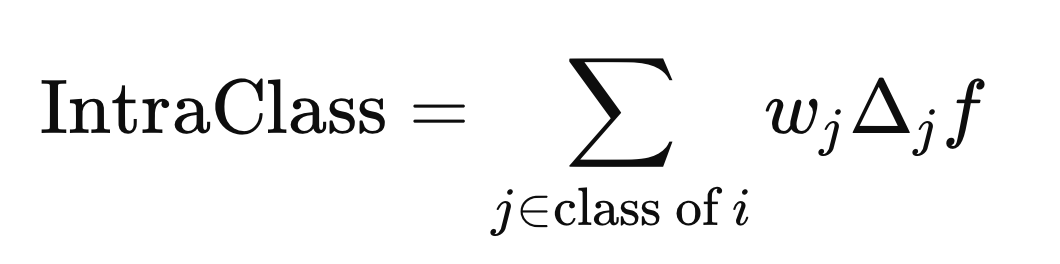
而类间距离则是使用与Y(i)类别标签不同的j元素计算得到的。

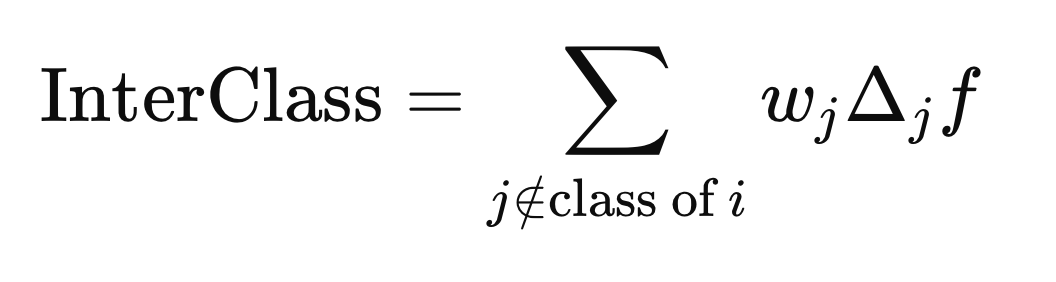
计算权重

对于样本X(i)，我们计算一个权重向量（W），其长度为N，如果X(j)远离X(i)，其权重应较小，反之，如果它靠近，则权重应较大。权重不应仅仅因为样本具有不同的类别标签而产生不利影响。由于F(i)尚未达到最优，用于定义邻域基础的变量仍然未知。引用的论文通过从权重细化的前几次迭代中计算出的平均权重来解决这一问题。

当F向量包含在定义两个样本之间的距离时，其被认为是在由F(i)定义的度量空间内。通过在另一个度量空间中定义距离来计算最优权重，我们将这个度量空间称为F(z)，其公式如下。

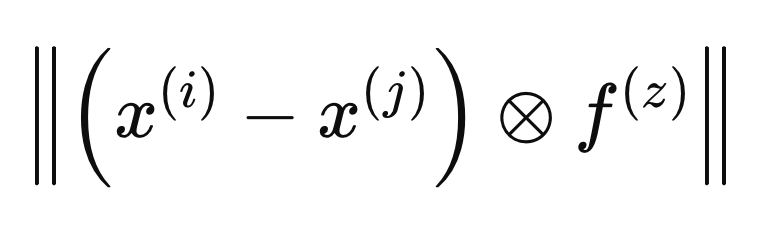
为了确保权重不会仅仅因为样本属于不同的类别而产生不利影响，我们在由F(z)定义的度量空间中，计算X(i)与所有同类别其他样本之间的最小距离。

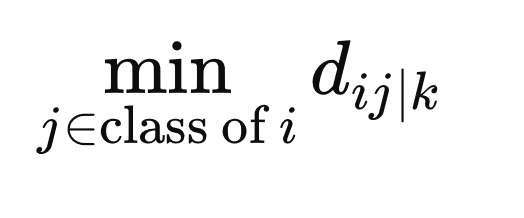
此外，我们还计算与X(i)不同类别样本之间的最小距离。

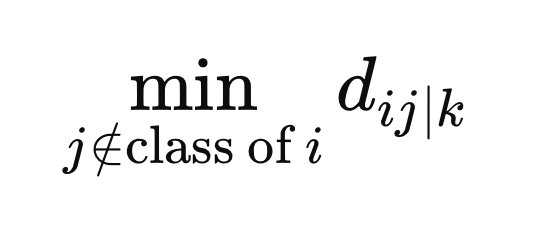
这些是定义权重所需的最终值。权重的计算是取所有度量空间的平均值，具体公式为距离与特定度量空间z中的最小距离之差的负指数。

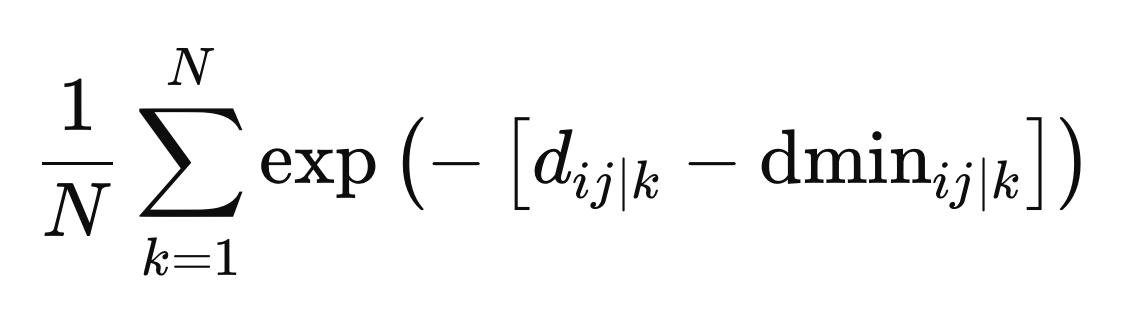
相互冲突的目标

在这一阶段，我们已经获得了最优权重，这使我们能够在类间分离和类内分离之间找到适当的平衡。这就涉及到调和两个相互冲突的目标：最小化类内分离（使同一类别的数据点尽可能相似）和最大化类间分离（使不同类别尽可能区分开来）。通常情况下，用同一组预测变量同时完美实现这两个目标是不可行的。

一种可行的方法是Epsilon-约束方法，它在这些相互冲突的目标之间寻找折中方案。该方法首先解决其中一个优化问题（通常是最大化问题），然后确保在最大化函数值保持在某个阈值以上的约束条件下解决最小化问题。

首先，我们最大化类间分离，并记录该函数的最大值，记为epsilon（ϵ），它代表了可能达到的最大类间分离。接下来，我们在参数β（取值范围为0到1）的不同值下最小化类内分离，同时约束最小化解的类间分离必须大于或等于βϵ。

参数β作为折中因子，平衡对两个目标的关注：当β设置为1时，类间分离获得完全优先权；而当β设置为0时，关注点则完全转向最小化类内分离。在这两个优化任务上都施加了四个约束条件：

• F的所有元素必须在0到1之间（包括0和1）。
• 一个F向量的元素之和必须小于或等于用户指定的超参数，该参数控制可以激活的最大预测变量数量。
• 一个F向量的元素之和必须大于或等于1，以确保为每个样本至少激活一个预测变量。
  

对于类内最小化，还有一个从初始最大化操作继承而来的附加约束：最大化函数的值必须至少等于β与ϵ的乘积。

所涉及的函数和约束都是线性的，这表明优化任务是线性规划问题。标准的线性规划问题旨在不超过指定阈值的约束条件下最大化目标函数。

线性规划涉及在一组线性约束条件下优化一个线性目标函数。目标函数通常用“z”表示，是决策变量的线性组合。约束条件以线性不等式或等式的形式表达，限制决策变量的取值。除了用户指定的约束条件外，决策变量和不等式右侧还存在隐含的非负性约束。

虽然标准形式假设决策变量为非负数，并且约束条件为“小于或等于”不等式，但这些限制可以通过变换来放宽。通过将不等式的两边同时乘以-1，我们可以处理“大于或等于”形式的不等式以及右侧为负值的情况。此外，涉及决策变量的非正系数可以通过创建新变量转换为正系数。

内点法是一种高效的算法，用于解决线性规划问题，尤其是在处理大规模优化任务时。我们的Python实现将采用这种方法来高效地找到最优解。一旦达到收敛，我们将获得一个最优的F(i)向量。然而，需要注意的是，这些值并不是所需的格式（要么是1，要么是0）。这在LFS方法的最后一步中得以修正。

Beta试验

计算出的F(i)向量的问题在于，它由实数值组成，而不是二进制值。LFS程序的目标是识别每个样本的最相关变量，这由一个二进制F矩阵表示，其中的值要么是0，要么是1。值为0表示相应的变量被认定不相关或被略过。

为了将F(i)向量的实数值转换为二进制值，我们使用蒙特卡洛方法来找到最佳的二进制等价物。这涉及到重复用户指定次数的过程，这是LFS方法的一个关键超参数。在每次迭代中，我们从一个二进制向量开始，其中每个预测候选变量最初都设置为1，使用连续的F(i)值作为每个预测变量的概率。然后我们检查二进制向量是否满足最小化过程的约束条件，并计算其目标函数值。具有最小目标函数值的二进制向量被选为最终的F(i)向量。

特征选择的后处理

LFS为每个样本独立选择最优的预测候选变量，这使得报告一个单一的确定性集合不切实际。为了解决这个问题，我们统计每个预测变量被包含在最优子集中的频率。允许用户设置一个阈值，并将最频繁出现的预测变量识别为最相关的。重要的是，这个集合中一个预测变量的相关性并不意味着它的单独价值；它的价值可能在于它与其他预测变量的相互作用。

这是LFS的一个关键优势：它能够识别出单独可能不显著但在与其他变量结合时有价值的预测变量。这个预处理步骤对于现代预测模型至关重要，这些模型擅长识别变量之间的复杂关系。通过消除不相关的预测变量，LFS简化了建模过程并提高了模型性能。

Python实现：LFSpy

在本节中，我们探讨了局部特征选择（LFS）算法的实际应用，首先关注其作为特征选择技术的使用，并简要讨论其数据分类能力。所有演示都将在Python中使用LFSpy包进行，该包实现了LFS算法的特征选择和数据分类方面。该包可在PyPI上找到，有关它的详细信息可以在那里找到。

首先，安装LFSpy包。

pip install LFSpy

接下来，从LFSpy导入LocalFeatureSelection类。

from LFSpy import LocalFeatureSelection

可以通过调用带参数的构造函数来创建LocalFeatureSelection的实例。

lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)

构造函数支持以下可选参数：

参数名称	数据类型	说明
α	整型	从所有候选预测变量中选择的最大预测变量数量。默认值为19。
γ	双精度型	一个容差水平，用于控制在局部区域内不同类别标签的样本与相同类别标签的样本的比例。默认值为0.2。默认值为0.2。
τ	整型	整个数据集的迭代次数（相当于传统机器学习中的“轮数”）。默认值为2，建议将此值设置为个位数，通常不超过5。
∑	双精度型	根据观测值的距离控制其权重。大于1的值会降低权重。默认值为1。
n_beta	整型	在将连续的F向量转换为其二进制等价物时测试的beta值的数量。
nrrp	整型	Beta试验的迭代次数。该值应该至少为500，并且随着训练数据集的大小增加而增加。默认值为2000。
knn	整型	特别适用于分类任务。它指定了分类时要比较的最近邻的数量。默认值为1。

在初始化了LFSpy类的实例之后，我们使用fit()方法，至少需要两个输入参数：一个二维矩阵，包含候选预测变量的训练样本，以及一个一维数组，包含相应的类别标签。

lfs.fit(xtrain,ytrain)

一旦模型拟合完成，调用fstar将返回F包含矩阵，该矩阵由1和0组成，用于指示所选择的特征。请注意，这个矩阵相对于训练样本的方向是转置的。

fstar = lfs.fstar

predict() 方法用于根据已学习的模型对测试样本进行分类，并返回与测试数据对应的类别标签。

predicted_classes = lfs.predict(test_samples)

score() 方法通过比较预测的类别标签和已知的正确标签来计算模型的准确率。它返回正确分类的测试样本所占的比例。

accuracy = lfs.score(test_data,test_labels)

LFSpy示例

在第一次实际演示中，我们在区间[−1,1]内生成了数千个均匀分布的随机变量。这些变量被排列成一个具有指定列数的矩阵。然后，我们根据两列任意列中的值是否同时为负或同时为正，为每一行创建一个{0, 1}标签的向量。本次演示的目的是确定LFS方法是否能够识别该数据集中最相关的预测变量。我们通过汇总F二进制包含矩阵中每个预测变量被选中的次数（由1表示）来评估结果。此测试的实现代码如下所示：

import numpy as np
import pandas as pd
from LFSpy import LocalFeatureSelection
from timeit import default_timer as timer

#number of random numbers to generate
datalen = 500 

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our training data
xtrain = data
ytrain = class_labels

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#start timer
start = timer()

#train the model
lfs.fit(xtrain,ytrain)

#output training duration
print("Training done in ", timer()-start , " seconds. ")

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
ibins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0])

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(original_crits.shape[0]):
   print( f" Variable at column {i}, selected {original_crits[i]} %")

运行LFSdemo.py的输出结果

Training done in  45.84896759999992  seconds. 
Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable at column 0, selected 19.0 %
Python   Variable at column 1, selected 81.0 %
Python   Variable at column 2, selected 87.0 %
Python   Variable at column 3, selected 20.0 %
Python   Variable at column 4, selected 18.0 %

令人兴奋的是，尽管这两个相关变量在预测类别中扮演着相同的角色，但其中一个被选择的频率略高于另一个。这表明数据中的一些细微差别可能会影响选择过程。可以明确的是，这两个变量被选择的频率都明显高于不相关的预测变量，这表明它们在确定类别中的重要性。可能是因为其单线程特性，该算法的执行速度相对较慢，在较大数据集上这可能会限制其性能。

LFS用于数据分类

鉴于LFS的局部性质，在构建分类器方面，比起传统的、具有全局偏差的特征选择方法更加繁琐。引用的论文讨论了一种提议的分类器架构，我们在这里不会深入探讨。感兴趣的读者可以参考引用的论文以获取完整细节。在本节中，我们将专注于实现。

LocalFeatureSelection类的predict()方法评估类别相似性。它接受与训练数据结构匹配的测试数据，并根据训练好的LFS模型所学习的模式返回预测的类别标签。在接下来的代码演示中，我们将扩展之前的脚本，构建一个LFS分类器模型，以JSON格式导出，使用MQL5脚本加载它，并对一个样本外的数据集进行分类。用于导出LFS模型的代码包含在JsonModel.py文件中。此文件定义了lfspy2json()函数，该函数将LocalFeatureSelection模型的状态和参数序列化到一个JSON文件中。这使得模型能够以一种易于在MQL5代码中读取和使用的方式保存，便于与MetaTrader 5集成。完整代码如下：

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com

from LFSpy import LocalFeatureSelection
import json 

MQL5_FILES_FOLDER = "MQL5\\FILES"
MQL5_COMMON_FOLDER = "FILES"

def lfspy2json(lfs_model:LocalFeatureSelection, filename:str):
    """
    function export a LFSpy model to json format 
    readable from MQL5 code.
    
    param: lfs_model should be an instance of LocalFeatureSelection
    param: filename or path to file where lfs_model
    parameters will be written to
    
    """
    if not isinstance(lfs_model,LocalFeatureSelection):
        raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "alpha":lfs_model.alpha,
            "gamma":lfs_model.gamma,
            "tau":lfs_model.tau,
            "sigma":lfs_model.sigma, 
            "n_beta":lfs_model.n_beta,
            "nrrp":lfs_model.nrrp,
            "knn":lfs_model.knn,
            "rr_seed":lfs_model.rr_seed,
            "num_observations":lfs_model.training_data.shape[1],
            "num_features":lfs_model.training_data.shape[0],
            "training_data":lfs_model.training_data.tolist(),
            "training_labels":lfs_model.training_labels.tolist(),
            "fstar":lfs_model.fstar.tolist()
          }
          
    
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

该函数接受一个LocalFeatureSelection对象和一个文件名作为输入。It serializes the model parameters as a JSON object and saves it under the specified file name. 该模块还定义了两个常量，MQL5_FILES_FOLDER和MQL5_COMMON_FOLDER，表示安装标准MetaTrader 5时可访问文件夹的目录路径。这只是与MetaTrader 5集成解决方案的一部分。另一部分是在MQL5代码中实现的，代码在lfspy.mqh中。这个包含文件定义了Clfspy类，它便于加载以JSON格式保存的LFS模型，用于推导目的。完整代码如下：

//+------------------------------------------------------------------+
//|                                                        lfspy.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>
//+------------------------------------------------------------------+
//|structure of model parameters                                     |
//+------------------------------------------------------------------+
struct LFS_PARAMS
  {
   int               alpha;
   int               tau;
   int               n_beta;
   int               nrrp;
   int               knn;
   int               rr_seed;
   int               sigma;
   ulong             num_features;
   double            gamma;
  };
//+------------------------------------------------------------------+
//|  class encapsulates LFSpy model                                  |
//+------------------------------------------------------------------+
class Clfspy
  {
private:
   bool              loaded;
   LFS_PARAMS        model_params;
   matrix train_data,
          fstar;
   vector            train_labels;
   //+------------------------------------------------------------------+
   //|  helper function for parsing model from file                     |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      model_params.alpha = (int)jsonmodel["alpha"].ToInt();
      model_params.tau = (int)jsonmodel["tau"].ToInt();
      model_params.sigma = (int)jsonmodel["sigma"].ToInt();
      model_params.n_beta = (int)jsonmodel["n_beta"].ToInt();
      model_params.nrrp = (int)jsonmodel["nrrp"].ToInt();
      model_params.knn = (int)jsonmodel["knn"].ToInt();
      model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt();
      model_params.gamma = jsonmodel["gamma"].ToDbl();

      ulong observations = (ulong)jsonmodel["num_observations"].ToInt();
      model_params.num_features = (ulong)jsonmodel["num_features"].ToInt();

      if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) ||
         !fstar.Resize(model_params.num_features,observations))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }


      for(int i=0; i<int(model_params.num_features); i++)
        {
         for(int j = 0; j<int(observations); j++)
           {
            if(i==0)
               train_labels[j] = jsonmodel["training_labels"][j].ToDbl();
            train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl();
            fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl();
           }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| helper classification function                                   |
   //+------------------------------------------------------------------+
   matrix            classification(matrix &testing_data)
     {
      int N = int(train_labels.Size());
      int H = int(testing_data.Cols());

      matrix out(H,2);

      for(int i = 0; i<H; i++)
        {
         vector column = testing_data.Col(i);
         vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn);
         if(!out.Row(result,i))
           {
            Print(__FUNCTION__, " row insertion failure ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| internal feature classification function                         |
   //+------------------------------------------------------------------+
   vector            class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn)
     {
      int N = int(targets.Size());
      int n_nt_cls_1 = (int)targets.Sum();
      int n_nt_cls_2 = N - n_nt_cls_1;
      int M = int(patterns.Rows());
      int NC1 = 0;
      int NC2 = 0;
      vector S = vector::Zeros(N);

      S.Fill(double("inf"));

      vector NoNNC1knn = vector::Zeros(N);
      vector NoNNC2knn = vector::Zeros(N);
      vector NoNNC1 = vector::Zeros(N);
      vector NoNNC2 = vector::Zeros(N);
      vector radious = vector::Zeros(N);
      double r = 0;
      int k = 0;
      for(int i = 0; i<N; i++)
        {
         vector fs = f_star.Col(i);
         matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
         vector testpr = test * fs;
         vector mtestpr = (-1.0 * testpr);
         matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false);
         vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0)));
         vector min1 = dist;
         np::sort(min1);
         vector min_uniq = np::unique(min1);
         int m = -1;
         int no_nereser = 0;
         vector NN(dist.Size());
         while(no_nereser<int(knn))
           {
            m+=1;
            double a1  = min_uniq[m];
            for(ulong j = 0; j<dist.Size(); j++)
               NN[j]=(dist[j]<=a1)?1.0:0.0;
            no_nereser = (int)NN.Sum();
           }
         vector bitNN = np::bitwiseAnd(NN,targets);
         vector Not = np::bitwiseNot(targets);
         NoNNC1knn[i] = bitNN.Sum();
         bitNN = np::bitwiseAnd(NN,Not);
         NoNNC2knn[i] = bitNN.Sum();
         vector A(fs.Size());
         for(ulong v =0; v<A.Size(); v++)
            A[v] = (fs[v]==0.0)?1.0:0.0;
         vector f1(patterns.Cols());
         vector f2(patterns.Cols());
         if(A.Sum()<double(M))
           {
            for(ulong v =0; v<A.Size(); v++)
               A[v] = (A[v]==1.0)?0.0:1.0;
            matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols());
            amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false);
            matrix patternsp = patterns*amask;
            vector testp = test*(amask.Col(0));
            vector testa = patternsp.Col(i) - testp;
            vector col = patternsp.Col(i);
            matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false);
            double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum()));
            vector Dist_pat  = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0)));
            vector eerep = Dist_pat;
            np::sort(eerep);
            int remove = 0;
            if(targets[i] == 1.0)
              {
               vector unq = np::unique(eerep);
               k = -1;
               NC1+=1;
               if(remove!=1)
                 {
                  int Next = 1;
                  while(Next == 1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() - 1.0;
                     double nocls2clst = f2tn.Sum();
                     if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum() - 1.0;
                        nocls2clst = f2tn.Sum();
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC1[i]>NoNNC2[i])
                        S[i] = 1.0;
                    }
                 }
              }
            if(targets[i] == 0.0)
              {
               vector unq = np::unique(eerep);
               k=-1;
               NC2+=1;
               int Next;
               if(remove!=1)
                 {
                  Next =1;
                  while(Next==1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() ;
                     double nocls2clst = f2tn.Sum() -1.0;
                     if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum();
                        nocls2clst = f2tn.Sum() -1.0;
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC2[i]>NoNNC1[i])
                        S[i] = 1.0;
                    }
                 }
              }
           }
         radious[i] = r;
        }
      vector q1 = vector::Zeros(N);
      vector q2 = vector::Zeros(N);
      for(int i = 0; i<N; i++)
        {
         if(NoNNC1[i] > NoNNC2knn[i])
            q1[i] = 1.0;
         if(NoNNC2[i] > NoNNC1knn[i])
            q2[i] = 1.0;
        }

      vector ntargs = np::bitwiseNot(targets);
      vector c1 = np::bitwiseAnd(q1,targets);
      vector c2 = np::bitwiseAnd(q2,ntargs);

      double sc1 = c1.Sum()/NC1;
      double sc2 = c2.Sum()/NC2;

      if(sc1==0.0 && sc2==0.0)
        {
         q1.Fill(0.0);
         q2.Fill(0.0);

         for(int i = 0; i<N; i++)
           {
            if(NoNNC1knn[i] > NoNNC2knn[i])
               q1[i] = 1.0;
            if(NoNNC2knn[i] > NoNNC1knn[i])
               q2[i] = 1.0;

            if(!targets[i])
               ntargs[i] = 1.0;
            else
               ntargs[i] = 0.0;
           }

         c1 = np::bitwiseAnd(q1,targets);
         c2 = np::bitwiseAnd(q2,ntargs);

         sc1 = c1.Sum()/NC1;
         sc2 = c2.Sum()/NC2;
        }

      vector out(2);

      out[0] = sc1;
      out[1] = sc2;

      return out;
     }
public:
   //+------------------------------------------------------------------+
   //|    constructor                                                   |
   //+------------------------------------------------------------------+
                     Clfspy(void)
     {
      loaded = false;
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+
                    ~Clfspy(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  load a LFSpy trained model from file                            |
   //+------------------------------------------------------------------+
   bool              load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false)
     {
      loaded = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();
      if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         loaded = fromJSON(js);
        }
      return loaded;
     }
   //+------------------------------------------------------------------+
   //|   make a prediction based specific inputs                        |
   //+------------------------------------------------------------------+
   vector            predict(matrix &inputs)
     {
      if(!loaded)
        {
         Print(__FUNCTION__, " No model available, Load a model first before calling this method ");
         return vector::Zeros(1);
        }

      if(inputs.Cols()!=train_data.Rows())
        {
         Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)");
         return vector::Zeros(1);
        }

      matrix testdata = inputs.Transpose();

      matrix probs = classification(testdata);
      vector classes = vector::Zeros(probs.Rows());

      for(ulong i = 0; i<classes.Size(); i++)
         if(probs[i][0] > probs[i][1])
            classes[i] = 1.0;

      return classes;

     }
   //+------------------------------------------------------------------+
   //| get the parameters of the loaded model                           |
   //+------------------------------------------------------------------+
   LFS_PARAMS        getmodelparams(void)
     {
      return model_params;
     }


  };
//+------------------------------------------------------------------+

在该类中，用户需要了解两个主要方法：

• load()方法接受一个文件名作为输入，该文件名应指向导出的LFS模型。
• predict()方法接受一个具有所需列数的矩阵，并返回一个类别标签向量，其长度与输入矩阵的行数相对应。
  

让我们看看这些在实践中是如何运作的。我们从Python代码开始。文件LFSmodelExportDemo.py使用随机生成的数字配置样本内和样本外的数据集。样本外数据被保存为一个CSV文件。使用样本内数据训练一个LFS模型，然后将其序列化并以JSON格式保存。我们在样本外数据上测试该模型，并记录结果，以便稍后与在MetaTrader 5中进行的相同测试做出比较。接下来展示Python代码：

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports
import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER
from os import path
from sklearn.metrics import accuracy_score, classification_report

#initialize MT5 terminal
if not mt5.initialize():
    print("MT5 initialization failed ")
    mt5.shutdown()
    exit() # stop the script if mt5 not initialized
  
#we want to get the path to the MT5 file sandbox
#initialize TerminalInfo instance    
terminal_info = mt5.terminal_info()

#model file name
filename = "lfsmodel.json"

#build the full path
modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename)

#number of random numbers to generate
datalen = 1000

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our data
train_size = 100
xtrain = data[:train_size,:]
ytrain = class_labels[:train_size]

#load testing data (out of sample)
test_data = data[train_size:,:]
test_labels = class_labels[train_size:]

#here we prepare the out of sample data for export using pandas
#the data will be exported in a single csv file
colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])]
testdata = pd.DataFrame(test_data,columns=colnames)

#the last column will be the target labels
testdata["c_labels"]=test_labels

#display first 5 samples
print("Out of sample dataframe head \n", testdata.head())
#display last 5 samples
print("Out of sample dataframe tail \n", testdata.tail())

#build the full path of the csv file
testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv")

#try save the file
try:
    testdata.to_csv(testdatafilepath)
except Exception as e:
    print(" Error saving iris test data ")
    print(e) 
else:
    print(" test data successfully saved to csv file ")  

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#train the model
lfs.fit(xtrain,ytrain)

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
bins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0])
index = np.argsort(percents)[::-1]

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(percents.shape[0]):
   print(f" Variable  {colnames[index[i]]}, selected {percents[index[i]]} %")


#conduct out of sample test of trained model
accuracy = lfs.score(test_data,test_labels)
print(f" Out of sample accuracy is {accuracy*100.0} %")


#export the model
try:
    lfspy2json(lfs,modelfilepath)
except Exception as e:
    print(" Error saving lfs model ")
    print(e)
else:
   print("lfs model saved to \n ", modelfilepath)

接下来，我们将焦点转向MetaTrader 5脚本LFSmodelImportDemo.mq5。在此，我们读取由Python脚本生成的样本外数据，并加载训练好的模型。然后对样本外数据集进行测试，并将结果与Python测试中获得的结果进行比较。以下是MQL5的相关代码：

//+------------------------------------------------------------------+
//|                                           LFSmodelImportDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<lfspy.mqh>
//script inputs
input string OutOfSampleDataFile = "testdata.csv";
input bool   OutOfSampleDataInCommonFolder = false;
input string LFSModelFileName = "lfsmodel.json";
input bool   LFSModelInCommonFolder = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder);
   
   if(testdata.Rows()<1)
    {
     Print(" failed to read csv file ");
     return;
    }
    
   
   vector testlabels = testdata.Col(testdata.Cols()-1);
   testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1);
   
  
   Clfspy lfsmodel;
   
   if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder))
    {
     Print(" failed to load the iris lfs model ");
     return;
    }
    
   vector y_pred = lfsmodel.predict(testdata);
   
   vector check = MathAbs(testlabels-y_pred);
   
   Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %");
  }
//+------------------------------------------------------------------+

运行Python脚本LFSmodelExportDemo.py的输出结果。

Python  Out of sample dataframe head 
Python         var_1     var_2     var_3     var_4     var_5  c_labels
Python  0  0.337773 -0.210114 -0.706754  0.940513  0.434695         1
Python  1 -0.009701 -0.119561 -0.904122 -0.409922  0.619245         1
Python  2  0.442703  0.295811  0.692888  0.618308  0.682659         1
Python  3  0.694853  0.244405 -0.414633 -0.965176  0.929655         0
Python  4  0.120284  0.247607 -0.477527 -0.993267  0.317743         0
Python  Out of sample dataframe tail 
Python          var_1     var_2     var_3     var_4     var_5  c_labels
Python  95  0.988951  0.559262 -0.959583  0.353533 -0.570316         0
Python  96  0.088504  0.250962 -0.876172  0.309089 -0.158381         0
Python  97 -0.215093 -0.267556  0.634200  0.644492  0.938260         0
Python  98  0.639926  0.526517  0.561968  0.129514  0.089443         1
Python  99 -0.772519 -0.462499  0.085293  0.423162  0.391327         0
Python  test data successfully saved to csv file 

Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable  var_3, selected 87.0 %
Python   Variable  var_2, selected 81.0 %
Python   Variable  var_4, selected 20.0 %
Python   Variable  var_1, selected 19.0 %
Python   Variable  var_5, selected 18.0 %
Python   Out of sample accuracy is 92.0 %
Python  lfs model saved to 
Python    C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json

运行MQL5脚本LFSmodelImportDemo.mq5的输出结果。

LFSmodelImportDemo (BTCUSD,D1)  Accuracy is 92.0 %

通过比较两者的结果，我们可以看出它们的输出一致，这表明模型导出的方法按预期正常运行。

结论

局部特征选择（Local Feature Selection, LFS）为特征选择提供了一种创新的方法，特别适合金融市场的动态环境。通过识别局部相关的特征，LFS克服了传统方法的局限性，这些传统方法依赖于单一的全局特征集。该算法对不同数据模式的适应性、管理非线性关系的能力以及平衡相互冲突目标的能力，使其成为构建机器学习模型的有力工具。尽管LFSpy包提供了LFS的实际实现，但在大规模数据集上，仍有进一步优化其计算效率的潜力。总而言之，LFS为数据复杂且不断演变的领域中的分类任务提供了一种有前景的方法。

文件名	说明
Mql5/include/np.mqh	包含用于各种矩阵和向量工具函数的通用定义的文件。
Mql5/include/lfspy.mqh	一个包含Clfspy类定义的文件，该类为MetaTrader 5程序中LFS模型的推导功能提供支持。
Mql5/scripts/JsonModel.py	一个本地Python模块，包含将LFS模型以JSON格式导出的功能定义。
Mql5/scripts/LFSdemo.py	一个Python脚本，展示如何使用LocalFeatureSelection类通过随机变量进行特征选择。
Mql5/scripts/LFSmodelExportDemo.py	一个Python脚本，展示如何将LFS模型导出以便在MetaTrader 5中使用。
Mql5/scripts/LFSmodelImportDemo.mq5	一个MQL5脚本，展示如何在MetaTrader 5程序中加载和使用导出的LFS模型。