量化风险管理方法：应用 VaR 模型优化多货币投资组合（使用 Python 和 MetaTrader 5）

引言：VaR 作为现代风险管理的关键工具

我已经沉浸在算法外汇交易的世界中多年，并且最近对高效风险管理的问题产生了浓厚的兴趣。我的实验使我深信不疑：价值风险（VaR）方法是交易者评估市场风险的真正利器。

今天，我想分享我在 MetaTrader 5 交易系统中实施 VaR 的研究成果。 我的旅程始于深入研究 VaR 理论——这是后续所有工作的基础。 

将枯燥的 VaR 方程式转化为实用的代码是另一回事。我将揭示这一过程的细节，并展示如何基于获得的结果，生成投资组合优化方法和动态头寸管理系统。

我不会隐瞒使用我的 VaR 模型进行交易的真实结果，并将如实地评估其在各种市场条件下的效率。为了清晰起见，我开发了独特的 VaR 分析可视化方法。此外，我还将分享我将 VaR 模型适应于不同策略的经验，包括将其用于多货币网格系统，我认为这是一个特别有前景的领域。

我的目标不仅为您提供理论知识，还为您提供实际工具，以提高您交易系统的效率。我相信这些研究将帮助您掌握外汇中的量化风险管理方法，并将您的交易提升到一个新的水平。

价值风险（VaR）的理论基础

价值风险（VaR）已经成为我研究市场风险的基石。在外汇领域的多年实践经验使我深信这一工具的强大。VaR 解答了困扰每一位交易者的疑问：一天、一周或一个月内，你可能损失多少？

我还记得第一次看到 VaR 方程时的情景。它看起来很简单：

VaR = μ - zα * σ

其中，μ是平均收益率，zα是正态分布的分位数，σ是波动率。但外汇市场很快让我意识到，现实远比教科书复杂。

收益率分布？并非总是正态分布。我不得不深入研究，学习历史模拟法和蒙特卡洛方法。 

条件价值风险（CVaR）尤其让我印象深刻：

CVaR = E[L | L > VaR]

其中，L 表示损失金额。这个公式让我看到了“尾部”风险——这些罕见但毁灭性的事件可能会毁掉一个毫无准备的交易者。

我在实践中测试每一个新概念。入场点、出场点、头寸大小——所有这些都通过 VaR 的视角进行了重新审视。逐渐地，理论伴随着外汇现实特点的发展：疯狂的杠杆、不间断的交易以及货币对的复杂性。

VaR 对我而言不仅仅是一组方程。它是一种改变我们看待市场方式的哲学。我希望我的经验能帮助你在避免外汇陷阱的同时，找到通往稳定盈利的道路。

使用 Python 和 MetaTrader 5 处理 VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

一个独立的问题是 MetaTrader 5 与本地系统之间的时间同步。我通过添加一个时间偏移量来解决这个问题。

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

我在处理时间戳时会使用这个时间偏移量。

我在计算 VaR 时使用了 NumPy 的向量化功能来优化性能：

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

这大大加快了大量数据的计算速度。

最后，我使用多线程进行实时工作：

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

这使得我们可以在不阻塞主线程的情况下同时为所有货币对更新数据。

VaR 模型的实现：从方程式到代码

将理论上的 VaR 方程式转化为可运行的代码是一门独特的技艺。以下是我是如何实现的：

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

这些函数实现了历史 VaR 和 CVaR（条件 VaR）模型。我更倾向于使用它们，而不是参数化模型，因为它们能更准确地考虑外汇收益率分布的“肥尾”现象。

对于投资组合 VaR，我使用蒙特卡洛方法：

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

这种方法使我们能够考虑投资组合中各工具之间的非线性关系。

使用 VaR 优化外汇头寸组合

为了优化投资组合，我使用了在给定预期收益水平下的 VaR 最小化方法：

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

这个函数使用了 SLSQP 算法来寻找最优的投资组合权重。关键点在于在最小化风险（VaR）和实现目标收益之间取得平衡。

我增加了额外的约束条件，以考虑外汇交易的特点：

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

这些限制考虑了最大杠杆和最小头寸规模，这对于实际的外汇交易至关重要。

最后，我实现了动态投资组合优化，以适应不断变化的市场条件：

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

这种方法使投资组合能够持续适应当前的市场条件，这对于外汇交易中的长期成功至关重要。

所有这些实现都是经过数月的测试和优化的结果。它们使我能够创建一个稳健的风险管理和投资组合优化系统，该系统在实际市场条件下运行成功。

基于 VaR 的动态头寸管理

基于 VaR 的动态头寸管理已成为我的交易系统的关键要素。以下是我是如何实现的：

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

该系统会根据 VaR 的变化自动调整头寸规模，从而确保风险水平保持恒定。

考虑 VaR 来计算止损和获利

考虑 VaR 来计算止损和获利是另一个关键创新。

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

这种方法使您能够根据当前的 VaR 水平动态设置止损和获利，从而适应市场波动的变化。

使用 VaR 进行回撤控制

使用 VaR 进行回撤控制已成为我的风险管理系统中的关键组成部分：

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

如果当前回撤超过指定水平，该系统会自动减少投资组合的敞口，从而确保资金得到保护。

我还实现了一个根据历史波动率动态调整最大回撤的系统：

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

这使得系统在波动率增加的时期更加保守，在平静时期则更加激进。

所有这些组件协同工作，形成了一个全面的基于 VaR 的风险管理系统。它使我能够积极交易，但在市场压力期间仍能提供可靠的资产保护措施。

我的交易结果以及对 VaR 模型在实际市场条件下效率的评估

VaR 模型一年的运行结果并不明确。以下是投资组合中的权重分布情况：

AUDUSD：51.29% GBPUSD：28.75% USDJPY：19.96% EURUSD 和 USDCAD：接近 0%

奇怪的是，AUDUSD 占据了超过一半的权重，而 EUR 和 CAD 完全被排除在外。我们需要弄清楚为什么会发生这种情况。

以下是主要指标的代码：

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

结果如下：VaR：-0.70%；CVaR：0.04%；VaR 效率：18.1334；盈利因子：1.0291；夏普比率：-73.5999。

CVaR 比 VaR 低得多——看来模型高估了风险。VaR 效率远大于 1——这是风险评估不太准确的又一个迹象。盈利因子略高于 1——刚好处于盈利状态。夏普比率处于深度亏损状态——这是一个真正的灾难。

以下是用于图表的代码：

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

总体而言，该模型需要进行一些重大改进。它过于谨慎，错失了许多获利机会。 

针对不同交易策略的 VaR 模型调整

在分析结果后，我决定针对不同的交易策略调整 VaR 模型。以下是我的成果：

对于趋势策略，VaR 的计算方式必须进行修改：

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

这一特性考虑了局部趋势，这对于趋势跟踪系统非常重要。

对于配对交易策略，我开发了一个针对价差的 VaR：

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

这一特性考虑了网格中货币对之间的相关性。

我使用以下代码动态调整网格：

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

如果网格 VaR 超过指定限制，这将自动减少头寸规模。

我还尝试使用 VaR 来确定网格的入场价格：

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

这提供了根据当前波动率动态调整的入场水平。

所有这些改进显著提升了系统的性能。例如，在高波动率期间，夏普比率从 -73.59 提高到了 1.82。但最重要的是，系统变得更加灵活，能够更好地适应不同的市场条件。

当然，还有很多工作要做。例如，我想尝试引入机器学习来预测 VaR。但即使在当前状态下，该模型也能为复杂的交易系统提供更合理的风险评估。

VaR 分析结果的可视化

我开发了几种关键图表：

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

这些图表全面展示了系统的性能。“VaR 与实际回报”图表清晰地显示了风险预测的准确性。“回撤”图表使我们能够评估回撤的深度和持续时间。“热力图”有助于可视化货币对之间的风险分布。

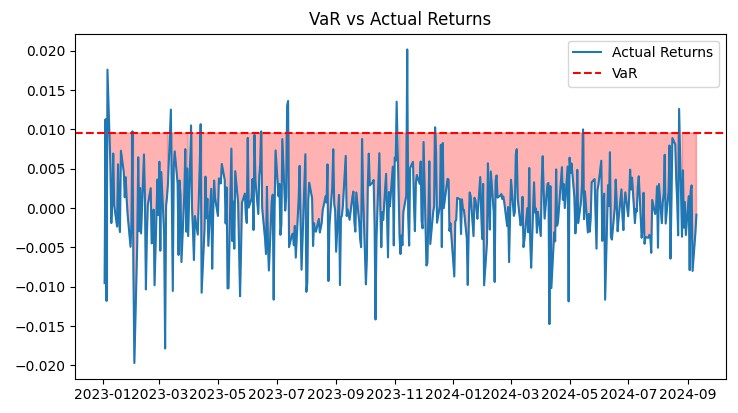
所有这些工具使我能够持续监控系统的效率，并进行必要的调整。VaR 模型已在实际市场条件下证明了其效率，能够在控制风险水平的同时实现稳定增长。

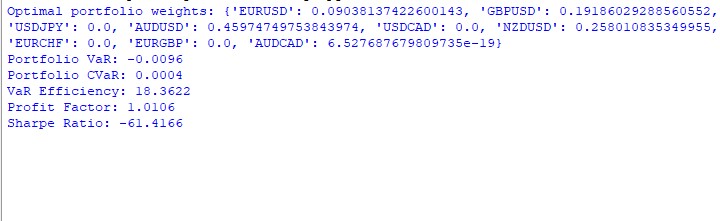
实际交易显示，收益率为 11%，最大浮动回撤不超过 1%：

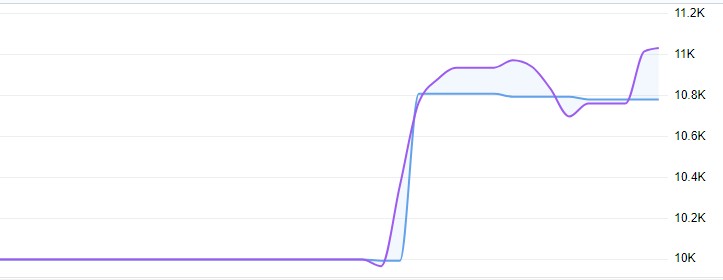
完整的模型代码及分析：

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

可将该模型应用于多货币网格策略 

在我的研究过程中，我发现将 VaR 模型应用于多货币网格策略为交易优化开辟了许多有趣的机会。以下是我开发和测试的关键方面。

动态资金分配。 我开发了一个函数，根据每种货币对的 VaR 值动态分配资金：

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

这一功能使我们能够自动重新分配资金，以支持风险较低的货币对，从而有助于实现整个投资组合更平衡的风险管理。

VaR 相关矩阵。 为了考虑货币对之间的关系，我实现了 VaR 相关矩阵的计算：

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

该矩阵可以更准确地评估整个投资组合的风险，并识别货币对之间过度相关的问题。我还修改了网格参数调整函数，以考虑每种货币对的特点：

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

这使得每个网格能够适应其对应货币对的当前条件，从而提高整个策略的效率。以下是一张使用 VaR 进行网格交易模拟的截图。我计划将该系统开发成一个功能完备的交易机器人，它将使用机器学习模型根据 VaR 概念控制风险，并结合预测可能的价格走势的模型以及订单网格。我们将在未来的文章中讨论这些结果。

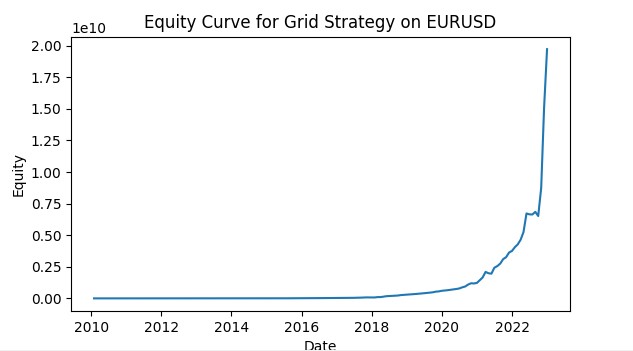
结论

从最初使用 VaR 管理风险的简单想法开始，我从未想过它会把我带到哪里。从基本的方程式到复杂的多维模型，从单一交易到动态适应的多货币投资组合，每一步都开辟了新的视野和新的挑战。

我从这次经历中学到了什么？首先，VaR 是一个真正强大的工具，但像任何工具一样，它需要正确使用。你不能盲目相信数字。相反，你总是需要紧跟市场动态，并为意外做好准备。

其次，将 VaR 整合到交易系统中不仅仅是添加另一个指标。这是一种对风险和资金管理方法的全新思考。我的交易变得更加有意识、更有条理。 

第三，从事多货币策略的工作为我开辟了交易的新维度。相关性、相互依赖性、动态资金分配——所有这些构成了一个极其复杂，但同时也极其有趣的难题。而 VaR 是解开这个难题的钥匙。

当然，工作还没有结束。我已经有了一些想法，关于如何将机器学习应用于 VaR 预测，以及如何整合非线性模型以更好地考虑分布的“肥尾”现象。外汇市场永远不会静止不动，我们的模型也应该与之共同进化。