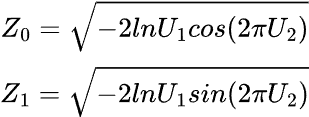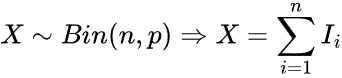MetaTrader 5 / Эксперты
English Deutsch 日本語
preview
Машинное обучение и Data Science (Часть 35): NumPy в MQL5 – искусство создания сложных алгоритмов с меньшим объемом кода

Машинное обучение и Data Science (Часть 35): NumPy в MQL5 – искусство создания сложных алгоритмов с меньшим объемом кода

MetaTrader 5 — Эксперты |
104 0
Omega J Msigwa
Omega J Msigwa

Содержание

Стоит только поверить, что вы можете, — и вы уже на полпути к цели

-- Теодор Рузвельт.

Введение

Ни один язык программирования не является полностью самодостаточным для решения всех возможных задач, которые мы можем себе представить, создавая код. Каждый язык программирования зависит от хорошо разработанных инструментов - библиотек, фреймворков и модулей, помогающих решать определенные проблемы и воплощать идеи в реальность.

MQL5 не является исключением. Разработанная в первую очередь для алгоритмической торговли, на ранних этапах ее функциональность в основном ограничивалась торговыми операциями. В отличие от своего предшественника, языка MQL4, MQL5 гораздо мощнее и функциональнее. Однако для создания полноценного торгового робота требуется нечто большее, чем просто вызов функций для совершения сделок купли и продажи.

Для работы в сложных условиях финансовых рынков трейдеры часто используют сложные математические методы, включая машинное обучение и искусственный интеллект (ИИ). Это привело к росту спроса на оптимизированные кодовые базы и специализированные фреймворки, способные эффективно обрабатывать сложные вычисления.

источник изображения: pexels.com

Для полного понимания статьи требуются базовые знания Python и NumPy.



Почему NumPy?

Что касается сложных вычислений в MQL5, у нас есть множество хороших библиотек, предоставляемых MetaQuotes, таких как Fuzzy, Stat, а также мощный Alglib (находится в MetaEditor в папке MQL5\Include\Math).

Эти библиотеки содержат множество функций, подходящих для программирования сложных советников с минимальными усилиями, однако большинство функций в них не отличаются гибкостью из-за чрезмерного использования массивов и указателей на объекты, не говоря уже о том, что для их правильного использования требуются математические знания.

После введения матриц и векторов язык MQL5 стал более универсальным и гибким в плане хранения данных и вычислений, особенно в отношении массивов, представляющих собой объекты, которые сопровождаются множеством встроенных математических функций, ранее требовавших ручной реализации.

Благодаря гибкости матриц и векторов, мы можем расширить их возможности до чего-то большего, создав набор различных математических функций, аналогичных тем, что присутствуют в NumPy (Numerical Python - библиотека Python, предлагающая набор высокоуровневых математических функций, включая поддержку многомерных массивов, маскированных массивов и матриц).

Можно с уверенностью сказать, что большинство функций, предлагаемых для работы с матрицами и векторами в MQL5, были вдохновлены NumPy, как это видно в документации. Синтаксис очень похож.


MQL5

 Python 
vector::Zeros(3);
vector::Full(10);
 
numpy.zeros(3)
numpy.full(10)

Согласно документации, подобный синтаксис был введен для того, чтобы "перенести алгоритмы и коды с языка Python на MQL5 с минимальными затратами. Таким образом, множество задач по обработке данных, решению математических уравнений, нейросетям и по машинному обучению можно решать с использованием готовых наработок и библиотек языка Python".

Это правда, но функций, предоставляемых матрицами и векторами, недостаточно. Нам по-прежнему не хватает множества важных функций, которые часто необходимы для перевода алгоритмов и кода из Python в MQL5. В этой статье мы реализуем некоторые из наиболее полезных функций и методов NumPy в MQL5, используя очень похожий синтаксис, чтобы значительно упростить перевод алгоритмов из языка программирования Python.

Чтобы синтаксис оставался похожим на синтаксис Python, мы будем использовать строчные буквы для обозначения названий функций. Начнем с методов инициализации векторов и матриц.


Инициализация векторов и матриц

Для работы с векторами и матрицами нам необходимы методы для их инициализации путем заполнения их некоторыми значениями. Ниже перечислены некоторые функции, необходимые для выполнения этой задачи.


Метод

 Описание 
template <typename T>
vector CNumpy::full(uint size, T fill_value) { return vector::Full(size, fill_value); }
template <typename T>
matrix CNumpy::full(uint rows, uint cols, T fill_value) { return matrix::Full(rows, cols, fill_value); }
 Создаем новый вектор/матрицу заданного размера/количества строк и столбцов, заполненную значением. 
vector CNumpy::ones(uint size) { return vector::Ones(size); }
matrix CNumpy::ones(uint rows, uint cols) { return matrix::Ones(rows, cols); }
 Создаем новый вектор заданного размера/матрицу с заданным количеством строк и столбцов, заполненную единицами. 
vector CNumpy::zeros(uint size) { return vector::Zeros(size); }
matrix CNumpy::zeros(uint rows, uint cols) { return matrix::Zeros(rows, cols); }
 Создаем вектор заданного размера/матрицу с заданным количеством строк и столбцов, заполненную нулями. 
matrix CNumpy::eye(const uint rows, const uint cols, const int ndiag=0) { return matrix::Eye(rows, cols, ndiag); }
 Построим матрицу, у которой на диагонали находятся единицы, а на остальных позициях — нули. 
matrix CNumpy::identity(uint rows) { return matrix::Identity(rows, rows); }
 Построим квадратную матрицу, у которой на главной диагонали будут единицы.

Несмотря на свою простоту, эти методы имеют решающее значение для создания матриц-заполнителей и векторов, которые часто используются в преобразованиях, заполнении и дополнении данных. 

Пример использования:

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Initialization
    
    // Vectors One-dimensional
    
    Print("numpy.full: ",np.full(10, 2));
    Print("numpy.ones: ",np.ones(10));
    Print("numpy.zeros: ",np.zeros(10));
    
    // Matrices Two-Dimensional
    
    Print("numpy.full:\n",np.full(3,3, 2));
    Print("numpy.ones:\n",np.ones(3,3));
    Print("numpy.zeros:\n",np.zeros(3,3));
    Print("numpy.eye:\n",np.eye(3,3));
    Print("numpy.identity:\n",np.identity(3));
 }


Математические функции

Это обширная тема, поскольку существует множество математических функций, которые необходимо реализовать и описать как для векторов, так и для матриц, и мы обсудим лишь некоторые из них. Начнем с математических констант.

Константы

Математические константы так же полезны, как и функции.


Константа

 Описание

numpy.e

  Постоянная Эйлера, основание натуральных логарифмов, постоянная Непера.

numpy.euler_gamma  

  Определяется как предельная разность между гармоническим рядом и натуральным логарифмом.

np.inf

  

 Представление (положительной) бесконечности с плавающей запятой согласно стандарту IEEE 754.

np.nan


 Представление Not a Number (NaN) с плавающей запятой согласно стандарту IEEE 754.
np.pi
 Приблизительно равно 3,14159, то есть отношению длины окружности к ее диаметру. 

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    Print("numpy.e: ",np.e);
    Print("numpy.euler_gamma: ",np.euler_gamma);
    Print("numpy.inf: ",np.inf);
    Print("numpy.nan: ",np.nan);
    Print("numpy.pi: ",np.pi);
 }

Функции

Ниже перечислены некоторые функции, присутствующие в классе CNumpy.

Метод
Описание

 
vector CNumpy::add(const vector&a, const vector&b) { return a+b; };
matrix CNumpy::add(const matrix&a, const matrix&b) { return a+b; };
 Добавляет два вектора/матрицы. 
vector CNumpy::subtract(const vector&a, const vector&b) { return a-b; };
matrix CNumpy::subtract(const matrix&a, const matrix&b) { return a-b; };
 Вычитает два вектора/матрицы. 
vector CNumpy::multiply(const vector&a, const vector&b) { return a*b; };
matrix CNumpy::multiply(const matrix&a, const matrix&b) { return a*b; };
 Умножает два вектора/матрицы. 
vector CNumpy::divide(const vector&a, const vector&b) { return a/b; };
matrix CNumpy::divide(const matrix&a, const matrix&b) { return a/b; };
 Делит два вектора/матрицы 
vector CNumpy::power(const vector&a, double n) { return MathPow(a, n); };
matrix CNumpy::power(const matrix&a, double n) { return MathPow(a, n); };
 Возводит все элементы матрицы/вектора a в степень n. 
vector CNumpy::sqrt(const vector&a) { return MathSqrt(a); }; 
matrix CNumpy::sqrt(const matrix&a) { return MathSqrt(a); };
 Вычисляет квадратный корень из каждого элемента вектора/матрицы a.

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    vector a = {1,2,3,4,5};
    vector b = {1,2,3,4,5};  
    
    Print("np.add: ",np.add(a, b));
    Print("np.subtract: ",np.subtract(a, b));
    Print("np.multiply: ",np.multiply(a, b));
    Print("np.divide: ",np.divide(a, b));  
    Print("np.power: ",np.power(a, 2));
    Print("np.sqrt: ",np.sqrt(a));
    Print("np.log: ",np.log(a));
    Print("np.log1p: ",np.log1p(a));
 }


Статистические функции

Их также можно отнести к математическим функциям, но в отличие от основных математических операций, эти функции помогают получить аналитические показатели на основе заданных данных. В машинном обучении они используются в основном для проектирования признаков и нормализации.

В таблице ниже представлены некоторые функции, реализованные в классе MQL5-Numpy.


Метод

 Описание 
double sum(const vector& v) { return v.Sum(); }
double sum(const matrix& m) { return m.Sum(); };
vector sum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Sum(axis); };
 Вычисляет сумму элементов вектора/матрицы, что также может быть выполнено для заданной оси (осей). 
double mean(const vector& v) { return v.Mean(); }
double mean(const matrix& m) { return m.Mean(); };
vector mean(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Mean(axis); };


Вычисляет среднее арифметическое значений элементов вектора/матрицы.

 
double var(const vector& v) { return v.Var(); }
double var(const matrix& m) { return m.Var(); };
vector var(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Var(axis); };


Вычисляет дисперсию значений элементов матрицы/вектора.

 
double std(const vector& v) { return v.Std(); }
double std(const matrix& m) { return m.Std(); };
vector std(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Std(axis); };


Возвращает стандартное отклонение значений элементов вектора/матрицы или элементов вдоль заданной оси.

 
double median(const vector& v) { return v.Median(); }
double median(const matrix& m) { return m.Median(); };
vector median(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Median(axis); };
  

Вычисляет медиану элементов вектора/матрицы.

 
double percentile(const vector &v, int value) { return v.Percentile(value); }
double percentile(const matrix &m, int value) { return m.Percentile(value); }
vector percentile(const matrix &m, int value, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Percentile(value, axis); }

Вычисляют указанный процентиль значений элементов вектора/матрицы или элементов вдоль заданной оси.

 
double quantile(const vector &v, int quantile_) { return v.Quantile(quantile_); } 
double quantile(const matrix &m, int quantile_) { return m.Quantile(quantile_); }
vector quantile(const matrix &m, int quantile_, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Quantile(quantile_, axis); }
  

Вычисляют указанный квантиль значений элементов матрицы/вектора или элементов вдоль указанной оси.

 
vector cumsum(const vector& v) { return v.CumSum(); };
vector cumsum(const matrix& m) { return m.CumSum(); };
matrix cumsum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumSum(axis); };

Возвращают кумулятивную сумму элементов матрицы/вектора, в том числе и по заданной оси.

 
vector cumprod(const vector& v) { return v.CumProd(); }
vector cumprod(const matrix& m) { return m.CumProd(); };
matrix cumprod(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumProd(axis); };
  

Возвращает кумулятивное произведение элементов массива/вектора, в том числе и по заданной оси.

 
double average(const vector &v, const vector &weights) { return v.Average(weights); }
double average(const matrix &m, const matrix &weights) { return m.Average(weights); }
vector average(const matrix &m, const matrix &weights, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Average(weights, axis); }


Вычисляет взвешенное среднее арифметическое значений матрицы/вектора.

 
ulong argmax(const vector& v) { return v.ArgMax(); }
ulong argmax(const matrix& m) { return m.ArgMax(); }
vector argmax(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMax(axis); };
  

Возвращают индекс максимального значения.


 
ulong argmin(const vector& v) { return v.ArgMin(); }
ulong argmin(const matrix& m) { return m.ArgMin(); }
vector argmin(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMin(axis); };
 Возвращают индекс минимального значения. 
double min(const vector& v) { return v.Min(); }
double min(const matrix& m) { return m.Min(); }
vector min(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Min(axis); };
 Возвращают минимальное значение в векторе/матрице, включая значения вдоль указанной оси. 
double max(const vector& v) { return v.Max(); }
double max(const matrix& m) { return m.Max(); }
vector max(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Max(axis); };
 Возвращают максимальное значение в векторе/матрице, включая значения вдоль указанной оси. 
double prod(const vector &v, double initial=1.0) { return v.Prod(initial); }
double prod(const matrix &m, double initial) { return m.Prod(initial); }
vector prod(const matrix &m, double initial, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Prod(axis, initial); }
  

Вычисляют произведение элементов матрицы/вектора, которое так же может выполняться по указанной оси.

 
double ptp(const vector &v) { return v.Ptp(); }
double ptp(const matrix &m) { return m.Ptp(); }
vector ptp(const matrix &m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Ptp(axis); }
  

Возвращают диапазон значений матрицы/вектора или указанной оси матрицы, эквивалентны результату Max() - Min(). Ptp - Peak to peak, от пика до пика.

Эти функции управляются встроенными статистическими функциями для векторов и матриц, как это видно в документации. Всё, что я сделал, это создал синтаксис, похожий на NumPy, и обернул эти функции.

Ниже приведен пример использования этих функций.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
//--- Statistical functions
   
     vector z = {1,2,3,4,5};
    
     Print("np.sum: ", np.sum(z));
     Print("np.mean: ", np.mean(z));
     Print("np.var: ", np.var(z));
     Print("np.std: ", np.std(z));
     Print("np.median: ", np.median(z));
     Print("np.percentile: ", np.percentile(z, 75));
     Print("np.quantile: ", np.quantile(z, 75));
     Print("np.argmax: ", np.argmax(z));
     Print("np.argmin: ", np.argmin(z));
     Print("np.max: ", np.max(z));
     Print("np.min: ", np.min(z));
     Print("np.cumsum: ", np.cumsum(z));
     Print("np.cumprod: ", np.cumprod(z));
     Print("np.prod: ", np.prod(z));
     
     vector weights = {0.2,0.1,0.5,0.2,0.01};
     Print("np.average: ", np.average(z, weights));
     Print("np.ptp: ", np.ptp(z));
}


Генераторы случайных чисел

NumPy имеет множество удобных подмодулей, одним из которых является random submodule (подмодуль случайных чисел). 

Подмодуль numpy.random предоставляет различные функции генерации случайных чисел на основе генератора случайных чисел PCG64 (начиная с NumPy 1.17+). Большинство этих методов основаны на математических принципах из теории вероятностей и статистических распределений.

В машинном обучении мы часто генерируем случайные числа для множества задач, в частности в качестве начальных весов для нейронных сетей и многих моделей, использующих итеративные методы градиентного спуска для обучения, а иногда мы даже генерируем случайные признаки, которые следуют статистическому распределению, чтобы получить выборочные тестовые данные для наших моделей.

Крайне важно, чтобы генерируемые нами случайные числа соответствовали статистическому распределению, чего мы не можем достичь, используя встроенные функции генерации случайных чисел в MQL5.

Во-первых, вот как можно установить начальное значение генератора случайных чисел для подмодуля CNumpy.random.

np.random.seed(42);


Равномерное распределение #

Мы генерируем случайные числа из равномерного распределения между некоторыми низкими и высокими значениями.

Формула:

где R - случайное число из [0,1].

 template <typename T>
 vector uniform(T low, T high, uint size=1)
  { 
    vector res = vector::Zeros(size);
    for (uint i=0; i<size; i++)
       res[i] = low + (high - low) * (rand() / double(RAND_MAX));  // Normalize rand()
    
    return res;
  }

Применение.

Внутри файла Numpy.mqh была создана отдельная структура CRandom, которая затем вызывается внутри класса CNumpy. Это позволяет нам вызывать структуру внутри класса, обеспечивая синтаксис, похожий на Python.

class CNumpy
  {
protected:
    
public:
                     CNumpy(void);
                    ~CNumpy(void);
                    
                    CRandom random;
  }
Print("np.random.uniform: ",np.random.uniform(1,10,10));

Результаты.

2025.03.16 15:03:15.102 Numpy  np.random.uniform: [8.906552323984496,9.274605548265022,7.828760643330179,9.355082857753228,2.218420972319712,5.772331919309061,3.76067384868923,6.096438489944151,1.93908505508591,8.107272560808131]

Мы можем визуализировать результаты, чтобы увидеть, равномерно ли распределены данные.



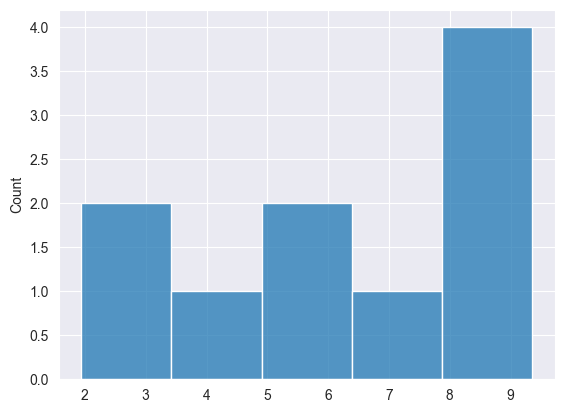
Нормальное распределение #

Метод используется во многих моделях машинного обучения, например, для инициализации весов нейронной сети.

Реализацию можно выполнить с помощью преобразования Бокса-Мюллера.

Формула:

где:

 являются случайными числами из [0,1]

 vector normal(uint size, double mean=0, double std=1)
   {
       vector results = {};  // Declare the results vector
       
       // We generate two random values in each iteration of the loop
       uint n = size / 2 + size % 2;  // If the size is odd, we need one extra iteration
   
       // Loop to generate pairs of normal numbers
       for (uint i = 0; i < n; i++)
       {
           // Generate two random uniform variables
           double u1 = MathRand() / 32768.0;  // Uniform [0,1] -> (MathRand() generates values from 0 to 32767)
           double u2 = MathRand() / 32768.0;  // Uniform [0,1]
   
           // Apply the Box-Muller transform to get two normal variables
           double z1 = MathSqrt(-2 * MathLog(u1)) * MathCos(2 * M_PI * u2);
           double z2 = MathSqrt(-2 * MathLog(u1)) * MathSin(2 * M_PI * u2);
   
           // Scale to the desired mean and standard deviation, and add them to the results
           results = push_back(results, mean + std * z1);
           if ((uint)results.Size() < size)  // Only add z2 if the size is not reached yet
               results = push_back(results, mean + std * z2);
       }
       
       // Return only the exact size of the results (if it's odd, we cut off one value)
       
       results.Resize(size);
       return results;
   }

Применение.

Print("np.random.normal: ",np.random.normal(10,0,1));

Результаты.

2025.03.16 15:33:08.791 Numpy test (US Tech 100,H1)     np.random.normal: [-1.550635379340936,0.963285267506685,0.4587699653416977,-0.4813064556591148,-0.6919587880027229,1.649030932484221,-2.433415738330552,2.598464400400878,-0.2363726420659525,-0.1131299501178828]



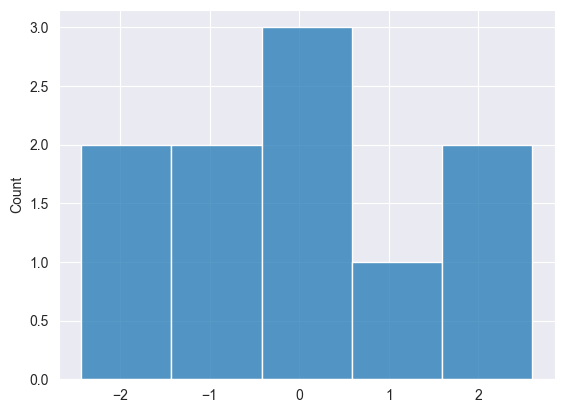
Экспоненциальное распределение #

Экспоненциальное распределение — это распределение вероятностей, описывающее время между событиями в процессе Пуассона, где события происходят непрерывно и независимо друг от друга с постоянной средней скоростью.

Задается формулой:

Для генерации случайных чисел, распределенных по экспоненциальному закону, мы используем метод обратного преобразования выборки. Формула следующая:

где:

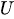  •  - это равномерно распределенное случайное число от 0 до 1.
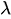  •  - параметр скорости.

 vector  exponential(uint size, double lmbda=1.0)
   {
      vector res = vector::Zeros(size);
      for (uint i=0; i<size; i++)
         res[i] = -log((rand()/RAND_MAX)) / lmbda;
          
      return res;
   }

Применение.

Print("np.random.exponential: ",np.random.exponential(10));

Результаты.

2025.03.16 15:57:36.124 Numpy test (US Tech 100,H1)     np.random.exponential: [0.4850272647406031,0.7617651806321184,1.09800210467871,2.658253432915927,0.5814831387699247,0.9920104404467721,0.7427922283035616,0.09323707153463576,0.2963563234048633,1.790326127008611]



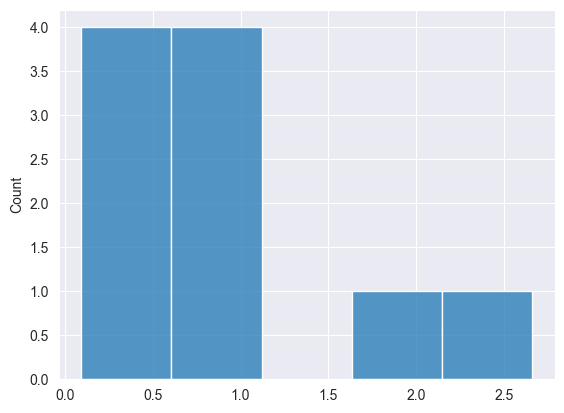
Биномиальное распределение #

Это дискретное распределение вероятностей, моделирующее количество успехов в фиксированном числе независимых испытаний, каждое из которых имеет одинаковую вероятность успеха.

Задается формулой:

Мы можем реализовать его следующим образом.

// Function to generate a single Bernoulli(p) trial
int bernoulli(double p)
  {
    return (double)rand() / RAND_MAX < p ? 1 : 0;
  }
// Function to generate Binomial(n, p) samples
vector binomial(uint size, uint n, double p)
  {
    vector res = vector::Zeros(size);
    
    for (uint i = 0; i < size; i++)
      {
        int count = 0;
        for (uint j = 0; j < n; j++)
          count += bernoulli(p); // Sum of Bernoulli trials

        res[i] = count;
      }
    
    return res;
}

Применение.

Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));

Результаты.

2025.03.16 19:35:20.346 Numpy test (US Tech 100,H1)     np.random.binomial: [2,1,2,3,2,1,1,4,0,3]



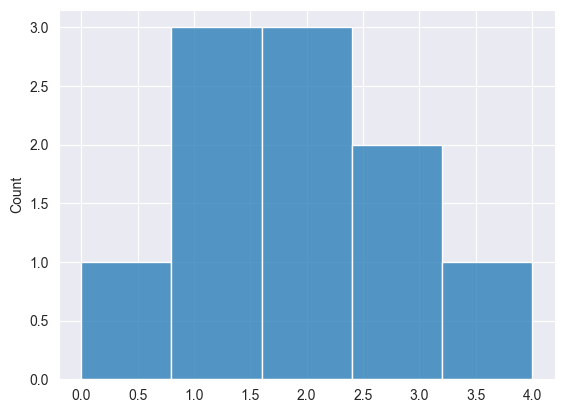
Распределение Пуассона #

Это распределение вероятностей, выражающее вероятность наступления заданного числа событий за фиксированный интервал времени или пространства при условии, что эти события происходят с постоянной средней частотой и независимо от времени, прошедшего с момента последнего события.

Формула.

где:

  •  - это количество вхождений (0,1,2...)
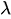  •  (лямбда) — средняя частота возникновения.
  • e - число Эйлера.

int poisson(double lambda)
   {
       double L = exp(-lambda);
       double p = 1.0;
       int k = 0;
   
       while (p > L)
       {
           k++;
           p *= MathRand() / 32767.0; // Normalize MathRand() to (0,1)
       }
       
       return k - 1; // Since we increment k before checking the condition
   }
// We generate a vector of Poisson-distributed values
vector poisson(double lambda, int size)
{
    vector result = vector::Zeros(size);
    for (int i = 0; i < size; i++)
        result[i] = poisson(lambda);
    
    return result;
}

Применение.

Print("np.random.poisson: ",np.random.poisson(4, 10));

Результаты.

2025.03.16 18:39:56.058 Numpy test (US Tech 100,H1)     np.random.poisson: [6,6,5,1,3,1,1,3,6,7]




Перетасовка #

При обучении моделей машинного обучения распознаванию закономерностей в данных мы часто перетасовываем образцы, чтобы помочь моделям понять закономерности, присутствующие в данных, а не их расположение.

Функция перетасовки очень удобна в подобных ситуациях.

Пример использования.

vector data = {1,2,3,4,5,6,7,8,9,10};
np.random.shuffle(data);

Print("Shuffled: ",data);

Результаты.

2025.03.16 18:55:36.763 Numpy test (US Tech 100,H1)     Shuffled: [6,4,9,2,3,10,1,7,8,5]


Случайный выбор #

Подобно функции перетасовки эта функция случайным образом выбирает значения из заданного одномерного массива, но с возможностью перетасовки как с заменой, так и без нее.

template<typename T>
vector<T> choice(const vector<T> &v, uint size, bool replace=false)

С заменой.

Значения не будут уникальными, одни и те же элементы могут повторяться в результирующем перетасованном векторе/массиве.

vector data = {1,2,3,4,5,6,7,8,9,10};

Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));

Результаты.

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=True: [5,3,9,2,1,3,4,7,8,3]

Без замены.

В результате перемешивания вектор будет содержать уникальные элементы, точно такие же, как и в исходном векторе, изменится только их порядок.

Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));

Результаты.

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=False: [8,4,3,10,5,7,1,9,6,2]

Все функции в одном месте.

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Random numbers generating
    
    np.random.seed(42);
    
    Print("---------------------------------------:");  
    Print("np.random.uniform: ",np.random.uniform(1,10,10));
    Print("np.random.normal: ",np.random.normal(10,0,1));
    Print("np.random.exponential: ",np.random.exponential(10));
    Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));
    Print("np.random.poisson: ",np.random.poisson(4, 10));
    
    vector data = {1,2,3,4,5,6,7,8,9,10};
    //np.random.shuffle(data);
    //Print("Shuffled: ",data);
    
    Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));
    Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));
 }


Быстрое преобразование Фурье (Fast Fourier Transform, FFT) #

Быстрое преобразование Фурье (FFT) — это алгоритм, который вычисляет дискретное преобразование Фурье (discrete Fourier transform, DFT) последовательности или его обратное (inverse, IDFT). Преобразование Фурье преобразует сигнал из его исходной области (часто временной или пространственной) в представление в частотной области и наоборот. DFT получают путем разложения последовательности значений на компоненты с различными частотами (подробности).

Эта операция полезна во многих областях, например:

  1. В обработке сигналов и звука она используется для преобразования звуковых волн во временной области в частотные спектры. При кодировании аудиоформатов и фильтрации шума.
  2. Для сжатия изображений и распознавания образов на изображениях.
  3. Специалисты по анализу данных часто используют FFT для извлечения признаков из данных временных рядов.

Подмодуль numpy.fft отвечает за работу с FFT.

В текущей версии CNumpy я реализовал только одномерные функции Standard FFT.

Прежде чем мы рассмотрим методы Standard FFT в классе, разберемся с функцией генерации частот DFT.

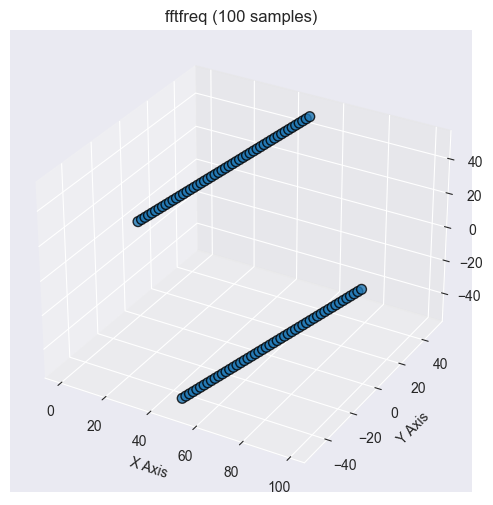
Частота FFT

При выполнении быстрого преобразования Фурье (FFT) над сигналом или данными выходные данные находятся в частотной области; для их интерпретации необходимо знать, какой частоте соответствует каждый элемент FFT. Вот тут-то и пригодится этот метод.

Функция возвращает частоты дискретного преобразования Фурье (DFT), соответствующие FFT заданного размера. Это помогает определить соответствующие частоты для каждого коэффициента FFT.

vector fft_freq(int n, double d)

Пример использования.

2025.03.17 11:11:10.165 Numpy test (US Tech 100,H1)     np.fft.fftfreq: [0,0.1,0.2,0.3,0.4,-0.5,-0.4,-0.3,-0.2,-0.1]



Стандартные быстрые преобразования Фурье #

FFT

Эта функция вычисляет FFT входного сигнала, преобразуя его из временной области в частотную. Это эффективный алгоритм для вычисления дискретного преобразования Фурье (DFT).

vector<complex> fft(const vector &x)

Эта функция построена на основе CFastFourierTransform::FFTR1D - функции, предоставляемой ALGLIB. Обратитесь к ALGLIB для более подробной информации.

Пример использования.

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
Print("np.fft.fft: ",np.fft.fft(signal));

Результаты.

2025.03.17 11:28:16.739 Numpy test (US Tech 100,H1)     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]

Обратное FFT

Функция вычисляет обратное быстрое преобразование Фурье (IFFT), которое преобразует данные из частотной области обратно во временную область. По сути, она сводит на нет эффект предыдущего метода np.fft.fft.

vector ifft(const vectorc &fft_values)

Пример использования.

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};

vectorc fft_res = np.fft.fft(signal); //perform fft
Print("np.fft.fft: ",fft_res); //fft results
Print("np.fft.ifft: ",np.fft.ifft(fft_res)); //Original signal

Результаты.

2025.03.17 11:45:04.537 Numpy test     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]
2025.03.17 11:45:04.537 Numpy test     np.fft.ifft: [-4.440892098500626e-17,0.09999999999999991,0.1999999999999999,0.2999999999999999,0.4,0.5,0.6,0.7,0.8000000000000002,0.9]


Линейная алгебра #

Линейная алгебра — это раздел математики, изучающий векторы, матрицы и линейные преобразования. Она лежит в основе многих областей, таких как физика, инженерия, наука о данных и т. д.

NumPy предоставляет модуль np.linalg, подмодуль, посвященный функциям линейной алгебры. Он предлагает практически все функции линейной алгебры, такие как решение линейных систем, вычисление собственных значений/векторов и многое другое.

Ниже приведены некоторые функции линейной алгебры, реализованные в классе CNumpy.


Метод

 Описание 
matrix inv(const matrix &m)  {  return m.Inv();  }

Вычисляет мультипликативную обратную матрицу квадратной обратимой матрицы методом Гаусса-Жордана.

 
double det(const matrix &m)  {  return m.Det();  }

Вычисляет определитель квадратной невырожденной матрицы.

 
matrix kron(const matrix &a, const matrix &b) { return a.Kron(b); }
matrix kron(const vector &a, const vector &b) { return a.Kron(b); }
matrix kron(const vector &a, const matrix &b) { return a.Kron(b); }
matrix kron(const matrix &a, const vector &b) { return a.Kron(b); }

Вычисляют произведение Кронекера двух матриц, матрицы и вектора, вектора и матрицы или двух векторов.

 
struct eigen_results_struct
  {
   vector eigenvalues;
   matrix eigenvectors;
  };

eigen_results_struct eig(const matrix &m) 
 {
   eigen_results_struct res;
   if (!m.Eig(res.eigenvectors, res.eigenvalues))
      printf("%s failed to calculate eigen vectors and values, error = %d",__FUNCTION__,GetLastError());
   
   return res;
 }

Функция вычисляет собственные значения и правые собственные векторы квадратной матрицы


 
double norm(const matrix &m, ENUM_MATRIX_NORM norm) {  return m.Norm(norm); }
double norm(const vector &v, ENUM_VECTOR_NORM norm) {  return v.Norm(norm); }

Возвращает норму матрицы или вектора (подробности).

 
svd_results_struct svd(const matrix &m)
  {
    svd_results_struct res;
    if (!m.SVD(res.U, res.V, res.singular_vectors))
      printf("%s failed to calculate the SVD");
    
    return res;
  }
 Вычисляет сингулярное разложение (Singular Value Decomposition, SVD).

 
vector solve(const matrix &a, const vector &b) { return a.Solve(b); }

Решает линейное матричное уравнение или систему линейных алгебраических уравнений.

 
vector lstsq(const matrix &a, const vector &b) { return a.LstSq(b); }

Вычисляет систему линейных алгебраических уравнений приблизительно (для неквадратных или вырожденных матриц).

 
ulong matrix_rank(const matrix &m) { return m.Rank(); }
 Функция вычисляет ранг матрицы, который представляет собой количество линейно независимых строк или столбцов в матрице. Это ключевое понятие для понимания пространства решений системы линейных уравнений. 
matrix cholesky(const matrix &m)
{
  vector values = eig(m).eigenvalues;
  
  for (ulong i=0; i<values.Size(); i++)
   {
    if (values[i]<=0)
       {
          printf("%s Failed Matrix is not positive definite",__FUNCTION__);
          return matrix::Zeros(0,0);
       }
   }
   
   matrix L;   
   if (!m.Cholesky(L))
      printf("%s Failed, Error = %d",__FUNCTION__, GetLastError());
      
   return L;
} 
 Разложение Холецкого используется для разложения положительно определенной матрицы на произведение нижнетреугольной матрицы и ее транспонированной матрицы. 
matrix matrix_power(const matrix &m, uint exponent) { return m.Power(exponent); }
 Вычисляет матрицу, возведенную в определенную целую степень. Если быть точнее, вычисляется , где - матрица, а - неотрицательное целое число.

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
    //--- Linear algebra
    
    
    matrix m = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    Print("np.linalg.inv:\n",np.linalg.inv(m));
    Print("np.linalg.det: ",np.linalg.det(m));
    Print("np.linalg.det: ",np.linalg.kron(m, m));
    Print("np.linalg.eigenvalues:",np.linalg.eig(m).eigenvalues," eigenvectors: ",np.linalg.eig(m).eigenvectors);
    Print("np.linalg.norm: ",np.linalg.norm(m, MATRIX_NORM_P2));
    Print("np.linalg.svd u:\n",np.linalg.svd(m).U, "\nv:\n",np.linalg.svd(m).V);
        
    
    matrix a = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    vector b = {1,2,3};
    
    Print("np.linalg.solve ",np.linalg.solve(a, b));
    Print("np.linalg.lstsq: ", np.linalg.lstsq(a, b));
    Print("np.linalg.matrix_rank: ", np.linalg.matrix_rank(a));
    Print("cholesky: ", np.linalg.cholesky(a));
    Print("matrix_power:\n", np.linalg.matrix_power(a, 2));
 }


Многочлены (степенные ряды) #

Подмодуль numpy.polynomial предоставляет набор мощных инструментов для создания, вычисления, дифференцирования, интегрирования и манипулирования многочленами. Он более численно устойчив, чем использование numpy.poly1d для операций над полиномами.

В библиотеке NumPy языка программирования Python существуют различные типы многочленов, но в нашем классе CNumpy-MQL5 я в настоящее время реализовал стандартную систему счисления по степеням (многочлен).

class CPolynomial: protected CNumpy
  {
protected:
   vector m_coeff;
      
   matrix vector21DMatrix(const vector &v)
    {
      matrix res = matrix::Zeros(v.Size(), 1);
      for (ulong r=0; r<v.Size(); r++)
         res[r][0] = v[r];
         
      return res;
    }
    
public:
                     CPolynomial(void);
                     CPolynomial(vector &coefficients); //for loading pre-trained model
                    ~CPolynomial(void);
                    
                     vector fit(const vector &x, const vector &y, int degree);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::~CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(vector &coefficients):
m_coeff(coefficients)
 {
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CPolynomial::fit(const vector &x, const vector &y, int degree)
 {
   //Constructing the vandermonde matrix
   matrix X = vander(x, degree+1, true);
   
   matrix temp1 =  X.Transpose().MatMul(X);
   matrix temp2 = X.Transpose().MatMul(vector21DMatrix(y));
   
   matrix coef_m = linalg.inv(temp1).MatMul(temp2);
   
   return (this.m_coeff = flatten(coef_m));
 }

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {     
    //--- Polynomial
    
    vector X = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
    vector y = MathPow(X, 3) + 0.2 * np.random.randn(10);  // Cubic function with noise
    
    CPolynomial poly;
    
    Print("coef: ", poly.fit(X, y, 3));
 }

Результаты.

2025.03.17 14:01:43.026 Numpy test (US Tech 100,H1)     coef: [-0.1905916844269999,2.3719065699851,-5.625684489899982,4.749058310806731]

Кроме того, в основном классе CNumpy есть вспомогательные функции для работы с полиномами, в том числе:


Функция

 Описание 
vector polyadd(const vector &p, const vector &q);
 Складывает два многочлена, выравнивая их по степени (длине коэффициентов). Если один из многочленов короче другого, перед сложением он дополняется нулями. 
vector polysub(const vector &p, const vector &q);
 Вычитает два многочлена. 
vector polymul(const vector &p, const vector &q);
 Умножает два многочлена, используя распределительное свойство, каждый член p умножается на каждый член q и результаты суммируются.
 
vector polyder(const vector &p, int m=1);
 Вычисляет производные многочлена p, производная вычисляется с помощью стандартного правила для производных. Каждый член     становится  . 
vector polyint(const vector &p, int m=1, double k=0.0)
 Вычисляет интеграл многочлена p, интеграл каждого члена   становится  . Метод позволяет производить вычисления m-го интеграла с постоянной интегрирования k, добавленной после интеграции. 
double polyval(const vector &p, double x);
 Вычисляет значение многочлена в заданной точке x путем суммирования членов многочлена, где каждый член вычисляется как  .   
struct polydiv_struct
  {
     vector quotient, 
            remainder;
  };

polydiv_struct polydiv(const vector &p, const vector &q);
 Эта функция делит два многочлена и возвращает частное и остаток.

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Polynomial utils
    
    vector p = {1,-3, 2};
    vector q = {2,-4, 1};
    
    Print("polyadd: ",np.polyadd(p, q));
    Print("polysub: ",np.polysub(p, q));
    Print("polymul: ",np.polymul(p, q));
    Print("polyder:", np.polyder(p));
    Print("polyint:", np.polyint(p)); // Integral of polynomial
    Print("plyval x=2: ", np.polyval(p, 2)); // Evaluate polynomial at x = 2
    Print("polydiv:", np.polydiv(p, q).quotient," ",np.polydiv(p, q).remainder);
 }


Другие часто используемые методы NumPy

Классифицировать все методы NumPy сложно, ниже приведены некоторые из наиболее полезных функций этого класса, которые мы еще не обсуждали.


Метод

 Описание 
vector CNumpy::arange(uint stop)
vector CNumpy::arange(int start, int stop, int step)
 Первая функция создает вектор с диапазоном значений в заданном интервале.

Второй вариант делает то же самое, но учитывает шаг увеличения значений. Эти две функции полезны для генерации вектора чисел в порядке возрастания.
 
vector CNumpy::flatten(const matrix &m)
vector CNumpy::ravel(const matrix &m) { return flatten(m); };
 Они преобразуют двумерную матрицу в одномерный вектор.

Часто в результате мы получаем матрицу, состоящую, возможно, из одной строки и одного столбца, которую для удобства использования необходимо преобразовать в вектор.		 
matrix CNumpy::reshape(const vector &v,uint rows,uint cols)
 Преобразует одномерный вектор в матрицу из строк и столбцов (cols). 
matrix CNumpy::reshape(const matrix &m,uint rows,uint cols)
 Преобразует двумерную матрицу в новую форму (rows и cols). 
matrix CNumpy::expand_dims(const vector &v, uint axis)
 Добавляет новый axis в одномерный вектор, превращая его в матрицу. 
vector CNumpy::clip(const vector &v,double min,double max)
 Функция ограничивает значения в векторе заданным диапазоном (между минимальным и максимальным значениями), что полезно для уменьшения количества экстремальных значений и удержания вектора в желаемом диапазоне. 
vector CNumpy::argsort(const vector<T> &v)
 Возвращает индексы, которые будут использоваться для сортировки массива. 
vector CNumpy::sort(const vector<T> &v)
 Сортирует массив в порядке возрастания. 
vector CNumpy::concat(const vector &v1, const vector &v2);
vector CNumpy::concat(const vector &v1, const vector &v2, const vector &v3);
 Объединяет несколько векторов в один большой вектор. 
matrix CNumpy::concat(const matrix &m1, const matrix &m2, ENUM_MATRIX_AXIS axis = AXIS_VERT)
Когда axis=0, матрица объединяется по строкам (укладывает m1 с матрицами m2 горизонтально).
При axis=1 матрица объединяется по столбцам (m1 укладывается с матрицами m2 вертикально).		 
matrix CNumpy::concat(const matrix &m, const vector &v, ENUM_MATRIX_AXIS axis = AXIS_VERT)
 При axis = 0 вектор добавляется в качестве новой строки (только если его размер соответствует количеству столбцов в матрице).

При axis = 1 вектор добавляется в качестве нового столбца (только если его размер соответствует количеству строк в матрице).		 
matrix CNumpy::dot(const matrix& a, const matrix& b);
double CNumpy::dot(const vector& a, const vector& b);
matrix CNumpy::dot(const matrix& a, const vector& b);
 Они вычисляют скалярное произведение (также известное как внутреннее произведение) двух матриц, векторов или матрицы и вектора. 
vector CNumpy::linspace(int start,int stop,uint num,bool endpoint=true)
 Функция создает массив равномерно расположенных чисел в заданном диапазоне (начало, конец). num = количество образцов, которые необходимо сгенерировать.
endpoint (default=true), включен стоп, при false стоп исклюается.		 
struct unique_struct
 {
   vector unique, count;
 };

unique_struct CNumpy::unique(const vector &v)
 Возвращает уникальные (unique) элементы вектора и подсчитанное количество их появлений (count).

Пример использования.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
    //--- Common methods
    
    vector v = {1,2,3,4,5,6,7,8,9,10};  
    
    Print("------------------------------------");  
    Print("np.arange: ",np.arange(10));
    Print("np.arange: ",np.arange(1, 10, 2));
    
    matrix m = {
      {1,2,3,4,5},
      {6,7,8,9,10}
    };
      
    Print("np.flatten: ",np.flatten(m));
    Print("np.ravel: ",np.ravel(m));
    Print("np.reshape: ",np.reshape(v, 5, 2));
    Print("np.reshape: ",np.reshape(m, 2, 3));
   
    Print("np.expnad_dims: ",np.expand_dims(v, 1));
    Print("np.clip: ", np.clip(v, 3, 8));
   
    //--- Sorting
   
    Print("np.argsort: ",np.argsort(v));
    Print("np.sort: ",np.sort(v));
   
    //--- Others
    
    matrix z = {
      {1,2,3},
      {4,5,6},
      {7,8,9},
    };
      
    Print("np.concatenate: ",np.concat(v,  v));
    Print("np.concatenate:\n",np.concat(z,  z, AXIS_HORZ));
    
    vector y = {1,1,1};
    
    Print("np.concatenate:\n",np.concat(z,  y, AXIS_VERT));
    Print("np.dot: ",np.dot(v, v));
    Print("np.dot:\n",np.dot(z, z));
    Print("np.linspace: ",np.linspace(1, 10, 10, true));
    
    Print("np.unique: ",np.unique(v).unique, " count: ",np.unique(v).count);
 }

Результаты.

NJ      0       16:34:01.702    Numpy test (US Tech 100,H1)     ------------------------------------
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [0,1,2,3,4,5,6,7,8,9]
LG      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [1,3,5,7,9]
QR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.flatten: [1,2,3,4,5,6,7,8,9,10]
QO      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.ravel: [1,2,3,4,5,6,7,8,9,10]
EF      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2]
NL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [3,4]
NK      0       16:34:01.703    Numpy test (US Tech 100,H1)      [5,6]
NQ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8]
HF      0       16:34:01.703    Numpy test (US Tech 100,H1)      [9,10]]
HD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2,3]
QD      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.expnad_dims: [[1,2,3,4,5,6,7,8,9,10]]
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.clip: [3,3,3,4,5,6,7,8,8,8]
FM      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.argsort: [0,1,2,3,4,5,6,7,8,9]
KD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.sort: [1,2,3,4,5,6,7,8,9,10]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate: [1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10]
FS      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3]
DM      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
CJ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]
IS      0       16:34:01.703    Numpy test (US Tech 100,H1)      [1,2,3]
DH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
CH      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3,1]
KN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6,1]
KH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9,1]]
JR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot: 385.0
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot:
JN      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[30,36,42]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [66,81,96]
RN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [102,126,150]]
RI      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.linspace: [1,2,3,4,5,6,7,8,9,10]
MQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.unique: [1,2,3,4,5,6,7,8,9,10] count: [1,1,1,1,1,1,1,1,1,1]


Разработка моделей машинного обучения с нуля с использованием MQL5-NumPy

Как я уже объяснял ранее, библиотека NumPy является основой многих моделей машинного обучения, реализованных на языке программирования Python, благодаря наличию огромного количества методов, помогающих работать с массивами, матрицами, базовой математикой и даже линейной алгеброй. Теперь, когда у нас есть аналогичный механизм закрытия в MQL5, давайте попробуем использовать его для реализации простой модели машинного обучения с нуля.

Рассмотрим в качестве примера модель линейной регрессии.

Я нашел этот код в интернете, это модель линейной регрессии, использующая градиентный спуск в функции обучения.

import numpy as np
from sklearn.metrics import mean_squared_error, r2_score

class LinearRegression:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        """
        Train the Linear Regression model using Gradient Descent.
        X: Input features (numpy array of shape [n_samples, n_features])
        y: Target values (numpy array of shape [n_samples,])
        """
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        for _ in range(self.epochs):
            y_pred = np.dot(X, self.weights) + self.bias  # Predictions
            
            # Compute Gradients
            dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))
            db = (1 / n_samples) * np.sum(y_pred - y)
            
            # Update Parameters
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

    def predict(self, X):
        """
        Predict output for the given input X.
        """
        return np.dot(X, self.weights) + self.bias

# Example Usage
if __name__ == "__main__":
    # Sample Data (X: Input features, y: Target values)
    X = np.array([[1], [2], [3], [4], [5]])  # Feature
    y = np.array([2, 4, 6, 8, 10])           # Target (y = 2x)

    # Create and Train Model
    model = LinearRegression(learning_rate=0.01, epochs=1000)
    model.fit(X, y)

    # Predictions
    y_pred = model.predict(X)

    # Evaluate Model
    print("Predictions:", y_pred)
    print("MSE:", mean_squared_error(y, y_pred))
    print("R² Score:", r2_score(y, y_pred))

Результат.

Predictions: [2.06850809 4.04226297 6.01601785 7.98977273 9.96352761]
MSE: 0.0016341843485627612
R² Score: 0.9997957269564297

Обратите внимание на функцию fit, в функции обучения у нас есть несколько методов NumPy. Поскольку у нас есть аналогичные функции в CNumpy, давайте реализуем их и в MQL5.

#include <MALE5\Numpy\Numpy.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
    // Sample Data (X: Input features, y: Target values)
    matrix X = {{1}, {2}, {3}, {4}, {5}};
    vector y = {2, 4, 6, 8, 10};

    // Create and Train Model
    CLinearRegression model(0.01, 1000);
    model.fit(X, y);

    // Predictions
    vector y_pred = model.predict(X);

    // Evaluate Model
    Print("Predictions: ", y_pred);
    Print("MSE: ", y_pred.RegressionMetric(y, REGRESSION_MSE));
    Print("R² Score: ", y_pred.RegressionMetric(y_pred, REGRESSION_R2));
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CLinearRegression
  {
protected:

   CNumpy np;
   double m_learning_rate;
   uint m_epochs;
   vector weights;
   double bias;
   
public:
                     CLinearRegression(double learning_rate=0.01, uint epochs=1000);
                    ~CLinearRegression(void);
                    
                    void fit(const matrix &x, const vector &y);
                    vector predict(const matrix &X);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::CLinearRegression(double learning_rate=0.01, uint epochs=1000):
 m_learning_rate(learning_rate),
 m_epochs(epochs)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::~CLinearRegression(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CLinearRegression::fit(const matrix &x, const vector &y)
 {
   ulong n_samples = x.Rows(), n_features = x.Cols();
   this.weights = np.zeros((uint)n_features);
   this.bias = 0.0;

//---
   
   for (uint i=0; i<m_epochs; i++)
      {
        matrix temp = np.dot(x, this.weights);
        vector y_pred = np.flatten(temp) + bias;
        
        // Compute Gradients
        
        temp = np.dot(x.Transpose(), (y_pred - y));
                
        vector dw = (1.0 / (double)n_samples) * np.flatten(temp);
        double db = (1.0 / (double)n_samples) * np.sum(y_pred - y);

        // Update Parameters
        
        this.weights -= this.m_learning_rate * dw;
        this.bias -= this.m_learning_rate * db;
      }
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLinearRegression::predict(const matrix &X)
 {
   matrix temp = np.dot(X, this.weights);
   
   return np.flatten(temp) + this.bias;
 }

Результаты.

RD      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) Predictions: [2.068508094061713,4.042262972785917,6.01601785151012,7.989772730234324,9.963527608958529]
KH      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) MSE: 0.0016341843485627612
RQ      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) R² Score: 1.0

Отлично! Мы получили те же результаты от этой модели, что и в коде на Python.


Что дальше?

У вас есть мощная библиотека и набор ценных методов, которые использовались для создания бесчисленных алгоритмов машинного обучения и статистического анализа на языке программирования Python, и ничто не мешает вам создавать сложные торговые роботы, способные производить сложные вычисления, подобные тем, которые вы часто видите в Python.

На данный момент в библиотеке по-прежнему отсутствует большинство функций, поскольку на их написание у меня ушли бы месяцы, поэтому не стесняйтесь добавлять свои собственные. Функции, присутствующие в библиотеке, — это те, которые я часто использую или которые мне нужны при работе с алгоритмами машинного обучения на языке MQL5.

Синтаксис Python в MQL5 иногда может вызывать путаницу, поэтому не стесняйтесь изменять имена функций на те, которые вам больше подходят.

Оставайтесь с нами и вносите свой вклад в разработку алгоритмов машинного обучения для языка MQL5 в этом GitHub-репозитории.


Таблица вложений

Имя файла Описание
Include\Numpy.mqh Клон NumPy для MQL5, все методы NumPy для MQL5 можно найти в этом файле.
Scripts\Linear regression from scratch.mq5 Скрипт, в котором реализован пример линейной регрессии с использованием библиотеки CNumpy.
Scripts\Numpy test.mq5  Скрипт вызывает все методы из библиотеки Numpy.mqh для тестирования.

Это площадка для применения всех методов, обсуждаемых в этой статье.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/17469

Прикрепленные файлы |
Загрузить ZIP
attachments.zip (16 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (Основные компоненты) Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (Основные компоненты)
В данной статье представлен практический подход к адаптации современного фреймворка для анализа финансовых потоков средствами MQL5. Рассмотрены ключевые компоненты модели — Depth-Wise свёртки с остаточными связями, конусные Super Kernel Block и модуль глобальной агрегации движения (GMA).
Знакомство с языком MQL5 (Часть 26): Советник по зонам поддержки/сопротивления — выявление, проверка пробоя и вход Знакомство с языком MQL5 (Часть 26): Советник по зонам поддержки/сопротивления — выявление, проверка пробоя и вход
В этой статье вы научитесь созданию советника на языке MQL5, который автоматически определяет зоны поддержки и сопротивления и исполняет сделки на их основе. Вы узнаете, как запрограммировать своего советника так, чтобы он выявлял эти ключевые рыночные уровни, осуществлял мониторинг отскоков цены и принимал торговые решения без ручного вмешательства.
Особенности написания экспертов Особенности написания экспертов
Написание и тестирование экспертов в торговой системе MetaTrader 4.
От новичка до эксперта: Торговля по RSI с учетом структуры рынка От новичка до эксперта: Торговля по RSI с учетом структуры рынка
В настоящей статье рассмотрим практические приемы торговли осциллятором Индекс относительной силы (RSI) с рыночной структурой. Наше внимание будет сосредоточено на паттернах изменения цен в канале, на том, как они обычно торгуются, и как можно использовать MQL5 для улучшения этого процесса. В итоге вы получите основанную на правилах автоматизированную систему канальной торговли и предназначенную для более точного и стабильного выявления возможностей продолжения тренда.