
Алгоритм кристаллической структуры — Crystal Structure Algorithm (CryStAl)
Содержание
Введение
В мои руки попал для исследования один из алгоритмов оптимизации, работа над которым выявила "подводные камни" реализации перспективной идеи. Знакомьтесь, Crystal Structure Algorithm (CryStAl) — метаэвристический алгоритм оптимизации, вдохновлённый физическим процессом формирования кристаллических структур. Он был предложен в 2021 году группой исследователей A.Kaveha, M.Kooshkebaghi и опубликован в статье Siamak Talatahari. CryStAl моделирует процесс образования кристаллов, где решения — это атомы, а поиск оптимума — это упорядочивание этих атомов в стабильную структуру. Алгоритм использует базис и решётку, как аналог пространственного распределения решений, симметрию и регулярность для формирования сбалансированной популяции, и энергетические критерии, чтобы отсеивать неустойчивые решения.
Реализация алгоритма
Разберем концепцию работы алгоритма CryStAl посредством подробного псевдокода всех его этапов:
Входные параметры алгоритма
Размер популяции кристаллов — сколько кристаллов будет в популяции (обычно 30)
Количество случайных кристаллов — сколько случайных кристаллов использовать для вычисления среднего значения Fc (обычно 3)
Размерность задачи — количество оптимизируемых переменных
Максимальное количество итераций — сколько раз алгоритм будет повторять цикл оптимизации
Границы поиска — минимальные и максимальные значения для каждой переменной
ЭТАП 1: ИНИЦИАЛИЗАЦИЯ ПОПУЛЯЦИИ
Создание начальных кристаллов
Для каждого кристалла в популяции и для каждой координаты (переменной) этого кристалла:
- Формула 3 — Случайная инициализация: Новая координата = Минимальная граница + Случайное число × (Максимальная граница - Минимальная граница), где Случайное число равномерно распределено от 0 до 1
Вычислить значение фитнес-функции для этого кристалла и записать персональные рекорды кристалла
Инициализация глобальных рекордов
Найти кристалл с максимальным значением фитнес-функции
Найти кристалл с минимальным значением фитнес-функции
ЭТАП 2: ОСНОВНОЙ ЦИКЛ ОПТИМИЗАЦИИ
Повторять следующие шаги от первой итерации до максимальной:
ШАГ 1: Вычисление средней позиции всех кристаллов (Cr_main)
Для каждой координаты: обнулить сумму для этой координаты
Для каждого кристалла в популяции: прибавить к сумме значение этой координаты у данного кристалла
Разделить сумму на количество кристаллов, получив среднее значение
Результат: получили вектор средних значений по всем координатам
ШАГ 2: Определение лучшего кристалла (Cr_b)
Установить индекс лучшего кристалла на первый кристалл
Для каждого следующего кристалла со второго по последний:
Если фитнес этого кристалла больше фитнеса текущего лучшего: обновить индекс лучшего кристалла на индекс этого кристалла
Результат: известен индекс кристалла с наилучшим значением фитнес-функции
ШАГ 3: Обновление позиций всех кристаллов
Для каждого кристалла в популяции:
Этап 3.1: Сохранение текущего состояния
Сохранить текущую позицию кристалла как старую позицию
Этап 3.2: Выбор стратегии обновления
Случайно выбрать одну из четырех стратегий обновления:
- Стратегия 0: Простое кубическое обновление
- Стратегия 1: Кубическое обновление с лучшим кристаллом
- Стратегия 2: Кубическое обновление со средним значением случайных кристаллов
- Стратегия 3: Комбинированное обновление с лучшим и средним
Этап 3.3: Применение выбранной стратегии
ЕСЛИ выбрана СТРАТЕГИЯ 0 — Простое кубическое обновление:
Для каждой координаты кристалла: сгенерировать случайное число r от 0 до 1
- Формула 4 — Новая координата = Старая координата + r × Средняя координата всех кристаллов
ИНАЧЕ ЕСЛИ выбрана СТРАТЕГИЯ 1 — С лучшим кристаллом:
Для каждой координаты кристалла: сгенерировать два случайных числа r1 и r2 от 0 до 1
- Формула 5 — Новая координата = Старая координата + r1 × Средняя координата всех кристаллов + r2 × Координата лучшего кристалла
ИНАЧЕ ЕСЛИ выбрана СТРАТЕГИЯ 2 — Со средним случайных кристаллов:
Подэтап 2.1: Вычисление среднего случайных кристаллов (Fc)
Для каждой координаты: обнулить сумму для этой координаты
Повторить заданное количество раз (обычно 3 раза): выбрать случайный кристалл из популяции (исключая текущий обрабатываемый)
Для каждой координаты: прибавить к сумме значение этой координаты у случайно выбранного кристалла
Для каждой координаты: разделить сумму на количество выбранных случайных кристаллов
Результат: получили среднее значение нескольких случайно выбранных кристаллов
Подэтап 2.2: Обновление позиции
Для каждой координаты кристалла: сгенерировать два случайных числа r1 и r2 от 0 до 1
- Формула 6 — Новая координата = Старая координата + r1 × Средняя координата всех кристаллов + r2 × Средняя координата случайных кристаллов
ИНАЧЕ выбрана СТРАТЕГИЯ 3 — Комбинированная:
Подэтап 3.1: Вычисление среднего случайных кристаллов (Fc)
(Выполняется точно так же, как в стратегии 2)
Подэтап 3.2: Обновление позиции
- Для каждой координаты кристалла: сгенерировать три случайных числа r1, r2 и r3 от 0 до 1
- Формула 7 — Новая координата = Старая координата + r1 × Средняя координата всех кристаллов + r2 × Координата лучшего кристалла + r3 × Средняя координата случайных кристаллов
Этап 3.4: Обработка выхода за границы (Boundary Handling)
Для каждой координаты нового положения кристалла: если координата меньше минимальной границы ИЛИ больше максимальной границы: кристалл вышел за допустимые границы — нужна коррекция
- Сгенерировать случайное число от 0 до 1
- Пересчитать координату внутри допустимых границ: Координата = Минимальная граница + Случайное число × (Максимальная граница - Минимальная граница)
Обновить позицию кристалла на новую рассчитанную позицию
ШАГ 4: Оценка новых позиций и обновление рекордов
Для каждого кристалла в популяции:
Этап 4.1: Вычисление фитнеса
Вычислить значение фитнес-функции для новой позиции кристалла
Этап 4.2: Обновление персональных рекордов кристалла
Если новое значение фитнеса лучше персонального лучшего значения: Обновить персональное лучшее значение фитнеса на текущее Сохранить текущую позицию как персональную лучшую позицию
Если новое значение фитнеса хуже персонального худшего значения: Обновить персональное худшее значение фитнеса на текущее Сохранить текущую позицию как персональную худшую позицию
Этап 4.3: Обновление глобальных рекордов
Если значение фитнеса этого кристалла лучше глобального лучшего: Обновить глобальное лучшее значение на фитнес этого кристалла Сохранить позицию этого кристалла как глобальную лучшую
Если значение фитнеса этого кристалла хуже глобального худшего: Обновить глобальное худшее значение на фитнес этого кристалла Сохранить позицию этого кристалла как глобальную худшую
ШАГ 5: Переход к следующей итерации
Перейти к следующей итерации основного цикла оптимизации
Конец основного цикла оптимизации
ЭТАП 3: ЗАВЕРШЕНИЕ РАБОТЫ АЛГОРИТМА
После выполнения всех итераций вернуть результат:
- Глобальную лучшую позицию (решение задачи оптимизации)
- Глобальное лучшее значение фитнес-функции
Диаграмма на рисунке ниже содержит схему основного цикла, визуализацию четырех стратегий и пример поискового пространства с кристаллами.

Рисунок 1. Блок-схема работы алгоритма CryStAl
Алгоритм CryStAl старается поддержать баланс между двумя важными аспектами оптимизации:
Исследованием (exploration) — изучение новых областей поискового пространства: обеспечивается стратегией 0 через движение к средней позиции, усиливается стратегией 2 через информацию от случайных кристаллов и помогает избежать застревания в локальных оптимумах.
Эксплуатацией (exploitation) — углубленный поиск вблизи хороших решений: реализуется стратегией 1 через движение к лучшему кристаллу, ускоряет сходимость к оптимуму и позволяет эффективно использовать найденную информацию.
Комбинированный подход:
- Стратегия 3 объединяет все три компонента
- Случайный выбор стратегий на каждой итерации обеспечивает адаптивность
- Каждая стратегия имеет равную вероятность выбора 25%
Роль ключевых компонентов:
Средняя позиция (Cr_main) — представляет центр масс популяции, направляет поиск к центральным областям исследованного пространства и обновляется каждую итерацию на основе текущих позиций всех кристаллов.
Лучший кристалл (Cr_b) — содержит лучшее найденное на данный момент решение, притягивает другие кристаллы в перспективную область, усиливает эксплуатацию найденных хороших решений.
Среднее случайных кристаллов (Fc) — представляет локальную информацию от соседей, добавляет стохастичность и разнообразие в поиск, помогает избежать преждевременной сходимости.
Теперь, когда мы подробно разобрались с принципами работы алгоритма, перейдем к его реализации в коде. Напишем класс "C_AO_CryStAl", который будет являться наследником класса "C_AO" и будет предназначен для реализации алгоритма "Crystal Structure Algorithm".
Конструктор:- Инициализируются два параметра: "popSize" (размер популяции кристаллов, по умолчанию 30) и "numRandomCrystals" (количество случайных кристаллов, используемых для одного из вычислений "Fc", по умолчанию 3).
- Эти параметры добавляются в структуру, предоставляющую информацию о параметрах алгоритма.
- Этот метод позволяет обновлять значения параметров "popSize" и "numRandomCrystals", используя данные из внешней структуры параметров.
- Проводится проверка, чтобы "numRandomCrystals" всегда был не меньше 1 и не больше, чем "popSize" минус 1, чтобы избежать некорректных вычислений.
- Init () — метод для инициализации алгоритма, требующий информацию о диапазонах и шагах входных переменных, а также о количестве эпох;
- Moving () — метод, реализующий шаг перемещения кристаллов в алгоритме;
- Revision () — метод, отвечающий за пересмотр или обновление состояния популяции.
- numRandomCrystals — количество случайных кристаллов, которое используется для вычисления "Fc".
- meanPosition — массив, хранящий среднее значение позиций всех кристаллов в популяции;
- bestCrystalIdx — индекс лучшего кристалла в текущей популяции;
- isFirstIteration — булевый флаг, указывающий, является ли текущая итерация первой после инициализации;
- CalculateMeanPosition () — метод для вычисления средней позиции кристаллов;
- CalculateFc () — метод для вычисления величины "Fc", которая является критерием, зависящим от выбранных кристаллов;
- SelectRandomCrystal () — метод для выбора случайного кристалла из популяции, с возможностью исключить указанный кристалл.
В целом, класс "C_AO_CryStAl" моделирует алгоритм оптимизации, основанный на поведении кристаллов. Он оперирует популяцией "кристаллов", каждый из которых имеет свою позицию. Алгоритм включает шаги для перемещения кристаллов, расчета их качественных характеристик и определения лучшего решения.
//———————————————————————————————————————————————————————————————————— class C_AO_CryStAl : public C_AO { public: //---------------------------------------------------------- ~C_AO_CryStAl () { } C_AO_CryStAl () { ao_name = "CryStAl"; ao_desc = "Crystal Structure Algorithm"; ao_link = "https://www.mql5.com/ru/articles/19899"; popSize = 30; // размер популяции кристаллов numRandomCrystals = 3; // количество случайных кристаллов для Fc ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "numRandomCrystals"; params [1].val = numRandomCrystals; } void SetParams () { popSize = (int)params [0].val; numRandomCrystals = (int)params [1].val; if (numRandomCrystals < 1) numRandomCrystals = 1; if (numRandomCrystals > popSize - 1) numRandomCrystals = popSize - 1; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP); void Moving (); void Revision (); //------------------------------------------------------------------ int numRandomCrystals; // количество случайных кристаллов для вычисления Fc private: //--------------------------------------------------------- double meanPosition []; // средняя позиция всех кристаллов (Cr_main) int bestCrystalIdx; // индекс лучшего кристалла bool isFirstIteration; // флаг первой итерации после инициализации void CalculateMeanPosition (); void CalculateFc (int currentCrystal, double &fcArray []); int SelectRandomCrystal (int excludeCrystal); }; //————————————————————————————————————————————————————————————————————
Метод "Init" предназначен для инициализации алгоритма "Crystal Structure Algorithm" перед началом его работы.
Сначала вызывается метод "StandardInit", который выполняет базовые подготовительные действия, общие для всех алгоритмов, унаследованных от "C_AO". Если этот базовый этап не удается, метод "Init" также завершается неудачно. Создается массив "meanPosition" (средняя позиция). Размер этого массива определяется переменной "coords", которая хранит количество измерений. Все элементы этого массива инициализируются нулевым значением. Это означает, что в начале работы алгоритма средняя позиция всех кристаллов считается равной нулю.
Установка начальных значений для флажков:- bestCrystalIdx (индекс лучшего кристалла) устанавливается в 0. Это предполагает, что при старте первый кристалл в популяции считается лучшим.
- isFirstIteration (флаг первой итерации) устанавливается в "true". Это указывает, что следующая выполняемая итерация будет первой после полной инициализации.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_CryStAl::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Инициализация массивов ArrayResize (meanPosition, coords); ArrayInitialize (meanPosition, 0.0); bestCrystalIdx = 0; isFirstIteration = true; return true; } //————————————————————————————————————————————————————————————————————
Метод "CalculateMeanPosition" предназначен для вычисления среднего положения всех "кристаллов" в популяции. Первым делом все элементы массива "meanPosition" (который хранит среднее по каждой координате) сбрасываются. Это делается для того, чтобы перед началом суммирования текущих позиций кристаллов, мы начинали с чистого листа.
Затем метод проходит по каждому кристаллу в популяции. Для каждого кристалла он также проходит по всем его координатам (определяемым "coords"). Значение каждой координаты текущего кристалла добавляется к соответствующему элементу массива "meanPosition". Таким образом, "meanPosition" постепенно накапливает сумму значений каждой координаты по всем кристаллам.
После того как суммирование завершено, метод снова проходит по всем координатам. Каждое накопленное значение в "meanPosition" делится на общее количество кристаллов "popSize". Это преобразование превращает сумму координат в их среднее значение. В результате выполнения этого метода, массив "meanPosition" будет содержать среднее значение каждой координаты по всем кристаллам в популяции.
//———————————————————————————————————————————————————————————————————— //--- Вычисление средней позиции всех кристаллов (Cr_main) void C_AO_CryStAl::CalculateMeanPosition () { // Обнуляем средние значения ArrayInitialize (meanPosition, 0.0); // Суммируем текущие позиции всех кристаллов for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { meanPosition [c] += a [i].c [c]; } } // Делим на количество кристаллов для получения среднего for (int c = 0; c < coords; c++) { meanPosition [c] /= (double)popSize; } } //————————————————————————————————————————————————————————————————————
Метод "CalculateFc" предназначен для вычисления так называемого "среднего значения случайно выбранных кристаллов". Он принимает на вход индекс текущего кристалла "currentCrystal" и массив "fcArray", в который будет записан результат.
В самом начале все элементы массива "fcArray" обнуляются. Это гарантирует, что мы начинаем суммирование с чистого листа для каждой новой позиции "Fc". Затем метод входит в цикл, который повторяется "numRandomCrystals" раз. В каждой итерации этого цикла:
- выбирается случайный индекс кристалла "randomCrystal". Важно отметить, что этот выбор делается таким образом, чтобы исключить сам "currentCrystal" (т.е. кристалл, для которого мы сейчас вычисляем "Fc");
- позиция (координаты) этого случайно выбранного кристалла добавляется к соответствующим элементам в массиве "fcArray". Таким образом, этот массив накапливает сумму координат всех выбранных случайных кристаллов.
В итоге, массив "fcArray" будет содержать координаты "среднего" кристалла, полученного путем усреднения позиций нескольких случайным образом выбранных кристаллов из популяции (исключая текущий).
//———————————————————————————————————————————————————————————————————— //--- Вычисление Fc (среднее значение случайно выбранных кристаллов) void C_AO_CryStAl::CalculateFc (int currentCrystal, double &fcArray []) { // Инициализируем массив нулями ArrayInitialize (fcArray, 0.0); // Выбираем numRandomCrystals случайных кристаллов (исключая текущий) for (int i = 0; i < numRandomCrystals; i++) { int randomCrystal = SelectRandomCrystal (currentCrystal); // Суммируем позиции выбранных кристаллов for (int c = 0; c < coords; c++) { fcArray [c] += a [randomCrystal].c [c]; } } // Вычисляем среднее значение for (int c = 0; c < coords; c++) { fcArray [c] /= (double)numRandomCrystals; } } //————————————————————————————————————————————————————————————————————
Метод "SelectRandomCrystal" предназначен для выбора случайного "кристалла" из всей популяции, но с одним важным условием: он не должен выбирать тот кристалл, который был указан как "excludeCrystal".
Метод запускает бесконечный цикл, который будет продолжаться до тех пор, пока не будет выполнено условие выхода. Внутри цикла генерируется случайный числовой индекс, который выбирается из диапазона, охватывающего все возможные "кристаллы" в популяции (от 0 до "popSize" минус 1).
После генерации случайного индекса, происходит проверка:
- если сгенерированный индекс "selected" равен индексу кристалла, который мы хотим исключить "excludeCrystal", то цикл продолжает работать, и генерируется новый случайный индекс;
- если сгенерированный индекс не равен "excludeCrystal", то условие выхода из цикла выполняется.
//———————————————————————————————————————————————————————————————————— //--- Выбор случайного кристалла (исключая указанный) int C_AO_CryStAl::SelectRandomCrystal (int excludeCrystal) { int selected; do selected = u.RNDminusOne (popSize); while (selected == excludeCrystal); return selected; } //————————————————————————————————————————————————————————————————————
Метод "Moving" является основным рабочим циклом алгоритма, который отвечает за эволюцию популяции "кристаллов" в каждой итерации. Если алгоритм запускается впервые, "revision" равен "false", он инициализирует позиции всех кристаллов в популяции. Для каждого кристалла и каждой его координаты генерируется случайное значение в диапазоне от 0 до 1. Это случайное значение затем масштабируется в заданный рабочий диапазон (rangeMin - rangeMax) для данной координаты. Применяется дискретизация, чтобы привести позицию к допустимому шагу "rangeStep". После инициализации устанавливается флаг "revision" в "true", чтобы последующие вызовы метода выполняли обновление, а не инициализацию.
После первой итерации сначала вычисляется средняя позиция всех кристаллов в популяции. Алгоритм находит кристалл с наилучшим значением функции приспособленности "f" на текущей итерации и запоминает его индекс.
Для каждого кристалла в популяции (перебирая от 0 до "popSize"):
- текущая позиция кристалла копируется во временное хранилище, которое будет использоваться как "старая позиция" (Cr_old) для расчетов;
- случайным образом выбирается одна из нескольких доступных стратегий обновления позиции (всего их четыре, пронумерованы от 0 до 3);
- для двух из четырех стратегий (стратегии 2 и 3) вычисляется "среднее значение случайно выбранных кристаллов" (Fc), которое также будет использовано в обновлении;
- в зависимости от выбранной стратегии, новая позиция кристалла "Cr_new" вычисляется на основе его старой позиции, средней позиции популяции, позиции лучшего кристалла и "Fc". Каждая стратегия использует свою комбинацию этих факторов и случайных чисел (r, r1, r2, r3) для внесения изменений;
- после вычисления новой позиции, она проверяется на соответствие заданным рабочим диапазонам (rangeMin - rangeMax) для каждой координаты. Если новая позиция выходит за допустимые границы, она корректируется путем генерации новой случайной позиции в пределах этих границ;
- к позиции снова применяется процедура дискретизации с помощью функции u.SeInDiSp ().
Метод "Moving" итеративно перемещает "кристаллы" в пространстве поиска, используя различные стратегии, основанные на текущей информации о популяции (средняя позиция, лучший кристалл) и случайных факторах.
//———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_CryStAl::Moving () { // Начальная инициализация популяции (формула 3) if (!revision) { // Инициализация популяции кристаллов случайным образом for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { double xi = u.RNDfromCI (0.0, 1.0); a [i].c [j] = rangeMin [j] + xi * (rangeMax [j] - rangeMin [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } // КРИТИЧНО: Вычисляем среднюю позицию и находим лучший кристалл ПЕРЕД обновлением CalculateMeanPosition (); // Находим лучший кристалл для текущей итерации bestCrystalIdx = 0; for (int i = 1; i < popSize; i++) { if (a [i].f > a [bestCrystalIdx].f) { bestCrystalIdx = i; } } // Основной цикл обновления позиций (формулы 4-7) for (int i = 0; i < popSize; i++) { // Сохраняем текущую позицию как старую (Cr_old) ArrayCopy (a [i].cP, a [i].c, 0, 0, coords); // Выбираем случайную стратегию (0-3) int strategy = u.RNDminusOne (5); // Подготавливаем массив для Fc (только для стратегий 2 и 3) double fc []; ArrayResize (fc, coords); if (strategy == 2 || strategy == 3) { CalculateFc (i, fc); } // Применяем выбранную стратегию обновления позиции switch (strategy) { case 0: // Стратегия 1: Simple cubicle (формула 4) // Cr_new = Cr_old + r * Cr_main for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].cP [c] + r * meanPosition [c]; } break; case 1: // Стратегия 2: Cubicle with the best crystals (формула 5) // Cr_new = Cr_old + r1 * Cr_main + r2 * Cr_b for (int c = 0; c < coords; c++) { double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].cP [c] + r1 * meanPosition [c] + r2 * a [bestCrystalIdx].c [c]; } break; case 2: // Стратегия 3: Cubicle with the mean crystals (формула 6) // Cr_new = Cr_old + r1 * Cr_main + r2 * Fc for (int c = 0; c < coords; c++) { double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].cP [c] + r1 * meanPosition [c] + r2 * fc [c]; } break; case 3: // Стратегия 4: Cubicle with the best and mean crystals (формула 7) // Cr_new = Cr_old + r1 * Cr_main + r2 * Cr_b + r3 * Fc for (int c = 0; c < coords; c++) { double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); double r3 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].cP [c] + r1 * meanPosition [c] + r2 * a [bestCrystalIdx].c [c] + r3 * fc [c]; } break; } // Проверка и коррекция границ для новой позиции for (int c = 0; c < coords; c++) { // Если вышли за границы, применяем boundary handling if (a [i].c [c] < rangeMin [c] || a [i].c [c] > rangeMax [c]) { // Генерируем новую случайную позицию в допустимом диапазоне double xi = u.RNDfromCI (0.0, 1.0); a [i].c [c] = rangeMin [c] + xi * (rangeMax [c] - rangeMin [c]); } // Применяем дискретизацию a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" отвечает за обновление и сохранение лучших найденных решений как на уровне каждого отдельного "кристалла" (персональное лучшее решение), так и на уровне всей популяции (глобальное лучшее решение).
Методика проходит по каждому "кристаллу" в популяции, чтобы оценить его текущее состояние. Для каждого кристалла выполняется сравнение его текущей оценки приспособленности "f" с его же лучшей когда-либо найденной ранее оценкой "fB". Если текущая оценка лучше, чем предыдущая лучшая, то обновляется персональная лучшая оценка "fB" текущим значением и позиция кристалла, соответствующая этой новой лучшей оценке, копируется в его персональное лучшее решение "cB".
Параллельно с обновлением персональных лучших решений, алгоритм отслеживает лучшее решение, найденное всей популяцией на текущий момент. Сравнивается также текущая оценка приспособленности "f" кристалла с общей лучшей оценкой популяции "fB". Если текущая оценка кристалла лучше, чем текущая глобальная лучшая, то обновляется глобальная лучшая оценка "fB" текущим значением и позиция кристалла, соответствующая этой новой глобальной лучшей оценке, копируется в глобальное лучшее решение "cB".
По завершении работы метода "Revision", в переменных "fB" и "cB" хранятся самые высокие значения функции приспособленности и соответствующие им координаты, найденные за все время работы алгоритма. Каждому кристаллу также присваивается его собственное наилучшее найденное решение.
//———————————————————————————————————————————————————————————————————— //--- Обновление и проверка результатов void C_AO_CryStAl::Revision () { // Обновляем лучшие и худшие решения для каждого кристалла for (int i = 0; i < popSize; i++) { // Обновляем персональное лучшее решение if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, coords); } // Обновляем глобальное лучшее решение if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } } //————————————————————————————————————————————————————————————————————
Результаты тестов
По результатам тестов алгоритм набирает очень скромные показатели. Обращает на себя внимание сам результат, 26.33%, который вписывается в показатель случайного поиска, random walk в нашей рейтинговой таблице. Итак, что это означает? Мы еще к этому вернемся.
CryStAl|Crystal Structure Algorithm|30.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.49130791883895686
25 Hilly's; Func runs: 10000; result: 0.3254668138312991
500 Hilly's; Func runs: 10000; result: 0.25762861219210875
=============================
5 Forest's; Func runs: 10000; result: 0.3770837459944563
25 Forest's; Func runs: 10000; result: 0.21650897859329796
500 Forest's; Func runs: 10000; result: 0.158890697466887
=============================
5 Megacity's; Func runs: 10000; result: 0.2938461538461538
25 Megacity's; Func runs: 10000; result: 0.1498461538461539
500 Megacity's; Func runs: 10000; result: 0.09889230769230854
=============================
All score: 2.36947 (26.33%)
Такие результаты не оставили меня равнодушным, и я решил внести несколько поправок, улучшить сходимость алгоритма, логика взаимодействия которого, как оказалось, не совсем эффективна, дала возможность пересмотреть некоторые нелогичные методики, сохранив при этом общую идею. Посмотрим, что в итоге получилось в модифицированной версии.
Формулировка Обновления Позиций (Стратегии 0-3): модификация использует другой стиль обновления, который выглядит как добавление смещения к текущей позиции a [i].c [c]. Формулы выглядят иначе, хотя используются те же концепции, в стратегии. Добавление некоторой доли разности между текущей позицией и средней позицией становится серьезным изменением в математической реализации.
Дополнительное Случайное Возмущение: вводится дополнительное условие "if (u.RNDprobab () < 0.1)". Если это условие выполняется с вероятностью 10%, то позиция кристалла обновляется с помощью a[i].c[c] = u.PowerDistribution (cB[c], rangeMin[c], rangeMax[c], 20), что уменьшает вероятность застревания алгоритма. Остальные стратегии применяются с вероятностью 90%.
Далее в сохранении Старой Позиции "a [i].c P": оригинальная версия сохраняет старую позицию в "a [i].cP" перед вычислением новой позиции. В модифицированной версии эта позиция не сохраняется и не используется, обновление происходит напрямую из текущей позиции "a [i].c [c]".
Обработка Границ: в оригинале, после применения стратегии обновления, метод проходит по всем координатам и если новая позиция вышла за границы, генерируем совершенно новую случайную позицию в допустимом диапазоне, в "C_AO_CryStAlm" сначала применяется стратегия обновления, а затем только дискретизация с помощью метода "u.SeInDiSp".
//———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_CryStAlm::Moving () { // Начальная инициализация популяции (формула 3) if (!revision) { // Инициализация популяции кристаллов случайным образом for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { double xi = u.RNDfromCI (0.0, 1.0); a [i].c [j] = rangeMin [j] + xi * (rangeMax [j] - rangeMin [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } // КРИТИЧНО: Вычисляем среднюю позицию и находим лучший кристалл ПЕРЕД обновлением CalculateMeanPosition (); // Основной цикл обновления позиций (формулы 4-7) for (int i = 0; i < popSize; i++) { // Выбираем случайную стратегию (0-3) int strategy = u.RNDminusOne (5); // Подготавливаем массив для Fc (только для стратегий 2 и 3) double fc []; ArrayResize (fc, coords); if (strategy == 2 || strategy == 3) { CalculateFc (i, fc); } for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.1) { a [i].c [c] = u.PowerDistribution (cB [c], rangeMin [c], rangeMax [c], 20); } else { // Применяем выбранную стратегию обновления позиции switch (strategy) { case 0: // Стратегия 1: Simple cubicle (формула 4) { // Cr_new = Cr_old + r * Cr_main double r = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].c [c] + r * (meanPosition [c] - a [i].c [c]); } break; case 1: // Стратегия 2: Cubicle with the best crystals (формула 5) { // Cr_new = Cr_old + r1 * Cr_main + r2 * Cr_b double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].c [c] + r1 * (meanPosition [c] - a [i].c [c]) + r2 * (cB [c] - a [i].c [c]); } break; case 2: // Стратегия 3: Cubicle with the mean crystals (формула 6) { // Cr_new = Cr_old + r1 * Cr_main + r2 * Fc double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].c [c] - r1 * (meanPosition [c] - a [i].c [c]) + r2 * (fc [c] - a [i].c [c]); } break; case 3: // Стратегия 4: Cubicle with the best and mean crystals (формула 7) { // Cr_new = Cr_old + r1 * Cr_main + r2 * Cr_b + r3 * Fc double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); double r3 = u.RNDfromCI (0.0, 1.0); a [i].c [c] = a [i].c [c] + r1 * (meanPosition [c] - a [i].c [c]) + r2 * (cB [c] - a [i].c [c]) + r3 * (fc [c] - a [i].c [c]); } break; } } // Применяем дискретизацию a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Инициализация у нас не изменилась. Для метода "CalculateMeanPosition" нет никаких отличий между версиями для "C_AO_CryStAl" и "C_AO_CryStAlm", а так же для метода "CalculateFc" и "SelectRandomCrystal". Метод "Revision" в обеих версиях C_AO_CryStAl и C_AO_CryStAlm реализован абсолютно идентично.
Посмотрим на новые результаты ниже: они подтверждают корректность моих теоретических предпосылок. Теперь выясним причины, по которым оригинальная версия превращает направленный поиск в случайное блуждание с дрейфом.
CryStAlm|Crystal Structure Algorithm M|30.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8065665859751701
25 Hilly's; Func runs: 10000; result: 0.5614723387106613
500 Hilly's; Func runs: 10000; result: 0.2909726108642525
=============================
5 Forest's; Func runs: 10000; result: 0.7522883470073202
25 Forest's; Func runs: 10000; result: 0.48674341114821484
500 Forest's; Func runs: 10000; result: 0.2101468006131327
=============================
5 Megacity's; Func runs: 10000; result: 0.48461538461538467
25 Megacity's; Func runs: 10000; result: 0.2701538461538461
500 Megacity's; Func runs: 10000; result: 0.11110769230769342
=============================
All score: 3.97407 (44.16%)
Когда мы сравниваем две версии алгоритма Crystal Structure Algorithm, на первый взгляд может показаться, что изменения минимальны. Оба метода инициализируют популяцию одинаково, оба вычисляют среднюю позицию, оба используют четыре стратегии обновления. Однако за этим внешним сходством скрываются фундаментальные различия, которые приводят почти кдвукратной разнице в производительности. Давайте разберем каждое изменение, чтобы понять, почему модифицированная версия настолько эффективнее.
Фундаментальная ошибка: абсолютное сложение вместо направленного движения. Чтобы понять ключевую проблему оригинального алгоритма, представим одномерную оптимизацию — ищем максимум функции в диапазоне от 0 до 100. Средняя позиция популяции (то место, куда притягиваются кристаллы) находится в точке 60. У нас есть три кристалла в разных позициях: первый в точке 10, второй в точке 60, третий в точке 90. Случайный коэффициент r для всех одинаковый - 0.5.
Оригинальная формула: x_new = x_old + r × mean
- Кристалл 1: 10 + 0.5 × 60 = 10 + 30 = 40 (сдвиг +30)
- Кристалл 2: 60 + 0.5 × 60 = 60 + 30 = 90 (сдвиг +30)
- Кристалл 3: 90 + 0.5 × 60 = 90 + 30 = 120 (сдвиг +30, ВЫХОД ЗА ГРАНИЦУ!)
Заметили проблему? ВСЕ ТРИ КРИСТАЛЛА СДВИНУЛИСЬ НА +30, независимо от того, где они находились! Первый кристалл был далеко слева от цели и двинулся вправо — нормально. Второй уже БЫЛ в цели и его оттолкнули вправо — абсурд. Третий был справа от цели, его оттолкнули ещё дальше вправо, и он вылетел за границы — катастрофа.
Это не "движение к цели". Это одинаковый толчок всех в одном направлении, как если бы подул сильный ветер и всех сдвинул на одинаковое расстояние. Причем направление и сила этого "ветра" определяются абсолютными значениями координаты цели, а не относительным положением кристаллов.
Модифицированная формула: x_new = x_old + r × (mean - x_old)
- Кристалл 1: 10 + 0.5 × (60 - 10) = 10 + 25 = 35 (прошел 50% пути к цели)
- Кристалл 2: 60 + 0.5 × (60 - 60) = 60 + 0 = 60 (уже в цели, остался на месте)
- Кристалл 3: 90 + 0.5 × (60 - 90) = 90 - 15 = 75 (прошел 50% пути НАЗАД к цели)
Видите разницу? Каждый кристалл движется К своей цели, пропорционально расстоянию до неё. Кто далеко — делает большой шаг. Кто близко — маленький. Кто уже на месте — стоит. Кто за целью — возвращается назад. Это именно то, что нужно для оптимизации.
Проблема 1: Взрыв при больших координатах. Если оптимизируемые переменные имеют диапазон, скажем, от 0 до 1000, и средняя позиция популяции оказывается в районе 600-700, то к КАЖДОМУ кристаллу добавляется число порядка 600-700 (умноженное на случайный коэффициент 0-1). Даже кристалл, который находится в позиции 650 (почти точно у цели!), получит смещение +300...+600 и улетит к границе 1000 или за неё. Алгоритм превращается в генератор случайных чисел на границах пространства.
Проблема 2: Зависимость от масштаба координат. Если у вас задача с переменными разного масштаба (например, x от 0 до 10, y от 0 до 1000), то смещения по y будут в 100 раз больше, чем по x, просто из-за разницы в масштабе! Это не имеет никакого отношения к тому, насколько далеко кристалл от оптимума по каждой координате.
Проблема 3: Все кристаллы двигаются в одном направлении. Когда вы добавляете одинаковый вектор ко всем кристаллам (пусть и с разными случайными коэффициентами), вся популяция смещается как единое целое в одном направлении. Это не "поиск оптимума", это "дрейф популяции". Представьте стаю птиц, которая должна искать корм, но вместо этого все птицы синхронно летят на северо-восток с небольшими случайными отклонениями. Это не поиск, это миграция.
Проблема 4: Постоянные переинициализации. Из-за огромных смещений кристаллы постоянно вылетают за границы. Алгоритму приходится их переинициализировать в случайных местах. Это означает, что **любая накопленная информация о направлении движения теряется**. Кристалл двигался к перспективной области, вылетел, его телепортировали в случайное место - вся история движения стёрта. По сути, алгоритм каждые несколько итераций сбрасывается к случайному поиску.
Память о лучшем решении: локальное против глобального. Второе важное изменение связано с тем, какое "лучшее решение" используется в формулах. Модифицированная версия ведет глобальный дневник рекордов. Когда кто-то нашёл высоту 3000 метров, это записывается и никогда не забывается. Даже если все исследователи потом спустились вниз, алгоритм помнит: "Лучшее место, которое мы когда-либо находили, было вот там, на высоте 3000". И именно к этой точке притягиваются остальные исследователи. Это особенно важно в задачах оптимизации, когда популяция может временно деградировать. Например, вы применили мутацию, и все решения стали хуже. В оригинале алгоритм начнет следовать за худшими решениями. В модификации он продолжит держать курс на реально лучшее найденное решение за всю историю работы.
Добавление интенсивной локальной эксплуатации. Третье ключевое изменение касается нового механизма, который отсутствует в оригинале. В модифицированной версии с вероятностью 10% каждая координата кристалла генерируется специальным способом вокруг глобального лучшего решения с помощью функции "PowerDistribution" с параметром 20. Оригинальный алгоритм работает как чистая метаэвристика: кристаллы движутся по всему пространству согласно своим стратегиям. Модифицированная версия добавляет элемент локального поиска: каждая десятая координата выскакивает в окрестность лучшего найденного решения. Параметр 20 в PowerDistribution означает очень сильную концентрацию — примерно как если бы вы искали ключи в радиусе полуметра от того места, где помните их последний раз. Это не случайная точка в этой области, а точка с очень высокой вероятностью оказаться совсем близко к центру.
Упрощение обработки границ. Четвертое изменение касается того, что происходит, когда кристалл пытается выйти за допустимые границы пространства поиска. В модифицированной версии координата просто передается функции "u.SeInDiSp", которая обрезает значение по границам и применяет дискретизацию. Почему это изменение стало возможным? Потому что благодаря правильным формулам движения, кристаллы в модифицированной версии крайне редко выходят за границы
В оригинальной версии из-за абсолютного сложения векторов кристаллы постоянно вылетают за границы, и переинициализация становится необходимостью. Но эта переинициализация дорого обходится: во-первых, она требует генерации случайных чисел и дополнительных вычислений, во-вторых, она превращает направленное движение в случайное перемещение. Кристалл мог двигаться в перспективном направлении, вылетел за границу и оказался в совершенно случайном месте, потеряв всю траекторию движения.
Оптимизация использования памяти. Пятое изменение выглядит технически незначительным, но демонстрирует понимание того, что действительно нужно для работы алгоритма. В оригинальной версии перед обновлением позиции кристалла его текущая позиция копируется в специальный массив cP (предыдущая позиция), а затем в формулах используется эта копия. Например, новая координата вычисляется как старая координата из массива cP плюс что-то ещё. В модифицированной версии этого копирования нет. Формула просто берет текущее значение координаты, вычисляет изменение и записывает результат обратно в ту же переменную.
Почему оригиналу нужна была копия? Потому что формула выглядела как "x_new = x_old + нечто". Чтобы вычислить правую часть, нужно было зафиксировать x_old до начала изменений. В модифицированной версии формула перестроена так, что можно работать непосредственно с текущим значением: "x = x + изменение". Для популяции из 30 кристаллов в 10-мерном пространстве это экономит 300 операций копирования данных на каждой итерации. Может показаться, что это мелочь, но когда алгоритм выполняет тысячи итераций, эти мелочи накапливаются.
На визуализации можем проследить, как модифицированная версия во время работы формирует "кристаллические формы", заметен также разброс значений на функциях малой и средней размерности.

CryStAlm на тестовой функции Hilly

CryStAlm на тестовой функции Forest

CryStAlm на тестовой функции Forest

CryStAlm на стандартной тестовой функции Ackley
В рейтинговой таблице алгоритм CryStAlm представлен ознакомительно, совсем немного не хватило для определения места.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 5 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 6 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 7 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 8 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 26 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 27 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 28 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 29 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 30 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 31 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 32 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 33 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 34 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 35 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 36 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 37 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 38 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 39 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 40 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 41 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 42 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 43 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 44 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| 45 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| CryStAlm | crystal_structure_algorithm_M | 0,80656 | 0,56147 | 0,29097 | 1,65900 | 0,75228 | 0,48674 | 0,21014 | 1,44916 | 0,48461 | 0,27015 | 0,11111 | 0,86587 | 3,974 | 44,16 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Красивая идея, разрушенная реализацией. Алгоритм Crystal Structure Algorithm появился в 2021 году с привлекательной концепцией: использовать принципы формирования кристаллических структур для глобальной оптимизации. Авторы предложили популяционный алгоритм, где "кристаллы" движутся под влиянием средней позиции популяции, лучшего найденного решения и случайно выбранных соседей. Четыре стратегии движения, элегантная математическая модель. На бумаге всё выглядело убедительно.
Проблема в том, что между концептуальной идеей и работающей реализацией находится критический этап — перевод физической метафоры в конкретные математические операции. И именно здесь оригинальный CryStAl терпит провал. Формулы, которые выглядят разумно в статье, на практике превращают направленный поиск в хаотичное блуждание. Это не просто история о "нашли баг и исправили", а фундаментальный урок о том, что в разработке метаэвристик концепция и математическая реализация должны находиться в согласии, иначе алгоритм работает не так, как задумывалось, или не работает вообще.
Разрыв между замыслом и исполнением. Давайте посмотрим, что авторы ХОТЕЛИ реализовать в оригинальном CryStAl. Идея четкая: кристаллы должны притягиваться к трём ключевым точкам — к средней позиции всей популяции (центр масс, глобальная информация), к лучшему найденному кристаллу (эксплуатация) и к среднему случайных соседей (локальная информация, разнообразие). Четыре стратегии комбинируют эти притяжения разными способами. В теории это создаёт баланс между исследованием нового пространства и углублением поиска в перспективных областях. Физическая аналогия красивая: атомы взаимодействуют с соседями и стремятся к равновесной конфигурации. Авторы ХОТЕЛИ реализовать "притяжение к цели", но НАПИСАЛИ "добавление вектора". Это разные операции!
Системная ошибка мышления: формулы вместо геометрии. Корень проблемы глубже, чем одна неправильная формула. Это ментальная ошибка при проектировании алгоритма: концентрация на формулах вместо понимания того, что эти формулы делают в геометрии пространства поиска. Авторы оригинального CryStAl написали: "кристалл движется к средней позиции, формула: x + r × mean". Они сконцентрировались на алгебраическом выражении, не визуализируя, что произойдет с кристаллами в разных частях пространства. Правильный подход требует задать вопросы:
- Что должно произойти с кристаллом, который уже находится в целевой точке? Ответ: он должен остаться там или сделать очень маленький шаг. Оригинальная формула выбрасывает его прочь. Модифицированная оставляет на месте (при x_old = mean получаем x + 0 × (mean - x) = x).
- Что должно произойти с кристаллом, который находится дальше цели? Ответ: он должен вернуться назад к цели. Оригинальная формула толкает его дальше в том же направлении. Модифицированная разворачивает (отрицательная разность даёт движение назад).
- Должна ли величина шага зависеть от абсолютных значений координат? Ответ: нет, она должна зависеть от расстояния до цели. Оригинал зависит от абсолютных значений. Модификация — от расстояний.
- Что происходит, когда переменные имеют разные масштабы? Оригинал: смещения по разным координатам несоразмерны их относительным расстояниям до цели. Модификация: смещения автоматически масштабируются относительными расстояниями.
Ответы на эти вопросы немедленно показывают, что формула x + r × target геометрически некорректна для моделирования притяжения. А формула x + r × (target - x) геометрически правильна: это интерполяция, движение на r-ю долю пути к цели, с естественными свойствами замедления при приближении.
Множество формул не спасают неправильную базу. Может возникнуть впечатление, что четыре стратегии CryStAl компенсируют проблемы друг друга. Стратегия 0 с одной целевой точкой работает плохо, но стратегия 3 с тремя целевыми точками должна быть лучше? На практике происходит обратное: умножение неправильных операций усугубляет проблему.
Формула стратегии 3: x_new = x_old + r1 × mean + r2 × best + r3 × fc, где fc - среднее случайных кристаллов. Теперь мы складываем ТРИ больших числа (абсолютные координаты трёх целевых точек). Возьмём пример: переменные от 0 до 1000, кристалл в [640, 430, 770], mean = [650, 420, 780], best = [645, 425, 775], fc = [655, 415, 785], коэффициенты r1 = r2 = r3 = 0.4.
Первая координата: 640 + 0.4 × 650 + 0.4 × 645 + 0.4 × 655 = 640 + 260 + 258 + 262 = 1420 - ещё дальше за границей!
Стратегия 3 должна была быть самой сложной и эффективной (балансирует глобальную, локальную информацию и эксплуатацию), но на практике она генерирует самые большие выбросы, потому что суммирует ещё больше абсолютных величин. Проблема не в количестве компонентов, а в том, что базовая операция (абсолютное сложение) фундаментально неправильна.
От случайного поиска к направленной оптимизации. Что реально делает оригинальный CryStAl на практике? После нескольких итераций устанавливается следующий режим работы: на каждом шаге популяция получает огромные смещения, большинство кристаллов вылетает за границы, их координаты переинициализируются случайно. Фактически каждые 2-3 итерации алгоритм генерирует новую почти случайную популяцию, сохраняя лишь небольшую долю координат от предыдущего поколения.
Модифицированный CryStAlm работает принципиально иначе. Кристаллы действительно движутся к целевым точкам, а не хаотично перемещаются. Траектории плавные и контролируемые. Выходы за границы редки. Популяция методично сходится к перспективным областям, сохраняя при этом разнообразие благодаря случайным стратегиям и механизму отталкивания. Каждая итерация накапливает информацию о ландшафте функции и использует её для следующих шагов и не стирает предыдущее состояние случайными регенерациями.
Методологический урок для исследователей. История CryStAl — это не просто пример неудачной реализации. Это системная проблема в разработке метаэвристических алгоритмов.
Более широкий контекст: эпидемия слабых алгоритмов. CryStAl не уникален. В литературе по метаэвристикам последних 15 лет сотни "новых" алгоритмов, вдохновленных разными метафорами и многие из них страдают той же болезнью: красивая идея, нестрогая реализация, тестирование на ограниченном наборе задач, публикация с заявками о конкурентоспособности. Потом другие исследователи берут эти алгоритмы как baseline, сравниваются с ними, создавая цепочку сравнений с фундаментально слабыми основаниями.
Модификация CryStAl в CryStAlm даёт нам глубокий анализ. Минимальные изменения в коде (переписать формулы движения, добавить PowerDistribution, использовать cB вместо bestCrystalIdx), но фундаментальные изменения в поведении.
Сравнение CryStAl и CryStAlm преподносит несколько критических уроков для сообщества исследователей в области метаэвристической оптимизации:
Урок 1: Концепция не равна реализации. Красивая идея алгоритма — это только начало. Перевод идеи в математические операции требует глубокого понимания геометрии пространства поиска. Формулы должны делать то, что вы хотите, а не просто выглядеть правдоподобно на бумаге. Проверяйте не только "что формула вычисляет", но и "что она делает с агентами в разных ситуациях".
Урок 2: Абстракция скрывает ошибки. Когда вы пишете "кристалл притягивается к средней позиции", легко пропустить, что формула реализует не притяжение, а параллельное смещение. Абстрактное мышление ("движение к цели") должно сопровождаться конкретной проверкой ("как именно изменятся координаты"). Всегда проверяйте формулы на конкретных числовых примерах.
Урок 3: Стандартные тесты недостаточны. Тестирование на CEC benchmark с нормализованными переменными может скрывать критические проблемы, которые проявляются на реалистичных масштабах или смешанных диапазонах. Добавляйте тесты с "неудобными" условиями: очень большие диапазоны, разные масштабы переменных, узкие оптимумы. Визуализируйте поведение алгоритма, не только результаты.
Урок 4: Множество механизмов не компенсирует неправильную базу. Если базовая операция (например, формула движения) некорректна, добавление сложных надстроек не поможет. Сначала убедитесь, что фундамент работает, потом добавляйте улучшения. Один правильный механизм лучше десяти неправильных.
Урок 5: Сравнения требуют проверки baseline. Если ваш новый алгоритм превосходит существующий, задайтесь вопросом: а работает ли тот baseline вообще? Быстрая проверка: сравните baseline со случайным поиском. Если разница мала - вы сравниваетесь с пустышкой, и ваш результат ничего не значит.
Урок 6: Детали реализации критически важны. Разница между "почти правильной" формулой и "правильной" может быть огромной для производительности. x + r × mean и x + r × (mean - x) отличаются на несколько символов в коде, но в 2 раза по качеству результатов. Детали имеют значение. Не игнорируйте их как "технические мелочи".
CryStAl демонстрирует, что метаэвристика — это не коллекция метафор и формул. Это инженерная дисциплина, где понимание того, как операции влияют на динамику поиска в пространстве решений, столь же важно, как и изначальная концепция. Красивая идея, реализованная небрежно, даёт алгоритм, который работает как случайный поиск. Та же идея, реализованная с пониманием геометрии и динамики, даёт работающий инструмент.
Для продвижения области вперед недостаточно генерировать новые метафоры. Нужно создавать алгоритмы, которые действительно делают то, что заявлено - направленно исследуют пространство, накапливают информацию, сходятся к оптимумам. И это требует не просто написать формулы, а глубоко проанализировать, правильно ли эти формулы реализуют замысел.
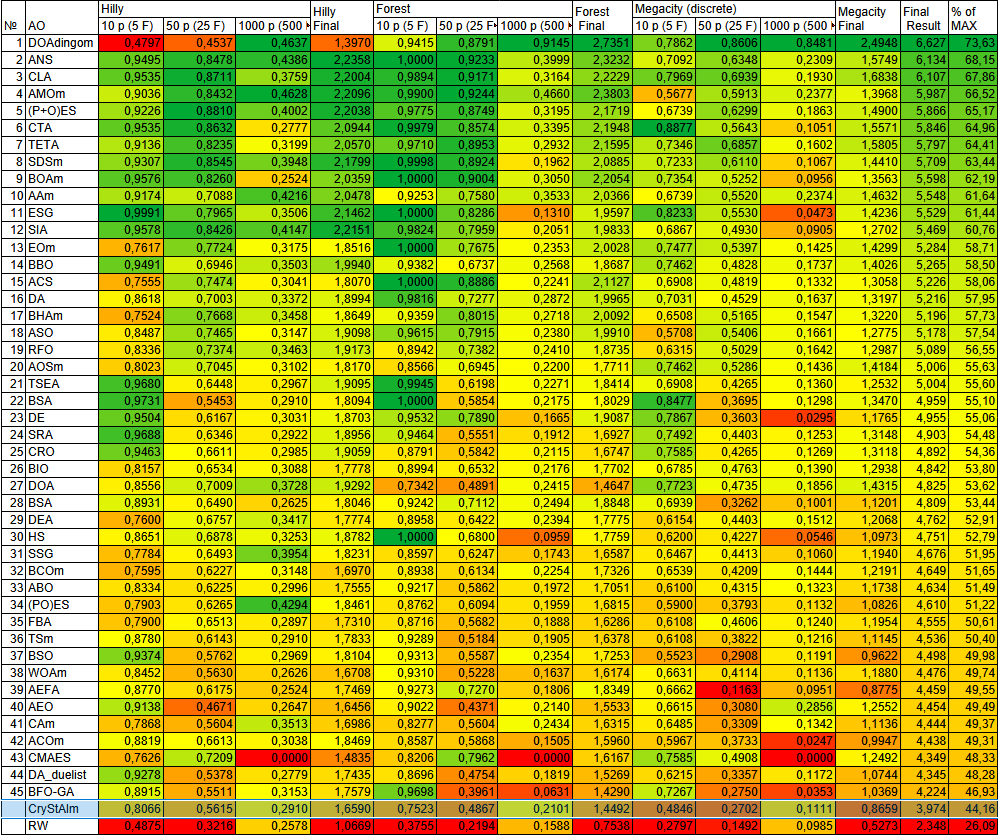
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
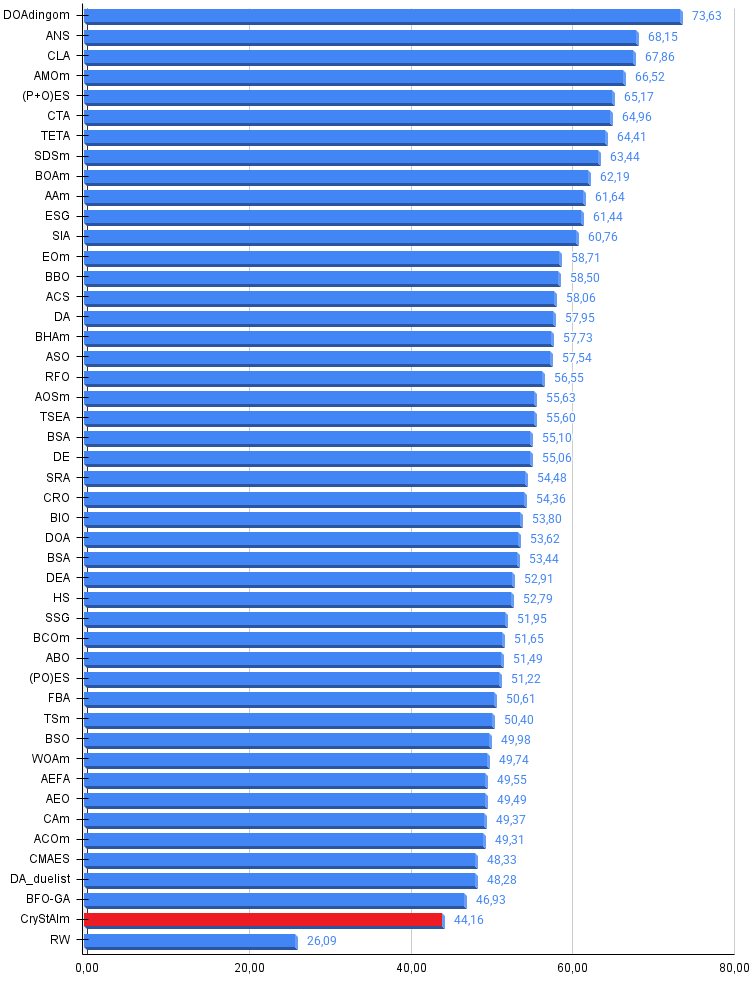
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма CryStAlm:
Плюсы:
- Относительно простая реализация.
- Быстрый.
- Стабильно средние результаты (желтый цвет, без серьёзных провалов на отдельных тестах).
Минусы:
- Разброс значений на функциях малой и средней размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_CryStAlm.mq5 | Скрипт | Испытательный стенд для CryStAlm |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 От новичка до эксперта: Торговля с использованием уровней Фибоначчи после публикации NFP
От новичка до эксперта: Торговля с использованием уровней Фибоначчи после публикации NFP
 Нейросети в трейдинге: Модели многократного уточнения прогнозов (RAFT)
Нейросети в трейдинге: Модели многократного уточнения прогнозов (RAFT)
 Нейросети в трейдинге: Модели многократного уточнения прогнозов (Основные компоненты)
Нейросети в трейдинге: Модели многократного уточнения прогнозов (Основные компоненты)
 От новичка до эксперта: Анимированный советник News Headline с использованием MQL5 (XI) - Корреляция при торговле на новостях
От новичка до эксперта: Анимированный советник News Headline с использованием MQL5 (XI) - Корреляция при торговле на новостях
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования