
Алгоритм Бизона — Bison Algorithm (BIA)
Содержание
Введение
В поисках лучшего оптимизационного метода, в этой статье познакомимся с Алгоритмом Бизона (Bison Algorithm, BIA) — это популяционный алгоритм оптимизации, вдохновлённый поведением роя, предназначенный для непрерывных задач с одной целевой функцией. Ключевыми особенностями BIA являются два основополагающих принципа, заимствованных из поведения бизонов, это способность к динамичному перемещению и оборонительная стратегия. Алгоритм был разработан чешскими исследователями в 2017 году и был опубликован в сборнике Lecture Notes in Computer Science (Springer) в 2019 году.
Бизоны — удивительные животные с огромной выносливостью и силой. Они способны развивать большую скорость и поддерживать её в течение получаса. Когда их окружают хищники, они склонны образовывать круг, в котором самые сильные особи находятся по периметру, а остальное стадо стремится оказаться внутри, чтобы занять безопасную позицию.
Эти два поведенческих паттерна были смоделированы в Алгоритме Бизона и применены в качестве техники оптимизации. Первый аспект, "скорость и выносливость", позволяет агентам алгоритма перемещаться по всему пространству поиска, исследуя новые и потенциально оптимальные области. Второй аспект, "оборонительный круг", моделирует механизм локального исследования и стабилизации, когда агенты собираются вокруг наиболее перспективных решений, защищая их от преждевременного отклонения и уточняя их позиции. Теперь посмотрим, как это действительно работает в алгоритме.
Реализация алгоритма
Вы наблюдаете за стадом бизонов в прерии. Им нужно найти самое лучшее пастбище с сочной травой и чистой водой. Но прерия огромна! Как же они это делают? Разделим стадо бизонов на две группы.
Основное стадо (80% бизонов) — это осторожные бизоны. Они держатся вместе, медленно передвигаются группой. "Безопасность в числах!" — их девиз.
Исследователи (20% бизонов) — это смелые молодые бизоны. Они бегут вперед в одном направлении, исследуя новые территории. "А что там, за холмом?" — думают они.
Сформированы две группы: 40 бизонов основного стада разбредаются по известной территории, а 10 бегунов собираются возле самого упитанного бизона (он явно знает, где хорошая трава!) и готовятся к забегу. Когда бизон из основного стада идет к новому месту, он сначала запоминает, где стоял. Делает несколько шагов (от 0 до 3.5 метров). Пробует траву. Если новая трава хуже, тогда возвращается обратно. "Лучше синица в руках..." Если бегун-исследователь нашел место лучше, чем у худшего в стаде бизона, то происходит их замена местами. Бегуны каждый день слегка меняют направление (на 10% влево или вправо). Так больше шансов найти что-то новое. Когда стадо собирается вокруг лучших бизонов, они не просто встают посередине. Вожак (самый упитанный) имеет "вес" 100, второй — 90, третий — 80... десятый — 10.
Теперь представьте, что:
- Пастбище = пространство поиска решений
- Качество травы = значение целевой функции
- Позиция бизона = потенциальное решение
- Лучшее пастбище = оптимальное решение
Диаграмма ниже показывает фазу инициализации — разделение популяции на роевую группу (80%) и бегущую группу (20%). Основной цикл итераций с четырьмя шагами: определение цели роения (выбор между лучшим бегуном или центром элиты), движение роевой группы к центру (вычисление центра элиты со взвешенным усреднением), движение бегунов по направлению исследования, проверка и обновление результатов.
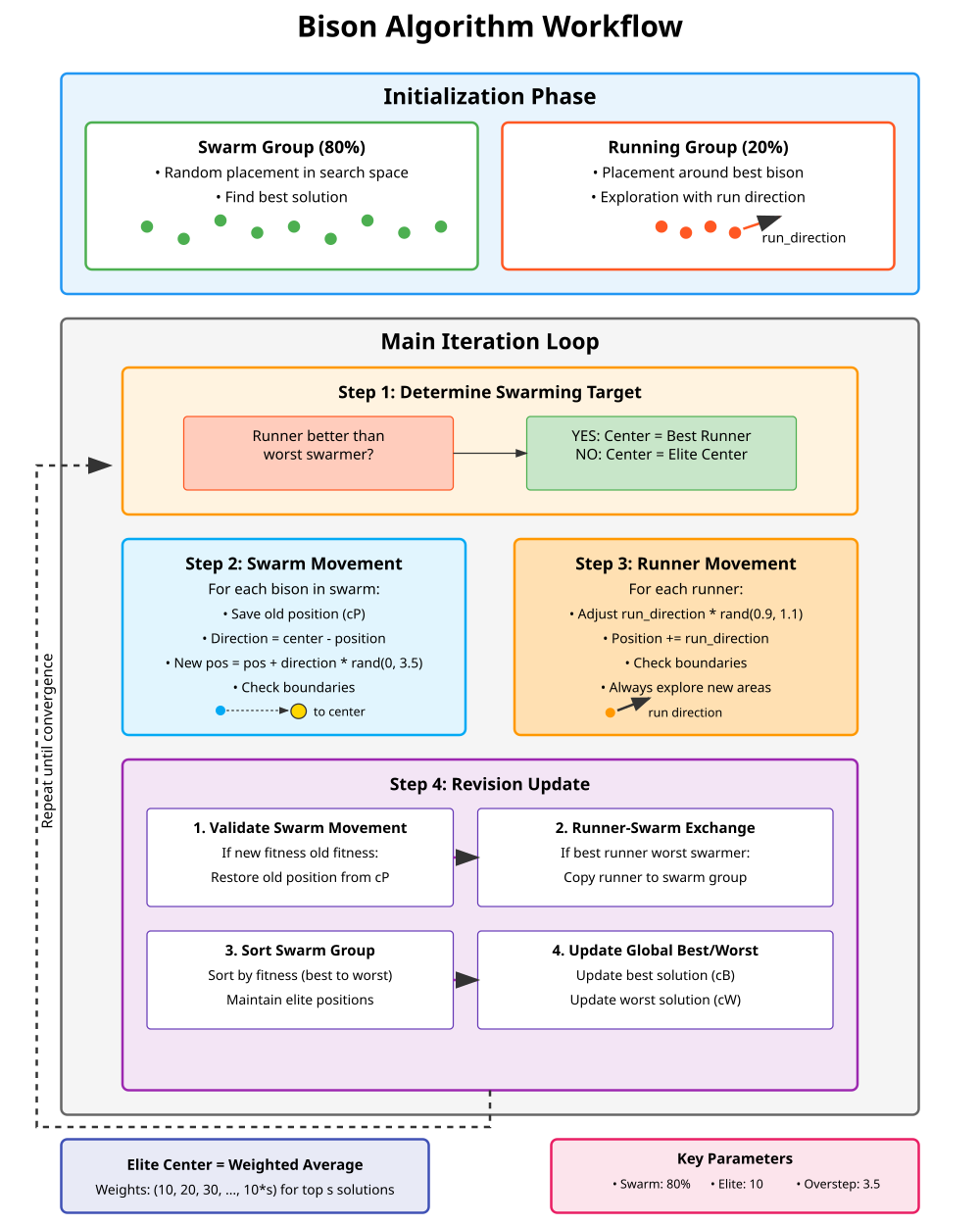
Рисунок 1. Схема работы стратегии алгоритма BIA
Ключевые параметры алгоритма. Цветовая схема: зеленый — роевая группа, оранжевый — бегущая группа, фиолетовый — фаза проверки и обновления, голубой — движение роя. Стрелки показывают поток выполнения и направления движения групп на иллюстрации.
Приступим к написанию псевдокода алгоритма DIA.
ИНИЦИАЛИЗАЦИЯ:
1. Создать популяцию из N бизонов
2. Разделить на группы:
- Роевая группа (80%): разместить случайно по всему пространству
- Бегущая группа (20%): разместить вокруг лучшего бизона роевой группы
3. Задать случайное направление бега для разведчиков
ОСНОВНОЙ ЦИКЛ (повторять до сходимости):
ВЫБОР ЦЕЛИ ДВИЖЕНИЯ:
- ЕСЛИ лучший из бегущей группы нашел место лучше худшего в стаде:
Цель = позиция лучшего из бегущей группы
- ИНАЧЕ:
Цель = взвешенный центр 10 лучших в стаде
ДВИЖЕНИЕ РОЕВОЙ ГРУППЫ:
- Для каждого бизона в стаде:
1. Сохранить текущую позицию
2. Вычислить направление к цели
3. Сделать шаг к цели (случайная длина от 0 до 3.5)
4. Проверить границы области поиска
ДВИЖЕНИЕ БЕГУЩЕЙ ГРУППЫ:
- Слегка изменить направление бега (×0.9-1.1)
- Для каждого индивида:
1. сдвинуться по направлению бега
2. проверить границы области поиска
ОЦЕНКА И ОБНОВЛЕНИЕ:
1. Проверка роевой группы:
- ЕСЛИ новая позиция хуже старой:
Вернуть старую позицию
2. Обмен между группами:
- ЕСЛИ лучший индивид из бегущей группы лучше худшего в стаде:
Заменить худшего в стаде на лучшего индивида
3. Сортировка:
- Отсортировать роевую группу по качеству
4. Обновление:
- Запомнить лучшее найденное решение
- Запомнить худшее решение
КОНЕЦ ЦИКЛА
ВЫЧИСЛЕНИЕ ВЗВЕШЕННОГО ЦЕНТРА:
- Взять 10 лучших решений
- Присвоить веса: 1-й получает вес 100, 2-й - 90, ..., 10-й - 10
- Центр = сумма(позиция × вес) / сумма(весов)
Теперь нам более понятно, как все работает, и мы можем приступить к написанию кода алгоритма. Класс реализует "Bison Algorithm" и указывает наследование от базового класса "C_AO".
Параметры алгоритма:- popSize — определяет общее число "индивидов" или "агентов" в популяции, участвующей в работе алгоритма.
- swarmGroupRate — задает долю (в процентах) от общего числа индивидов, которая будет составлять "роевую группу".
- eliteGroupSize — определяет количество самых лучших индивидов, которые формируют "элитную группу" для вычисления центра.
- overstep — устанавливает максимальный шаг, который может сделать "роевая группа" при своем движении.
В конструкторе устанавливаются значения по умолчанию для всех параметров. Метод "SetParams" позволяет обновить значения параметров алгоритма, используя данные из внешнего источника (представленного массивом "params").
Функциональность:
- Init — метод для начальной инициализации алгоритма, с использованием диапазонов значений для параметров.
- Moving — метод, отвечающий за движение или обновление состояния индивидов в популяции.
- Revision — метод используется для пересмотра и корректировки поведения индивидов или параметров.
- ComputeCenter — приватный метод для вычисления центра элитной группы.
- CheckIfRunnerBetter — приватный метод, проверяет, является ли какой-либо "бегущий" индивид лучше других.
- swarmGroupSize — рассчитывается на основе "popSize" и "swarmGroupRate", определяет фактическое количество особей в роевой группе.
- runningGroupSize — размер "бегущей" группы (подгруппа в общей популяции).
- runDirection — массив, хранящий направление движения для каждого индивида.
- center — массив, хранящий координаты центра элитной группы.
В целом, класс "C_AO_BisonAlgorithm" представляет собой блок, реализующий поисковую стратегию, основанную на концепции популяции, роевых и элитных групп, и имеющий настраиваемые параметры.
class C_AO_BisonAlgorithm : public C_AO { public: //---------------------------------------------------------- ~C_AO_BisonAlgorithm () { } C_AO_BisonAlgorithm () { ao_name = "BIA"; ao_desc = "Bison Algorithm"; ao_link = "https://www.mql5.com/ru/articles/19444"; popSize = 50; // размер популяции swarmGroupRate = 0.8; // доля роевой группы от популяции (80%) eliteGroupSize = 10; // размер элитной группы для вычисления центра (s параметр) overstep = 3.5; // максимальный шаг роевой группы ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "swarmGroupRate"; params [1].val = swarmGroupRate; params [2].name = "eliteGroupSize"; params [2].val = eliteGroupSize; params [3].name = "overstep"; params [3].val = overstep; } void SetParams () { popSize = (int)params [0].val; swarmGroupRate = params [1].val; eliteGroupSize = (int)params [2].val; overstep = params [3].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); private: void ComputeCenter (); bool CheckIfRunnerBetter (); //------------------------------------------------------------------ public: double swarmGroupRate; // доля роевой группы int eliteGroupSize; // размер элитной группы (s параметр) double overstep; // максимальный шаг роевой группы private: //--------------------------------------------------------- int swarmGroupSize; // размер роевой группы int runningGroupSize; // размер бегущей группы double runDirection []; // направление бега double center []; // центр элитной группы }; //————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_BisonAlgorithm" отвечает за первоначальную настройку алгоритма перед началом его работы. Сначала метод пытается выполнить общую, стандартизированную часть инициализации, используя передаваемые ей диапазоны значений для параметров и количество эпох. Если эта стандартная часть не удается, весь процесс инициализации прерывается. Далее, исходя из общего размера популяции и заданного коэффициента, вычисляется количество особей, которые будут относиться к "роевой группе". Оставшиеся особи формируют "бегущую группу".
Для обеспечения корректной работы алгоритма размеры этих групп проходят проверку. Гарантируется, что роевая группа всегда будет иметь хотя бы одного члена, а также, что она не займет всю популяцию (оставляя место для бегущей группы). Аналогично проверяется, что элитная группа не меньше одного и не превышает по размеру роевую группу, являясь ее подмножеством.
Выделяется память для служебных массивов. Массив, предназначенный для хранения направления движения особей (для каждого измерения пространства поиска), и массив для хранения координат центра элитной группы, оба изменяют свой размер до количества измерений, определенных в системе. Если все предыдущие шаги выполнены успешно, метод возвращает "true", алгоритм готов к работе.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_BisonAlgorithm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Вычисляем размеры групп swarmGroupSize = (int)MathFloor (popSize * swarmGroupRate); runningGroupSize = popSize - swarmGroupSize; // Корректировка размеров групп if (swarmGroupSize < 1) swarmGroupSize = 1; if (swarmGroupSize >= popSize) swarmGroupSize = popSize - 1; if (eliteGroupSize < 1) eliteGroupSize = 1; if (eliteGroupSize > swarmGroupSize) eliteGroupSize = swarmGroupSize; // Инициализация вспомогательных массивов ArrayResize (runDirection, coords); ArrayResize (center, coords); return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" класса "C_AO_BisonAlgorithm" является ядром алгоритма, отвечающим за одну итерацию или шаг эволюции популяции. Он состоит из двух основных фаз: первоначальной инициализации популяции (если алгоритм запускается впервые) и последующих шагов обновления позиций особей.
Фаза 1: Первоначальная инициализация (при первом запуске): если алгоритм запускается впервые (флаг "revision" установлен в "false"), выполняется следующая последовательность действий:
- Генерация роевой группы. Особи, входящие в роевую группу, инициализируются случайными значениями в пределах заданных для каждого параметра диапазонов. После генерации эти значения могут быть дополнительно скорректированы, чтобы соответствовать шагу изменения параметров.
- Поиск лучшего бизона. Среди всех особей роевой группы находится та, которая имеет наилучшую приспособленность (наибольшее значение целевой функции).
- Генерация бегущей группы. Остальные особи популяции (бегущая группа) инициализируются вокруг найденного лучшего бизона. Их позиции генерируются случайным образом в некоторой окрестности лучшего решения, а затем также корректируются, в соответствии с диапазонами и шагами параметров.
- Инициализация вектора направления движения. Для каждой размерности пространства поиска генерируется случайный вектор направления движения. Величина этого вектора зависит от общего диапазона значений параметра, и его знак (положительный или отрицательный) также выбирается случайно.
- Установка флага инициализации. Флаг "revision" устанавливается в "true", начальная инициализация завершена, и в дальнейшем будут выполняться только шаги обновления.
Фаза 2: Основной цикл итерации (последующие шаги): когда начальная инициализация уже проведена, метод выполняет следующие шаги для каждой итерации:
Определение цели роения. Алгоритм проверяет, не является ли какое-либо решение из бегущей группы лучше, чем текущая "цель роения".- Если решение из бегущей группы оказывается лучше, то эта цель роения (центроид) устанавливается равной этому лучшему решению.
- В противном случае, вычисляется новый центроид, который представляет собой среднюю позицию лучших решений популяции.
- Сначала сохраняются текущие позиции и значения приспособленности особи.
- Затем новая позиция рассчитывается путем движения от текущей позиции в направлении целевой точки роения. Величина этого движения определяется случайным фактором, который регулирует "перешагивание" через цель.
- Полученная новая позиция затем корректируется, чтобы оставаться в пределах допустимых диапазонов и учитывать шаг параметров.
Корректировка вектора направления движения. Вектор направления, используемый бегущей группой, немного изменяется случайным образом. Это придает некоторую вариативность в движении бегунов.
Движение бегущей группы. Каждая особь бегущей группы перемещается, используя скорректированный вектор направления.
- Новая позиция вычисляется путем добавления вектора направления к текущей позиции.
- Затем эта новая позиция корректируется, чтобы оставаться в пределах допустимых диапазонов и учитывать шаг параметров.
Таким образом, метод "Moving" моделирует поведение группы особей: часть группы (роевая) движется к общей цели, реагируя на лучшие решения, а другая часть (бегущая) следует за скорректированным вектором направления, который также может изменяться.
/———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_BisonAlgorithm::Moving () { // Начальная инициализация популяции if (!revision) { // Генерация роевой группы случайным образом for (int i = 0; i < swarmGroupSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } // Находим лучшее решение среди роевой группы для инициализации бегунов int bestIdx = 0; double bestFit = a [0].f; for (int i = 1; i < swarmGroupSize; i++) { if (a [i].f > bestFit) { bestFit = a [i].f; bestIdx = i; } } // Генерация бегущей группы вокруг лучшего бизона double neighbourhood = (rangeMax [0] - rangeMin [0]) / 15.0; for (int i = swarmGroupSize; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = a [bestIdx].c [j] + u.RNDfromCI (-neighbourhood, neighbourhood); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } // Генерация run direction = random((ub-lb)/45, (ub-lb)/15) for (int j = 0; j < coords; j++) { double range = rangeMax [j] - rangeMin [j]; runDirection [j] = u.RNDfromCI (range / 45.0, range / 15.0); if (u.RNDprobab () < 0.5) runDirection [j] = -runDirection [j]; } revision = true; return; } //------------------------------------------------------------------ // Основной цикл итерации // 1. Определяем цель роения (swarming target) if (CheckIfRunnerBetter ()) { // Если runner лучше swarmer, center = runner // center уже установлен в CheckIfRunnerBetter } else { // Иначе вычисляем центр сильнейших решений ComputeCenter (); } // 2. Движение роевой группы for (int i = 0; i < swarmGroupSize; i++) { // Сохраняем старые позиции в cP и фитнес в fP ArrayCopy (a [i].cP, a [i].c, 0, 0, coords); a [i].fP = a [i].f; // Вычисляем нового кандидата позиции for (int c = 0; c < coords; c++) { double direction = center [c] - a [i].c [c]; a [i].c [c] = a [i].c [c] + direction * u.RNDfromCI (0.0, overstep); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } // 3. Корректировка run direction вектора for (int j = 0; j < coords; j++) { runDirection [j] = runDirection [j] * u.RNDfromCI (0.9, 1.1); } // 4. Движение бегущей группы for (int i = swarmGroupSize; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].c [c] + runDirection [c]; a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" класса "C_AO_BisonAlgorithm" предназначен для обновления состояния популяции после выполнения одного шага движения и оценки приспособленности особей, а также для подведения итогов итерации.
Коррекция роевой группы. Для каждой особи в роевой группе проверяется, является ли ее новая позиция (рассчитанная на предыдущем шаге) лучше, чем ее предыдущая (сохраненная) позиция. Если новая позиция хуже, особь возвращается к своей предыдущей, лучшей позиции. Таким образом особи роевой группы не ухудшают свое результаты.
Сравнение бегущей группы с роевой:
- Находится лучшая особь в бегущей группе (с самой высокой приспособленностью) и худшая особь в роевой группе (с самой низкой приспособленностью).
- Если лучшая особь из бегущей группы оказывается лучше, чем худшая особь из роевой группы, то худшая особь из роевой группы заменяется лучшей особью из бегущей группы. Это позволяет более сильным решениям из бегущей группы проникать в роевую группу.
- Создается временная копия всех особей роевой группы.
- Эта временная копия сортируется по убыванию приспособленности (от лучшего к худшему).
- После сортировки, особи из отсортированной временной копии копируются обратно в основную популяцию. Это гарантирует, что в роевой группе всегда будут находиться лучшие решения, найденные на данный момент.
- Лучшее глобальное решение. Сравнивается приспособленность лучшей особи в роевой группе (которая теперь является лучшим решением после сортировки) с текущим лучшим глобальным решением. Если лучшая особь роевой группы лучше, обновляется глобальное лучшее решение.
- Худшее глобальное решение. Просматриваются все особи в популяции (и роевой, и бегущей), чтобы найти самую слабую особь. Если обнаружена особь со значением приспособленности ниже текущего худшего глобального решения, то худшее глобальное решение обновляется.
Таким образом, метод "Revision" играет роль "приемщика результатов", который отбирает лучшие решения, поддерживает порядок и обновление в роевой группе, и отслеживает общий прогресс алгоритма, сохраняя лучшее и худшее найденное решение.
//———————————————————————————————————————————————————————————————————— //--- Обновление и проверка результатов void C_AO_BisonAlgorithm::Revision () { // 1. Для роевой группы: обновляем позиции только если новая позиция лучше for (int i = 0; i < swarmGroupSize; i++) { // Если новая позиция хуже старой, возвращаем старую if (a [i].f < a [i].fP) { ArrayCopy (a [i].c, a [i].cP, 0, 0, coords); a [i].f = a [i].fP; } } // 2. Проверяем, не нашел ли runner лучшее решение чем swarmer double bestRunnerFitness = -DBL_MAX; int bestRunnerIdx = -1; double worstSwarmerFitness = DBL_MAX; int worstSwarmerIdx = -1; for (int i = swarmGroupSize; i < popSize; i++) { if (a[i].f > bestRunnerFitness) { bestRunnerFitness = a[i].f; bestRunnerIdx = i; } } for (int i = 0; i < swarmGroupSize; i++) { if (a[i].f < worstSwarmerFitness) { worstSwarmerFitness = a[i].f; worstSwarmerIdx = i; } } // Если runner лучше худшего swarmer, копируем runner в swarming group if (bestRunnerIdx >= 0 && worstSwarmerIdx >= 0 && bestRunnerFitness > worstSwarmerFitness) { ArrayCopy (a[worstSwarmerIdx].c, a[bestRunnerIdx].c, 0, 0, coords); a[worstSwarmerIdx].f = a[bestRunnerIdx].f; } // 3. Сортировка роевой группы // Создаем временный массив для сортировки только роевой группы S_AO_Agent swarmTemp []; ArrayResize (swarmTemp, swarmGroupSize); // Копируем роевую группу for (int i = 0; i < swarmGroupSize; i++) { swarmTemp[i].Init(coords); ArrayCopy (swarmTemp[i].c, a[i].c, 0, 0, coords); swarmTemp[i].f = a[i].f; ArrayCopy (swarmTemp[i].cP, a[i].cP, 0, 0, coords); swarmTemp[i].fP = a[i].fP; } // Сортируем S_AO_Agent tempSorted []; ArrayResize (tempSorted, swarmGroupSize); u.Sorting (swarmTemp, tempSorted, swarmGroupSize); // Копируем обратно отсортированную роевую группу for (int i = 0; i < swarmGroupSize; i++) { ArrayCopy (a[i].c, swarmTemp[i].c, 0, 0, coords); a[i].f = swarmTemp[i].f; ArrayCopy (a[i].cP, swarmTemp[i].cP, 0, 0, coords); a[i].fP = swarmTemp[i].fP; } // 4. Обновляем глобальное лучшее и худшее решение if (a[0].f > fB) { fB = a[0].f; ArrayCopy (cB, a[0].c, 0, 0, WHOLE_ARRAY); } // Находим худшее во всей популяции for (int i = 0; i < popSize; i++) { if (a[i].f < fW) { fW = a[i].f; ArrayCopy (cW, a[i].c, 0, 0, WHOLE_ARRAY); } } } //————————————————————————————————————————————————————————————————————
Метод "CheckIfRunnerBetter" служит для определения, содержит ли бегущая группа более перспективное решение, чем те, что присутствуют в роевой группе. Если такое решение найдено, оно становится новой "целью" для роения.
Поиск лучшего "бегуна". Метод сначала сканирует всех особей, относящихся к "бегущей группе" (не являющихся частью роевой). Он находит особь с наилучшей приспособленностью (самое высокое значение целевой функции) среди всех "бегунов" и сохраняет ее индекс и значение приспособленности.
Поиск худшего "роя". Затем метод анализирует особей, входящих в "роевую группу". Он находит особь с наихудшей приспособленностью (самое низкое значение целевой функции) среди роя.
Сравнение и определение цели. После этого происходит сравнение:
- Если наилучший "бегун" имеет приспособленность выше, чем у худшего "роя", это означает, что бегущая группа действительно нашла более качественное решение.
- В этом случае, позиция (координаты) наилучшего "бегуна" присваивается переменной, обозначающей "центр" или "цель роения". Метод возвращает значение, указывающее, что цель роения была обновлена.
Возврат результата:
- Если наилучший "бегун" оказался лучше худшего из "роя", метод сообщает об этом, возвращая утвердительное значение.
- В противном случае (если ни один "бегун" не превзошел худшего из "роя"), метод сообщает об этом, возвращая отрицательное значение, и "центр роения" остается прежним.
Таким образом, этот метод позволяет динамически менять направление поиска: если появляются более сильные решения в "исследовательской" бегущей группе, они становятся ориентиром для "социальной" роевой группы.
//———————————————————————————————————————————————————————————————————— //--- Проверка, лучше ли runner чем swarmer bool C_AO_BisonAlgorithm::CheckIfRunnerBetter () { // Находим лучшего runner double bestRunnerFitness = -DBL_MAX; int bestRunnerIdx = -1; for (int i = swarmGroupSize; i < popSize; i++) { if (a[i].f > bestRunnerFitness) { bestRunnerFitness = a[i].f; bestRunnerIdx = i; } } // Находим худшего swarmer double worstSwarmerFitness = DBL_MAX; for (int i = 0; i < swarmGroupSize; i++) { if (a[i].f < worstSwarmerFitness) { worstSwarmerFitness = a[i].f; } } // Если runner лучше swarmer, устанавливаем его как центр if (bestRunnerIdx >= 0 && bestRunnerFitness > worstSwarmerFitness) { ArrayCopy (center, a[bestRunnerIdx].c, 0, 0, coords); return true; } return false; } //————————————————————————————————————————————————————————————————————
Метод "ComputeCenter" вычисляет новую "целевую" позицию (центр) для роевой группы, основываясь на самых лучших найденных решениях. Вот как он работает:
- Обнуление целевой позиции. Сначала все компоненты будущей целевой позиции (центра) обнуляются. Это подготавливает их к накоплению новых значений.
- Определение количества лучших решений. Метод выбирает, сколько именно лучших решений будет использоваться для расчета центра. Он берет минимальное значение из двух параметров:
- eliteGroupSize — максимальное количество "элитных" решений, которые могут быть учтены;
- swarmGroupSize — размер текущей роевой группы;
- Это гарантирует, что мы используем либо все заданные элитные решения, либо столько, сколько есть в роевой группе, если элитных решений меньше.
- Назначение весов. Создается набор весов для каждого из выбранных лучших решений. Эти веса увеличиваются линейно: первое решение получает меньший вес, второе — больший, и так далее, до последнего. Конкретно, веса задаются как 10, 20, 30... до s * 10, где s —количество учитываемых лучших решений. Эти веса показывают, насколько значимым является каждое решение при вычислении центра.
- Накопление общей суммы весов. Все рассчитанные веса суммируются. Эта общая сумма понадобится для нормализации.
- Взвешенное суммирование позиций. Теперь для каждой размерности (координаты) позиции:
- берется значение соответствующей координаты из каждого из s лучших решений;
- это значение координаты умножается на вес соответствующего лучшего решения. Важно отметить, что веса применяются в обратном порядке: самое лучшее решение (первое в отсортированном списке) получается самый большой вес, второе — следующий по величине, и так далее.
- результаты этих умножений для всех s лучших решений суммируются для данной координаты.
- Нормализация. Полученная сумма взвешенных координат для каждой размерности делится на общую сумму всех весов. Это делает расчет "средневзвешенным", гарантируя, что итоговая позиция центра находится в некоторой "средней" области лучших найденных решений, при этом более качественные решения имеют большее влияние.
В результате, метод "ComputeCenter" создает новую "целевую" позицию, которая является своего рода "средним" лучшим решением, но с предпочтением для наиболее качественных из них, что помогает направлять дальнейший поиск роя.
//———————————————————————————————————————————————————————————————————— //--- Вычисление центра элитной группы void C_AO_BisonAlgorithm::ComputeCenter () { // Обнуляем центр for (int j = 0; j < coords; j++) { center [j] = 0.0; } // Вычисляем взвешенный центр из s лучших решений double weights []; int s = MathMin(eliteGroupSize, swarmGroupSize); ArrayResize (weights, s); double totalWeight = 0.0; // weight = (10, 20, 30, ..., 10*s) for (int i = 0; i < s; i++) { weights[i] = (i + 1) * 10.0; totalWeight += weights[i]; } // center = sum(weight[i] * position[i]) / sum(weights) for (int j = 0; j < coords; j++) { for (int i = 0; i < s; i++) { center[j] += (weights[s - 1 - i] * a[i].c[j]) / totalWeight; } } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Результаты, как видим, средние, на дискретной функции Megacity несколько ниже, алгоритм труднее справляется с дискретными задачами.Bison|Bison Algorithm|50.0|0.8|10|3.5|
=============================
5 Hilly's; Func runs: 10000; result: 0.761847128451914
25 Hilly's; Func runs: 10000; result: 0.4002698460741261
500 Hilly's; Func runs: 10000; result: 0.25201531651422443
=============================
5 Forest's; Func runs: 10000; result: 0.7620992740937584
25 Forest's; Func runs: 10000; result: 0.45225292646780135
500 Forest's; Func runs: 10000; result: 0.19295587559803248
=============================
5 Megacity's; Func runs: 10000; result: 0.48769230769230765
25 Megacity's; Func runs: 10000; result: 0.19876923076923075
500 Megacity's; Func runs: 10000; result: 0.10058461538461608
=============================
All score: 3.60849 (40.09%)
На визуализации работы алгоритма BIA заметен достаточно большой разброс результатов не только на функциях малой размерности (зеленые линии), но и на функциях средней размерности (голубые линии).
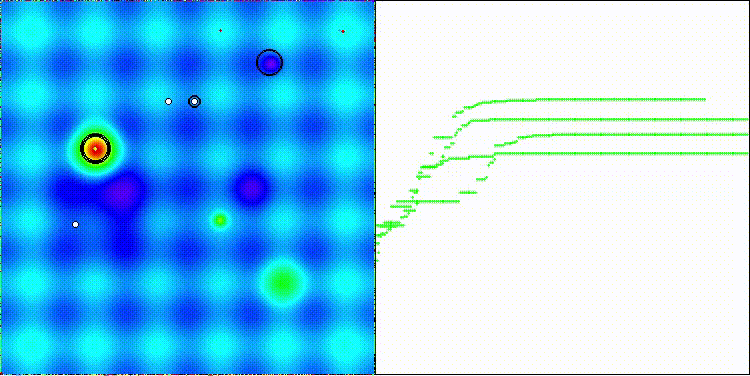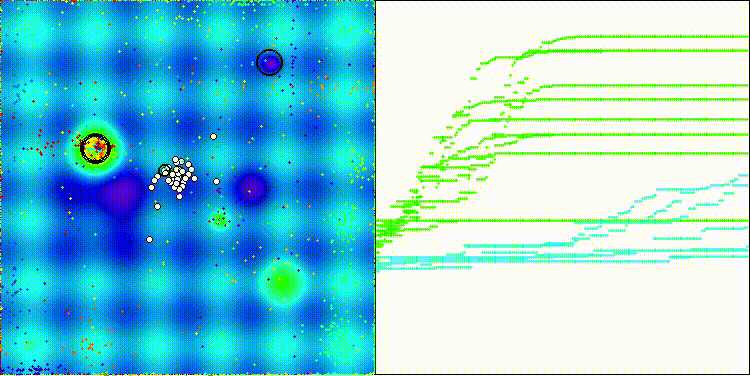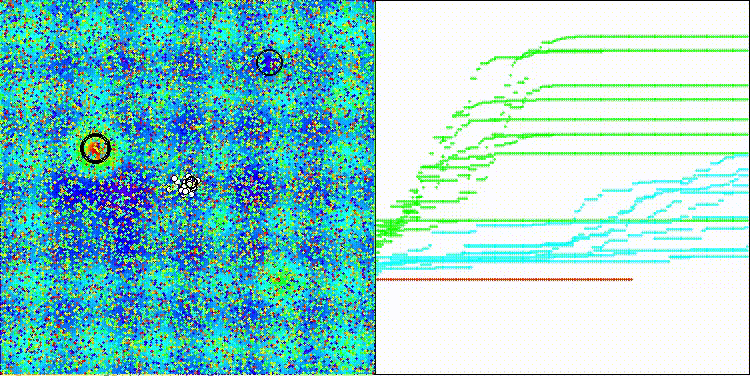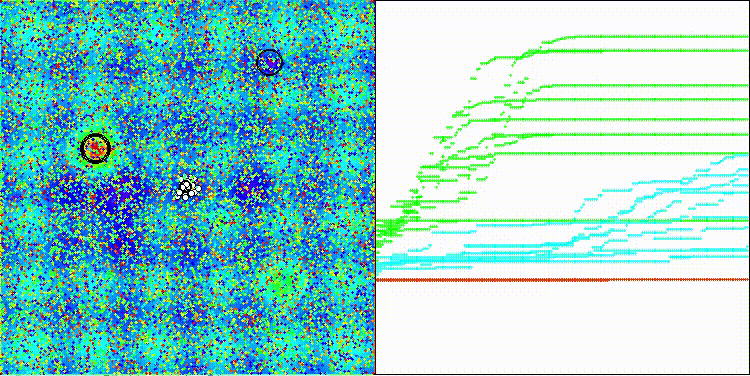
BIA на тестовой функции Hilly
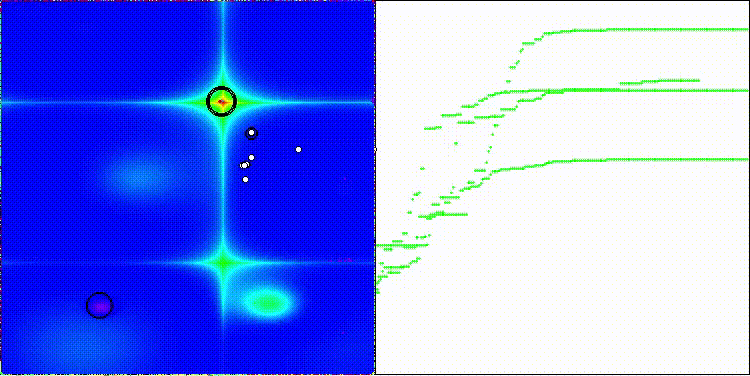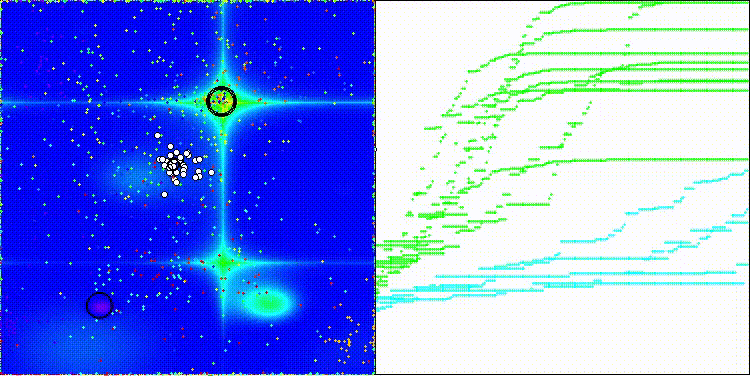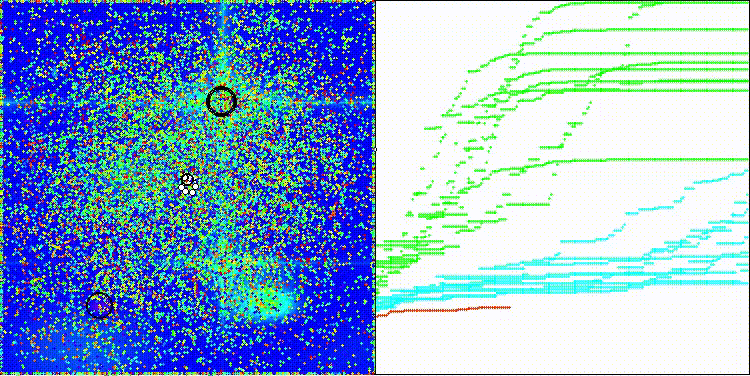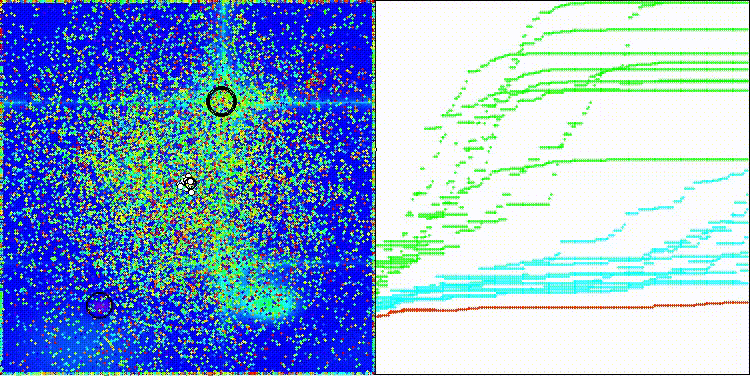
BIA на тестовой функции Forest
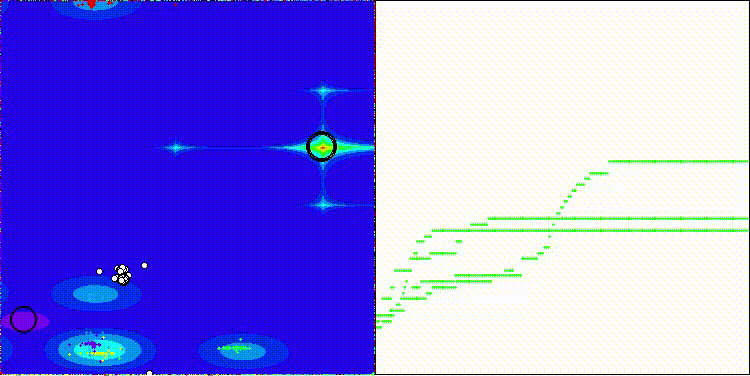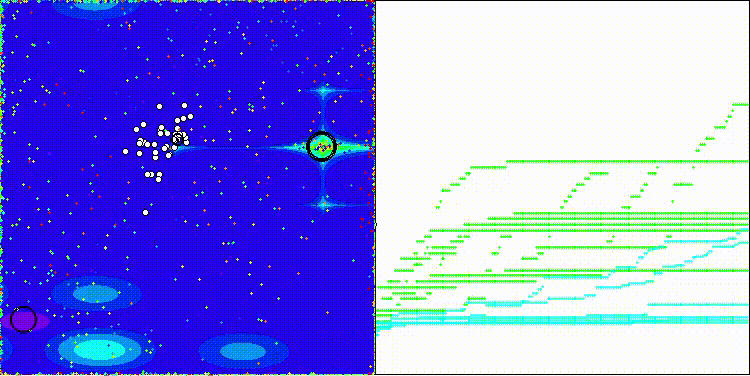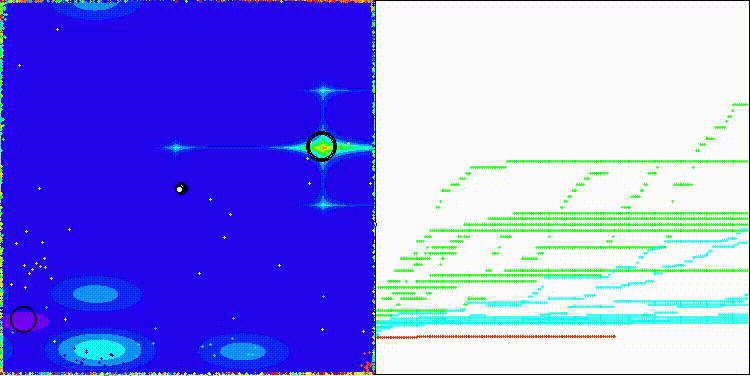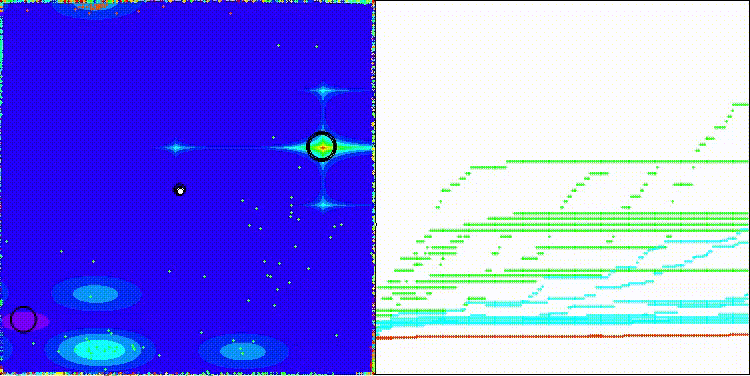
BIA на тестовой функции Megacity
В рейтинговой таблице популяционных методов оптимизации алгоритм BIA представлен ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 13 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 14 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 15 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 16 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 17 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 18 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 19 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 20 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 21 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 22 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 23 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 24 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 25 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 26 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 27 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 28 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 29 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 30 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 31 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 32 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 33 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 34 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 35 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 36 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 37 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 38 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 39 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 40 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 41 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 42 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 43 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| 44 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| BIA | bison_algorithm | 0,76185 | 0,40027 | 0,25201 | 1,41413 | 0,76210 | 0,45225 | 0,19296 | 1,40731 | 0,48769 | 0,19877 | 0,10058 | 0,78704 | 3,608 | 40,09 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Bison Algorithm представляет интересную концепцию разделения на исследователей и эксплуататоров, но в текущей реализации уступает современным метаэвристикам. Основная ценность — в идее явного разделения ролей, которая может быть успешно интегрирована в гибридные подходы.
Результаты тестирования показывают, что алгоритм демонстрирует средние показатели, не достигая уровня топовых метаэвристик, и испытывает трудности с решением дискретных задач. Для попадания в рейтинговую таблицу необходима существенная доработка механизмов движения и адаптации параметров. Алгоритм может найти применение в задачах, где важна простота реализации и интерпретируемость, но не требуется максимальная точность.
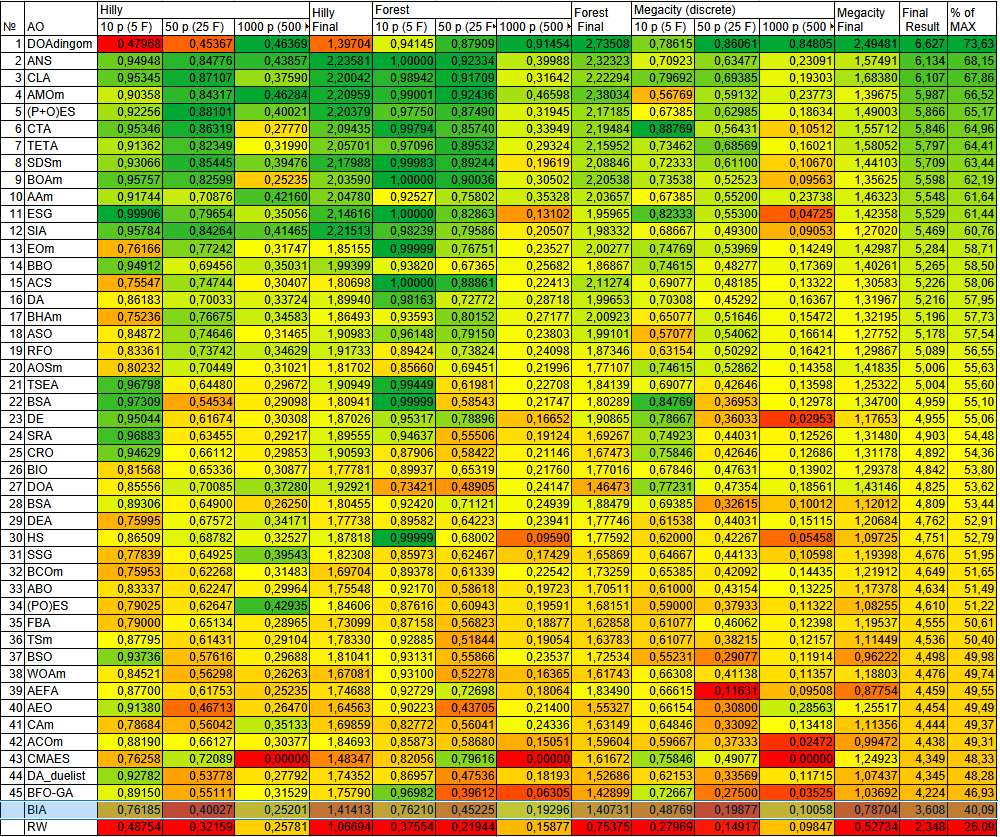
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
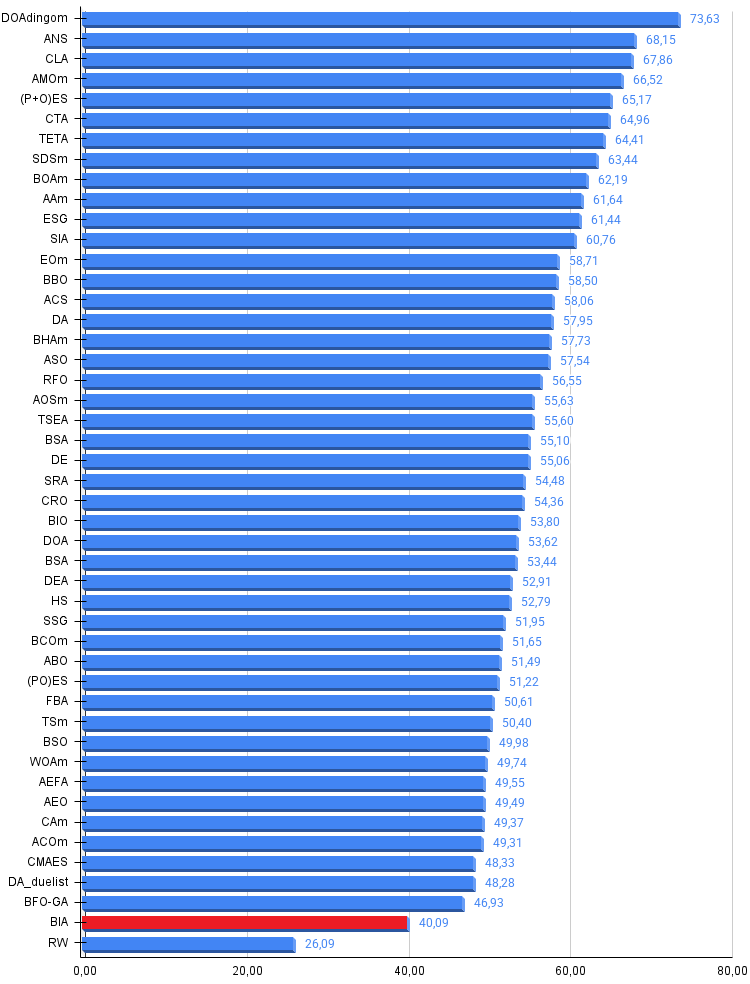
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма BIA:
Плюсы:
- Простая реализация.
- Быстрый.
Минусы:
- Разброс значений на функциях малой и средней размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_BIA.mq5 | Скрипт | Испытательный стенд для BIA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Искусство ведения логов (Часть 3): Изучение обработчиков для сохранения логов
Искусство ведения логов (Часть 3): Изучение обработчиков для сохранения логов
 Создание пользовательской системы определения рыночного режима на языке MQL5 (Часть 1): Индикатор
Создание пользовательской системы определения рыночного режима на языке MQL5 (Часть 1): Индикатор
 Разрабатываем мультивалютный советник (Часть 29): Доработка конвейера
Разрабатываем мультивалютный советник (Часть 29): Доработка конвейера
 Символьное уравнение прогнозирования цены с использованием SymPy
Символьное уравнение прогнозирования цены с использованием SymPy
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования