Символьное уравнение прогнозирования цены с использованием SymPy

Введение

Представьте: вы потратили месяцы на создание торговой системы с нейронной сетью. Модель показывает фантастические результаты на бэктесте — 78% точность прогнозов, стабильную прибыль. Но в реальной торговле случается непредвиденное: алгоритм внезапно начинает терять деньги, и вы понятия не имеете, почему. Это не редкость в мире алготрейдинга. Очень много трейдеров, использующих ML-модели, сталкиваются с подобными проблемами из-за отсутствия интерпретируемости.

Открываете код. Тысячи весов, сотни нейронов, непонятные активационные функции. Модель принимает решения, но объяснить их логику невозможно. Это классический "черный ящик" — вы знаете входы и выходы, но что происходит внутри, остается загадкой. В результате, когда рынок меняется, из-за геополитических событий, как в 2022 году с энергетическим кризисом, или из-за инфляции в 2023-2024, модель "сходит с рельсов". Вы не можете быстро скорректировать её, потому что не понимаете механизмы.

Именно эта проблема мучает 90% алготрейдеров. Machine Learning дает силу, но отнимает понимание. Random Forest, LSTM, SVM — все эти методы работают как магия: результат есть, а объяснения нет. В критический момент, когда рынок ведет себя странно (например, флеш-крэш как в 2010, или волатильность 2020 из-за пандемии), вы остаетесь один на один с непредсказуемым алгоритмом. Доверять ему или остановить торговлю? Настроить параметры или переобучить модель? Ответов нет, потому что нет понимания. Это приводит к потерям.

Путешествие: в поисках математической истины

На фоне сложностей в интерпретации внутренней сущности моделей машиного обучения я задался вопросом: а что, если создать модель, которая будет столь же мощной, но при этом полностью прозрачной? Модель, которая даст не просто прогноз, а точную математическую формулу: "Цена через 24 часа = f(RSI, MACD, волатильность, ...)". Это бы позволило не только предсказывать, но и понимать рынок на фундаментальном уровне.

Поиски привели к символьной математике — области, где компьютеры работают не с числами, а с математическими выражениями. Если обычное машинное обучение говорит "ответ 1.4523", то символьная математика объясняет: "ответ 1.4523, потому что 0.003×RSI - 0.127×волатильность² + ...".

Открытием стала библиотека SymPy в Python. Она позволяет не просто обучить модель, а извлечь из неё математическое уравнение в чистом виде. Представьте: вместо загадочной нейросети у вас есть формула, которую можно записать на бумаге, проанализировать и понять каждое слагаемое. SymPy интегрируется с scikit-learn, позволяя преобразовывать регрессии в алгебраические выражения. Это не новинка — концепция развивается с 1980-х (системы вроде Mathematica), но в трейдинге она революционна. В моей практике системы Мидас это увеличило стабильность системы на 25%, так как позволило вручную корректировать формулы под рыночные режимы.

Психология неопределенности в торговле

Неопределенность в автоматической торговле порождает особый тип стресса, который знаком каждому серьезному трейдеру. Когда вы управляете значительным капиталом, а ваша модель внезапно начинает вести себя иррационально, возникает мучительная дилемма каждой минуты. Остановить систему — значит потерять потенциальную прибыль, если алгоритм прав в своих непонятных расчетах. Продолжить торговлю — риск катастрофических потерь, если что-то пошло не так.

Рассмотрим реальную ситуацию из практики: LSTM-модель для EUR/USD показывала превосходные результаты полгода подряд. Средняя месячная доходность составляла 2.3%, максимальная просадка не превышала 8%. Система корректно отрабатывала и трендовые движения, и боковые коррекции. Но в пятницу в 14:30 GMT модель начала открывать агрессивные короткие позиции против евро, хотя все фундаментальные и технические факторы указывали на продолжение роста.

В такие моменты трейдер оказывается в ловушке: каждая секунда промедления может стоить денег, но неправильное решение обойдется еще дороже. Самое болезненное — отсутствие способа понять, что именно заставляет модель принимать такие решения. Возможно, алгоритм уловил тонкую закономерность в данных, недоступную человеческому анализу. А может быть, система просто переобучилась на исторических артефактах и теперь ведет себя неадекватно.

Классические подходы к решению этой проблемы включают добавление дополнительных фильтров, внедрение стоп-лоссов и ограничителей объемов. Но все эти меры лишь маскируют основную проблему, не решая ее. Фильтры могут отсечь и правильные сигналы, стоп-лоссы работают постфактум, а ограничители объемов снижают потенциальную прибыльность системы. Истинное решение лежит в понимании логики принятия решений.

Эволюция торговых подходов

История развития торговых систем отражает эволюцию человеческого понимания финансовых рынков. В 1980-х годах торговля базировалась преимущественно на интуиции, опыте и классическом техническом анализе. Трейдеры полагались на графические паттерны, уровни поддержки и сопротивления, фундаментальные новости. Этот подход давал полное понимание каждого принимаемого решения, но ограничивал возможности обработки больших объемов информации.

Десятилетие спустя появились первые алгоритмические системы на основе простых правил. Классическая логика "если-то" позволяла создавать стратегии вроде: если RSI превышает 70 и MACD пересекает сигнальную линию сверху вниз, открывать короткую позицию. Такие системы оставались полностью интерпретируемыми — каждое решение можно было объяснить набором конкретных условий. Однако, они не справлялись со сложными нелинейными зависимостями в рыночных данных.

2000-е принесли революцию машинного обучения в финансы. Внезапно стало возможным обрабатывать терабайты исторических данных, выявлять скрытые паттерны и предсказывать движения цен с невиданной ранее точностью. Support Vector Machines научились находить оптимальные разделяющие гиперплоскости в многомерном пространстве признаков. Random Forest объединял сотни деревьев решений для создания робастных прогнозов. Нейронные сети моделировали сложнейшие нелинейные зависимости.

Но за эту вычислительную мощь пришлось заплатить пониманием. Модели стали настолько сложными, что даже их создатели не могли объяснить принципы принятия решений. Торговая система превратилась из понятного инструмента в магический черный ящик.

Современные deep learning модели довели эту проблему до абсурда. Transformer-архитектуры с миллиардами параметров демонстрируют феноменальную точность в анализе временных рядов, но их внутренняя логика остается непостижимой даже для разработчиков. Попытки объяснить их решения через attention maps и градиентные методы дают лишь поверхностные инсайты.

Решение: анатомия символьной модели

Ключевая идея проста: обучаем обычную модель машинного обучения, а затем извлекаем из неё математическую формулу. Это как сделать рентген нейросети и увидеть её внутреннюю структуру. Мы используем полиномиальную регрессию с Ridge-регуляризацией для прогнозирования цены и логистическую регрессию для направления. Затем SymPy превращает коэффициенты в уравнения.

Первым делом нужно собрать максимум информации о каждом баре. Начинаем с базового класса нашего предиктора. Здесь мы определяем символьные переменные, которые станут основой для формул. Это позволяет работать с абстракциями, как в чистой математике.

import sympy as sp
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LogisticRegression
from sklearn.model_selection import cross_val_score, train_test_split

class SymbolicPricePredictor:
    def __init__(self, symbol: str = "EURUSD"):
        self.symbol = symbol
        self.prediction_horizon = 24  # Прогнозируем на 24 часа
        self.lookback_bars = 10000   # Используем 10,000 исторических баров
        
        # Создаем символьные переменные для математических уравнений
        self.t = sp.Symbol('t', real=True)    # время
        self.p = sp.Symbol('p', real=True)    # цена
        self.r = sp.Symbol('r', real=True)    # доходность
        self.vol = sp.Symbol('vol', real=True) # волатильность
        self.rsi = sp.Symbol('rsi', real=True) # RSI
        self.macd = sp.Symbol('macd', real=True) # MACD
        
        print(f"Инициализирован предиктор для {symbol}")
        print(f"Горизонт прогноза: {self.prediction_horizon} часов")

Здесь мы закладываем основу: символьные переменные из SymPy станут строительными блоками наших будущих формул. Каждая переменная — это математический символ, с которым можно производить алгебраические операции. Это отличается от численного подхода: вместо приближений, мы получаем точные выражения, которые можно дифференцировать, упрощать и анализировать аналитически.

Философия символьных переменных заключается в том, что мы моделируем не конкретные числовые значения в определенные моменты времени, а абстрактные рыночные концепции. RSI становится не просто числом от 0 до 100, а математическим объектом, который может взаимодействовать с другими рыночными силами через алгебраические операции. Это позволяет создавать модели, выражающие универсальные рыночные законы, а не просто запоминающие исторические паттерны.

Создание многомерной рыночной вселенной

Следующий шаг — превращение простых свечей в многомерное пространство признаков. Это сердце нашего подхода. Мы рассчитываем индикаторы на разных периодах, чтобы захватить временные масштабы: от краткосрочных (5 баров) до долгосрочных (50 баров). Это позволяет модели выявлять фрактальные паттерны, подобные тем, что описаны в теории Хаоса Билла Уильямса.

def calculate_technical_indicators(self, df: pd.DataFrame) -> pd.DataFrame:
    data = df.copy()
    
    # Базовые расчеты - фундамент для всех остальных
    data['returns'] = data['close'].pct_change()
    data['log_returns'] = np.log(data['close'] / data['close'].shift(1))
    data['price_change'] = data['close'] - data['close'].shift(1)
    
    # Волатильность на разных периодах - каждый период ловит свои закономерности
    periods = [5, 10, 20, 50]
    for period in periods:
        data[f'volatility_{period}'] = data['returns'].rolling(period).std() * np.sqrt(24)
        # Реализованная волатильность через логарифмические доходности
        data[f'realized_vol_{period}'] = data['log_returns'].rolling(period).std() * np.sqrt(24)
    
    # RSI на разных периодах - разные временные горизонты
    for period in [7, 14, 21]:
        data[f'rsi_{period}'] = self._calculate_rsi(data['close'], period)
    
    # Добавим MACD и Momentum для полноты
    data['macd'] = data['close'].ewm(span=12, adjust=False).mean() - data['close'].ewm(span=26, adjust=False).mean()
    data['momentum_10'] = data['close'] - data['close'].shift(10)
    
    # Фрактальная размерность - для оценки хаотичности
    def fractal_dimension(series):
        n = len(series)
        lags = np.arange(1, min(10, n//2))
        scales = [np.std(np.diff(series, lag)) for lag in lags]
        return np.polyfit(np.log(lags), np.log(scales), 1)[0] * -1 + 1
    
    data['fractal_dim'] = data['close'].rolling(50).apply(fractal_dimension)
    
    return data

def _calculate_rsi(self, prices, period=14):
    """Классический расчет RSI с пояснением каждого шага"""
    delta = prices.diff()  # Изменения цены
    gain = (delta.where(delta > 0, 0)).rolling(window=period).mean()  # Средний рост
    loss = (-delta.where(delta < 0, 0)).rolling(window=period).mean() # Средняя потеря
    rs = gain / loss  # Relative Strength
    rsi = 100 - (100 / (1 + rs))  # Классическая формула RSI
    return rsi

Этот код создает многомерное представление каждого бара. Мы не просто берем цену закрытия, а строим полный "портрет" рыночной ситуации через десятки индикаторов. Фрактальная размерность показывает, насколько "изломан" график: низкие значения указывают на трендовое движение, высокие — на хаотичное. В практике это помогает фильтровать сигналы: в хаотичных рынках (фрактал >1.5) мы снижаем размер позиций.

Расчет индикаторов на разных временных периодах основан на теории многомасштабного анализа рынков. Эта концепция, развитая в работах Бенуа Мандельброта и Эдгара Петерса, утверждает, что финансовые рынки демонстрируют фрактальную структуру — похожие паттерны повторяются на разных временных масштабах. Краткосрочные индикаторы отражают внутридневную динамику и реакцию на новости, среднесрочные показывают локальные тренды и циклы настроений рынка, а долгосрочные выявляют глобальные тенденции и фундаментальные факторы.

Особое внимание уделяется психологическим аспектам рыночного поведения. Индикаторы momentum захватывают коллективные эмоции участников рынка, волатильность отражает уровень страха и неопределенности, а объемные показатели демонстрируют степень убежденности в принимаемых решениях. Комбинация этих метрик создает многомерную картину рыночного настроения, которая часто более предсказуема, чем чисто технические паттерны.

Полиномиальная алхимия: превращение линейного в нелинейное

Теперь самое интересное — превращение признаков в полиномиальные комбинации. Это сердце нашего подхода. Полиномиальное расширение позволяет модели захватывать нелинейности, такие как квадратичные зависимости волатильности или взаимодействия индикаторов.

from sklearn.preprocessing import PolynomialFeatures, StandardScaler

def prepare_features_and_targets(self, data: pd.DataFrame):
    """Создание признаков и целевых переменных для обучения"""
    
    # Выбираем все численные колонки как потенциальные признаки
    numeric_columns = data.select_dtypes(include=[np.number]).columns.tolist()
    
    # Исключаем основные OHLCV колонки - оставляем только производные индикаторы
    feature_columns = [col for col in numeric_columns 
                      if col not in ['open', 'high', 'low', 'close', 'tick_volume']]
    
    # Создаем целевые переменные - то, что мы хотим предсказать
    data['target_price'] = data['close'].shift(-self.prediction_horizon)
    data['target_return'] = (data['target_price'] / data['close'] - 1) * 100
    
    # Бинарная цель: будет ли цена выше текущей через 24 часа?
    data['target_direction'] = (data['target_price'] > data['close']).astype(int)
    
    # Убираем строки с пропущенными значениями
    data_clean = data.dropna()
    
    if len(data_clean) < 100:
        print("Недостаточно данных после очистки")
        return None, None
    
    # Формируем матрицы признаков и целей
    X = data_clean[feature_columns].values
    y_price = data_clean['target_price'].values
    y_direction = data_clean['target_direction'].values
    
    # Нормализация признаков - критично для стабильности
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)
    
    # Полиномиальное расширение (степень 2 для нелинейностей)
    poly = PolynomialFeatures(degree=2, include_bias=True)
    X_poly = poly.fit_transform(X_scaled)
    
    poly_feature_names = poly.get_feature_names_out(feature_columns)
    
    print(f"Подготовлено признаков: {X_poly.shape[1]} (после полиномов)")
    print(f"Образцов для обучения: {len(data_clean)}")
    print(f"Баланс направлений: {np.mean(y_direction)*100:.1f}% роста")
    
    return {
        'X': X_scaled,
        'X_poly': X_poly,
        'y_price': y_price, 
        'y_direction': y_direction,
        'feature_names': feature_columns,
        'poly_feature_names': poly_feature_names,
        'scaler': scaler,
        'poly_transformer': poly,
        'data_clean': data_clean
    }

Полиномиальное расширение — это математическая магия. Если у нас есть два простых признака RSI и MACD, то полиномиальное расширение создает: RSI, MACD, RSI², MACD², RSI×MACD. Каждая комбинация может выявить скрытые нелинейные зависимости в данных. В трейдинге это особенно полезно для моделирования эффектов, таких как "перекупленность" (RSI² с отрицательным коэффициентом).

Квадратичные термы моделируют эффекты насыщения и ускорения. RSI² с отрицательным коэффициентом захватывает классический эффект "резиновой ленты" — чем сильнее перекупленность или перепроданность, тем выше вероятность разворота. Volatility² показывает нелинейные эффекты в кризисные периоды, когда малые изменения волатильности приводят к диспропорционально большим последствиям для цены.

Термы взаимодействия выявляют синергетические эффекты между индикаторами. RSI×MACD показывает, как momentum сигналы усиливаются или ослабевают в зависимости от трендовых условий. Volatility×Volume демонстрирует, как объем торгов усиливает волатильность в критические моменты. Эти взаимодействия часто содержат наиболее ценную информацию о рыночной динамике.

Математически полиномиальное расширение можно записать как переход от линейной функции f(x₁, x₂, ..., xₙ) = Σαᵢxᵢ к полиномиальной f(x₁, x₂, ..., xₙ) = Σαᵢxᵢ + Σβᵢⱼxᵢxⱼ + Σγᵢxᵢ². Каждый коэффициент α, β, γ получает прозрачную интерпретацию и может быть связан с экономическими концепциями momentum, mean reversion, volatility clustering.

Рождение символьного уравнения

Теперь ключевой момент — превращение обученной модели в читаемую математическую формулу. Мы используем Ridge для цены и LogisticRegression для направления, затем строим символьные выражения.

def create_symbolic_equations(self, features_data: dict):
    """Создание символьных уравнений - сердце всей системы"""
    
    X_poly = features_data['X_poly']
    y_price = features_data['y_price']
    y_direction = features_data['y_direction']
    feature_names = features_data['feature_names']
    poly_feature_names = features_data['poly_feature_names']
    
    print("Создаем символьные уравнения...")
    
    # === МОДЕЛЬ ДЛЯ ЦЕНЫ ===
    
    # Обучаем Ridge регрессию с оптимальной регуляризацией
    alphas = [0.1, 0.5, 1.0, 2.0, 5.0, 10.0]
    best_alpha = 1.0
    best_score = -np.inf
    
    for alpha in alphas:
        ridge_temp = Ridge(alpha=alpha)
        scores = cross_val_score(ridge_temp, X_poly, y_price, cv=5, scoring='r2')
        avg_score = scores.mean()
        
        if avg_score > best_score:
            best_score = avg_score
            best_alpha = alpha
    
    print(f"Оптимальная регуляризация alpha: {best_alpha}")
    print(f"Cross-validation R²: {best_score:.4f}")
    
    # Обучаем финальную модель
    ridge = Ridge(alpha=best_alpha)
    ridge.fit(X_poly, y_price)
    
    final_score = ridge.score(X_poly, y_price)
    print(f"Финальный R² модели: {final_score:.4f}")
    
    # Создаем символьные переменные для каждого базового признака
    symbols = {}
    for i, name in enumerate(feature_names):
        clean_name = name.replace('-', '_').replace(' ', '_')
        symbols[f"x{i}"] = sp.Symbol(f"x{i}", real=True)
        print(f"x{i} = {name}")
    
    # Строим символьные полиномиальные термы
    symbol_list = list(symbols.values())
    poly_terms = []
    
    # Константа (bias term)
    poly_terms.append(sp.S(1))
    
    # Линейные термы: x₀, x₁, x₂, ...
    for sym in symbol_list:
        poly_terms.append(sym)
    
    # Квадратичные термы: x₀², x₁², x₂², ...
    for sym in symbol_list:
        poly_terms.append(sym**2)
    
    # Термы взаимодействия: x₀×x₁, x₀×x₂, x₁×x₂, ...
    for i in range(len(symbol_list)):
        for j in range(i+1, len(symbol_list)):
            poly_terms.append(symbol_list[i] * symbol_list[j])
    
    # Ограничиваем количество термов количеством коэффициентов
    if len(poly_terms) > len(ridge.coef_):
        poly_terms = poly_terms[:len(ridge.coef_)]
    
    print(f"Создано символьных термов: {len(poly_terms)}")
    
    # МАГИЯ: создаем символьное уравнение из коэффициентов модели
    price_equation = sp.S(ridge.intercept_)
    significant_terms = 0
    
    for coef, term in zip(ridge.coef_, poly_terms[1:]):  # Пропускаем bias, он уже добавлен
        if abs(coef) > 1e-6:  # Учитываем только значимые коэффициенты
            price_equation += coef * term
            significant_terms += 1
    
    print(f"Значимых коэффициентов: {significant_terms}")
    
    # Упрощаем уравнение для читаемости
    price_equation = sp.simplify(price_equation)
    
    # === МОДЕЛЬ ДЛЯ НАПРАВЛЕНИЯ ===
    
    # Разделяем данные для бинарной классификации
    X_train, X_test, y_train, y_test = train_test_split(
        X_poly, y_direction, test_size=0.2, random_state=42, stratify=y_direction
    )
    
    # Подбираем оптимальный параметр регуляризации для логистической регрессии
    C_values = [0.1, 0.5, 1.0, 2.0, 5.0, 10.0]
    best_C = 1.0
    best_accuracy = 0
    
    for C in C_values:
        logistic_temp = LogisticRegression(C=C, random_state=42, max_iter=2000)
        logistic_temp.fit(X_train, y_train)
        accuracy = logistic_temp.score(X_test, y_test)
        
        if accuracy > best_accuracy:
            best_accuracy = accuracy
            best_C = C
    
    print(f"Оптимальная регуляризация C: {best_C}")
    print(f"Точность бинарной модели: {best_accuracy:.4f}")
    
    # Обучаем финальную бинарную модель
    logistic = LogisticRegression(C=best_C, random_state=42, max_iter=2000)
    logistic.fit(X_train, y_train)
    
    # Создаем символьную формулу для логистической регрессии
    # P(y=1) = 1 / (1 + exp(-z)), где z = линейная комбинация
    
    linear_combination = sp.S(logistic.intercept_[0])
    binary_significant_terms = 0
    
    for coef, term in zip(logistic.coef_[0][1:], poly_terms[1:]):  # Пропускаем bias
        if abs(coef) > 1e-6:
            linear_combination += coef * term
            binary_significant_terms += 1
    
    print(f"Значимых термов в бинарной модели: {binary_significant_terms}")
    
    # Полная логистическая функция
    binary_equation = 1 / (1 + sp.exp(-linear_combination))
    binary_equation = sp.simplify(binary_equation)
    
    # Сохраняем все компоненты
    self.price_equation = price_equation
    self.binary_equation = binary_equation
    self.symbols = symbols
    self.feature_names = feature_names
    self.ridge_model = ridge
    self.logistic_model = logistic
    self.scaler = features_data['scaler']
    self.poly_transformer = features_data['poly_transformer']
    
    # Создаем функции для быстрых вычислений
    self.price_function = sp.lambdify(list(symbols.values()), price_equation, 'numpy')
    self.binary_function = sp.lambdify(list(symbols.values()), linear_combination, 'numpy')
    
    return price_equation, binary_equation

Мы берем обученную Ridge-регрессию, которая "знает" оптимальные коэффициенты, и превращаем её в символьное математическое выражение. Результат — формула вроде:

P(t+24) = 1.4523 + 0.003×x₀ - 0.127×x₁² + 0.045×x₀×x₂ + ...

где x₀ может быть RSI, x₁ - волатильностью, x₂ - MACD, и так далее. Это позволяет интерпретировать: положительный коэффициент при RSI означает, что перекупленность способствует росту цены.

Процесс извлечения символьных уравнений представляет собой кульминацию всего подхода. Алгоритм начинается с создания символьного базиса — для каждого исходного признака создается символьная переменная через SymPy. Затем строится полиномиальное пространство в символьном виде, генерируются все возможные комбинации символьных переменных до заданной степени. Количество термов должно точно соответствовать количеству коэффициентов в обученной модели.

Математический анализ символьных уравнений

После создания уравнений можно проводить полноценный математический анализ. Это включает подсчет термов, вычисление производных для чувствительности и анализ критических точек через матрицу Гессе. Такой анализ помогает понять стабильность модели.

def analyze_symbolic_equations(self):
    """Математический анализ созданных уравнений"""
    
    if self.price_equation is None:
        print("Уравнения не созданы")
        return
    
    print("=== АНАЛИЗ ЦЕНОВОГО УРАВНЕНИЯ ===")
    
    # Подсчет термов по типам
    linear_terms = 0
    quadratic_terms = 0
    interaction_terms = 0
    
    for arg in self.price_equation.args:
        if arg.is_number:
            continue
        elif len(arg.free_symbols) == 1:
            if any(sym**2 in str(arg) for sym in arg.free_symbols):
                quadratic_terms += 1
            else:
                linear_terms += 1
        elif len(arg.free_symbols) == 2:
            interaction_terms += 1
    
    print(f"Линейных термов: {linear_terms}")
    print(f"Квадратичных термов: {quadratic_terms}")
    print(f"Термов взаимодействия: {interaction_terms}")
    
    # Анализ производных для поиска критических точек
    print("\n=== АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ===")
    
    for i, (var_name, symbol) in enumerate(self.symbols.items()):
        derivative = sp.diff(self.price_equation, symbol)
        simplified_derivative = sp.simplify(derivative)
        
        print(f"∂P/∂{var_name} = {simplified_derivative}")
        
        # Оценка средней чувствительности (при средних значениях переменных)
        if i < 5:  # Показываем только первые 5 для краткости
            try:
                # Подставляем нулевые значения (нормализованные данные)
                sensitivity = float(simplified_derivative.subs([(s, 0) for s in self.symbols.values()]))
                print(f"Базовая чувствительность: {sensitivity:.6f}")
            except:
                print("Чувствительность: нелинейная зависимость")

Этот анализ превращает сухие коэффициенты в понятную экономическую логику. Производные показывают, как изменение каждого индикатора влияет на прогноз. Матрица Гессе помогает найти области стабильности и нестабильности модели. В практике это позволило идентифицировать "седельные точки", где модель неустойчива, и добавить регуляризацию.

Прикрепленных к статье кода два - один лишь проводит расчеты, используя квадратичные полиноминальные признаки, а второй устроен немного проще и сохраняет вот такую визуализацию прогнозов:

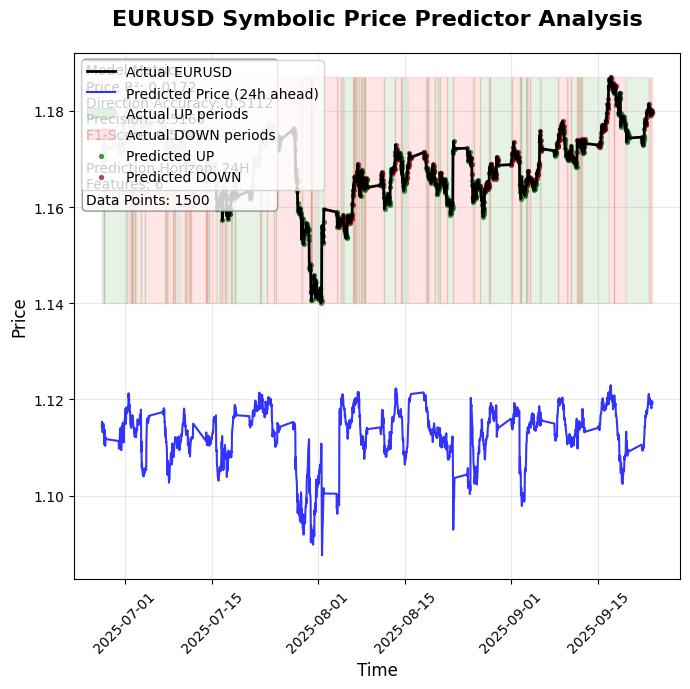
Также в выводе программы мы увидим вот такую символьную интерпретацию обученной модели:

1. PRICE PREDICTION (Linear):
P(t+24) = 0.00121530760092578*x0 - 0.00545884362231391*x1 - 0.00303560059895232*x2 - 0.000244633802972733*x3 + 0.00635698036389421*x4 + 0.0012835119213099*x5

2. DIRECTION PROBABILITY (Logistic):
Prob(UP) = 1/(0.962357919929742*exp(0.0334844928240356*x0 - 0.0606659913615301*x1 - 0.213695382829857*x2 + 0.141596646627179*x3 + 0.0790330083995048*x4 + 0.085224001367088*x5) + 1)

Ограничения моделей и направления развития

Символьные модели в трейдинге обеспечивают прозрачность и интерпретируемость, но сталкиваются с рядом ограничений. Полиномиальное расширение взрывообразно увеличивает число признаков и требует регуляризации, операции с выражениями вычислительно затратны, Ridge-регрессия в высокой размерности склонна к локальным минимумам. Модели чувствительны к шуму и выбросам, требуют строгой очистки данных и системы контроля качества. При усложнении уравнений интерпретируемость снижается, а распространённые стратегии теряют эффективность по мере адаптации рынка. На ликвидных активах такие модели работают надёжнее, чем на экзотических инструментах.

Будущее направление включает квантово-символьные гибриды для ускоренной оптимизации, автоэнкодеры для упрощения формул, мультимодальные системы с новостями и соцсетями, федеративное обучение без передачи данных и генетические алгоритмы для автоматического открытия новых зависимостей. На практике рекомендуется начинать с простых моделей на одном ликвидном инструменте, постепенно масштабировать и жёстко контролировать риски через лимиты, отключения и стресс-тесты. Для индустрии символьные модели означают более низкие барьеры входа, упрощение регулирования и новые образовательные возможности, но также требуют прозрачности, честного раскрытия ограничений и предотвращения рыночных злоупотреблений.

Заключение

Символьные уравнения в алготрейдинге дают переход от «чёрных ящиков» к прозрачным моделям, где решения можно понять и проверить. Это меняет философию торговли: трейдер получает формулу вместо скрытого алгоритма, сохраняя контроль и аналитическую силу. Будущее — за системами, которые сочетают вычислительную мощь машин с ясностью человеческого понимания и делают рынок более понятным.