
Нейросети в трейдинге: Интеграция теории хаоса в прогнозирование временных рядов (Окончание)
Введение
Продолжаем построение собственного видения подходов, предложенных авторами фреймворка Attraos. В предыдущей статье мы познакомились с теоретическими аспектами фреймворка. Напомню, что в нем для решения задач прогнозирования временных рядов используются принципы теории хаоса.
Архитектура фреймворка Attraos представляет собой сложную многокомпонентную систему, в которой объединены методы нелинейного анализа, машинного обучения и вычислительной оптимизации. Использование метода реконструкции фазового пространства (Phase Space Reconstruction — PSR) позволяет Attraos моделировать скрытые динамические процессы и учитывать нелинейные взаимосвязи между различными рыночными переменными. Это делает возможным выявление устойчивых структур в рыночных данных и их использование для повышения качества прогнозирования предстоящего ценового движения.
Одной из ключевых особенностей Attraos является блок динамической памяти с несколькими разрешениями (Multi-Resolution Dynamic Memory Unit — MDMU), который позволяет модели сохранять исторические паттерны ценового движения и адаптироваться к изменяющимся рыночным условиям. Это особенно важно для финансовых рынков, где паттерны могут повторяться в различных временных интервалах с разной амплитудой и интенсивностью. Модель динамически адаптируется к изменяющейся структуре финансовых рынков, обеспечивая более точные прогнозы на разных временных горизонтах.
Применение стратегии локальной эволюции в частотной области позволяет адаптироваться к изменяющимся рыночным условиям, усиливая различия аттракторов. Это помогает модели минимизировать ошибки и контролировать отклонения аттракторов, обеспечивая стабильность и высокую точность прогнозов.
Авторская визуализация фреймворка Attraos представлена ниже.
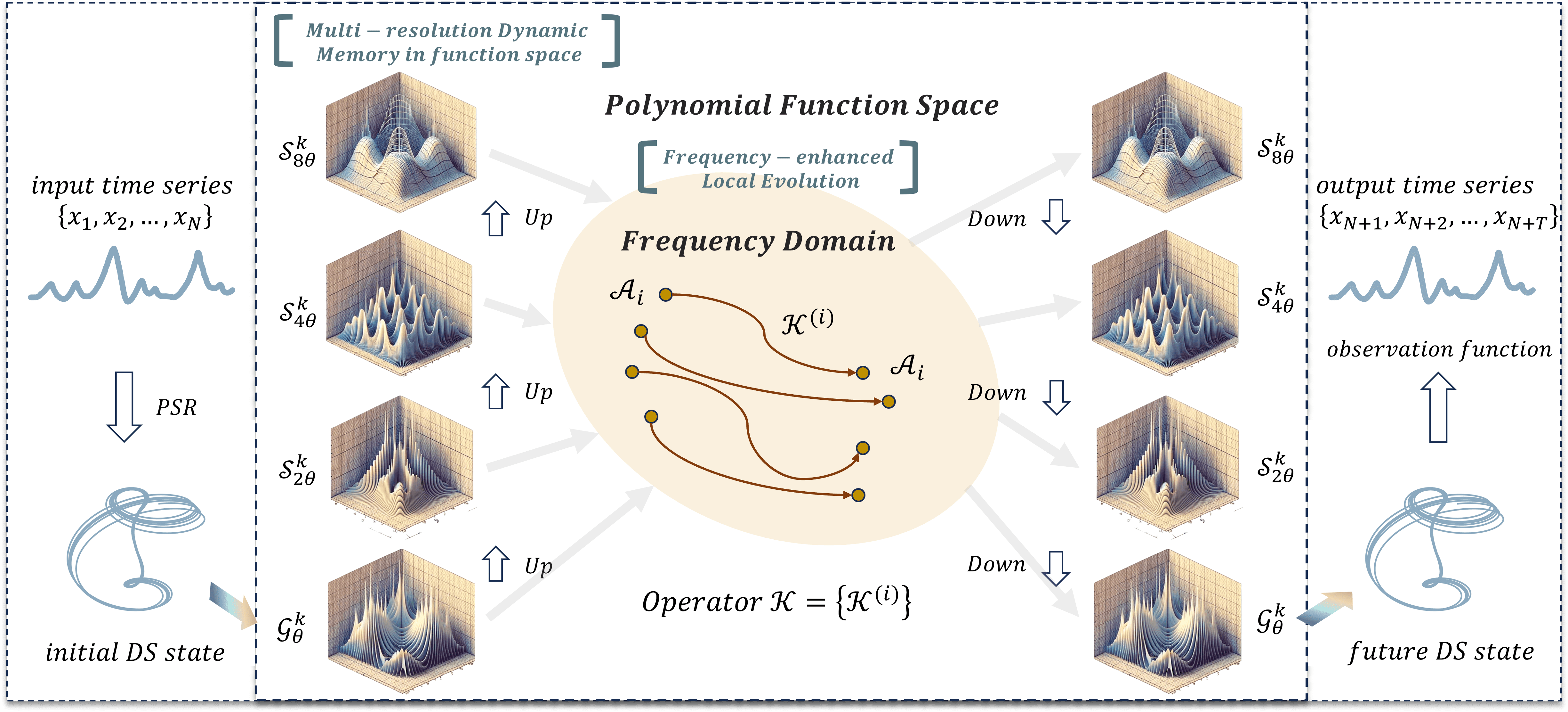
В практической части предыдущей статьи мы реализовали базовые компоненты на стороне OpenCL-программы. И сегодня переходим к созданию объектов в основной программе.
Построение объекта Attraos
Алгоритм Attraos начинается с модуля PSR, который трансформирует анализируемый временной ряд в фазовое пространство с учетом временного заданного лага. Данный процесс представляет собой ключевой этап предварительной обработки данных, позволяя выявить скрытые зависимости, структуру временного ряда и возможные латентные паттерны в динамике.
Многомерный временной ряд обычно представляется в виде матрицы, каждая строка содержит параметры анализируемый системы в некоторой временной точке t. Однако, в нашем случае, данные хранятся в одномерных буферах, а их матричное представление носит условный характер. При этом структура данных организована таким образом, что в буфере последовательно хранятся значения векторов, описывающих состояние системы во временной точке. Размер такого вектора задается параметром window. Следовательно, для создания подпоследовательностей с некоторым временным лагом, достаточно пропорционально увеличить значение параметра window и, соответственно, уменьшить длину последовательности. Таким образом, процесс трансформации временного ряда в фазовое пространство не требует дополнительных вычислительных ресурсов и реализуется исключительно за счет выбора архитектуры модели.
Все последующие операции фреймворка мы выстроим в рамках объекта CNeuronAttraos, структура которого представлена ниже.
class CNeuronAttraos : public CNeuronBaseOCL { protected: CNeuronBaseOCL cOne; CNeuronBaseOCL cX_norm; CNeuronConvOCL cA; CNeuronConvOCL cX_proj; CNeuronBaseOCL cDelta; CNeuronBaseOCL cB; CNeuronBaseOCL cC; CNeuronConvOCL cD; CNeuronBaseOCL cH; CNeuronConvOCL cDelta_proj; CNeuronBaseOCL cDeltaA; CNeuronBaseOCL cDeltaB; CNeuronBaseOCL cDeltaBX; CNeuronBaseOCL cDeltaH; CNeuronBaseOCL cHS; //--- virtual bool PScan(void); virtual bool PScanCalcGradient(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronAttraos(void) {}; ~CNeuronAttraos(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronAttraos; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
В представленной структуре нового класса, помимо стандартного набора переопределяемых виртуальных методов, мы видим довольно большое количество внутренних объектов. Они выполняют разные функции и обеспечивают взаимодействие между элементами класса. Использование внутренних объектов помогает организовать код более эффективно. Каждый из них отвечает за свою часть работы, что делает систему модульной и удобной для внесения изменений. В процессе реализации методов нового объекта мы более подробно рассмотрим функционал каждого из внутренних компонентов. Это позволит понять их назначение и оценить их роль в общей структуре.
Все внутренние объекты объявлены статично, что исключает необходимость их динамического создания и удаления. Благодаря этому, конструктор и деструктор класса остаются пустыми, поскольку управление памятью для этих объектов выполняется автоматически. А инициализация всех объявленных и унаследованных объектов осуществляется в методе Init. В параметрах данного метода получаем константы, позволяющие однозначно определить архитектуру создаваемого объекта. Думаю, что структура параметров в данном случае у вас не вызывает вопросов.
bool CNeuronAttraos::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false; SetActivationFunction(None);
В теле метода, как обычно, сразу вызываем одноименный метод родительского класса, в теле которого уже организованы минимально необходимые точки контроля и процесс инициализации унаследованных интерфейсов.
Тут же мы явным образом отключаем функцию активации для нашего объекта, так как все процессы осуществляются с использованием внутренних объектов. А унаследованные интерфейсы используются только для обмена данных на глобальном уровне.
После успешного выполнения операций метода родительского класса, мы переходим к инициализации объявленных объектов. Здесь вначале инициализируем объекты двух матриц обучаемых параметров:
- A — матрица переходов состояний;
- D — матрицу остаточных связей с исходными данными.
Поскольку эти матрицы будут умножаться на полные матрицы, содержащие все элементы анализируемой последовательности, нам необходимо сразу повторить их значения по числу элементов в последовательности. Это позволит избежать дополнительных операций копирования и оптимизировать процесс обратного распространения градиента ошибки.
Как и ранее, для организации обучаемых параметров мы используем небольшую модель из двух последовательных слоёв. Первый слой содержит фиксированное значение, а второй генерирует необходимый тензор путем умножения внутренних обучаемых параметров на фиксированное число первого слоя. Такой подход позволяет нам использовать существующие алгоритмы нейронных слоев для обучения параметров без создания дополнительного функционала. С целью минимизирования количества обучаемых параметров второго слоя, обычно в первом слое используется всего один элемент.
Однако, в данном случае, нам необходимо на выходе второго слоя получить тензор с повторяющимися значениями. Для этого мы повторим фиксированные значения в первом слое заданное количество раз. В качестве второго слоя будем использовать сверточный слой с числом фильтров равным количеству обучаемых параметров. Размер окна и шаг свёртки установим равными 1, чтобы каждый элемент тензора на выходе зависел только от одного исходного значения.
int index = 0; if(!cOne.Init(0, index, OpenCL, units_count, optimization, iBatch)) return false; if(!cOne.getOutput().Fill(1)) return false; cOne.SetActivationFunction(None); //--- index++; if(!cA.Init(0, index, OpenCL, 1, 1, window * window_key, units_count, 1, optimization, iBatch)) return false; cA.SetActivationFunction(MinusSoftPlus); CBufferFloat *w = cA.GetWeightsConv(); if(!w || !w.Fill(0)) return false;
Так как первый слой в данном случае не имеет обучаемых параметров, то мы можем использовать его и для генерации второй матрицы обучаемых параметров. Поэтому далее мы инициализируем только второй объект генерации необходимых обучаемых параметров.
index++; if(!cD.Init(0, index, OpenCL, 1, 1, window, units_count, 1, optimization, iBatch)) return false; cD.SetActivationFunction(None); w = cD.GetWeightsConv(); if(!w || !w.Fill(1)) return false;
Обратите внимание, что при инициализации объектов мы заполняем матрицы обучаемых параметров фиксированными значениями. Это несколько отличается от общего подхода заполнения обучаемых параметров случайными значениями. Фиксированная инициализация актуальна в ситуациях, когда модель должна сохранять определённые свойства на ранних этапах обучения, или начальные условия оказывают значительное влияние на конечное распределение параметров. В данном случае, это позволяет избежать резких флуктуаций на старте и способствует более плавной адаптации модели к данным.
Остальные параметры модели пространства состояний мы создадим зависимыми от исходных данных, что позволит адаптировать их к особенностям анализируемой последовательности. Для их генерации используем сверточный слой, который сразу генерирует значения всех сущностей модели. Такой подход обеспечивает эффективную обработку данных, так как свертка выполняется параллельно по всей последовательности, что значительно ускоряет вычисления.
Однако, перед генерацией параметров модели пространства состояний мы сначала нормализуем исходные данные. Нормализация позволяет устранить влияние различий в масштабе исходных значений, что делает процесс оптимизации более гладким и предсказуемым.
//--- index++; if(!cX_norm.Init(0, index, OpenCL, window * units_count, optimization, iBatch)) return false; cX_norm.SetActivationFunction(None); index++; if(!cX_proj.Init(0, index, OpenCL, window, window, 4 * window_key, units_count, 1, optimization, iBatch)) return false; cX_proj.SetActivationFunction(None);
Далее нам предстоит разделить сгенерированные параметры модели на отдельные сущности. И для хранения данных создадим дополнительные объекты, наименование которых укажет на сущность записанных данных.
index++; if(!cDelta.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cDelta.SetActivationFunction(None); index++; if(!cB.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cB.SetActivationFunction(None); index++; if(!cC.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cC.SetActivationFunction(None); index++; if(!cH.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cH.SetActivationFunction(None);
Следующим шагом инициализируем объект, отвечающий за генерацию параметров экспоненциального затухания скрытых состояний. Этот компонент играет ключевую роль в управлении динамикой информации, передаваемой через последовательность, регулируя степень сохранения или затухания прошлых состояний.
index++; if(!cDelta_proj.Init(0, index, OpenCL, window_key, window_key, window, units_count, 1, optimization, iBatch)) return false; cDelta_proj.SetActivationFunction(SoftPlus);
Использование SoftPlus в качестве функции активации обеспечивает наличие только положительных значений на выходе.
Далее мы инициализируем еще несколько объектов хранения промежуточных результатов вычислений. Все они имеют одинаковый размер.
index++; if(!cDeltaA.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaA.SetActivationFunction(None); index++; if(!cDeltaB.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaB.SetActivationFunction(None); index++; if(!cDeltaBX.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaBX.SetActivationFunction(None); index++; if(!cDeltaH.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaH.SetActivationFunction(None); index++; if(!cHS.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cHS.SetActivationFunction(None); //--- return true; }
И завершаем работу метода инициализации, вернув логический результат выполнения операций вызывающей программе.
Обратите внимание, что в данном объекте мы не сохранили параметры архитектуры в отдельных локальных переменных. В рамках данной реализации мы решили не создавать дополнительных переменных, которые постоянно хранят значения, сохраненные во внутренних объектах. Вместо них мы планируем использовать локальные переменные, которые заполняем в начале методов прямого и обратного проходов.
После завершения работы по инициализации объекта, мы переходим к построению алгоритма прямого прохода, который организуем в методе feedForward. В параметрах данного метода получаем указатель на объект исходных данных.
bool CNeuronAttraos::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units = cD.GetUnits();
В теле метода мы сначала загрузим из внутренних объектов параметры исходных данных, которые не сохранили на стадии инициализации. А затем сгенерируем тензоры обучаемых параметров модели.
if(!cA.FeedForward(cOne.AsObject())) // (Units, Window, WindowKey) return false; if(!cD.FeedForward(cOne.AsObject())) // (Units, Window)) return false;
На следующем шаге нормализуем исходные данные и сгенерируем контекстно-зависимые параметры модели.
if(!NeuronOCL || !SumAndNormilize(NeuronOCL.getOutput(), NeuronOCL.getOutput(), cX_norm.getOutput(), window, true, 0, 0, 0, 0.5f)) return false; if(!cX_proj.FeedForward(cX_norm.AsObject())) // (Units, 4*WindowKey) return false;
После чего разделим их на отдельные сущности.
if(!DeConcat(cDelta.getOutput(), cB.getOutput(), cC.getOutput(), cH.getOutput(), cX_proj.getOutput(), window_key, window_key, window_key, window_key, units)) // 4*(Units, WindowKey) return false;
И сгенерируем параметры адаптивного временного шага.
if(!cDelta_proj.FeedForward(cDelta.AsObject())) // (Units, Window) return false;
На этом подготовительный этап завершен, и мы переходим к построению алгоритма MDMU, который отвечает за моделирование динамики временного ряда. Состояние модели обновляется по рекуррентному уравнению:
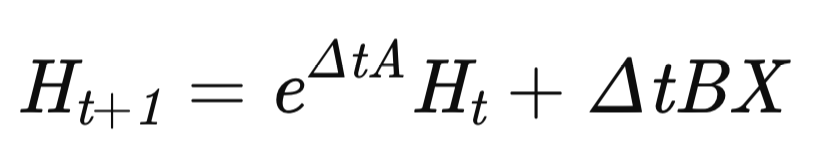
где Δt — адаптивный временной шаг.
Вначале мы вычислим экспоненциальное значение в первом слагаемом. Только функцию экспоненты заменим на SoftPlus, который обладает некоторыми преимуществами.
if(!DiagMatMul(cDelta_proj.getOutput(), cA.getOutput(), cDeltaA.getOutput(), window, window_key, units, SoftPlus)) // (Units, Window, WindowKey) return false;
SoftPlus растет медленнее экспоненты, что снижает риск резкого увеличения матрицы переходов. Благодаря этому, градиенты изменяются плавно, и обучение становится стабильнее.
Экспонента сильно меняет динамику при малых изменениях Δ. SoftPlus делает изменения мягкими, что снижает вероятность резких скачков в скрытых состояниях.
В шумных данных SoftPlus уменьшает влияние выбросов. Ее рост ограничен логарифмической функцией. Это делает модель более устойчивой.
Затем вычислим значения второго слагаемого путем последовательного умножения матриц.
if(!MatMul(cDelta_proj.getOutput(), cB.getOutput(), cDeltaB.getOutput(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false; if(!DiagMatMul(cX_norm.getOutput(), cDeltaB.getOutput(), cDeltaBX.getOutput(), window, window_key, units, None)) // (Units, Window, WindowKey) return false;
И скорректируем матрицу динамического регулятора изменений скрытых состояний на скорость изменения скрытого состояния.
if(!MatMul(cDelta_proj.getOutput(), cH.getOutput(), cDeltaH.getOutput(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false;
После подготовки всех необходимых данных, мы скорректируем скрытые состояния системы с помощью алгоритма параллельного сканирования, который мы реализовали в прошлой статье на стороне OpenCL. В данном случае достаточно вызвать метод-обертку кернела PScan.
if(!PScan()) return false;
Метод вызова кернела построен по стандартному алгоритму, и мы не будем останавливаться на его детальном рассмотрении в рамках данной статьи. Полный код указанного метода можно найти во вложении к статье (в файле NeuroNet.cl).
Далее нам остается сгенерировать прогнозное состояние анализируемой системы. Для этого мы умножаем матрицу обновленного скрытого состояния на матрицу проекции скрытых состояний.
if(!MatMul(cHS.getOutput(), cC.getOutput(), Output, window, window_key, 1, units)) // (Units, Window, 1) return false;
Нормализованные данные исходного состояния умножим на коэффициенты прямых связей.
if(!ElementMult(cD.getOutput(), cX_norm.getOutput(), PrevOutput)) // (Units, Window)) return false;
И суммируем результаты двух операций.
if(!SumAndNormilize(Output, PrevOutput, Output, window, false, 0, 0, 0, 1)) // (Units, Window)) return false;
Дополнительно добавим полученные исходные данные, создав магистраль остаточных связей.
if(!SumAndNormilize(Output, NeuronOCL.getOutput(), Output, window, false, 0, 0, 0, 1)) // (Units, Window)) return false; //--- return true; }
Такой подход позволяет объединить информацию о скрытых состояниях и краткосрочных зависимостях в исходных данных.
На этом завершается алгоритм прямого прохода нашего видения фреймворка Attraos. Возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода.
Следующим этапом мы переходим к построению алгоритмов обратного прохода нашего объекта. В рамках данной статьи рассмотрим метод распределения градиентов ошибки calcInputGradients. В параметрах метода, как и ранее, получаем указатель на объект исходных данных. Только на этот раз нам предстоит передать в него размер ошибки, в соответствии с влиянием исходных данных на конечный результат работы модели.
bool CNeuronAttraos::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
В теле метода сразу проверяем актуальность полученного указателя, так как передать данные мы можем только в действительный объект. В противном случае все дальнейшие операции теряют смысл.
Далее мы, как и в методе прямого прохода, сохраним в локальные переменные параметры исходных данных.
uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units = cD.GetUnits();
Далее мы распределяем градиент ошибки от уровня результатов по соответствующим информационным потокам. Напомню, что в ходе прямого прохода мы задействовали 3 информационных потока передачи данных:
- модель пространства состояний;
- прямые связи с коэффициентом;
- остаточные связи.
Вначале мы распределим градиент ошибки между коэффициентами прямой связи и нормализованными исходными данными.
if(!ElementMultGrad(cD.getOutput(), cD.getGradient(), cX_norm.getOutput(), cX_norm.getPrevOutput(), Gradient, cD.Activation(), None)) // (Units, Window)) return false;
Затем передадим данные на второй информационный поток, где распределим градиент ошибки между скрытыми состояниями системы и коэффициентами их проекции.
if(!MatMulGrad(cHS.getOutput(), cHS.getGradient(), cC.getOutput(), cC.getGradient(), Gradient, window, window_key, 1, units)) // (Units, Window, 1) return false;
При необходимости скорректируем полученные результаты на производные соответствующих функций активации.
if(cHS.Activation() != None) { if(!DeActivation(cHS.getOutput(), cHS.getGradient(), cHS.getGradient(), cHS.Activation())) return false; } if(cC.Activation() != None) { if(!DeActivation(cC.getOutput(), cC.getGradient(), cC.getGradient(), cC.Activation())) return false; }
Далее распределим градиент ошибки через модуль параллельного сканирования, путем вызова метода-обертки соответствующего кернела.
if(!PScanCalcGradient()) return false;
Полученные значения распределяем между соответствующими сущностями. Вначале передадим градиент ошибки на скрытые состояния и параметры адаптивного временного шага.
if(!MatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getGradient(), cH.getOutput(), cH.getGradient(), cDeltaH.getGradient(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false;
А затем опустим градиент ошибки на уровень нормализованных исходных данных.
if(!DiagMatMulGrad(cX_norm.getOutput(), cX_norm.getGradient(), cDeltaB.getOutput(), cDeltaB.getGradient(), cDeltaBX.getGradient(), window, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cX_norm.getGradient(), cX_norm.getPrevOutput(), cX_norm.getPrevOutput(), window, false, 0, 0, 0, 1)) return false;
Здесь следует обратить внимание, что мы уже ранее передавали значения градиента ошибки в объект нормализованных исходных данных. Поэтому, на данном этапе, мы суммируем данные двух информационных потоков.
Тут же распределяем градиент ошибки между коэффициентами влияния исходных данных на скрытое состояние и параметрами адаптивного временного шага.
if(!MatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getPrevOutput(), cB.getOutput(), cB.getGradient(), cDeltaB.getGradient(), window, 1, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cDelta_proj.getGradient(), cDelta_proj.getPrevOutput(), cDelta_proj.getGradient(), window, false, 0, 0, 0, 1)) return false;
Данные на уровне параметров адаптивного временного шага суммируем с ранее накопленными значениями.
Далее нам предстоит опустить градиент ошибки на уровень матрицы эволюции скрытого состояния, но вначале скорректируем полученные значения на производную функции активации.
if(!DeActivation(cDeltaA.getOutput(), cDeltaA.getGradient(), cDeltaA.getGradient(), SoftPlus)) return false;
А затем, распределим значения между сущностями.
if(!DiagMatMulGrad(cDelta_proj.getOutput(), cDelta_proj.getPrevOutput(), cA.getOutput(), cA.getGradient(), cDeltaA.getGradient(), window, window_key, units)) // (Units, Window, WindowKey) return false; if(!SumAndNormilize(cDelta_proj.getGradient(), cDelta_proj.getPrevOutput(), cDelta_proj.getGradient(), window, false, 0, 0, 0, 1)) return false;
На данном этапе мы снова суммируем значения градиента ошибки на уровне параметров адаптивного временного шага. Но на этот раз, это последний информационный поток в данном направлении. И теперь корректируем накопленные значения на производную соответствующей функции активации.
if(cDelta_proj.Activation() != None) { if(!DeActivation(cDelta_proj.getOutput(), cDelta_proj.getGradient(), cDelta_proj.getGradient(), cDelta_proj.Activation())) return false; }
После чего спускаем градиент ошибки до уровня адаптивных временных шагов.
if(!cDelta.calcHiddenGradients(cDelta_proj.AsObject())) return false;
Теперь мы получили градиенты ошибки на уровне всех контекстно-зависимых сущностей. Мы собираем полученные значение в единый тензор.
if(!Concat(cDelta.getGradient(), cB.getGradient(), cC.getGradient(), cH.getGradient(), cX_proj.getGradient(), window_key, window_key, window_key, window_key, units)) // 4*(Units, WindowKey) return false;
После чего спускаем градиент ошибки до уровня нормализованных исходных данных.
if(!cX_norm.calcHiddenGradients(cX_proj.AsObject())) return false; if(!SumAndNormilize(cX_norm.getGradient(), cX_norm.getPrevOutput(), cX_norm.getGradient(), window, false, 0, 0, 0, 1)) return false;
Напомню, что в объект нормализованных исходных данных мы уже дважды передавали градиент ошибки. Следовательно, полученные на данном этапе данные прибавляем к ранее накопленным значениям.
Сюда же мы прибавляем значения по магистрали остаточных связей, после чего, передаем накопленные значения на уровень исходных данных, предварительно скорректировав их на производную соответствующей функции активации.
if(!SumAndNormilize(cX_norm.getGradient(), Gradient, cX_norm.getGradient(), window, false, 0, 0, 0, 1)) return false; if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cX_norm.getGradient(), NeuronOCL.Activation())) return false; //--- return true; }
На этом мы завершаем работу метода распределения градиента ошибки и возвращаем логический результат работы вызывающей программе.
С методом обновления параметров модели updateInputWeights я предлагаю вам ознакомиться самостоятельно. В нем мы лишь вызываем одноименные методы четырех внутренних объектов, содержащих обучаемые параметры.
И здесь хочется сказать несколько слов об алгоритмах методов сохранения и восстановления объекта. Наш новый класс содержит довольно много внутренних объектов, но только 4 из них содержат обучаемые параметры. Следовательно, при сохранении, нам достаточно записать на диск только информацию об этих внутренних объектах.
bool CNeuronAttraos::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; //--- if(!cA.Save(file_handle)) return false; if(!cD.Save(file_handle)) return false; if(!cX_proj.Save(file_handle)) return false; if(!cDelta_proj.Save(file_handle)) return false; //--- return true; }
Но возникает вопрос в восстановлении работоспособности объекта. В методе Load мы сначала загружаем с диска ранее сохраненные данные.
bool CNeuronAttraos::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; //--- if(!LoadInsideLayer(file_handle, cA.AsObject())) return false; if(!LoadInsideLayer(file_handle, cD.AsObject())) return false; if(!LoadInsideLayer(file_handle, cX_proj.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDelta_proj.AsObject())) return false;
Затем запишем в локальные переменные параметры архитектуры объекта.
uint window = cX_proj.GetWindow(); uint window_key = cX_proj.GetFilters() / 4; uint units_count = cD.GetUnits();
Дальнейший алгоритм повторяет процесс инициализации объектов временного хранения данных.
if(!cOne.Init(0, 0, OpenCL, units_count, optimization, iBatch)) return false; if(!cOne.getOutput().Fill(1)) return false; cOne.SetActivationFunction(None); int index = 3; if(!cX_norm.Init(0, index, OpenCL, window * units_count, optimization, iBatch)) return false; cX_norm.SetActivationFunction(None); index += 2; if(!cDelta.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cDelta.SetActivationFunction(None); index++; if(!cB.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cB.SetActivationFunction(None); index++; if(!cC.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cC.SetActivationFunction(None); index++; if(!cH.Init(0, index, OpenCL, window_key * units_count, optimization, iBatch)) return false; cH.SetActivationFunction(None); index += 2; if(!cDeltaA.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaA.SetActivationFunction(None); index++; if(!cDeltaB.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaB.SetActivationFunction(None); index++; if(!cDeltaBX.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaBX.SetActivationFunction(None); index++; if(!cDeltaH.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cDeltaH.SetActivationFunction(None); index++; if(!cHS.Init(0, index, OpenCL, window * window_key * units_count, optimization, iBatch)) return false; cHS.SetActivationFunction(None); //--- return true; }
Такой подход позволяет нам оптимизировать процесс сохранения данных и восстановления работоспособности объекта, а так же использование дискового пространства.
На этом мы завершаем рассмотрение алгоритмов построения фреймворка Attraos средствами MQL5. С полным кодом класса CNeuronAttraos и всех его методов вы можете ознакомиться во вложении.
Архитектура модели
После реализации алгоритмов фреймворка Attraos, мы переходим к описанию архитектуры обучаемых моделей. В рамках данного эксперимента мы обучаем две модели с использованием подходов мультизадачного обучения. Архитектура обеих моделей представлена в методе CreateDescriptions. В параметрах метода получаем указатели на 2 динамических массива, в которые нам и предстоит передать описание архитектуры моделей.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
В теле метода сразу проверяем актуальность полученных указателей и, при необходимости, создаем новые экземпляры объектов.
Первой мы опишем архитектуру актера, который и будет использовать реализованные выше подходы фреймворка Attraos. Как обычно, модель начинается с полносвязного слоя исходных данных и следующего за ним слоя пакетной нормализации данных. Такой подход позволяет нам передавать в модель сырые исходные данные, получаемые от терминала. При этом их первичная обработка в виде нормализации осуществляется уже средствами модели.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Далее мы используем первый слой архитектуры Attraos. В данном случае, для трансформации исходных данных в фазовое пространство используем временной лаг в 5 шагов, что соответствует 5 минутам на минутном таймфрейме.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*5; // 5 min descr.count = HistoryBars/5; // 24 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Для следующего слоя мы увеличиваем временной шаг до 15 элементов.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*15; // 15 min descr.count = HistoryBars/15; // 8 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
А в третьем до 30.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAttraos; descr.window = BarDescr*30; // 30 min descr.count = HistoryBars/30; // 4 descr.window_out = 256; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Здесь следует обратить внимание, что на выходе каждого объекта CNeuronAttraos мы получаем результат в размерности исходных данных. Поэтому следующим свертночным слоем понижаем размерность тензора в 3 раза.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count=descr.count = HistoryBars/3; descr.window = BarDescr*3; descr.step = descr.window; int prev_window=descr.window_out = BarDescr; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
За которым следует голова принятия решений из 3 последовательных полносвязных слоев.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Полученный результат мы нормализуем.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
И добавляем блок риск-менеджмента.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Модель вероятностей направления предстоящего движения полностью перенесена из предыдущих работ без изменений. И позвольте не приводить её описание в рамках данной статьи. Полное описание архитектуры обучаемых моделей представлено во вложении. Там же вы найдете полный код программ обучения моделей и взаимодействия с окружающей средой, которые так же были перенесены из предыдущих работ без изменений.
Тестирование
На протяжении двух статей мы проделали значительный объем работы, адаптируя и развивая идеи, заложенные авторами фреймворка Attraos. И теперь подошли к одному из ключевых этапов — проверке работоспособности и эффективности реализованных методов на реальных исторических данных. Этот процесс является решающим в оценке практической применимости модели и её способности выявлять закономерности, обеспечивая стабильные результаты в различных рыночных условиях.
Для обучения модели была использована выборка, включающая исторические котировки валютной пары EURUSD на таймфрейме M1 за весь 2024 год. Все параметры анализируемых индикаторов остаются установленными по умолчанию, без дополнительной оптимизации. Такой подход позволяет исключить влияние внешних факторов, таких как подгонка параметров под конкретные исторические данные, и сосредоточиться исключительно на фундаментальном качестве работы модели. Важно отметить, что использование неизмененных параметров индикаторов также позволяет оценить способность модели адаптироваться к реальной рыночной динамике без необходимости постоянного вмешательства и перенастройки.
Как и ранее, обучение модели осуществляется в 2 этапа. На первом этапе устанавливаем размер пакета обучения равным 1, что позволяет на каждой итерации процесса обучения использовать абсолютно случайное состояние из обучающей выборки. Это позволяет нам максимально приблизить работу модели в новом состоянии. Однако, этого недостаточно для корректного обучения блока риск-менеджмента. Поэтому на втором этапе мы увеличиваем размер пакета до 60, что позволяет нам корректировать работу модели и блока риск-менеджмента на 60 последовательных состояниях окружающей среды. При использовании минутного таймфрейма, это соответствует одному часу.
Для тестирования обученной модели использованы данные за Январь-Февраль 2025 года. Этот период выбран, чтобы обеспечить строгую проверку способности модели работать на новых, ранее не встречавшихся данных. При этом все остальные параметры эксперимента остаются неизменными, что гарантирует чистоту эксперимента, воспроизводимость результатов и корректность последующего сравнения. Такой подход исключает влияние случайных факторов и позволяет объективно оценить качество работы алгоритмов.
Результаты тестирования представлены ниже.
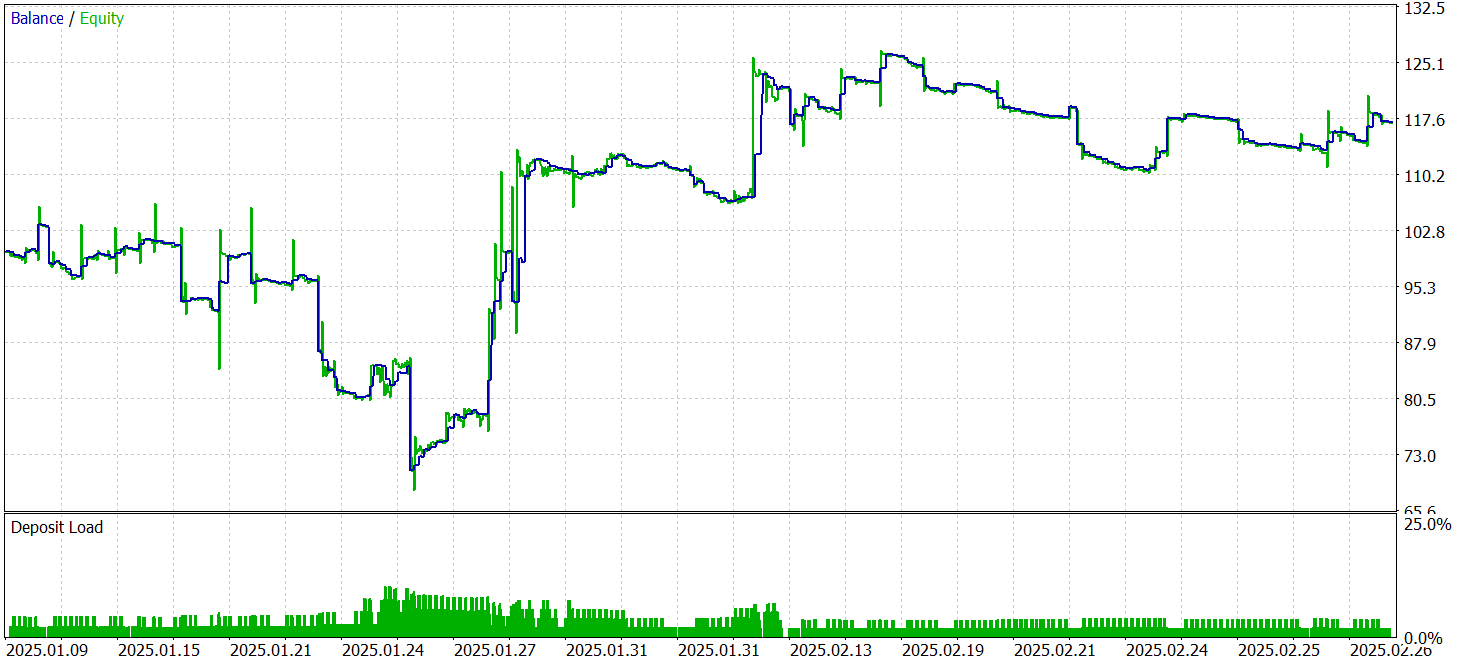
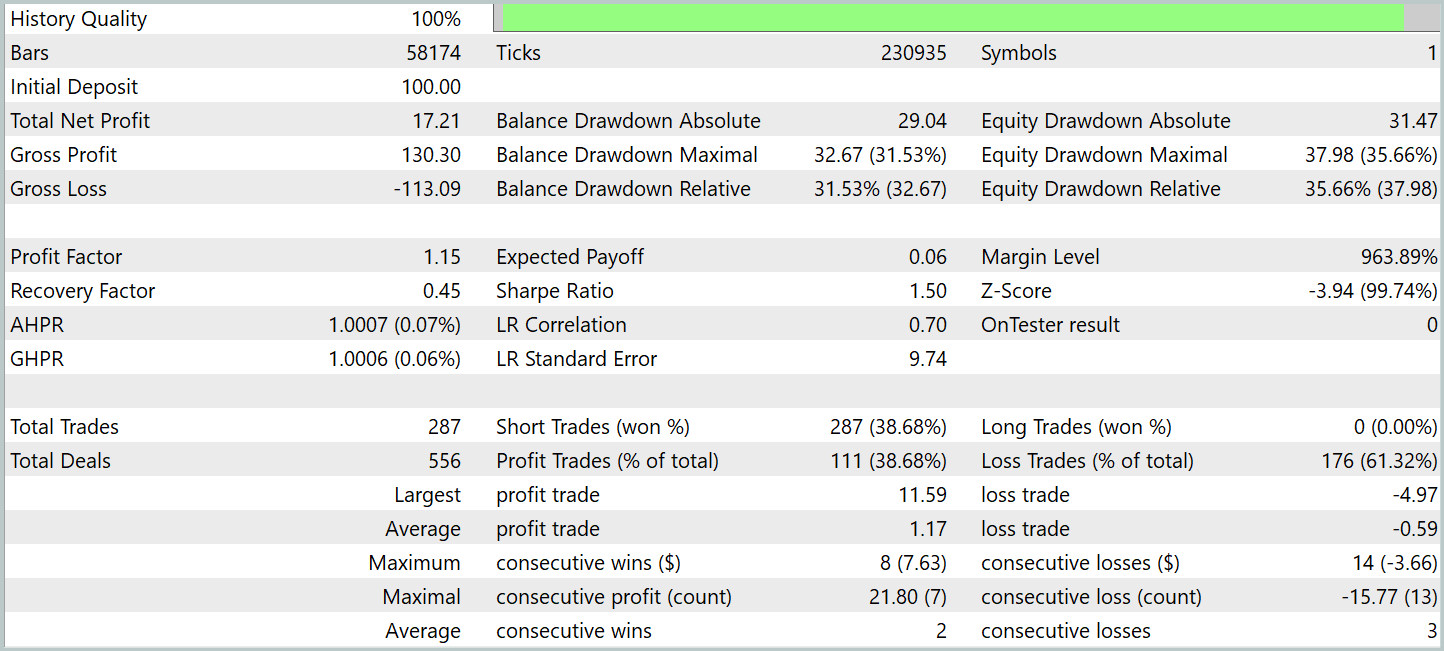
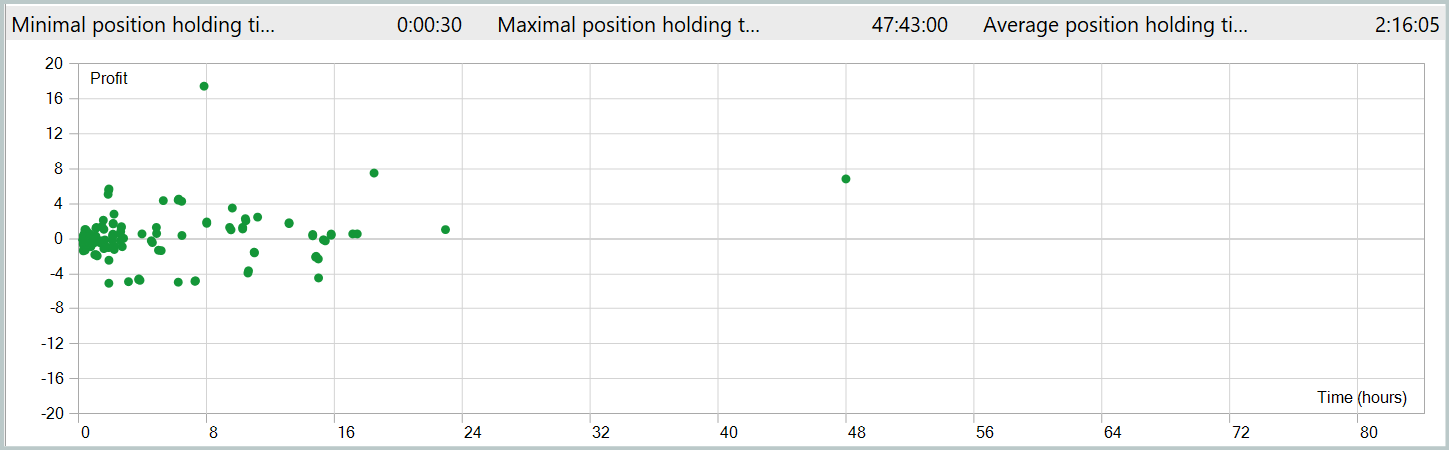
За период тестирования модель осуществила 287 торговых операций, из которых почти 39% были закрыты с прибылью. Несмотря на относительно невысокий процент успешных сделок, стратегия продемонстрировала положительный результат за счет соотношения прибыли и убытков. В частности, средний размер прибыли на успешной сделке оказался вдвое выше среднего убытка, что позволило компенсировать менее удачные операции, выйти на общий положительный финансовый результат и зафиксировать показатель профит-фактор на уровне 1.15.
Среднее время удержания позиции превысило 2 часа, что свидетельствует о склонности модели к краткосрочным и среднесрочным торговым решениям. Однако, особое внимание привлекает случай максимального удержания позиции, которое составило почти двое суток. Данный факт требует дополнительного анализа.
Заключение
Мы познакомились с фреймворком Attraos, который использует концепции теории хаоса для решения задач прогнозирования временных рядов. Авторы фреймворка интегрируют подходы нелинейного анализа, реконструкции фазового пространства, динамическую память с различными уровнями разрешения и адаптивные алгоритмы. Эти технологии помогают строить более точные прогнозы и адаптировать торговые модели к изменяющимся условиям рынка.
В практической части мы реализовали собственное видение предложенных подходов средствами MQL5, построили и обучили модели на реальных исторических данных. Результаты тестирования обученной модели на исторических данных не входящих в обучающую выборку свидетельствуют о возможности модели генерировать прибыль на новых данных. Однако результаты выявили и некоторые проблемы. В частности мы видим длительное удержание некоторых позиций. И график баланса не настолько гладок, как бы нам того хотелось. Из этого можно сделать вывод, что модель имеет потенциал, но необходима дополнительная работа по её оптимизации.
Обратите внимание, что сделанные выводы актуальны только для данной реализации. Авторская версия в данной работе не тестировалась.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Бильярдный алгоритм оптимизации — Billiards Optimization Algorithm (BOA)
Бильярдный алгоритм оптимизации — Billiards Optimization Algorithm (BOA)
 Переосмысливаем классические стратегии (Часть V): Анализ нескольких инструментов в валютной паре USDZAR
Переосмысливаем классические стратегии (Часть V): Анализ нескольких инструментов в валютной паре USDZAR
 MQL5-советник, интегрированный в Telegram (Часть 3): Отправка скриншотов графиков с подписями из MQL5 в Telegram
MQL5-советник, интегрированный в Telegram (Часть 3): Отправка скриншотов графиков с подписями из MQL5 в Telegram
 Машинное обучение и Data Science (Часть 29): Как отбирать лучшие форекс-данные для обучения ИИ
Машинное обучение и Data Science (Часть 29): Как отбирать лучшие форекс-данные для обучения ИИ
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования