Trading de arbitragem no Forex: sistema de negociação matricial para retorno ao valor justo com limitação de risco

Introdução

No mundo do trading algorítmico, existe um número infinito de estratégias, mas apenas algumas delas possuem elegância matemática e uma lógica fundamental que está na base dos mercados financeiros. Hoje quero apresentar a você um sistema que incorpora exatamente essas qualidades, a arbitragem matricial no mercado Forex, baseada no conceito de valor justo das moedas.

Imagine um mercado em que oito das principais moedas mundiais formam uma rede complexa de relações, na qual cada par de moedas deve estar em equilíbrio ideal com todos os demais. Em teoria, essa rede deveria ser perfeitamente balanceada, mas na prática observamos imperfeições microscópicas constantes, isto é, desvios temporários do valor justo, que criam oportunidades únicas de extração de lucro.

Esses desvios não são apenas ruído aleatório. Eles representam desequilíbrios que o mercado, mais cedo ou mais tarde, corrige, retornando ao estado de equilíbrio. É justamente essa inevitabilidade matemática que aprenderemos a utilizar em nosso sistema de negociação, sem depender de indicadores técnicos ou análises subjetivas, mas baseando-nos apenas na lógica implacável dos números e das probabilidades.

O que torna essa estratégia especialmente atraente é sua universalidade e independência dos regimes de mercado. Enquanto a maioria dos sistemas funciona apenas em determinadas condições, como tendência, lateralização ou alta volatilidade, nosso sistema matricial opera em qualquer conjuntura de mercado, pois se apoia em leis matemáticas fundamentais, e não em sentimentos passageiros do mercado.

Neste artigo, não apenas apresentaremos o conceito teórico, mas também demonstraremos um sistema de negociação totalmente automatizado, implementado na linguagem MQL5, que coloca essa ideia em prática, com gerenciamento de risco inteligente, tamanho de posição adaptativo e uma matriz visual de desequilíbrios para monitorar oportunidades de mercado em tempo real. Vamos mergulhar em um mundo onde a precisão matemática encontra os mercados financeiros, criando uma abordagem elegante para extrair lucro das imperfeições do sistema monetário global.

Princípio de funcionamento do sistema de arbitragem matricial

Na base do nosso sistema matricial está um conceito que pode ser chamado de "arbitragem triangular com esteroides". A arbitragem triangular tradicional pressupõe a busca por desequilíbrios entre três pares de moedas. Nosso sistema leva essa abordagem a um nível fundamentalmente novo, criando uma matriz multidimensional de relações entre todas as principais moedas do mercado Forex.

Fundamento matemático da estratégia

Cada moeda em nosso sistema é representada como um vértice em um grafo multidimensional, onde as arestas são as taxas de câmbio entre as moedas. Um sistema idealmente balanceado deve possuir a propriedade da transitividade: se conhecemos a taxa EUR/USD e a USD/JPY, então a taxa EUR/JPY deve ser o produto delas. No entanto, na realidade, o mercado Forex é um organismo vivo, no qual surgem constantemente ineficiências temporárias.

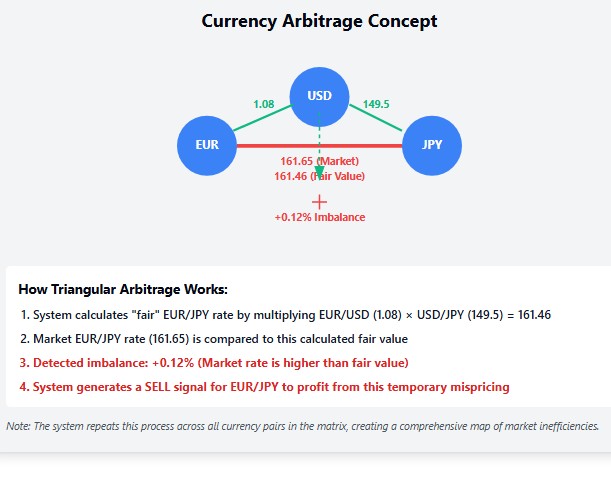
Nosso sistema acompanha essas ineficiências, calculando para cada par de moedas o seu "valor justo" com base em todos os outros pares de moedas. Quando o preço de mercado atual se desvia de forma significativa desse valor justo calculado, surge uma oportunidade potencial de entrada no mercado.

Arquitetura do sistema de negociação

O EA cria e atualiza constantemente uma matriz de tamanho 8×8, que representa as relações entre as principais moedas: EUR, USD, GBP, JPY, CHF, CAD, AUD e NZD. Cada célula da matriz contém não apenas a taxa atual, mas exatamente a taxa "justa", calculada levando em consideração todas as taxas cruzadas possíveis.

// Матрица курсов валют (справедливые значения)
// Используем одномерный массив для реализации двумерной матрицы
double g_currency_matrix[];

Um ponto técnico importante: no código, utilizamos um array unidimensional para a implementação eficiente da matriz bidimensional, o que garante um uso mais eficiente da memória e aumenta o desempenho do EA ao trabalhar com um grande número de pares de moedas.

Processo de cálculo do valor justo

O processo de determinação do valor justo começa com a inicialização da matriz, onde os elementos da diagonal são preenchidos com unidades. Afinal, a taxa de uma moeda em relação a ela mesma é sempre igual a 1, isso é um axioma do nosso sistema. Em seguida, a matriz é preenchida com as taxas de mercado atuais, aquelas mesmas cotações que vemos no terminal.

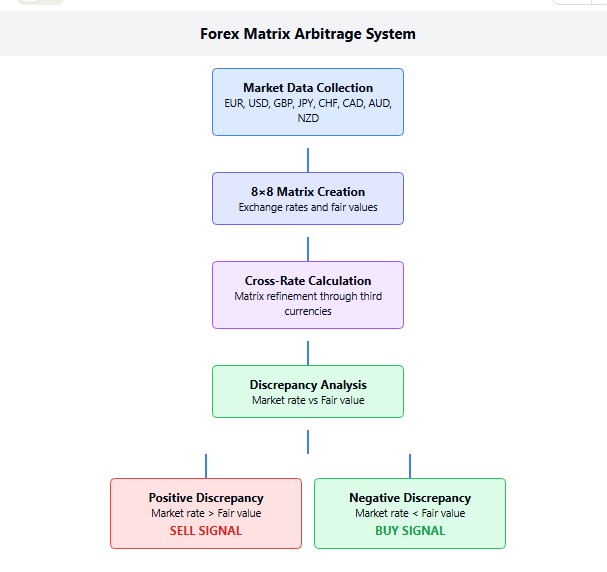
Mas a verdadeira magia começa na etapa seguinte, o refinamento iterativo de todos os valores da matriz. Aqui ocorre o cálculo de todas as taxas cruzadas possíveis, quando o sistema analisa as relações entre moedas por meio de terceiras moedas. Imagine isso como a exploração de "caminhos alternativos", se for possível obter uma taxa EUR/JPY mais vantajosa por meio do dólar, o sistema irá identificar isso.

Especialmente elegante é o algoritmo de cálculo das taxas cruzadas:

void CalculateCrossRatesArbitrage()
{
   // Несколько итераций для уточнения матрицы
   for(int iterations = 0; iterations < 3; iterations++)
   {
      for(int i = 0; i < g_currencies_count; i++)
      {
         for(int j = 0; j < g_currencies_count; j++)
         {
            if(i == j) continue;
            
            for(int k = 0; k < g_currencies_count; k++)
            {
               if(k == i || k == j) continue;
               
               double ik_value = GetMatrixValue(i, k);
               double kj_value = GetMatrixValue(k, j);
               
               if(ik_value != 0 && kj_value != 0)
               {
                  double triangleRate = ik_value * kj_value;
                  double current_value = GetMatrixValue(i, j);
                  
                  if(current_value == 0)
                     SetMatrixValue(i, j, triangleRate);
                  else
                     SetMatrixValue(i, j, (current_value * 0.7 + triangleRate * 0.3));
                  
                  current_value = GetMatrixValue(i, j);
                  if(current_value != 0)
                     SetMatrixValue(j, i, 1.0 / current_value);
               }
            }
         }
      }
   }
}

Observe o ajuste fino na forma dos coeficientes de peso 0.7 e 0.3. Esses não são números aleatórios, mas o resultado de inúmeros testes. Damos maior peso às cotações diretas, mas ao mesmo tempo não ignoramos as informações obtidas por meio das taxas cruzadas. Essa proporção cria o equilíbrio ideal entre a estabilidade e a sensibilidade do sistema às ineficiências do mercado.

Lógica de negociação e gerenciamento de risco

Após a criação da matriz de valores justos, chega o momento da tomada de decisões de negociação. O sistema calcula o desvio percentual do preço de mercado atual em relação ao valor justo para cada par de moedas. Isso é expresso por uma fórmula elegante:

g_market_rates[i].discrepancy = (g_market_rates[i].median / g_market_rates[i].fair_value - 1.0) * 100.0;

Quando o desvio ultrapassa o limite definido pelo usuário, o sistema identifica uma oportunidade potencial de extração de lucro. Um desvio negativo significa que o mercado está subvalorizando a moeda em relação ao seu valor justo, isto é, um sinal de compra. Um desvio positivo indica sobrevalorização, que é um sinal de venda.

O gerenciamento de risco inteligente não é apenas uma função adicional, mas uma parte inseparável do nosso sistema. A função de cálculo do tamanho da posição considera não apenas o nível de risco definido pelo usuário, mas também as particularidades de cada par de moedas: valor do ponto, volatilidade, tamanhos mínimo e máximo de lote. Isso permite que o sistema se adapte a diferentes condições de mercado e mantenha o mesmo nível de risco, independentemente do instrumento negociado.

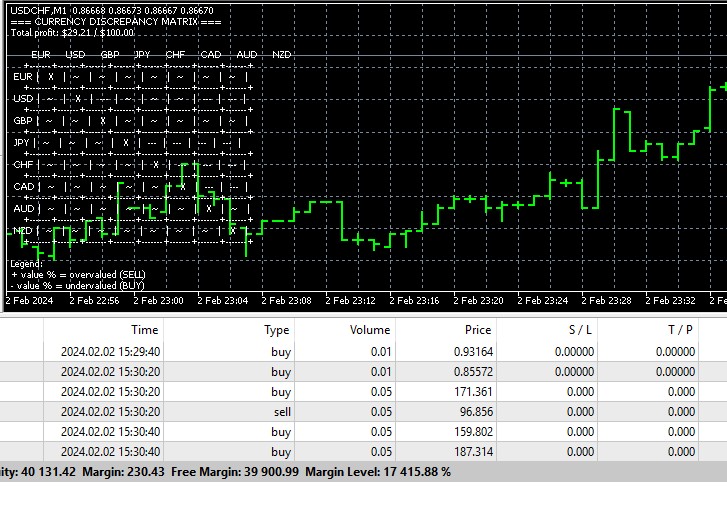
Visualização e monitoramento

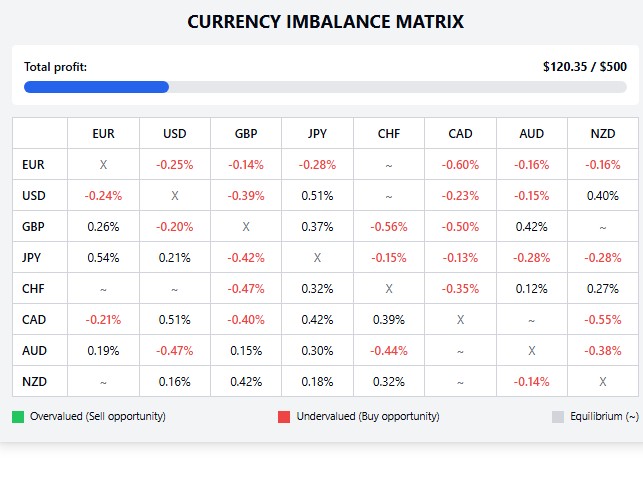
Um dos maiores tesouros do nosso sistema é a visualização da matriz de desequilíbrios cambiais diretamente no gráfico. Isso não é apenas um conjunto de números abstratos, mas um mapa interativo de oportunidades, que é atualizado em tempo real a cada movimento do mercado:

=== CURRENCY IMBALANCE MATRIX ===
Total profit: $120.35 / $500.00
       EUR     USD     GBP     JPY     CHF     CAD     AUD     NZD   
    +-------+-------+-------+-------+-------+-------+-------+-------+
 EUR |   X   |+0.15% |-0.31% | ~ | ~ |-0.52% | ~ |
    +-------+-------+-------+-------+-------+-------+-------+-------+
 USD |-0.15% |   X   |+0.24% | ~ |-0.11% | ~ |+0.42% | ~ |
    +-------+-------+-------+-------+-------+-------+-------+-------+
...

Essa visualização funciona como um radar de alta precisão, identificando instantaneamente oportunidades de arbitragem no mercado Forex. Valores positivos são destacados em verde, sinalizando a sobrevalorização do par de moedas e uma potencial oportunidade de venda. Valores negativos são coloridos em vermelho, indicando subvalorização e uma oportunidade favorável de compra. O símbolo "~" indica pares de moedas em estado de equilíbrio relativo, que no momento atual não apresentam interesse para nossa estratégia de negociação.

Encerramento automático da negociação

A psicologia do trading é uma das áreas mais complexas dos mercados financeiros. Nosso sistema aborda esse aspecto ao oferecer um mecanismo de encerramento automático da negociação quando a meta de lucro definida é atingida. O trader define o nível de lucro desejado e, quando ele é alcançado, o sistema fecha todas as posições e interrompe a negociação até a próxima inicialização.

Esse mecanismo é um verdadeiro guardião contra a ganância, um dos inimigos mais perigosos do trader. Quando o sistema atinge o objetivo, ele não se deixa seduzir pela possibilidade de ganhar "um pouco mais", mas fixa o lucro de forma disciplinada.

A essência do nosso sistema matricial pode ser expressa em uma única frase: "Elegância matemática a serviço da eficiência financeira". Não tentamos prever o movimento do mercado nem analisar notícias. Em vez disso, criamos um modelo matemático de relações justas entre as moedas e extraímos lucro dos desvios temporários do mercado em relação a esse modelo. Trata-se de uma abordagem que funciona independentemente dos regimes de mercado, pois se baseia em princípios matemáticos fundamentais, e não em tendências de mercado passageiras.

Na próxima parte do artigo, vamos nos aprofundar nos aspectos práticos da configuração do sistema, analisar os parâmetros ideais para diferentes condições de mercado e examinar os resultados de backtests em dados históricos que abrangem diversos regimes de mercado.

Configuração ideal dos parâmetros do sistema

A arte de criar um sistema de negociação realmente eficiente reside menos na invenção de novos indicadores ou métodos de análise e mais no ajuste fino dos parâmetros. Em nosso sistema de arbitragem matricial, as configurações-chave são o valor do desvio mínimo para entrada no mercado, o nível de risco e a abordagem para o cálculo do tamanho da posição.

O parâmetro MinDiscrepancy exige atenção especial. Um valor muito baixo levará a entradas frequentes no mercado com desvios pequenos, que podem ser apenas ruído aleatório. Um valor muito alto significa que o sistema deixará passar muitas oportunidades. Com base em inúmeros testes, recomendamos começar com esse parâmetro na faixa de 0.05-0.1%. Para pares que envolvem o iene, um valor mais alto pode ser ideal, em torno de 0.15%, levando em consideração sua volatilidade tradicionalmente maior.

O gerenciamento de risco por meio do parâmetro MaxRisk é o seu escudo de proteção no mundo do trading cambial. Recomendamos nunca ultrapassar o valor de 0.02, isto é, 2% do saldo, mesmo para as estratégias mais agressivas. Traders conservadores podem reduzir esse valor para 0.01 ou até 0.005, sacrificando o lucro potencial em favor de uma maior estabilidade.

O cálculo automático do tamanho do lote ( AutoLots ) é uma poderosa ferramenta de adaptação do sistema a diferentes condições de mercado. Quando essa opção está ativada, o sistema determina de forma independente o tamanho ideal da posição, levando em conta a volatilidade atual e o valor do ponto para o par de moedas específico. Isso permite manter o mesmo nível de risco em todas as operações, independentemente do instrumento negociado.

Timing de atualização da matriz e dos sinais de negociação

A frequência de atualização da matriz de valores justos exerce uma influência significativa sobre a eficiência do sistema. Atualizações excessivamente frequentes podem gerar "ruído" desnecessário nos cálculos, enquanto atualizações muito raras podem resultar em oportunidades perdidas. Em nossa implementação, utilizamos um temporizador com intervalo de 5 segundos:

EventSetTimer(5); // Обновление каждые 5 секунд

Esse intervalo não foi escolhido por acaso, pois garante um equilíbrio entre a atualidade dos dados e a carga computacional. Ao trabalhar com processadores mais rápidos, é possível experimentar a redução desse intervalo para 2 ou 3 segundos, obtendo uma reação ainda mais ágil aos desequilíbrios do mercado.

É interessante notar que, em períodos de alta volatilidade do mercado, por exemplo, durante a divulgação de notícias econômicas importantes, o sistema pode apresentar resultados especialmente impressionantes. Movimentos bruscos de preço frequentemente criam desequilíbrios temporários entre pares de moedas, e nosso sistema os identifica com eficiência. No entanto, é importante ter cautela ao negociar em momentos de volatilidade extrema, pois spreads ampliados podem afetar de forma significativa a rentabilidade da estratégia.

Ajuste fino dos cálculos matriciais

Uma das características mais interessantes do nosso sistema é o mecanismo de refinamento iterativo da matriz de valores justos. Na implementação atual, utilizamos três iterações:

for(int iterations = 0; iterations < 3; iterations++)
{
   // Расчет кросс-курсов...
}

O aumento do número de iterações pode, em teoria, elevar a precisão dos cálculos, mas ao custo de uma maior carga computacional. Nossos testes mostram que três iterações oferecem o equilíbrio ideal entre precisão e desempenho.

Outro parâmetro de ajuste fino são os coeficientes de peso utilizados na média entre a taxa direta e a taxa calculada por meio das taxas cruzadas:

SetMatrixValue(i, j, (current_value * 0.7 + triangleRate * 0.3));

O aumento do peso atribuído ao triangleRate tornará o sistema mais sensível às oportunidades de arbitragem, mas também pode elevar a quantidade de sinais falsos. A redução desse coeficiente, ao contrário, resulta em uma estratégia mais conservadora, com menos operações, porém com uma taxa potencialmente mais alta de entradas bem-sucedidas.

O parâmetro de lucro alvo TotalProfitTarget merece atenção especial. Sua definição funciona como um tipo de contrato disciplinar do trader consigo mesmo. Assim que o objetivo é alcançado, o sistema fecha todas as posições e interrompe a negociação até a próxima inicialização. Isso protege o trader da tentação de "melhorar um pouco o resultado", algo que frequentemente leva à perda do lucro já obtido.

Adaptação do sistema às condições de mercado em constante mudança

O mercado Forex é um organismo vivo, que está em constante evolução. Aquilo que funcionava ontem pode não funcionar amanhã. Como o nosso sistema matricial se adapta a essas condições mutáveis?

Em primeiro lugar, o próprio conceito de busca por desvios em relação ao valor justo torna o sistema relativamente resistente às mudanças de regime de mercado. Ele não depende de tendências de longo prazo nem de padrões estáveis de comportamento do preço, mas extrai lucro de desequilíbrios de curto prazo, que existem independentemente da direção geral do mercado.

Em segundo lugar, a abordagem sistemática de otimização de parâmetros permite adaptar a estratégia às condições atuais do mercado. Recomenda-se realizar periodicamente, por exemplo, uma vez por trimestre, uma reotimização dos parâmetros com base nos dados históricos mais recentes, para que o sistema se "ajuste" ao caráter atual do mercado.

Na próxima parte do artigo, analisaremos as capacidades avançadas do nosso sistema matricial, incluindo entradas e saídas adaptativas, integração com outros métodos de análise e possibilidades de escalonamento da estratégia para um número maior de pares de moedas e instrumentos.

Capacidades avançadas do sistema de arbitragem matricial

O verdadeiro poder do nosso sistema matricial se revela plenamente quando começamos a explorar suas capacidades avançadas. Desde algoritmos adaptativos de entrada e saída até a integração com fontes adicionais de informação de mercado. O potencial para o desenvolvimento criativo do conceito central é praticamente ilimitado.

Algoritmos adaptativos de entrada e saída

A implementação padrão do nosso sistema utiliza um valor fixo de desvio mínimo para entrada no mercado. No entanto, o mercado Forex é dinâmico, e a volatilidade de pares de moedas individuais está em constante mudança. Imagine o quanto o sistema poderia se tornar mais eficiente se o limite de entrada se adaptasse automaticamente à volatilidade atual do mercado.

Podemos modificar o nosso sistema adicionando o cálculo do desvio padrão móvel dos desequilíbrios para cada par de moedas. Em seguida, o valor de MinDiscrepancy será ajustado automaticamente, aumentando em períodos de alta volatilidade e diminuindo em momentos mais tranquilos. Essa adaptabilidade eleva significativamente a eficiência do sistema, especialmente em períodos de transição, quando o caráter do mercado muda de forma abrupta.

Uma abordagem semelhante pode ser aplicada também ao algoritmo de saída das posições. Em vez do simples fechamento da posição ao surgir um sinal oposto, o sistema pode utilizar um trailing stop adaptativo, que acompanha o preço a uma distância proporcional à volatilidade atual. Isso permite maximizar o lucro no caso de continuação do movimento do preço na direção favorável.

Integração com correlação cambial

Nosso sistema matricial já leva em conta implicitamente as correlações entre os pares de moedas por meio do cálculo dos valores justos. No entanto, podemos ir além e adicionar uma análise explícita de correlação, que ajudará a otimizar a estrutura das posições abertas.

Imagine uma situação em que o sistema gera simultaneamente sinais de compra para EUR/USD e de venda para GBP/USD. Esses pares frequentemente apresentam alta correlação positiva, o que torna essas operações opostas especialmente atraentes do ponto de vista da relação risco/retorno. Na prática, criamos um hedge que nos protege contra movimentos amplos do mercado e permite extrair lucro do movimento relativo entre as moedas.

Por outro lado, se o sistema gera sinais na mesma direção para pares altamente correlacionados, por exemplo, compra de EUR/USD e compra de AUD/USD, essa combinação aumenta a concentração de risco. Nesse caso, pode-se implementar um algoritmo que selecione apenas um dos pares, aquele com a maior relação risco/retorno esperada.

Otimização da eficiência computacional

À medida que o sistema é expandido para um número maior de pares de moedas, a eficiência computacional torna-se criticamente importante. Nossa implementação atual utiliza uma abordagem simples, porém eficiente, com um array unidimensional para armazenar a matriz bidimensional. Essa solução economiza significativamente memória e aumenta a velocidade dos cálculos.

No entanto, é possível avançar ainda mais. Para sistemas muito grandes, por exemplo, que abrangem todos os pares de moedas majors, minors e exóticos, pode-se implementar matrizes esparsas, que armazenam apenas os elementos não nulos. Isso é especialmente eficiente, pois no início da operação do sistema a maioria das células da matriz de valores justos não está preenchida.

Outra possibilidade de otimização são os cálculos paralelos. Processadores modernos possuem múltiplos núcleos, e o algoritmo de refinamento iterativo da matriz pode ser paralelizado, acelerando significativamente os cálculos em sistemas de grande porte.

Seleção dinâmica de pares de moedas

Na implementação atual, o sistema trabalha com um conjunto fixo de oito moedas principais. No entanto, é possível desenvolver um algoritmo que selecione dinamicamente os pares de moedas para análise com base em sua liquidez, volatilidade e na eficiência histórica do sistema nesses pares.

// Динамический отбор валютных пар
void SelectOptimalCurrencyPairs()
{
   CArrayString potential_pairs; // Все доступные пары
   
   // Заполнение списка всех доступных пар
   // ...
   
   // Оценка каждой пары по нескольким критериям
   for(int i = 0; i < potential_pairs.Total(); i++)
   {
      double liquidity = EstimateLiquidity(potential_pairs.At(i));
      double volatility = EstimateVolatility(potential_pairs.At(i));
      double historical_performance = EstimateHistoricalPerformance(potential_pairs.At(i));
      
      // Комбинированная оценка
      double score = CalculateCombinedScore(liquidity, volatility, historical_performance);
      
      // Сохранение оценки
      // ...
   }
   
   // Выбор лучших пар для текущего торгового цикла
   // ...
}

Essa abordagem permite que o sistema se adapte às condições de mercado em constante mudança, concentrando-se nos pares de moedas mais promissores no momento atual.

Negociação de instrumentos derivativos

Os princípios do nosso sistema matricial são aplicáveis não apenas ao mercado Forex à vista, mas também a instrumentos derivativos, como futuros e opções sobre moedas. Uma direção especialmente interessante é o uso do sistema para negociação de opções, onde desequilíbrios temporários na precificação podem criar oportunidades adicionais de arbitragem.

O sistema pode ser modificado para calcular a volatilidade "justa" para diferentes prazos de expiração e strikes de opções, identificando situações em que os prêmios de mercado se desviam significativamente dos valores teoricamente justos. Essa abordagem abre um mundo completamente novo de possibilidades para traders experientes.

Escalonamento para outras classes de ativos

Embora o nosso sistema tenha sido desenvolvido para o mercado Forex, sua concepção é universal e pode ser adaptada para outros instrumentos financeiros inter-relacionados. Imagine a aplicação do método matricial a pares de criptomoedas, onde as ineficiências de precificação costumam ser ainda mais pronunciadas do que nos mercados tradicionais.

Outra direção interessante é a arbitragem intermercado, em que o sistema analisa as relações entre diferentes classes de ativos: moedas, taxas de juros, commodities e índices. Por exemplo, existem correlações históricas bem conhecidas entre o dólar australiano e os preços do ouro, ou entre o dólar canadense e o petróleo. Desvios temporários nessas correlações podem representar oportunidades de negociação bastante interessantes.

Considerações finais

O sistema de arbitragem matricial incorpora uma profunda ideia filosófica: os mercados tendem ao equilíbrio, mas nunca o alcançam por completo. É justamente nessas oscilações constantes entre o caos e a ordem que se escondem as oportunidades de extração de lucro.

Nosso sistema não tenta prever o movimento futuro dos preços com base em padrões históricos ou fatores fundamentais. Em vez disso, ele cria um modelo matemático de um mercado "ideal" e extrai lucro dos desvios temporários do mercado real em relação a esse modelo. Essa abordagem torna o sistema resistente às mudanças de regimes e tendências de mercado, pois ele não trabalha com tendências ou correções, mas com desequilíbrios relativos, que existem em qualquer ambiente de mercado.

Em uma era em que o aprendizado de máquina e as redes neurais se tornam cada vez mais populares no trading algorítmico, nosso sistema matricial nos lembra da força dos métodos matemáticos clássicos. Ele demonstra que, às vezes, a aplicação elegante de princípios simples pode ser mais eficaz do que modelos complexos que exigem treinamento com grandes volumes de dados.

Colocamos em suas mãos uma ferramenta poderosa que, quando utilizada corretamente, pode se tornar um valioso complemento ao seu arsenal de negociação. Lembre-se de que a chave para o sucesso no trading algorítmico não está apenas na qualidade do próprio algoritmo, mas também na disciplina e na aplicação metódica. Comece com configurações conservadoras, teste cuidadosamente o sistema em diferentes condições de mercado e, gradualmente, adapte-o ao seu próprio estilo e objetivos de negociação.

O sistema de arbitragem matricial não é apenas um robô de negociação, é uma nova forma de enxergar o mercado, que permite ver estrutura e ordem onde outros veem apenas o caos de movimentos aleatórios de preços. Bem-vindo ao mundo do trading matemático!