Redes neurais em trading: Modelos híbridos de sequências de grafos (GSM++)

Nos últimos anos, os transformadores de grafos, adaptados de aplicações em processamento de linguagem natural e visão computacional, têm recebido atenção especial. A capacidade deles de modelar dependências de longo alcance e lidar de forma eficaz com estruturas financeiras irregulares os torna uma ferramenta promissora para tarefas como previsão de volatilidade, detecção de anomalias de mercado e construção de estratégias de investimento otimizadas. No entanto, os transformadores clássicos enfrentam uma série de problemas fundamentais, incluindo alto custo computacional e dificuldade de adaptação a estruturas de grafos desordenadas.

Os autores do trabalho "Best of Both Worlds: Advantages of Hybrid Graph Sequence Models" propõem um modelo unificado de sequências de grafos GSM++, que combina os pontos fortes de diferentes arquiteturas para criar um método eficiente de representação e processamento de grafos. Ele é baseado em três etapas principais: tokenização do grafo, codificação local dos nós e codificação global das dependências. Essa abordagem permite considerar tanto as conexões locais quanto as globais do sistema financeiro, tornando o modelo universal e aplicável a uma ampla gama de tarefas.

O elemento-chave do modelo proposto é o método desenvolvido de tokenização hierárquica de grafos, que possibilita transformar os dados de mercado em uma representação sequencial compacta, preservando suas características topológicas e temporais. Diferente dos métodos tradicionais de codificação de séries temporais, essa abordagem melhora a qualidade da extração de características e simplifica o processamento de grandes volumes de dados de mercado. A combinação da tokenização hierárquica com uma arquitetura híbrida, que inclui mecanismos de transformadores e modelos recorrentes, permite alcançar resultados superiores em diferentes tarefas. Isso torna o método proposto uma ferramenta eficaz para lidar com dados financeiros complexos.

Pesquisas empíricas e análises teóricas realizadas pelos autores do framework GSM++ mostram que o modelo proposto não apenas concorre com os transformadores de grafos tradicionais, mas também os supera em várias características essenciais.

Algoritmo GSM++

O modelo unificado de sequências de grafos representa uma abordagem conceitual que inclui três etapas principais: tokenização, codificação local e codificação global. Esse método permite representar e analisar de forma eficiente estruturas de grafos complexas, o que é especialmente importante no contexto dos mercados financeiros. Sistemas de mercado complexos, que envolvem muitos participantes e interações, exigem o uso de ferramentas de modelagem poderosas, capazes de identificar dependências não lineares e correlações ocultas.

Tokenização desempenha um papel fundamental na transformação da estrutura do grafo em uma representação sequencial, necessária para o processamento de dados com o uso de modelos de sequências. Distinguem-se os seguintes métodos principais de tokenização: tokenização de nós ou arestas, e tokenização de subgrafos. A escolha do método de tokenização exerce grande influência sobre a eficiência do modelo, pois determina quão completamente a informação estrutural do grafo será preservada e quais características da sua organização serão consideradas na análise posterior.

A tokenização de nós ou arestas pressupõe que o grafo seja tratado como uma sequência de elementos correspondentes, sem levar em conta suas inter-relações. Para preservar a informação estrutural, é necessário um codificador posicional ou estrutural adicional. A principal desvantagem desse método é sua alta complexidade computacional, já que o comprimento da sequência corresponde ao número de nós ou arestas, o que dificulta o treinamento dos modelos. No entanto, esse método pode ser útil em situações em que é necessário considerar informações detalhadas sobre cada elemento do sistema, como na construção de estratégias individuais para ativos com base em suas características microscópicas. No contexto do trading de alta frequência, essa abordagem permite analisar com maior precisão o impacto das flutuações de curto prazo do mercado e identificar padrões de negociação anômalos.

A tokenização de subgrafos possibilita a redução dos custos computacionais ao representar o grafo como sequências de subgrafos, aumentando a capacidade do modelo de considerar a estrutura local. Essa abordagem é especialmente útil em aplicações financeiras, como na análise de modelos de negociação, em que os subgrafos podem corresponder a clusters de ativos relacionados ou a grupos de investidores. As interações entre ativos frequentemente apresentam uma natureza oculta de rede, e o uso de subgrafos permite revelar padrões de mercado persistentes, o que é fundamental em tarefas de investimento em portfólio, avaliação de liquidez e estratégias de arbitragem.

Cada um dos métodos de tokenização possui suas vantagens e limitações, portanto a escolha do método específico depende da natureza da tarefa. Em alguns casos, abordagens combinadas, que unem as propriedades de ambas as estratégias de tokenização, permitem alcançar um melhor equilíbrio entre a precisão da representação dos dados e a eficiência computacional.

Com base nessas ideias, os autores do framework GSM++ propuseram um algoritmo de tokenização hierárquica, fundamentado na clusterização de nós por similaridade (Hierarchical Affinity Clustering — HAC).

O algoritmo começa considerando cada vértice do grafo como um cluster separado. Em seguida, a cada etapa, dois clusters são unidos pelo aresta "menos custosa", calculada a partir da similaridade de suas codificações. Esse processo continua até que todo o grafo seja unificado em um único cluster. O resultado é uma árvore hierárquica, onde a raiz representa o grafo inteiro e as folhas correspondem aos nós originais.

Essa abordagem tem duas vantagens importantes. Primeiro, ela organiza os nós de modo que elementos semelhantes fiquem mais próximos uns dos outros, o que melhora a representação do grafo nos modelos. Segundo, ela possibilita a codificação dos grafos em diferentes níveis de detalhamento, permitindo uma análise flexível da estrutura. Foram desenvolvidas duas variantes de tokenização: a travessia em profundidade (DFS) e a travessia em largura (BFS). O método DFS gera sequências de nós que refletem sua posição hierárquica. Já o método BFS cria sequências em que os nós são ordenados de forma que elementos semelhantes estejam próximos entre si.

A metodologia de tokenização proposta preserva a estrutura local do grafo e funciona de forma eficiente com modelos recorrentes, especialmente em tarefas que exigem a análise da conectividade global.

Adicionalmente, é utilizado o método de codificação posicional hierárquica, que leva em conta os caminhos mínimos entre os nós e sua posição dentro da hierarquia dos clusters. Experimentos demonstraram que esse tipo de codificação melhora a qualidade da representação dos grafos.

Como, dependendo da estrutura do grafo e da tarefa a ser resolvida, diferentes nós podem exigir diferentes métodos de tokenização, foi proposto o método Mix of Tokenization (MoT). Ele permite que cada nó utilize o método de codificação mais adequado, escolhendo os tokenizadores ótimos e combinando suas representações.

Após a etapa de tokenização, os dados são transformados em uma representação vetorial com o objetivo de explorar as características locais do grafo. Nesse estágio, são mais comumente utilizadas redes neurais convolucionais em grafos (GNN), pois elas identificam de maneira eficiente as dependências locais entre os nós. No contexto dos mercados financeiros, esse passo auxilia na análise das correlações entre ativos, na detecção de anomalias locais e na construção de previsões baseadas em dados de microestrutura. Graças à sua adaptabilidade e à capacidade de extrair padrões complexos, as redes neurais em grafos são aplicadas tanto na automação do trading quanto na previsão da volatilidade do mercado.

O codificação global desempenha um papel crucial no estudo das dependências de longo prazo dentro do grafo. Nessa etapa, aplica-se a codificação sequencial para identificar relações complexas entre os elementos da estrutura. Em aplicações financeiras, isso possibilita modelar tendências macroeconômicas, analisar os impactos de fatores globais sobre os mercados e construir estratégias fundamentadas na interconexão profunda dos dados. Tendências de longo prazo em dados financeiros, como os efeitos da política monetária ou das crises econômicas globais, exigem o uso de algoritmos robustos, capazes de capturar dependências complexas em diferentes horizontes temporais.

Ao escolher o modelo de sequência para o aprendizado em grafos, surge a questão: qual modelo será o mais eficiente? De acordo com a abordagem adotada, é possível combinar diferentes codificadores de sequência com distintos métodos de tokenização, gerando diversas arquiteturas potenciais. No entanto, ainda não há uma compreensão clara sobre quais delas são mais adequadas para tarefas específicas em grafos.

As tarefas de contagem consistem em determinar a quantidade de nós de um determinado tipo dentro do grafo. Modelos que utilizam mecanismos de atenção sem dependências causais não conseguem resolver essas tarefas corretamente. Surge, então, a questão: poderiam os modelos recorrentes, que consideram a ordem, solucionar esse problema?

Verifica-se que, se a largura do modelo recorrente corresponder ao número de diferentes classes de nós, ele é capaz de contar sua quantidade com precisão. Isso confirma a eficácia dos modelos recorrentes em tarefas nas quais a estrutura sequencial tem mais relevância do que a própria topologia do grafo.

Algumas tarefas em grafos, como o raciocínio algorítmico, exigem a obediência rigorosa à ordem dos nós. Os modelos de sequência modernos, em sua maioria, utilizam dependências causais, e isso precisa ser considerado ao integrá-los em modelos de grafos. Pesquisas mostram que o excesso de compressão da informação pode levar à perda de representatividade. Em modelos recorrentes, a sensibilidade aos dados de entrada diminui à medida que aumenta a distância entre os elementos, enquanto nos transformadores ela permanece constante. No entanto, ambos os modelos estão sujeitos ao colapso das representações com o aumento da profundidade.

A informação localizada no início da sequência tem mais chances de ser preservada. Isso gera um efeito em forma de U, no qual os tokens posicionados no começo e no fim da sequência mantêm melhor seu significado em comparação com os tokens do meio. Esse comportamento é observado tanto em transformadores quanto em modelos recorrentes. Por esse motivo, ao organizar os nós em sequência, é importante posicionar os elementos relevantes próximos uns dos outros para reforçar sua influência mútua.

As tarefas relacionadas à determinação da conectividade do grafo exigem uma análise global de sua estrutura. A conectividade pode ser tratada como um problema de classificação binária. Pesquisas mostram que transformadores com determinada profundidade e tamanho de embeddings conseguem resolver essas tarefas de forma eficiente. Entretanto, modelos recorrentes e transformadores com atenção limitada requerem uma quantidade significativamente maior de parâmetros ou maior profundidade para atingir resultados equivalentes.

Os modelos recorrentes apresentam maior eficiência quando os dados possuem uma ordem natural e a tokenização leva em consideração a estrutura do grafo. Um parâmetro essencial é a localidade do nó, que define a distância máxima entre vértices vizinhos. Para grafos com localidade restrita, pode-se construir um modelo recorrente compacto, capaz de determinar a conectividade. No entanto, transformadores com número fixo de parâmetros não conseguem lidar de forma eficaz com essas tarefas.

Ao escolher o modelo, é fundamental compreender os compromissos que surgem ao aplicá-los em tarefas de análise de grafos. A avaliação de diferentes arquiteturas permite destacar alguns pontos principais:

1. Transformadores demonstram alta eficiência na resolução de tarefas de conectividade em grafos utilizando um número mínimo de parâmetros. Eles são especialmente úteis quando o grafo apresenta uma estrutura complexa e exige processamento paralelo. A capacidade de gerar representações dependentes de contexto os torna uma ferramenta poderosa para a análise de redes e grafos complexos.
2. Redes neurais recorrentes (RNN) funcionam bem em grafos onde as conexões entre os vértices possuem uma estrutura claramente localizada. Nesses casos, elas demandam menos parâmetros e cálculos, tornando-se mais eficientes em termos de energia e adequadas para lidar com dados em fluxo contínuo.
3. Modelos híbridos, que combinam RNN e transformadores, permitem unir as vantagens de ambas as arquiteturas. Eles oferecem um equilíbrio entre a complexidade computacional e a precisão das previsões, sendo especialmente úteis em tarefas que exigem tanto contexto global quanto detalhes locais.
4. Modelos de espaço de estados mostram alta eficácia em situações em que a ordem estrita dos elementos é fundamental. Eles possuem propriedades de memória de longo prazo, o que os torna valiosos para a análise de séries temporais e o modelamento de sequências de ações em sistemas baseados em agentes.
5. Atenção esparsa reduz os custos computacionais dos transformadores, sobretudo ao trabalhar com grafos de grande escala. Contudo, para que seja utilizada de forma eficiente, é necessário desenvolver mecanismos adicionais capazes de identificar as conexões mais relevantes entre os vértices, o que pode aumentar a complexidade da implementação do modelo.

Assim, a escolha do modelo depende da estrutura dos dados brutos e dos recursos computacionais disponíveis. Os transformadores são adequados para grafos complexos com dependências globais bem definidas, RNN, são ideais para sequências localizadas, enquanto os modelos de espaço de estados funcionam melhor em tarefas que exigem uma ordem estrita de execução das operações. As abordagens híbridas permitem equilibrar a eficiência computacional e a precisão das previsões, tornando-se uma escolha versátil para muitas aplicações práticas.

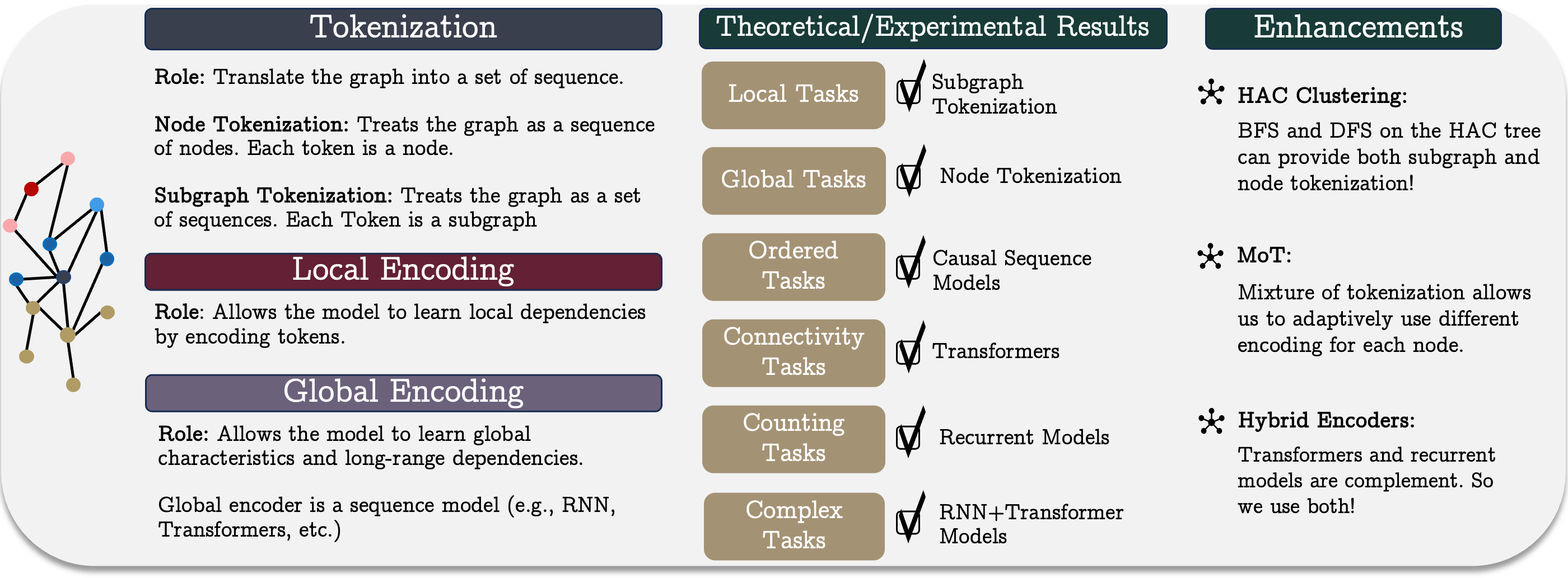
Com base nos resultados da análise realizada no trabalho dos autores, foi apresentado o framework GSM++, que inclui a tokenização hierárquica dos nós por similaridade, redes neurais convolucionais em grafos como codificador local e um codificador global híbrido, que contém os módulos Mamba e Transformer.

Implementação em MQL5

Após a análise dos aspectos teóricos dos métodos propostos pelos autores do framework GSM++, passamos à parte prática do nosso trabalho. Nesta seção, concentramos nossa atenção na implementação de nossa própria visão dos métodos estudados, utilizando os recursos e as possibilidades oferecidas pela linguagem de programação MQL5.

Vale ressaltar que, embora mantenhamos a concepção geral estabelecida nas abordagens originais, nossa implementação será significativamente diferente nos detalhes.

Antes de tudo, em nossa versão, optamos por não utilizar a clusterização hierárquica baseada em similaridade (HAC). Afinal, acredito que você concorda que as velas formadas no gráfico de um instrumento financeiro são objetos dinâmicos e em constante mudança, que não podem ser padronizados de forma simples. Sua análise e clusterização representam um processo complexo e multifacetado, que exige uma abordagem muito mais profunda e abrangente.

Portanto, assim como anteriormente, utilizaremos módulos treináveis para a tokenização das representações dos bares analisados. Essa abordagem nos permite manter a flexibilidade e a adaptabilidade do modelo em condições de dados reais, o que é especialmente importante no trabalho com os mercados financeiros.

No entanto, em nossa implementação aplicamos o algoritmo de tokenização mista (MoT), mas em uma forma ligeiramente modificada e adaptada às especificidades da nossa tarefa. Os autores do framework GSM++ sugerem o uso de um modelo treinável de clusterização para selecionar os dois algoritmos de tokenização mais relevantes e, em seguida, somar seus valores para obter a representação final. Já nós, diferentemente dessa proposta, iremos preparar quatro variantes distintas de tokens para cada barra e combinar seus valores por meio do algoritmo Attention Pooling, emprestado do framework R-MAT.

Esse método possibilita uma melhora significativa na qualidade da análise, pois considera um maior número de aspectos dos dados e permite destacar com mais precisão as informações relevantes. Em nosso trabalho, para a tokenização, utilizaremos as seguintes variantes:

• Tokenização de nós — neste caso, cada barra será tratada como um elemento individual de análise, com o qual o modelo trabalhará para extrair informações.
• Tokenização de arestas — aqui, o foco estará nas interações entre duas barras vizinhas, permitindo identificar conexões relevantes entre diferentes partes dos dados.
• Tokenização de subgrafos — esse método nos permitirá formar estruturas mais complexas, levando em conta as relações entre múltiplos bares dentro de um mesmo grupo.
• Tokenização de subgrafos de sequências unitárias individuais — essa variante prevê uma análise mais detalhada das sequências estruturais, possibilitando o processamento dos dados em um nível mais profundo.

A aplicação dos métodos de tokenização escolhidos possibilita considerar tanto os elementos isolados quanto suas inter-relações, o que eleva de forma significativa a qualidade da representação das informações de cada barra e melhora a eficiência geral do modelo. A unificação de todos esses tokens através do Attention Pooling permitirá que o modelo se adapte de maneira flexível e concentre sua atenção nas características mais relevantes, otimizando o processo de tomada de decisão.

Para implementar essa solução, criaremos um novo objeto CNeuronMoT, cuja estrutura é apresentada a seguir.

class CNeuronMoT  :  public CNeuronMHAttentionPooling
  {
protected:
   CNeuronConvOCL             cNodesTokenizer;
   CNeuronConvOCL             cEdgesTokenizer;
   CNeuronConvOCL             cSubGraphsTokenizer;
   CLayer                     cUnitarSubGraphsTokenizer;
   CNeuronBaseOCL             cConcatenate;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoT(void){};
                    ~CNeuronMoT(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Como objeto pai, utilizamos neste caso o objeto CNeuronMHAttentionPooling, no qual já está implementado o algoritmo Attention Pooling, previsto para ser utilizado na saída do módulo, a fim de combinar as diferentes variantes de tokenização. Essa abordagem apresenta várias vantagens essenciais.

Em primeiro lugar, o uso da classe pai nos permite evitar redundância de código, eliminando a necessidade de reimplementar o módulo Attention Pooling em outros objetos ou componentes. Em vez disso, integramos uma versão já pronta e otimizada desse algoritmo, mantendo um alto nível de abstração e facilitando a manutenção do código.

Em segundo lugar, a execução de todas as operações de unificação e processamento dos tokens se resume à chamada do funcional já implementado na classe pai. Isso simplifica de maneira significativa a arquitetura do sistema e contribui para uma utilização mais eficiente dos recursos, uma vez que a classe pai já contém todos os métodos e algoritmos necessários para o trabalho com atenção. Assim, minimizamos a duplicação de funcionalidades e aumentamos a modularidade e a escalabilidade do sistema.

Na estrutura do novo objeto, vemos o já conhecido conjunto de métodos virtuais sobrescrevíveis, que constituem uma parte essencial da implementação do nosso modelo. Esses métodos nos oferecem flexibilidade e a possibilidade de personalizar o comportamento do objeto de acordo com as especificidades da tarefa.

Além disso, a classe contém alguns objetos internos que desempenham um papel fundamental na construção do nosso algoritmo. A função de cada um deles será explicada com mais detalhes no processo de implementação dos métodos da classe, onde analisaremos de forma aprofundada sua operação e interação.

Todos os objetos internos são declarados estaticamente, o que nos permite deixar o construtor e o destrutor da classe vazios. Já a inicialização de todos os objetos declarados e herdados é realizada no método Init.

bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint units_count,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch))
      return false;

Nos parâmetros do método recebemos constantes que descrevem a dimensionalidade dos dados brutos. Aqui, é importante destacar que, nesta implementação, espera-se que os resultados sejam obtidos na mesma dimensionalidade. Por isso, os parâmetros recebidos são imediatamente passados ao método de mesmo nome da classe pai, na qual já estão implementadas as inicializações de todos os objetos herdados e interfaces.

Após a execução bem-sucedida das operações do método da classe pai, passamos à inicialização dos novos objetos declarados. O primeiro deles é o objeto de tokenização de nós. Sua função é desempenhada por uma camada convolucional, na qual a janela de convolução, seu passo e o número de filtros possuem os mesmos valores, equivalentes ao vetor que descreve um elemento da sequência.

Essa abordagem nos permite trabalhar de forma eficiente com sequências de dados, onde cada elemento (ou nó) é representado como um vetor que corresponde a determinadas características. Por meio da convolução, conseguimos extrair importantes características locais, que servirão de base para o processamento e a tokenização subsequente dos dados. A igualdade dos valores desses parâmetros com o vetor de descrição do elemento possibilita a integração harmoniosa da camada convolucional à estrutura geral do modelo, garantindo sua eficiência e consistência em todas as etapas do processamento.

int index = 0;
if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cNodesTokenizer.SetActivationFunction(SoftPlus);

Em seguida, inicializamos a camada convolucional de tokenização de arestas. Diferente do objeto anterior, aqui utilizamos uma janela de convolução equivalente a dois elementos completos da sequência analisada. Esse método permite modelar as interações e conexões entre elementos vizinhos, o que é essencial para uma análise mais profunda da estrutura dos dados.

index++;
if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cEdgesTokenizer.SetActivationFunction(SoftPlus);

Vale destacar que o uso de uma janela de convolução dupla com passo unitário, em termos gerais, leva à redução da sequência em 1 elemento. No entanto, a posterior combinação dos tokens exige a compatibilidade da dimensionalidade dos tensores em todas as etapas. Por essa razão, não alteramos o comprimento da sequência em nossa camada convolucional, o que implica no preenchimento dos elementos ausentes no final da sequência com valores nulos.

De maneira análoga, inicializamos a camada convolucional de tokenização de subgrafos, ampliando a janela de convolução para 3 elementos da sequência, mantendo todos os demais parâmetros inalterados.

index++;
if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cSubGraphsTokenizer.SetActivationFunction(SoftPlus);

Para todos os níveis de tokenização aplicamos a função de ativação SoftPlus. Essa escolha é motivada por uma série de vantagens que essa função oferece. SoftPlus é uma função suave e monótona, que evita variações bruscas e melhora a estabilidade do treinamento. Diferentemente do ReLU, SoftPlus não possui transição abrupta de zero para valores positivos, o que ajuda a prevenir o problema dos chamados "neurônios mortos".

Além disso, SoftPlus tem a propriedade de que sua derivada é sempre positiva, o que contribui para uma boa diferenciabilidade e atualizações mais suaves dos pesos durante a propagação reversa do erro. Isso é particularmente importante em redes neurais complexas, nas quais são necessários ajustes precisos e estáveis dos parâmetros em todas as etapas do aprendizado.

O uso do SoftPlus em todos os níveis de tokenização permite criar um modelo mais flexível e estável, garantindo fluidez e robustez no seu funcionamento, o que é crucial ao lidar com o processamento e a análise de sequências de dados complexas.

A geração de tokens em termos de sequências unitárias do conjunto multivariado de séries temporais analisado, entretanto, segue um procedimento um pouco diferente. Para realizar esse funcional, precisamos executar algumas operações sequenciais, que serão reunidas em um modelo interno, armazenando os ponteiros para os objetos em um array dinâmico chamado cUnitarSubGraphsTokenizer.

Primeiro, preparamos um array dinâmico e declaramos variáveis locais para o armazenamento temporário dos ponteiros dos objetos.

cUnitarSubGraphsTokenizer.Clear();
cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL);
CNeuronConvOCL *conv = NULL;
CNeuronTransposeOCL *transp = NULL;

Para facilitar o trabalho com sequências unitárias individuais, realizamos a transposição dos dados brutos.

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }

Em seguida, utilizamos a camada convolucional para a geração de tokens de subgrafos. Aqui, assim como anteriormente, analisamos subgrafos compostos por 3 elementos. A única diferença é que, neste caso, cada elemento é representado por um único valor, e o número de variáveis analisadas corresponde à quantidade de sequências unitárias em estudo.

index++;
conv = new CNeuronConvOCL();
if(!conv ||
   !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(conv))
  {
   delete conv;
   return false;
  }
conv.SetActivationFunction(SoftPlus);

Esse método nos possibilita analisar de forma mais detalhada as transições e os padrões dentro das sequências unitárias individuais.

Os valores obtidos são então transpostos de volta ao estado original.

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }
transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

E o "toque final" consiste na inicialização do objeto responsável pela concatenação dos resultados gerados pelos diferentes métodos de tokenização.

   index++;
   if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch))
      return false;
   cConcatenate.SetActivationFunction(None);
//---
   return true;
  }

É importante destacar que desativamos intencionalmente a função de ativação para o objeto de concatenação de dados. Naturalmente, em nossa implementação utilizamos as mesmas funções de ativação para todos os objetos de geração de tokens, e poderíamos tê-la transferido para o objeto de concatenação, o que simplificaria ligeiramente o algoritmo de distribuição do gradiente do erro durante a propagação reversa. No entanto, de forma geral, admitimos a possibilidade de uso de diferentes funções de ativação para cada objeto de geração de tokens. Nesse cenário, a atribuição de uma função de ativação ao objeto de concatenação apenas distorceria os dados. 

Ao final do método de inicialização, retornamos o resultado lógico da execução das operações ao programa chamador e encerramos sua execução.

A próxima etapa do nosso trabalho é a construção do método de propagação para frente feedForward. Seu algoritmo é bastante simples.

bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cNodesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cEdgesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cSubGraphsTokenizer.FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto que contém os dados brutos, o qual é imediatamente repassado aos métodos de mesmo nome dos objetos internos responsáveis pelos diferentes níveis de tokenização.

Para a geração de tokens no contexto das sequências unitárias, estruturamos um laço de iteração sobre os objetos do modelo interno.

   CNeuronBaseOCL *prev = NeuronOCL, *current = NULL;
   for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++)
     {
      current = cUnitarSubGraphsTokenizer[i];
      if(!current ||
         !current.FeedForward(prev))
         return false;
      prev = current;
     }

Todos os tokens gerados são reunidos em um único tensor, compatível com a dimensionalidade dos elementos da sequência analisada.

   if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(),
              cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(),
              cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits))
      return false;

O objeto resultante é então transmitido ao método de mesmo nome da classe pai, responsável por produzir a representação final do grafo.

   return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
  }

O resultado lógico da execução das operações é retornado ao programa chamador, encerrando a execução do método.

Por trás da aparente simplicidade do método de propagação para frente, existe o uso paralelo de 4 fluxos de informação, o que traz certas dificuldades na organização do processo de distribuição do gradiente do erro. Seu algoritmo é implementado no método calcInputGradients.

bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método, recebemos um ponteiro para o mesmo objeto de dados brutos. Só que, desta vez, precisamos transmitir a ele o gradiente do erro, correspondente ao grau de influência dos dados brutos sobre o resultado do modelo. Esses dados só podem ser passados a um objeto válido, portanto a primeira operação do método consiste em verificar a validade do ponteiro recebido.

Em seguida, distribuímos o gradiente do erro, recebido dos objetos subsequentes do modelo, até o nível do objeto de concatenação dos tokens, utilizando os recursos da classe pai.

if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject()))
   return false;

Depois, repassamos os valores obtidos para os fluxos de informação correspondentes.

CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1];
if(!current ||
   !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(),
             cSubGraphsTokenizer.getGradient(), current.getGradient(),
             cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits))
   return false;

Nosso próximo passo é distribuir o gradiente do erro por todos os fluxos de informação.

É importante lembrar que, a partir do objeto de concatenação, recebemos o gradiente do erro ainda não corrigido pela derivada da função de ativação. Portanto, antes de iniciar as operações de cada fluxo, precisamos ajustar os valores de acordo com a derivada da função de ativação correspondente.

Primeiro, distribuímos o gradiente do erro pelo fluxo das sequências unitárias. Inicialmente, verificamos a existência de uma função de ativação e, se necessário, corrigimos os valores obtidos.

if(current.Activation() != None &&
   !DeActivation(current.getOutput(), current.getGradient(),
                 current.getGradient(), current.Activation()))
   return false;

Depois, organizamos um laço de iteração reversa sobre os objetos do modelo interno, chamando sucessivamente seus métodos de mesmo nome.

for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--)
  {
   current = cUnitarSubGraphsTokenizer[i];
   if(!current ||
      !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1]))
      return false;
  }

Em seguida, propagamos o gradiente do erro até o nível dos dados brutos.

if(!NeuronOCL.calcHiddenGradients(current.AsObject()))
   return false;

Nesse estágio, transmitimos o gradiente do erro aos dados brutos apenas por um fluxo. Ainda precisamos conduzir os erros pelos três fluxos restantes.

Para preservar os dados já processados, realizamos a substituição do ponteiro para o buffer de gradientes do erro dos dados brutos.

CBufferFloat *temp = NeuronOCL.getGradient();
if(!NeuronOCL.SetGradient(current.getPrevOutput(), false))
   return false;

E somente quando temos certeza da preservação dos dados anteriores, passamos os gradientes pelos demais fluxos. Nessa etapa, verificamos a presença de funções de ativação e, quando necessário, corrigimos os valores de acordo com a derivada da função de ativação correspondente.

if(cNodesTokenizer.Activation() != None &&
   !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(),
                 cNodesTokenizer.getGradient(), cNodesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

Depois, propagamos o gradiente do erro até o nível dos dados brutos e o somamos aos valores previamente acumulados. Repetimos as mesmas operações para o fluxo seguinte.

if(cEdgesTokenizer.Activation() != None &&
   !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(),
                 cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

if(cSubGraphsTokenizer.Activation() != None &&
   !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(),
                 cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

Após a transmissão bem-sucedida dos gradientes do erro por todos os fluxos de informação, retornamos os ponteiros ao estado inicial e encerramos o método, retornando previamente o resultado lógico das operações ao programa chamador.

   if(!NeuronOCL.SetGradient(temp, false))
      return false;
//---
   return true;
  }

Com isso, concluímos a análise dos algoritmos de construção dos métodos do objeto de tokenização mista adaptativa CNeuronMoT. O código completo desse objeto e de todos os seus métodos pode ser consultado no anexo.
 
Infelizmente, chegamos ao limite do espaço desta publicação, mas nosso trabalho ainda não está concluído. Faremos uma breve pausa e daremos continuidade na próxima parte do artigo.

Considerações finais

Neste artigo, exploramos uma abordagem inovadora para o uso de modelos híbridos de sequências de grafos (GSM++), que combinam a força das estruturas em grafo com a análise sequencial de dados. Esses modelos proporcionam alta precisão em previsão e análise, permitindo processar de maneira eficiente dados financeiros complexos. Além disso, otimizam a utilização de recursos computacionais, o que os torna especialmente valiosos ao lidar com grandes volumes de informação. Um dos principais diferenciais do GSM++ é sua capacidade de adaptação às rápidas mudanças nas condições de mercado.

Na parte prática do nosso trabalho, demos início à implementação da nossa própria visão dos métodos propostos e desenvolvemos o módulo de tokenização mista. No próximo artigo, continuaremos essa construção até sua conclusão lógica, validando a eficiência dos métodos implementados com base em dados históricos reais.

Referências

• Best of Both Worlds: Advantages of Hybrid Graph Sequence Models
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com código de programa em OpenCL