Negociamos opções sem opções (Parte 1): Fundamentos da teoria e emulação por meio de ativos subjacentes

Introdução

O instrumento financeiro chamado opção desperta um interesse cada vez maior entre os participantes das negociações em bolsa. Basta dizer que, nos últimos anos, quando a bolsa de Moscou MOEX realizava competições entre investidores individuais, o LCH, os traders de opções invariavelmente ocupavam posições premiadas na seção de derivativos do concurso. E isso em condições de concorrência elevada durante a realização do evento.

A teoria matemática das opções é relativamente complexa e não trivial para compreensão e cálculos manuais, porém existe um número bastante grande dos chamados calculadores de opções, programas que permitem calcular qualquer combinação de opções. Como regra, negocia-se um conjunto de opções com diferentes parâmetros, as chamadas estruturas de opções. Mas sobre isso, nas próximas partes do artigo.

Neste artigo é descrita a emulação de opções por meio da compra/venda do ativo subjacente. Esse método permite criar (emular) uma opção sintética com quaisquer parâmetros necessários, inclusive inexistentes no mercado real. Por exemplo, criar um instrumento exótico como uma opção sobre uma opção, ou uma opção sobre um spread, bem como outros tipos de ativos subjacentes reais ou sintéticos.

Fundamentos da teoria das opções

• 1. Definições

Opção é um instrumento financeiro derivativo, o chamado derivativo (da palavra inglesa "derivative"), que concede o direito, mas não a obrigação, ao participante das negociações de:

• comprar o ativo subjacente, opção Call
• vender o ativo subjacente, opção Put
  

Para o vendedor da opção, que também é o contraparte do comprador, o acordo não é um direito, mas uma obrigação de realizar a operação, se a opção for Call, vender o ativo subjacente ao comprador, se a opção for Put, comprar o ativo subjacente do comprador, em troca do que ele recebe um prêmio do comprador.

A compra ou venda do ativo subjacente ocorre por um preço fixo em uma data previamente determinada no futuro, a data de expiração, ou antes da data de expiração. Após a execução, expiração, da opção, o participante das negociações recebe em sua conta a quantidade correspondente do ativo subjacente comprado ou vendido, ações, futuros, moeda, no caso de opções com entrega, ou o equivalente em dinheiro, o resultado da execução da opção, no caso de opções liquidadas financeiramente.

• 2. Termos

Ativo subjacente, ação, índice, moeda, mercadoria ou outro instrumento sobre o qual a opção é emitida.

Strike, preço previamente acordado pelo qual o ativo subjacente pode ser comprado ou vendido, também chamado de preço de exercício da opção, da palavra inglesa "strike".

Prêmio, o custo da opção que o comprador paga ao vendedor pela aquisição do direito de comprar ou vender o ativo subjacente por um determinado preço em um determinado momento.

Expiração, data de término da validade da opção, da palavra inglesa "expiration", data até a qual o comprador pode exercer seu direito de compra ou venda do ativo subjacente.

• 3. Tipos de opções

• 3.1. Pela possibilidade de exercício

Americanas, podem ser exercidas em qualquer dia até a expiração, normalmente custam mais caro que as europeias;

Europeias, podem ser exercidas somente na data de expiração;

Bermudas, exercício em datas determinadas.

• 3.2. Pelo tipo de liquidação

Com entrega, entrega do ativo subjacente;

Liquidadas financeiramente, liquidação em dinheiro.

• 3.3. Pelo mercado negociado

De bolsa, padronizadas, negociadas em bolsas, por exemplo, CBOE, MOEX;

De balcão (OTC), condições individuais entre contrapartes.

• 4. A essência do instrumento opção

A opção é um bom meio de hedge, da palavra inglesa hedge, cerca, proteção, ou seja, proteção dos investimentos. O preço da opção, prêmio da opção, determina quanto você está disposto a pagar para eliminar, parcial ou totalmente, o risco. Por exemplo, você decidiu proteger, fazer hedge, de um ativo em rublos contra o risco de valorização do rublo em relação ao dólar americano, por um período de meio ano. Suponhamos que, dentro de seis meses, você precisará de um determinado montante em rublos para uma grande compra.

Uma das opções de hedge é comprar diretamente o próprio ativo subjacente, dólares por rublos. Porém, aqui surgem novos riscos, se nesses seis meses o rublo começar a se fortalecer em relação ao dólar, você perderá na conversão inversa para rublos, possivelmente uma quantia significativa. Por exemplo, a taxa mudou de 100 rublos por dólar para 80 rublos por dólar, o que significa que você perderá 20% do valor inicial em rublos.

A segunda opção de hedge é a compra de uma opção Put sobre o ativo RUB/USD com prazo de expiração de meio ano e strike aproximadamente igual à taxa atual do rublo em relação ao dólar, digamos, 100 rublos por dólar. Pagando o prêmio da opção, poderemos, ao longo de seis meses, vender nossa opção Put e receber o ativo subjacente, rublos, à taxa de 100 rublos por dólar. Mesmo que até lá o rublo se fortaleça para, é assustador imaginar, 50 rublos por dólar. Como resultado, pagaremos apenas o prêmio da opção.

De forma análoga, é possível proteger seu ativo em rublos contra a desvalorização do rublo. Nesse caso, é necessário comprar uma opção Call com strike aproximadamente igual à taxa atual do rublo em relação ao dólar.

• 5. Modelo de opções de Black-Scholes

O modelo de Black-Scholes é uma fórmula matemática desenvolvida em 1973 por Fischer Black, Myron Scholes e, indiretamente, Robert Merton, para o cálculo do preço justo de opções europeias. O preço justo, neste caso, é o preço que satisfaz tanto o comprador quanto o vendedor da opção. Por esse trabalho, Scholes e Merton receberam o Prêmio Nobel de Economia em 1997, Fischer Black faleceu antes e não foi premiado.

Preço, prêmio, da opção Call:

Preço, prêmio, da opção Put:

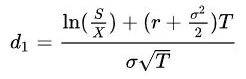
onde:

• S - preço atual do ativo subjacente
• X - preço de strike da opção
• r - taxa de juros livre de risco, capitalizada continuamente
• T - tempo até a expiração, em anos
• N(d) - função cumulativa da distribuição normal padrão
• σ - volatilidade do ativo subjacente

O modelo é construído com base em várias premissas:

1. mercado absolutamente eficiente, ausência de possibilidade de arbitragem;
2. taxa de juros livre de risco, constante e conhecida;
3. volatilidade do ativo subjacente, constante;
4. ausência de dividendos, posteriormente o modelo foi aprimorado;
5. distribuição lognormal dos preços do ativo, os preços não podem ser negativos;
6. tempo contínuo, a negociação ocorre sem interrupções;
7. ausência de comissões e impostos.

As principais desvantagens do modelo decorrem das premissas apresentadas acima:

• o mercado não é eficiente, com certa aproximação apenas os instrumentos mais líquidos podem ser considerados como tal;
• a volatilidade do ativo subjacente muda com muita frequência e de forma contínua para ser considerada constante;
• a distribuição está longe de ser lognormal, os mercados reais possuem "caudas pesadas", riscos de crash, além disso, movimentos bruscos de preços são ignorados;
• não é adequado para opções americanas.

Existem modelos alternativos de precificação de opções que levam em conta alguns dos fatores listados acima:

• modelo de Heston, volatilidade estocástica
• modelo Bayesiano, consideração de macrofatores
• métodos de aprendizado de máquina, redes neurais para previsão de preços de opções.

• 6. "Gregos"

Os chamados "gregos" são indicadores estatísticos da sensibilidade do preço da opção à variação de diferentes parâmetros, preço de strike, volatilidade, preço atual do ativo subjacente, data de expiração e assim por diante. Do ponto de vista matemático, os "gregos" são derivadas parciais da fórmula de Black-Scholes. Conceitualmente, são utilizados os seguintes principais indicadores:

• Delta (Delta), mostra como o valor da opção se altera quando o preço do ativo subjacente muda. É calculada como a razão entre a variação do valor da opção e a variação do valor do ativo. Se o valor da delta for negativo, isso significa que, com o aumento do valor do ativo, o valor da opção irá cair. Para opções Call, a delta é positiva; para opções Put, é negativa. Este é o indicador mais importante, que será utilizado na emulação de opções.
• Gamma (Gamma), mostra como o valor da delta muda quando o preço do ativo subjacente se altera. Essencialmente, é a segunda derivada do preço da opção em relação ao preço do ativo subjacente. Para opções cuja expiração ainda está distante, a gamma é mínima. Seu valor cresce à medida que a data de expiração se aproxima.
• Theta (Teta), mostra como o valor da opção muda em função da proximidade do tempo de expiração. É calculada como a razão entre a variação do valor da opção e a variação do tempo até a expiração. O valor da theta é sempre apresentado como negativo, pois reduz o valor da opção.
• Vega (Vega), mostra como o valor da opção muda quando a volatilidade esperada se altera. É calculada como a razão entre a variação do valor da opção e a variação da volatilidade esperada. O maior valor de vega é observado em opções cujo preço de strike está mais próximo do preço de mercado atual do ativo. Essas opções são as mais sensíveis à variação da volatilidade esperada. O valor da vega diminui à medida que a data de expiração da opção se aproxima.
• Volatilidade implícita (Implied Volatility, IV), um indicador importante que não pertence aos "gregos", mas é utilizado na fórmula de Black-Scholes. É calculada com base em negociações reais de contratos de opções específicas. Além disso, a volatilidade pode ser calculada de diferentes formas: pelo método de ajuste à fórmula de Black-Scholes, apenas no strike central, ponderando-a por diferentes strikes, com ou sem consideração das ofertas, e assim por diante. Na emulação, partiremos do pressuposto de que o ativo subjacente não possui opções reais nem ofertas sobre elas, ou que elas não estão disponíveis para nós.

Portanto, em vez da volatilidade implícita, utilizaremos a volatilidade histórica (Historical Volatility, HV), calculada para os intervalos: dia, semana, mês. O intervalo depende do período de tempo até a expiração da opção. Do ponto de vista matemático, a volatilidade histórica é um indicador estatístico da dispersão dos dados em relação ao seu valor médio ao longo de um determinado período de tempo. Ela é calculada como o desvio padrão multiplicado pela raiz quadrada do número de períodos de tempo T. Para os nossos objetivos, é adequado utilizar os períodos de tempo dia, semana e mês.

Emulação de opções

• 1. Necessidade de emulação

A necessidade de emulação é ditada por vários fatores, listados abaixo:

• Ausência física de uma opção sobre o ativo subjacente desejado. Por exemplo, na corretora de criptomoedas Bybit são negociadas opções apenas sobre três ativos spot: BTC, ETH e SOL. Além disso, até recentemente, na bolsa de Moscou MOEX não existiam opções sobre ações.
• Tipo de opção inadequado quanto ao tempo de expiração. Por exemplo, na MOEX, para opções sobre ações existem apenas opções europeias, com execução somente no último dia. Isso restringe o leque de estratégias de negociação com opções, eliminando as especulativas.
• Liquidez insuficiente para abertura ou encerramento antecipado de opções. Na MOEX, apenas opções sobre os futuros ou ações mais líquidos permitem abrir ou fechar rapidamente uma posição em opções. Isso pode levar tanto à perda de lucro quanto à obtenção de um prejuízo não sistêmico. Além disso, esse fator dificulta o uso de estratégias de scalping, nas quais a velocidade de abertura e fechamento das posições em opções é decisiva.

• 2. Comparação entre opções reais e virtuais

Critério de comparação	Opção real	Opção virtual
Pagamento do custo, prêmio, na compra da opção	Há pagamento	Não há pagamento
Recebimento de prêmio na venda da opção	Há prêmio	Não há prêmio
Existência de decaimento temporal da opção à medida que a data de expiração se aproxima	Há decaimento temporal	Não há decaimento temporal
Influência de "aftershocks" e do contexto de notícias	Não influencia no caso geral	Influencia a qualidade da emulação de opções
Flexibilidade na escolha do tempo de expiração	Inexistente, definido pela bolsa	Definido pelo usuário
Possibilidade de usar tempos curtos de expiração, um dia, algumas horas, dezenas de minutos	Inexistente	Qualquer tempo de expiração
Necessidade de monitoramento constante das posições	Não é necessário no caso geral	É necessário monitoramento constante

Em negrito estão destacadas as qualidades positivas de cada variante. Como se pode ver na tabela, ambas as variantes de opções possuem seus pontos positivos e seus pontos negativos. Como era de se esperar, não existe nada perfeito em nosso mundo real.

• 3. Requisitos das condições de negociação para o uso da emulação de opções

Como para a emulação de opções são utilizadas operações com o ativo subjacente, é desejável minimizar comissões e outros custos operacionais de negociação, tais como: slippage, spreads elevados, swaps para posições abertas. Todos eles pioram a qualidade da opção virtual, especialmente em períodos curtos de expiração. No restante, não há requisitos especiais quanto às condições de negociação.

Para afirmar que uma posição no ativo subjacente é equivalente a uma opção, é necessário compreender que, em cada momento no tempo, a opção possui um determinado valor de delta (Delta). Se a quantidade do ativo subjacente coincidir com a delta da opção, então essas posições serão equivalentes naquele momento específico, ou seja, gerarão o mesmo lucro ou prejuízo.
 
Vamos analisar com mais detalhes como construir a emulação.

Suponha que seja necessário comprar ou vender uma opção ou várias opções sobre um mesmo ativo subjacente. Primeiro, vamos calcular, isso pode ser feito, por exemplo, no site da bolsa de Moscou MOEX, se estivermos falando de opções negociadas em bolsa, a delta dessa posição como se ela tivesse sido criada por meio de opções.
Consideremos um exemplo. Suponha que planejamos comprar 100 opções Call dentro do dinheiro para participar da alta com alavancagem e risco limitado. A delta de uma opção é igual a 0.5. A delta total do portfólio de 100 opções será igual a 0.5 * 100 = 50. Para criar um portfólio equivalente, basta comprar 50 unidades do ativo subjacente. Então, em ambos os portfólios, a delta coincidirá e será igual a 50.

No entanto, ao comprar uma opção, em geral, pode-se esquecê-la até a própria expiração. Já com a emulação, tudo é um pouco diferente. Aqui, ao longo de todo o seu período de vida, é necessário garantir a equivalência com o portfólio de opções, pois o preço de mercado está mudando o tempo todo. Portanto, serão necessários ajustes, rebalanceamentos, ou seja, compra ou venda da quantidade faltante ou excedente de unidades do ativo subjacente. Com que frequência e em que momento realizar os rebalanceamentos? Isso pode ser feito com um determinado passo de tempo, uma vez por hora, uma vez por dia, ou com um passo baseado na delta, quando a delta variar em +/-1, +/-2 e assim por diante. Também existem outras variantes.

Vamos continuar com o nosso exemplo. Foi criado um portfólio de 50 unidades compradas do ativo subjacente, ou seja, equivalente a 100 opções Call. Ao final do dia, o mercado subiu um pouco, e a delta de uma opção Call aumentou para 0.53, a delta do portfólio aumentou para 0.53 * 100 = 53. Então, para manter a equivalência, devemos comprar mais 3 unidades do ativo subjacente. Se no dia seguinte as cotações recuarem abaixo do nível de entrada, e a delta da opção diminuir, digamos, para 0.48, teremos que vender 5 unidades do ativo subjacente. Dessa forma, a equivalência dos portfólios é mantida.

Por que o perfil da posição de opção emulada irá repetir o perfil das opções compradas? Porque, quando o preço sobe, a delta aumenta, e o trader compra mais ativo subjacente. Quanto mais a opção entra "dentro do dinheiro", maior será a quantidade de unidades do ativo subjacente que teremos no portfólio, passando assim a obter lucro com a alta, de forma semelhante a uma opção Call comprada. Se o preço cair, passaremos a vender o ativo subjacente, reduzindo a quantidade de unidades até zero. Com isso, garante-se a limitação das perdas em caso de queda, assim como ocorre com uma opção Call.

Agora, com mais detalhes sobre o rebalanceamento. Este é o ponto principal na emulação. É dessas operações que, de fato, depende o resultado final. As correções devem ser realizadas de forma sistemática, seguindo um algoritmo previamente adotado; caso contrário, são possíveis prejuízos imprevistos. Por exemplo, se a cotação subir bruscamente de uma delta 0.5 para uma delta 0.6 e o rebalanceamento for perdido, isto é, não forem compradas 10 unidades do ativo subjacente, então o ativo subjacente, no pior dos casos, pode não retornar a essa faixa até a expiração. No dia seguinte, a delta pode já ser 0.65, e seremos obrigados a comprar 15 unidades com delta 0.65, em vez de comprar 10 unidades com delta 0.6 e 5 com delta 0.65. Naturalmente, é necessário utilizar um robô de negociação para realizar a emulação da opção.

O cenário ideal é quando o futuro é negociado 24 horas por dia, permitindo realizar correções de forma contínua. No entanto, correções muito frequentes podem levar a prejuízos adicionais que, à primeira vista, parecem absolutamente desnecessários. Se o mercado, em termos de delta, se moveu ao longo de três dias da seguinte forma: 0.50, 0.55, 0.50, então, seguindo o algoritmo de rebalanceamento, precisaremos primeiro comprar 5 unidades com delta 0.55 e, no dia seguinte, vender 5 unidades com delta 0.50, com o que, naturalmente, fixaremos prejuízos. Portanto, se por algum motivo o trader tiver perdido a correção no segundo dia, nada de grave terá acontecido, o preço não mudou. Mas o mercado também pode se mover de forma monotônica para um dos lados, por isso o rebalanceamento precisa ser feito regularmente.

A desvantagem dos “rebalanceamentos por tempo” é a presença de movimentos bruscos de preço, quando o mercado cresce ou cai vários por cento em um curto intervalo de tempo. Isso é combatido com sucesso pelos métodos de correção “por passo de delta”, porém, às vezes, também ocorrem falhas neles, quando fisicamente não é possível realizar a operação ao preço planejado devido a um movimento extremamente rápido e a um grande slippage. Nesses casos, os robôs de negociação ajudam, pois “ajustam” a posição de forma mais rápida e precisa durante os “espasmos” do mercado.

É evidente que, com flutuações do ativo subjacente para cima e para baixo, nós, com nossos rebalanceamentos, apenas fixamos a cada vez um pequeno prejuízo. De fato, no exemplo da compra de uma opção Call, o trader compra o ativo subjacente caro e vende barato. Se o ativo subjacente, ao longo de toda a vida da posição, não sair do lugar, a estratégia será deficitária devido à manutenção da delta. Mas, ao comprar uma opção, também se paga um prêmio por ela. E se ela não entrar “dentro do dinheiro”, o prêmio igualmente se perde. O decaimento temporal corrói a opção; na emulação, os prejuízos podem ser gerados pelo rebalanceamento.

As compras e vendas do ativo subjacente para manter a delta são pequenas operações deficitárias, cujo prejuízo total ao longo de todo o período é aproximadamente igual ao prêmio da opção. É claro que o prêmio depende da volatilidade IV no momento da compra. Quanto maior a IV, mais, segundo os traders, o mercado tende a “oscilar”. Quanto maior a IV, mais cara é a opção. O mesmo ocorre com a emulação: quanto mais frequentemente o mercado oscilou, mais volátil ele foi, mais cara acabou sendo a emulação. Quanto mais intensas forem as oscilações, maiores serão as perdas, de forma semelhante ao aumento do custo da opção com o crescimento da volatilidade.

A emulação se justifica se, ao longo da vida da opção, o ativo subjacente apresentou baixa volatilidade, e raramente foi necessário realizar rebalanceamentos, ou o tamanho das perdas decorrentes deles foi pequeno. Nesse caso, emular a opção é mais vantajoso do que comprá-la na bolsa com uma IV elevada. Afinal, a volatilidade realizada ao longo da vida do portfólio acabou sendo muito menor do que a IV. Aqui também é válida a analogia com uma opção vendida. Por exemplo, se você vendeu uma opção com volatilidade de 52%, e se realiza uma volatilidade de 60%, então, devido à manutenção da neutralidade em delta, o resultado será negativo. Se, por outro lado, se realizar uma volatilidade de 45%, a venda se torna vantajosa, pois os custos de rebalanceamento serão menores do que o prêmio.

A emulação perde para a compra direta da opção se a volatilidade realizada superar a IV no momento da criação do portfólio. Afinal, correções frequentes devido à alta “nervosidade” do mercado excederão o valor do prêmio da opção. Por outro lado, se emularmos uma opção curta, então, com uma volatilidade realizada maior, a emulação acaba sendo mais vantajosa do que a venda direta da opção.

O que mais é necessário saber ao criar uma opção de forma artificial?  Vamos lembrar que a precificação da opção é determinada, principalmente, por três fatores: tempo até a expiração, preço do ativo subjacente, volatilidade implícita. Mantidas as demais condições iguais, cada um desses fatores afeta a opção à sua maneira. Pode-se dizer que o valor de uma opção comum é uma função de três variáveis. Já a opção emulada consiste apenas no ativo subjacente, cujo preço não depende do nível da volatilidade implícita nem do tempo. O preço da opção “artificial” é função apenas do preço do ativo subjacente.  Isso é bom ou ruim?  É evidente que essa circunstância pode atuar tanto a favor quanto contra.

Antes de implementar a emulação, vamos analisar os aspectos práticos do algoritmo. Para isso, construiremos gráficos da dependência da delta da opção e do P&L, lucro/prejuízo, em relação ao preço do ativo subjacente. Esses gráficos foram obtidos no site da MOEX para uma opção sobre o futuro SBRF com strike 31000 e data de expiração em 18.06.2025. Os gráficos são válidos para a data de 22.05.2025. O preço atual, correspondente à linha vertical pontilhada, naquele momento era igual a 30800.

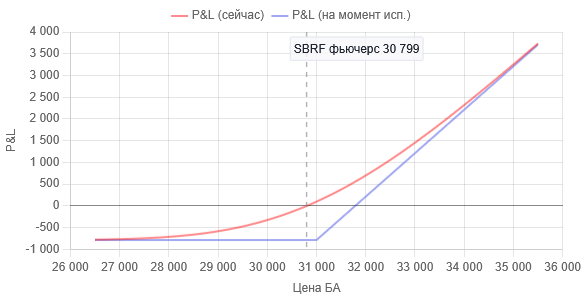
Fig.1 Dependência do lucro/prejuízo (P&L) da opção Call comprada com strike 31000 do preço do ativo subjacente. P&L expresso em rublos por um contrato. Linha vertical pontilhada — momento de construção dos gráficos. Para esse momento o P&L é negativo e igual a - 23,92 rublos.

Linha vermelha — para o momento atual (22.05.2025), linha azul — no momento da expiração (18.06.2025), ou seja, quando T = 1 na fórmula Black-Scholes.

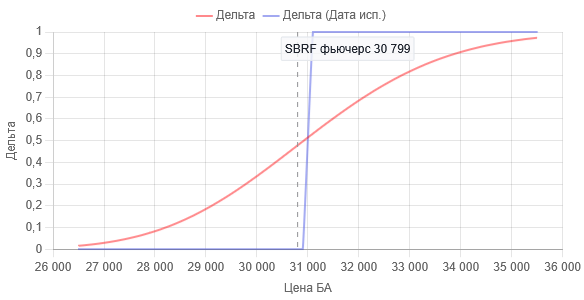
Fig.2 Dependência do valor Delta da opção Call comprada com strike 31000 do preço do ativo subjacente para um contrato. Linha vertical pontilhada — momento de construção dos gráficos. Para este momento, o Delta é 0,48.

Linha vermelha — para o momento atual (22.05.2025), linha azul — no momento da expiração (18.06.2025), ou seja, quando T = 1 na fórmula Black-Scholes.

Os gráficos apresentados acima decorrem diretamente da fórmula de Black-Scholes. Como pode ser visto no gráfico da fig.1, ao comprar uma opção Call pagamos um prêmio ao vendedor no valor de aproximadamente 789 rublos por contrato. Ou seja, já começamos no prejuízo. Diferentemente da opção emulada, na qual, em uma primeira aproximação, pode-se negligenciar a comissão pela compra do ativo subjacente. Mas há também uma boa notícia: em qualquer queda do preço do ativo subjacente, superior ao valor do prêmio, nossos prejuízos não irão para um negativo infinito. Nisso reside a diferença fundamental entre a compra de uma opção Call e a compra, por exemplo, de uma ação, no segundo caso, em caso de queda do preço, as perdas não são limitadas.

Desenvolvemos a emulação de opções em MQL5

A partir da fig. 2 é possível ver que a Delta varia, para um contrato de uma opção Call comprada, no intervalo de 0 até +1. Vamos passar, no eixo X do gráfico da Delta, de preços absolutos para variações em pontos. Para isso, subtrairemos dos preços o preço de strike, neste caso, 31000. O gráfico obtido terá a seguinte aparência:

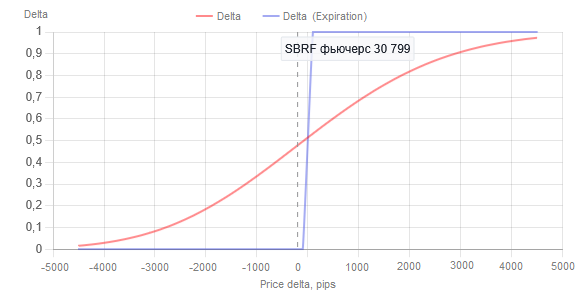
Fig.3 Dependência do valor do Delta da opção Call comprada com strike 31000 da variação do preço do ativo subjacente relativo ao strike para uma única opção. Linha vertical pontilhada — momento de construção dos gráficos. Para este momento, o Delta é 0,48.

Linha vermelha — para o momento atual (22.05.2025), linha azul — no momento da expiração (18.06.2025), ou seja, quando T = 1 na fórmula Black-Scholes.

Naturalmente, o gráfico resultante não difere qualitativamente em nada do original, exceto pela escala no eixo X. Como na fórmula de Black-Scholes aparece a volatilidade implícita (IV), e ela, em geral, não nos é conhecida, a única opção adequada é utilizar, em seu lugar, a volatilidade histórica (HV). Para opções mensais, será a HV média do mês; para opções semanais, a HV média da semana, e assim por diante.

Para facilitar a comparação de gráficos com diferentes ativos subjacentes e para obter a possibilidade de criar opções sobre instrumentos sintéticos, um portfólio composto por diferentes ativos, será conveniente utilizar variações relativas de preços, normalizando essas variações pela volatilidade histórica calculada HV.

Então, a variação relativa em relação ao preço price é expressa pela seguinte relação: Relative Price(price) = (price - Strike) / HV.

Suponhamos que, para o período de expiração, tenhamos calculado HV = 5000. Em princípio, isso é visível na fig.3. Obteremos um gráfico do seguinte tipo:

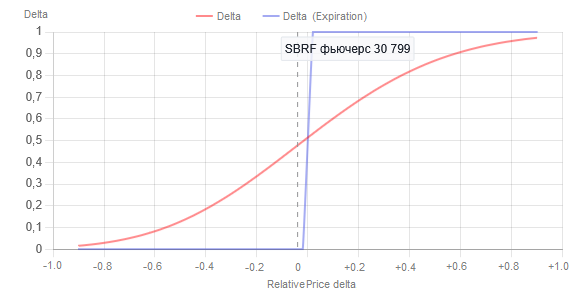
Fig.4 Dependência do valor do Delta da opção Call comprada com strike 31000 em relação à variação relativa do preço, normalizada pela volatilidade histórica do ativo subjacente para uma única opção. Linha vertical pontilhada — momento de construção dos gráficos. Para este momento, o Delta é 0,48.

Linha vermelha — para o momento atual (22.05.2025), linha azul — no momento da expiração (18.06.2025), ou seja, quando T = 1 na fórmula Black-Scholes.

Vê-se que, quando o preço é igual ao strike, a Delta é igual a 0.5. O gráfico da delta, mostrado pela linha vermelha, nada mais é do que a sigmoide conhecida na matemática e no aprendizado de máquina, da forma: 1 \ (1 + exp(-K \ (x - S))), onde S = 0, e K, no caso geral, é desconhecido e ajustado experimentalmente. Em termos conceituais, o coeficiente K depende do período de expiração. Conhecendo o valor da delta no momento atual, 0.48, ao preço atual do ativo subjacente, 30800, podemos calcular o valor de K; para este momento no tempo, ele é igual a 2 e irá mudar, aumentar, à medida que a expiração da opção se aproxima.

Para fins de emulação, vamos ignorar o decaimento temporal da opção e a variação de K; ele será constante durante todo o tempo de vida da opção. Isso terá um efeito positivo no P&L da opção Call comprada e negativo no P&L da opção Put comprada. No geral, no P&L do portfólio de opções, a influência será pequena.

Se igualarmos o parâmetro S na sigmoide 1 \ (1 + exp(-K \ (x - S))) a 0.5, então o gráfico da dependência da delta em relação à variação relativa de preço será deslocado ao longo do eixo X para a direita em um valor S, e obteremos, no zero, um valor próximo de zero, a sigmoide tende assintoticamente a 0 e a 1. Essa forma é mais conveniente para os fins de emulação e de normalização pelo intervalo de volatilidade, o que utilizaremos já no desenvolvimento do expert em MQL.

Assim, temos todos os dados iniciais necessários para escrever o código em MQL5 para a emulação de uma opção sobre um ativo subjacente arbitrário. A saber: a fórmula da função de emulação, o preço de strike, a volatilidade histórica e a compreensão dos processos que ocorrem no mercado ideal de Black-Scholes.

• 1. Classe base

Vamos emular os seguintes tipos de opções:

• compra do direito de comprar o ativo subjacente — opção Long Call
• compra do direito de vender o ativo subjacente — opção Long Put
• venda do direito de comprar o ativo subjacente — opção Short Call
• venda do direito de vender o ativo subjacente — opção Short Put

Definiremos todos os tipos de opções suportados na forma de uma enumeração:

// ---------------------------------------------------------------------
//  Тип опциона:
// ---------------------------------------------------------------------
enum ENUM_OPTION_TYPE
{
   ENUM_OPTION_CALL_LONG,                 // Long Call
   ENUM_OPTION_CALL_SHORT,                // Short Call
   ENUM_OPTION_PUT_LONG,                  // Long Put
   ENUM_OPTION_PUT_SHORT,                 // Short Put
};

A classe base é derivada da classe padrão do MQL "CObject". Isso foi feito para que seja possível utilizar facilmente as listas padrão do MQL "CList" para manipulação de objetos e criação de estruturas de opções de qualquer complexidade. Isso será abordado no próximo artigo da série.

Os principais membros de dados da classe base:

• tipo de opção — campo 'type_enum'
• preço de strike — campo ''strike''
• valor atual da delta da opção — campo 'delta'
• preço para normalização da opção pela volatilidade — campo 'norm_price'

Além disso, existe um conjunto de campos auxiliares que serão necessários nas classes derivadas da classe base. A classe base é abstrata, com a definição obrigatória, nas classes derivadas, do método "GetSigmoidValue". Esse método é diferente para diferentes tipos de opções dentro do modelo de Black-Scholes. Esse mesmo enfoque permitirá, no futuro, adicionar outros tipos de opções, por exemplo, utilizando métodos de aprendizado de máquina e/ou outros modelos de precificação.

// =====================================================================
// Базовый класс опциона - порожден от 'CObject', чтобы можно было
// помещать в списки.
// =====================================================================
class TOptionBase : public CObject
{
protected:
   ENUM_OPTION_TYPE  type_enum;
   double  strike;
   double  shift;
   double  koeff_K;
   double  koeff_S;
   int     digits;
   double  norm_price;
   double  delta;

   double  norm_koeff;
   bool    range_inited_Flag;

public:
   // ---------------------------------------------------------------------
   //  Конструктор:
   // ---------------------------------------------------------------------
   TOptionBase(const ENUM_OPTION_TYPE _type, const double _k, const double _s, const int _digits)
   :
   CObject(),
   type_enum(_type),
   strike(0.0),
   shift(0.0),
   koeff_K(_k),
   koeff_S(_s),
   digits(_digits),
   range_inited_Flag(false),
   delta(0.0),
   norm_koeff(0.0)
   {
   }

public:
   // ---------------------------------------------------------------------
   //  Установить диапазон нормировки дельты для центрального страйка:
   // ---------------------------------------------------------------------
   void SetRange(const double _strike, const double _norm_price)
   {
     this.strike = _strike;
     this.norm_price = _norm_price;
     this.norm_koeff = 1.0 / (this.norm_price - this.strike);
     this.range_inited_Flag = true;
   }
   // ---------------------------------------------------------------------
   //  Рассчитать значение нормированной дельты для заданной цены:
   // ---------------------------------------------------------------------
   double UpdateDelta(const double _price)
   {
     if(this.range_inited_Flag == false)
     {
       this.delta = 0.0;
     }
     else
     {
       this.delta = NormalizeDouble(this.GetSigmoidValue((_price - this.strike) * this.norm_koeff), 5);
     }

     return(this.delta);
   }
   // ---------------------------------------------------------------------
   //  Получить значение вычисленной ранее нормированной дельты:
   // ---------------------------------------------------------------------
   double Delta()
   {
     return(this.delta);
   }
   // ---------------------------------------------------------------------
   //  Получить флаг инциализации диапазона для дельты:
   // ---------------------------------------------------------------------
   bool    IsRangeInited()
   {
     return(this.range_inited_Flag);
   }
protected:
   // ---------------------------------------------------------------------
   //  Получить значение нормированной дельты:
   // ---------------------------------------------------------------------
   virtual double GetSigmoidValue(const double _x) = 0;
};
// ---------------------------------------------------------------------

• 2. Particularidades do funcionamento em condições reais

Na emulação da opção, precisamos escolher com que variação da delta deve ser realizado o rebalanceamento das posições. Isso limita a precisão da emulação por um lado, mas, por outro, permite controlar os gastos com comissões na abertura e no fechamento de posições. Utilizamos os parâmetros do ativo subjacente, Vmin_size, volume mínimo da posição aberta, e Vmin_delta_size, variação mínima do volume da posição.

Também definiremos o número de rebalanceamentos das posições quando a delta variar no intervalo, em valor absoluto, |0.0...1.0|. Esse número de rebalanceamentos N será definido como um parâmetro externo. Assim, o volume total das posições variará de 0 até (Vmin_size + Vmin_delta_size * (N - 1)).

Como regra, Vmin_size é igual a Vmin_delta_size, mas isso não é obrigatório. Por padrão, adotaremos o número de rebalanceamentos igual a dez no intervalo de delta |0.0...1.0|.

• 3. Opção Long Call

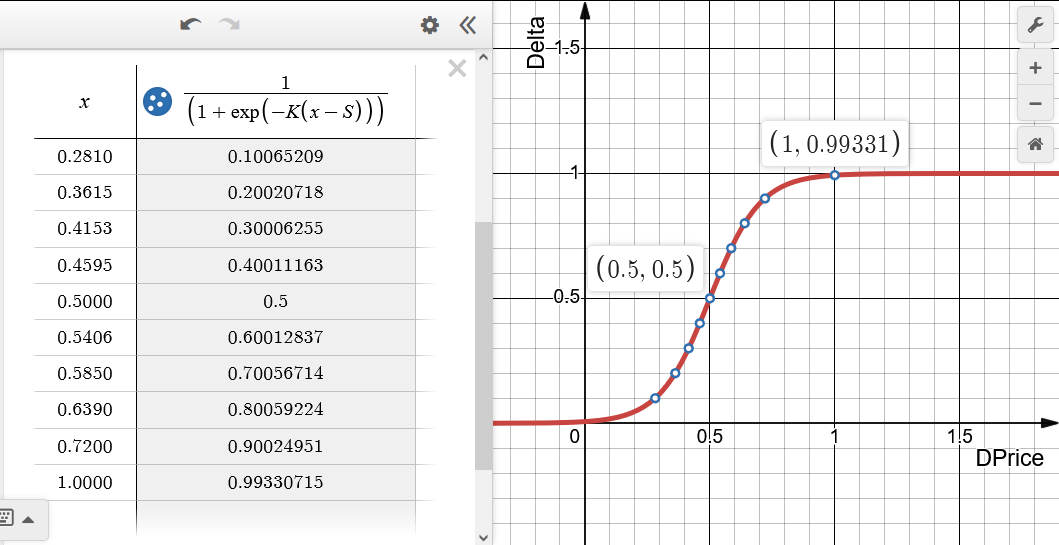
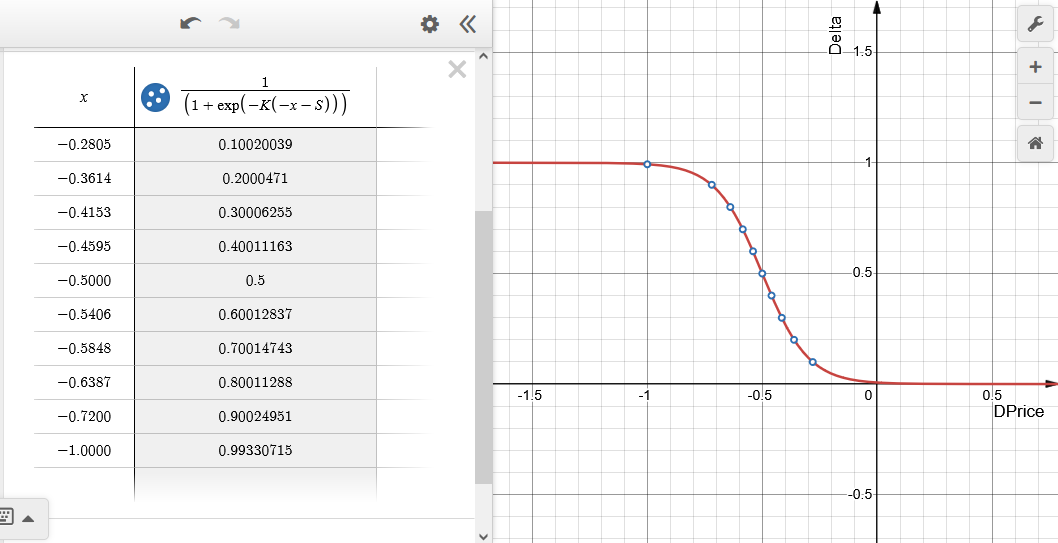
Fig.5 Dependência do valor da Delta da variação relativa do preço DPrice (x na tabela) para a opção emulada Long Call (compra de Call). S = 0.5, K = 10. O intervalo da delta é dividido em dez partes iguais.

Ao preço de strike corresponde o ponto zero DPrice = 0. Quando o valor da delta está próximo de um, diz-se que a opção está "profundamente dentro do dinheiro"; nesse caso, ela se comporta como uma posição comprada no ativo subjacente de volume máximo. À medida que o preço se aproxima do strike, o volume da posição no ativo subjacente é reduzido e se torna igual a zero quando a opção está "fora do dinheiro", ou seja, quando a delta é próxima de zero. A opção real, nesse caso, entra em prejuízo no valor do prêmio.

// =====================================================================
// Classe de opção do tipo "Long Call"
// =====================================================================
class OptionLongCall : public TOptionBase
{
public:
    // ------------------------------------------------------------------
    // Construtor:
    // ------------------------------------------------------------------
    OptionLongCall(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_CALL_LONG, _k, _s, _digits)
    {
    }

protected:
    // ------------------------------------------------------------------
    // Obter o valor da delta normalizada:
    // ------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(1.0 / (1.0 + MathExp(-this.koeff_K * (_x - this.koeff_S))));
    }
};
// ------------------------------------------------------------------

• 4. Opção Long Put

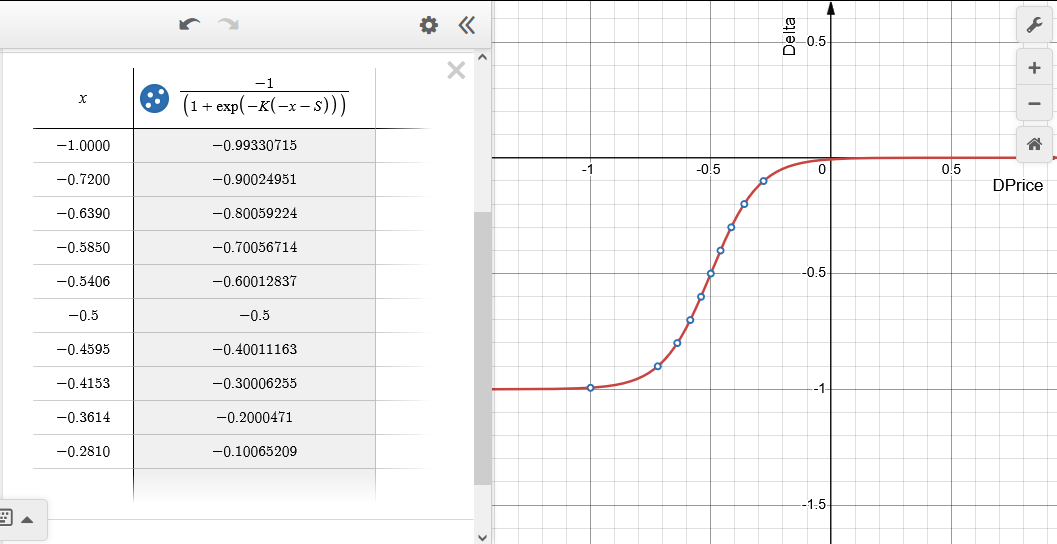
Fig.6 Dependência do valor da Delta da variação relativa do preço DPrice (x na tabela) para a opção emulada Long Put (compra de Put). S = 0.5, K = 10. O intervalo da delta é dividido em dez partes iguais.

Ao preço de strike corresponde o ponto zero DPrice = 0. Quando o valor da delta está próximo de menos um, diz-se que a opção está "profundamente dentro do dinheiro"; nesse caso, ela se comporta como uma posição vendida no ativo subjacente de volume máximo. À medida que o preço se aproxima do strike, o volume da posição no ativo subjacente é reduzido e se torna igual a zero quando a opção está "fora do dinheiro", ou seja, quando a delta é próxima de zero. A opção real, nesse caso, entra em prejuízo no valor do prêmio.

// =====================================================================
// Classe de opção do tipo "Long Put"
// =====================================================================
class OptionLongPut : public TOptionBase
{
public:
    // ------------------------------------------------------------------
    // Construtor:
    // ------------------------------------------------------------------
    OptionLongPut(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_PUT_LONG, _k, _s, _digits)
    {
    }

protected:
    // ------------------------------------------------------------------
    // Obter o valor da delta normalizada:
    // ------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(-1.0 / (1.0 + MathExp(-this.koeff_K * (-_x - this.koeff_S))));
    }
};
// ------------------------------------------------------------------

• 5. Opção Short Call

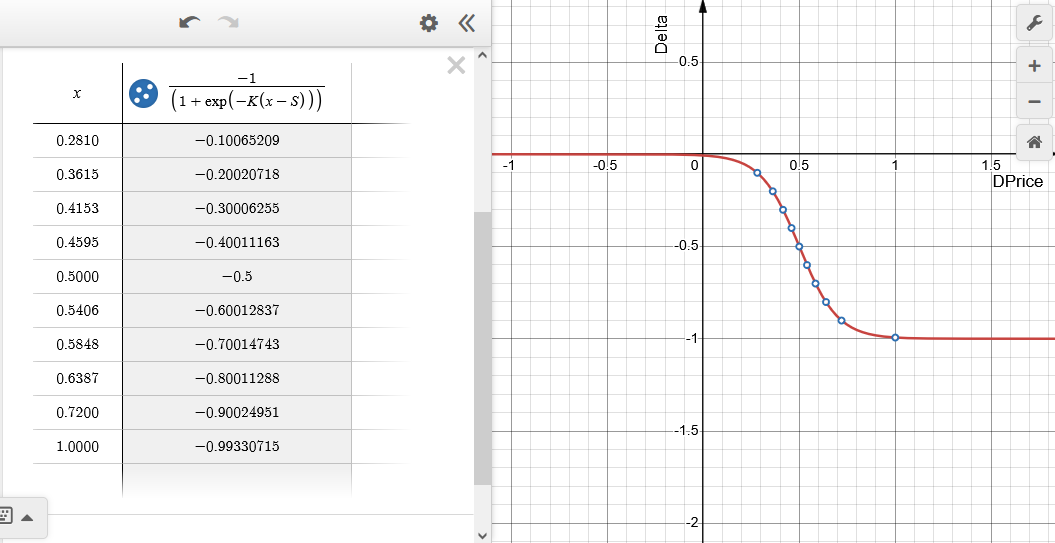
Fig.7 Dependência do valor da Delta da variação relativa do preço DPrice (x na tabela) para a opção emulada Short Call (venda de Call). S = 0.5, K = 10. O intervalo da delta é dividido em dez partes iguais.

Ao preço de strike corresponde o ponto zero DPrice = 0. Quando o valor da delta está próximo de menos um, diz-se que a opção está "profundamente dentro do dinheiro"; nesse caso, ela se comporta como uma posição vendida no ativo subjacente de volume máximo. À medida que o preço se aproxima do strike, o volume da posição no ativo subjacente é reduzido e se torna igual a zero quando a opção está "fora do dinheiro", ou seja, quando a delta é próxima de zero. A opção real, nesse caso, passa a ter lucro no valor do prêmio.

// =====================================================================
// Classe de opção do tipo "Short Call"
// =====================================================================
class OptionShortCall : public TOptionBase
{
public:
    // ------------------------------------------------------------------
    // Construtor:
    // ------------------------------------------------------------------
    OptionShortCall(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_CALL_SHORT, _k, _s, _digits)
    {
    }

protected:
    // ------------------------------------------------------------------
    // Obter o valor da delta normalizada:
    // ------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(-1.0 / (1.0 + MathExp(-this.koeff_K * (_x - this.koeff_S))));
    }
};
// ------------------------------------------------------------------

• 6. Opção Short Put

Fig.8 Dependência do valor da Delta da variação relativa do preço DPrice (x na tabela) para a opção emulada Short Put (venda de Put). S = 0.5, K = 10. O intervalo da delta é dividido em dez partes iguais.

Ao preço de strike corresponde o ponto zero DPrice = 0. Quando o valor da delta está próximo de um, diz-se que a opção está "profundamente dentro do dinheiro"; nesse caso, ela se comporta como uma posição vendida no ativo subjacente de volume máximo. À medida que o preço se aproxima do strike, o volume da posição no ativo subjacente é reduzido e se torna igual a zero quando a opção está "fora do dinheiro", ou seja, quando a delta é próxima de zero. A opção real, nesse caso, passa a ter lucro no valor do prêmio.

// =====================================================================
// Classe de opção do tipo "Short Put"
// =====================================================================
class OptionShortPut : public TOptionBase
{
public:
    // ------------------------------------------------------------------
    // Construtor:
    // ------------------------------------------------------------------
    OptionShortPut(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_PUT_SHORT, _k, _s, _digits)
    {
    }

protected:
    // ------------------------------------------------------------------
    // Obter o valor da delta normalizada:
    // ------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(1.0 / (1.0 + MathExp(-this.koeff_K * (-_x - this.koeff_S))));
    }
};
// ------------------------------------------------------------------

• 7. Particularidades do cálculo do volume da posição no ativo subjacente

Para calcular o volume da posição, precisamos converter o valor da delta do intervalo |0.0...1.0| para o intervalo de valores inteiros |0...10|. E já esse valor inteiro será multiplicado pelo volume da variação mínima do lote, obtendo assim o valor necessário do volume da posição. 

Suponhamos que o número de "subintervalos" da delta seja igual a dez. Apenas multiplicando a delta por dez e convertendo o resultado para um tipo inteiro, não atingiremos o objetivo. Isso porque, quando a delta oscila em torno de qualquer limite de um "subintervalo", o volume também oscilará de forma síncrona com a delta. Vamos explicar com um exemplo: suponha que a delta seja igual a 0.090, o volume então será (int)(0.090 * 10) = 0, isto é, a posição está ausente, e depois ela aumente para 0.101, o volume então será (int)(0.101 * 10) = 1 em seguida, no próximo tick, após um curto intervalo de tempo, volte a diminuir para 0.090, o volume novamente se tornará igual a 0. Ou seja, nós, na prática, compramos e quase imediatamente vendemos a posição, resultando em um rebalanceamento sem sentido da posição, que pode se repetir muitas vezes em poucos segundos. Isso é o chamado "chattering", ou tremulação do sinal.

Portanto, ao converter a delta para o volume desejado, deve existir um certo "histerese" no rebalanceamento da posição. Isso é alcançado distinguindo a direção do rebalanceamento, o que é necessário: reduzir ou aumentar a posição atual no ativo subjacente, e levando em consideração o valor anterior do volume da posição.

Introduziremos o conceito de nível de emulação da opção. Explicação: se for definida a correspondência |0.0...1.0| -> |0...10| (ver explicações acima), então consideraremos que o nível de emulação da opção varia de zero até dez. O número de níveis é definido como um parâmetro externo ao método de cálculo, N. O nível de emulação, assim como a delta, será considerado em módulo. E separadamente utilizaremos o sinal do nível de emulação da opção — {0, +1, -1}. Se for 0, então a posição está fechada.

• 8. Cálculo do volume da posição no ativo subjacente em MQL5

A forma de implementar a "histerese" no cálculo do nível atual de emulação da opção é tabular, por meio do uso de dois arrays:

• IncreaseLevel_Array — determina o nível de emulação da opção quando ele aumenta.
• DecreaseLevel_Array — determina o nível de emulação da opção quando ele diminui.

Isso é feito no método UpdateOptionLevel, que recebe dois parâmetros de entrada:

• _delta — a delta atual da opção.
• _curr_level — o nível atual de emulação da opção, calculado anteriormente, ou 0 se esta for a primeira chamada do método.

O construtor da classe OptionContractsVolume recebe dois argumentos como parâmetros:

• _ZeroDelta — o valor da delta correspondente ao nível zero de emulação da opção. Pode variar de 0.001 a 0.099.
• _LevelsNumber — o número de níveis de emulação da opção. Quanto maior o número de níveis, mais suave e precisa será a emulação, porém maior será o lote negociado no ativo subjacente, devido à discretização da sua variação.

No construtor são preenchidos os arrays IncreaseLevel_Array e DecreaseLevel_Array e são inicializadas diversas variáveis auxiliares, ver o código-fonte com comentários.

// =====================================================================
//      Класс расчета объема контракта базового актива для опциона:
// =====================================================================
class OptionContractsVolume
{
  int IncreaseLevel_Array[];          // уровень эмуляции опциона при его увеличении
  int DecreaseLevel_Array[];          // уровень эмуляции опциона при его уменьшении
  // ---------------------------------------------------------------------
protected:
  double  ZeroDelta;                  // значение дельты, соответствующее нулевому уровню уровню эмуляции опциона
  int     LevelsNumber;               // число уровней эмуляции опциона
  // ---------------------------------------------------------------------
  int     zero_delta;                 // целое значение дельты, соответствующее нулевому уровню эмуляции опциона
  int     curr_option_level_sign;     // текуший знак уровня эмуляции опциона
  int     curr_option_level;          // текуший уровень эмуляции опциона
  // ---------------------------------------------------------------------
  int     curr_inc_level;
  int     curr_dec_level;
  // ---------------------------------------------------------------------
  int     curr_contracts_index;
  // ---------------------------------------------------------------------
  bool    is_contracts_updated_Flag;

public:
  // ---------------------------------------------------------------------
  //  Конструктор:
  // ---------------------------------------------------------------------
  OptionContractsVolume(const double _ZeroDelta, const int _levels_number)
  :
  ZeroDelta(_ZeroDelta),
  LevelsNumber(_levels_number),
  curr_option_level_sign(0),
  curr_option_level(0),
  curr_inc_level(0),
  curr_dec_level(0),
  is_contracts_updated_Flag(false)
  {
    this.zero_delta = (int)(NormalizeDouble(this.ZeroDelta, 3) * 1000.0);

    // Выделим память для массивов, хранящих уровни эмуляции:
    ArrayResize(this.IncreaseLevel_Array, (this.LevelsNumber + 1) * 100 + 1);
    ArrayResize(this.DecreaseLevel_Array, (this.LevelsNumber + 1) * 100 + 1);

    // Заполним массив в сторону увеличения:
    for(int i = 0; i < this.LevelsNumber + 1; i++)
    {
      ArrayFill(this.IncreaseLevel_Array, i * this.LevelsNumber * 100, this.LevelsNumber * 100, i);
    }
    ArrayFill(this.IncreaseLevel_Array, (this.LevelsNumber + 1) * 100, 1, this.LevelsNumber);

    // Заполним массив в сторону уменьшения:
    ArrayFill(this.DecreaseLevel_Array, 0,    zero_delta,  0);
    ArrayFill(this.DecreaseLevel_Array, zero_delta,  this.LevelsNumber * 100 - zero_delta + 1,  1);
    for(int i = 2; i < this.LevelsNumber + 1; i++)
    {
      ArrayFill(this.DecreaseLevel_Array, i * this.LevelsNumber * 100,  this.LevelsNumber * 100,  i);
    }
    ArrayFill(this.DecreaseLevel_Array, (this.LevelsNumber + 1) * 100, 1, this.LevelsNumber);
  }
  // ---------------------------------------------------------------------
  //  Рассчитать уровень эмуляции опциона для заданной дельты:
  // ---------------------------------------------------------------------
  //  - если произошло изменении уровня, возвращает 'true'.
  // ---------------------------------------------------------------------
  bool  UpdateOptionLevel(const double _delta, const int _curr_level)
  {
    this.is_contracts_updated_Flag = false;

    //  Определим направление торговли:
    int delta_int = (int)(NormalizeDouble(_delta, 3) * 1000.0);
    this.curr_option_level_sign = 0;
    if(delta_int > zero_delta / 2)
    {
      this.curr_option_level_sign = 1;
    }
    else if(delta_int < -zero_delta / 2)
    {
      this.curr_option_level_sign = -1;
    }

    //  Текущий индекс для массивов, исходя из 'Delta' с точностью 3 знака после запятой:
    this.curr_contracts_index = (int)MathAbs(delta_int);
    if(this.curr_contracts_index > ((this.LevelsNumber + 1) * 100))
    {
      //  Индекс не должен превыщать размер массива (здесь опцион глубоко в деньгах):
      this.curr_contracts_index = (this.LevelsNumber + 1) * 100;
    }

    //  Текущий уровень эмуляции опционов (0...N) в сторону УВЕЛИЧЕНИЯ:
    this.curr_inc_level = this.IncreaseLevel_Array[this.curr_contracts_index];

    //  Текущий уровень эмуляции опционов (0...N) в сторону УМЕНЬШЕНИЯ:
    this.curr_dec_level = this.DecreaseLevel_Array[this.curr_contracts_index];

    //  Если уровень эмуляции опционов (0...N) по сравнению с текущим, УВЕЛИЧИЛСЯ:
    if(this.curr_inc_level > _curr_level)
    {
      this.curr_option_level = this.curr_inc_level;
      this.is_contracts_updated_Flag = true;
      return(true);
    }

    //  Если, уровень эмуляции опционов (0...N) по сравнению с текущим УМЕНЬШИЛСЯ:
    if(this.curr_dec_level < _curr_level)
    {
      this.curr_option_level = this.curr_dec_level;

      this.is_contracts_updated_Flag = true;
      return(true);
    }

    return(false);
  }
};
// ---------------------------------------------------------------------

O texto completo do código está contido no arquivo OptionEmulatorA1.mqh no anexo deste artigo.

Considerações finais 

Assim, analisamos uma variante de emulação de opções por meio do ativo subjacente, que é uma ferramenta relativamente complexa e poderosa, que:

• permite criar estratégias de opções complexas e não padronizadas;
• oferece mais flexibilidade do que as opções padrão;
• exige um entendimento profundo de modelos matemáticos;
• é eficiente com uma gestão de riscos adequada.

Esse método é especialmente útil quando é necessário:

• hedge de grandes portfólios,
• criação de estratégias de opções exóticas,
• negociação em mercados com baixa liquidez de opções.

A seguir será considerada a parte prática, a condução e o rebalanceamento de posições no ativo subjacente utilizando as funções de negociação do MQL5.