MQL5 Wizard techniques you should know (Part 49): Aprendizaje por refuerzo con optimización de políticas proximales

Introducción

Continuamos nuestra serie sobre el asistente MQL5, donde últimamente estamos alternando entre patrones simples de indicadores comunes y algoritmos de aprendizaje por refuerzo. Tras haber analizado los patrones de indicadores (Alligator de Bill Williams) en el último artículo, volvemos ahora al aprendizaje por refuerzo, donde en esta ocasión el algoritmo que vamos a examinar es la Optimización de Política Proximal (Proximal Policy Optimization, PPO). Se informa que este algoritmo, publicado por primera vez hace siete años, es el algoritmo de aprendizaje por refuerzo elegido para ChatGPT. Por lo tanto, es evidente que existe cierto entusiasmo en torno a este enfoque del aprendizaje por refuerzo. El algoritmo PPO tiene como objetivo optimizar la política (la función que define las acciones del actor) de manera que mejore el rendimiento general, evitando cambios drásticos que podrían hacer que el proceso de aprendizaje se volviera inestable.

No lo hace de forma independiente, sino que trabaja en conjunto con otros algoritmos de aprendizaje por refuerzo, algunos de los cuales hemos visto en esta serie, que, en términos generales, se dividen en dos categorías. Algoritmos basados en políticas y algoritmos basados en valores. Ya hemos visto ejemplos de cada uno de ellos en la serie y, quizás para recapitular, los algoritmos basados en políticas que vimos fueron Q-Learning y SARSA. Solo hemos considerado un método basado en el valor, y ese es la diferencia temporal. Entonces, ¿en qué consiste exactamente el PPO?

Como se ha mencionado anteriormente, el «problema» que resuelve PPO es evitar que la política cambie demasiado durante las actualizaciones. La tesis que sustenta esto es que, si no se interviene en la gestión de la frecuencia y la magnitud de las actualizaciones, el agente podría: olvidar lo que ha aprendido, tomar decisiones erráticas o rendir peor en el entorno. De este modo, PPO garantiza que las actualizaciones sean pequeñas pero significativas. PPO funciona comenzando con una política predefinida con sus parámetros. Las políticas son simplemente funciones que definen las acciones de los actores en función de las recompensas y los estados del entorno.

Dada una política, la interacción del agente con el entorno se llevaría a cabo con el fin de recopilar datos. Esta «recopilación de datos» permitiría comprender la relación entre estado, acción y recompensa, así como las probabilidades de las diversas acciones emprendidas en el marco de esa política. Una vez establecido esto, lo siguiente es definir la función objetivo. Como se menciona en la introducción anterior, PPO consiste en moderar la magnitud de las actualizaciones en el aprendizaje por refuerzo, y para ello utilizamos una función de «recorte». Esta función se define mediante la siguiente ecuación:

Donde:

• r t (θ)=πθ(at∣st)/πθ old (at∣st) es la relación de probabilidad entre la nueva política (con parámetros θ) y la antigua política (con parámetros θ old​).
• Â t es la estimación de la ventaja en el momento t, que mide cuánto mejor es una acción en comparación con la acción promedio en un estado dado.
• ϵ es un hiperparámetro (a menudo 0,1 o 0,2) que controla el rango de recorte, limitando el tamaño del paso de la actualización de la política.

La estimación de la ventaja se puede definir de varias maneras, sin embargo, la que utilizamos en nuestra implementación se indica a continuación:

Donde:

• Q(s t ,a t ) es el valor Q (rendimiento esperado) por realizar la acción a t ​ en el estado s t ​.
• V(s t ) es la función de valor para el estado s t ​, que representa el rendimiento esperado si seguimos la política desde ese estado en adelante.

Este método de cuantificación de la función de ventaja hace hincapié en la dependencia o el uso de algoritmos basados en políticas y algoritmos basados en valores, a lo que también aludimos anteriormente. Una vez que hemos definido nuestra función objetivo, procedemos a realizar actualizaciones en nuestra política. La actualización ajusta los parámetros de la política con el objetivo de maximizar la función objetivo recortada. Esto garantiza que los cambios en la política sean graduales y no se ajusten excesivamente a los datos recientes. Este proceso se repite al interactuar con el entorno utilizando la política actualizada, recopilando datos continuamente y perfeccionando la política.

¿Por qué es popular el PPO? Bueno, es más fácil de implementar en comparación con optimizadores de políticas más antiguos como la optimización de políticas de región de confianza, proporciona actualizaciones estables gracias al recorte (cuya fórmula destacamos anteriormente), es muy eficiente, ya que funciona bien con las redes neuronales modernas y puede manejar tareas a gran escala. También es versátil, ya que puede funcionar bien tanto en espacios continuos como discretos. Otra forma de considerar la intuición detrás de PPO sería imaginar que uno está aprendiendo a jugar un juego. Si cambias drásticamente tu enfoque del juego después de cada intento, de forma continua, acabarás perdiendo las pocas buenas maniobras o tácticas que hayas podido aprender al principio. El PPO sirve como una forma de garantizar que, a medida que aprendes el juego, solo realices cambios pequeños, graduales y deliberados, evitando cambios radicales que podrían empeorar tu rendimiento.

En muchos sentidos, este es el debate entre exploración y explotación que el aprendizaje por refuerzo pretende abordar. Y se puede argumentar que, al inicio de la mayoría de los procesos de aprendizaje, son necesarios cambios radicales en el enfoque que faciliten más la exploración que la explotación. En estas situaciones iniciales, el PPO no sería muy útil, claramente. No obstante, dado que puede aplicarse a la mayoría de las disciplinas y campos de aprendizaje, los defensores se encuentran más en una fase de ajuste que de descubrimiento inicial, por lo que el PPO goza de gran popularidad. Con este fin, el PPO se utiliza ampliamente en robótica, por ejemplo, para enseñar a los robots a caminar o manipular objetos, o en videojuegos en los que, por ejemplo, se entrena a la IA para jugar a juegos complejos como el ajedrez o Dota.

El papel de los PPO en el aprendizaje por refuerzo para los operadores bursátiles

El PPO, como algoritmo de política que funciona junto con otros algoritmos básicos de aprendizaje por refuerzo, no tiene muchas alternativas. Las pocas disponibles que merecen ser mencionadas son las redes Deep Q-Networks, que ya analizamos en un artículo anterior aquí, Asynchronous Advantage Actor-Critic, que aún no hemos visto, y Trusted Region Policy Optimization, que ya hemos mencionado anteriormente. Consideremos cómo se distingue PPO de cada una de estas implementaciones. Si empezamos con DQN, este utiliza Q-Learning y puede tener problemas de inestabilidad debido a las grandes actualizaciones de políticas, especialmente en espacios de acción continuos. Por espacios de acción continuos se entiende los ciclos RL en los que la elección del actor no está predefinida por opciones enumerables como comprar-vender-mantener, sino que se establece mediante un número de coma flotante o doble en casos de uso como determinar el tamaño ideal de la posición para la próxima operación.

Sin embargo, se podría decir que PPO es más estable y fácil de implementar, ya que no necesita una red de destino separada ni siquiera experiencia en reproducción, un concepto que exploraremos en un artículo futuro. Al contar con un proceso de entrenamiento simplificado, PPO funciona directamente tanto en espacios de acción discretos como continuos, mientras que DQN es más adecuado para espacios discretos.

En comparación con Asynchronous Advantage Actor-Critic (A3C), A3C (un algoritmo de políticas que aún no hemos considerado en esta serie) tiende a utilizar múltiples ciclos de RL (o agentes) para actualizar una política compartida en diferentes momentos, lo que suele aumentar la complejidad del modelo en el que se presentan los múltiples ciclos de RL. Por otro lado, PPO depende de actualizaciones sincrónicas y recortes de políticas para mantener un proceso de aprendizaje estable sin actualizaciones excesivamente agresivas que puedan suponer un riesgo de colapso de la política.

La optimización de políticas de región de confianza (Trust Region Policy Optimization, TRPO) también presenta algunas diferencias notables en comparación con la optimización de políticas de región de confianza (TRPO). Entre ellas destaca el hecho de que TRPO utiliza un complejo proceso de optimización para limitar los cambios en las políticas, un proceso que a menudo requiere resolver un problema de optimización con restricciones. Por otro lado, PPO simplifica esto mediante el recorte, como se mencionó anteriormente, donde, al restringir las actualizaciones, se puede obtener eficiencia computacional sin dejar de alcanzar niveles similares de estabilidad y rendimiento.

Hay algunas características más del PPO que vale la pena compartir aquí en la introducción, así que las repasaremos antes de pasar al cuerpo principal. PPO, como ya se ha destacado anteriormente, utiliza un mecanismo de recorte para las actualizaciones de políticas con el objetivo inmediato de evitar actualizaciones demasiado drásticas. Sin embargo, la consecuencia quizás no deseada de esto es proporcionar un equilibrio entre la explotación y la exploración, un principio clave en el aprendizaje por refuerzo. Esto puede ser beneficioso para los operadores, especialmente en entornos de alta volatilidad, donde la sobreexplotación de las recompensas podría ser una tarea inútil, y en cambio, mantener la pólvora seca para obtener una visión a largo plazo de los mercados es una estrategia más adecuada.

Sin embargo, en los casos en los que se justifica cierta exploración, PPO puede aplicar la regularización de entropía, lo que evitaría que el algoritmo se volviera demasiado confiado en una acción concreta, de modo que se inclinara menos por recortar las actualizaciones de la política. Consideraremos la regularización de la entropía en un artículo futuro.

El PPO también es eficaz a la hora de gestionar o tratar grandes espacios de acción. Esto se debe a que su marco actor-crítico le permite pronosticar mejor los valores del dominio del actor, incluso cuando son continuos, como ya se ha mencionado anteriormente; pero, más allá de eso, su reducción de la varianza de las actualizaciones de políticas, gracias al uso de una función de pérdida sustitutiva, puede dar lugar a un comportamiento más coherente en todas las operaciones, incluso en casos en los que el RL opera en entornos muy volátiles, como los que se observan en el mercado de divisas.

PPO también escala bien dado que no depende del almacenamiento de grandes buffers de reproducción de experiencias que a menudo consumen muchos recursos. Podría decirse que esta ventaja podría hacerla adecuada para casos de uso tales como el comercio de alta frecuencia con muchos instrumentos o incluso configuraciones de reglas comerciales complejas.

La PPO puede ser eficiente en el aprendizaje con datos limitados. Esta eficiencia en la toma de muestras de datos, en comparación con sus pares, lo hace muy eficaz para entornos donde la obtención de datos de mercado puede resultar inhibida o costosa. Este es un escenario muy preocupante para muchas empresas que necesitan probar sus estrategias durante largos períodos de tiempo en términos de historial, sobre una base de ticks reales, por ejemplo. Si bien el probador de estrategias de MetaTrader puede generar datos de ticks si no hay ticks reales disponibles, por regla general, suele preferirse probar la estrategia con datos de ticks reales del bróker comercial previsto.

Este volumen de datos de ticks reales rara vez está disponible en cantidad suficiente para muchos corredores e incluso en los casos en que se dispone de los años necesarios para el período de prueba, una revisión de calidad podría revelar lagunas significativas en el conjunto de datos. Este es un tipo de problema especial para los datos financieros porque, si se compara con otros campos, como el desarrollo de videojuegos o simulaciones, la generación de grandes cantidades de datos y el entrenamiento posterior suele ser sencillo. Además, las señales clave a menudo dependen de eventos raros, como caídas o auges del mercado, y estos no aparecen con la suficiente frecuencia como para que los modelos aprendan de ellos.

La PPO 'evita' estos problemas al ser inherentemente eficiente en el uso de muestras, ya que es capaz de aprender de volúmenes limitados de datos. La necesidad de grandes volúmenes de datos para generar políticas adecuadas no es un requisito previo para la PPO. Esto se debe en parte a la estimación de ventajas, que permite hacer un mejor uso de los datos de mercado disponibles en porciones más pequeñas y en menos episodios. Esto puede ser clave cuando se intenta modelar eventos raros pero importantes, ya que PPO aprende de manera incremental tanto de las buenas como de las malas transacciones, incluso cuando enfrenta escasez de datos.

Para la mayoría de los sistemas comerciales, las "recompensas", que generalmente se cuantifican como ganancias o pérdidas, de cualquier decisión pueden retrasarse significativamente. Esta situación presenta desafíos ya que resulta problemático asignar crédito a una acción específica tomada anteriormente. Por ejemplo, al ingresar en una posición larga en un momento particular, el beneficio podría recién obtenerse días o incluso semanas después, lo que claramente desafía los algoritmos de RL a la hora de aprender qué acciones o estados del entorno precipitan con precisión qué recompensas.

Este escenario se ve aún más debilitado por el ruido y la aleatoriedad del mercado, que son tan inherentes a gran parte de la acción de los precios del mercado que hacen difícil discernir si un resultado positivo fue resultado de una buena decisión o de un movimiento ad hoc del mercado. La función de ventaja, cuya ecuación se ha compartido anteriormente, ayuda a PPO a estimar mejor la recompensa esperada de una acción específica al considerar tanto el valor (ponderación de largo plazo V(st )) como también los valores Q del emparejamiento estado-acción (representados como Q(st , at )) de modo que las decisiones tomadas estén mejor equilibradas hacia ambos extremos.

Configuración de la clase de señal PPO en MQL5

Entonces, para implementar esto en MQL5, utilizaremos la clase 'Cql' que ha sido nuestra fuente principal a través de todos los artículos de aprendizaje de refuerzo. Necesitamos realizar cambios para ampliarlo y adaptarlo a PPO, y el primero de ellos es la introducción de una estructura de datos para manejar los datos de PPO. El listado de los mismos se presenta a continuación:

//+------------------------------------------------------------------+
//| PPO                                                              |
//+------------------------------------------------------------------+
struct Sppo
{  matrix            policy[];
   matrix            gradient[];
};

En la estructura de datos anterior hay dos matrices que se redimensionan según la cantidad de acciones disponibles para el actor en el ciclo de aprendizaje de refuerzo. Cada una de las matrices, tanto para el gradiente como para la política, se dimensiona según el número de estados por el número de estados, en el típico modo cuadrado. Por lo tanto, la matriz de políticas sirve como nuestro equivalente Q-Map, ya que registra los pesos y, por lo tanto, la probabilidad de selección de cada acción en cada estado. Nos ceñiremos a los mismos estados ambientales simples que hemos estado utilizando en estas series de mercados alcistas, bajistas y con fluctuaciones. Para resumir, estos tres estados se registran tanto en un horizonte temporal corto como en un horizonte temporal más largo.

Al definir horizontes temporales, la mayoría de las personas gravitarían hacia los marcos temporales y, por ejemplo, buscarían si la acción del precio de un valor determinado es alcista o bajista en el marco temporal diario y luego repetirían este proceso en el marco temporal de una hora para obtener los dos conjuntos de métricas. Lo que elegimos y hemos estado usando en estas series para definir nuestros horizontes temporales ha sido mucho más simple, ya que simplemente usamos un rezago de un número determinado de barras de precios para separar lo que es de corto plazo de lo que es de largo plazo.

Este valor rezagado es un parámetro de entrada ajustable que denominamos 'Signal_PPO_RL_Scale' o m_scale dentro del código de clase de señal y el proceso de mapeo de las dos tendencias de acción del precio se captura en la función de obtención de salida, que se compartirá más adelante en este artículo. Por ahora, sin embargo, si volvemos a PPO, la implementación de esto al modificar la clase Cql implica principalmente la introducción de 2 nuevas funciones. La función de política de establecimiento y la función de obtención de recorte. Al determinar la próxima acción del actor, no llamamos a ninguna de estas funciones; de hecho, podrían ser funciones protegidas en la clase Cql.

La configuración de la política se llama dentro de la función de configuración de la política y la función de compensación de la política. Su listado se presenta a continuación:

//+------------------------------------------------------------------+
//| PPO policy update function                                       | 
//+------------------------------------------------------------------+
void Cql::SetPolicy()
{  matrix _policies;
   _policies.Init(THIS.actions, Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _policies.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies[i][GetMarkov(ii, iii)] += Q_PPO.policy[i][ii][iii];
         }
      }
   }
   vector _probabilities;
   _probabilities.Init(Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _probabilities.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies.Row(i).Activation(_probabilities, AF_SOFTMAX);
            double _old = _probabilities[states[1]];
            double _new = _probabilities[states[0]];
            double _advantage = Q_SA[i][ii][iii] - Q_V[ii][iii];
            double _clip = GetClipping(_old, _new, _advantage);
            Q_PPO.gradient[i][ii][iii] = (_new - _old) * _clip;
         }
      }
   }
   for(int i = 0; i < THIS.actions; i++)
   {  for(int ii = 0; ii < int(Q_PPO.policy[i].Rows()); ii++)
      {  for(int iii = 0; iii < int(Q_PPO.policy[i].Cols()); iii++)
         {  Q_PPO.policy[i][ii][iii] += THIS.alpha * Q_PPO.gradient[i][ii][iii];
         }
      }
   }
}

Dentro de esta función, cubrimos esencialmente 3 pasos para actualizar los valores de la política para nuestra estructura PPO, cuyo código compartimos anteriormente. Estos valores de política guían la selección de la siguiente acción en la función de acción y, al ser una función antigua a la que hemos hecho referencia en artículos anteriores, su uso aquí es relevante porque hemos realizado más revisiones a su listado, como se detalla aquí:

//+------------------------------------------------------------------+
//| Choose an action using epsilon-greedy approach                   |
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   //printf(__FUNCSIG__+" next state is: %i, with best act as: %i ",_next_state,_best_act);
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   states[1] = states[0];
   states[0] = GetMarkov(_next_row, _next_col);
   td_value = Q_V[_next_row][_next_col];
   td_policies[1][0] = td_policies[0][0];
   td_policies[1][1] = td_policies[0][1];
   td_policies[1][2] = td_policies[0][2];
   td_policies[0][0] = _next_row;
   td_policies[0][1] = td_value;
   td_policies[0][2] = _next_col;
   q_sa_act = 1;
   q_ppo_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[q_sa_act][_next_row][_next_col])
      {  q_sa_act = i;
      }
      if(Q_PPO.policy[i][_next_row][_next_col] > Q_PPO.policy[q_ppo_act][_next_row][_next_col])
      {  q_ppo_act = i;
      }
   }
//update last acts
   acts[1] = acts[0];
   acts[0] = q_ppo_act;
}

Sin embargo, volviendo a la función de política establecida y sus tres pasos, el primero de ellos cuantifica el peso total de la política para cada acción en todos los estados. En esencia, es una forma de aplanar la matriz de estados del entorno mediante una función get-Markov que devuelve un índice único a partir de dos valores de índice (que representan patrones a corto y largo plazo). Una vez que estemos armados con estos pesos acumulativos para cada acción en la matriz que hemos denominado '_policies', podemos proceder a calcular los gradientes de actualización para nuestros pesos de políticas.

Los gradientes que se almacenan en la matriz de gradientes que introdujimos en la estructura PPO anterior actualizan nuestros pesos de políticas, de forma muy similar a como una red neuronal actualiza sus pesos. Sin embargo, obtener los valores del gradiente, como en la mayoría de las redes neuronales modernas, es todo un proceso. Primero, necesitamos definir un vector '_probabilities' cuyo tamaño coincida con el índice aplanado de los estados del entorno. En este caso es 3 x 3, lo que da como resultado 9. Otra introducción o cambio a la clase Cql que hemos realizado con PPO es la introducción de la matriz de estados de tamaño 2. Esta matriz simplemente registra o almacena en búfer los dos últimos índices de estado del entorno que ha "experimentado" el actor, y el propósito de este registro es ayudar a actualizar los gradientes.

Entonces, con la matriz '_policies' donde para cada acción y índice de estado aplanado tenemos el peso acumulado de la política, obtenemos una distribución de probabilidad en todos los estados para cada acción. Ahora bien, dado que la ponderación de la política puede ser negativa, necesitamos normalizar los valores brutos en el rango de 0 a 1, y una de las formas más sencillas de lograr esto es utilizando las funciones de activación integradas con activación SoftMax. Realizamos estas activaciones en forma consecutiva y una vez realizadas obtenemos probabilidades para el estado anterior y el estado del entorno actual. Nuevamente, aquí utilizamos índices aplanados para mayor brevedad.

La otra métrica importante que necesitamos obtener en esta etapa es la ventaja. Recordemos que, como se mencionó anteriormente, esta ventaja nos ayuda a normalizar o equilibrar nuestras actualizaciones de pesos de políticas para tener en cuenta tanto los pesos basados en la acción del estado a corto plazo como los pesos basados en el valor a largo plazo, un proceso que hace que las selecciones de acciones de PPO sean mejores para combinar la acción del precio a corto plazo con las recompensas a largo plazo como ya se argumentó anteriormente. Esta ventaja se obtiene restando la matriz de pesos Q-Value que presentamos en el artículo sobre la diferencia temporal de la matriz de pares estado-acción que presentamos en nuestro primer artículo sobre el aprendizaje por refuerzo. Ambos cambian de nombre, pero su funcionamiento y principios siguen siendo los mismos.

Con esta ventaja, calculamos entonces cuánto debemos recortar las actualizaciones. Como se mencionó en las introducciones anteriores, PPO se distingue de otros algoritmos de gestión de políticas debido a la forma en que modera sus actualizaciones al garantizar que no sean demasiado drásticas y que sean en su mayoría incrementales para el éxito a largo plazo. La determinación de '_clip' se realiza mediante la función get-clipping, cuya fuente se comparte a continuación:

//+------------------------------------------------------------------+
//| Helper function to compute the clipped PPO objective             |
//+------------------------------------------------------------------+
double Cql::GetClipping(double OldProbability, double NewProbability, double Advantage)
{  double _ratio = NewProbability / OldProbability;
   double _clipped_ratio = fmin(fmax(_ratio, 1 - THIS.epsilon), 1 + THIS.epsilon);
   return fmin(_ratio * Advantage, _clipped_ratio * Advantage);
}

El código de esta función es muy breve y la probabilidad anterior no debe ser cero; de lo contrario, se puede agregar un valor épsilon al denominador para comprobarlo. Una vez que tenemos el '_clip' que en esencia es una fracción normalizada, multiplicamos esto por la diferencia entre las dos probabilidades. Es de destacar aquí que la ventaja y también el producto entre el clip y la diferencia de probabilidad pueden ser positivos o negativos. Esto implica que los gradientes de actualización también pueden tener signo, es decir, ser negativos o positivos.

Esto conduce a las actualizaciones reales de los pesos de las políticas, que como se mencionó anteriormente, son muy similares a la actualización de pesos de la red neuronal y también, al estar basadas en los gradientes anteriores, pueden ser negativas o positivas. Esta firma de pesos de la política PPO es la razón por la que necesitamos activar, mediante SoftMax, las sumas de pesos de cada acción al calcular las distribuciones de probabilidad resaltadas en la segunda fase de establecimiento de la política. Una vez que se actualizan los pesos de las políticas, se utilizan de la siguiente manera en la función de acción modificada cuyo listado actualizado se compartió anteriormente.

El ajuste de la antigua función de Acción es muy pequeño, ya que simplemente verificamos la magnitud del peso de la política donde se selecciona la acción con el peso más alto, siguiendo nuestro régimen de actualización de PPO mencionado anteriormente. Dada la siguiente acción, ahora podemos recuperar esto con la función de obtención de salida que también, como ya se reiteró anteriormente, define las matrices de estado del entorno y la lista para esto se proporciona a continuación. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalPPO::GetOutput(Cql *QL, int RewardSign)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = RewardSign*_in_row[m_scale - 1];
      double _reward_max = RewardSign*_in_row.Max();
      double _reward_min = RewardSign*_in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float, RewardSign);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
   }
}

Al igual que la función de acción anterior, es muy similar a la que hemos estado usando en los artículos sobre aprendizaje por refuerzo, con cambios prácticamente inexistentes (salvo algunas omisiones clave), dado que las funciones clave que llamamos ahora con PPO están ocultas; concretamente, la función de política de configuración y la función de recorte de obtención. Claramente, parece una versión diluida de la salida de obtención que hemos estado usando. A modo de resumen de lo mencionado anteriormente, la 'escala m' puede verse aquí como nuestro rezago que separa las tendencias del mercado en el horizonte temporal corto de las tendencias a largo plazo mientras se utiliza un único marco temporal. El lector puede explorar alternativas que utilicen marcos temporales diferentes, pero en ese caso habría que añadir un marco temporal alternativo como entrada. Los cambios 'significativos' que tenemos en la clase de señal personalizada están en las funciones de condición larga y corta, cuyo código se comparte a continuación:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::LongCondition(void)
{  int result = 0;
   GetOutput(RL_BUY, 1);
   if(RL_BUY.q_ppo_act==0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::ShortCondition(void)
{  int result = 0;
   GetOutput(RL_SELL, -1);
   if(RL_SELL.q_ppo_act==2)
   {  result = 100;
   }
   return(result);
}

La lista es casi idéntica a la que hemos estado usando, con la principal diferencia siendo la referencia a 'q_ppo_act' en oposición a la acción que se seleccionó puramente a partir del proceso de decisión de Markov.

Informes y análisis del Probador de estrategias

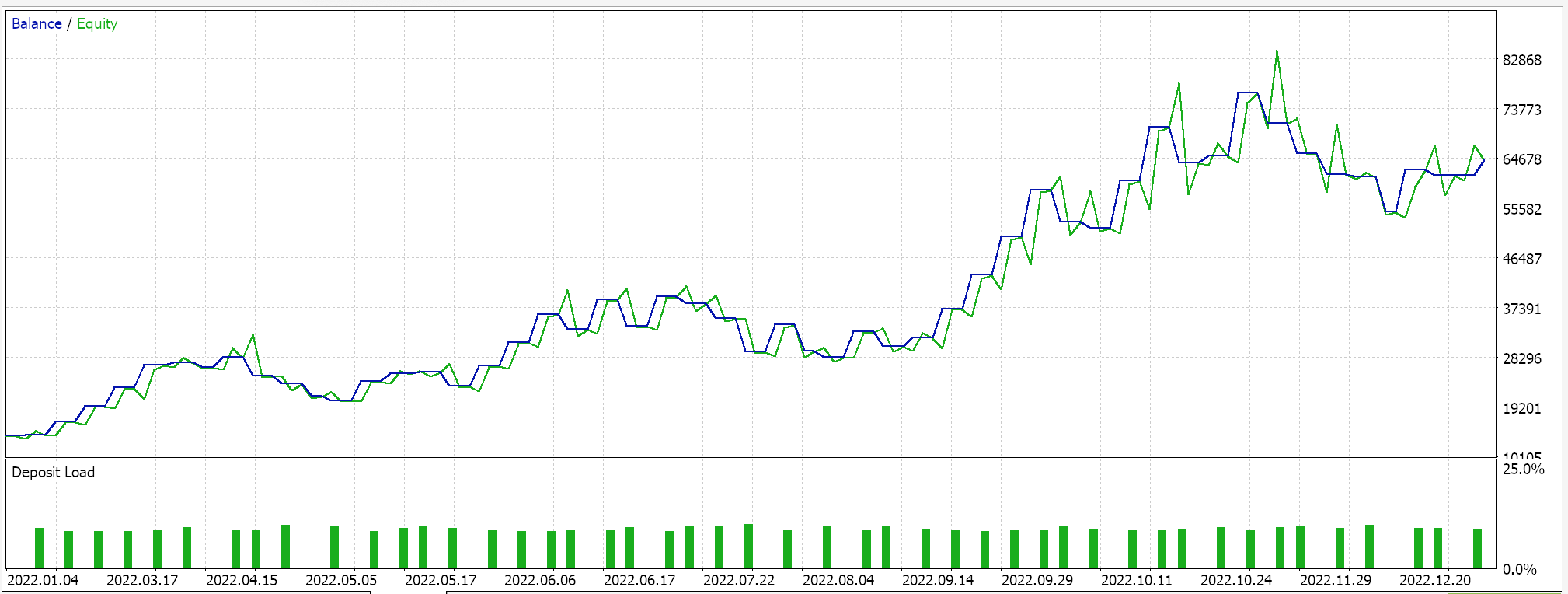
Assemblamos esta clase de señal personalizada en un Asesor Experto utilizando el Asistente MQL5 (MQL5 Wizard). Para los lectores nuevos, hay guías aquí y aquí sobre cómo hacerlo. Si extraemos algunos ajustes favorables de la optimización del GBP JPY durante el año 2022 en el marco temporal de 4 horas, nos presentan los siguientes resultados:

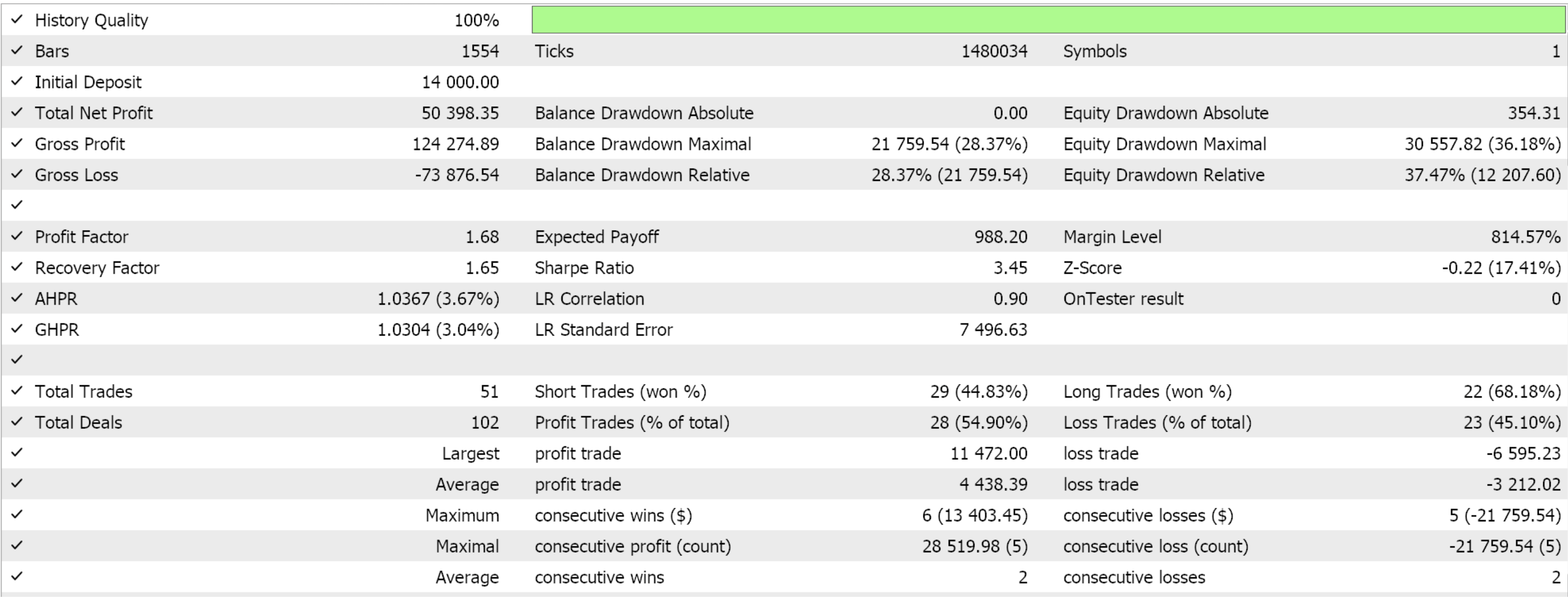
Como siempre, los resultados aquí presentados tienen como objetivo mostrar el potencial de la señal personalizada. Las configuraciones de entrada utilizadas para este informe no se validan de forma cruzada y, por lo tanto, no se comparten. Se invita al lector a participar en esto adaptándolo a sus expectativas.

Mi filosofía al respecto es que cualquier Asesor Experto, ya sea para usarse de manera totalmente automatizada o para respaldar un sistema de trading manual, nunca puede contribuir con más del 50% a todo el "sistema de trading". Las emociones humanas son siempre la otra mitad. Así, incluso si le presentas "el Santo Grial" a alguien que no está familiarizado con sus complejidades o su funcionamiento, es probable que se vuelva impulsivo y cuestione muchas de sus decisiones comerciales clave. Entonces, al presentar una señal personalizada sin sus configuraciones "grial", se invita al lector no solo a comprender por qué el Asesor Experto puede haber tenido un desempeño favorable en el corto período optimizado que se presenta en los artículos, sino también a comprender por qué puede no tener un desempeño similar en diferentes períodos de prueba, y estas dos piezas de información deberían ayudar a comenzar el proceso de revelar configuraciones que pueden funcionar durante períodos más amplios.

Creo que este proceso en el que el trader desarrolla su propia configuración o combina diferentes señales personalizadas en un Asesor Experto funcional es la forma en que compensan su 50%.

Conclusión

Hemos analizado otro algoritmo de aprendizaje de refuerzo, la optimización de políticas proximales, y es un método muy popular y eficaz gracias a su moderación de las actualizaciones de políticas durante los episodios de aprendizaje de refuerzo.

El algoritmo PPO presenta un enfoque pionero para el aprendizaje de refuerzo, combinando estabilidad y adaptabilidad de políticas, que son cruciales para aplicaciones del mundo real como el comercio. Su estrategia de recorte personalizada admite acciones tanto discretas como continuas y ofrece una eficiencia escalable sin una dependencia intensiva de recursos, lo que la hace invaluable para sistemas complejos que enfrentan una amplia variedad de condiciones de mercado.

Nombre del archivo	Descripción
Cql.mqh	Clase fuente de aprendizaje por refuerzo.
SignalWZ_49.mqh	Archivo de clase de señal personalizada.
wz_49.mqh	Asistente para crear un asesor experto cuyo encabezado sirve para mostrar los archivos utilizados.