Información mutua como criterio para la selección de características paso a paso

Introducción

La información mutua es una herramienta valiosa para identificar predictores efectivos, especialmente cuando se trata de relaciones complejas y no lineales. Puede descubrir dependencias que otros métodos podrían pasar por alto, lo que lo hace especialmente adecuado para modelos que pueden explotar dichas complejidades. Este artículo explora la aplicación de la información mutua en la selección de características, centrándose en el algoritmo propuesto por Hanchuan Peng, Fuhui Long y Chris Ding en su artículo de investigación titulado "Selección de características basada en información mutua: criterios de máxima dependencia, máxima relevancia y Redundancia mínima".

Comenzaremos analizando la estimación de información mutua para variables continuas y luego profundizaremos en el proceso de selección de características en sí. Finalmente, ilustraremos la efectividad del algoritmo mediante ejemplos que involucran conjuntos de datos sintéticos y del mundo real.

Estimación de la información mutua de variables continuas

La información mutua, denotada como I(X;Y), cuantifica la información compartida entre dos variables aleatorias, X e Y. Para las variables discretas, su cálculo es relativamente sencillo e implica la suma de las probabilidades conjuntas y marginales.

Sin embargo, las variables continuas plantean un desafío importante debido a su rango infinito de valores posibles. Un enfoque común para abordar esto implica discretizar las variables continuas en contenedores y luego aplicar la fórmula de información mutua discreta. Lamentablemente, la precisión de este método es muy sensible al ancho del contenedor o al número de contenedores elegidos, lo que puede generar una variabilidad sustancial en la información mutua estimada.

Para calcular información mutua para variables continuas, debemos pasar de sumas discretas a integrales continuas. Esto requiere conocimiento de las funciones de densidad de probabilidad conjunta y marginal (PDF), que a menudo no están disponibles debido a los datos limitados. La técnica de la ventana Parzen proporciona una solución al aproximar los PDF directamente a partir de los datos. Este método implica colocar una función de ventana sobre los datos y calcular una suma ponderada de los puntos de datos dentro de la ventana. El peso asignado a cada punto de datos disminuye con su distancia desde el centro de la ventana. Al mover esta ventana a través del espacio de datos y calcular la suma ponderada en cada punto, podemos construir una estimación de la función de densidad de probabilidad.

Esta técnica es particularmente útil en escenarios donde la distribución subyacente es desconocida o compleja. Al adaptar la forma y el tamaño de la ventana, podemos ajustar la suavidad y la precisión de la estimación de densidad. Sin embargo, es importante tener en cuenta que la elección de los parámetros de la ventana puede afectar significativamente la calidad de la estimación. La efectividad de la estimación de densidad de Parzen depende de la selección de una función de ponderación apropiada, que idealmente debería integrarse a la unidad y exhibir un decaimiento rápido a medida que el argumento se aleja de cero. Una opción popular para esta función de ponderación es la función gaussiana, caracterizada por un parámetro de escala, sigma.

Sin embargo, determinar el valor óptimo de sigma es una tarea difícil, que a menudo resulta en una variabilidad significativa en la densidad estimada. Esta sensibilidad a la elección de sigma es una desventaja importante del método de la ventana de Parzen, lo que lo hace menos que ideal para tareas como la evaluación de candidatos a predictores, donde la estimación precisa de la densidad es un requisito previo.

Una alternativa al método de la ventana de Parzen para estimar información mutua entre variables continuas es la partición adaptativa. La partición adaptativa ofrece una mejora significativa respecto del enfoque ingenuo de agrupamiento fijo. Al subdividir iterativamente regiones con alto contenido de información, la partición adaptativa enfoca eficazmente los recursos computacionales en las áreas más relevantes del espacio de datos. Este enfoque específico produce estimaciones más precisas de la información mutua, en particular cuando se trata de distribuciones complejas y no uniformes. Una fortaleza clave del particionamiento adaptativo radica en su capacidad de adaptarse a la estructura de datos subyacente. El proceso de partición recursiva garantiza que las regiones con dependencias significativas se subdividan aún más, mientras que las regiones con información mínima permanecen intactas. Este enfoque dinámico evita los errores comunes del binning fijo, que puede suavizar o sobreajustar los datos.

Además, la partición adaptativa incorpora pruebas estadísticas para guiar el proceso de partición. Al evaluar la significancia estadística de posibles subdivisiones, la partición adaptativa puede distinguir entre información genuina y ruido aleatorio. Esto ayuda a evitar el sobreajuste, que de otro modo podría conducir a estimaciones infladas de la información mutua. El problema principal del método ingenuo es que presta excesiva atención a las áreas del dominio bivariado con pocos o ningún caso, mientras que potencialmente descuida las regiones densas donde se encuentra la mayor parte de la información.  

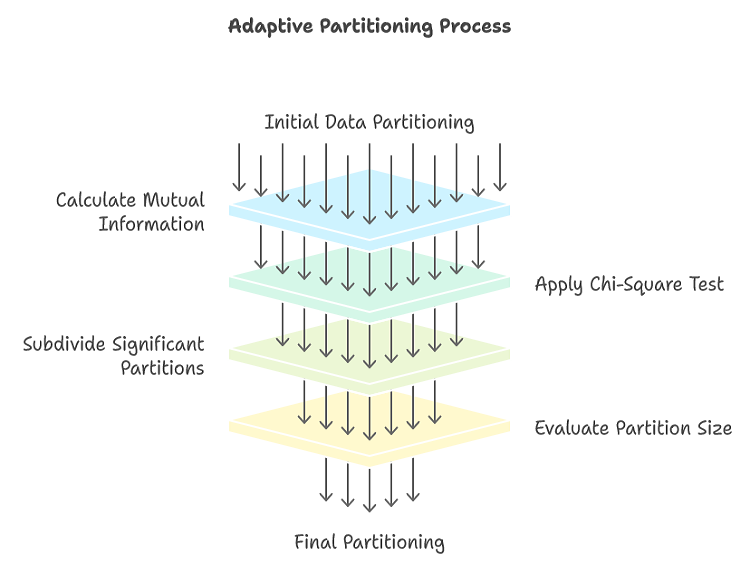
La partición adaptativa comienza con una partición de grano grueso del espacio de datos. Para cada partición, se calcula la información mutua entre las variables. Si este valor supera un umbral predefinido, la partición se subdivide en subparticiones más pequeñas. Este proceso de partición recursiva continúa hasta que se cumple un criterio de detención. Si el proceso de partición se detiene demasiado pronto, las particiones resultantes pueden ser demasiado burdas, lo que causa una pérdida de detalle y un sesgo descendente en la información mutua estimada. Por el contrario, si el proceso de partición continúa durante demasiado tiempo, las particiones pueden llegar a tener un tamaño excesivamente fino, lo que produce un sobreajuste y una estimación inflada de la información mutua debido al ruido.

Para determinar si una partición debe subdividirse aún más, se utiliza una prueba de chi-cuadrado. Esta prueba evalúa la independencia entre las dos variables dentro de la partición. La partición se divide en cuatro subparticiones, creando una tabla de contingencia de 2x2. Se cuenta el número de puntos de datos que caen en cada una de las cuatro subparticiones. Bajo la hipótesis nula de independencia entre las dos variables, el número esperado de puntos de datos en cada subpartición se calcula en función de los totales marginales. Luego, la estadística de chi-cuadrado calculada se compara con un valor crítico de la distribución de chi-cuadrado con 1 grado de libertad. Si el valor calculado excede el valor crítico, se rechaza la hipótesis nula de independencia, lo que indica una relación significativa entre las dos variables dentro de la partición.

Si la prueba de chi-cuadrado es significativa, la partición se subdivide en particiones más pequeñas. Este proceso continúa recursivamente hasta que las particiones se vuelven suficientemente homogéneas o se cumple el criterio de detención. Si la prueba de chi-cuadrado no es significativa, la partición se considera homogénea y no es necesaria ninguna subdivisión adicional.

Para abordar la posibilidad de una relación más compleja dentro de una partición que podría pasar desapercibida con una simple división de 2x2, el algoritmo incorpora una verificación adicional. Si la prueba de chi-cuadrado 2x2 no detecta una relación significativa, pero la partición sigue siendo relativamente grande, se realiza una división 4x4 más refinada. Luego se aplica una prueba de chi-cuadrado a esta partición de 4x4 para evaluar la presencia de una distribución no aleatoria. Si la prueba 4x4 tampoco detecta una relación significativa, la partición se considera homogénea y se calcula su contribución a la información mutua general. En este caso no es necesaria ninguna subdivisión adicional.

Si la prueba de chi-cuadrado 2x2 o 4x4 indica una distribución no uniforme dentro de una partición, la partición se subdivide en cuatro subparticiones más pequeñas. Estas subparticiones se manejan de forma diferente comprobando su tamaño. Si una subpartición es demasiado pequeña, se considera terminal. Se calcula su contribución a la información mutua general y la partición ya no se considera para una subdivisión posterior. De lo contrario, si una subpartición es suficientemente grande, se marca como candidata para una subdivisión futura.

La estadística estándar de prueba de chi-cuadrado de dos por dos se muestra en la siguiente ecuación.

Particionamiento adaptativo en MQL5

La clase Capm en mutualinfo.mqh implementa el algoritmo de partición adaptativa para estimar información mutua para variables continuas. Para gestionar el proceso de particionamiento recursivo, utiliza la estructura personalizada IntStack. Esta estructura contiene información sobre las particiones y cualquier subpartición contenida en ella. La estructura cuenta con seis miembros, que se detallan a continuación:

• Xstart y Xstop: definen el rango de índices para una variable dentro de la partición envolvente actual.
• Ystart y Ystop: definen el rango de índices para una segunda variable dentro de la partición envolvente actual.
• DataStart y DataStop: especifican los índices de inicio y finalización de los puntos de datos dentro de una partición envolvente, marcando las subparticiones.
  

//+------------------------------------------------------------------+
//| int type stack structure                                         |
//+------------------------------------------------------------------+
struct IntStack
  {
   int Xstart ;     // X value (rank) at which this rectangle starts
   int Xstop ;      // And stops
   int Ystart ;     // Ditto for Y
   int Ystop ;
   int DataStart ;  // Starting index into indices for the cases in this
   int DataStop ;   // rectangle, and the (inclusive) ending index
  };

El constructor Capm toma tres argumentos:

• no_split: un indicador booleano que determina cómo manejar valores que son aproximadamente iguales. Si se establece como verdadero, el algoritmo garantiza que dichos valores se agrupen durante la partición, evitando que se separen en particiones diferentes.
• dep_vals: Un vector que contiene los valores de una de las variables a analizar. Esta variable suele ser aquella cuya información mutua se calculará frente a muchas otras variables.
• chi_critical_value: Un umbral para las pruebas de chi-cuadrado utilizadas en el proceso de partición. Este valor determina el nivel de significancia para las pruebas e influye en la profundidad de la partición. Los valores entre 4,0 y 8,0 son generalmente adecuados, siendo 6,0 una opción común con utilidad universal.
  

//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
Capm::Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0)
  {
   m_no_split = no_split;
   m_size = int(dep_vals.Size()) ;
   m_chi_crit = chi_critical_value;

   if(ArrayResize(m_indices,m_size)<0 || !m_tempvals.Resize(m_size) || ArrayResize(m_ranks,m_size)<0
      || (m_no_split && ArrayResize(m_tied_ranks,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return;
     }

   for(int i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = dep_vals[i] ;
      m_indices[i] = i ;
     }

   qsortdsi(0, m_size-1, m_tempvals, m_indices) ;

   for(int i=0 ; i<m_size ; i++)
     {
      m_ranks[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         m_tied_ranks[i] = 1 ;
      else
         m_tied_ranks[i] = 0 ;
     }
  }

El constructor de la clase Capm comienza estableciendo el indicador no_split, que determina si se deben tener en cuenta los vínculos en los datos, y chi_critical_value, que establece el umbral para la prueba de chi-cuadrado utilizada para identificar relaciones significativas entre variables. A continuación, el constructor asigna memoria para que las matrices almacenen los datos, los rangos y los valores vinculados. Copia los valores de las variables en un vector temporal y los ordena. Los índices originales de los puntos de datos se conservan en la matriz m_indices. Por último, el constructor asigna rangos a los puntos de datos ordenados e identifica cualquier valor empatado, marcándolos en la matriz m_tied_ranks si el indicador no_split está configurado.

//+------------------------------------------------------------------+
//| Mutual information using the Adaptive partitioning method        |
//+------------------------------------------------------------------+
class Capm
  {

public:
                     Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0) ;
                    ~Capm(void) ;
   double            fit(vector &raw) ;

private:
   bool               m_no_split;  // respect ties
   int m_size ;                        // Number of cases
   int m_ranks[] ;                     // 'Dependent' variable ranks
   int m_tied_ranks[] ;                // tied[i] != 0 if case with rank i == case with rank i+1
   double m_chi_crit ;                 // Chi-square test criterion
   int               m_indices[];      // indices
   vector            m_tempvals;       // temp values
  } ;

El método fit() de la clase Capm está diseñado para estimar la información mutua entre una variable (proporcionada al constructor) y otra variable suministrada como argumento. Toma un solo vector como entrada, que representa los valores de una segunda variable. Este vector debe tener la misma dimensión que el vector proporcionado al constructor. Al llamar al método fit() varias veces con diferentes vectores, podemos calcular de manera eficiente la información mutua entre una variable y varias variables.

//+------------------------------------------------------------------+
//|  mutual information for continuous variables                     |
//+------------------------------------------------------------------+
double Capm::fit(vector &raw)
  {
   int i, k, ix, iy, nstack, splittable ;
   int current_indices[], x[], fullXstart, fullXstop, fullYstart, fullYstop, ipos ;
   int trialXstart[4], trialXstop[4], trialYstart[4], trialYstop[4] ;
   int ipx, ipy, xcut[4], ycut[4], iSubRec, x_tied[], ioff ;
   int X_AllTied, Y_AllTied ;
   int centerX, centerY, currentDataStart, currentDataStop ;
   int actual[4], actual44[16] ;
   vector expected(16), xfrac(4), yfrac(4) ;
   double diff, testval;
   double px, py, pxy, MI ;

   IntStack stack[];

   if(ArrayResize(stack,1,256)<0)
     {
      Print(__FUNCTION__," arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   if(ArrayResize(current_indices,m_size)<0 || ArrayResize(x,m_size)<0
      || (m_no_split && ArrayResize(x_tied,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = raw[i] ;
      m_indices[i] = i ;
     }

   if(!qsortdsi(0, m_size-1, m_tempvals, m_indices))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      x[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         x_tied[i] = 1 ;
      else
         x_tied[i] = 0 ;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_indices[i] = i ;
     }

   stack[0].Xstart = 0 ;
   stack[0].Xstop = m_size-1 ;
   stack[0].Ystart = 0 ;
   stack[0].Ystop = m_size-1 ;
   stack[0].DataStart = 0 ;
   stack[0].DataStop = m_size-1 ;
   nstack = 1 ;

   MI = 0.0 ;
   while(nstack > 0)
     {

      --nstack ;
      fullXstart = stack[nstack].Xstart ;
      fullXstop = stack[nstack].Xstop ;
      fullYstart = stack[nstack].Ystart ;
      fullYstop = stack[nstack].Ystop ;
      currentDataStart = stack[nstack].DataStart ;
      currentDataStop = stack[nstack].DataStop ;


      centerX = (fullXstart + fullXstop) / 2 ;
      X_AllTied = (x_tied.Size())  && (x_tied[centerX] != 0) ;
      if(X_AllTied)
        {
         for(ioff=1 ; centerX-ioff >= fullXstart ; ioff++)
           {
            if(! x_tied[centerX-ioff])
              {
               X_AllTied = 0 ;
               centerX -= ioff ;
               break ;
              }
            if(centerX + ioff == fullXstop)
               break ;
            if(! x_tied[centerX+ioff])
              {
               X_AllTied = 0 ;
               centerX += ioff ;
               break ;
              }
           }
        }

      centerY = (fullYstart + fullYstop) / 2 ;
      Y_AllTied = (m_tied_ranks.Size())  && (m_tied_ranks[centerY] != 0) ;
      if(Y_AllTied)
        {
         for(ioff=1 ; centerY-ioff >= fullYstart ; ioff++)
           {
            if(! m_tied_ranks[centerY-ioff])
              {
               Y_AllTied = 0 ;
               centerY -= ioff ;
               break ;
              }
            if(centerY + ioff == fullYstop)
               break ;
            if(! m_tied_ranks[centerY+ioff])
              {
               Y_AllTied = 0 ;
               centerY += ioff ;
               break ;
              }
           }
        }

      if(X_AllTied  ||  Y_AllTied)
         splittable = 0 ;
      else
        {
         trialXstart[0] = trialXstart[1] = fullXstart ;
         trialXstop[0] = trialXstop[1] = centerX ;
         trialXstart[2] = trialXstart[3] = centerX+1 ;
         trialXstop[2] = trialXstop[3] = fullXstop ;
         trialYstart[0] = trialYstart[2] = fullYstart ;
         trialYstop[0] = trialYstop[2] = centerY ;
         trialYstart[1] = trialYstart[3] = centerY+1 ;
         trialYstop[1] = trialYstop[3] = fullYstop ;

         for(i=0 ; i<4 ; i++)
            expected[i] = (currentDataStop - currentDataStart + 1) *
                          (trialXstop[i]-trialXstart[i]+1.0) / (fullXstop-fullXstart+1.0) *
                          (trialYstop[i]-trialYstart[i]+1.0) / (fullYstop-fullYstart+1.0) ;

         actual[0] = actual[1] = actual[2] = actual[3] = 0 ;
         for(i=currentDataStart ; i<=currentDataStop ; i++)
           {
            k = m_indices[i] ;
            if(x[k] <= centerX)
              {
               if(m_ranks[k] <= centerY)
                  ++actual[0] ;
               else
                  ++actual[1] ;
              }
            else
              {
               if(m_ranks[k] <= centerY)
                  ++actual[2] ;
               else
                  ++actual[3] ;
              }
           }

         testval = 0.0 ;
         for(i=0 ; i<4 ; i++)
           {
            diff = fabs(actual[i] - expected[i]) - 0.5 ;
            testval += diff * diff / expected[i] ;
           }

         splittable = (testval > m_chi_crit)  ?  1 : 0 ;

El método comienza inicializando una pila para administrar el proceso de partición. Todo el conjunto de datos se inserta inicialmente en la pila como partición raíz. Posteriormente, el algoritmo extrae iterativamente una partición de la pila y evalúa su homogeneidad. Se aplica una prueba de chi-cuadrado para evaluar la significancia estadística de cualquier relación potencial entre las variables dentro de la partición. Si la prueba indica una relación significativa, la partición se divide en cuatro subparticiones y cada subpartición se vuelve a colocar en la pila para su posterior consideración. Este proceso continúa hasta que todas las particiones cumplen el criterio de detención o se vuelven homogéneas.

if(! splittable && fullXstop-fullXstart > 30 && fullYstop-fullYstart > 30)
           {
            ipx = fullXstart - 1 ;
            ipy = fullYstart - 1 ;
            for(i=0 ; i<4 ; i++)
              {
               xcut[i] = (fullXstop - fullXstart + 1) * (i+1) / 4 + fullXstart - 1 ;
               xfrac[i] = (xcut[i] - ipx) / (fullXstop - fullXstart + 1.0) ;
               ipx = xcut[i] ;
               ycut[i] = (fullYstop - fullYstart + 1) * (i+1) / 4 + fullYstart - 1 ;
               yfrac[i] = (ycut[i] - ipy) / (fullYstop - fullYstart + 1.0) ;
               ipy = ycut[i] ;
              }
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  expected[ix*4+iy] = xfrac[ix] * yfrac[iy] *
                                      (currentDataStop - currentDataStart + 1) ;
                  actual44[ix*4+iy] = 0 ;
                 }
              }
            for(i=currentDataStart ; i<=currentDataStop ; i++)
              {
               k = m_indices[i] ;
               for(ix=0 ; ix<3 ; ix++)
                 {
                  if(x[k] <= xcut[ix])
                     break ;
                 }
               for(iy=0 ; iy<3 ; iy++)
                 {
                  if(m_ranks[k] <= ycut[iy])
                     break ;
                 }
               ++actual44[ix*4+iy] ;
              }
            testval = 0.0 ;
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  diff = fabs(actual44[ix*4+iy] - expected[ix*4+iy]) - 0.5 ;
                  testval += diff * diff / expected[ix*4+iy] ;
                 }
              }
            splittable = (testval > 3 * m_chi_crit)  ?  1 : 0 ;
           }
        }

      if(splittable)
        {

         for(i=currentDataStart ; i<=currentDataStop ; i++)
            current_indices[i] = m_indices[i] ;

         ipos = currentDataStart ;
         for(iSubRec=0 ; iSubRec<4 ; iSubRec++)
           {

            if(actual[iSubRec] >= 3)
              {
               stack[nstack].Xstart = trialXstart[iSubRec] ;
               stack[nstack].Xstop = trialXstop[iSubRec] ;
               stack[nstack].Ystart = trialYstart[iSubRec] ;
               stack[nstack].Ystop = trialYstop[iSubRec] ;
               stack[nstack].DataStart = ipos ;
               stack[nstack].DataStop = ipos + actual[iSubRec] - 1 ;
               ++nstack ;
               if(ArrayResize(stack,nstack+1,256)<0)
                 {
                   Print(__FUNCTION__," arrayresize error ", GetLastError());
                   return EMPTY_VALUE;
                 }

               if(iSubRec == 0)
                 {
                  for(i=currentDataStart ; i<=currentDataStop ; i++)
                    {
                     k = current_indices[i] ;
                     if(x[k] <= centerX  &&  m_ranks[k] <= centerY)
                        m_indices[ipos++] = current_indices[i] ;
                    }
                 }
               else
                  if(iSubRec == 1)
                    {
                     for(i=currentDataStart ; i<=currentDataStop ; i++)
                       {
                        k = current_indices[i] ;
                        if(x[k] <= centerX  &&  m_ranks[k] > centerY)
                           m_indices[ipos++] = current_indices[i] ;
                       }
                    }
                  else
                     if(iSubRec == 2)
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] <= centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
                     else
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] > centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
              }

            else
              {
               if(actual[iSubRec] > 0)
                 {
                  px = (trialXstop[iSubRec] - trialXstart[iSubRec] + 1.0) / m_size ;
                  py = (trialYstop[iSubRec] - trialYstart[iSubRec] + 1.0) / m_size ;
                  pxy = (double) actual[iSubRec] / m_size ;
                  MI += pxy * log(pxy / (px * py)) ;
                 }
              }
           }
        }
      else
        {
         px = (fullXstop - fullXstart + 1.0) / m_size ;
         py = (fullYstop - fullYstart + 1.0) / m_size ;
         pxy = (currentDataStop - currentDataStart + 1.0) / m_size ;
         MI += pxy * log(pxy / (px * py)) ;
        }
     }

   return MI;

Para las particiones que se consideran homogéneas, ya sea debido a una prueba de chi-cuadrado no significativa o a un número mínimo de puntos de datos, se calcula la información mutua. Este cálculo implica estimar las distribuciones de probabilidad conjunta y marginal dentro de la partición y aplicar la fórmula siguiente.

El proceso continúa de forma recursiva, con particiones que se dividen y evalúan hasta que no es posible realizar más divisiones significativas. La estimación final de la información mutua se obtiene sumando las contribuciones de todas las particiones terminales, lo que proporciona una estimación integral basada en la estructura de los datos. Si el método encuentra un error, devuelve el equivalente a la constante EMPTY_VALUE incorporada de MQL5. En una próxima sección, utilizaremos la clase Capm en la implementación de un algoritmo de selección de características paso a paso.

Selección de predictores utilizando información mutua

Al aplicar información mutua a la tarea de selección de características, nuestro objetivo es identificar un subconjunto de predictores de un conjunto más amplio de predictores candidatos que maximice la dependencia conjunta con una variable objetivo. Esta dependencia conjunta es una generalización de información mutua, donde una de las cantidades es una colección de variables en lugar de una sola variable. El cálculo de la dependencia conjunta para subconjuntos más grandes de predictores se vuelve computacionalmente intratable debido a la maldición de la dimensionalidad. Esto ocurre porque la partición multidimensional requerida de los datos genera celdas extremadamente dispersas, especialmente a medida que aumenta el número de dimensiones (predictores).

Además, la gran cantidad de posibles combinaciones de características puede resultar abrumadora incluso para conjuntos de características de tamaño moderado. Esta explosión combinatoria hace que no sea práctico buscar exhaustivamente todos los subconjuntos posibles, lo que requiere el uso de estrategias de búsqueda eficientes.

Un enfoque común para la selección de características es la selección gradual hacia adelante. Este método comienza con un modelo vacío y agrega iterativamente la característica que proporciona la mayor mejora al rendimiento del modelo, según lo medido por un criterio elegido. Si bien este enfoque es eficiente, tiene la limitación de ser codicioso. Es posible que no se detecten combinaciones óptimas de características, como en los casos en que dos características, al combinarse, proporcionan un poder de predicción significativamente mejor que cualquiera de ellas por sí sola. Esto se debe a que el algoritmo se centra en mejoras incrementales en cada paso, pasando por alto potencialmente las relaciones sinérgicas entre las características.

Si bien existen otras técnicas, como los métodos de orden superior y la selección hacia atrás, la selección progresiva hacia adelante sigue siendo la opción más práctica debido a su eficiencia computacional, especialmente cuando se trabaja con grandes conjuntos de datos y recursos computacionales limitados. Además, cuando se aplica al contexto específico de dependencia conjunta, la selección gradual hacia adelante exhibe una propiedad sorprendente: puede aproximarse de manera efectiva al subconjunto de características óptimo, aunque no optimice explícitamente la medida de dependencia conjunta.

Peng, Long y Ding propusieron un algoritmo de selección de características basado en información mutua, conocido como criterio de máxima relevancia, mínima redundancia (MRMR). Este algoritmo aproxima de manera eficiente el subconjunto de características óptimo sin calcular explícitamente la dependencia conjunta, lo cual resulta computacionalmente intratable. El criterio MRMR se basa en el concepto de relevancia y redundancia. La relevancia de un conjunto de características S para la variable objetivo Y se define como la información mutua promedio entre Y y cada característica en S.

Aquí ∣S∣ es el número de características en S e I(Xi,Y) es la información mutua entre la característica Xi e Y.

Si bien maximizar la relevancia es intuitivo, puede conducir a un subconjunto de características subóptimo debido a la redundancia. Si simplemente seleccionamos características en función de su relevancia individual para la variable objetivo, podemos terminar con un conjunto de características altamente correlacionadas que brinden poca información adicional. Para abordar esta cuestión, debemos considerar no sólo la relevancia de una característica, sino también su redundancia con las características ya seleccionadas.

La redundancia de un candidato a predictor Xi​ con respecto a un conjunto de características ya seleccionado S se define como la información mutua promedio entre Xi​ y cada característica en S:

Donde I(Xi,Xj) es la información mutua entre la característica candidata Xi y la característica Xj ya en S.

Es importante señalar que la expresión matemática para la redundancia es idéntica a la expresión para la relevancia. La única diferencia radica en la interpretación. Cuando calculamos la información mutua entre una característica candidata y la variable objetivo, la denominamos relevancia. Sin embargo, cuando calculamos la información mutua entre una característica candidata y una característica que ya está en el conjunto seleccionado, lo llamamos redundancia.

Básicamente, ambos conceptos implican medir la cantidad de información compartida entre dos variables, pero el contexto determina si se considera relevante o redundante. En relevancia, nos preocupa la relación entre la característica y la variable objetivo, mientras que en redundancia, nos centramos en cuánta superposición existe entre la característica candidata y las características ya seleccionadas.

En resumen, el algoritmo MRMR funciona de la siguiente manera:

1. La característica con la mayor información mutua con la variable objetivo Y se selecciona como la primera característica.
2. En cada paso subsiguiente, el algoritmo selecciona la característica que maximiza el siguiente criterio.
   

Este criterio equilibra la relevancia de la característica para la variable objetivo Y (es decir, I(X_i, Y)) con su redundancia con la característica ya seleccionada. El aspecto destacable del algoritmo MRMR es que aproxima eficazmente el subconjunto de características óptimo, aunque optimizar directamente la dependencia conjunta es computacionalmente intratable. Este resultado, aunque no es inmediatamente obvio, está matemáticamente probado en el artículo original.

Para evaluar la significancia estadística de las características seleccionadas, se pueden emplear dos pruebas de permutación de Monte Carlo (MCP):

• Significación de características individuales: esta prueba evalúa la significación de cada característica individual comparando su relevancia para la variable objetivo con una distribución nula obtenida mediante permutación. Al permutar los valores de las características, creamos una distribución nula que supone que la característica no tiene relación con el objetivo. Si la relevancia observada es significativamente mayor que los valores permutados, podemos concluir que es probable que la característica sea verdaderamente informativa.
• Significación general del modelo: esta prueba evalúa la significancia de todo el conjunto de características seleccionadas comparando la suma acumulada de la relevancia de las características individuales con una distribución nula obtenida mediante permutación. Al permutar los valores de la variable objetivo, creamos una distribución nula que supone que las características no tienen relación con el objetivo. Si la relevancia acumulada observada es significativamente mayor que los valores permutados, podemos concluir que es probable que el conjunto de características seleccionado sea predictivo de la variable objetivo.
  

Implementación MQL5 de selección por pasos basada en información mutua

La clase Cmrmr en mutualinfo.mqh implementa el algoritmo MRMR y toma los siguientes parámetros en su constructor:

• num_reps: El número de réplicas para las pruebas de permutación de Monte Carlo. Si se establece este valor en un valor menor o igual a 1, se deshabilitan las pruebas.
• max_preds: El número máximo de características que se seleccionarán.
• chisquare_thresh: El umbral de la prueba de chi-cuadrado para el método de partición adaptativa utilizado para estimar información mutua.
• m_verbose: Un indicador booleano para controlar si se debe mostrar una salida detallada durante la ejecución del algoritmo.
  

//+-----------------------------------------------------------------------+
//|Relevance minus redundancy for building an optimal subset of predictors|
//+-----------------------------------------------------------------------+
class Cmrmr
  {
private:
   int               m_max_preds;
   int               m_reps;
   bool              m_verbose;
   int               m_samples;
   int               m_vars;
   matrix            m_preds;
   vector            m_target;
   vector            m_crits;
   double            m_chisquare_thresh;
   ulong             m_selected_vars[];
   matrix            m_critical_values;
   vector            mutualinfo(int which_size,int &which[],vector &targs);
public:
                     Cmrmr(int num_reps,int max_preds, double chisquare_thresh,bool verbose);
                    ~Cmrmr(void);
   bool              StepWise(matrix &predictors, vector &targets);
   matrix            GetCriticalValues(void);
   bool              GetSelectedVars(ulong &output[]);
  };

Para iniciar el proceso de selección de características utilizando la clase Cmrmr, necesitamos instanciar un objeto de esta clase y luego llamar a su método StepWise(). El método StepWise() toma dos entradas principales:

• Una matriz de variables predictoras candidatas: esta matriz debe contener los datos de todas las características potenciales que un profesional desea considerar.
• Un vector de la variable de destino: este vector debe contener los valores de una variable de destino.

El método devuelve un valor booleano que indica el éxito o el fracaso del proceso de selección de características. El método StepWise() de la clase Cmrmr inicializa las estructuras de datos necesarias y luego procede al bucle de prueba MCP. Si no se solicitan pruebas MCP (`num_reps` es menor o igual a 1), el bucle se ejecuta solo una vez. Dentro del bucle, el método calcula la información mutua entre cada predictor candidato y la variable objetivo utilizando una instancia de la clase Capm.

//+------------------------------------------------------------------+
//|  Stepwise feature selection based on mutual information          |
//+------------------------------------------------------------------+
bool Cmrmr::StepWise(matrix &predictors,vector &targets)
  {
   if(m_selected_vars.Size())
      ArrayFree(m_selected_vars);

   m_preds = predictors;
   m_samples = int(m_preds.Rows());
   m_vars = int(m_preds.Cols());
   m_max_preds = m_max_preds>=m_vars?m_vars:m_max_preds;
   m_target = targets;
   
   
   int i, j, k, ivar, irep;
   int index[], stepwise_mcpt_count[], solo_mcpt_count[], stepwise_ivar[], which_preds[],original_stepwise_ivar[] ;

   int nkept,best_ivar;
   vector casework(m_samples), sorted(m_samples), mutual(m_vars);
   vector crit(m_vars), relevance(m_vars), original_relevance(m_vars), current_crits(m_vars), sorted_crits(m_vars);
   double best_crit, dtemp, group_pvalue,solo_pvalue;
   vector stepwise_crit(m_vars), original_stepwise_crit(m_vars);
   double sum_relevance;
   vector original_sum_relevance(m_vars), sum_redundancy(m_vars);
   vector target = m_target;

   best_crit = -DBL_MAX;
   best_ivar = -1;
   nkept = m_max_preds;

   if(ArrayResize(index,m_vars)<0 || ArrayResize(stepwise_mcpt_count,m_vars)<0 ||
      ArrayResize(solo_mcpt_count,m_vars)<0 || ArrayResize(which_preds,m_vars)<0 || ArrayResize(stepwise_ivar,m_vars)<0 ||
      ArrayResize(original_stepwise_ivar,m_vars)<0)
     {
      Print(__FUNCTION__," array resize error ", GetLastError());
      return false;
     }

   int unif_error;
   for(irep=0 ; irep<m_reps ; irep++)
     {
      if(irep)
        {
         i = m_samples ;
         while(i > 1)
           {
            j = (int)(MathRandomUniform(0.0,1.0,unif_error) * i);
            if(unif_error)
              {
               Print(__FUNCTION__," Mathrandomuniform error ", GetLastError());
               return false;
              }
            if(j >= i)
               j = i - 1 ;
            dtemp = target[--i] ;
            target[i] = target[j] ;
            target[j] = dtemp ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         which_preds[i] = i ;

      crit = mutualinfo(m_vars,which_preds,target);

      for(ivar=0 ; ivar<m_vars ; ivar++)
        {
         relevance[ivar] = crit[ivar] ;
         if(ivar == 0  ||  crit[ivar] > best_crit)
           {
            best_crit = crit[ivar] ;
            best_ivar = ivar ;
           }
        }

      stepwise_crit[0] = best_crit ;
      stepwise_ivar[0] = best_ivar ;
      sum_relevance = best_crit ;
      if(irep == 0)
        {

         original_stepwise_crit[0] = best_crit ;
         original_stepwise_ivar[0] = best_ivar ;
         original_sum_relevance[0] = sum_relevance ;
         stepwise_mcpt_count[0] = 1 ;

         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            index[ivar] = ivar ;
            original_relevance[ivar] = sorted_crits[ivar] = current_crits[ivar] = crit[ivar] ;
            solo_mcpt_count[ivar] = 1 ;
           }

         if(!qsortdsi(0, m_vars-1, sorted_crits, index))
           {
            Print(__FUNCTION__, " failed qsort ");
            return false;
           }

         if(m_verbose)
            Print("       Variable         MI") ;

         for(i=m_vars-1 ; i>=0 ; i--)
           {
            k = index[i] ;

            if(m_verbose)
               PrintFormat("%15s %12.4lf",string(k), current_crits[k]) ;
           }
        }

      else
        {
         if(sum_relevance >= original_sum_relevance[0])
            ++stepwise_mcpt_count[0] ;
         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            if(relevance[ivar] >= original_relevance[ivar])
               ++solo_mcpt_count[ivar] ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         sum_redundancy[i] = 0.0 ;

      for(nkept=1 ; nkept<m_max_preds ; nkept++)
        {

         if(irep == 0 && m_verbose)
           {
            Print("Predictors so far   Relevance   Redundancy   Criterion") ;
            for(i=0 ; i<nkept ; i++)
              {
               k = stepwise_ivar[i] ;
               PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), relevance[k], relevance[k] - stepwise_crit[i], stepwise_crit[i]) ;
              }
           }

         k = 0 ;
         for(i=0 ; i<m_vars ; i++)
           {
            for(j=0 ; j<nkept ; j++)
              {
               if(stepwise_ivar[j] == i)
                  break ;
              }
            if(j == nkept)
               which_preds[k++] = i ;
           }
         if(k != (m_vars - nkept))
           {
            Print(__FUNCTION__, " failed assertion ", __LINE__);
            return false;
           }

         k = stepwise_ivar[nkept-1] ;

         casework = m_preds.Col(k);

         crit = mutualinfo(m_vars-nkept,which_preds,casework);

         for(i=0 ; i<(m_vars-nkept) ; i++)
           {
            k = which_preds[i] ;
            sum_redundancy[k] += crit[i] ;
            index[i] = k ;
            sorted_crits[i] = current_crits[i] = ((relevance[k] - sum_redundancy[k]) / double(nkept)) ;
            if(i == 0  ||  current_crits[i] > best_crit)
              {
               best_crit = current_crits[i] ;
               best_ivar = k ;
              }
           }

         stepwise_crit[nkept] = best_crit ;
         stepwise_ivar[nkept] = best_ivar ;
         sum_relevance += relevance[best_ivar] ;

         if(irep == 0)
           {
            original_stepwise_crit[nkept] = best_crit ;
            original_stepwise_ivar[nkept] = best_ivar ;
            original_sum_relevance[nkept] = sum_relevance ;
            stepwise_mcpt_count[nkept] = 1 ;

            if(!qsortdsi(0, m_vars-nkept-1, sorted_crits, index))
              {
               Print(__FUNCTION__, " failed qsort ");
               return false;
              }

            if(m_verbose)
              {
               Print("Additional candidates, in order of decreasing relevance minus redundancy") ;
               Print("       Variable     Relevance   Redundancy   Criterion") ;

               for(i=m_vars-nkept-1 ; i>=0 ; i--)
                 {
                  k = index[i] ;
                  PrintFormat("%15s %12.4lf %12.4lf %12.4lf",
                              string(k), relevance[k], sum_redundancy[k] / nkept,
                              relevance[k] - sum_redundancy[k] / nkept) ;
                 }
              }
           }

         else
           {
            if(sum_relevance >= original_sum_relevance[nkept])
               ++stepwise_mcpt_count[nkept] ;
           }

        }

     }
//---
   m_critical_values = matrix::Zeros(nkept,m_reps>1?5:3);
//---
   if(ArrayResize(m_selected_vars,nkept)<0)
     {
      Print(__FUNCTION__, " failed array resize ", GetLastError());
      return false;
     }
//---
   if(m_verbose)
     {
      if(m_reps > 1)
         Print("Final predictors ||  Relevance ||  Redundancy || Criterion  ||  Solo pval || Group pval") ;
      else
         Print("Final predictors  ||  Relevance ||  Redundancy ||  Criterion") ;
     }
//---
   for(i=0 ; i<nkept ; i++)
     {
      k = original_stepwise_ivar[i] ;
      m_selected_vars[i] = ulong(k);

      m_critical_values[i][0] = original_relevance[k];
      m_critical_values[i][1] = original_relevance[k] - original_stepwise_crit[i];
      m_critical_values[i][2] = original_stepwise_crit[i];

      if(m_critical_values.Cols()>3)
        {
         group_pvalue = (double) stepwise_mcpt_count[i] / (double) m_reps;
         solo_pvalue = (double) solo_mcpt_count[k] / (double) m_reps;
         m_critical_values[i][3] = solo_pvalue;
         m_critical_values[i][4] = group_pvalue;
        }

      if(m_verbose)
        {
         if(m_reps > 1)
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf    %8.3lf    %8.3lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2],solo_pvalue,group_pvalue) ;
         else
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2]);
        }
     }

   return true;

  }

El método mutualinfo(), que es un método privado dentro de la clase Cmrmr, es responsable de estimar la información mutua entre un predictor dado y la variable objetivo utilizando el método de partición adaptativa. Devuelve un vector de aproximaciones de información mutua para los predictores seleccionados especificados como índices de columna para mutualinfo().

//+------------------------------------------------------------------+
//| continuous mutual infomation                                     |
//+------------------------------------------------------------------+
vector Cmrmr::mutualinfo(int which_size,int &which[],vector &targs)
  {
   vector res = vector::Zeros(m_vars);

   res.Fill(-DBL_MAX);

   vector vars;

   Capm mia(true,targs,m_chisquare_thresh);

   for(int i = 0; i<which_size; i++)
     {
      vars = m_preds.Col(which[i]);
      res[i] = mia.fit(vars);
     }

   return res;

  }

El método StepWise() almacena los valores de información mutua calculados en el vector "relevancia", ya que estos valores serán necesarios en iteraciones posteriores para calcular el término de redundancia. La característica con la mayor información mutua se selecciona como la primera característica y su información se almacena en las variables stepwise_crit y stepwise_ivar. Además, se inicializa la variable sum_relevance para realizar un seguimiento de la relevancia acumulativa de las características seleccionadas, que se utilizarán más adelante para la prueba MCP.

Para la replicación inicial no permutada, el algoritmo almacena los valores originales de relevancia y criterio para la primera característica seleccionada. También inicializa contadores para la prueba de significancia del modelo general y pruebas de significancia de características individuales. Además, se genera una tabla que muestra la información mutua de cada característica candidata con la variable objetivo para brindar información sobre las clasificaciones iniciales de las características. Esta tabla ayuda a visualizar el proceso de selección inicial y sirve como referencia para la comparación con los valores permutados durante la fase de prueba de significancia.

Si no estamos en la replicación inicial no permutada, el algoritmo procede a realizar las dos pruebas MCP, diseñadas para evaluar la significancia estadística del conjunto de características seleccionado por el algoritmo MRMR. Para gestionar de manera eficiente la redundancia en evolución a medida que se agregan nuevas características al conjunto seleccionado, el algoritmo utiliza la matriz `sum_redundancy`. La matriz se inicializa con ceros. Esta matriz se utiliza para almacenar la redundancia acumulativa de cada característica candidata en relación con las características que ya se han seleccionado.

Al principio, como no se selecciona ninguna característica, todos los valores de esta matriz se establecen en cero. Cuando se agrega una nueva característica al conjunto seleccionado, se debe actualizar su redundancia con cada una de las características candidatas restantes. La redundancia de una característica con respecto al conjunto seleccionado creciente se define como la información mutua promedio entre la característica candidata y las características ya seleccionadas. Se calcula la información mutua entre la nueva característica y cada una de las características candidatas restantes. Esto cuantifica cuánta información comparte la nueva función con cada una de las funciones seleccionadas. El valor de redundancia de cada característica restante se actualiza agregando el valor de información mutua entre la característica recién agregada y la característica existente.

Después de actualizar los valores de redundancia, el algoritmo calcula el criterio MRMR (máxima relevancia, mínima redundancia) para cada una de las características candidatas restantes. El criterio MRMR se calcula restando la redundancia promedio de cada característica de su relevancia. Una vez calculado el criterio MRMR para todas las características candidatas restantes, se selecciona la característica con la puntuación MRMR más alta. El algoritmo repite este proceso iterativamente, actualizando la matriz `sum_redundancy` y recalculando el criterio MRMR cada vez que se agrega una nueva característica. A medida que se seleccionan más características, la redundancia de las características restantes con el conjunto seleccionado se actualiza continuamente, lo que garantiza que el proceso de selección de características considere las relaciones evolutivas entre las características.

Si esta es la réplica inicial no permutada, los valores originales de estas cantidades se conservan para una comparación posterior durante las pruebas de permutación. De lo contrario, se incrementan los contadores de las pruebas de permutación "grupo" y "solo". Después de completar el número deseado de iteraciones, el algoritmo concluye mostrando una tabla que resume las características seleccionadas, su relevancia y sus valores p de las pruebas de permutación. Después de llamar a `StepWise()` y ejecutarlo exitosamente, se puede invocar `GetCriticalValues()` para obtener una matriz de la tabla de valores mostrada en modo detallado. Mientras tanto, `GetSelectedVars()` recupera los índices de las variables seleccionadas (columnas) correspondientes a la propiedad `m_max_preds` de la clase.

//+------------------------------------------------------------------+
//| get the matrix of decision variables                             |
//| matrix rows arranged in terms of descending relevance of each    |
//| candidate predictor. Most relevant predictors critical values are|
//| in the first row, etc.                                           |
//| Column 0 is the calculated relevance                             |
//| Column 1 is the calculated redundancy                            |
//| Column 2 is the calculated Stepwise Mutual information           |
//| Column 3 and 4 will exist only if MCP test is specified          |
//| Column 3 is the Solo probability value                           |
//| Column 4 are the Group probability values                        |
//+------------------------------------------------------------------+
matrix Cmrmr::GetCriticalValues(void)
{
  return m_critical_values;
}
//+--------------------------------------------------------------------------+
//|get the indices of the most relevant predictors as determined by algorithm|
//+--------------------------------------------------------------------------+
bool Cmrmr::GetSelectedVars(ulong &output[])
{
 return (ArrayCopy(output,m_selected_vars)>0);
}

En la siguiente sección, veremos cómo se aplica la clase Cmrmr utilizando conjuntos de datos sintéticos y del mundo real.

Ejemplos de relevancia menos redundancia

Para ilustrar eficazmente la aplicación del algoritmo MRMR, comenzaremos aplicándolo a un conjunto de datos sintéticos. El conjunto de datos consta de 100 muestras y 10 variables predictoras potenciales (características). La variable objetivo Y se construye sumando las primeras cuatro columnas de la matriz, por lo que la relación entre el objetivo y los predictores es determinista para estas columnas. Sin embargo, las columnas 4 a 7 no brindan información real sobre el objetivo y sirven como características irrelevantes. Las variables en las columnas 8 y 9 son combinaciones de variables en los índices de columna {1,3} y {0,2} respectivamente.

//---
   MathSrand(125);

   matrix rdata(100,10);

   rdata.Random(0.0,1.0);

   vector dep = rdata.Col(0) + rdata.Col(1) + rdata.Col(2) + rdata.Col(3);

   vector sum02 = rdata.Col(0) + rdata.Col(2);

   vector sum13 = rdata.Col(1) + rdata.Col(3);

   if(!rdata.Col(sum13,8) || !rdata.Col(sum02,9))
     {
      Print(" Failed column insertion ", GetLastError());
      return;
     }

El objetivo es utilizar el algoritmo MRMR para identificar las columnas como los predictores más relevantes. Este experimento se implementa en el script RelevanceMinusRedundancy.mq5, que permite la personalización de varios hiperparámetros, incluida la cantidad de permutaciones de Monte Carlo y la cantidad máxima de características a seleccionar. El script está configurado para ejecutarse en modo detallado, proporcionando resultados detallados durante el proceso de selección de características.

//inputs
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;

La salida inicial del script RelevanceMinusRedundancy.mq5 son los valores de información mutua individuales entre cada predictor candidato y la variable objetivo. Organizados en orden descendente de información mutua, lo que permite una fácil identificación de las características más relevantes.

Variable         MI
      9       0.2675
      8       0.1696
      0       0.1662
      3       0.1336
      2       0.0823
      1       0.0645
      6       0.0000
      7       0.0000
      4       0.0000
      5       0.0000

Como era de esperar, la primera característica seleccionada por el algoritmo MRMR es la que tiene la mayor información mutua individual con la variable objetivo. En este caso es el que está en el índice de la columna 9.

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675

La segunda característica seleccionada es la variable en el índice de columna 8. Observando los resultados del análisis, esta variable tiene alta relevancia y también una redundancia mínima con la primera variable seleccionada.

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675
            8       0.1696       0.0000       0.1696

La tercera característica seleccionada demuestra cómo la redundancia afecta el proceso de selección. Aunque las características en las columnas 0, 1, 2 y 3 están directamente relacionadas con la variable objetivo, su alta redundancia con las características ya seleccionadas (columnas 8 y 9) reduce su criterio MRMR general. Por lo tanto, el algoritmo selecciona características menos directamente relacionadas que tienen menor redundancia con el conjunto existente. Sólo después de seleccionar algunas características no relacionadas, el algoritmo comenzará a priorizar las características en las columnas 0, 1, 2 y 3, a medida que disminuye su redundancia con el conjunto seleccionado.

Additional candidates, in order of decreasing relevance minus redundancy
Variable     Relevance   Redundancy   Criterion
    5       0.0000       0.0000       0.0000
    4       0.0000       0.0000       0.0000
    7       0.0000       0.0000       0.0000
    6       0.0000       0.0000       0.0000
    1       0.0645       0.0600       0.0044
    0       0.1662       0.1351       0.0311
    2       0.0823       0.1426      -0.0603
    3       0.1336       0.1781      -0.0445

Si bien las variables irrelevantes en este ejemplo sintético no tenían relevancia alguna, es importante señalar que en escenarios del mundo real las características irrelevantes aún pueden exhibir cierto grado de relación con la variable objetivo, lo que genera una redundancia distinta de cero. En tales casos, el algoritmo MRMR equilibra eficazmente la relevancia y la redundancia, priorizando las características que proporcionan información única.

Final predictors ||  Relevance ||  Redundancy || Criterion  || Solo pval|| Group pval
9                     0.2675        0.0000       0.2675       0.010       0.010
8                     0.1696        0.0000       0.1696       0.010       0.010
4                     0.0000        0.0000       0.0000       1.000       0.010
5                     0.0000        0.0000       0.0000       1.000       0.010
6                     0.0000        0.0000       0.0000       1.000       0.010
7                     0.0000        0.0000       0.0000       1.000       0.010
1                     0.0645        0.0738      -0.0093       0.010       0.010
0                     0.1662        0.1811      -0.0149       0.010       0.010
2                     0.0823        0.1077      -0.0254       0.010       0.010
3                     0.1336        0.1584      -0.0247       0.010       0.010

Los valores p obtenidos de las pruebas de permutación de Monte Carlo proporcionan información valiosa sobre la significancia estadística de las características seleccionadas. Los valores p más bajos indican evidencia más fuerte de que la característica es verdaderamente informativa y no se debe al azar. Un umbral de valor p de 0,05 se utiliza comúnmente para determinar la significación estadística.

A continuación se muestra una demostración del algoritmo en un conjunto de datos más realista. El script StepWiseFeatureSelectionByMutualInformation.mq5 proporciona una aplicación práctica del algoritmo MRMR en datos financieros. Se basa en la premisa de predecir el rendimiento futuro de un símbolo específico utilizando un conjunto de indicadores técnicos. El script calcula cuatro indicadores: Money Flow Index (MFI), Moving Average (MA), Bears Power y Bulls Power, para una serie de períodos retrospectivos. Estos indicadores sirven como características candidatas para el proceso de selección de características. Mediante la aplicación del algoritmo MRMR, el script tiene como objetivo identificar la combinación más informativa de indicadores que pueda predecir de manera eficaz los rendimientos futuros. Esto implica seleccionar características que sean relevantes para la variable objetivo (rendimientos futuros) y minimizar la redundancia con otras características seleccionadas.

//+------------------------------------------------------------------+
//|                  StepWiseFeatureSelectionByMutualInformation.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#resource "\\Indicators\\LogReturns.ex5"
#include<mutualinfo.mqh>
#include<ErrorDescription.mqh>
//+------------------------------------------------------------------+
//|indicator type                                                    |
//+------------------------------------------------------------------+
enum SELECT_INDICATOR
  {
   MFI=0,//MFI
   MA,//MA
   BEARS,//BEARS
   BULLS//BULLS
  };
//--- input parameters
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;
input bool VerboseOutPut = false;
input uint     period_inc=2;//lookback increment
input uint     max_lookback=6;
input ENUM_MA_METHOD         AppliedMA = MODE_SMA;
input ENUM_APPLIED_PRICE     AppliedPrice = PRICE_CLOSE;
input datetime SampleStartDate=D'2019.12.31';
input datetime SampleStopDate=D'2022.12.31';
input string   SetSymbol="BTCUSD";
input ENUM_TIMEFRAMES SetTF = PERIOD_D1;
//----
string predictor_names[];                      // variable names
int size_sample,                      //training set size
    size_observations,                //size of of both training and testing sets combined
    maxperiod,                        //maximum lookback
    indicator_handle=INVALID_HANDLE;  //long moving average indicator handle
//---
vector indicator[];                   //indicator indicator values;
//---
matrix feature_matrix;          //full matrix of features;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---get relative shift of sample set
   int samplestart,samplestop,num_features;
   samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate);
   samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate);
   num_features = int((max_lookback/period_inc)*4);
//---check for errors from ibarshift calls
   if(samplestart<0 || samplestop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(samplestart - samplestop) + 1 ;
   maxperiod=int(max_lookback);
//---check for input errors
   if(size_observations<=0 || maxperiod<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---allocate memory
   if(ArrayResize(indicator,num_features+1)<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//----get the full collection of indicator values
   int period_len;
   int k=0;
//---
   for(SELECT_INDICATOR select_indicator = 0; select_indicator<4; select_indicator++)
     {
      for(int iperiod=0; iperiod<int((indicator.Size()-1)/4); iperiod++)
        {
         period_len=int((iperiod+1) * period_inc);
         int try
               =10;
         predictor_names.Push(EnumToString(select_indicator)+"_"+string(period_len));
         while(try)
           {
            switch(select_indicator)
              {
               case MFI:
                  indicator_handle=iMFI(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,VOLUME_TICK);
                  break;
               case MA:
                  indicator_handle=iMA(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,0,AppliedMA,AppliedPrice);
                  break;
               case BEARS:
                  indicator_handle=iBearsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
               case BULLS:
                  indicator_handle=iBullsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
              }

            if(indicator_handle==INVALID_HANDLE)
               try
                  --;
            else
               break;
           }

         if(indicator_handle==INVALID_HANDLE)
           {
            Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError());
            return;
           }

         Comment("copying data to buffer for indicator ",period_len);
         try
               = 0;
         while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try
                  <10)
              {
               try
                  ++;
               Sleep(5000);
              }

         if(try
               <10)
               ++k;
         else
           {
            Print("error copying to indicator buffers ",GetLastError());
            Comment("");
            return;
           }

         if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle))
            indicator_handle=INVALID_HANDLE;
        }
     }

//---resize matrix
   if(!feature_matrix.Resize(size_observations,indicator.Size()-1))
     {
      Print(__LINE__);
      Print(ErrorDescription(GetLastError()));
      Comment("");
      return;
     }
//---copy collected data to matrix
   for(ulong i = 0; i<feature_matrix.Cols(); i++)
      if(!feature_matrix.Col(indicator[i],i))
        {
         Print(__LINE__);
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
//---
   int try
         = 10;
   while(try
            >-1 && indicator_handle == INVALID_HANDLE)
        {
         indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\LogReturns",0,1,1);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not initialize returns indicator ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      try
            = 10;
     }
//---
   while(try
            >-1 && !indicator[indicator.Size()-1].CopyIndicatorBuffer(indicator_handle,0,samplestop-1,size_observations))
        {
         Sleep(2000);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not collect returns indicator info ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      IndicatorRelease(indicator_handle);
      Comment("");
     }
//--- display the dataset
   string console;
   for(uint i = 0; i<predictor_names.Size(); i++)
      console+=StringFormat(" %12s ",predictor_names[i]);
   console+=" NextBar Returns (Target) ";
   Print(console);
   for(ulong i = 0; i<feature_matrix.Rows(); i++)
     {
      console = "";
      for(ulong j = 0; j<feature_matrix.Cols(); j++)
         console += StringFormat(" %12.6lf ",feature_matrix[i][j]);
      console+=StringFormat(" %12.6lf ",indicator[indicator.Size()-1][i]);
      Print(console);
     }
//---
   Cmrmr mstep(NumReplications,MaxPredictors,ChiSquareThreshold,VerboseOutPut);
//---
   if(!mstep.StepWise(feature_matrix,indicator[indicator.Size()-1]))
      return;
//---
   Print(" Final predictor labels ");
   ulong variables[];
   if(mstep.GetSelectedVars(variables))
     {
      for(uint i = 0; i<variables.Size(); i++)
         Print(predictor_names[variables[i]]);
     }
   return;
  }
//+------------------------------------------------------------------+

A continuación se muestra un fragmento del conjunto de datos de indicadores recopilados del terminal MetaTrader 5, junto con la variable objetivo en la última columna. En total, hay 12 predictores candidatos (indicadores).

MFI_2         MFI_4         MFI_6          MA_2          MA_4          MA_6       BEARS_2       BEARS_4       BEARS_6       BULLS_2       BULLS_4       BULLS_6  NextBar Returns(Target)
0.000000     53.151442     46.921608   7213.654000   7279.552750   7260.007333    -76.371267   -101.867797   -107.113146     87.265733     61.769203     56.523854     -0.003564
0.000000     26.316595     34.451328   7180.962000   7244.558000   7255.420333    -41.795089    -70.889078    -83.462247     42.344911     13.250922      0.677753     -0.032447
0.000000      0.000000     36.720977   7053.740000   7133.697000   7204.281833   -127.731696   -210.813447   -251.244462    153.948304     70.866553     30.435538      0.054562

Lo que sigue son los resultados del análisis del predictor utilizando los parámetros predeterminados del script. Primero, miramos la tabla de valores de información mutua. Aquí vemos que algunos indicadores tienen cero información mutua con el objetivo. El indicador de media móvil con una longitud de período de 6 tiene la mayor información mutua en relación con el objetivo.

PS          Variable         MI
ND                 5       0.0308
LG                 4       0.0293
MJ                 3       0.0279
GM                 6       0.0227
JP                 9       0.0182
IS                 1       0.0165
MF                 8       0.0135
JI                 7       0.0126
HL                 0       0.0000
JO                 2       0.0000
GS                10       0.0000
HD                11       0.0000

Naturalmente, MA_6 es la primera selección realizada por el algoritmo. Dado que se ha realizado la primera selección, será interesante ver si hay otros candidatos predictores que compartan información con ella (MA_6). Esto se puede inferir examinando los valores de redundancia a continuación.

ME   Predictors so far   Relevance   Redundancy   Criterion
GH                 5       0.0308       0.0000       0.0308
II   Additional candidates, in order of decreasing relevance minus redundancy
FE          Variable     Relevance   Redundancy   Criterion
LE                 0       0.0000       0.0095      -0.0095
ED                 1       0.0165       0.0869      -0.0704
FD                 2       0.0000       0.1149      -0.1149
PE                11       0.0000       0.2768      -0.2768
ID                 8       0.0135       0.3251      -0.3116
NS                 7       0.0126       0.3492      -0.3366
CR                10       0.0000       0.3484      -0.3484
ES                 6       0.0227       0.4030      -0.3802
IS                 9       0.0182       0.4285      -0.4103
CR                 3       0.0279       2.5363      -2.5084
DR                 4       0.0293       3.0096      -2.9803

MFI_2 será la próxima elección para el algoritmo, ya que tiene la menor redundancia entre todos los predictores candidatos restantes, a pesar de tener cero relevancia para la variable objetivo. Además, observe cómo los predictores en los índices de columna 3 y 4 (MA_2 y MA_4, respectivamente) tienen los niveles más altos de redundancia con MA_6. Esto tiene sentido, ya que son el mismo indicador calculado con longitudes de ventana más cortas. A continuación se muestra el conjunto de predictores después de dos selecciones más, ambas sin relevancia alguna para la variable objetivo. Cabe destacar el principal predictor en el conjunto de candidatos que no han sido seleccionados. El algoritmo comienza a considerar predictores relevantes debido al efecto dilutivo que las dos últimas selecciones tuvieron sobre los predictores seleccionados como grupo.

PQ   Predictors so far   Relevance   Redundancy   Criterion
FL                 5       0.0308       0.0000       0.0308
JK                 0       0.0000       0.0095      -0.0095
DK                 2       0.0000       0.1796      -0.1796
EE  Additional candidates, in order of decreasing relevance minus redundancy
JH         Variable     Relevance   Redundancy   Criterion
CH                6       0.0227       0.1469      -0.1241
PH                9       0.0182       0.1465      -0.1283
GI               10       0.0000       0.2024      -0.2024
PG                7       0.0126       0.2133      -0.2007
PF               11       0.0000       0.2308      -0.2308
GG                8       0.0135       0.2664      -0.2529
QG                1       0.0165       0.4679      -0.4514
KF                3       0.0279       0.8840      -0.8561
LF                4       0.0293       1.0372      -1.0079

Concluimos nuestro comentario sobre los resultados saltando hacia adelante y mostrando el conjunto final de predictores elegidos por el algoritmo.

OQ  Predictores finales ||  Relevancia ||  Redundancia || Criterio  ||  Valor p individual || Valor p del grupo
HN                5       0.0308       0.0000       0.0308       0.010       0.010
DJ                0       0.0000       0.0095      -0.0095       1.000       0.010
JG                2       0.0000       0.1796      -0.1796       1.000       0.010
HD                6       0.0227       0.1620      -0.1393       0.010       0.010
FQ                9       0.0182       0.2023      -0.1842       0.010       0.010
DL               11       0.0000       0.2798      -0.2798       1.000       0.010
KJ                1       0.0165       0.2932      -0.2767       0.010       0.010
OG                7       0.0126       0.3298      -0.3172       0.010       0.010
OE               10       0.0000       0.4151      -0.4151       1.000       0.010
JP                8       0.0135       0.4585      -0.4450       0.010       0.010
RN   Final predictor labels
NO  MA_6
DE  MFI_2
NN  MFI_6
KP  BEARS_2
DJ  BULLS_2
FL  BULLS_6
PQ  MFI_4
MK  BEARS_4
FM  BULLS_4
OF  BEARS_6

Conclusión

En este artículo, hemos explorado la aplicación de la información mutua en la selección de características, centrándonos en el algoritmo MRMR (Max-Dependency, Max-Relevance, Min-Redundancy) propuesto por Peng, Long y Ding. Comenzamos analizando la estimación de información mutua para variables continuas, destacando su capacidad para capturar dependencias complejas y no lineales entre las características y la variable objetivo. A través de nuestra exploración del algoritmo MRMR, demostramos cómo equilibra eficazmente los objetivos en competencia de maximizar la relevancia para la variable objetivo mientras minimiza la redundancia con características ya seleccionadas.

Al agregar iterativamente características basadas en sus puntajes MRMR y evaluar su significancia estadística a través de pruebas de permutación de Monte Carlo, el algoritmo garantiza que el conjunto de características seleccionado proporcione los predictores más informativos y únicos para el modelo. Los ejemplos sintéticos y del mundo real ilustraron la utilidad práctica del algoritmo MRMR en escenarios de datos del mundo real, donde las características irrelevantes y la multicolinealidad a menudo complican la selección de características. La capacidad del algoritmo MRMR para priorizar características relevantes y evitar las redundantes garantiza que siga siendo una herramienta valiosa en el proceso de selección de características, especialmente en los casos donde las relaciones entre las variables son intrincadas y no lineales.

Todo el código al que se hace referencia en el artículo se adjunta a continuación. La siguiente tabla describe todos los archivos de código fuente que acompañan al artículo.

Nombre del archivo	Descripción
MQL5/include/np.mqh	Un archivo de encabezado de funciones de utilidad de matriz y vector.
MQL5/include/mutualinfo.mqh	Un archivo de encabezado que contiene la definición de la clase Capm que implementa el método de partición adaptativa para estimar la información mutua de variables continuas. Y la definición de la clase Cmrmr que implementa la selección de características paso a paso basada en información mutua.
MQL5/scripts/RelevanceMinusRedundancy.mq5	Un script que demuestra el uso de la clase Cmrmr usando datos sintéticos
MQL5/scripts/StepWiseFeatureSelectionByMutualInformation.mq5	Otro script que también demuestra la aplicación de la clase Cmrmr en un conjunto de datos más realista.