William-Gann-Methoden (Teil II): Gann Square Indikator erstellen

Einführung

William Delbert Gann, ein legendärer Händler und technischer Analyst des frühen 20. Jahrhunderts, hinterließ ein reiches Erbe an Marktanalyseinstrumenten und -techniken. Unter seinen zahlreichen Entwicklungen nimmt das 9er-Quadrat einen besonderen Platz ein. Es ist ein geheimnisvolles und vielseitiges Werkzeug, das Elemente der Geometrie, Numerologie und Astrologie miteinander verbindet.

Das Gann‘sche 9er-Quadrat ist eine spiralförmige Zahlenfolge, die in einem 9x9-Quadrat angeordnet ist. Dieses Instrument wird zur Vorhersage wichtiger Preisniveaus und Zeitzyklen auf den Finanzmärkten verwendet. Trotz seines esoterischen Charakters zieht das 9er-Quadrat weiterhin die Aufmerksamkeit moderner Händler auf sich, die nach unkonventionellen Ansätzen zur Marktanalyse suchen.

In diesem Artikel tauchen wir in die Welt des Gann'schen 9er-Quadrats ein und versuchen, sein Konzept in das digitale Zeitalter zu übertragen, indem wir einen Indikator für die MetaTrader 5-Plattform mit Hilfe der Programmiersprache MQL5 erstellen. Unser Ziel ist es, ein Tool zu entwickeln, das es Händlern ermöglicht, die Prinzipien des 9er-Quadrats in ihrem Handel zu visualisieren und anzuwenden, indem es die Weisheit von Gann mit moderner Technologie kombiniert.

Wir werden die theoretischen Grundlagen des 9er-Quadrats erläutern, den Prozess der Erstellung des Indikators Schritt für Schritt nachvollziehen und seine praktische Anwendung sowie mögliche Grenzen diskutieren. Ganz gleich, ob Sie ein erfahrener Entwickler von Handelssystemen sind oder sich einfach nur für unkonventionelle Methoden der Marktanalyse interessieren, dieser Artikel wird Ihnen wertvolle Informationen und praktische Fähigkeiten vermitteln, mit denen Sie Ihren analytischen Werkzeugkasten erweitern können.

Begeben wir uns auf eine faszinierende Reise in die Fußstapfen von William Gann und schlagen wir eine Brücke zwischen seinen brillanten Ideen und der modernen Welt des algorithmischen Handels.

Theoretische Grundlage des Gann‘schen 9er-Quadrats

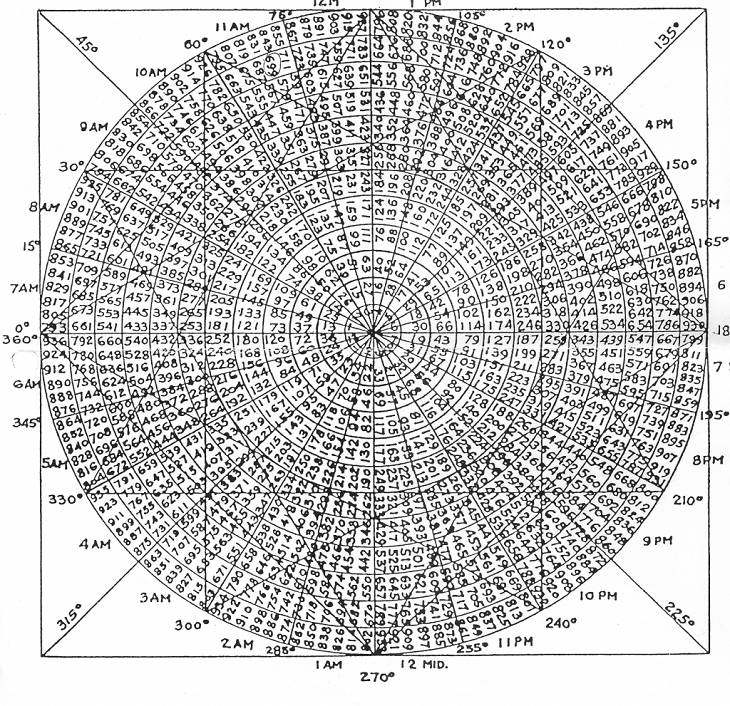
Das 9er-Quadrat von Gann ist ein einzigartiges technisches Analyseinstrument, das Elemente der Geometrie, Numerologie und Astrologie kombiniert. Die Methode basiert auf der Idee, dass sich Preise und Zeit auf den Finanzmärkten in spiralförmigen Mustern bewegen, die als Zahlenfolge in einem 9x9-Quadrat dargestellt werden können.

Die Konstruktion von Quadrat 9 beginnt mit der zentralen Zelle, die die Nummer 1 erhält. Die Zahlen werden dann gegen den Uhrzeigersinn spiralförmig angeordnet und füllen das Quadrat bis 81 (9x9). Jede neunte Zahl in dieser Folge bildet ein „Kardinalkreuz“ (cardinal cross) - ein Schlüsselpunkt, den Gann für die Marktanalyse als besonders wichtig erachtete.

Nach der Gann-Theorie entsprechen die Zahlen im 9er-Quadrat den Preisniveaus und Zeitintervallen. Er war der Meinung, dass der Markt dazu neigt, auf diese Niveaus zu reagieren und Wendepunkte, Unterstützung oder Widerstand zu schaffen. Besondere Bedeutung kommt dabei Zahlen zu, die auf einer Linie liegen oder in einem harmonischen Verhältnis zueinander stehen.

Gann verknüpfte das 9er-Quadrat auch mit astrologischen Konzepten und erklärte, dass die Winkel zwischen den Zahlen im Quadrat bestimmten planetarischen Aspekten entsprechen. Dadurch wird die Analyse um eine zeitliche Dimension erweitert, die es uns ermöglicht, nicht nur die Preisniveaus, sondern auch mögliche Termine für wichtige Marktereignisse vorherzusagen.

Es ist wichtig zu beachten, dass die Interpretation des 9er-Quadrats oft subjektiv ist und Erfahrung erfordert. Händler nutzen dieses Instrument auf unterschiedliche Weise: Einige konzentrieren sich auf Kursniveaus, andere auf Zeitzyklen, und wieder andere kombinieren beide Ansätze.

Trotz seines esoterischen Charakters zieht das Gann'sche 9er-Quadrat weiterhin die Aufmerksamkeit moderner Händler auf sich. Ihr Wert liegt in ihrer Fähigkeit, eine einzigartige Perspektive auf Marktbewegungen zu bieten, die die traditionellen Methoden der technischen Analyse ergänzen kann.

Im Rahmen der Erstellung eines MetaTrader 5-Indikators besteht unsere Aufgabe darin, diese theoretischen Konzepte in Algorithmen umzusetzen, die in der Lage sind, spezifische Handelssignale und visuelle Darstellungen zu erzeugen. Dadurch können Händler die Ideen von Gann in die moderne digitale Handelsumgebung integrieren.

Mathematischer Apparat des Gann‘schen 9er-Quadrats

Trotz seiner esoterischen Wurzeln hat das Gann'sche 9er-Quadrat eine klare mathematische Struktur. Das Verständnis dieser Struktur ist entscheidend für die Erstellung eines genauen und effizienten Indikators. Schauen wir uns die grundlegenden mathematischen Prinzipien an, die dem 9er-Quadrat zugrunde liegen:

• Aufbau des Quadrats - Das 9er-Quadrat ist eine spiralförmige Folge von Zahlen von 1 bis 81, die in einer 9x9-Matrix angeordnet sind. Mathematisch lässt sich dies als eine Funktion der (x, y)-Koordinaten zum Quadrat darstellen.
• Spiralfolge - die Zahlen sind in einer Spirale gegen den Uhrzeigersinn angeordnet. Dies kann durch parametrische Gleichungen der Spirale in diskreter Form beschrieben werden.
• Winkelbeziehungen - Gann legte besonderen Wert auf Winkelbeziehungen zwischen Zahlen. Diese Beziehungen können durch trigonometrische Funktionen ausgedrückt werden, wobei die Position der quadrierten Zahlen berücksichtigt wird.
• Preisprojektionen - Verschiedene mathematische Transformationen, oft mit Logarithmus oder Quadratwurzeln, werden verwendet, um quadratische Zahlen in Preisniveaus umzuwandeln.
• Zeitzyklen - Der zeitliche Aspekt des 9er-Quadrats kann durch modulare Arithmetik ausgedrückt werden, wobei jede vollständige Umdrehung der Spirale einem bestimmten Zyklus entspricht.
• Kardinalkreuz - Die Zahlen, die das Kardinalkreuz bilden (jede neunte Zahl), können als arithmetische Progression mit einem Schritt von 9 ausgedrückt werden.
• Harmonische Beziehungen - Harmonische Beziehungen zwischen Zahlen in einem Quadrat können durch einfache Zahlenverhältnisse oder Winkel in Grad beschrieben werden.
• Quadratwurzel des Preises - Gann verwendete in seinen Berechnungen häufig die Quadratwurzel des Preises, was eine weitere Ebene der mathematischen Manipulation darstellt.
• Modulare Arithmetik - Viele Berechnungen im 9er-Quadrat beruhen auf den Prinzipien der modularen Arithmetik, insbesondere mit Modulo 9.

Um einen Indikator in MQL5 zu erstellen, müssen wir diese mathematischen Konzepte in spezifische Algorithmen umwandeln. Dazu gehört die Entwicklung von Funktionen zur Berechnung des 9er-Quadrats, zur Berechnung von Winkelverhältnissen, zur Projektion von Zahlen auf eine Preisskala und zur Bestimmung von Zeitzyklen.

Es ist wichtig, darauf hinzuweisen, dass die Mathematik des 9er-Quadrats zwar genau ist, ihre Auslegung und Anwendung auf die Märkte jedoch weitgehend subjektiv bleibt. Unser Ziel bei der Entwicklung des Indikators ist es, den Nutzern ein flexibles Werkzeug an die Hand zu geben, mit dem sie auf der Grundlage präziser mathematischer Berechnungen mit verschiedenen Aspekten der Gann-Theorie experimentieren können.

Vorbereiten der Erstellung eines Indikators

Beginnen wir mit der Definition der Grundfunktionen unseres Gann'schen 9er-Quadrat Indikators. Wir müssen das Quadrat selbst auf dem Chart darstellen, wichtige Kursniveaus berechnen und Zeitzyklen anzeigen. Dann werden wir über die Einstellungen nachdenken, die den Nutzern zur Verfügung stehen. Dies können sein: die Ausgangszahl für Quadrat 9, die Skala für die Umrechnung in Preise und die Wahl der Farben für Linien und Text.

Es ist wichtig zu planen, wie wir Daten speichern werden. Wir benötigen ein Array mit Zahlen des 9er-Quadrats sowie Listen, um die berechneten Preise und Daten zu speichern.

Der nächste Schritt ist die Entwicklung der grundlegenden Algorithmen. Wir müssen Funktionen erstellen, um das 9er-Quadrat zu erzeugen, seine Zahlen in Preisniveaus zu übersetzen und Daten für Zeitzyklen zu berechnen. Lassen Sie uns überlegen, wie wir all diese Informationen am besten auf dem Chart darstellen können. Wir müssen entscheiden, wie das 9er-Quadrat selbst angezeigt werden soll und wo Preisniveaus und Daten platziert werden sollen.

Vergessen wir nicht die Tests. Bereiten wir Methoden zur Überprüfung der Genauigkeit unserer Berechnungen vor und testen wir den Indikator auf verschiedenen Zeitskalen. Es ist auch wichtig, die Eigenschaften der Arbeit in MQL5 zu studieren, insbesondere in Bezug auf die Erstellung von grafischen Elementen und verfügbaren mathematischen Funktionen.

Mit dieser Vorbereitung wird eine solide Grundlage für die Erstellung eines effizienten und nutzerfreundlichen Gann'schen 9er-Quadrat Indikators geschaffen.

Die Struktur des Gann'schen 9er-Quadrat Indikator-Codes

Bei der Entwicklung des Gann'schen 9er-Quadrat Indikators für MetaTrader 5 ist es wichtig, eine klare und logische Codestruktur zu schaffen. Dadurch wird es einfacher, den Indikator zu verstehen, zu debuggen und weiter zu verbessern. Schauen wir uns die wichtigsten Komponenten an, die in unserem Code enthalten sein müssen.

Zunächst müssen wir die Variablen deklarieren und initialisieren. Definieren wir globale Variablen, um die Indikatoreinstellungen zu speichern, und erstellen wir Arrays, um die Daten und berechneten Werten des 9er-Quadrats zu speichern.

• Die Funktion OnInit() wird zur Initialisierung der Indikatorparameter und zur Erstellung der erforderlichen grafischen Objekte verwendet.
• Die Funktion OnDeinit() löscht alle erstellten grafischen Objekte, wenn der Indikator gelöscht wird.
• Die Funktion OnCalculate() ist die Hauptfunktion des Indikators, die bei jedem Tick aufgerufen wird. Hier werden die wichtigsten Berechnungen durchgeführt und die Anzeige aktualisiert.

Umsetzung der Schlüsselkomponenten des Indikators

Schauen wir uns den „leeren“ Code für das 9er-Quadrat an:

//+------------------------------------------------------------------+
//|                                                      GannSquare9 |
//|                                          Copyright 2024, Shtenco |
//|                          https://www.mql5.com/ru/users/koshtenko |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, Evgeniy Koshtenko"
#property link      "https://www.mql5.com/ru/users/koshtenko"
#property version   "1.00"
#property description "Gann Square of 9 Price and Time Levels Indicator"
#property indicator_chart_window

// Input parameters
input double StartNumber = 1;  // Starting number for the Gann Square
input color PriceLevelColor = clrDodgerBlue;  // Color of the price levels
input color TimeLevelColor = clrRed;  // Color of the time levels
input int LevelsToShow = 50;  // Number of levels to display
input datetime EndDate = D'2024.08.14 00:00';  // End date for calculations
input double PriceStepDivisor = 10.0;  // Divisor for price step (higher value = more levels)

// Global variables
double price_levels[];
datetime time_levels[];
double price_scale;
int time_scale;

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
// Validate inputs
   if(StartNumber <= 0 || LevelsToShow <= 0 || EndDate <= 0 || PriceStepDivisor <= 0)
     {
      Print("Invalid input parameters");
      return INIT_PARAMETERS_INCORRECT;
     }

// Calculate scales
   CalculateScales();

// Calculate and draw levels
   CalculateLevels();
   DrawLevels();

   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
// No calculations needed for this indicator
   return(rates_total);
  }

//+------------------------------------------------------------------+
//| Calculate price and time scales                                  |
//+------------------------------------------------------------------+
void CalculateScales()
  {
   double current_price = SymbolInfoDouble(_Symbol, SYMBOL_BID);
   price_scale = current_price / (StartNumber * StartNumber);

   datetime current_time = TimeCurrent();
   time_scale = (int)MathMax(1, (EndDate - current_time) / (86400 * StartNumber * StartNumber));  // in days
  }

//+------------------------------------------------------------------+
//| Calculate price and time levels                                  |
//+------------------------------------------------------------------+
void CalculateLevels()
  {
   ArrayResize(price_levels, LevelsToShow);
   ArrayResize(time_levels, LevelsToShow);

   for(int i = 0; i < LevelsToShow; i++)
     {
      double price_square = MathPow(StartNumber + i / PriceStepDivisor, 2);
      int time_square = (StartNumber + i) * (StartNumber + i);

      price_levels[i] = price_scale * price_square;
      time_levels[i] = EndDate - time_scale * time_square * 86400;  // Convert days to seconds
     }
  }

//+------------------------------------------------------------------+
//| Draw levels on the chart                                         |
//+------------------------------------------------------------------+
void DrawLevels()
  {
   for(int i = 0; i < LevelsToShow; i++)
     {
      // Draw price level
      string price_name = "GannPriceLevel_" + IntegerToString(i);
      ObjectCreate(0, price_name, OBJ_HLINE, 0, 0, price_levels[i]);
      ObjectSetInteger(0, price_name, OBJPROP_COLOR, PriceLevelColor);
      ObjectSetInteger(0, price_name, OBJPROP_STYLE, STYLE_SOLID);
      ObjectSetInteger(0, price_name, OBJPROP_WIDTH, 1);
      ObjectSetString(0, price_name, OBJPROP_TOOLTIP, "Gann Price Level " + DoubleToString(price_levels[i], _Digits));

      // Draw time level
      string time_name = "GannTimeLevel_" + IntegerToString(i);
      ObjectCreate(0, time_name, OBJ_VLINE, 0, time_levels[i], 0);
      ObjectSetInteger(0, time_name, OBJPROP_COLOR, TimeLevelColor);
      ObjectSetInteger(0, time_name, OBJPROP_STYLE, STYLE_DOT);
      ObjectSetInteger(0, time_name, OBJPROP_WIDTH, 1);
      ObjectSetString(0, time_name, OBJPROP_TOOLTIP, "Gann Time Level " + TimeToString(time_levels[i], TIME_DATE|TIME_MINUTES));
     }
  }

//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectsDeleteAll(0, "GannPriceLevel_");
   ObjectsDeleteAll(0, "GannTimeLevel_");
  }
//+------------------------------------------------------------------+

Dieser Indikator ist eine moderne Interpretation des Konzepts des 9er-Quadrats von William Gann, angepasst an die MetaTrader 5 Plattform. Es visualisiert Preis- und Zeitebenen auf der Grundlage der Gann-Prinzipien und bietet Händlern ein einzigartiges Werkzeug für Marktanalysen und Handelsentscheidungen.

Indikator-Eingänge:

• StartNumber — Anfangszahl für die Konstruktion des 9er-Quadrats,
• PriceLevelColor und TimeLevelColor — Farben für die Anzeige von Preis- bzw. Zeitebenen,
• LevelsToShow — Anzahl der anzuzeigenden Ebenen,
• EndDate — Enddatum für Berechnungen und Tests mit historischen Daten,
• PriceStepDivisor — Frequnz der Preisstufen.

Globale Variablen werden zum Speichern und Verarbeiten von Daten verwendet. In den Arrays price_levels[] und time_levels[] werden die berechneten Preis- bzw. Zeitstufen gespeichert. Die Variablen price_scale und time_scale werden zur Skalierung von Preis- und Zeitwerten verwendet.

Die Funktion CalculateScales() ermittelt automatisch die Skalen für Preis und Zeit auf der Grundlage des aktuellen Preises des Instruments und des angegebenen Enddatums. CalculateLevels() führt Preis- und Zeitstufenberechnungen durch. Die Kursniveaus werden mit einer quadratischen Funktion und einem zusätzlichen Divisor berechnet, um die Häufigkeit der Niveaus zu erhöhen, während die Zeitniveaus auf dem Quadrat einer Zahl basieren, was der Gann-Theorie entspricht. DrawLevels() ist für die Visualisierung der Daten zuständig, indem horizontale Linien für Preisniveaus und vertikale Linien für Zeitebenen im Chart erstellt werden. 

Der Indikator bietet Händlern eine visuelle Darstellung von Preis- und Zeitebenen, die auf den Prinzipien des Gann'schen 9er-Quadrats basieren. Dies kann besonders für Händler nützlich sein, die sich für nicht-traditionelle technische Analysemethoden interessieren und nach zusätzlichen Instrumenten zur Bestätigung ihrer Handelsideen suchen.

Zu den Merkmalen dieser Implementierung gehören die Möglichkeit, die Häufigkeit der Preisniveaus für eine detailliertere Analyse anzupassen, die Flexibilität bei der Wahl des Enddatums für die historische Analyse und eine Kombination von Preis- und Zeitebenen in einem einzigen Chart.

Mögliche Verbesserungen des Indikators umfassen das Hinzufügen von Warnungen, wenn der Preis oder die Zeit wichtige Niveaus erreicht, die Implementierung einer automatischen Aktualisierung der Niveaus, wenn sich der Preis signifikant ändert, die Integration mit anderen Gann-Analysemethoden, um ein umfassendes Handelssystem zu schaffen, und die Optimierung der Leistung, um auf größeren Zeitrahmen und mit einer großen Anzahl von Niveaus zu arbeiten.

Visualisierung des Quadrats der 9 Ebenen auf dem Chart

Die Kursniveaus werden als horizontale Linien im Chart angezeigt. Jede Linie stellt ein potenzielles Unterstützungs- oder Widerstandsniveau dar, das auf der Grundlage des Gann'schen 9er-Quadrats berechnet wurde. Die Farbe dieser Linien wird durch den nutzerdefinierten Parameter PriceLevelColor bestimmt, sodass Händler die Anzeige an ihre Präferenzen und ihren Chart-Stil anpassen können. Die horizontalen Linien werden entlang der vertikalen Achse des Charts verteilt, wobei ihre Dichte durch den Parameter PriceStepDivisor gesteuert wird. So können Händler die Anzahl der angezeigten Kursniveaus anpassen und ein Gleichgewicht zwischen Detailgenauigkeit und Lesbarkeit des Charts finden.

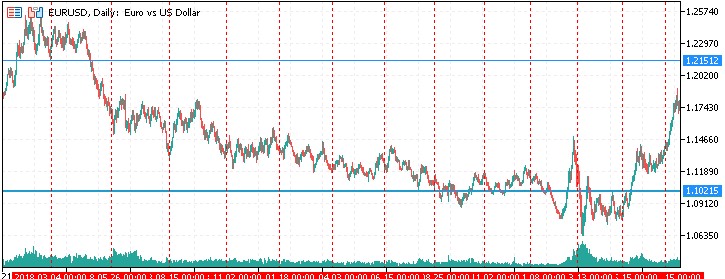
Die Zeitebenen werden als vertikale Linien im Chart dargestellt. Diese Linien stellen wichtige Zeitpunkte auf der Grundlage der quadratischen Progression der Gann-Zahlen dar. Die Farbe der Zeitlinien wird durch den Parameter TimeLevelColor festgelegt, wodurch sie leicht von den Preisniveaus unterschieden werden können. Vertikale Linien werden entlang der horizontalen Achse des Charts verteilt, beginnend mit dem angegebenen Enddatum (Parameter EndDate), und bewegen sich in der Zeit rückwärts. Dies gibt Händlern die Möglichkeit, potenzielle Umkehrpunkte oder wichtige Daten in der Zukunft zu sehen sowie historische Daten zu analysieren.

Zeitquadrate und Zeitzyklen

Das Quadrieren der Zeit und Zeitzyklen sind Schlüsselkonzepte in der Theorie von William Gann, die sich im 9er-Quadrat widerspiegeln. Diese Ideen beruhen auf der Annahme, dass Marktbewegungen bestimmten Zeitmustern folgen, die vorhergesagt und für Handelsentscheidungen genutzt werden können.

time_scale = (int)MathMax(1, (EndDate - current_time) / (86400 * StartNumber * StartNumber));  // in days

Das Konzept der Quadratur der Zeit legt nahe, dass wichtige Marktereignisse häufig in Intervallen auftreten, die Quadrate ganzer Zahlen sind. Beispielsweise können größere Marktumschwünge nach 4, 9, 16, 25, 36, 49, 64, 81 Tagen oder in längeren Zeiträumen auf der Grundlage dieser Zahlen auftreten. Im Zusammenhang mit dem 9er-Quadrat entsprechen diese Zahlen den Schlüsselpunkten der Spirale.

Die Gleichung ist das Schlüsselelement bei der Berechnung der Zeitskala für den Gann'schen 9er-Quadrat Indikator. Werfen wir einen Blick auf seine Bestandteile und seine Bedeutung:

1. EndDate − aktuelle_Zeit: Dies ist die Differenz zwischen dem angegebenen Enddatum und der aktuellen Uhrzeit. Das Ergebnis wird in Sekunden angegeben.
2. 86400: Dies ist die Anzahl der Sekunden eines Tages (24 Stunden * 60 Minuten * 60 Sekunden).
3. StartNummer * StartNummer: Dies ist das Quadrat der Ausgangszahl, die zur Skalierung der Zeitleiste verwendet wird.
4. (EndDate − current_time) / (86400 * StartNumber * StartNumber): In diesem Teil der Gleichung wird die Zeitdifferenz von Sekunden in Tage umgerechnet und dann durch das Quadrat der Ausgangszahl dividiert. Dadurch entsteht eine nichtlineare Zeitskala, die den Grundsätzen des Gann‘schen 9er-Quadrats entspricht.
5. MathMax(1, ...): Diese Funktion stellt sicher, dass das Ergebnis mindestens 1 ist. Dies verhindert die Division durch Null oder negative Werte.
6. (int): Umwandlung des Ergebnisses in einen Integer-Typ, da der Zeitrahmen in ganzen Tagen ausgedrückt werden sollte.

Die Idee hinter dieser Gleichung ist, eine Zeitleiste zu erstellen, die immer kürzer wird, je näher sie dem aktuellen Datum kommt. Dies spiegelt Ganns Konzept der Beschleunigung von Zeit- und Marktzyklen wider.

Je größer die StartNummer ist, desto stärker wird die Zeitleiste komprimiert. Dadurch können Händler den Indikator für verschiedene Zeithorizonte anpassen.

Die Verwendung des Quadrats von StartNumber (StartNumber * StartNumber) im Nenner führt zu einer nicht linearen Verteilung der Zeitebenen, was mit den Grundsätzen des Gann'schen 9er-Quadrats übereinstimmt, bei dem die Bedeutung der Zahlen quadratisch zunimmt.

Beschleunigung der Zeitzyklen zusammen mit der Beschleunigung der Marktzyklen

Eines der interessanten Merkmale dieses Indikators besteht darin, dass die Zeitzyklen, die auf den Prinzipien des Gann'schen 9er-Quadrats beruhen, näher aneinander liegen, je näher sie dem aktuellen Datum kommen. Dieses Phänomen kann als Ausdruck der im modernen Finanzumfeld zu beobachtenden Beschleunigung der Marktzyklen interpretiert werden.

In den letzten Jahrzehnten haben wir in der Tat eine erhebliche Beschleunigung der Marktprozesse erlebt. Börsencrashs, die früher alle paar Jahre oder sogar Jahrzehnte auftraten, sind heute viel häufiger zu beobachten. Dies ist auf eine Reihe von Faktoren zurückzuführen, darunter die Globalisierung der Finanzmärkte, die Entwicklung der Informationstechnologie und des algorithmischen Handels sowie die zunehmende Geschwindigkeit der Informationsverbreitung. Vielleicht ist dies auf die allmähliche Entwicklung zur technologischen Singularität zurückzuführen. 

Der Gann-Indikator 9er-Quadrat spiegelt diese Beschleunigung indirekt wider, indem er Zeitzyklen anzeigt, die sich immer mehr auf die Gegenwart zubewegen. Diese visuelle Darstellung kann Händlern helfen, das heutige schnelllebige Marktumfeld, in dem die Zyklen immer schneller werden, besser zu verstehen und sich darauf einzustellen.

Diese Beschleunigung kann als ein Zeichen für die technologische Entwicklung und die Entwicklung der Finanzmärkte gesehen werden. Mit dem Aufkommen des Hochfrequenzhandels, der sofortigen Verbreitung von Nachrichten über soziale Medien und der zunehmenden Verfügbarkeit von Handelsplattformen für Kleinanleger reagieren die Märkte heute schneller auf Ereignisse als je zuvor. Früher waren die Trends viel dauerhafter und vorhersehbarer. 

Es ist wichtig zu beachten, dass der Indikator diese Beschleunigung zwar widerspiegelt, aber nicht direkt vorhersagt. Vielmehr stellt sie ein visuelles Instrument dar, das Händlern helfen kann, das Konzept der sich beschleunigenden Marktzyklen zu verstehen und in ihre Analysen zu integrieren.

Prüfung von Indikatoren

Schauen wir uns die Ergebnisse des Indikators anhand historischer Daten an. Wir haben EURUSD als Vermögenswert und 1,00 als Ausgangspunkt für die Berechnung der Niveaus gewählt.

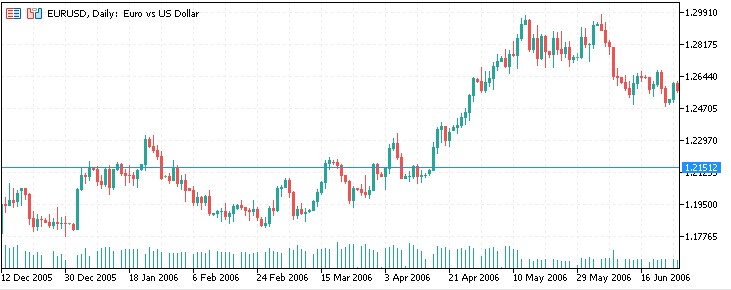
Ein weiteres Segment:

Und noch eine:

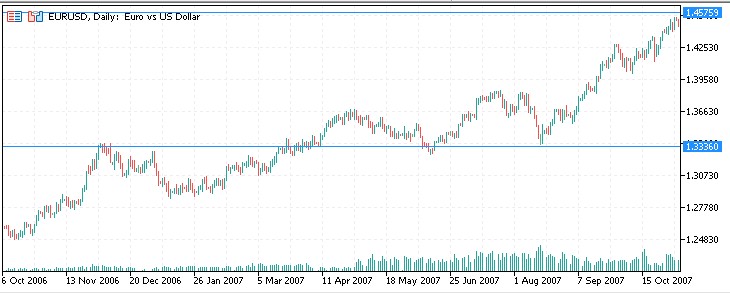
2008:

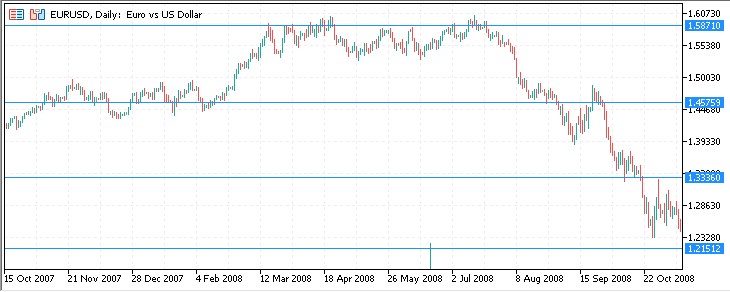
2010 sehen wir wieder eine Reaktion auf die Werte:

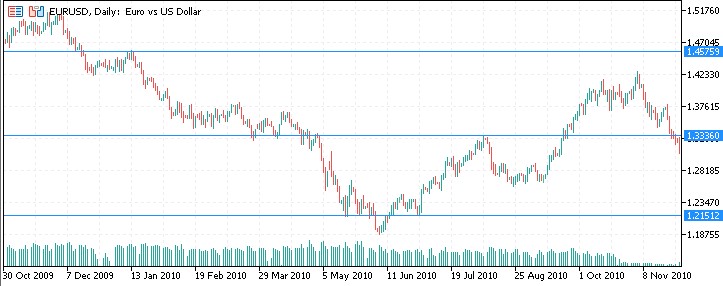
2011:

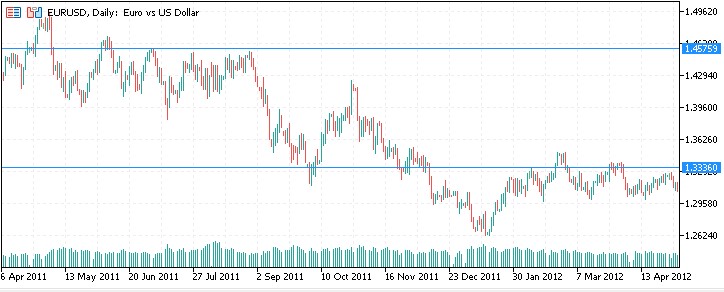
2012:

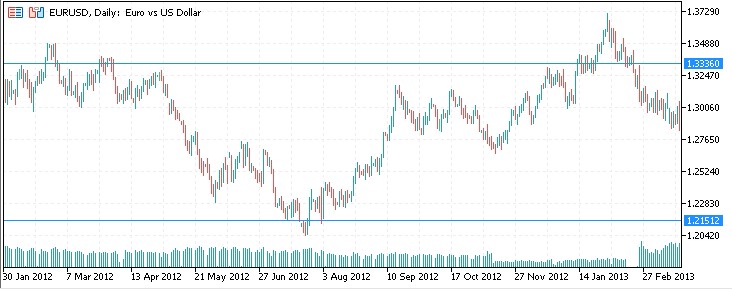
2020:

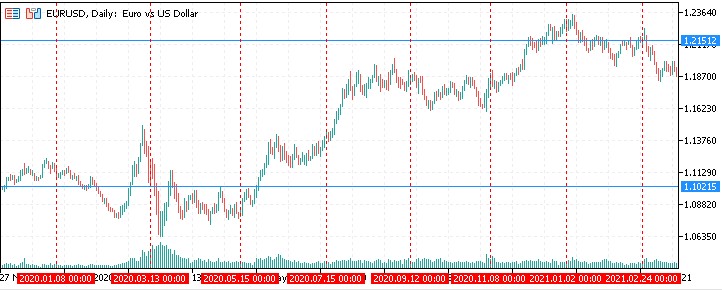
Aktueller Zeitraum: Zurzeit befindet sich EURUSD genau auf dem Niveau des Gann'schen 9er-Quadrats.

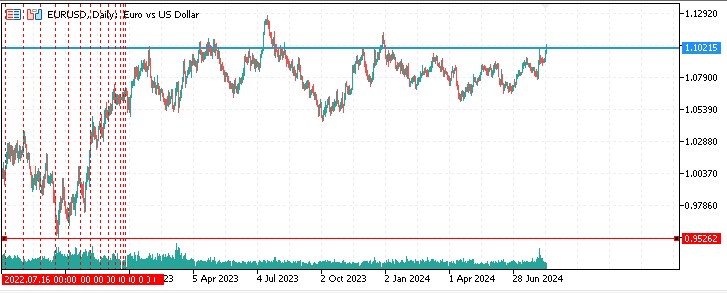
Was die Zeitzyklen durch Time Squaring betrifft, so habe ich keine statistisch signifikanten Preisreaktionen darauf festgestellt.

Mögliche Verbesserungen

Eine interessante Option scheint das Hinzufügen von Alarmen zu sein, wenn der Kurs das 9er-Quadrat berührt. Es ist auch möglich, bei der Preisaktualisierung eine automatische Neuberechnung der Quadratmeterzahlen vorzunehmen. 

Es wäre auch interessant, die Gann-Box und das Gann-Gitter in Form von Indikatoren zu implementieren und alle Entwicklungen in einem komplexen System zu kombinieren.

Aussichten für die Erstellung eines EA auf der Grundlage von 9er-Quadrat

Es ist auch möglich, einen EA zu erstellen, der auf einem Rebound von den quadratischen Ebenen basiert. Ich sehe es als einen halbautomatischen EA, der möglicherweise mit Chart-Objekten verknüpft ist. Ein solcher EA könnte den Händlern die Arbeit erleichtern, indem er ihren Handelsanweisungen auf der einen oder anderen Ebene folgt.

Schlussfolgerung

Die Entwicklung des Gann'schen 9er-Quadrat Indikators für die MetaTrader 5 Plattform ist ein interessantes und ehrgeiziges Projekt, das klassische Ideen der technischen Analyse mit modernen Handelstechnologien verbindet. Dieser Indikator bietet Händlern ein einzigartiges Marktanalyseinstrument, das Elemente der Preis- und Zeitanalyse kombiniert.

Die Umsetzung des Konzepts des 9er-Quadrats in Form eines digitalen Indikators macht diese komplexe Theorie zugänglicher und für ein breites Spektrum von Händlern anwendbar. Die Möglichkeit, Preis- und Zeitebenen in einem einzigen Chart zu visualisieren, ermöglicht eine umfassende Analyse der Marktbewegungen, was vor allem im Kontext der heutigen, sich schnell verändernden Märkte nützlich sein kann.

Es ist wichtig, darauf hinzuweisen, dass die Interpretation von Ganns 9er-Quadrat Signale trotz ihrer mathematischen Grundlage weitgehend subjektiv bleibt. 

Insgesamt zeigt dieses Projekt, wie historische Methoden der technischen Analyse an moderne Handelstechnologien angepasst werden können, um neue Instrumente für Händler zu schaffen. Dies unterstreicht den bleibenden Wert der klassischen Ideen und ihr Potenzial im Kontext moderner Finanzmärkte.