Von der Grundstufe bis zur Mittelstufe: Operatoren

Einführung

Die hier vorgestellten Materialien sind ausschließlich für Bildungszwecke bestimmt. Die Anwendung sollte unter keinen Umständen zu einem anderen Zweck als zum Erlernen und Beherrschen der vorgestellten Konzepte verwendet werden.

Im vorherigen Artikel „Von der Grundstufe zur Mittelstufe: Variablen (III)“ haben wir uns mit vordefinierten Variablen und einer interessanten Art der Interpretation von Funktionen beschäftigt. Alles, was bisher besprochen wurde, führt jedoch zu einer gemeinsamen Herausforderung, einer der größten Schwierigkeiten, mit denen neue Programmierer konfrontiert sind, insbesondere diejenigen, die an kleinen persönlichen Projekten arbeiten. Diese Herausforderung ergibt sich aus der Existenz unterschiedlicher Datentypen.

Wie in „Von der Grundstufe zur Mittelstufe: Variablen (II)“ erwähnt, klassifiziert MQL5 Daten in verschiedene Typen. Um jedoch Datentypen richtig erklären zu können, müssen wir den richtigen Kontext herstellen. Dieser Kontext ist genau das Hauptthema dieses Artikels: die Basisoperatoren. Das Verständnis dieser Operatoren ist unerlässlich, um Datentypen effektiv zu diskutieren.

Manche mögen denken, dass dieses Thema einfach ist und nicht behandelt werden muss. Aber gerade weil es trivial erscheint, ist es wichtig. Viele Kodierungsfehler entstehen durch ein Missverständnis dieses grundlegenden Konzepts.

Damit wären wir schon beim ersten Thema dieses Artikels angelangt.

Datentypen und Operatoren

In nicht typisierten Sprachen ist die Diskussion über Operatoren und Datentypen oft überflüssig. Eine Operation wie z. B. 10 geteilt durch 3 wird ohne Probleme das erwartete Ergebnis liefern. In einer stark typisierten Sprache wie MQL5 sowie in C und C++ führt diese einfache Division jedoch nicht zu einem einzigen Ergebnis, sondern zu zwei unterschiedlichen Resultaten. Und in einigen Fällen sogar noch mehr, aber wir werden diese zusätzlichen Fälle in einer späteren Diskussion untersuchen. Im Moment konzentrieren wir uns auf die Möglichkeit, zwei unterschiedliche Ergebnisse zu erzielen.

Warten Sie eine Sekunde. Zwei Ergebnisse? Das macht doch keinen Sinn! Sie denken jetzt vielleicht: Sind Sie verrückt? Jedes Mal, wenn wir 10 durch 3 dividieren, erhalten wir 3,3333... Es gibt keine andere mögliche Antwort! Nun, wenn Sie das denken, dann ist dieser Artikel genau das Richtige für Sie. Ziel ist es, zu verdeutlichen, dass beim Programmieren nicht immer alles so funktioniert, wie es auf den ersten Blick erscheinen mag.

Lassen Sie uns zunächst einen Fall untersuchen, der einfacher ist als der Umgang mit wiederkehrenden Dezimalzahlen, aber dennoch zeigt, wie eine einzige Operation zwei völlig unterschiedliche Ergebnisse liefern kann. Im Folgenden sehen wir uns ein einfaches Codebeispiel an. Und zwar so:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print(5 / 2);
7. }
8. //+------------------------------------------------------------------+

Code 01

Dieser einfache Code 01 dient zur Veranschaulichung eines interessanten Konzepts, das häufig für erhebliche Verwirrung sorgt. Man könnte meinen, dass man das Ergebnis der in Zeile sechs durchgeführten Operation bereits kennt, ohne den Code im MetaTrader 5-Terminal ausgeführt zu haben. Aber ich frage Sie: Wissen Sie wirklich, welcher Wert angezeigt werden wird? Die Antwort mag Sie überraschen, denn sie hängt vom Datentyp ab, der für die Berechnung verwendet wird. Das erwartete Ergebnis ist natürlich 2,5. Wenn Sie jedoch Code 01 ausführen, werden Sie feststellen, dass das Terminal stattdessen 2 ausgibt. Aber warum? Weiß der Computer nicht, wie man einen so einfachen Ausdruck berechnet? Nein, der Computer kann von Natur aus nicht rechnen. In Wirklichkeit sind Computer hervorragend in der Addition, aber schrecklich in den meisten anderen mathematischen Operationen.

„Moment mal, wollt ihr uns reinlegen?“ Ganz und gar nicht! Auch wenn es wie ein Trick erscheinen mag, ist dies eine grundlegende Tatsache: Computer können nur addieren. Selbst dann haben sie Schwierigkeiten mit Brüchen. Wenn man einen Computer bittet, zwei Bruchzahlen zu addieren, kann es sein, dass er nicht immer das richtige Ergebnis liefert. Es kommt darauf an, wie die Zahlen im Speicher des Computers dargestellt werden.

Computer verstehen nur Nullen und Einsen, d.h. Ein- und Aus-Zustände. Sie erkennen nicht von sich aus Zahlen wie 2 oder 3. Stattdessen stützen sie sich auf boolesche Logik, um Daten zu verarbeiten und Berechnungen durchzuführen. Und indem sie dies auf eine bestimmte Weise tun, führen sie die Berechnungen durch, die wir von ihnen verlangen. Wenn ich aber 5 geteilt durch 2 in einen Taschenrechner eingebe, erhalte ich 2,5. Warum liefert MQL5 also 2 statt 2,5?

Genau an dieser Stelle kommen die Datentypen ins Spiel. In Zeile sechs sind beide Werte vom Typ Ganzzahl. Infolgedessen bestimmt der Compiler, dass die Ausgabe ebenfalls eine ganze Zahl sein muss. Im Gegensatz dazu können die Ergebnisse eines Taschenrechners entweder ganze Zahlen oder Fließkommazahlen (in der Programmierung auch als Dezimalzahlen bezeichnet) sein. Dies ist der Punkt, an dem viele Programmierer, insbesondere Anfänger, verwirrt sind. In dynamisch typisierten Sprachen ist das Ergebnis immer das gleiche. In stark typisierten Sprachen wie MQL5 gibt es jedoch mehrere mögliche Ergebnisse, je nachdem, wie Sie den Datentyp definieren.

Um den Code 01 so zu ändern, dass das korrekte Ergebnis von 2,5 angezeigt wird, müssen wir ihn wie im folgenden Beispiel gezeigt ändern:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print((double)(5 / 2));
7. }
8. //+------------------------------------------------------------------+

Code 02

Wenn wir die Änderungen in Code 02 vornehmen, wird das Ergebnis nun eindeutig sein. Dieser Vorgang wird als Typecasting oder Typkonvertierung bezeichnet. Die MQL5-Dokumentation bietet eine detaillierte Erklärung dieses Konzepts, ebenso wie viele andere Referenzen zu Programmiersprachen.

Im Fall von MQL5 können Sie im Abschnitt Typkonvertierung nachlesen, wie die implizite Konvertierung funktioniert, wobei immer ein komplexerer Typ, typischerweise double, bevorzugt wird. Eine solche Illustration ist unten abgebildet.

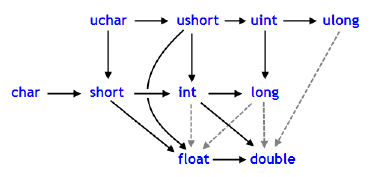
Abbildung 01

Da in der Dokumentation bereits erläutert wird, wie Datentypen im Verhältnis zueinander skaliert werden, werden wir hier nicht näher darauf eingehen. Neugierige Leser werden sich jedoch fragen: Warum ist das so?

Wenn Sie dies verstehen, werden Sie viele andere Konzepte besser begreifen. Warum führt zum Beispiel die Durchführung einer mathematischen Operation manchmal zu einem falschen oder unsinnigen Ergebnis? Warum erscheint ein Wert zunächst richtig, aber bei späterer Verwendung falsch?

Diese Unstimmigkeiten sind darauf zurückzuführen, wie die Daten im Speicher eines Computers dargestellt werden. Um dies richtig zu erklären, sollten wir ein neues Thema einführen.

Bitbreite

Am Ende des Artikels „Von der Grundstufe bis zur Mittelstufe: Variablen (II)“ haben wir uns eine Tabelle angesehen, die die Grenzwerte für verschiedene Datentypen im Speicher anzeigt. Es gibt jedoch ein wichtiges Detail: Fließkommatypen (double und float) werden nicht auf die gleiche Weise dargestellt wie Ganzzahltypen (int, ushort, etc.). Im Moment konzentrieren wir uns ausschließlich auf ganzzahlige Werte. Fließkommazahlen bedürfen einer tieferen Erklärung, die wir später behandeln werden. Dies ist von entscheidender Bedeutung, denn blindes Vertrauen in eine Gleitkommaberechnung kann zu schwerwiegenden Ungenauigkeiten führen.

Lassen Sie uns zunächst die ganzzahligen Werte in ihre grundlegendste Einheit zerlegen: Bits. Der höchste Wert, den ein Typ darstellen kann, entspricht 2, erhöht um die Anzahl der verwendeten Bits. Mit 4 Bits können Sie zum Beispiel 16 verschiedene Werte darstellen. Mit 10 Bit können Sie 1024 Werte darstellen usw.

Dies gilt jedoch nur für positive Werte. Negative Zahlen erfordern eine kleine Anpassung. Bei ganzen Zahlen mit Vorzeichen wird der Bereich durch 2 hoch (Anzahl der Bits - 1), vom negativen Gegenstück dieses Wertes minus 1, bestimmt. Das mag zunächst verwirrend klingen, ist aber in der Praxis ganz einfach. Mit denselben vier Bits, die aber sowohl positive als auch negative Werte darstellen, können wir zum Beispiel von -8 bis 7 gehen. Mit 10 Bits können wir von -512 bis 511 gehen. Aber warten Sie einen Moment. Müsste es nicht -8 bis 8 oder -512 bis 512 sein? Denn wenn wir 8 und 7 addieren, erhalten wir 15 und nicht 16, und wenn wir 512 und 511 addieren, erhalten wir 1023 und nicht 1024. Warum ist das so? Der fehlende Wert ist Null. Die Null nimmt eine Position im Bereich ein, weshalb die Zählung leicht abweichend erscheint.

Zur weiteren Klärung müssen wir verstehen, wie negative Zahlen im Speicher abgelegt werden. Schauen wir uns die folgende Abbildung an:

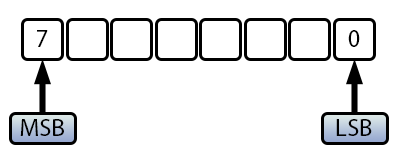
Abbildung 02

Hier sehen wir einen 8-Bit-Wert, der entweder ein Zeichen ohne Vorzeichen (uchar) oder ein Zeichen mit Vorzeichen (char) darstellen kann. Der Unterschied liegt im Most Significant Bit (MSB). Bei uchar (ohne Vorzeichen), wo alle Werte positiv sind (gekennzeichnet durch das Präfix u), spielt das MSB keine Rolle, sodass Werte von 0 bis 255 (insgesamt 256 Werte) möglich sind. Bei char (mit Vorzeichen) bestimmt jedoch das MSB, ob der Wert positiv oder negativ ist. Ist das MSB gleich eins, ist der Wert negativ, ist das MSB gleich null, ist der Wert positiv. Aus diesem Grund können wir positive Werte von 0 bis 127 zählen. Da die Null jedoch vorzeichenlos ist und dies der einzige Fall ist, in dem das MSB eingeschaltet ist und die anderen Bits nicht, wird sie als -128 interpretiert, es gibt also keine „negative Null“. Dies erklärt auch, warum die Zählung bei negativen Werten immer einen zusätzlichen Wert gegenüber der Hälfte der möglichen Werte aufweist.

Interessant, nicht wahr? Aber jetzt wird alles nur noch besser. Wenn Sie die obige Erklärung verstanden haben, dann wissen Sie bereits, wie die Funktion ABS oder MathAbs, die in vielen Programmiersprachen vorhanden ist, einen negativen Wert in einen positiven umwandeln kann. Um diese Umwandlung durchzuführen, müssen wir nur den Zustand des MSB ändern.

Wenn wir jedoch nicht darauf achten, was wir tun, kann uns das Unerwartete widerfahren. Wenn Sie zum Beispiel zwei positive Werte, z. B. 100 und 40, addieren, erhalten Sie einen negativen Wert. „Moment - was? Wenn beide Zahlen positiv sind, muss auch die Summe positiv sein!“ In der Alltagsmathematik ist das richtig. Aber in der Computerbranche funktionieren die Dinge nicht immer wie erwartet. Lassen Sie uns dieses Phänomen anhand des folgenden Codebeispiels untersuchen. Sehen Sie sich den nachstehenden Code an:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     char    value1 = 100,
07.             value2 = 40,
08.             Result;
09. 
10.     Result = value1 + value2;
11.     Print(value1, " + ", value2, " = ", Result);
12. }
13. //+------------------------------------------------------------------+

Code 03

Nach der Ausführung dieses Codes erscheint das folgende Ergebnis auf dem Bildschirm:

Abbildung 03

Heilige Jungfrau Maria! Was ist das? Das ist doch UNMÖGLICH. Nein, liebe Leserin, lieber Leser, das ist definitiv nicht unmöglich. Genau aus diesem Grund musste dieser Artikel geschrieben werden. Sie müssen verstehen, dass sich in einer stark typisierten Sprache die Wahl des richtigen Datentyps direkt auf das berechnete Ergebnis auswirkt. Viele Programmierer haben erhebliche Schwierigkeiten, weil sie dieses grundlegende Konzept nicht begreifen. Schlimmer noch, viele werden in die Irre geführt, weil sie sich dieser scheinbar einfachen Dinge nicht bewusst sind. Wenn Sie diese jedoch nicht richtig verstehen, werden Sie anfällig für falsche Zusicherungen von Genauigkeit und Sicherheit.

An dieser Stelle werden Sie vielleicht denken: „Also gut, wir verwenden einen Datentyp, der Werte bis 127 für positive Zahlen und -128 für negative Zahlen darstellen kann. Wäre es nicht besser, einen größeren Typ zu verwenden, z. B. einen int, der 32 statt 8 Bits verwendet?“ Ja, lieber Leser, das scheint eine vernünftige Lösung zu sein. Doch das ist nicht das eigentliche Problem. Das Problem ist, dass irgendwann der maximal darstellbare Wert erreicht wird, und wenn das passiert, wird die Berechnung unweigerlich auf irgendeine Weise fehlschlagen. Denken Sie daran, dass wir es nach wie vor nur mit Integer-Typen zu tun haben. Fließkommazahlen machen die Sache noch komplizierter.

Bevor man sich mit der Gleitkommaarithmetik befasst, ist es daher wichtig, zunächst die Ganzzahloperationen zu verstehen. Es ist jedoch wichtig zu erwähnen, dass es nicht immer möglich ist, einen größeren Datentyp zu verwenden. Diese Einschränkung wird besonders deutlich, wenn es um Zeichenketten geht. An dieser Stelle wird es noch komplizierter. Zeichenketten oder Zeichensequenzen können entweder eine 8-Bit- oder eine 16-Bit-Kodierung verwenden. In den meisten Fällen verlassen sich die Computer auf die ASCII-Tabelle. Es handelt sich um einen 8-Bit-Kodierungsstandard aus den Anfängen der Computertechnik. Da ASCII jedoch für die Darstellung bestimmter Zeichen unzureichend war, mussten zusätzliche Kodierungsverfahren entwickelt werden. Dies führte zur Einführung von 16-Bit-Zeichenkodierungen in einigen Programmen. Die Verwendung einer 16-Bit-Kodierung bietet jedoch nicht unendlich viele Möglichkeiten. Sie erweitert einfach den Bereich von 256 Werten auf 65.536 Werte, indem sie das höchstwertige Bit (MSB) auf Position 15 verschiebt.

Dennoch ist eine Zeichenkette letztlich nichts anderes als ein Array mit einfacheren Werten, das jedoch eine viel größere Bandbreite an Darstellungsmöglichkeiten bietet. In MQL5 können Sie beispielsweise einen 128-Bit-Wert erstellen, obwohl der größte vordefinierte Typ (ulong) auf 64 Bit beschränkt ist. Aber wie ist das möglich? Es ist eigentlich ganz einfach. Wenn Sie verstehen, wie jedes Bit in einer Sequenz zu einem Wert beiträgt, wenn es ein- oder ausgeschaltet ist, können Sie die entsprechenden Werte der aktiven Bits summieren. Auf diese Weise geschieht etwas fast Magisches: Sie erhalten die Möglichkeit, jeden erdenklichen Wert darzustellen.

Genau aus diesem Grund ergibt sich bei der Addition von 100 und 40 in Code 03 das Ergebnis -116. Das liegt daran, dass -116 in diesem Zusammenhang +140 entspricht. Auf den ersten Blick mag dies absurd erscheinen, aber wenn man die Werte in binärer Form betrachtet, ergibt sich folgendes Bild:

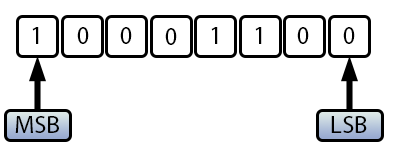
Abbildung 04

Mit anderen Worten, ein und derselbe Binärwert kann in einem Fall als positiv und in einem anderen Fall als negativ interpretiert werden, allein aufgrund der Art und Weise, wie das MSB behandelt wird. Aus diesem Grund müssen Sie vor allem bei der Erstellung von Schleifen äußerst vorsichtig sein. Wenn sie nicht richtig gehandhabt werden, können diese typbezogenen Probleme dazu führen, dass sich sowohl Berechnungen als auch Schleifen unvorhersehbar verhalten, selbst wenn alles korrekt zu funktionieren scheint. Fehler bei der Typenauswahl oder die Überschreitung der Höchstgrenze eines bestimmten Typs können dazu führen, dass ein ganzes Programm außer Kontrolle gerät.

An einer Stelle haben wir erwähnt, dass dieses Problem durch die Verwendung eines größeren Datentyps gelöst werden könnte. Aber warum funktioniert dieser Ansatz in einigen Fällen und in anderen nicht? Die Antwort liegt darin, wie das MSB verschoben wird. Dieser Effekt ist in der folgenden Abbildung zu sehen:

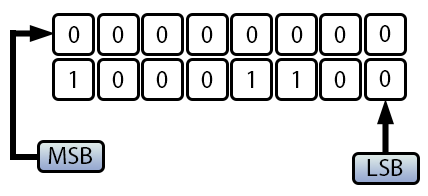
Abbildung 05

Das Konzept ist einfach, nicht wahr? Damit sind die Grundlagen der arithmetischen Operationen für den Moment abgedeckt. Alles, was wir bisher besprochen haben, bezieht sich jedoch auf arithmetische Operatoren. Es gibt eine weitere wichtige Kategorie von Operatoren, die wir als Nächstes untersuchen müssen: logische Operatoren. Um diese Konzepte zu erklären und richtig zu trennen, werden wir uns einem neuen Thema zuwenden.

Logische Operatoren

Logische Operatoren arbeiten auf Bitebene. Obwohl sie manchmal auf Bytes oder ganze Bitsätze angewandt werden können, sind sie in erster Linie für die Funktion auf Bit-Ebene konzipiert. Auf den ersten Blick mag dies etwas verwirrend erscheinen, aber mit der Zeit werden Sie sehen, dass es Sinn macht. Im Gegensatz zu arithmetischen Operatoren, die für die Durchführung von Berechnungen verwendet werden, werden logische Operatoren für die Auswertung von Bedingungen verwendet. In der Regel wird mit logischen Operationen geprüft, ob Werte bestimmte Bedingungen erfüllen. Da diese Operatoren am effektivsten sind, wenn sie zusammen mit Kontrollstrukturen verwendet werden, werden wir hier nur einen kurzen Überblick geben, um Sie auf die kommenden Themen vorzubereiten.

Obwohl logische Operatoren in Verbindung mit bedingten Anweisungen sinnvoller sind, können sie auch zur Durchführung kleinerer Operationen verwendet werden. In der Tat ist jede CPU-Operation in Wirklichkeit logischer als Arithmetik. Obwohl die Arithmetic Logic Unit (ALU) sowohl für Arithmetik als auch für Logik steht, sind logische Operationen für die CPU-Funktionalität grundlegend.

Bei den logischen Operatoren gibt es vor allem AND, OR, NOT und in einigen, aber nicht allen Programmiersprachen XOR. Darüber hinaus gibt es Rechts- und Linksverschiebungen. Diese einfachen Operationen dienen als Grundlage für die gesamte Rechenlogik. In Wirklichkeit kann man aus diesen Grundoperationen alles machen. Genau nach diesem Prinzip arbeitet die ALU, das „Gehirn“ der CPU.

An diesem Punkt schauen Sie vielleicht in die MQL5-Dokumentation (oder in die Referenz einer anderen Programmiersprache) und fragen sich: „Es gibt aber noch weitere logische Operatoren, wie z.B. größer als (>), kleiner als (<), und andere. Warum sind sie hier nicht enthalten?“ Gute Frage, lieber Leser. Einige Sprachen bieten zur Vereinfachung zusätzliche logische Operatoren oder Vergleichsfunktionen. Auf der Hardware-Ebene sind diese Operationen jedoch weitaus einfacher als in den Programmiersprachen dargestellt. Um es klar zu sagen: Dies ist keine Kritik an diesen Umsetzungen. Sie erleichtern die Programmierung sogar erheblich. Die einfachste Art, zwei Werte zu vergleichen, ist zum Beispiel die Subtraktion. Eine alternative Methode ist jedoch die Anwendung einer bitweisen XOR-Operation. Wenn alle Bits übereinstimmen, ist das Ergebnis Null. Wenn ein Bit abweicht, sind die Werte nicht gleich. Bei der Subtraktion können wir das MSB analysieren, um festzustellen, ob das Ergebnis Null (gleich), negativ (kleiner als) oder positiv (größer als) ist. So können wir numerische Beziehungen ohne explizite Vergleichsoperatoren herstellen.

Um dieses Konzept zu verdeutlichen, sehen wir uns ein einfaches Beispiel an, in dem bestimmt wird, ob ein Wert größer, kleiner oder gleich einem anderen ist. Dazu verwenden wir den folgenden Codeabschnitt:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     short   value1 = 230,
07.             value2 = 250;
08. 
09.     Print("Result #1: ", value1 - value2);
10.     Print("Result #2: ", value2 - value1);
11.     Print("Result #3: ", value2 ^ value1);
12. }
13. //+------------------------------------------------------------------+

Code 04

Hier haben wir ein einfaches und typisches Wertanalysesystem. Wenn dieser Code ausgeführt wird, sehen Sie das folgende Ergebnis im Terminal:

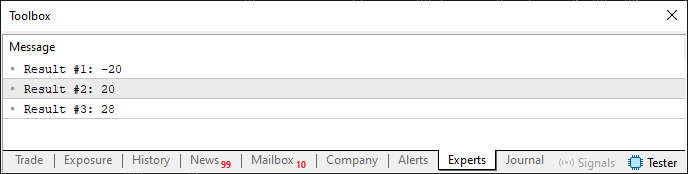
Abbildung 06

Achten Sie nun auf das, was vorhin über die Bestimmung, ob ein Wert größer, kleiner oder gleich einem anderen ist, gesagt wurde. Um die Sache noch interessanter zu machen, verwenden wir einen 16-Bit-Wert mit Vorzeichen, mit dem wir 65.536 verschiedene Werte darstellen können. Da es sich jedoch um einen Wert mit Vorzeichen handelt, d. h. er kann sowohl negative als auch positive Zahlen enthalten, reicht der Bereich von -32.768 bis 32.767. Wenn wir uns auf die Analyse von Werten innerhalb eines 8-Bit-Bereichs beschränken, werden wir keine Probleme haben, zu bestimmen, ob ein Wert größer, kleiner oder gleich einem anderen ist. Aber mit 16-Bits können wir einen viel breiteren Bereich darstellen, von -255 bis 255, was hervorragend ist. Allerdings gibt es Möglichkeiten, dies noch besser zu machen. Aber darauf wollen wir jetzt noch nicht eingehen, denn es gibt ein paar Konzepte, die zunächst erklärt werden müssen. Dennoch ist Code 04 ziemlich faszinierend und macht Spaß.

Schauen wir uns also an, was hier passiert. Da Wert1 eindeutig kleiner ist als Wert2, ergibt die Subtraktion des einen vom anderen einen negativen Wert, was bestätigt, dass der erste Wert tatsächlich kleiner ist. Dies geschieht in Zeile 9 von Code 04. Subtrahiert man dagegen Wert1 von Wert2, wie in Zeile 10 gezeigt, ist das Ergebnis positiv, was bedeutet, dass Wert2 größer ist als Wert1. Schließlich führen wir in Zeile 11 einen Vergleich durch, um zu prüfen, ob die Werte gleich sind. Da das Ergebnis ungleich Null ist, können wir mit Sicherheit feststellen, dass die Werte nicht gleich sind.

Dieses Konzept ist recht interessant, und es wird noch faszinierender, wenn man feststellt, dass es in der ALU keine Subtraktionsoperation gibt. Tatsächlich ist jede Operation, die in der ALU durchgeführt wird, im Grunde nur eine Summe, kombiniert mit einigen logischen Operationen. Sogar die Additionsoperation kann im Kern auf logische Operationen reduziert werden.

Um dies jedoch richtig zu demonstrieren, müssten wir einige Kontrollfunktionen verwenden. Da die Kontrollfunktionen in diesem Artikel noch nicht erläutert wurden, werden wir nicht näher darauf eingehen, wie diese auf ALU-Ebene implementiert werden könnten. Aber keine Sorge, wir werden das in zukünftigen Artikeln behandeln. Wenn Sie erst einmal verstanden haben, wie man diese Techniken implementiert, können Sie MQL5 für viel fortgeschrittenere und spannendere Aufgaben als die Erstellung von Indikatoren, Skripten und Expert Advisors verwenden.

Ob ich diese Umsetzung demonstrieren werde, ist noch ungewiss, da das Hauptziel hier rein pädagogisch ist. Aber ich werde darüber nachdenken.

Ich stimme zu, dass Verschiebungsoperatoren immer noch nicht richtig dargestellt werden, da sie in der MQL5-Dokumentation kaum erwähnt werden. Diese Operatoren haben jedoch einen ganz bestimmten Zweck und sind auf die Erfüllung bestimmter Aufgaben ausgerichtet. Aus diesem Grund werden sie in den meisten gängigen MQL5-Codes nicht verwendet, insbesondere bei der Arbeit mit Indikatoren und Expert Advisors. Bei der Arbeit mit Bildern in einer mit MQL5 erstellten Anwendung werden diese Operatoren jedoch sehr viel häufiger verwendet.

Wenn sie jedoch für ganz bestimmte Tätigkeiten bestimmt sind, können sie auch für andere Zwecke verwendet werden. Eine solche Aufgabe wird untersucht, sobald wir uns mit den Kontrollfunktionen befassen.

Abschließende Überlegungen

In diesem Artikel haben wir einige wichtige Details der Programmierung behandelt, die einen wesentlichen Unterschied machen, wenn man in einer stark typisierten Sprache arbeitet. Auch wenn einige der erörterten Konzepte für viele neu sein mögen, haben wir nur an der Oberfläche dessen gekratzt, was es zu diesem Thema gibt. Daher rate ich Ihnen, lieber Leser, sich die Zeit zu nehmen, die grundlegende MQL5-Dokumentation zu studieren, um Ihr Verständnis der hier vorgestellten Konzepte zu vertiefen. Außerdem empfehle ich Ihnen, sich mit der booleschen Logik zu befassen, die trotz ihrer Einfachheit viele der Berechnungen vereinfachen wird, die Ihnen bei Ihren Programmieraufgaben begegnen. Wenn man weiß, wie man mit positiven und negativen Werten arbeitet und wie sich diese Nuancen auswirken, macht das auf lange Sicht einen großen Unterschied.

In den beigefügten Dateien sind drei der vier hier besprochenen Codes enthalten, sodass Sie sie in Ihrem eigenen Tempo studieren können. Im nächsten Artikel werden wir uns mit Kontrollfunktionen oder Operatoren beschäftigen. Dann wird es richtig spannend, und der eigentliche Spaß beginnt. Bis bald!