Bivariate Copulae in MQL5 (Teil 1): Implementierung von Gauß- und Studentische t-Copulae für die Modellierung von Abhängigkeiten

Einführung

Copula-basierte Handelsstrategien bieten einen interessanten alternativen Ansatz zur statistischen Arbitrage, indem sie die Abhängigkeit zwischen zwei Handelsinstrumenten mithilfe einer Copula-Funktion modellieren. Der traditionelle Paarhandel stützt sich auf vorübergehende Abweichungen von einer erwarteten langfristigen Beziehung, und eine Copula kann zur Modellierung dieser Beziehung verwendet werden, um Handelsmöglichkeiten zu identifizieren. Der theoretische Vorteil der Verwendung von Copulae liegt in ihrer Fähigkeit, nicht-lineare und asymmetrische Abhängigkeiten zwischen Handelsinstrumenten zu erfassen.

In diesem Sinne markiert dieser Artikel den Beginn einer Serie über die Implementierung von Werkzeugen für Copula-basierte Handelsstrategien. In diesem ersten Teil werden die Grundlagen der statistischen Copulae im Zusammenhang mit dem Paarhandel und der Modellierung von Abhängigkeiten untersucht. Wir präsentieren auch MQL5-Code für die Vorverarbeitung von Datensätzen vor der Anpassung von Copula-Modellen. Der breitere Schwerpunkt der Reihe wird eine Bibliothek sein, die häufig verwendete Copula-Modelle implementiert. Zunächst werden in diesem Artikel Implementierungen der Gauß'schen und der Studentischen t-Copulae vorgestellt.

Wichtige Grundlagen der Copula-Theorie

Um mit Copulas arbeiten zu können, müssen drei miteinander verbundene Konzepte verstanden werden.

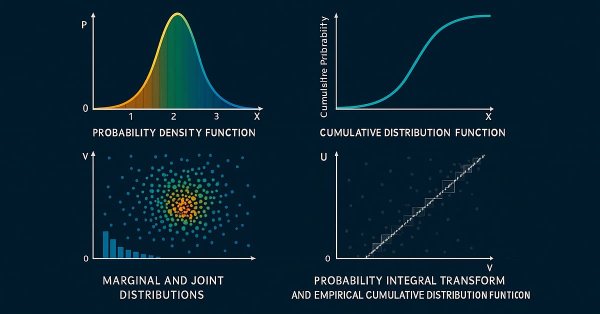
Die Wahrscheinlichkeitsdichtefunktion. Bei der Untersuchung statistischer Verteilungen beschreibt die Wahrscheinlichkeitsdichtefunktion (Probability Density Function, PDF) die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable X einen bestimmten Wert x annimmt. Im Gegensatz zu einer diskreten Wahrscheinlichkeitsmassenfunktion ordnet die PDF die Wahrscheinlichkeiten nicht direkt bestimmten Werten zu. Stattdessen stellt sie eine Dichte dar, sodass die Wahrscheinlichkeit, dass X in ein bestimmtes Intervall [a,b] fällt, durch das Integral der PDF über diesen Bereich gegeben ist.

Die kumulative Verteilungsfunktion. Die kumulative Verteilungsfunktion (Cumulative Distribution Function, CDF), die auf der PDF aufbaut, gibt die Wahrscheinlichkeit an, dass eine Zufallsvariable X einen Wert annimmt, der kleiner oder gleich x ist. Die CDF ist eine nicht-abnehmende Funktion, die von 0 bis 1 reicht und eine vollständige Beschreibung der Wahrscheinlichkeitsverteilung einer Zufallsvariablen liefert.

Marginale und gemeinsame Verteilungen. Wenn man mit mehreren Zufallsvariablen arbeitet, muss man zwischen Randverteilungen und gemeinsamen Verteilungen unterscheiden. Eine Randverteilung beschreibt die Wahrscheinlichkeitsverteilung einer einzelnen Variablen innerhalb einer größeren Menge, wobei der Einfluss der anderen Variablen praktisch ignoriert wird. Im Gegensatz dazu charakterisiert eine gemeinsame Verteilung die kollektive Wahrscheinlichkeitsverteilung aller Variablen in einem Datensatz.  

Die Wahrscheinlichkeitsintegraltransformation. Die Wahrscheinlichkeitsintegraltransformation (Probability Integral Transform, PIT) ist ein grundlegendes Konzept der Wahrscheinlichkeitstheorie und ein wichtiger Baustein für das Verständnis der Copulae. Er besagt, dass, wenn X eine kontinuierliche Zufallsvariable ist, deren CDF = F(X), dann ist die transformierte Variable U=F(X) ist gleichmäßig auf dem Intervall [0,1] verteilt. Mit anderen Worten: Unabhängig davon, ob X einer Normal-, Exponential- oder einer anderen kontinuierlichen Verteilung folgt, wird es durch die Anwendung seiner eigenen CDF in eine Variable mit einer Gleichverteilung auf [0,1] umgewandelt.

Das PIT ermöglicht die Abbildung jeder kontinuierlichen Zufallsvariablen auf das Einheitsintervall, wodurch sie effektiv standardisiert wird, während ihre probabilistische Struktur erhalten bleibt. Durch die Umwandlung von Randbedingungen in gleichmäßige Verteilungen können wir analysieren, wie die Variablen ohne den Einfluss ihrer individuellen Verteilungen miteinander verbunden sind. Dieser einheitliche Raum ist genau der Ort, an dem Copulae wirken, denn sie erfassen die Abhängigkeitsstruktur zwischen den Variablen, sobald die Marginale auf diese Weise transformiert worden sind.

Empirische kumulative Verteilungsfunktion. Wenn die tatsächliche zugrundeliegende Verteilung einer Variablen unbekannt ist, können wir die empirische kumulative Verteilungsfunktion (Empirical Cumulative Distribution Function, ECDF) als Schätzung für die tatsächliche CDF verwenden. Für eine Stichprobe von N Beobachtungen, x1, x2, ...,xN ist die ECDF definiert als:

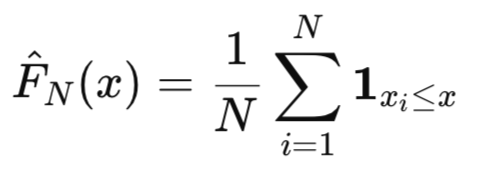
die eine Funktion angibt, die gleich 1 ist, wenn x_i <= x, und andernfalls 0.

Die Verwendung der ECDF zur Durchführung der PIT wird häufig als nicht-parametrischer Ansatz zur Schätzung bezeichnet, da er nicht von einer bestimmten Verteilungsform für die Randwerte ausgeht. Die transformierten Datenpunkte sind die Eingaben, die zur Anpassung der Copula selbst verwendet werden.

Die Datei linear_cdf.mqh enthält die Definition der Klasse CLinearCDF, die zur Schätzung der ECDF eines Datensatzes verwendet wird. Die Klasse erzeugt eine ECDF mit linearer Interpolation zwischen den Stufen der Standard-ECDF. Dadurch wird das Ergebnis effektiv geglättet, während die Übereinstimmung mit der Standard-ECDF an den Stichprobenpunkten erhalten bleibt.

//+------------------------------------------------------------------+
//|                                                   linear_cdf.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Arrays/ArrayDouble.mqh>
#include<Arrays/ArrayObj.mqh>
#include "ecdf.mqh"
//+------------------------------------------------------------------+
//|CArray objects                                                    |
//+------------------------------------------------------------------+
class CArrayDoubles:public CArrayObj
  {
   virtual bool      CreateElement(const int index)
     {
      m_data[index] = new CArrayDouble();
      return m_data[index]!=NULL;
     }
  };
//+------------------------------------------------------------------+
//| ecdf quantile transformer                                        |
//+------------------------------------------------------------------+
class CLinearCDF
  {
protected:
   CSpline1DInterpolantShell* m_shells[];
   CArrayDoubles      m_internal;
   CArrayDouble      *m_arrays[];
   double            m_ub,m_lb;
   ulong             m_cols;
   void              clean_up(void)
     {

      for(uint i = 0; i<m_shells.Size(); i++)
         delete m_shells[i];
      for(uint i = 0; i<m_arrays.Size(); i++)
         delete m_arrays[i];
      m_internal.Clear();
     }
public:
                     CLinearCDF(void)
     {
      m_cols = 0;
     }
                    ~CLinearCDF(void)
     {
      clean_up();
     }
   bool              save(const int filehandle)
     {
      if(!m_cols)
         return false;
      return m_internal.Save(filehandle);
     }
   bool              load(const int filehandle)
     {
      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      if(m_internal.Load(filehandle))
        {
         int n_arrays = m_internal.Total();
         m_cols = ulong((n_arrays-1)/2);
         ArrayResize(m_shells,int(m_cols));
         ArrayResize(m_arrays,int(m_cols*2)+1);
         double xa[],ya[];
         m_arrays[0] = m_internal.At(0);
         m_ub = m_arrays[0].At(0);
         m_lb = m_arrays[0].At(1);
         for(int i = 0; i<int(m_cols); i++)
           {
            m_arrays[i*2+1] = m_internal.At(i*2+1);
            m_arrays[i*2+2] = m_internal.At(i*2+2);
            ArrayResize(xa,m_arrays[i*2+1].Total());
            for(int j = 0; j<m_arrays[i*2+1].Total(); j++)
               xa[j] = m_arrays[i*2+1][j];
            ArrayResize(ya,m_arrays[i*2+2].Total());
            for(int j = 0; j<m_arrays[i*2+2].Total(); j++)
               ya[j] = m_arrays[i*2+2][j];
            m_shells[i] = new CSpline1DInterpolantShell();
            CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
           }
         return true;
        }
      else
         return false;
     }
   bool              fit(matrix &data,double upper_bound = 1.0-1.e-5,double lower_bound = 1.e-5)
     {
      if(upper_bound<=lower_bound)
        {
         Print(__FUNCTION__, " invalid inputs ");
         return false;
        }

      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      m_ub = upper_bound;
      m_lb = lower_bound;
      m_cols = data.Cols();
      vector v;
      double xa[],ya[];
      vector slopes;
      vector slope_samples;
      CECDF m_ecdf;
      ArrayResize(m_shells,int(m_cols));
      ArrayResize(m_arrays,int(m_cols*2)+1);
      m_arrays[0] = new CArrayDouble();
      if(!m_arrays[0].Add(m_ub) || !m_arrays[0].Add(m_lb) || !m_internal.Add(m_arrays[0]))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      for(uint i = 0; i<m_shells.Size(); i++)
        {
         v = data.Col(i);
         if(!m_ecdf.fit(v))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }

         np::quickSort(v,true,0,long(v.Size()-1));
         slopes = np::unique(v);
         slope_samples = m_ecdf.ecdf(slopes);
         m_shells[i] = new CSpline1DInterpolantShell();
         if(!np::vecAsArray(slopes,xa) || !np::vecAsArray(slope_samples,ya))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }
         m_arrays[i*2+1] = new CArrayDouble();
         m_arrays[i*2+2] = new CArrayDouble();
         if(!m_arrays[i*2+1].AddArray(xa) || !m_arrays[i*2+2].AddArray(ya) ||!m_internal.Add(m_arrays[i*2+1])||!m_internal.Add(m_arrays[i*2+2]))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }
         CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
        }

      return true;
     }

   matrix            to_quantile(matrix &in)
     {
      if(in.Cols()!=m_cols)
        {
         Print(__FUNCTION__, " invalid input ");
         return matrix::Zeros(0,0);
        }

      vector temp;
      matrix out(in.Rows(),m_cols);
      for(ulong i = 0; i<m_cols; ++i)
        {
         temp  = in.Col(i);
         for(ulong j = 0; j<in.Rows(); ++j)
            out[j][i] = MathMax(MathMin(CAlglib::Spline1DCalc(m_shells[i],temp[j]),m_ub),m_lb);
        }

      return out;
     }
  };
//+------------------------------------------------------------------+

Die Methode fit() nimmt eine Matrix mit einer beliebigen Anzahl von Spalten an, die als Variablen eines multivariaten Datensatzes angenommen werden. Die optionalen Eingabeparameter upper_bound und lower_bound definieren Beschränkungen, die Werte von genau 0 oder 1 verhindern. Intern wird die Standard-ECDF an eindeutigen sortierten Stichprobenpunkten abgetastet. Auf der Grundlage dieser Punkte und ihrer entsprechenden ECDF-Werte wird dann ein eindimensionales lineares Interpolationsmodell erstellt. 

//+------------------------------------------------------------------+
//|                                                    ECDF_Demo.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ECDF/linear_cdf.mqh>
//--- input parameters
input string   FirstSymbol = "NZDUSD";
input string   SecondSymbol = "AUDUSD";
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2024.01.01 00:00:01';
input ulong HistoryLength = 1000;
input bool Use_Returns = false;
input int DisplayDuration = 30;//display duration in seconds
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---download symbol data
   vector syA,syB;
   if(!syA.CopyRates(FirstSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      !syB.CopyRates(SecondSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      syA.Size()!=syB.Size())
     {
      Print("Error downloading price data ", ::GetLastError());
      return;
     }
//---optionally transform to returns
   if(Use_Returns)
     {
      syA = np::diff(log(syA));
      syB = np::diff(log(syB));
     }
//---create matrix container and fill it
   matrix xy(syA.Size(),2);
   if(!xy.Col(syA,0) || !xy.Col(syB,1))
     {
      Print(" column insertion error ", GetLastError());
      return ;
     }
//---build ECDF model
   CLinearCDF qd;
   if(!qd.fit(xy))
     {
      Print(" CLinearCDF failure ");
      return;
     }
//---transform raw values to quantiles
   matrix yx = qd.to_quantile(xy);
//---display QQ plot
   np::scatter_plot(yx.Col(0),yx.Col(1),"Q-Q plot",FirstSymbol,SecondSymbol,true,0,0,0,0,500,500,true,30);
//---
  }
//+------------------------------------------------------------------

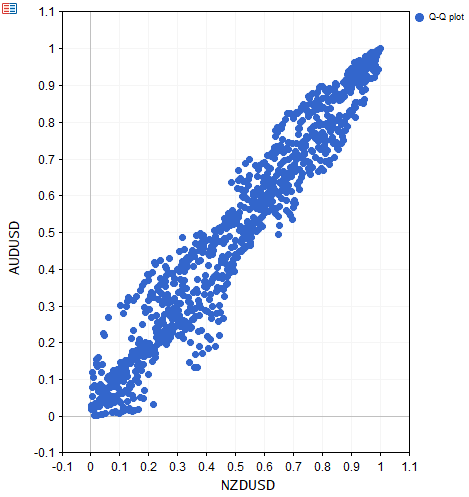
Das Skript ECDF_Demo.ex5 demonstriert die Verwendung der Klasse CLinearCDF, indem es auf einen bivariaten Datensatz von Preisen angewendet wird. Die transformierten Werte werden dann zur Darstellung der Quantil-zu-Quantil-Darstellung (Q-Q) der Daten verwendet. 

Definieren einer Copula

Eine Copula ist eine multivariable kumulative Verteilungsfunktion, die die Abhängigkeitsstruktur zwischen Zufallsvariablen unabhängig von deren Randverteilungen erfasst. Vereinfacht ausgedrückt ist eine Copula ein mathematischer Mechanismus, der es uns ermöglicht, die Abhängigkeit zwischen Variablen vom individuellen Verhalten der einzelnen Variablen zu entkoppeln.

Bei gegebenen Zufallsvariablen, die jeweils ihre eigene Randverteilung haben, verbindet eine Copula diese Randverteilungen zu einer gemeinsamen Verteilung, indem sie beschreibt, wie die Variablen zueinander in Beziehung stehen, unabhängig von der Form ihrer individuellen Verteilungen. Diese Trennung von Rändern und Abhängigkeit ist für die moderne multivariate Analyse von zentraler Bedeutung, insbesondere wenn die Annahme der Normalität oder der linearen Abhängigkeit unangemessen ist. Dies wird mathematisch durch das Theorem von Sklar formalisiert. Der Satz von Sklar besagt, dass es für jede kontinuierliche gemeinsame Verteilungsfunktion F eine eindeutige Copula C gibt, die so beschaffen ist, dass:

wobei F1(x1) und F2(x2) sind die marginalen CDFs von X1 und X2.

Die Fähigkeit einer Copula, die Abhängigkeit von zwei oder mehr Zufallsvariablen zu erfassen, kann mit einem Maß für die Assoziation, wie dem Korrelationskoeffizienten, verglichen werden. Der Unterschied besteht darin, dass eine Copula zusätzliche Informationen über die Art des Zusammenhangs zwischen den Variablen liefert, im Gegensatz zur Beschränkung auf eine einzige Zahl.

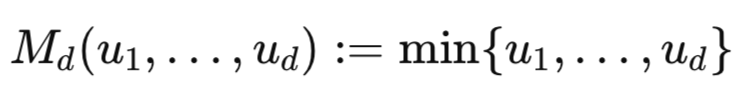
Genauso wie der Korrelationskoeffizient zwischen -1 und 1 begrenzt ist, gelten für Copulae ähnliche Grenzen, die sogenannten Fréchet-Hoeffding-Grenzen. Die unteren und oberen Fréchet-Hoeffding-Grenzen sind Funktionen, die die größte negative und positive Abhängigkeit definieren, die durch eine bestimmte Copula erfasst werden kann. Die Fréchet-Hoeffding-Grenzen sind selbst Copulae, wobei d der Dimensionalität oder der Anzahl der Variablen entspricht.

Abhängigkeit von den Rändern

Die Einzigartigkeit der einzelnen Copula-Funktionen ermöglicht es ihnen, verschiedene Arten von Abhängigkeitsstrukturen zu erfassen. Eine Eigenschaft einer Copula, die in der Regel für Finanzanwendungen von Interesse ist, ist ihre Fähigkeit, die Abhängigkeit der Ränder zu modellieren. Die Randabhängigkeit ist ein Maß für die Korrelation zwischen Zufallsvariablen, wenn sie Extremwerte aufweisen. Die Art der Abhängigkeit der Ränder, die eine Copula modellieren kann, bestimmt, wie die Struktur mit gemeinsamen Extremereignissen umgeht. Der obere Rand bezieht sich auf extrem hohe Werte in einer Verteilung, während der untere Rand extrem niedrigen Werten entspricht. Die Abhängigkeit der Ränder wird durch deren Abhängigkeitskoeffizienten (λ) quantifiziert, der als Grenzwert für eine bedingte Wahrscheinlichkeit berechnet wird. Die Abhängigkeit der Ränder ist schwer zu quantifizieren, ohne sie in Form einer Copula auszudrücken.

Die Abhängigkeit des unteren Rands misst die Wahrscheinlichkeit, dass eine Variable extrem niedrig ist, wenn die andere Variable ebenfalls extrem niedrig ist.

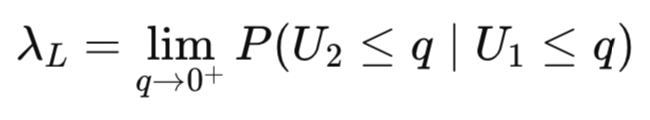
Die Abhängigkeit des oberen Rands misst die Wahrscheinlichkeit, dass eine Variable extrem hoch ist, wenn die andere Variable ebenfalls extrem hoch ist.

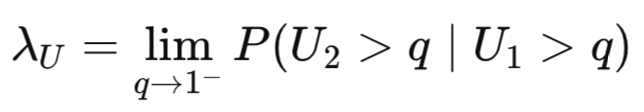
Copula-Typen

Copulae können in breite Klassen und Familien eingeteilt werden, die bestimmte funktionale Formen definieren. Die Art von Copulae, die wir in dieser Artikelserie beschreiben werden, sind parametrisch. Dies sind Copulae, die durch Parameter charakterisiert sind, die die Abhängigkeitsmerkmale, die sie erfassen, quantifizieren.

Elliptische Copulae sind eine Klasse von multivariaten Copulae, die von elliptischen Verteilungen abgeleitet sind, wie z. B. die multivariaten Normal- (Gauß-) und Studentische t-Verteilungen. Sie werden in erster Linie durch ein Assoziationsmaß parametrisiert, das die lineare Abhängigkeitsstruktur zwischen den Variablen abbildet. Die beiden gebräuchlichsten elliptischen Copulae sind die Gauß'sche und die Studentische t-Copulae. Im nächsten Abschnitt befassen wir uns mit der Implementierung von bivariaten elliptischen Copulae, beginnend mit der bivariaten Gauß‘schen Copula.

Bivariate Gauß‘sche Copula

Die bivariate Gauß‘sche Copula ist von der bivariaten Normalverteilung abgeleitet. Sie ist durch einen einzigen Parameter gekennzeichnet: den linearen Korrelationskoeffizienten (ρ) der zugrunde liegenden bivariaten Normalverteilung. Dieser Parameter bestimmt die Stärke und Richtung der Abhängigkeit zwischen den beiden Zufallsvariablen. Die Gauß‘sche Copula ist radialsymmetrisch und wegen ihrer rechnerischen Nachvollziehbarkeit beliebt, obwohl sie eine schwache Randabhängigkeit aufweist. Das bedeutet, dass sie starke, gleichzeitige Extremereignisse in den Variablen nicht angemessen erfasst.

In der Header-Datei gaussian.mqh ist die Klasse CGaussian aufgeführt, die eine bivariate Gauß‘sche Copula implementiert. CGaussian ist ein Abkömmling der abstrakten Klasse CBivariateCopula, die in base.mqh definiert ist, und ist die Grundlage für alle bivariaten Copulae-Implementierungen, die wir beschreiben werden.

//+------------------------------------------------------------------+
//| base copula class                                                |
//+------------------------------------------------------------------+
class CBivariateCopula:public CObject
  {
private:
   int               m_len;
protected:
   double            m_eps;
   double            m_theta;
   double            m_rho;
   double            m_nu;
   double            m_threshold;
   ENUM_COPULA_TYPE  m_copula_type;
   vector            m_bounds;
   double            m_tau;
   matrix            m_cov;
   virtual bool      check_theta(void) 
     {
       return (m_theta>m_bounds.Min() < m_theta < m_bounds.Max());  
     }
   virtual double    pdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    cdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    condi_cdf(double u,double v) { return EMPTY_VALUE; }
   virtual vector    pdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    condi_cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual double    theta_hat(const double tau){ return EMPTY_VALUE; }
   void              preprocess(double &u, double &v)
     {
      u = MathMin(MathMax(m_eps,u),1.0-m_eps);
      v = MathMin(MathMax(m_eps,v),1.0-m_eps);
     }
   void              preprocess(vector &u, vector &v)
     {
      u.Clip(m_eps,1.0-m_eps);
      v.Clip(m_eps,1.0-m_eps);
     }
   double            kendalTau(const vector &vec1,const vector &vec2)
     {
      double tau = double("nan");
      ulong size=vec1.Size();
      if(size==0 || vec2.Size()!=size)
        {
         Print(__FUNCTION__, " size of input vectors donot match ");
         return(tau);
        }
      //---
      long cnt1=0,cnt2=0,cnt=0;
      //---
      for(long i=0; i<long(size); i++)
        {
         for(long j=i+1; j<long(size); j++)
           {
            double delta1=vec1[i]-vec1[j];
            double delta2=vec2[i]-vec2[j];
            double delta=delta1*delta2;
            if(delta==0)
              {
               if(delta1!=0)
                  cnt1++;
               if(delta2!=0)
                  cnt2++;
              }
            else
              {
               cnt1++;
               cnt2++;
               if(delta>0.0)
                  cnt++;
               else
                  cnt--;
              }
           }
        }
      //--- calculate Kendall tau
      long den=cnt1*cnt2;
      if(den==0)
        {
         Print(__FUNCTION__, " failed zero check at line 76");
         return tau;
        }
      tau=double(cnt)/MathSqrt(den);
      //---
      return(tau);
     }

public:
                     CBivariateCopula(void)
     {
      m_len = 6;
      m_eps = 1.e-5;
      m_theta = m_rho = m_nu = EMPTY_VALUE;
      m_copula_type = WRONG_VALUE;
      m_cov  = matrix::Zeros(0,0);
      m_bounds = vector::Zeros(2);
      m_bounds[0] = -DBL_MIN;
      m_bounds[1] = DBL_MAX;
     }
                    ~CBivariateCopula(void)
     {
     }
   double            Get_theta(void)  { return m_theta; }
   double            Get_tau(void)    { return m_tau;   }
   double            Get_rho(void)    { return m_rho;   }
   matrix            Get_covar(void)  { return m_cov;   }
   double            Get_nu(void)     { return m_nu;    }
   double            Get_threshold(void) { return m_threshold; }
   double            Get_eps(void)    { return m_eps;   }
   virtual void              Set_theta(double theta) {  m_theta = theta; }
   virtual void              Set_tau(double tau) { m_tau = tau; }
   virtual void              Set_threshold(double threshold) { m_threshold = threshold; }
   virtual void              Set_nu(double nu) { m_nu = nu; }
   virtual void              Set_rho(double rho) { m_rho = rho; }
   virtual void              Set_eps(double eps) { m_eps = eps; }
   virtual matrix            Sample(ulong num_samples) { return matrix::Zeros(0,0); }
   virtual void              Set_covariance(matrix &cov)
     {
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
     }
   virtual double    Fit(vector &u, vector&v)
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
       {
        Print(__FUNCTION__, " Invalid input variable(s) ");
        return EMPTY_VALUE;
       }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(!check_theta())
        Print(__FUNCTION__, " Invalid theta " );
      return  m_theta;
     }
   double            Log_likelihood(vector &u, vector &v)
     {
      if(u.Size()!=v.Size())
        {
         Print(__FUNCTION__, " vectors are not of equal length ");
         return EMPTY_VALUE;
        }
      
      vector ll = pdf(u,v);

      return (log(ll)).Sum();
     }
   double            Copula_PDF(double u, double v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   double            Copula_CDF(double u, double v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   double            Conditional_Probability(double u, double v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   vector            Copula_PDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   vector            Copula_CDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   vector            Conditional_Probability(vector& u, vector& v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   double            Theta(double tau = 0.0)
     {
      if(!tau && m_tau)
         return theta_hat(m_tau);
      else
         if(tau)
            return theta_hat(tau);
         else
           {
            Print(__FUNCTION__ " invalid input parameter 'tau' ");
            return EMPTY_VALUE;
           }
     }

   virtual bool      Save(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileWriteLong(file_handle,-1)==sizeof(long))
           {
            //---
            if(FileWriteInteger(file_handle,int(m_copula_type),INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteInteger(file_handle,m_len,INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteDouble(file_handle,m_eps)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_theta)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_tau)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_rho)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_nu)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_threshold)!=sizeof(double))
               return false;
            return true;
           }
        }
      return false;
     }
   virtual bool      Load(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileReadLong(file_handle)==-1)
           {
            //---
            m_copula_type = ENUM_COPULA_TYPE(FileReadInteger(file_handle,INT_VALUE));

            if(FileReadInteger(file_handle,INT_VALUE)!=m_len)
               return false;

            ResetLastError();
            m_eps=FileReadDouble(file_handle);
            m_theta=FileReadDouble(file_handle);
            m_tau=FileReadDouble(file_handle);
            m_rho=FileReadDouble(file_handle);
            m_nu=FileReadDouble(file_handle);
            m_threshold=FileReadDouble(file_handle);
            if(GetLastError())
              {
               Print(__FUNCTION__, " possible read error ", GetLastError());
               return false;
              }
            return true;
           }
        }
      return false;
     }
   virtual int       Type(void)
     {
      return int(m_copula_type);
     }
  };

Es ermöglicht die Spezifikation von Copula-Modellen auf zwei Arten. Ein Modell kann explizit definiert werden, indem die Accessor-Methoden verwendet werden, um relevante Copula-Parameter zu setzen. Alternativ kann ein Modell erstellt werden, indem es mit Hilfe der Methode Fit() an einen bivariaten Datensatz einheitlicher Variablen (die marginalen CDFs der Rohwerte) angepasst wird. Bei Erfolg gibt die Methode einen anderen Wert als die Konstante EMPTY_VALUE zurück.

Die Dichte einer Copula wird durch Aufruf der Methode Copula_PDF() ausgewertet, während Copula_CDF() die gemeinsame kumulative Verteilungsfunktion der Copula auswertet. Die bedingte CDF der Copula wird durch Aufruf der Methode Conditional_Probability() berechnet. Alle soeben genannten Methoden sind überladen und akzeptieren skalare und vektorielle Eingaben. Die Methode Sample() wird verwendet, um synthetische Datensätze zu erzeugen, die mit den Modellparametern einer Copula übereinstimmen. Schließlich ermöglichen Load() und Save() die Serialisierung und Deserialisierung von Copula-Modellen zur Persistenz.

Die Erstellung einer expliziten bivariaten Gauß‘schen Copula erfordert die Angabe einer zwei-mal-zwei Kovarianzmatrix.

virtual void Set_covariance(matrix& cov) override
     {
      if(cov.Rows()!=2 || cov.Cols()!=2)
       {
        Print(__FUNCTION__," invalid input: expecting 2x2 matrix ");
        return;
       }
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
      m_tau = (2.0/M_PI) * MathArcsin(m_rho);
      m_theta = theta_hat(m_tau);
     }

Das Skript SampleEllipticCopula.ex5 prüft, ob die synthetischen Daten, die aus einer elliptischen Copula gesampelt wurden, mit den angegebenen Modellparametern übereinstimmen. Die vom Nutzer konfigurierbaren Eingänge mit dem Präfix Covar geben die Elemente einer Kovarianzmatrix an. Der Parameter Degree_Of_Freedom ist für den Test einer Gauß‘schen Copula nicht relevant. Der Parameter Größe bestimmt die Anzahl der zu erzeugenden Stichproben.

//+------------------------------------------------------------------+
//|                                         SampleEllipticCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Copulas/Bivariate/gaussian.mqh>
#include<Copulas/Bivariate/t.mqh>
//+------------------------------------------------------------------+
//|  enum                                                            |
//+------------------------------------------------------------------+
enum ENUM_ELPT_COPULA
 {
  GAUSSIAN=0,//Gaussian
  STUDENT//Student
 };
//--- input parameters
input ENUM_ELPT_COPULA copula_to_sample_from = GAUSSIAN;
input double Covar_0_0_ = 2.0;
input double Covar_0_1_ = 0.5;
input double Covar_1_0_ = 0.5;
input double Covar_1_1_ = 2.0;
input double Degrees_Of_Freedom = 5.0;
input ulong Size = 1000;

Das Programm verwendet die Methode Sample(), um synthetische Daten zu erzeugen, die später in einem Streudiagramm angezeigt werden. Die inverse CDF-Funktion der Gauß‘schen Standardverteilung wird dann auf den Datensatz angewendet, bevor die Korrelationsmatrix geschätzt wird.

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---
   CBivariateCopula *copula = NULL;
//---
   double set_theta = 0.0;
   switch(copula_to_sample_from)
    {
     case GAUSSIAN:
       copula = (CBivariateCopula*)new CGaussian();
       copula.Set_covariance(covar);
       break;
     case STUDENT:
       copula = (CBivariateCopula*)new CStudent();
       copula.Set_covariance(covar);
       copula.Set_nu(Degrees_Of_Freedom);
       break;
    }
//---
   Print("Specified correlation parameter of ", EnumToString(copula_to_sample_from)," copula :",copula.Get_rho());
   matrix samples = copula.Sample(Size);
   matrix inv_samples = samples;
   
   for(ulong i = 0; i<inv_samples.Rows(); ++i)
     for(ulong j =0; j<inv_samples.Cols(); ++j)
          inv_samples[i,j] = copula_to_sample_from == GAUSSIAN?CAlglib::InvNormalCDF(inv_samples[i,j]):studentTQuantile(inv_samples[i,j],Degrees_Of_Freedom);
          
   Print("Correlation of matrix of variable sampled from  ", EnumToString(copula_to_sample_from)," copula :\n", inv_samples.CorrCoef(false));      
   string cname = EnumToString((ENUM_COPULA_TYPE)copula.Type());
//---
   delete copula;
//---display scatter plot
   np::scatter_plot(inv_samples.Col(0),inv_samples.Col(1),cname+" Scatter plot","X","Y",true,0,0,0,0,500,300,true,10);  
//---
  }

Hier ist die Ausgabe von zwei Durchläufen. Das erwartete Ergebnis ist eine Matrix mit Off-Diagonal-Elementen, die in etwa dem Korrelationsparameter des Copula-Modells entsprechen. Beachten Sie, dass die Anzahl der angegebenen Stichproben das Ergebnis beeinflusst. Je größer die Anzahl der Stichproben ist, desto näher liegt die Ausgabe am angegebenen Korrelationsparameter.

CQ      0       14:06:16.963    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of GAUSSIAN copula :0.24999999999999994
DJ      0       14:06:17.021    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  GAUSSIAN copula :
DG      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2497651923653427]
RK      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)         [0.2497651923653427,1]]

Im nächsten Abschnitt wenden wir uns der anderen elliptischen Copula zu: Studentische t-Copula.

Bivariate Studentische t-Copula

Die bivariate Studentische t-Copula ist eine der bekanntesten Alternativen zur Gauß‘sche Copula, da sie die Abhängigkeit der Ränder erfasst, was die Gauß‘sche Copula nicht kann. Die Studentische t-Copula wird durch zwei Parameter definiert: den Korrelationskoeffizienten und die Freiheitsgrade, die üblicherweise mit ρ bzw. ν bezeichnet werden. Im Gegensatz zur Gauß'schen Copula weist die t-Copula eine Abhängigkeit der Ränder ungleich Null auf, was bedeutet, dass Extremereignisse in einer Variablen die Wahrscheinlichkeit von Extremen in der anderen Variable erhöhen.

wobei:

• t ρ , ν tρ,ν​ = CDFder bivariaten Studentische t-Verteilung mit Korrelation ρ ρ und ν ν Freiheitsgraden,
• t ν − 1 tν−1​ = inverse CDF (Quantilsfunktion) der univariaten t-Verteilung mit ν ν Freiheitsgraden,
• u , v ∈ [ 0 , 1 ] u,v∈[0,1].

Die Abhängigkeit in der t-Copula ist an den Rändern stärker als in der Mitte – im Gegensatz zur Gauß‘sche Copula, die eine gleichmäßige Abhängigkeit über die gesamte Verteilung aufweist. Dies macht es besonders geeignet für die Modellierung von Finanzrenditen, bei denen gemeinsame Crashs oder Booms häufiger auftreten, als Gauß‘sche Modelle vorhersagen würden. Mit zunehmendem Freiheitsgradparameter (ν) nimmt die Abhängigkeit der oberen und unteren Ränder ab. In der Tat konvergiert die Studentische t-Copula zu einer Gauß‘sche Copula, wenn die Freiheitsgrade sich der Unendlichkeit nähern. Umgekehrt gilt: Je geringer die Freiheitsgrade sind, desto größer ist die Abhängigkeit vom Rand.

Die Studentische t-Copula ist in t.mqh als Klasse CStudent implementiert, die wiederum eine Unterklasse von CBivariateCopula ist.

//+------------------------------------------------------------------+
//|                                                            t.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
#ifndef _NP_
#include<np.mqh>
#endif
#include<Math/Stat/T.mqh>
//+------------------------------------------------------------------+
//|utilities for Student's t distribution: Cheng Algorithm           |
//+------------------------------------------------------------------+
double            chengFuAlgo(double probability,double df)
  {
   double k = ceil(df*0.5);
   double a = 1.0 - probability;
   double qi = EMPTY_VALUE;
   if(a!=0.5)
     {
      qi = sqrt(2.0*pow(1.0-2.0*a,2.0)/(1.0 - pow(1.0-2.0*a,2.0)));
      double i = 0.0;
      double gy,j;
      while(i<20.0)
        {
         gy = 0.0;
         j = 0.0;
         while(j<=k-1.0)
           {
            gy+=MathFactorial(int(2*j))/pow(2.0,2.0*j)/pow(MathFactorial(int(j)),2.0)*pow(1.0+pow(qi,2.0)/(2.0*k),-j);
            j+=1.0;
           }
         qi = 1.0/sqrt(1.0/(2.0*k)*(pow(gy/1.0-2.0*a,2.0) - 1.0));
         i+=1.0;
        }
      if(a>0.5)
         return -qi;
      else
         return qi;
     }
   else
      return 0.0;
  }
//+------------------------------------------------------------------+
//| Hills algorithm                                                  |
//+------------------------------------------------------------------+
double            hillsAlgo(double probability,double df)
  {
   double z,a,b,c,x,y,d;
   z = a = b = c = x = y = d = EMPTY_VALUE;
   bool neg = false;
   if(probability>0.5)
     {
      z = 2.0*(1.0-probability);
     }
   else
     {
      neg = true;
      z = 2.0*probability;
     }
   a = 1.0/(df - 0.5);
   b = 48.0/(a*a);
   c = ((20700.0*a/b - 98.0)*a - 16.0)*a + 96.36;
   d = ((94.5/(b + c) - 3.0)/b + 1.0)*sqrt(a*M_PI/2.0)*df;
   x = z*d;
   y = pow(x,(2.0/df));

   if(y>0.05 + a)
     {
      x = CAlglib::InvNormalCDF(z*0.5);
      y = x*x;
      if(df<5.0)
         c = c+0.3*(df-4.5)*(x+0.6);
      c = c + (((0.05*d*x - 5.0)*x - 7.0)*x - 2.0)*x + b;
      y = (((((0.4*y + 6.3)*y + 36.0)*y + 94.5)/c - y - 3.0)/b + 1.0)*x;
      y = a*y*y;
      if(y > 0.002)
         y = exp(y) - 1.0;
      else
         y = y + 0.5*y*y;
     }
   else
      y = ((1.0/(((df + 6.0)/(df*y) - 0.089*d - 0.822)*(df + 2.0)*3.0) + 0.5/(df + 4.0))*y - 1.0)*(df + 1.0)/(df + 2.0) + 1.0/y;
   double q = sqrt(df*y);
   return (neg)?-1.0*q:q;
  }
//+------------------------------------------------------------------+
//| Student's t Inverse CDF                                          |
//+------------------------------------------------------------------+
double            studentTQuantile(double probability, double df)
  {
   if(df == 1.0)
      return tan(M_PI*(probability-1.0/2.0));
   else
      if(df == 2.0)
         return (2.0*probability-1.0)*sqrt(2.0/(4.0*probability*(1.0-probability)));
      else
         if(df == 4.0)
           {
            double a = 4.0*probability*(1.0 - probability);
            double q = cos(1.0/3.0*acos(sqrt(a)))/sqrt(a);
            return np::sign(probability - 0.5)*2.0*sqrt(q-1.0);
           }
         else
            if(!MathMod(df,2.0))
               return chengFuAlgo(probability,df);
            else
               return hillsAlgo(probability,df);
  }
//+------------------------------------------------------------------+
//| Student T Probability Density Function                           |
//+------------------------------------------------------------------+
double studentTDensity(double x, double df)
  {
   return CAlglib::GammaFunction((df + 1.0)/2.0)/(sqrt(df*M_PI)*CAlglib::GammaFunction(df/2.0))*pow((1.0 + pow(x,2.0)/df),(-((df + 1.0)/2.0)));
  }
//+------------------------------------------------------------------+
//| Bivariate Student Copula                                         |
//+------------------------------------------------------------------+
class CStudent : public CBivariateCopula
  {
private:
   virtual double    theta_hat(const double tau) override
     {
      return sin(tau*M_PI/2.0);
     }
   matrix            generate_corr_student(ulong num, matrix& cov, double nu_)
     {
      vector means = vector::Zeros(2);
      matrix normal = np::multivariate_normal(means,cov,num);

      double chi[];
      if(!MathRandomChiSquare(nu_,int(num),chi))
        {
         Print(__FUNCTION__, " Math random chisquare error ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out = matrix::Zeros(num,2);

      for(ulong i = 0; i<out.Rows(); i++)
        {
         double chisqrt = sqrt(chi[i]/nu_);
         out[i,0] = normal[i,0]/chisqrt;
         out[i,1] = normal[i,1]/chisqrt;
        }
      return out;
     }
   double            bvtdist(double z1,double z2, vector& mu, matrix& cov, double df)
     {
      double x1 = z1 - mu[0];
      double x2 = z2 - mu[1];
      double det_cov = cov[0,0]*cov[1,1]-cov[0,1]*cov[1,0];

      double xt = (-2.0*cov[0,1]*x1*x2+cov[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
      double numerator = CAlglib::GammaFunction((2.0+df)/2.0);
      double denominator = (CAlglib::GammaFunction(df/2.0)*df*M_PI*sqrt(det_cov)*pow(1.0+xt/df,(2.0+df)/2.0));
      return numerator/denominator;
     }
   //+------------------------------------------------------------------+
   //|  inner integral function object                                  |
   //+------------------------------------------------------------------+
   class CInnerInt : public CIntegrator1_Func
     {
   private:
      double            m_x;
      double            m_rho;
      matrix            m_corr;
      vector            m_mu;
      double            m_nu;
   public:
      //---
                     CInnerInt(void)
        {
         m_mu = vector::Zeros(2);
        }
                    ~CInnerInt(void) {}
      void              Set(double x, double rho, double nu)
        {
         m_x = x;
         m_nu = nu;
         m_rho = rho;
         matrix crr = {{1.0, m_rho}, {m_rho, 1.0}};
         m_corr = crr;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         double x1 = m_x - 0.0;
         double x2 = x - 0.0;
         double det_cov = m_corr[0,0]*m_corr[1,1]-m_corr[0,1]*m_corr[1,0];

         double xt = (-2.0*m_corr[0,1]*x1*x2+m_corr[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
         double numerator = CAlglib::GammaFunction((2.0+m_nu)/2.0);
         double denominator = (CAlglib::GammaFunction(m_nu/2.0)*m_nu*M_PI*sqrt(det_cov)*pow(1.0+xt/m_nu,(2.0+m_nu)/2.0));
         y =  numerator/denominator;
        }
     };
   //+------------------------------------------------------------------+
   //|  outer integral function object                                  |
   //+------------------------------------------------------------------+
   class COuterInt : public CIntegrator1_Func
     {
   public:
      double            ay_limit;
      double            by_limit;
      double            nu;
      double            rho;
      //---
                     COuterInt(void) {}
                    ~COuterInt(void) {}
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         CInnerInt fint;
         //---
         fint.Set(x,rho,nu);
         //---
         CAutoGKStateShell s;
         //---
         double integral;
         //---
         CObject ob;
         //---
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(ay_limit,by_limit,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,ob);
         //---
         CAlglib::AutoGKResults(s,integral,rep);
         //---
         CAutoGKReport report = rep.GetInnerObj();
         //---
         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);
         //---
         y = integral;
        }
     };
protected:
   virtual double    pdf(double u,double v) override
     {
      double y1,y2;
      y1 = studentTQuantile(u,m_nu);
      y2 = studentTQuantile(v,m_nu);
      vector means = vector::Zeros(2);
      matrix corr = {{1.0,m_rho},{m_rho,1.0}};
      double numerator = bvtdist(y1,y2,means,corr,m_nu);
      double denominator,pdf1,pdf2;
      pdf1 = studentTDensity(y1,m_nu);
      pdf2 = studentTDensity(y2,m_nu);
      denominator = pdf1*pdf2;
      return numerator/denominator;
     }
   virtual double    cdf(double u,double v) override
     {
      double uu,vv;
      uu = MathMax(u,1.e-6);
      vv = MathMax(v,1.e-6);
      //---
      int errcode = 0;
      //---
      COuterInt fout;
      fout.rho = m_rho;
      fout.nu = m_nu;
      fout.ay_limit = double(LONG_MIN);
      fout.by_limit = studentTQuantile(vv,m_nu);
      double ax_limit = double(LONG_MIN);
      double bx_limit = studentTQuantile(uu,m_nu);
      //---
      CObject obj;
      CAutoGKStateShell ss;
      //---
      double outer_integral;
      CAutoGKReportShell repp;
      //---
      CAlglib::AutoGKSmooth(ax_limit,bx_limit,ss);
      //---
      CAlglib::AutoGKIntegrate(ss,fout,obj);
      //---
      CAlglib::AutoGKResults(ss,outer_integral,repp);
      //---
      CAutoGKReport report = repp.GetInnerObj();
      //---
      if(report.m_terminationtype<0.0)
         Print(__FUNCTION__, " integration error ",report.m_terminationtype);
      //---
      return MathMax(MathMin(outer_integral,1.0),0.0);
     }
   virtual double    condi_cdf(double u,double v) override
     {
      double inv_u,inv_v;
      int errcode = 0;
      inv_u = studentTQuantile(u,m_nu);
      inv_v = studentTQuantile(v,m_nu);
      double numerator,denominator;
      numerator = (inv_u-m_rho*inv_v)*sqrt(m_nu+1.0);
      denominator = sqrt((1.0-pow(m_rho,2.))*(pow(inv_v,2.0)+m_nu));
      double tcdf = MathCumulativeDistributionT(numerator/denominator,m_nu+1.0,errcode);
      if(errcode)
        {
         Print(__FUNCTION__, " mathcdf error ", errcode);
         return EMPTY_VALUE;
        }
      return tcdf;
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = pdf(u[i],v[i]);
      return out;
     }
   virtual vector    cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = cdf(u[i],v[i]);
      return out;
     }
   virtual vector    condi_cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = condi_cdf(u[i],v[i]);
      return out;
     }
public:
                     CStudent(void)
     {
      m_copula_type = STUDENT_COPULA;
     }
                    ~CStudent(void)
     {
     }

   virtual matrix    Sample(ulong num_samples) override
     {
      matrix spairs = generate_corr_student(num_samples,m_cov,m_nu);
      matrix out = spairs;
      int err1,err2;
      err1 = err2 = 0;
      for(ulong i = 0; i<spairs.Rows(); ++i)
        {
         out[i,0] = MathCumulativeDistributionT(spairs[i,0],m_nu,err1);
         out[i,1] = MathCumulativeDistributionT(spairs[i,1],m_nu,err2);
         if(err1 || err2)
           {
            Print(__FUNCTION__, " mathcdf error ", err1?err1:err2);
            return matrix::Zeros(0,0);
           }
        }
      return out;
     }
   virtual double    Fit(vector &u, vector&v) override
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
        {
         Print(__FUNCTION__, " Invalid input variable(s) ");
         return EMPTY_VALUE;
        }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(m_nu == EMPTY_VALUE)
         m_nu = fit_nu(u,v);
      matrix vals = matrix::Zeros(u.Size(),2);
      for(ulong i = 0; i<vals.Rows(); ++i)
        {
         vals[i,0] = studentTQuantile(u[i],m_nu);
         vals[i,1] = studentTQuantile(v[i],m_nu);
        }
      m_cov = vals.Cov(false);
      m_rho = m_cov[0,1]/(sqrt(m_cov[0,0])*sqrt(m_cov[1,1]));
      return m_rho;
     }
  };

//+------------------------------------------------------------------+

Nachfolgend sehen Sie die Ausgabe von zwei Durchläufen von SampleEllipticCopula.ex5, wobei die entsprechende t-Copula-Option ausgewählt wurde.

IM      0       14:07:00.097    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of STUDENT copula :0.24999999999999994
NQ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  STUDENT copula :
GF      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2441795870726779]
MJ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)         [0.2441795870726779,1]]

Tests und Validierung

Um den Rest der Methoden beider Copula-Implementierungen zu testen, haben wir die Skripte TestBivariateGaussianCopula.ex5 und TestBivariateStudentTCopula.ex5. Beide Skripte erstellen spezifische Copula-Modelle und werten den PDF-, CDF- und bedingten CDF-Code aus. Diese Tests wurden aus den Unit-Tests des Python-Pakets ArbitrageLab reproduziert, auf dem der vorgestellte MQL5-Code basiert. So können wir überprüfen, ob der MQL5-Code genauso funktioniert wie die ursprüngliche Python-Implementierung.

//+------------------------------------------------------------------+
//|                                  TestBivariateGaussianCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
//--- input parameters
#include<Copulas/Bivariate/gaussian.mqh>
//---
 double Covar_0_0_ = 2.0;
 double Covar_0_1_ = 0.5;
 double Covar_1_0_ = 0.5;
 double Covar_1_1_ = 2.0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---   
   CGaussian norm_copula;
   norm_copula.Set_covariance(covar);
//---   
   Print("Rho ", norm_copula.Get_rho());
   Print("Joint cdf(0.7,0.0001) ",norm_copula.Copula_CDF(0.7,0.0001));
   Print("Joint cdf(0.0001,0.7) ",norm_copula.Copula_CDF(0.0001,0.7));
   Print("Joint cdf(0.7,1.0) ",norm_copula.Copula_CDF(0.7,1.0));
   Print("Joint cdf(0.5,0.7) ",norm_copula.Copula_CDF(0.5,0.7));
//---   
   Print("Joint pdf(0.5,0.7) ",norm_copula.Copula_PDF(0.5,0.7));
   Print("Joint pdf(0.7,0.5) ",norm_copula.Copula_PDF(0.7,0.5));
   Print("Joint pdf(0.6,0.7) ",norm_copula.Copula_PDF(0.6,0.7));
//---   
   Print("Conditional CDF (U<=0.5|V=0.7) ",norm_copula.Conditional_Probability(0.5,0.7));
  }
//+------------------------------------------------------------------+

Hier sind die Ergebnisse für den Test der Methoden aus CGaussian.

KR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Rho 0.24999999999999994
JR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,0.0001) 0.00009407442939459683
JG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.0001,0.7) 0.00009407442939459683
KK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999973036455064
FL      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.5,0.7) 0.38494413131861455
IR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0233716657780745
KG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0233716657780745
LK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.0580116369285744
EP      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.4461479582632463

Zum Vergleich sehen Sie hier den Python-Code für den Einheitstest für die Gauß‘sche Copula.

def test_gaussian(self):
        """
        Test Gaussian copula class.
        """

        cov = [[2, 0.5], [0.5, 2]]
        cop = GaussianCopula(cov=cov)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Gaussian Copula')
        self.assertEqual(descr['Class Name'], 'Gaussian')
        self.assertEqual(descr['cov'], cov)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0.7, 1e-4), cop.C(1e-4, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1e-8), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), 0.7, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.5, 0.7), 0.384944, delta=1e-4)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.023371665778, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.058011636928, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.446148, delta=1e-4

Als Nächstes folgen die Ergebnisse für die Klasse CStudent.

ER      0       14:40:34.138    TestBivariateStudentTCopula (XAUEUR,D1) Rho 0.24999999999999994
JG      0       14:40:35.369    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.2) 0.000006839679521344817
JD      0       14:40:36.613    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.2,0.0) 0.000006839679521344818
HK      0       14:40:38.041    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999969941893684
PO      0       14:40:39.584    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,0.7) 0.6999969941893683
OR      0       14:40:41.280    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,1.0) 0.9999810861796908
RF      0       14:40:42.452    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.0) 0.0000010861794979038194
HJ      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.3,0.7) 0.23534922600994124
DL      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0915055449624917
FP      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0915055449624917
MD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.1416004955531887
DD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.441518430406228
MG      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Loglikelihood 2.135711666815534

Einheitstest für Studentische t-Copula.

def test_student(self):
        """
        Test Student copula class (Student-t).
        """

        cov = [[2, 0.5], [0.5, 2]]
        nu = 5
        cop = StudentCopula(cov=cov, nu=nu)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Student-t Copula')
        self.assertEqual(descr['Class Name'], 'Student')
        self.assertEqual(descr['cov'], cov)
        self.assertEqual(descr['nu (degrees of freedom)'], nu)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)
        # More to be added here for test on C(U<=u, V<=v)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.09150554, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.1416005, delta=1e-4)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0, 0.2), cop.C(0.2, 0), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(1, 1), 1, delta=1e-4)
        self.assertAlmostEqual(cop.C(0, 0), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.3, 0.7), 0.23534923332657925, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.4415184293094455, delta=1e-4)

        # Check theta(tau)
        self.assertAlmostEqual(cop.theta_hat(2 * np.arcsin(0.2) / np.pi), 0.2, delta=1e-4)

        # log_ml function in ccalc
        u = np.array([0.1, 0.21, 0.5, 0.8])
        v = np.array([0.01, 0.25, 0.4, 0.7])
        new_cop = StudentCopula(nu=5)
        new_cop.fit(u, v)
        ll = new_cop.get_log_likelihood_sum(u=u,
                                            v=v)
        self.assertAlmostEqual(ll, 2.1357117471178584, delta=1e-5

Wie aus der Ausgabe ersichtlich ist, scheint die Bibliothek korrekt zu funktionieren.

Schlussbemerkungen

Vergleicht man die bisher implementierten elliptischen Copulae, so ist die t-Copula möglicherweise besser für die Modellierung von gemeinsamen Extremereignissen geeignet. Eine asymmetrische Abhängigkeit der Ränder kann jedoch nicht erfasst werden. Dies ist der Fall, wenn die Abhängigkeit an einem Rand stärker ist als am anderen. Hierfür wären archimedische Copulae wie Clayton oder Gumbel nützlicher.

Im nächsten Teil dieser Artikelserie werden wir archimedische Copulae und ihre Implementierung in MQL5 besprechen. Sobald wir eine gute Anzahl von Copulae implementiert haben, werden wir uns damit befassen, wie Copulae auf den Paarhandel angewendet werden können.

Datei oder Ordner	Beschreibung
MQL5/include/np.mqh	Eine Header-Datei mit verschiedenen Vektor- und Matrix-Hilfsfunktionen.
MQL5/include/Copulas/Bivariate	Dieser Ordner enthält alle Header-Dateien der Coplulae-Implementierungen.
MQL5/include/ECDF	Dieser Ordner enthält die Header-Dateien für die in diesem Artikel beschriebene empirische CDF-Implementierung.
MQL5/script/ECDF_Demo.mq5	Dieses Skript demonstriert die Anwendung der im Artikel beschriebenen empirischen CDF-Implementierung.
MQL5/script/TestBivariateGaussianCopula.mq5	Dieses Skript demonstriert die Verwendung der Klasse CGaussian.
MQL5/script/TestBivariateStudentTCopula.mq5	Dieses Skript demonstriert die Verwendung der Klasse CStudent.
MQL5/script/SampleEllipticCopula.mq5	Dieses Skript demonstriert das Sampling aus einer elliptischen Copula.