Neuronales Netz in der Praxis: Pseudoinverse (I)

Einführung

Ich freue mich, Sie zu einem neuen Artikel über neuronale Netze begrüßen zu dürfen.

Im vorherigen Artikel „Neuronales Netz in der Praxis: Geradenfunktion“ haben wir darüber gesprochen, wie algebraische Gleichungen verwendet werden können, um einen Teil der gesuchten Informationen zu bestimmen. Dies ist notwendig, um eine Gleichung zu formulieren, in unserem speziellen Fall eine Geradengleichung, da unser kleiner Datensatz tatsächlich als eine Gerade ausgedrückt werden kann. Das gesamte Material zur Erklärung der Funktionsweise neuronaler Netze ist nicht einfach darzustellen, wenn man nicht weiß, auf welchem Niveau die Mathematikkenntnisse der einzelnen Leser liegen.

Obwohl viele denken, dass dieser Prozess viel einfacher und unkomplizierter wäre, vor allem, wenn man bedenkt, dass es viele Bibliotheken im Internet gibt, die versprechen, dass man sein eigenes neuronales Netzwerk entwickeln kann, ist die Realität, dass es nicht so einfach ist.

Ich möchte keine falschen Erwartungen wecken: Ich werde Ihnen nicht erzählen, dass Sie mit praktisch keinen Kenntnissen oder Erfahrungen etwas wirklich Praktisches schaffen können, mit dem Sie Geld verdienen können, indem Sie neuronale Netze oder künstliche Intelligenz für den Handel am Markt nutzen. Wenn Ihnen jemand das sagt, dann lügt er definitiv.

Die Erstellung selbst des einfachsten neuronalen Netzes ist in vielen Fällen eine schwierige Aufgabe. Hier möchte ich Ihnen zeigen, wie Sie etwas schaffen können, das Sie dazu inspiriert, dieses Thema zu vertiefen. Neuronale Netze sind seit mindestens mehreren Jahrzehnten Gegenstand der Forschung. Wie in den drei vorangegangenen Artikeln über künstliche Intelligenz erwähnt, ist das Thema viel komplexer, als viele Menschen denken.

Die Verwendung einer bestimmten Funktion bedeutet nicht, dass unser neuronales Netz besser oder schlechter sein wird, sondern nur, dass wir Berechnungen mit einer bestimmten Funktion durchführen werden. Dies bezieht sich auf das, was wir heute in diesem Artikel sehen werden.

Im Vergleich zu den ersten drei Artikeln in dieser Reihe über neuronale Netze könnten Sie nach dem heutigen Artikel daran denken, aufzugeben. Das sollten Sie nicht. Denn ein und derselbe Artikel kann Sie auch dazu bringen, sich mit dem Thema zu vertiefen. Hier werden wir uns ansehen, wie Pseudo-Inversionsberechnungen mit reinem MQL5 implementiert werden können. Auch wenn es nicht so beängstigend aussieht, wird der heutige Code für Anfänger viel schwieriger sein, als wir es gerne hätten, also keine Angst. Studieren Sie den Code sorgfältig und in Ruhe, ohne zu hetzen. Ich wiederum habe versucht, den Code so einfach wie möglich zu gestalten. Als solches ist es nicht auf eine effiziente und schnelle Ausführung ausgelegt. Im Gegenteil, sie ist bestrebt, so lehrreich wie möglich zu sein. Da wir jedoch die Matrixfaktorisierung verwenden werden, ist der Code selbst etwas komplexer als das, was viele zu sehen oder zu programmieren gewohnt sind.

Und ja, bevor es jemand erwähnt, ich weiß, dass MQL5 eine Funktion namens PInv hat, die genau das tut, was wir in diesem Artikel sehen werden. Ich weiß auch, dass MQL5 Funktionen für Matrixoperationen hat. Aber hier werden wir keine Berechnungen mit Matrizen durchführen, wie sie in MQL5 definiert sind, sondern wir werden Arrays verwenden, die zwar ähnlich sind, aber eine etwas andere Logik für den Zugriff auf Elemente im Speicher haben.

Pseudoinverse

Die Durchführung dieser Berechnung gehört nicht zu den schwierigsten Aufgaben, solange dem Entwickler alles klar ist. Im Grunde müssen wir einige Multiplikationen und andere einfache Operationen mit nur einer Matrix durchführen. Die Ausgabe wird eine Matrix sein, die das Ergebnis aller internen Faktorisierungen der Pseudoinverse ist.

An dieser Stelle müssen wir etwas klarstellen. Die Pseudoinverse kann auf zwei Arten faktorisiert werden: In einem Fall werden die Werte innerhalb der Matrix nicht ignoriert, und im anderen Fall wird der minimale Grenzwert für die in der Matrix vorhandenen Elemente verwendet. Wird diese Mindestgrenze nicht erreicht, ist der Wert dieses Elements in der Matrix gleich Null. Diese Bedingung wird nicht von mir auferlegt, sondern von den Regeln, die in das Berechnungsmodell eingebettet sind, das von allen Programmen zur Berechnung der Pseudoinverse verwendet wird. Jeder dieser Fälle hat einen ganz bestimmten Zweck. Was wir hier sehen, ist also NICHT die endgültige Berechnung der Pseudoinverse. Wir werden eine Berechnung durchführen, deren Ziel es ist, ähnliche Ergebnisse zu erzielen wie mit Programmen wie MatLab, SciLab und anderen, die ebenfalls die Pseudoinverse implementieren.

Da MQL5 auch Pseudoinverse berechnen kann, können wir die Ergebnisse, die wir mit der von uns implementierten Anwendung erhalten, mit den gleichen Ergebnissen vergleichen, die wir mit der Pseudoinverse-Funktion der MQL5-Bibliothek erhalten. Dies ist notwendig, um zu prüfen, ob alles korrekt ist. Ziel dieses Artikels ist es also nicht nur, Pseudoinversionsberechnungen durchzuführen, sondern auch zu verstehen, was dahinter steckt. Das ist wichtig, denn wenn Sie wissen, wie Berechnungen funktionieren, können Sie verstehen, warum und wann Sie eine bestimmte Methode in unserem neuronalen Netz verwenden sollten.

Beginnen wir mit der Implementierung des einfachsten Codes zur Verwendung der Pseudoinverse aus der MQL5-Bibliothek. Dies ist der erste Schritt, um sicherzustellen, dass die Berechnung, die wir später erstellen werden, tatsächlich funktioniert. Bitte ändern Sie den Code nicht, ohne ihn vorher zu überprüfen. Wenn Sie vorher etwas ändern, erhalten Sie möglicherweise andere Ergebnisse als die hier gezeigten. Probieren Sie also zuerst den Code aus, den ich Ihnen zeigen werde. Dann, und nur dann (wenn Sie es wünschen), ändern Sie ihn, um besser zu verstehen, was vor sich geht, aber nehmen Sie bitte keine Änderungen am Code vor, bevor Sie die ursprüngliche Version getestet haben.

Die Originalcodes sind im Anhang zu diesem Artikel zu finden. Schauen wir uns den ersten an. Der vollständige Code ist nachstehend aufgeführt:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart()
05. {
06.     matrix M_A {{1, -100}, {1, -80}, {1, 30}, {1, 100}};
07. 
08.     Print("Moore–Penrose inverse of :");
09.     Print(M_A);
10.     Print("is :");
11.     Print(M_A.PInv());
12. }
13. //+------------------------------------------------------------------+

Das Ergebnis der Codeausführung ist in der folgenden Abbildung dargestellt:

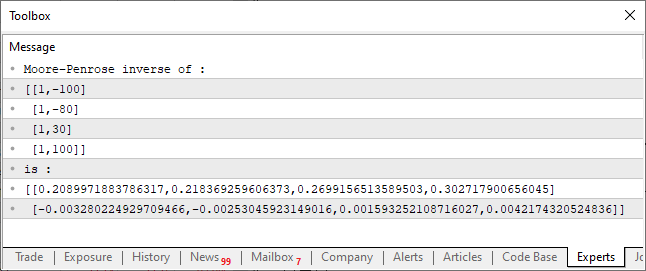
Dieser sehr einfache Code, den Sie oben sehen können, kann die Pseudoinverse einer Matrix berechnen. Das Ergebnis wird auf der Konsole angezeigt, wie in der Abbildung dargestellt. Alles ist ganz einfach. Achten Sie jedoch auf den Aufbau des Codes, dies ist ein sehr spezifischer Punkt bei der Erstellung von Codes. Mit Hilfe einer Matrix und eines Vektors erhalten wir eine ganze Reihe von möglichen und sehr funktionellen Operationen. Diese Operationen sind in der Standardbibliothek von MQL5 enthalten und können auch in die Standardbibliotheken anderer Sprachen aufgenommen werden.

Das ist zwar sehr nützlich, aber es gibt Fälle, in denen der Code auf eine bestimmte Weise ausgeführt werden muss oder soll. Entweder, weil wir ihn irgendwie optimieren wollen, oder einfach, weil wir keinen Code erzeugen wollen, der auf andere Weise ausgeführt werden kann. Letztendlich ist der Grund dafür nicht so wichtig. Obwohl viele Leute sagen, dass C/C++-Programmierer gerne das Rad neu erfinden, ist das bei uns nicht der Fall. In diesem Artikel sehen wir uns gemeinsam an, was hinter diesen komplexen Berechnungen steckt. Sie sehen das Ergebnis, haben aber keine Ahnung, wie es zustande gekommen ist. Jede Forschung, bei der man nicht versteht, woher genau dieses Ergebnis kommt und nicht ein anderes, ist keine echte Forschung, sondern nur Glaube. Mit anderen Worten, man sieht es und glaubt es einfach, aber man weiß nicht, ob es wahr ist oder nicht, man muss es einfach glauben. Und echte Programmierer können nicht blind vertrauen, sie müssen anfassen, sehen, schmecken und erleben, um wirklich an das zu glauben, was sie schaffen. Schauen wir uns nun an, wie das in der Abbildung gezeigte Ergebnis zustande gekommen ist. Wenden wir uns also einem neuen Thema zu.

Verstehen der Berechnungen hinter der Pseudoinverse

Wenn Sie sich damit zufrieden geben, nur die Ergebnisse zu sehen, ohne zu wissen, wie sie zustande gekommen sind, ist das großartig. Das bedeutet, dass dieses Thema für Sie nicht mehr von Nutzen ist und Sie Ihre Zeit nicht damit verschwenden sollten, es zu lesen. Aber wenn Sie verstehen wollen, wie die Berechnungen durchgeführt werden, sollten Sie vorbereitet sein. Obwohl ich versuchen werde, den Prozess so weit wie möglich zu vereinfachen, müssen Sie dennoch aufmerksam sein. Ich werde die Verwendung komplexer Formeln so weit wie möglich vermeiden, aber Ihre Aufmerksamkeit ist hier trotzdem wichtig, da der Code, den wir erstellen werden, viel komplizierter aussehen kann, als er tatsächlich ist. Beginnen wir mit dem Folgenden: Die Pseudoinverse wird grundsätzlich mit Hilfe der Matrixmultiplikation und der Inversen berechnet.

Diese Multiplikation ist ganz einfach. Viele Leute verwenden zu diesem Zweck einige Mittel, die ich persönlich für unnötig halte. In den Artikeln, in denen wir über Matrizen gesprochen haben, haben wir eine Methode zur Durchführung der Multiplikation besprochen, aber diese Methode war für ein ziemlich spezifisches Szenario gedacht. Hier brauchen wir eine etwas allgemeinere Methode, weil wir einige Dinge anders machen müssen als in dem Artikel über Matrizen.

Um die Sache zu vereinfachen, werden wir uns den Code in kleinen Teilen ansehen, die jeweils etwas Bestimmtes erklären. Beginnen wir mit der Multiplikation, die unten zu sehen ist:

01. //+------------------------------------------------------------------+
02. void Generic_Matrix_A_x_B(const double &A[], const uint A_Row, const double &B[], const uint B_Line, double &R[], uint &R_Row)
03. {
04.     uint A_Line = (uint)(A.Size() / A_Row),
05.          B_Row  = (uint)(B.Size() / B_Line);
06. 
07.     if (A_Row != B_Line)
08.     {
09.         Print("Operation cannot be performed because the number of rows is different from that of columns...");
10.         B_Row = (uint)(1 / MathAbs(0));
11.     }
12.     if (!ArrayIsDynamic(R))
13.     {
14.         Print("Response array must be of the dynamic type...");
15.         B_Row = (uint)(1 / MathAbs(0));
16.     }
17.     ArrayResize(R, A_Line * (R_Row = B_Row));
18.     ZeroMemory(R);
19.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == B_Row ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
20.         for (uint c = 0; c < A_Row; c++)
21.             R[cp] += (A[Ai + c] * B[Bi + (c * B_Row)]);
22. }
23. //+------------------------------------------------------------------+

Wenn Sie sich dieses Stück Code ansehen, fühlen Sie sich vielleicht schon verwirrt. Jemand hat vielleicht Angst, als ob der Weltuntergang bevorsteht. Andere möchten vielleicht Gott um Vergebung für alle ihre Sünden bitten. Aber Spaß beiseite, dieser Code ist sehr einfach, auch wenn er ungewöhnlich oder extrem komplex erscheint.

Sie finden es vielleicht schwierig, weil es sehr komprimiert ist und viele Dinge gleichzeitig zu passieren scheinen. Ich entschuldige mich bei den Anfängern, aber diejenigen von Ihnen, die meine Artikel verfolgt haben, kennen bereits meinen Stil, Code zu schreiben, und Sie werden sehen, dass dies mein typischer Stil ist. Lassen Sie uns nun herausfinden, was hier vor sich geht. Im Gegensatz zu dem zuvor gezeigten Code ist dieser Code allgemein, er hat sogar einen Test, der überprüft, ob wir zwei Matrizen multiplizieren können. Das ist recht nützlich, wenn auch nicht sehr praktisch für uns.

In der zweiten Zeile steht die Prozedurendeklaration. Wir müssen darauf achten, dass wir Parameter an den richtigen Stellen deklarieren und übergeben. Dann wird die Matrix A mit der Matrix B multipliziert und das Ergebnis in die Matrix R eingefügt. Wir müssen angeben, wie viele Spalten Matrix A hat und wie viele Zeilen Matrix B hat. Das letzte Argument gibt die Anzahl der Spalten in der Matrix R zurück. Der Grund für die Rückgabe der Anzahl der Spalten in der R-Matrix wird später erklärt, also machen Sie sich darüber vorerst keine Gedanken.

Gut. In der vierten und fünften Zeile werden wir die restlichen Werte berechnen, damit wir sie nicht manuell angeben müssen. In Zeile 7 führen wir dann einen kleinen Test durch, um zu sehen, ob Matrizen multipliziert werden können, sodass die Reihenfolge, in der die Matrizen übergeben werden, von Bedeutung ist. Darin unterscheidet er sich von dem Code für skalare Berechnungen: Bei Matrixberechnungen müssen wir sehr vorsichtig sein.

Wenn die Multiplikation fehlschlägt, wird in der neunten Zeile eine Meldung an die MetaTrader 5 Konsole ausgegeben. Und gleich danach, in Zeile zehn, wird ein RUN-TIME-Fehler ausgelöst, der dazu führt, dass die Anwendung, die versucht, die Matrixmultiplikation durchzuführen, geschlossen wird. Wenn ein solcher Fehler auf der Konsole erscheint, müssen Sie prüfen, ob die Meldung auch in der neunten Zeile erscheint. In diesem Fall liegt der Fehler nicht in dem betreffenden Codefragment, sondern an der Stelle, an der dieser Code aufgerufen wird. Ich weiß, dass es nicht sehr nett ist, die Anwendung bei einem RUN-TIME-Fehler zum Schließen zu zwingen, geschweige denn elegant, aber auf diese Weise verhindern wir, dass die Anwendung uns falsche Ergebnisse anzeigt.

Jetzt kommt der Teil, der viele Leute erschreckt: In Zeile 17 weisen wir Speicher zu, um die gesamte Ausgabe zu speichern. Die Matrix R muss also im Aufrufer eine dynamische Form haben. Verwenden Sie kein statisches Array, da dies in Zeile 12 erkannt wird und der Code mit einem RUN-TIME-Fehler und einer Meldung in Zeile 14 beendet wird, die den Grund für das Beenden angibt.

Eines der Details dieser Fehlererzeugungsmethode besteht darin, dass die Anwendung bei der Ausführung versucht, durch Null zu dividieren, was den Prozessor veranlasst, eine interne Unterbrechung auszulösen. Diese Unterbrechung veranlasst das Betriebssystem, Maßnahmen gegen die Anwendung zu ergreifen, die die Unterbrechung verursacht hat, und sie zum Schließen zu zwingen. Selbst wenn das Betriebssystem nichts unternimmt, geht der Prozessor in den Interrupt-Modus über, wodurch er sich selbst in einem eingebetteten System, das für die Ausführung einer Anwendung konzipiert ist, beendet.

Es ist zu beachten, dass ich hier einen Trick anwende, um zu verhindern, dass der Compiler erkennt, dass ein RUN-TIME-Fehler erzeugt wird. Wenn ich es anders machen würde als im Code gezeigt, würde der Compiler den Code nicht kompilieren, obwohl die Zeile, die den RUN-TIME-Fehler verursacht, in normalen Situationen kaum ausgeführt wird. Wenn Sie ein Programm zwangsweise beenden müssen, können Sie eine ähnliche Technik anwenden, die immer funktioniert. Das ist allerdings nicht sehr elegant, denn der Nutzer könnte sich über Ihre Anwendung oder über Sie, der sie geschrieben hat, ärgern. Nutzen Sie diesen Ansatz also mit Bedacht.

In Zeile 18 wird alles, was sich im zugewiesenen Speicher befindet, vollständig gelöscht. Normalerweise machen einige Compiler die Bereinigung selbst, aber nach einiger Zeit der Programmierung in MQL5 habe ich festgestellt, dass es natürlich nicht bereinigt dynamisch zugewiesenen Speicher. Ich glaube, das liegt daran, dass dynamisch zugewiesener Speicher in MetaTrader 5 für die Verwendung in Indikatorpuffern vorgesehen ist. Und da diese Puffer aktualisiert werden, wenn Daten empfangen und berechnet werden, ist es sinnlos, den Speicher zu löschen. Außerdem nimmt eine solche Reinigung viel Zeit in Anspruch, die für andere Aufgaben verwendet werden kann. Wir müssen also diese Bereinigung vornehmen und sicherstellen, dass wir keine unnötigen Werte in unseren Berechnungen verwenden. Bitte beachten Sie dies in Ihren Programmen, wenn Sie dynamisch zugewiesenen Speicher verwenden und dieser nicht als Nutzerindikatorpuffer verwendet wird.

Nun kommt der interessanteste Teil des Verfahrens: Wir multiplizieren die Matrix A mit der Matrix B und setzen das Ergebnis in die Matrix R. Dies geschieht in zwei Zeilen. Zeile 19 mag auf den ersten Blick sehr kompliziert erscheinen, aber wir sollten sie in ihre Bestandteile zerlegen. Die Idee ist, die Multiplikation zweier Matrizen völlig dynamisch und universell zu gestalten. Das heißt, es spielt keine Rolle, ob es mehr oder weniger Zeilen oder Spalten gibt, wenn das Verfahren diesen Punkt erreicht hat, werden die Matrizen multipliziert.

Genauso wie die Reihenfolge der Matrizen das Ergebnis beeinflusst, wirkt sich hier in Zeile 19 auch die Reihenfolge der Operationen auf das Ergebnis aus. Um nicht zu lang zu werden, werde ich die Erklärung vereinfachen. Um zu verstehen, was hier vor sich geht, lesen wir den Code so, wie er geschrieben ist, d. h. von links nach rechts, Begriff für Begriff. Dies ist die Art und Weise, wie der Compiler sie verarbeitet, um die ausführbare Datei zu erstellen, was zwar verwirrend erscheinen mag, es aber nicht ist. Der Code ist sehr prägnant und unterscheidet sich von dem, was die meisten Menschen verwenden. In jedem Fall geht es darum, Spalte für Spalte aus der Matrix A zu lesen und den Wert zu multiplizieren, indem man Zeile für Zeile aus der Matrix B liest. Aus diesem Grund beeinflusst die Reihenfolge der Koeffizienten das Ergebnis. Sie brauchen sich keine Gedanken darüber zu machen, wie Matrix B organisiert ist (Zeile oder Spalte), sie kann genauso organisiert sein wie Matrix A und die Multiplikation wird trotzdem gelingen.

Die erste der Operationen, die erforderlich sind, um den Wert der Pseudoinverse zu erhalten, ist fertig. Schauen wir uns nun die Art der Berechnungen an, die wir durchführen müssen, damit wir wissen, was wir noch implementieren müssen. Wir brauchen vielleicht keine allgemeine Lösung wie bei der Multiplikation, sondern etwas Spezifischeres, um den Wert der Pseudoinverse zu bestimmen.

Die Formel zur Berechnung der Pseudoinverse lautet wie folgt.

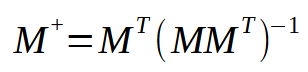
In dieser Formel steht M für die verwendete Matrix. Beachten Sie, dass es immer dasselbe ist. Bei der Betrachtung dieser Formel fällt jedoch auf, dass wir eine Multiplikation zwischen der ursprünglichen Matrix und ihrer transponierten Matrix durchführen müssen. Dann nehmen wir das Ergebnis und finden den Wert der inversen Matrix. Schließlich multiplizieren wir die transponierte Matrix mit dem Ergebnis der Inversion. Klingt einfach, nicht wahr? Hier können wir mehrere Abkürzungen erstellen. Um eine perfekte Abkürzung zu schaffen, müssten wir natürlich ein Verfahren modellieren, das nur die Pseudoinverse berechnen kann. Die Entwicklung eines solchen Verfahrens ist zwar nicht schwierig, aber es ist viel schwieriger zu erklären, wie es funktioniert. Um besser zu verstehen, wovon ich spreche, sollten wir Folgendes tun: Ich werde die Multiplikation der transponierten und der ursprünglichen Matrix in einem Verfahren zusammenfassen. Wenn wir uns an der Universität mit diesem Thema beschäftigen, werden wir normalerweise gebeten, es in zwei Blöcken zu behandeln. Das heißt, wir erstellen zunächst die transponierte Matrix und verwenden dann das Multiplikationsverfahren, um das Endergebnis zu erhalten. Es ist jedoch möglich, ein Verfahren zu erstellen, das diese beiden Schritte nicht umfasst und sie in einem Schritt ausführt. Obwohl dies sehr einfach zu implementieren ist, kann der Code schwer zu verstehen sein.

Im folgenden Code sehen wir, wie der in Klammern dargestellte Vorgang in der obigen Abbildung ausgeführt wird.

01. //+------------------------------------------------------------------+
02. void Matrix_A_x_Transposed(const double &A[], const uint A_Row, double &R[], uint &R_Row)
03. {
04.     uint BL = (uint)(A.Size() / A_Row);
05.     if (!ArrayIsDynamic(R))
06.     {
07.         Print("Response array must be of the dynamic type...");
08.         BL = (uint)(1 / MathAbs(0));
09.     }
10.     ArrayResize(R, (uint) MathPow(R_Row = (uint)(A.Size() / A_Row), 2));
11.     ZeroMemory(R);
12.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == BL ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
13.         for (uint c = 0; c < A_Row; c++)
14.             R[cp] += (A[c + Ai] * A[c + (Bi * A_Row)]);
15. }
16. //+------------------------------------------------------------------+

Beachten Sie, dass dieser Teil des Codes dem vorherigen sehr ähnlich ist, mit der Ausnahme, dass die Zeile, die das Ergebnis erzeugt, in den beiden Teilen leicht unterschiedlich ist. Dieses Snippet ist jedoch in der Lage, die notwendigen Berechnungen durchzuführen, um die ursprüngliche Matrix mit ihrer transponierten Matrix zu multiplizieren, was uns die Erstellung der transponierten Matrix erspart. Wir können diese Art der Optimierung umsetzen. Natürlich könnten wir in demselben Verfahren noch mehr Funktionen anhäufen, zum Beispiel eine inverse Matrix erzeugen oder sogar die Multiplikation der inversen Matrix mit der Transposition der Eingabematrix durchführen. Aber wie Sie sich bereits vorstellen können, verkompliziert jeder dieser Schritte das Verfahren, nicht global, sondern lokal. Deshalb ziehe ich es vor, sie Ihnen nach und nach vorzustellen, damit Sie verstehen können, worum es geht, und die Konzepte sogar ausprobieren können, wenn Sie wollen.

Aber da ich das Rad nicht neu erfinden will, werden wir nicht alles in einer Funktion zusammenfassen. Ich habe diesen Teil nur gezeigt, um Ihnen zu verdeutlichen, dass nicht alles, was wir in der Schule lernen, in der Praxis angewendet wird. Oft werden Prozesse optimiert, um ein bestimmtes Problem zu lösen. Und wenn man etwas optimiert, kann man die Aufgabe viel schneller erledigen als mit einem allgemeineren Verfahren.

Als Nächstes werden wir Folgendes tun: Wir haben bereits eine Multiplikationsrechnung. Als Nächstes benötigen wir eine Berechnung, die die Inverse der resultierenden Matrix erzeugt. Es gibt mehrere Möglichkeiten, diese Umkehrung zu programmieren. Obwohl es nur wenige mathematische Möglichkeiten gibt, dies auszudrücken, können sich die Programmiermethoden erheblich unterscheiden, sodass ein Algorithmus schneller ist als ein anderer. Was uns aber wirklich interessiert, ist das richtige Ergebnis, und wie wir es erzielen, ist nicht so wichtig.

Um die Inverse einer Matrix zu berechnen, bevorzuge ich eine spezielle Methode, bei der die Determinante der Matrix verwendet wird. An dieser Stelle können Sie eine andere Methode verwenden, um die Determinante zu finden, aber aus Gewohnheit ziehe ich es vor, die SARRUS-Methode zu verwenden. Ich denke, es ist einfacher, auf diese Weise zu programmieren. Für diejenigen, die damit nicht vertraut sind, werde ich es erklären: Die Sarrus-Methode berechnet die Determinante auf der Grundlage der Werte der Diagonalen. Das Programmieren ist etwas sehr Interessantes. Im folgenden Ausschnitt sehen Sie einen Vorschlag, wie Sie dies tun können. Es funktioniert für jede Matrix, oder besser gesagt, jedes Array, solange es quadratisch ist.

01. //+------------------------------------------------------------------+
02. double Determinant(const double &A[])
03. {
04. #define def_Diagonal(a, b)  {                                                                                                                       \
05.                 Tmp = 1;                                                                                                                            \
06.                 for (uint cp = a, cc = (a == 0 ? 0 : cp - 1), ct = 0; (a ? cp > 0 : cp < A_Row); cc = (a ? (--cp) - 1 : ++cp), ct = 0, Tmp = 1)     \
07.                 {                                                                                                                                   \
08.                     do {                                                                                                                            \
09.                         for (; (ct < A_Row); cc += b, ct++)                                                                                         \
10.                             if ((cc / A_Row) != ct) break; else Tmp *= A[cc];                                                                       \
11.                         cc = (a ? cc + A_Row : cc - A_Row);                                                                                         \
12.                     }while (ct < A_Row);                                                                                                            \
13.                     Result +=  (Tmp * (a ? -1 : 1));                                                                                                \
14.                 }                                                                                                                                   \
15.                             }
16. 
17.     uint A_Row, A_Size = A.Size();
18.     double Result, Tmp;
19. 
20.     if (A_Size == 1)
21.         return A[0];
22.     Tmp = MathSqrt(A_Size);
23.     A_Row = (uint)MathFloor(Tmp);
24.     if ((A_Row != (uint)MathCeil(Tmp)) || (!A_Size))
25.     {
26.         Print("The matrix needs to be square");
27.         A_Row = (uint)(1 / MathAbs(0));
28.     }
29.     if (A_Row == 2)
30.         return (A[0] * A[3]) - (A[1] * A[2]);
31.     Result = 0;
32. 
33.     def_Diagonal(0, A_Row + 1);
34.     def_Diagonal(A_Row, A_Row - 1);
35. 
36.     return Result;
37. 
38. #undef def_Diagonal
39. }
40. //+------------------------------------------------------------------+

Mit diesem schönen Fragment, das hier zu sehen ist, lässt sich der Wert der Determinante der Matrix ermitteln. Hier tun wir etwas so Wunderbares, dass der Code nicht einmal einer Erklärung bedarf.

In der vierten Zeile haben wir ein Makro definiert. Dieses Makro kann ein Array, oder in unserem Fall ein Array innerhalb eines Arrays, diagonal durchlaufen. Genau so wird es gemacht. Die Mathematik, die hinter diesem Code steckt, ermöglicht es Ihnen, den Wert der Diagonalen eine nach der anderen zu berechnen, sowohl in Richtung der Hauptdiagonale als auch in Richtung der Nebendiagonale, und zwar auf elegante und effiziente Weise. Beachten Sie, dass wir im Code nur das Array angeben müssen, das unsere Matrix enthält. Der zurückgegebene Wert ist die Determinante dieser Matrix. Die Sarrus-Methode, wie sie in diesem Code implementiert ist, hat jedoch eine Einschränkung: Wenn die Matrix 1x1 Dimensionen hat, ist die Determinante die Matrix selbst, und sie wird sofort zurückgegeben, wie in Zeile 21 zu sehen ist. Wenn das Array leer oder nicht quadratisch ist, wird in Zeile 27 ein RUN-TIME-Fehler ausgegeben, sodass der Code nicht weiter ausgeführt werden kann. Wenn die Matrix 2x2 groß ist, läuft die Berechnung der Diagonalen nicht durch das Makro, sondern wird davor in Zeile 30 durchgeführt. In allen anderen Fällen wird die Berechnung der Determinante durch ein Makro durchgeführt: Zunächst wird in Zeile 33 die Hauptdiagonale und in Zeile 34 die Nebendiagonale berechnet. Wenn du nicht verstehst, was vor sich geht, schau dir das Bild unten an, auf dem ich alles deutlich zeige. Dies ist für diejenigen, die mit der SARRUS-Methode nicht vertraut sind.

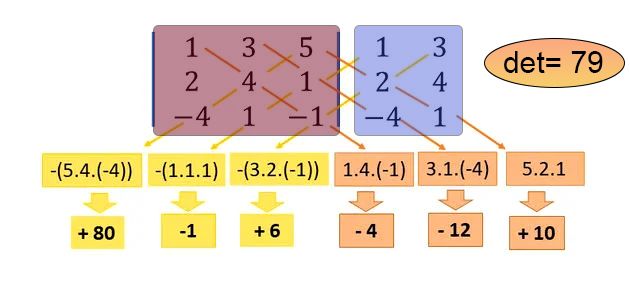
In diesem Bild stellt der rote Bereich die Matrix dar, für die wir die Determinante berechnen wollen, und der blaue Bereich ist eine virtuelle Kopie einiger Elemente der Matrix. Der Makrocode führt genau die in der Abbildung gezeigte Berechnung durch und gibt die Determinante zurück, die in diesem Beispiel 79 ist.

Abschließende Überlegungen

Nun, liebe Leserinnen und Leser, sind wir am Ende eines weiteren Artikels angelangt. Wir haben jedoch noch nicht alle notwendigen Verfahren zur Berechnung des Wertes der Pseudoinverse implementiert. Darüber werden wir im nächsten Artikel sprechen, in dem wir uns eine Anwendung ansehen werden, die diese Aufgabe erfüllt. Man kann zwar sagen, dass wir den Code aus dem Anhang dieses Artikels verwenden können, aber das Problem ist, dass er uns nicht die Freiheit gibt, jede Art von Struktur zu verwenden. Um die Pseudoinverse (PInv) zu verwenden, müssen wir tatsächlich mit einem Matrixtyp arbeiten. In dem Beispiel, das ich zur Erläuterung der Berechnungen zeige, können wir eine beliebige Datenmodellierung verwenden. Wir müssen nur die notwendigen Änderungen vornehmen, um alles nutzen zu können. Wir sehen uns im nächsten Artikel.