
Neuronale Netze leicht gemacht (Teil 95): Reduzierung des Speicherverbrauchs in Transformermodellen
Einführung
Die Einführung der Transformer-Architektur im Jahr 2017 führte zum Aufkommen von Large Language Models (LLMs), die bei der Lösung von Problemen der Verarbeitung natürlicher Sprache gute Ergebnisse erzielen. Schon bald wurden die Vorteile von Ansätzen der Self-Attention (Selbstaufmerksamkeit) von Forschern in praktisch allen Bereichen des maschinellen Lernens übernommen.
Aufgrund seines autoregressiven Charakters ist der Transformer-Decoder jedoch durch die Speicherbandbreite begrenzt, die zum Laden und Speichern der Entitäten von Key und Value (Schlüssel, Wert) bei jedem Zeitschritt benötigt wird (bekannt als KV-Caching). Da dieser Cache linear mit der Modellgröße, der Stapelgröße und der Kontextlänge skaliert, kann er sogar den Speicherbedarf der Modellgewichte übersteigen.
Dieses Problem ist nicht neu. Es gibt verschiedene Ansätze zur Lösung des Problems. Die am weitesten verbreiteten Methoden beinhalten eine direkte Reduzierung der verwendeten KV-Köpfe (heads). Im Jahr 2019 schlugen die Autoren des Dokuments „Fast Transformer Decoding: One Write-Head is All You Need“ den Algorithmus Multi-Query Attention (MQA) vor, der nur eine Schlüssel- und Wertprojektion für alle Aufmerksamkeitsköpfe auf der Ebene einer Schicht verwendet. Dadurch wird der Speicherverbrauch für den KV-Cache um 1/Köpfe reduziert. Diese erhebliche Verringerung des Ressourcenverbrauchs führt zu einer gewissen Verschlechterung der Modellqualität und -stabilität.
Die Autoren der Methode der Grouped-Query Attention (GQA), beschrieben im Artikel GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints (2023), stellte eine Zwischenlösung für die Aufteilung mehrerer KV-Köpfe in mehrere Aufmerksamkeitsgruppen vor. Effizienz der KV-Cache-Größenreduzierung bei Verwendung von GQA ist gleich Gruppen/Köpfe. Mit einer angemessenen Anzahl von Köpfen kann GQA in verschiedenen Tests nahezu mit dem Basismodell gleichziehen. Allerdings ist die Reduzierung der Cache-Größe KV bei Verwendung von MQA immer noch auf 1/Köpfe begrenzt. Für manche Anwendungen ist dies möglicherweise nicht ausreichend.
Um über diese Einschränkung hinauszugehen, haben die Autoren des Dokuments MLKV: Multi-Layer Key-Value Heads for Memory Efficient Transformer Decoding einen mehrstufigen Algorithmus zur gemeinsamen Nutzung von Schlüssel und Wert (MLKV) vorgeschlagen. Sie gehen bei der gemeinsamen Nutzung von KV noch einen Schritt weiter. MLKV teilt die KV-Köpfe nicht nur zwischen den Aufmerksamkeitsköpfen einer Ebene, sondern auch zwischen den Aufmerksamkeitsköpfen anderer Ebenen auf. KV-Köpfe können für Aufmerksamkeitskopfgruppen in einer Schicht und/oder für Aufmerksamkeitskopfgruppen in nachfolgenden Schichten verwendet werden. Im Extremfall kann ein KV-Kopf für alle Aufmerksamkeitsköpfe aller Ebenen verwendet werden. Die Autoren der Methode experimentieren mit verschiedenen Konfigurationen, die sie als gruppierte Abfrage sowohl auf der gleichen Ebene als auch zwischen verschiedenen Ebenen verwenden. Auch bei Konfigurationen, bei denen die Anzahl der KV-Köpfe geringer ist als die der Schichten. Die in diesem Artikel vorgestellten Experimente zeigen, dass diese Konfigurationen einen vernünftigen Kompromiss zwischen Leistung und erzielter Speichereinsparung darstellen. Die praktische Reduzierung des Speicherbedarfs auf 2/Schichten der ursprünglichen KV-Cache-Größe führt nicht zu einer signifikanten Verschlechterung der Qualität des Modells.
1. Die Methode MLKV
Die Methode MLKV ist eine logische Fortführung der Algorithmen MQA und GQA. Bei den genannten Methoden wird die Größe des KV-Cache durch die Verringerung der KV-Köpfe reduziert, die von einer Gruppe von Aufmerksamkeitsköpfen innerhalb einer einzigen Selbstaufmerksamkeits-Schicht gemeinsam genutzt werden. Ein völlig erwarteter Schritt ist die gemeinsame Nutzung der Entitäten von Schlüssel und Wert zwischen den Schichten der Selbstaufmerksamkeit. Dieser Schritt kann durch die jüngsten Forschungen über die Rolle des Blocks des Vorwärtsdurchgangs im Algorithmus des Transformers gerechtfertigt sein. Es wird davon ausgegangen, dass der angegebene Block den „Key-Value“-Speicher simuliert, der verschiedene Ebenen von Informationen verarbeitet. Am interessantesten ist für uns jedoch die Beobachtung, dass Gruppen von aufeinanderfolgenden Schichten ähnliche Dinge berechnen. Genauer gesagt befassen sich die unteren Ebenen mit oberflächlichen Mustern und die oberen Ebenen mit mehr semantischen Details. Daraus lässt sich schließen, dass die Aufmerksamkeit an Gruppen von Schichten delegiert werden kann, während die notwendigen Berechnungen im Block des Vorwärtsdurchgangs verbleiben. Intuitiv können KV-Köpfe von Schichten mit ähnlichen Zielen gemeinsam genutzt werden.
Die Autoren des Verfahrens MLKV haben diese Ideen weiterentwickelt und bieten einen mehrstufigen Schlüsselaustausch an. MLKV teilt die KV-Köpfe nicht nur unter den Abfrage-Aufmerksamkeitsköpfen in derselben Schicht der Selbstaufmerksamkeit, sondern auch unter den Aufmerksamkeitsköpfen in anderen Schichten. Dadurch kann die Gesamtzahl der KV-Köpfe im Transformer reduziert werden, wodurch ein noch kleinerer KV-Cache möglich wird.
MLKV kann wie folgt geschrieben werden:

Im Folgenden zeigt der Autor eine Visualisierung des Vergleichs der Methoden zur Reduzierung der KV-Cache-Größe.
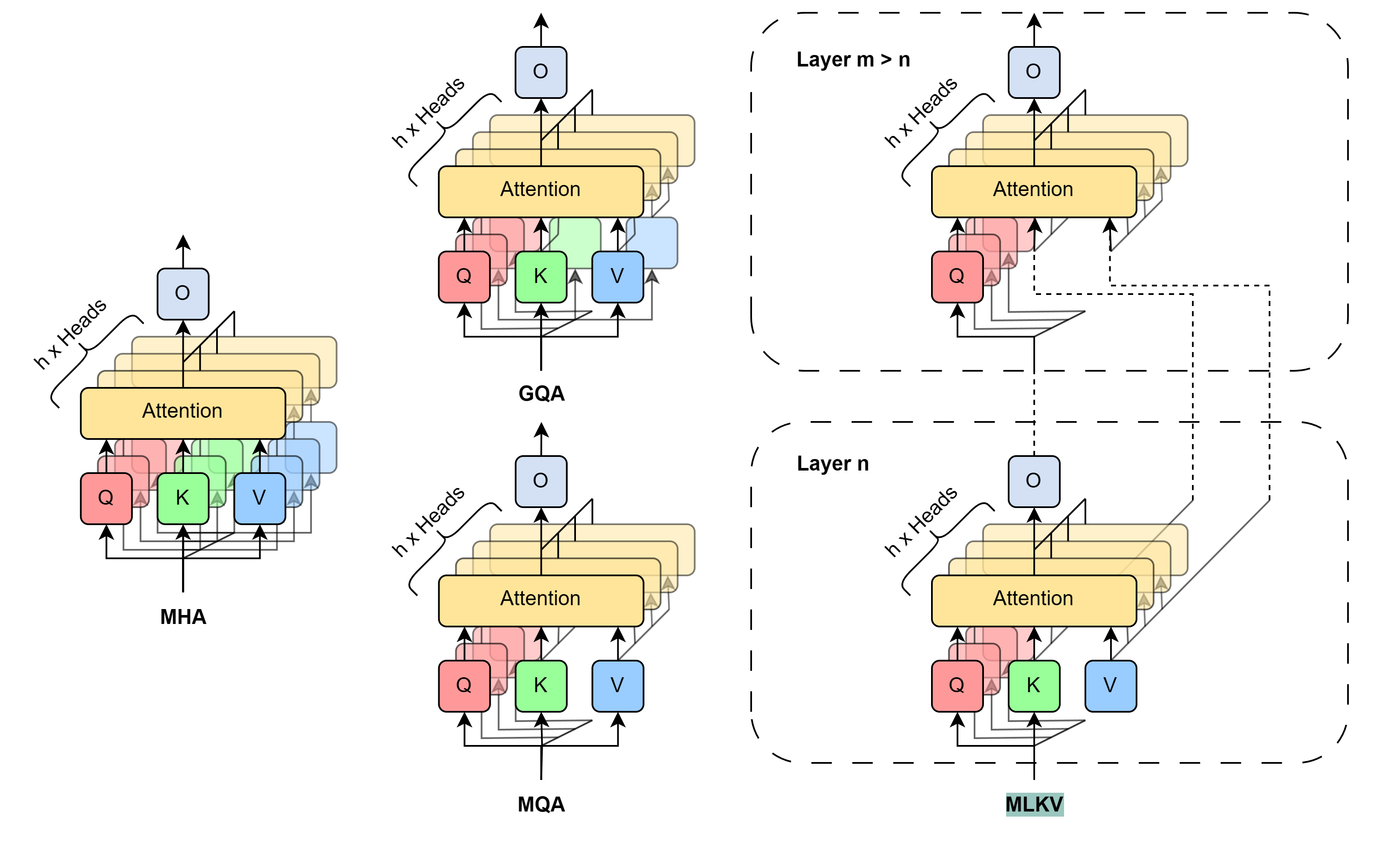
Die von den Autoren der Methode durchgeführten Experimente zeigen einen klaren Kompromiss zwischen Gedächtnis und Genauigkeit. Die Designer müssen selbst entscheiden, was sie opfern wollen. Außerdem gibt es viele Faktoren zu berücksichtigen. Wenn die Anzahl der KV-Köpfe größer oder gleich der Anzahl der Schichten ist, ist es immer noch besser, GQA/MQA anstelle von MLKV zu verwenden. Die Autoren der Methode gehen davon aus, dass das Vorhandensein von mehreren KV-Köpfen in mehreren Schichten wichtiger ist als das Vorhandensein mehrerer KV-Köpfe in einer Schicht. Mit anderen Worten, es sollten KV-Köpfe zuerst auf der Ebene der Schichten (GQA/MQA) und dann schichtübergreifend (MLKV) geopfert werden.
Für speicherintensivere Situationen, bei denen die Anzahl der KV-Köpfe geringer ist als die Anzahl der Schichten, ist die einzige Möglichkeit MLKV. Diese Konstruktionslösung ist praktikabel. Die Autoren der Methode fanden heraus, dass MLKV sehr ähnlich wie MQA funktioniert, wenn die Aufmerksamkeitsköpfe auf weniger als die Hälfte der Anzahl der Schichten reduziert werden. Das bedeutet, dass es eine relativ einfache Lösung sein sollte, wenn der KV-Cache nur halb so groß sein soll wie der von MQA.
Wenn ein niedrigerer Wert benötigt wird, können wir die Anzahl der KV-Köpfe bis zu 6 Mal weniger als die Anzahl der Schichten verwenden, ohne dass sich die Qualität stark verschlechtert. Alles, was darunter liegt, ist fragwürdig.
2. Implementierung in MQL5
Wir haben uns kurz mit der theoretischen Beschreibung der vorgeschlagenen Ansätze befasst. Nun können wir zu ihrer praktischen Umsetzung mit MQL5 übergehen. Hier werden wir die Methode MLKV anwenden. Meiner Meinung nach ist dies ein allgemeinerer Ansatz, während MQA und GQA als Spezialfälle von MLKV dargestellt werden können.
Die akuteste Frage bei der bevorstehenden Implementierung ist, wie Informationen zwischen den neuronalen Schichten übertragen werden können. In diesem Fall habe ich beschlossen, den bestehenden Algorithmus für den Datenaustausch zwischen den Objekten der neuronalen Schichten nicht zu verkomplizieren. Stattdessen werden wir einen mehrschichtigen Sequenzblock verwenden, den wir bereits mehrfach implementiert haben. Wir verwenden CNeuronMLMHAttentionOCL als übergeordnete Klasse für die kommende Implementierung.
2.1 Implementierung auf der OpenCL-Seite
Beginnen wir mit der Vorbereitung der Kernel auf der OpenCL-Programmseite. Beachten Sie, dass wir in der ausgewählten übergeordneten Klasse einen verketteten Tensor für die parallele Generierung der Entitäten Query, Key und Value verwendet haben. Der gesamte Mechanismus der Aufmerksamkeit wurde auf dieser Grundlage aufgebaut. Da wir jedoch eine unterschiedliche Anzahl von Köpfen für Query und Key verwenden sowie Key aus einer anderen Ebene verwenden, sollten wir darüber nachdenken, die genannten Entitäten in 2 separate Tensoren aufzuteilen. Etwas Ähnliches haben wir auch schon bei der Konstruktion von Blöcken der Kreuz-Beziehungen gemacht.
Das bedeutet, dass wir die Vorteile des bestehenden Codes nutzen und den Cross-Attention-Kernel-Algorithmus leicht anpassen können. Wir müssen lediglich einen weiteren Kernel-Parameter hinzufügen, der die Anzahl der KV-Köpfeangibt (im Code rot hervorgehoben).
__kernel void MH2AttentionOut(__global float *q, ///<[in] Matrix of Querys __global float *kv, ///<[in] Matrix of Keys __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention int dimension, ///< Dimension of Key int heads_kv )
Um im Hauptteil des Kernels den zu analysierenden KV-Kopf zu bestimmen, müssen wir den Rest aus der Division des aktuellen Aufmerksamkeitskopfes durch die Gesamtzahl der KV-Köpfe nehmen.
const int h_kv = h % heads_kv;
Fügen wir eine Verschiebungsanpassung im Tensor-Puffer Key-Value hinzu.
const int shift_k = 2 * dimension * (k + h_kv); const int shift_v = 2 * dimension * (k + heads_kv + h_kv);
Der weitere Kernel-Code bleibt unverändert. Ähnliche Änderungen wurden am Kernel-Code des Rückwärtsdurchgangs MH2AttentionInsideGradients vorgenommen. Der vollständige Code dieser Kernel ist im Anhang verfügbar.
Damit ist unsere Arbeit auf der Seite von OpenCL abgeschlossen. Kommen wir nun zur Hauptseite des Programms. Hier müssen wir zunächst die Funktionalität des zuvor erstellten Codes wiederherstellen. Denn ein zusätzlicher Parameter in den oben genannten Kerneln führt zu Fehlern beim Aufruf. Wir suchen also alle Aufrufe dieser Kernel und fügen die Datenübermittlung einem neuen Parameter hinzu.
Ich möchte Sie daran erinnern, dass wir bisher die gleiche Anzahl von Zielen für Query und Query verwendet haben.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_MH2AttentionInsideGradients, def_k_mh2aig_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
2.2 Erstellen der Klasse MLKV
Lassen Sie uns unser Projekt fortsetzen. Im nächsten Schritt werden wir eine mehrschichtige Aufmerksamkeitsblockklasse unter Verwendung der MLKV-Ansätze erstellen: CNeuronMLMHAufmerksamkeitMLKV. Wie bereits erwähnt, wird die neue Klasse ein direktes Kind der Klasse CNeuronMLMHAttentionOCL sein. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronMLMHAttentionMLKV : public CNeuronMLMHAttentionOCL { protected: uint iLayersToOneKV; uint iHeadsKV; CCollection KV_Tensors; CCollection KV_Weights; CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronMLMHAttentionMLKV(void) {}; ~CNeuronMLMHAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLMHAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Wie Sie sehen können, haben wir in der vorgestellten Klassenstruktur 2 Variablen eingeführt, um die Anzahl der KV-Köpfe (iHeadsKV) und die Häufigkeit der Aktualisierung des Key-Value-Tensors (iLayersToOneKV) zu speichern.
Wir haben auch Key-Value-Tensor-Speicher-Sammlungen und Gewichtsmatrizen für ihre Bildung hinzugefügt(KV_Tensors bzw. KV_Weights ).
Darüber hinaus haben wir einen Temp-Puffer hinzugefügt, um Zwischenwerte von Fehlergradienten aufzuzeichnen.
Die Methoden der Klasse sind Standardmethoden, und ich denke, Sie kennen ihren Zweck bereits. Wir werden sie im Laufe des Umsetzungsprozesses eingehender prüfen.
Wir deklarieren alle internen Objekte als statisch und können daher den Konstruktor und Destruktor der Klasse leer lassen. Die Initialisierung aller verschachtelten Objekte und Variablen wird in der Methode Init durchgeführt. Wie üblich enthalten die Parameter dieser Methode alle Informationen, die zur Erstellung des gewünschten Objekts erforderlich sind.
bool CNeuronMLMHAttentionMLKV::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir sofort die entsprechende Methode der Basisklasse aller neuronalen Schichten CNeuronBaseOCL auf.
Beachten Sie, dass wir auf das Objekt der Basisklasse und nicht auf die direkte übergeordnete Klasse zugreifen. Dies hängt mit der Aufteilung der Entitäten von Query, Key und Value in zwei Tensoren zusammen, was zu einer Änderung der Größe einiger Datenpuffer führt. Dieser Ansatz zwingt uns jedoch dazu, nicht nur neue Objekte zu initialisieren, sondern auch solche, die von der übergeordneten Klasse geerbt wurden.
Nach erfolgreicher Ausführung der Initialisierungsmethode der Basisklasse speichern wir die erhaltenen Klassenparameter in internen Variablen.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1);
Der nächste Schritt besteht darin, die Größen aller zu erstellenden Puffer zu berechnen.
uint num_q = iWindowKey * iHeads * iUnits; //Size of Q tensor uint num_kv = 2 * iWindowKey * iHeadsKV * iUnits; //Size of KV tensor uint q_weights = (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of Q tenzor uint kv_weights = 2 * (iWindow + 1) * iWindowKey * iHeadsKV; //Size of weights' matrix of KV tenzor uint scores = iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = iWindow * iUnits; //Size of out tensore uint w0 = (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Als Nächstes fügen wir eine Schleife mit einer Anzahl von Iterationen hinzu, die der Anzahl der internen Schichten des zu erstellenden Aufmerksamkeitsblocks entspricht.
for(uint i = 0; i < iLayers; i++) {
Im Hauptteil der Schleife erstellen wir eine weitere verschachtelte Schleife, in der wir zunächst Puffer zum Speichern von Daten erstellen. Bei der zweiten Iteration der verschachtelten Schleife legen wir Puffer für die Aufzeichnung der entsprechenden Fehlergradienten an.
CBufferFloat *temp = NULL; for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Hier erstellen wir zunächst die Tensoren der Entität Query. Dann erstellen wir die entsprechenden Tensoren für die Erfassung der Entitäten von Key-Value. Letztere sollte jedoch einmal pro iLayersToOneKV-Iteration der Schleife erstellt werden.
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
Als Nächstes erstellen wir nach dem Transformer-Algorithmus Puffer, um die Tensoren der Abhängigkeits-Koeffizientenmatrix, die mehrköpfige Aufmerksamkeit und ihre komprimierte Darstellung zu speichern.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Als Nächstes fügen wir den Block des Puffers für den Vorwärtsdurchgang hinzu.
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
//--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Beachten Sie, dass wir bei der Erstellung von Puffern zur Speicherung der Ausgänge und Fehlergradienten der zweiten Schicht des FeedForward-Blocks zunächst die Schichtnummer überprüfen. Da wir für die letzte Schicht keine neuen Puffer erstellen werden, speichern wir Zeiger auf die bereits erstellten Puffer der Ergebnisse und Fehlergradienten unserer Klasse CNeuronMLMHAttentionMLKV. So vermeiden wir unnötiges Kopieren von Daten beim Datenaustausch mit der nächsten Schicht.
Nach der Erstellung von Puffern für die Speicherung von Zwischenergebnissen und entsprechenden Fehlergradienten werden wir Puffer für die Matrizen der trainierbaren Parameter unserer Klasse erstellen. Ich muss sagen, dass es auch hier eine ausreichende Anzahl von ihnen gibt. Zunächst wird eine Gewichtsmatrix mit zufälligen Parametern erstellt und initialisiert, um die Query-Entität zu erzeugen.
//--- Initialize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Die Parameter für die Generierung des Key-Value-Tensors werden auf ähnliche Weise erzeugt. Auch sie werden einmal pro iLayersToOneKV der internen Ebenen erstellt.
//--- Initialize KV weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
Als Nächstes erstellen wir Kompressionsparameter für die Ergebnisse der mehrköpfigen Aufmerksamkeit.
//--- Initialize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Und zu guter Letzt sind die Parameter des FeedForward-Blocks zu nennen.
//--- Initialize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Während des Modelltrainings benötigen wir Puffer, um die Momente aller oben genannten Parameter aufzuzeichnen. Wir werden diese Puffer in einer verschachtelten Schleife erstellen, deren Anzahl der Iterationen von der gewählten Optimierungsmethode abhängt.
//--- for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(q_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(kv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
//--- Initialize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Nachdem wir alle Sammlungen unserer Aufmerksamkeitsblockpuffer erstellt haben, initialisieren wir einen weiteren Hilfspuffer, den wir zum Schreiben von Zwischenwerten verwenden werden.
if(!Temp.BufferInit(MathMax(num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
Achten Sie bei jedem Schritt darauf, den Fortschritt der Arbeiten zu kontrollieren. Und am Ende der Methode geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.
Die Methoden AttentionOut und AttentionInsideGradients stellen die von uns angepassten Kernel in die Ausführungswarteschlange. Wir werden ihre Algorithmen jetzt jedoch nicht im Detail erörtern. Der Algorithmus für die Aufnahme eines Kernels in die Ausführungswarteschlange bleibt unverändert:
- Festlegung des Aufgabenbereichs.
- Übergabe aller notwendigen Parameter an den Kernel.
- Einstellen des Kernels in die Ausführungswarteschlange.
Der Code für diesen Algorithmus wurde bereits mehrfach in dieser Artikelserie beschrieben. Die Methoden für die Einreihung der ursprünglichen Version der Kernel, die wir geändert haben, wurden in dem Artikel beschrieben, der der Methode ADAPT gewidmet ist. Bitte lesen Sie daher die beigefügten Codes für weitere Einzelheiten.
Wir gehen nun dazu über, den Algorithmus der Vorwärtsdurchgangsmethode feedForward zu betrachten. In den Methodenparametern erhalten wir einen Zeiger auf das Objekt der vorherigen Schicht, das in diesem Fall die Eingaben liefert.
bool CNeuronMLMHAttentionMLKV::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
Im Hauptteil der Methode wird zunächst die Relevanz des empfangenen Zeigers geprüft. Danach deklarieren wir einen lokalen Zeiger auf den Tensor-Puffer von Key-Value und führen eine Schleife durch alle internen Schichten unseres Blocks.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
Im Schleifenkörper erzeugen wir zunächst den Tensor von Query. Und dann erzeugen wir den Tensor Key-Value. Beachten Sie, dass wir letztere nicht bei jeder Iteration über die internen Schichten erzeugen, sondern nur alle Schichten iLayersToOneKV. Mathematisch gesehen ist die Kontrolle dieser Bedingung recht einfach: Es muss sichergestellt werden, dass der Index der aktuellen Ebene ohne Rest durch die Anzahl der Ebenen des Tensors Key-Value teilbar ist. Es ist zu beachten, dass bei der ersten Schicht mit dem Index „0“ auch der Rest der Teilung fehlt.
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; }
Wir speichern den Zeiger auf den Puffer der erzeugten Entitäten in der lokalen Variablen, die wir zuvor deklariert haben. Auf diese Weise können wir in späteren Iterationen der Schleife leicht auf sie zugreifen.
Nach der Erstellung aller erforderlichen Entitäten führen wir Vorwärtsdurchgänge der Kreuz-Aufmerksamkeit durch. Ihre Ergebnisse werden in den Ausgabepuffer der mehrköpfigen Aufmerksamkeit geschrieben.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Anschließend komprimieren wir die resultierenden Daten auf die Größe der Originaldaten.
//--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false;
Anschließend werden die Ergebnisse des Blocks Selbstaufmerksamkeit mit den Eingabedaten nach dem Transformer-Algorithmus zusammengefasst und die erhaltenen Werte normalisiert.
//--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
Als Nächstes leiten wir die Daten durch den Block von FeedForward.
//--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false;
Dann summieren wir die Daten aus den 2 Threads wieder auf und normalisieren sie.
//--- Sum and normalize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- return true; }
Nachdem wir alle Iterationen unserer Schleife durch die internen neuronalen Schichten erfolgreich abgeschlossen haben, geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.
Nach der Implementierung der Verfahren für den Vorwärtsdurchgang folgt die Konstruktion der Algorithmen der Rückwärtsdurchgänge. Hier führen wir die Optimierung der Modellparameter durch, um die maximal wahre Funktion auf dem Trainingsdatensatz zu finden. Wie Sie wissen, ist der Rückwärtsdurchgangs-Algorithmus in 2 Stufen aufgebaut. Zunächst wird der Fehlergradient auf alle Elemente des Modells übertragen, wobei deren Auswirkungen auf das Gesamtergebnis berücksichtigt werden. Diese Funktion ist in der Methode calcInputGradients implementiert. In der zweiten Stufe (Methode updateInputWeights) führen wir eine direkte Optimierung der Parameter in Richtung des Antigradienten durch.
Wir beginnen unsere Arbeit an der Implementierung des Rückwärtsdurchgangs-Algorithmus mit der Methode calcInputGradients zur Ausbreitung von Fehlergradienten. Als Parameter erhält diese Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. Während des Vorwärtsdurchgangs spielten sie die Rolle der Eingangsdaten. In diesem Stadium schreiben wir das Ergebnis der Methodenoperationen in den Fehlergradientenpuffer des erhaltenen Objekts.
bool CNeuronMLMHAttentionMLKV::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false;
Im Methodenrumpf wird die Relevanz des empfangenen Zeigers geprüft. Danach erstellen wir 2 lokale Variablen, um Zeiger auf Datenpuffer zu speichern, die zwischen den internen Schichten übergeben werden.
CBufferFloat *out_grad = Gradient;
CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);
Nach ein wenig Vorarbeit erstellen wir eine umgekehrte Schleife über die internen neuronalen Schichten.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1);
In dieser Schleife wird zunächst festgestellt, ob der Fehlergradientenpuffer der Entitäten von Key-Value geändert werden muss.
Wie wir gesehen haben, impliziert die Methode MLKV, dass ein Tensor der Entitäten von Key-Value für mehrere Selbstaufmerksamkeits-Blöcke verwendet wird. Bei der Organisation des Vorwärtsdurchgangs haben wir die entsprechenden Mechanismen implementiert. Nun müssen wir die Weitergabe des Fehlergradienten an die entsprechende Ebenen vonKey-Value organisieren. Und natürlich summieren wir die Fehlergradienten der verschiedenen Ebenen.
Der weitere Aufbau des Algorithmus kommt der Fortpflanzung des Fehlergradienten bei Objekten der Kreuz-Aufmerksamkeit sehr nahe. Zunächst wird der von der nachfolgenden Schicht erhaltene Fehlergradient durch den Vorwärtsdurchgangs-Block propagiert.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None)) return false; CBufferFloat *temp = FF_Tensors.At(i * 6 + 3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), FF_Tensors.At(i * 6), temp, iWindow, 4 * iWindow, LReLU)) return false;
Wir haben die Daten von 2 Threads im Vorwärtsdurchgang summiert. Nun summieren wir den Fehlergradienten über dieselben Daten-Threads im Rückwärtsdurchgang.
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false)) return false; out_grad = temp;
Im nächsten Schritt teilen wir den erhaltenen Fehlergradienten in Aufmerksamkeitsköpfe auf.
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None)) return false;
Anschließend wird der Fehlergradient auf die Entitäten Query, Key und Value übertragen. Hier werden wir kleine Zweige des Algorithmus organisieren. Denn wir müssen den Fehlergradienten des Tensors Key-Value aus mehreren internen Schichten summieren. Bei der Ausführung der der Verbreitungsmethode des Fehlergradienten werden die zuvor erfassten Daten jedes Mal gelöscht und mit neuen Daten überschrieben. Daher schreiben wir den Fehlergradienten nur beim ersten Aufruf direkt in den Tensor-Puffer von Key-Value.
//--- Passing gradient to query, key and value if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; }
In anderen Fällen schreiben wir den Fehlergradienten zunächst in einen Hilfspuffer. Dann addieren wir die erhaltenen Werte zu den zuvor gesammelten.
else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
Als Nächstes müssen wir den Fehlergradienten an die Ebene der Vorgängerschicht weitergeben. Mit „Vorgängerschicht“ ist hier in erster Linie die interne Vorgängerschicht gemeint. Bei der Verarbeitung der untersten Ebene wird der Fehlergradient jedoch an den Puffer des in den Methodenparametern enthaltenen Objekts übergeben.
Zunächst definieren wir einen Zeiger auf das Objekt, das den Fehlergradienten empfängt.
CBufferFloat *inp = NULL; if(i == 0) { inp = prevLayer.getOutput(); temp = prevLayer.getGradient(); } else { temp = FF_Tensors.At(i * 6 - 1); inp = FF_Tensors.At(i * 6 - 4); }
Danach wird der Fehlergradient von der Entität Query nach unten durchlaufen.
if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), inp, temp, iWindow, iWindowKey * iHeads, None)) return false;
Wir summieren den Fehlergradienten über 2 Datendreiecke (Query + "through").
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
Das Einzige, was in dem oben beschriebenen Algorithmus fehlt, ist der Fehlergradient aus den Entitäten Key und Value. Wie Sie sich erinnern, werden diese Einheiten nicht aus jeder internen Schicht gebildet. Dementsprechend werden wir den Fehlergradienten nur auf die Daten übertragen, die zu ihrer Bildung verwendet wurden. Aber es gibt einen Punkt. Zuvor haben wir bereits den Fehler von der Entität Query und dem Through-Thread in den Gradientenpuffer der Eingabedaten geschrieben. Daher schreiben wir den Fehlergradienten zunächst in einen Hilfspuffer und fügen ihn dann zu den zuvor erfassten Daten hinzu.
//--- if((i % iLayersToOneKV) == 0) { if(IsStopped() || !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; }
Am Ende der Schleifeniterationen übergeben wir einen Zeiger auf den Fehlergradientenpuffer, um die Operationen der nächsten Schleifeniteration durchzuführen.
if(i > 0) out_grad = temp; } //--- return true; }
Bei jedem Schritt überprüfen wir das Ergebnis der Operationen. Und nachdem alle Iterationen der Schleife erfolgreich abgeschlossen wurden, übergeben wir das logische Ergebnis der Methodenoperationen an das aufrufende Programm.
Wir haben den Fehlergradienten auf alle internen Objekte und die vorherige Schicht übertragen. Der nächste Schritt ist die Anpassung der Modellparameter. Diese Funktion ist in der Methode updateInputWeights implementiert. Wie bei den beiden oben beschriebenen Methoden erhalten wir in den Parametern einen Zeiger auf das Objekt der vorherigen Ebene.
bool CNeuronMLMHAttentionMLKV::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false; CBufferFloat *inputs = NeuronOCL.getOutput();
Im Methodenrumpf prüfen wir die Relevanz des empfangenen Zeigers und speichern den Zeiger auf den Ergebnispuffer des empfangenen Objekts sofort in einer lokalen Variablen.
Als Nächstes erstellen wir eine Schleife durch alle internen Schichten und aktualisieren die Modellparameter.
for(uint l = 0; l < iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(l * 2 + 1), inputs, (optimization == SGD ? QKV_Weights.At(l * 2 + 1) : QKV_Weights.At(l * 3 + 1)), (optimization == SGD ? NULL : QKV_Weights.At(l * 3 + 2)), iWindow, iWindowKey * iHeads)) return false;
Ähnlich wie bei der Vorwärtsdurchgangs-Methode passen wir zunächst die Parameter für die Generierung des Query-Tensors an.
Dann aktualisieren wir die Parameter für die Erzeugung des Tensors Key-Value. Auch hier ist zu beachten, dass diese Parameter nicht bei jeder Iteration der Schleife angepasst werden. Die Anpassung der Parameter des Tensors Key-Value in der allgemeinen Schleife erleichtert jedoch die Synchronisierung mit dem richtigen Eingabepuffer und macht den Code übersichtlicher.
if(l % iLayersToOneKV == 0) { uint l_kv = l / iLayersToOneKV; if(IsStopped() || !ConvolutuionUpdateWeights(KV_Weights.At(l_kv * (optimization == SGD ? 2 : 3)), KV_Tensors.At(l_kv * 2 + 1), inputs, (optimization == SGD ? KV_Weights.At(l_kv*2 + 1) : KV_Weights.At(l_kv*3 + 1)), (optimization == SGD ? NULL : KV_Weights.At(l_kv * 3 + 2)), iWindow, 2 * iWindowKey * iHeadsKV)) return false; }
Der Selbstaufmerksamkeits-Block enthält keine trainierbaren Parameter. Die Parameter erscheinen jedoch in der Ebene, in der wir die Ergebnisse der mehrköpfigen Aufmerksamkeit auf die Größe der Eingabedaten komprimieren. Im nächsten Schritt passen wir diese Parameter an.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9)), FF_Tensors.At(l * 6 + 3), AO_Tensors.At(l * 2), (optimization == SGD ? FF_Weights.At(l * 6 + 3) : FF_Weights.At(l * 9 + 3)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 6)), iWindowKey * iHeads, iWindow)) return false;
Danach müssen wir nur noch die Parameter des Vorwärtsdurchgangs-Blocks anpassen.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(l * 6 + 4), FF_Tensors.At(l * 6), (optimization == SGD ? FF_Weights.At(l * 6 + 4) : FF_Weights.At(l * 9 + 4)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 7)), iWindow, 4 * iWindow)) return false; //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 2), FF_Tensors.At(l * 6 + 5), FF_Tensors.At(l * 6 + 1), (optimization == SGD ? FF_Weights.At(l * 6 + 5) : FF_Weights.At(l * 9 + 5)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 8)), 4 * iWindow, iWindow)) return false;
Wir übergeben einen Zeiger auf den Eingabepuffer für die nachfolgende innere neuronale Schleife und fahren mit der nächsten Iteration der Schleife fort.
inputs = FF_Tensors.At(l * 6 + 2); } //--- return true; }
Nachdem alle Iterationen der Schleife erfolgreich abgeschlossen wurden, geben wir das logische Ergebnis der durchgeführten Operationen an den Aufrufer zurück.
Damit ist die Beschreibung der Klassenmethoden unseres neuen Aufmerksamkeitsblocks abgeschlossen, die die von den Autoren der Methode MLKV vorgeschlagenen Ansätze umfasst. Der vollständige Code dieser Klasse und alle ihre Methoden sind im Anhang verfügbar.
Wie bereits erwähnt, sind die genannten Methoden MQA und GQA Spezialfälle von MLKV. Sie können einfach mit der erstellten Klasse implementiert werden, indem man in den Parametern der Klasseninitialisierungsmethode „layers_to_one_kv=1“ angibt. Wenn der Wert des Parameters heads_kv gleich der Anzahl der Aufmerksamkeitsköpfe für die Entität Query ist, erhalten wir einen reinen Transformer. Wenn weniger, dann bekommen wir GQA. Wenn heads_kv gleich „1“ ist, handelt es sich um die MQA-Implementierung.
Bei der Vorbereitung dieses Artikels habe ich auch eine aufmerksamkeitsübergreifende Klasse erstellt, die die Ansätze von MLKV - CNeuronMLCrossAttentionMLKV nutzt. Seine Struktur wird im Folgenden dargestellt.
class CNeuronMLCrossAttentionMLKV : public CNeuronMLMHAttentionMLKV { protected: uint iWindowKV; uint iUnitsKV; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); public: CNeuronMLCrossAttentionMLKV(void) {}; ~CNeuronMLCrossAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key,uint heads, uint window_kw, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLCrossAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
Diese Klasse ist als Nachfolger der oben beschriebenen Klasse CNeuronMLMHAttentionMLKV aufgebaut. Ich musste nur kleine Korrekturen an den Methoden vornehmen, die Sie im Anhang finden.
2.3 Modellarchitektur
Wir haben die von den Autoren der MLKV-Methode vorgeschlagenen Ansätze in MQL5 implementiert. Nun können wir zur Beschreibung der Architektur der lernfähigen Modelle übergehen. Es sei darauf hingewiesen, dass wir im Gegensatz zu einer Reihe von Artikeln der letzten Zeit heute die Architekturen des Environmental State Encoder nicht anpassen werden. Wir werden der Architektur der Modelle von Akteur und Kritiker neue Objekte hinzufügen. Die Architektur dieser Modelle wird in der Methode CreateDescriptions festgelegt.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
In den Parametern erhält die Methode Zeiger auf 2 dynamische Arrays zur Erfassung der sequenziellen Architektur der Modelle. Im Hauptteil der Methode werden die empfangenen Zeiger überprüft und gegebenenfalls neue Objektinstanzen erstellt.
Zunächst beschreiben wir die Architektur des Akteurs. Wir füttern das Modell mit einer Beschreibung des Kontostands und der offenen Positionen.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Die empfangenen Daten werden von einer vollverknüpften Schicht vorverarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Dann fügen wir eine neue Ebene der mehrstufigen Querbeobachtung mit MLKV-Ansätzen hinzu.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); }
Diese Schicht vergleicht den aktuellen Kontostand mit der Vorhersage der bevorstehenden Preisbewegung, die aus dem Environment State Encoder stammt.
Hier verwenden wir 8 Aufmerksamkeitsköpfe für Query und nur 2 für den Key-Value-Tensor.
{
int temp[] = {8, 2};
ArrayCopy(descr.heads, temp);
}
Insgesamt erstellen wir 9 verschachtelte Ebenen in unserem Block. Alle 3 Schichten wird ein neuer Key-Value-Tensor erzeugt.
descr.layers = 9; descr.step = 3;
Zur Optimierung der Modellparameter verwenden wir die Adam-Methode.
descr.window_out = 32; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Nach dem Aufmerksamkeitsblock werden die Daten von 2 vollständig verbundenen Schichten verarbeitet.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Am Ausgang des Modells erstellen wir eine stochastische Politik des Akteurs, die Aktionen in einem bestimmten Bereich optimaler Werte erlaubt.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Darüber hinaus nutzen wir die Ansätze der FreDF-Methode, um Aktionen im Frequenzbereich zu koordinieren.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
In ähnlicher Weise bauen wir ein Modell des Kritikers. Anstelle des Kontostands füttern wir das Modell mit einem Vektor von Aktionen, die durch die Politik des Akteurs generiert werden.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Auch diese Daten werden von einer voll vernetzten Schicht vorverarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Es folgt ein Block für die Kreuz-Aufmerksamkeit.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); } { int temp[] = {8, 2}; ArrayCopy(descr.heads, temp); } descr.window_out = 32; descr.step = 3; descr.layers = 9; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Die Ergebnisse der Datenverarbeitung im Kreuz-Aufmerksamkeit-Block durchlaufen 3 vollständig verbundene Schichten.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Am Ausgang des Modells wird ein Vektor der erwarteten Belohnungen gebildet.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Außerdem fügen wir eine FreDF-Schicht für die Konsistenz der Belohnungunen im Frequenzbereich hinzu.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Die Expert Advisors für die Datenerhebung und das Training der Modelle haben sich nicht geändert. Den vollständigen Code können Sie im Anhang sehen. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme.
3. Tests
Wir haben die vorgeschlagenen Methoden umgesetzt. Kommen wir nun zur letzten Phase unserer Arbeit: dem Testen der vorgeschlagenen Ansätze an realen Daten.
Wie immer verwenden wir zum Trainieren der Modelle reale historische Daten des Instruments EURUSD mit dem Zeitrahmen H1 für das gesamte Jahr 2023. Wir sammeln Daten für den Trainingsdatensatz, indem wir Umweltinteraktions-EAs im MetaTrader 5 Strategie-Tester ausführen.
Beim ersten Start werden unsere Modelle mit zufälligen Parametern initialisiert. Infolgedessen erhalten wir Durchgänge mit völlig willkürlichen Strategien, die bei weitem nicht optimal sind. Um dem Trainingsdatensatz profitable Läufe hinzuzufügen, empfehle ich, die Ansätze der Methode Real-ORL bei der Sammlung von Quelldaten zu verwenden.
Nach dem Sammeln des anfänglichen Trainingsdatensatzes trainieren wir zunächst den Environment State Encoder, indem wir das Programm“.../MLKV/StudyEncoder.mq5“ in Echtzeit auf einem Chart im MetaTrader 5 Terminal ausführen. Dieser EA arbeitet nur mit dem Trainingsdatensatz und analysiert die Abhängigkeiten in den historischen Daten der Preisbewegung. Schon ein einziger Durchgang reicht aus, um ihn zu trainieren, unabhängig von den Handelsergebnissen. Daher trainieren wir den State Encoder, bis der Vorhersagefehler nicht mehr abnimmt, ohne den Trainingsdatensatz zu aktualisieren.
Dabei ist zu beachten, dass die anschließend trainierten Modelle Akteur und Kritiker die gewonnenen Vorhersagen indirekt nutzen. Um ein optimales Ergebnis zu erzielen, müssen wir die aktuellen Trends im Zustand der Umwelt und ihre Stärke im verborgenen Zustand des Encoders extrahieren, auf den dann die Modelle Actor und Critic zugreifen.
Nachdem wir beim Training des Environment State Encoders das gewünschte Ergebnis erzielt haben, gehen wir zum Training der Actor-Politik und der Genauigkeit der Handlungsbewertung des Kritikers über. Die zweite Stufe der Modellbildung ist iterativ. Der springende Punkt ist, dass die Variabilität des analysierten Finanzmarktumfelds sehr hoch ist. Wir können nicht alle möglichen Varianten der Interaktion zwischen dem Agenten und der Umwelt erfassen. Daher führen wir nach mehreren Iterationen des Trainings der Modelle Akteur und Kritiker eine weitere Iteration der Sammlung von Trainingsdaten durch. Dieser Prozess soll den zuvor gesammelten Trainingsdatensatz mit Daten über die Interaktion mit der Umwelt in einem bestimmten Bereich der aktuellen Politik des Akteurs ergänzen, wodurch diese verfeinert und optimiert werden kann.
So wechseln sich mehrere Iterationen des Trainings der Modelle Akteur und Kritiker mit Operationen zur Aktualisierung des Trainingsdatensatzes ab. Dieser Vorgang wird so oft wiederholt, bis die gewünschte Akteurspolitik erreicht ist.
Um das trainierte Modell zu testen, verwenden wir historische Daten vom Januar 2023, die nicht im Trainingsdatensatz enthalten sind. Andere Parameter werden so verwendet, wie sie in den Iterationen der Trainingsdatensammlung verwendet wurden.
Ich muss zugeben, dass es mir beim Training der Modelle für diesen Artikel nicht gelungen ist, eine Strategie zu finden, die auf dem Testdatensatz Gewinne erzielt. Offensichtlich handelt es sich dabei um den Einfluss des Modellabbauprozesses, auf den die Autoren in ihrer ursprünglichen Arbeit hingewiesen hatten.
Die Testergebnisse werden im Folgenden vorgestellt.
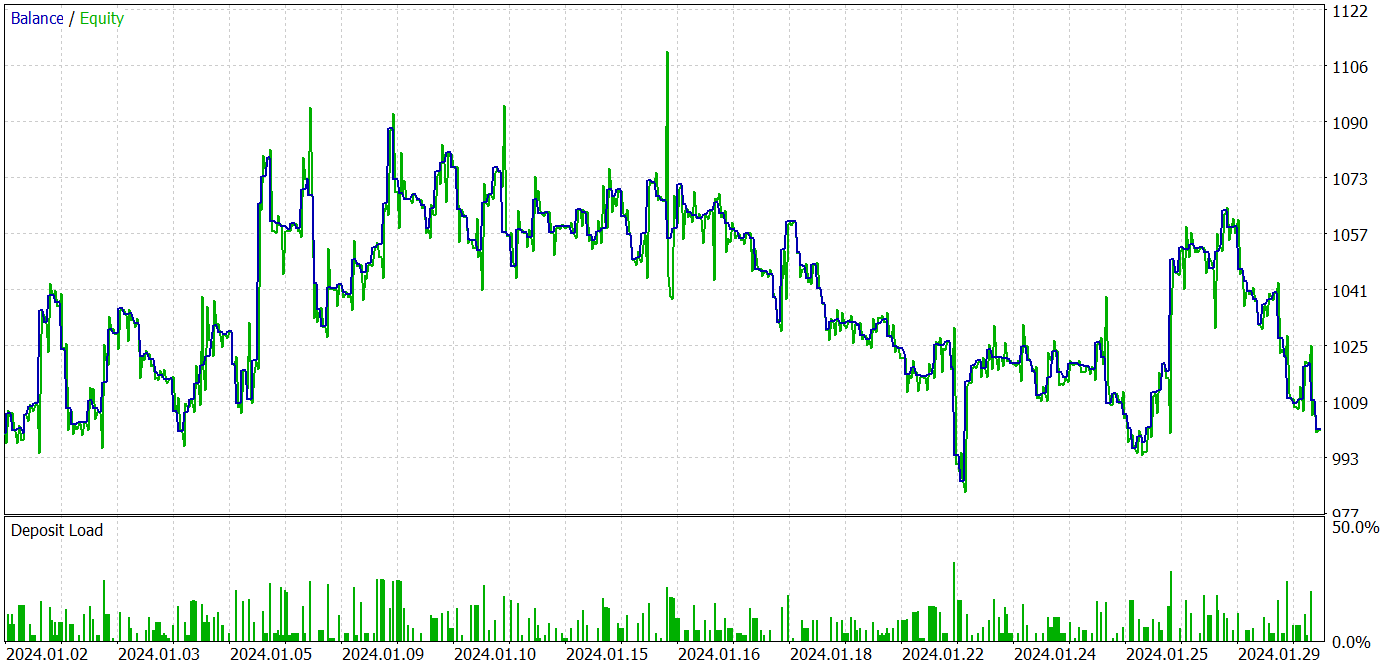
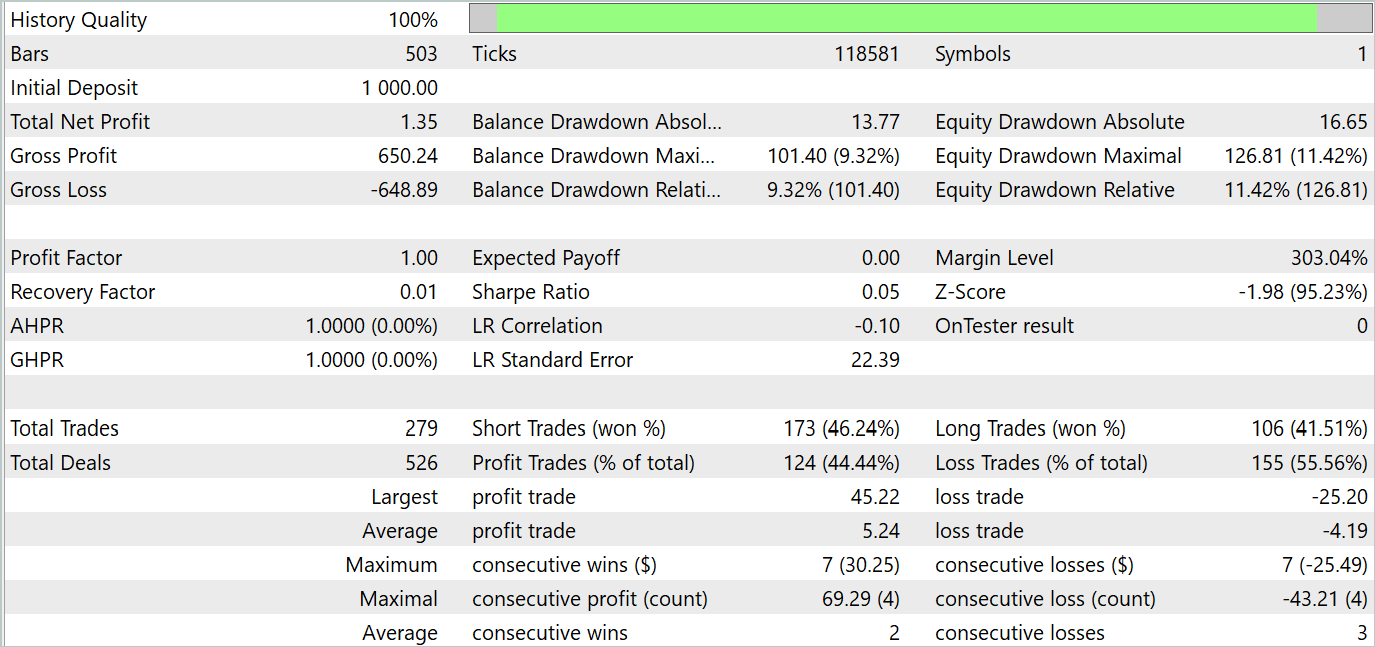
Aus den Testergebnissen geht hervor, dass die Rentabilität bei neuen Daten nahe bei 0 schwankt. Insgesamt sind die maximalen und durchschnittlichen Gewinne höher als bei ähnlichen Verlustindikatoren. Die Gewinnquote von 44,4 % erlaubte es jedoch nicht, während des Testzeitraums einen Gewinn zu erzielen.
Schlussfolgerung
In diesem Artikel haben wir eine neue Methode MLKV (Multi-Layer Key-Value) kennengelernt, die einen innovativen Ansatz zur effizienteren Speichernutzung in Transformers darstellt. Die Hauptidee besteht darin, die KV-Zwischenspeicherung auf mehrere Schichten auszudehnen, was den Speicherverbrauch erheblich reduzieren kann.
Im praktischen Teil des Artikels haben wir die vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben die Modelle mit echten Daten trainiert und getestet. Unsere Tests haben gezeigt, dass die vorgeschlagenen Ansätze die Kosten für die Ausbildung und den Betrieb des Modells erheblich senken können. Dies geht jedoch auf Kosten der Leistung des Modells. Als Schlussfolgerung sollten wir einen ausgewogenen Ansatz wählen, um einen Kompromiss zwischen den Kosten und der Leistung des Modells zu finden.
Referenzen
- MLKV: Multi-Layer Key-Value Heads for Memory Efficient Transformer Decoding
- Andere Artikel aus dieser Reihe
In diesem Artikel verwendete Programme
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Trainings-EA des Modells |
| 4 | StudyEncoder.mq5 | EA | Trainings-EA des Encoders |
| 5 | Test.mq5 | EA | Modeltest-EA |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15117
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Algorithmus zur chemischen Reaktionsoptimierung (CRO) (Teil II): Zusammenstellung und Ergebnisse
Algorithmus zur chemischen Reaktionsoptimierung (CRO) (Teil II): Zusammenstellung und Ergebnisse
 Neuronales Netz in der Praxis: Pseudoinverse (I)
Neuronales Netz in der Praxis: Pseudoinverse (I)
 Datenwissenschaft und ML (Teil 31): CatBoost AI-Modelle für den Handel verwenden
Datenwissenschaft und ML (Teil 31): CatBoost AI-Modelle für den Handel verwenden
 Neuronale Netze leicht gemacht (Teil 94): Optimierung der Eingabereihenfolge
Neuronale Netze leicht gemacht (Teil 94): Optimierung der Eingabereihenfolge
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Und wie erkennt man, dass das Netz etwas gelernt hat und nicht nur zufällige Signale erzeugt?
Die stochastische Politik des Akteurs geht von einer gewissen Zufälligkeit der Handlungen aus. Im Laufe des Lernprozesses wird der Streubereich der Zufallswerte jedoch stark eingeengt. Der Punkt ist, dass bei der Organisation einer stochastischen Politik 2 Parameter für jede Aktion trainiert werden: der Mittelwert und die Varianz der Streuung der Werte. Beim Training der Politik tendiert der Mittelwert zum Optimum und die Varianz zu 0.
Um zu verstehen, wie zufällig die Aktionen des Agenten sind, führe ich mehrere Testläufe für dieselbe Strategie durch. Wenn der Agent zufällige Aktionen generiert, werden die Ergebnisse aller Durchläufe sehr unterschiedlich ausfallen. Bei einer trainierten Strategie ist der Unterschied in den Ergebnissen unbedeutend.
Die stochastische Politik des Akteurs geht von einer gewissen Zufälligkeit der Handlungen aus. Im Laufe des Trainings wird der Bereich der Streuung der Zufallswerte jedoch stark eingeengt. Der Punkt ist, dass bei der Organisation einer stochastischen Politik 2 Parameter für jede Aktion trainiert werden: der Mittelwert und die Varianz der Streuung der Werte. Beim Training der Politik tendiert der Mittelwert zum Optimum und die Varianz zu 0.
Um zu verstehen, wie zufällig die Aktionen des Agenten sind, führe ich mehrere Testläufe für dieselbe Strategie durch. Wenn der Agent zufällige Aktionen generiert, werden die Ergebnisse aller Durchläufe sehr unterschiedlich ausfallen. Bei einer trainierten Strategie wird der Unterschied in den Ergebnissen unbedeutend sein.
Verstanden, danke.