周期与交易

概述

交易者面临的主要任务是预测价格走势。交易者会基于某种模型构建自己的预测。其中，最简单且直观的模型之一便是价格周期性波动模型。

任何周期性模式背后的基本思想是，各种因素相互作用，从而形成价格走势周期。这些周期可能在持续时间和强度上有所不同。如果您了解这些周期的参数，那么交易操作将变得非常简单：在周期达到最低点时开立多头仓位，在周期达到最高点时卖出平仓。

让我们看一下该模型如何应用于实践中。

简单周期

在描述周期时，我们通常会运用正弦和余弦三角函数。但周期也可以用另一种方式来定义——借助有限差分。

例如，让我们考虑一个方程，其中二阶差分与时间序列的值成正比：

这是一个简谐振荡器方程。乍一看，它并无特别之处。但这个方程有一个有趣的特性。如果R比值介于0到4的范围内，那么这个方程只能对应正弦曲线。这个比值取决于N周期时长。换句话说，其值可以选择为使方程仅对特定频率的周期做出反应：

现在，让我们看一下这个方程如何用于实践中。如果我们将它应用于p[]价格，就需要确定价格围绕其波动的m水平值。

为了避免计算这个平均水平的值，我将采用一个小技巧。让我们回忆一下，当周期达到最大值或最小值时，数学上会发生什么。在这些时刻，一阶导数会改变符号。

我们将使用原方程的一阶差分，而不是导数。这就是交易者的难题——从差分中寻找差分。但这种方法大大简化了计算。我们只需要设定R比值。方程的最终形式如下：

接下来，我将称此类方程为交易算法方程。基于这个方程，我们可以创建交易策略。首先，我要做一个小小的补充——我们可以使用任何常规的移动平均线，而不是当前价格。该策略的本质非常简单。当方程的符号发生变化时，进行开仓和平仓操作：

• 从负变正——开多仓，平空仓；
• 从正变负——开空仓，平多仓。

EA的资金变化如下图所示：

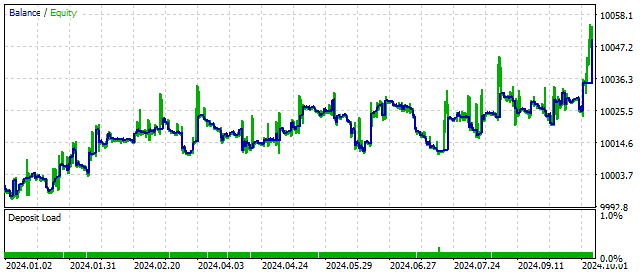
这个交易策略是有前景的。但它还需要一些改进。

阻尼周期

我们之前讨论的策略有一个严重的缺点。其基于这样的假设：周期将持续相当长的时间。然而在现实生活中，周期取决于许多外部因素，并且可能在开始不久后就几乎消失。

为了消除这个缺点，我们可以使用带有振荡阻尼的简谐振荡器模型。这样的周期方程也是通过有限差分设定的：

S参数决定了振荡衰减的速度。其值越高，阻尼发生得越快。该参数的临界值可以通过以下方程找出：

从此值开始，振荡器的运动将变为非振荡性。

我们已知如何处理这样类似的方程。我们需要找到其一阶差分，这将生成交易信号。

通过添加一个新参数，交易策略可能会变得更加灵活和盈利。例如，这是S取临界值时的资金变化情况。

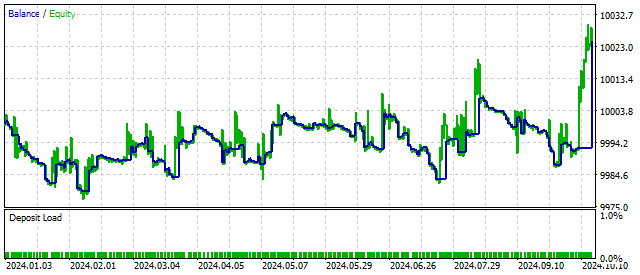
根据定义，参数S应为正值。但这个要求并非强制性的。如果我们为该参数设置一个负值，原方程将描述振幅不断增大的振荡。这样，EA就可以对周期的开始做出反应，并有可能提高盈利能力。在这种情况下，交易结果可能如下所示：

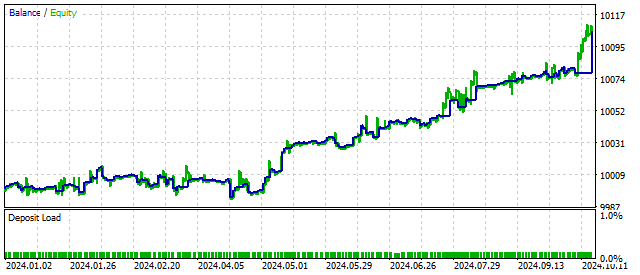
由此可见，使周期模型更加复杂可以优化交易结果。让我们尝试进一步复杂化这个模型。

艾略特波浪（Elliott Waves）

艾略特波浪理论早已广为人所知，并在交易中得到了广泛应用。让我们尝试将周期模型应用于艾略特波浪。

前五个艾略特波浪可以模拟为两个具有不同振幅和周期的正弦波之和：

在这种情况下，应满足以下条件：

结果，我们可以得到类似这样的图形：

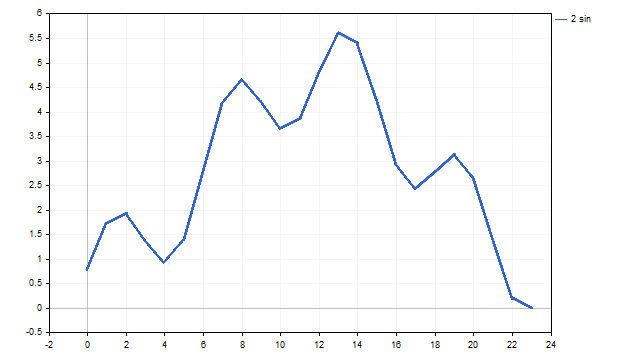
它看起来并不完全像书本上的图形——有点棱角分明，但非常相似。

我们可以使用有限差分来模拟两个正弦波的和：

其中， —— 价格读数索引为i时，n阶有限差分的值。我们已知如何处理这个方程 —— 从差分之和中找到差分，并获取交易信号：

通过两个正弦波的和使得EA能够适应更复杂的市场情况。使用该交易算法既可以增加市场进入的次数，也可以提高盈利能力。

这是基于艾略特波浪理论的EA可能展示的结果：

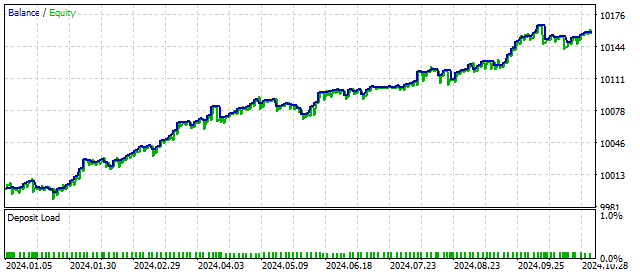
由此可见，即使对周期模型进行略微地复杂化，也能带来正向的结果。

广义简谐振荡器

我们已经研究了三种基于简谐振荡器的模型。这些模型中的每一个都是基于其自身的初始假设构建的。但最终，我们还是得到了部分有限差分之和。

我们可以构建一个更普遍的模型。这个模型的本质非常简单——首先我们取一个预定阶数的差分，并将它们加到较低阶数的差分上，直到一阶差分。在此情况下，每个低阶差分都取其自身的权重比。

例如，我取了七阶差分。那么，交易算法的方程将如下所示：

这类模型可以包含各种各样的周期组合及其行为。我们之前已经知晓，使模型更加复杂可以改善交易结果。在此情况下，资金变化可能如下所示：

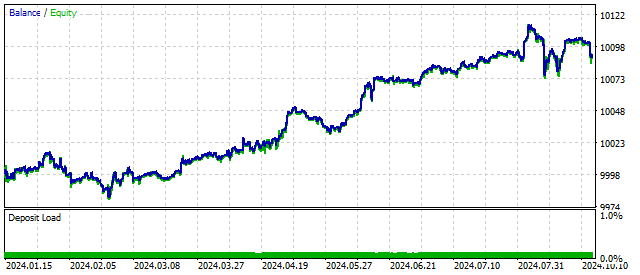
增加主差分的阶数能使模型更加灵活。广义振荡器将仅对特定的价格组合做出反应。换句话说，它在寻找特定的模式。同时，您需要牢记，振荡器的阶数越高，其模式出现的频率就越低。

该算法的另一个特点是，比率可以在非常广泛的范围内变化。甚至评估这些范围也可能很困难。另一方面，比率的选择允许您配置算法，使其能够对价格行为中的非周期性模式做出反应。

非线性振荡器

线性模型简单直观。然而，市场上的价格行为也可能呈现非线性的特征。例如，使用非线性模型能够更轻松地描述价格的急剧变化。非线性模型的主要优势在于它们能够描述极为复杂的时间序列行为。当您听到“混沌”和“随机性”这样的词汇时，那么极有可能遇到的是非线性模型。

最简单的模型之一是符号振荡器（signature oscillator）。其方程在许多方面与简谐振荡器相似。该模型使用符号函数作为非线性函数。交易算法的方程如下：

其中“sign”为符号函数。

得益于这一特性，该振荡器可以在5种不同模式下运行。模式切换取决于价格走势。振荡器的非线性特性让我们有理由相信，借助它进行交易将更加灵活和稳定。使用该算法的账户余额变化可能如下所示：

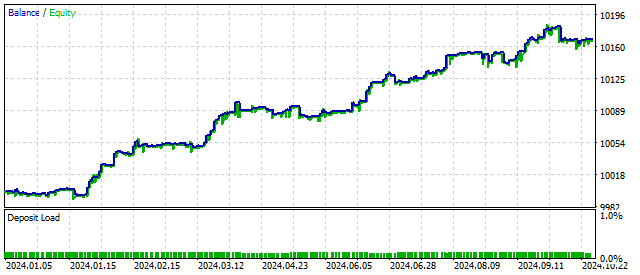
现在，我们来考虑一个具有二次非线性的振荡器。其方程非常简单：

为了在实践中应用这个方程，我们需要对其进行一些改进。

首先，我们需要确定一个价格围绕其波动的平均水平。我要提醒的是，我们可以使用价格的平滑值（简单移动平均线，SMA）来代替实际价格。那么，平均水平将等于移动平均线的平均值。

乍一看，计算平均值的平均值似乎有点令人望而生畏。1910年，安德烈·马尔可夫（Andrey Markov）发表了著作《有限差分计算》。在这部著作中，他阐明：对大量简单移动平均线取平均值，等同于对时间序列的所有值应用线性加权移动平均线（LWMA）。有限差分再次简化了计算。

二次振荡器交易算法的方程如下：

二次非线性允许振荡器更平滑地切换运行模式，但振幅更大。这样可以改善交易结果。

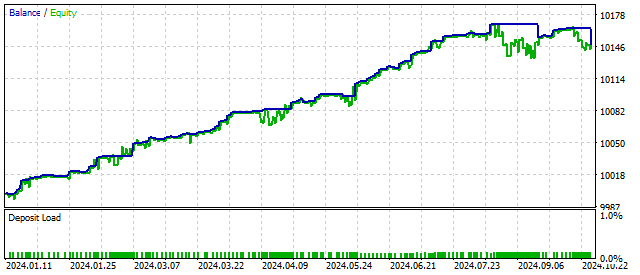
二次非线性的另一个例子是范德波尔振荡器（van der Pol oscillator）。该振荡器是模拟确定性混沌的首批范例之一。由于范德波尔方程的特性，其不仅在振动理论中得到应用，还在物理学、生物学等其他领域也得到应用。

范德波尔振荡器本身是对二次非线性振荡器的一种改进，其交易算法方程如下：

乍一看，该振荡器应该是不稳定的。但实际上，它的参数可以在相当大的范围内变化，而不会影响交易结果。

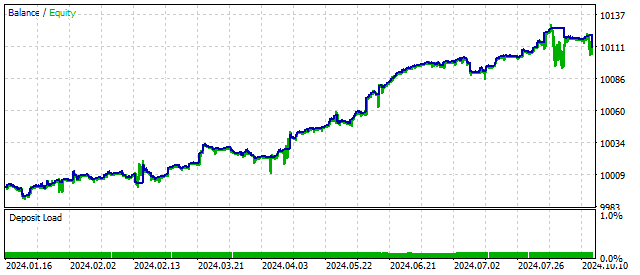
1918年，格奥尔格·达芬（Georg Duffing）探究具有三次非线性的振荡器方程。这种振荡器也可以模拟混沌价格行为。但它还有一个特点：根据外部条件及其参数的不同，可以处于两种稳定的状态。

达芬振荡器交易算法的方程是三次谐波振荡器与三次二项式之和：

该振荡器的性能与其他非线性模型相当。

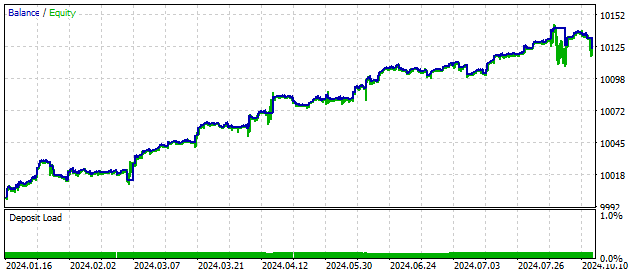
通常来说，可以创建很多非线性模型。任何非线性函数都可以成为混沌生成器。前面三种振荡器的非线性是基于一些物理原理和理念。经济物理学是一个实用的方向，但并非在任何时候都必须遵循。

例如，我将基于对数函数为交易算法添加非线性：

您可能会问：这些对数是从哪里来的，我添加它们的依据是什么？我的回答很简单——我想这么做。

但如果我有时间思考答案，那就会有所不同。连续价格之间的差异是多少？假设有100点。那么这些价格的对数之间的差异是多少呢？除了0之外还有其他吗？这是我的新答案：左边是一个常规振荡器，右边是一个可以影响开仓的过滤器。只有当价格大幅波动时，过滤器才会发挥作用。我们来检查一下它的工作情况。

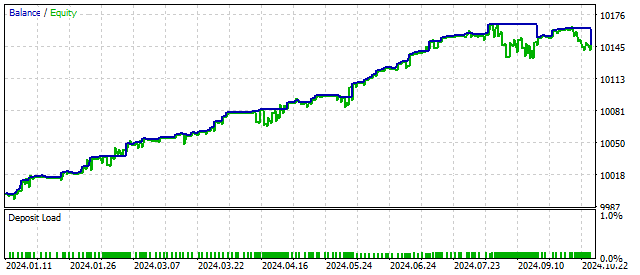
结果与二次非线性振荡器的运行情况相似。过滤器起作用了。但重要的一点是要牢记，在将所有想法应用于实践之前，应先在测试器中进行测试。

外部作用力

到目前为止，我们一直在研究自主振荡器。想象一下一个钟摆。其均匀地从一侧摆动到另一侧。它的周期一次又一次地重复。为什么这个钟摆会摆动，为什么会以这种特定的方式摆动——这些问题我们无法回答。这是一个自由运行振荡器的例子。

现在，推一下那个钟摆。先向一个方向推，再向另一个方向推。钟摆的周期开始发生变化——它的瞬时频率和振幅发生了变化。在外部作用力的影响下，钟摆不再是自主控制了。

让我们尝试将同样的方法应用于简谐振荡器。其方程将发生变化，如下所示：

其中F[n]是外部作用力。这种力是什么样的，它是如何作用的，方向如何——我一无所知。我只是假设它存在。现在的问题是：对模型进行这样的复杂化是否合理？让我们来回答这个问题。

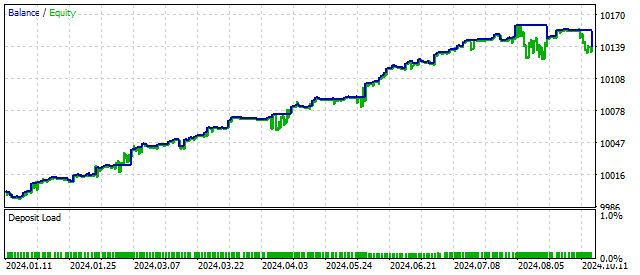
我之所以得出这个结果，是假设这个外部作用力与价格值的关系如下：

我做出此假设只有一个原因——我在整篇文章中都谈到了有限差分，而在这个例子中，我也使用了二阶差分的比率。您可以自由地做出自己的假设。例如，外部作用力可能与收盘价和开盘价之差、成交量等有关。您还可以添加非线性元素

毕竟，这种未知的力可能取决于多个组成部分。尽可能多地总结，并且尽可能长时间地总结。您所做的任何假设都可能对交易结果产生积极影响。

结论

正如您所见，在交易中使用周期性模式是相当合理的。这类模型的主要优势在于，它们有数百种参数组合，能够在很长一段时间内给出稳定的结果。交易者需要选择几十种互不相关的选项。

在本文中，我只提及了一些最常用的振荡器。还有相当多的解决方案可用于构建周期性模型（以及其他方面）。

我在以下条件下对EA进行了测试：欧元兑美元（EURUSD），H1时间框架，2024年1月1日至2024年10月30日。

撰写本文时使用了以下程序：

名称	类型	描述
简谐振荡器（Harmonic Oscillator）	EA	iPeriod - 移动平均周期 Type - 移动平均类型 R - 振荡器比率，允许值：1...399
阻尼简谐振荡器（Damped Harmonic Oscillator）	EA	S - 阻尼比，允许值：-1000...+1000
艾略特波浪（Elliott wave）	脚本	A1、A2 - 正弦波的振幅 N1、N2 - 正弦波的周期 Width - 线宽 Pause - 显示结果的延迟时间 Screenshot - 如果为“true”，则创建图像并保存在“Files”文件夹中
艾略特波浪（Elliott Waves）	EA	R、S - 振荡器比率，可接受值：0...1000
广义简谐振荡器	EA	比率允许值：-1000...+1000
符号振荡器（Sign Oscillator）	EA
二次振荡器（Quadratic Oscillator）	EA
范德波尔振荡器（Van der Pol Oscillator）	EA
达芬振荡器（Duffing Oscillator）	EA
对数振荡器（Log Oscillator）	EA
非自主振荡器（Non-Autonomous Oscillator）	EA