
使用经典机器学习方法预测汇率:逻辑回归(logit)模型和概率回归(probit)模型
引言
金融市场研究者始终面临一道难题:在众多数学模型中,如何挑选出能够预测交易品种未来走势的最佳方案?迄今为止,已涌现出大量此类模型。于是问题随之而来:面对方法浩如烟海,该如何避免迷失方向?初学者若想借助机器学习进行预测,又该从哪里入手、重点聚焦哪些模型?若将预测任务简化为一个二选一的问题——“明天的收盘价会高于今天吗?”——那么最顺理成章的选择便是二元分类模型。其中,逻辑回归(logit)和概率回归(probit)既简单又应用广泛。这些方法属于最常见的机器学习范式——有监督学习。
有监督学习的任务,则是教会模型把一组输入 {x}(预测变量或特征)映射到一组输出 {y}(目标或标签)。在本文中,我们只预测两种市场状态——货币对价格上涨或下跌。因此标签只有两类:y ∊ {1,0}。作为预测变量,我们使用价格模式,即经过标准化、并带有指定滞后的价格增量。这些数据将构成我们的 {x, y} 训练集,用于估计模型参数。基于训练好的分类器,预测模型被实现为称为LogitExpert的EA。
二元逻辑(logit)回归和概率(probit)回归
先简要回顾理论部分。最简单的二元选择模型是线性概率模型,其中成功事件的概率 P(yn=1|xn) 是解释变量的线性函数:
P(yn=1|xn) = w0*1 + w1x1 + w2x2 + … + wkxk
遗憾的是,这种模型存在一个严重缺陷:预测值可能大于 1 或小于 0,从而无法将其解释为概率。为解决这一问题,人们提出用已知的概率分布函数对线性函数的输出进行转换。
probit 模型基于标准正态分布 N(0,1):
P(yn=1|xn) = F(xnw)=μn
-
n —— 表示观测(样本)序号的下标,
-
yn —— 类别标签,
-
F( ) —— 正态分布函数(激活函数),
-
xn —— 特征向量,
-
w —— 模型参数向量,
-
xnw —— logit 或前激活值(特征向量与参数向量的点积)
xnw = w0*1 + w1x1 + w2x2 + … + wkxk
而 logit 模型则基于逻辑分布:
P(yn=1|xn) = L(xnw) = exp(xnw)/(1 + exp(xnw)) = μn
逻辑分布与正态分布的分布函数非常接近,在区间 [-1.2, 1.2] 内几乎重合。因此,除非概率接近 0 或 1,否则 logit 与 probit 模型往往给出相似的结果。将特征向量代入这些模型,我们就能计算出类别标签的概率,进而判断未来价格走势的方向概率。
准备数据
在估计模型参数之前,需要先定义特征,将其标准化,并以适当形式提供给寻找最优参数(即最小化损失函数)的函数。负责这一任务的函数是GetDataset:
-
InpCount_ —— 设置训练样本数量
-
lag_ —— 用于分析的特征数量(带滞后的价格增量)
-
string X —— 用于计算特征的货币对
-
string y —— 用于计算标签的货币对
-
int start —— 开始采集训练样本的K线编号
作为示例,我们使用货币对价格的滞后量作为特征。例如,若将参数 lag_ 设为 4,则特征为 x{return-4,return-3,return-2,return-1}},最终可获得 (InpCount_ - lag_) 个训练样本。
//+------------------------------------------------------------------+ //|Get data for analysis: features and corresponding labels | //+------------------------------------------------------------------+ bool GetDataset(int InpCount_,int lag_,int start,matrix &Input_X,vector & Target_y,string X,string y) { matrix rates; matrix target; target.CopyRates(y, PERIOD_CURRENT, COPY_RATES_OHLC, start+1, InpCount_); rates.CopyRates(X, PERIOD_CURRENT, COPY_RATES_OHLC, start+2, InpCount_-1); rates = rates.Transpose(); target = target.Transpose(); int Class_ []; ArrayResize(Class_,InpCount_); for(int i=0; i<InpCount_; i++) { if(target[i,3] > target[i,0]) Class_[i] = 1; else Class_[i] = 0; } vector label=vector::Zeros(InpCount_-lag_); for(int i=0; i<InpCount_-lag_; i++) { label[i] = Class_[i+lag_]; // class label } matrix returns=matrix::Zeros(InpCount_-lag_, lag_); for(int j=0; j<lag_; j++) { for(int i=0; i<InpCount_-lag_; i++) { returns[i,j] =rates[i+j,3] - rates[i+j,0] ; // Input Data } } vector cols_mean=returns.Mean(0); vector cols_std=returns.Std(0); mean_ = cols_mean[lag_-1]; std_ = cols_std[lag_-1]; for(int j=0; j<lag_; j++) { for(int i=0; i<InpCount_-lag_; i++) { returns[i,j] = (returns[i,j] - cols_mean[lag_-1])/cols_std[lag_-1]; } } Input_X = returns; Target_y = label; return true; }
在输出端,我们得到了特征矩阵 Input_X 与标签向量 Target_y。训练集构建完成后,接下来进入参数估计阶段。
模型参数估计
最常用的参数估计方法是最大似然法。在二元情形下,logit 与 probit 模型均假设因变量y 服从伯努利分布。若此假设成立,则对数似然函数可写为:
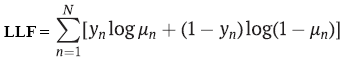
-
yn —— 类别标签,
-
μn —— 使用 logit 或 probit 回归得到的类别预测概率;
-
N —— 训练样本数量
为了估计参数,需要最大化该函数。然而在机器学习中通常以最小化损失函数为目标,且多数优化器均针对“最小化”进行配置,因此只需对对数似然函数取负号。结果即是所谓的负对数似然(NLL)。我们将使用L-BFGS 二阶拟牛顿优化算法来最小化损失函数,该算法已在Alglib库中实现。 这一数值方法通常用于求解 logit 与 probit 模型的参数。另一种常用的优化方法是迭代加权最小二乘法(IRLS)。
//+------------------------------------------------------------------+ //| Derived class from CNDimensional_Func | //+------------------------------------------------------------------+ class CNDimensional_Logit : public CNDimensional_Func { public: CNDimensional_Logit(void) {} ~CNDimensional_Logit(void) {} virtual void Func(CRowDouble &w,double &func,CObject &obj); }; //+------------------------------------------------------------------+ //| Objective Function: Logit Negative loglikelihood | //+------------------------------------------------------------------+ void CNDimensional_Logit::Func(CRowDouble &w,double &func,CObject &obj) { double LLF[],probit[],probitact[]; vector logitact; ArrayResize(LLF,Rows_); ArrayResize(probit,Rows_); vector params=vector::Zeros(Cols_); for(int i = 0; i<Cols_; i++) { params[i] = w[i]; // vector of parameters } vector logit=vector::Zeros(Rows_); logit = Input_X_gl.MatMul(params); for(int i=0; i <Rows_; i++) { probit[i] = logit[i]; } if(probit_) MathCumulativeDistributionNormal(probit,0,1,probitact); // Probit activation else logit.Activation(logitact,AF_SIGMOID); // Logit activation //--------------------to avoid NAN error when calculating logarithm ------------------------------------ if(probit_) { for(int i = 0; i<Rows_; i++) { if(probitact[i]==1) probitact[i]= 0.999; if(probitact[i]==0) probitact[i]= 0.001; } } else { for(int i = 0; i<Rows_; i++) { if(logitact[i]==1) logitact[i]= 0.999; if(logitact[i]==0) logitact[i]= 0.001; } } //------------------------------------------------------------------------------------------------- double L2_reg; if(L2_) L2_reg = 0.5 * params.Dot(params); // L2_regularization else L2_reg =0; //------------------ calculate loss function------------------------------------------------------------- if(probit_) { for(int i = 0; i<Rows_; i++) { LLF[i]=target_y_gl[i]*MathLog(probitact[i]) + (1-target_y_gl[i])*MathLog(1-probitact[i]) ; if(!MathIsValidNumber(LLF[i])) { break; } } } else { for(int i = 0; i<Rows_; i++) { LLF[i]=target_y_gl[i]*MathLog(logitact[i]) + (1-target_y_gl[i])*MathLog(1-logitact[i]); if(!MathIsValidNumber(LLF[i])) { break; } } } func = -MathSum(LLF) + L2_reg/(Rows_*C_); // Negative Loglikelihood + L2_regularization //------------------------------------------------------------------------------------------------------ func_ = func; }
然而,仅计算参数估计值并不足够;我们还希望获得这些估计值的标准误,以判断各个特征的显著性。
例如,流行的机器学习库 scikit-learn 在 logit 模型中并未提供这一信息。我已为 logit 与 probit 模型计算了标准差,因此可以直观地看到哪些具体特征对预测具有统计显著性。这也是我倾向于在 MQL 中自行编写 logit 模型代码,而非借助 ONNX 把现成机器学习包模型直接转换过来的原因之一。另一个原因是:我需要一个动态模型,能在每根 K 线或任意指定的时间框架上重新优化分类器参数。
不过,让我们回到损失函数。需要指出的是,它仍需进一步修正。要点在于:与先进的神经网络方法一样,我们的分类器也容易出现过拟合。其表现之一便是参数估计值异常偏大;为避免这一负面现象,需要一种能够限制估计值的方法。该方法即 L2 正则化:
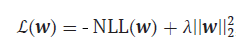
-
λ = 1/С , С = (0,1]
我们只需在现有损失函数中加上参数向量的 L2 范数平方,再乘上超参数 λ。λ 越大,对较大参数的惩罚越强,正则化效果也越明显。
负责估计分类器参数的函数为 FitLogitRegression:
- bool L2 = false —— 默认关闭 L2 正则化;
- double C = 1.0 —— 正则化强度超参数,值越小,对优化参数的限制越强;
- bool probit = false —— 默认启用 logit 模型;
- double alpha —— LR 统计量卡方分布的显著性水平 α
该函数以特征矩阵为输入,并为其增加一个取值恒为 1 的条件或哑变量。以便估计模型中的截距参数 w₀。除参数估计外,该函数还计算它们的协方差矩阵,用于求标准差。
//+------------------------------------------------------------------+ //| Finding the optimal parameters for the Logit or Probit model | //+------------------------------------------------------------------+ vector FitLogitRegression(matrix &input_X, vector &target_y,bool L2 = false, double C=1.0,bool probit = false,double alpha = 0.05) { L2_=L2; probit_ = probit; C_ = C; double w[],s[]; CObject obj; CNDimensional_Logit ffunc; CNDimensional_Rep frep; ulong Rows = input_X.Rows(); ulong Cols = input_X.Cols(); matrix One=matrix::Ones(int(Rows),int(Cols+1)); for(int i=0;i<int(Cols); i++) { One.Col(input_X.Col(i),i+1); // design matrix } input_X = One; Cols = input_X.Cols(); Rows_ = int(Rows); Cols_ = int(Cols); Input_X_gl = input_X; target_y_gl = target_y; ArrayResize(w,int(Cols)); ArrayResize(s,int(Cols)); //--- initialization ArrayInitialize(w,0.0); ArrayInitialize(s,1.0); //--- optimization stop conditions double epsg=0.000001; double epsf=0.000001; double epsx=0.000001; double diffstep=0.000001; int maxits=0; //------------------------------ CMinLBFGSStateShell state; CMinLBFGSReportShell rep; CAlglib::MinLBFGSCreateF(1,w,diffstep,state); CAlglib::MinLBFGSSetCond(state,epsg,epsf,epsx,maxits); CAlglib::MinLBFGSSetScale(state,s); CAlglib::MinLBFGSOptimize(state,ffunc,frep,0,obj); CAlglib::MinLBFGSResults(state,w,rep); Print("TerminationType ="," ",rep.GetTerminationType()); Print("IterationsCount ="," ",rep.GetIterationsCount()); vector parameters=vector::Zeros(Cols); for(int i = 0; i<int(Cols); i++) { parameters[i]= w[i]; } Print("Parameters = "," ",parameters); //-------Likelihood Ratio Test LR----------------------------------------- double S = target_y.Sum(); // number of "success" ulong All = target_y.Size(); // all data double L0 = S*MathLog(S/All) + (All-S)*MathLog((All-S)/All); // Log-likelihood for the trivial model // Print("L0 = ",L0); // Print("LLF = ",func_); double LR; LR = 2*(-func_ - L0); // Likelihood Ratio Test LR int err; double Chi2 = MathQuantileChiSquare(1-alpha,Cols-1,err); // If H0 true ---> Chi2Distribution(alpha,v) Print("LR ",LR," ","Chi2 = ",Chi2); //-------------------------------------------------------------------------------- //-------------- calculate if model significant or not if(LR > Chi2) ModelSignificant = true; else ModelSignificant = false; //---------------------------------------------------- //-------------Estimation of the covariance matrix of parameters for the Probit model------------ vector logit = input_X.MatMul(parameters); // vector activation; logit.Activation(activation,AF_SIGMOID); // Logit activation double probit_SE[],probitact[]; ArrayResize(probit_SE,Rows_); for(int i=0; i <Rows_; i++) { probit_SE[i] = logit[i]; } if(probit_) { ulong size_parameters = parameters.Size(); matrix CovProbit=matrix::Zeros(int(size_parameters),int(size_parameters)); int err; vector a_=vector::Zeros(Rows_); vector b=vector::Zeros(Rows_); vector c=vector::Zeros(Rows_); vector xt=vector::Zeros(int(size_parameters)); for(int i = 0; i<Rows_; i++) { a_[i] = MathPow((MathProbabilityDensityNormal(probit_SE[i],0,1,err)),2); b[i] = MathCumulativeDistributionNormal(probit_SE[i],0,1,err); c[i] = a_[i]/(b[i]*(1-b[i])); xt = input_X.Row(i); CovProbit = CovProbit + c[i]*xt.Outer(xt); } CovProbit = CovProbit.Inv(); vector SE; SE = CovProbit.Diag(0); SE = MathSqrt(SE); // standard errors of parameters Print("Probit_SE = ", SE); } else { //-------------Estimation of the covariance matrix of parameters for the Logit model------------ vector v = vector::Zeros(Rows_); for(int i = 0; i<Rows_; i++) { v[i] = activation[i]*(1-activation[i]); } matrix R,Hesse,X,a,CovLogit; R.Diag(v,0); X = input_X.Transpose(); a = X.MatMul(R); Hesse = a.MatMul(input_X); CovLogit = Hesse.Inv(); vector SE; SE = CovLogit.Diag(0); SE = MathSqrt(SE); // standard errors of parameters Print("Logit_SE = ", SE); //----------------------------------------------- } return parameters; }
参数估计及其协方差矩阵计算完成后,我们便可进入预测阶段。
预测
负责预测类别标签(即生成买入或卖出信号)的函数是Trade_PredictedTarget。该函数接收已优化的参数作为输入,并输出预测的类别标签。随后 LogitExpert EA 根据预测结果生成开仓规则。规则十分简洁:若收到买入信号(signal = 1),则开立多头仓位;若已持有多头,则继续持有;若收到卖出信号,则立即平掉多头并开立空头仓位。
LogitExpert EA 的实现代码
//+------------------------------------------------------------------+ //| LogitExpert.mq5 | //| Eugene | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Eugene" #property link "https://www.mql5.com" #property version "1.00" #include <\LogitReg.mqh> #include <Trade\Trade.mqh> #include <Trade\PositionInfo.mqh> CTrade m_trade; CPositionInfo m_position; sinput string symbol_X = "EURUSD"; // Input symbol sinput string symbol_y = "EURUSD"; // Target symbol input bool _probit_ = false; // Probit model input int InpCount = 20; // Depth of history input int _lag_ = 4; // Number of features input bool _L2_ = false; // L2_regularization input double _C_ = 1; // C(0,1) inverse of regularization strength input double alpha_ = 0.05; // Significance level Alpha (0,1) input int reoptimize_step = 2; // Reoptimize step #define MAGIC_NUMBER 23092024 int prev_bars = 0; MqlTick ticks; double min_lot; vector params_; matrix _Input_X; vector _Target_y; static int count_ = 0; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { m_trade.SetExpertMagicNumber(MAGIC_NUMBER); m_trade.SetTypeFillingBySymbol(Symbol()); m_trade.SetMarginMode(); min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Print(__FUNCTION__," Deinitialization reason code = ",reason); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if(!isnewBar(PERIOD_CURRENT)) return; double step; step = count_ % reoptimize_step; //------------------------------------Train Dataset------------------------------------------------- int start = 0; if(step == 0) { GetDataset(InpCount,_lag_,start,_Input_X,_Target_y,symbol_X,symbol_y); params_ = FitLogitRegression(_Input_X,_Target_y,_L2_,_C_,_probit_,alpha_); } count_ = count_+1; //-------------------------------------------------------------------------------------------------- //--- Get trade signal int signal = Trade_PredictedTarget(params_,start,_lag_,InpCount,symbol_X); Comment("Trade signal: ",signal," ","ModelSignificant: ",ModelSignificant); //--------------------------------------------- //--- Open trades based on Signals SymbolInfoTick(Symbol(), ticks); if(signal==1) { if(!PosExists(POSITION_TYPE_BUY) && ModelSignificant) { m_trade.Buy(min_lot,Symbol(), ticks.ask); PosClose(POSITION_TYPE_SELL); } else { PosClose(POSITION_TYPE_SELL); } } else { if(!PosExists(POSITION_TYPE_SELL) && ModelSignificant) { m_trade.Sell(min_lot,Symbol(), ticks.bid); PosClose(POSITION_TYPE_BUY); } else { PosClose(POSITION_TYPE_BUY); } } } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| Function tracks the occurrence of a new bar event | //+------------------------------------------------------------------+ bool isnewBar(ENUM_TIMEFRAMES TF) { if(prev_bars == 0) prev_bars = Bars(Symbol(), TF); if(prev_bars != Bars(Symbol(), TF)) { prev_bars = Bars(Symbol(), TF); return true; } return false; } //+------------------------------------------------------------------+ //|Function determines whether there is an open buy or sell position | //+------------------------------------------------------------------+ bool PosExists(ENUM_POSITION_TYPE type) { for(int i=PositionsTotal()-1; i>=0; i--) if(m_position.SelectByIndex(i)) if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type) return true; return false; } //+------------------------------------------------------------------+ //|The function closes a long or short trade | //+------------------------------------------------------------------+ void PosClose(ENUM_POSITION_TYPE type) { for(int i=PositionsTotal()-1; i>=0; i--) if(m_position.SelectByIndex(i)) if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type) if(!m_trade.PositionClose(m_position.Ticket())) printf("Failed to close position %d Err=%s",m_position.Ticket(),m_trade.ResultRetcodeDescription()); }
这款 EA 与其他做法相比,有两处关键差异:第一,它允许每隔 reoptimize_step 根 K 线就对分类器参数做一次重新优化;第二,它不仅估计模型参数,还会计算这些参数的标准差——这一点常被忽视。仅仅在样本上找到“最优”参数是不够的,还必须检验这些参数乃至整体模型是否显著。若参数不显著,那么忽略这类交易信号反而更合理。
因此,该 EA 还内置了模型显著性检验流程。零假设 H₀:所有模型参数均为 0(H₀: w₁ = w₂ = w₃ = … = wₖ = 0);备择假设 H₁:至少有一个参数不为 0,即模型对预测有用。检验使用似然比(LR)统计量,它衡量设定模型与平凡模型之间的差异:
LR = 2(LLF – LLF0)
- LLF —— 所求模型的对数似然值;
- LLF₀ —— 零假设下平凡模型的对数似然值。
p₀ = Σ(yₙ = 1) / N —— 样本中“成功”的比例;
LLF0 = N(p0*Ln(p0) + (1- p0)*Ln(1 – p0))
LR 越大,说明完整模型相对常规模型越好。当零假设成立时,LR 统计量服从自由度 v = 特征数量 的 χ² 分布。若计算出的 LR 值落入拒绝域,即 LR > X2crit (α; v = lag_),则拒绝 H₀,此时交易信号被视为有效,EA 才会开仓。
这只是其中一种可行的场景。GBPUSD,日线:
超参数
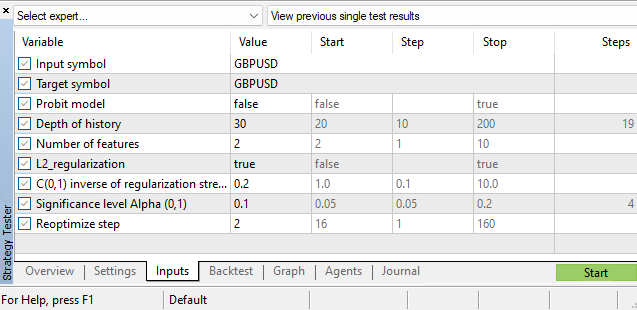
除了对分类器模型本身的参数进行评估之外,我们还需要评估许多超参数:
- 历史深度
- 特征数量
- 显著性水平
- 再优化步长
从 MetaTrader 5 的策略测试器中挑选这些超参数。一个可进一步提升 EA 表现的方案是构建历史深度参数与市场当前状态的依赖关系函数——即像我们对 logit 与 probit 模型参数所做的那样,让它也成为动态变量。不过,那将是另一个故事。提示一下,可参阅我的文章《作为时间序列非平稳性指标的双样本 Kolmogorov-Smirnov 检验》,其中探讨了构造“失序”指标的问题。
结论
在本文中,我们探讨了带有二元输出指标的回归模型,学习了如何估计这些模型的参数,并实现了用于测试与调参的 LogitExpert 交易 EA。其独特之处在于,它能够基于最新且最相关的数据,实时重训练分类器参数。
我们特别关注了参数标准误的估计,这要求我们计算 logit 与 probit 模型的协方差矩阵。
似然比准则被用来检验整个分类器模型方程的显著性,该统计量用于过滤掉统计上不可靠的交易信号。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/16029
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 从新手到专家:MQL5中的协作式调试指南
从新手到专家:MQL5中的协作式调试指南
 人工喷淋算法(ASHA)
人工喷淋算法(ASHA)


所有问题请向外汇市场和有效市场假说陛下提问。
这个标题有误导之嫌。
谢谢你,有趣的好文章。
我认为,您已经可以尝试在一日游中使用基本数据了。这并不是批评文章,而是一种思维方式。我想知道如何将宏观经济数据与价格数据充分 "混合"。例如,问题在于它们的变化很少。也许,宏观经济也可以在某种程度上用于价格预处理--例如,从名义汇率到实际汇率的过渡。
因此,标题具有误导性。
为什么?它使用了一个分类预测模型来进行预测。它能正确计算输入模型的内容。那有什么问题?该模型不能击败天真的预测?我可没这么说)
"用传统方法预测汇率是不可能的......"
"用传统方法预测汇率是不可能的......"