
Вычисление коэффициента Херста
Введение
Определение динамики рынка — одна из главных задач трейдера. Решить ее с помощью стандартных инструментов технического анализа зачастую очень сложно. Например, МА или MACD могут указывать на наличие тренда, но без дополнительных инструментов мы не можем оценить, насколько он силен, устойчив и является ли он вообще трендом — вполне возможно, что это кратковременный всплеск, который затухнет в ближайшем будущем.
Вспомним аксиому: чтобы успешно торговать на Forex, важно всегда знать чуть больше, чем другие участники рынка. В таком случае вы будете на шаг впереди, сможете
выбирать наиболее выгодные моменты входа и быть уверенными в
прибыльности сделки. Успешный трейдинг — это сочетание сразу нескольких преимуществ. Это и выставление ордеров на покупку и продажу точно в моменты перелома тренда, и успешный анализ по фундаментальным и техническим данным, и, конечно, полное отсутствие эмоций и сантиментов. Всё это — ключи к успешной карьере трейдера.
Комплексным решением многих проблем в области оценки состояния рынка может стать фрактальный анализ. Этим инструментом часто незаслуженно пренебрегают трейдеры и инвесторы, но фрактальный анализ временных рядов помогает эффективно оценить наличие и устойчивость тренда на рынке. Коэффициент Херста — одна из базовых величин фрактального анализа.
Прежде чем непосредственно перейти к вычислениям, вкратце рассмотрим основные положения фрактального анализа и познакомимся поближе с коэффициентом Херста.
1. Теория фрактального рынка (FMT). Фрактальный анализ
Фрактал — математическое множество, обладающее свойством самоподобия. Иными словами, это объект, в точности или приближённо совпадающий с частью себя самого — то есть, целое имеет ту же форму, что и одна или более частей. Самый показательный пример фрактальной структуры — «фрактальное дерево»:

Понятию самоподобия можно дать более глубокое определение: объект, обладающий этим «качеством», является статистически подобным в различных масштабах — пространственных или временных.
В контексте рынка значение слова "фрактальный" означает "повторяющийся" или "цикличный".
Фрактальная размерность – характеристика того, каким образом предмет или некий процесс заполняет пространство. Она описывает, как меняется структура предмета при изменении масштаба. Проецируя это определение на финансовые (в нашем случае — валютные) рынки, можно постулировать, что фрактальная размерность определяет степень «изрезанности» или изменчивости временного ряда. Соответственно, прямая линия имеет размерность d, равную единице, случайное блуждание — d=1.5, а для фрактального временного ряда 1<d<1.5 или 1.5<d<1.
«Цель гипотезы фрактального рынка состоит в том, чтобы дать модель поведения инвестора и движений рыночной цены, которые соответствуют нашим наблюдениям… В любой конкретный момент времени цены не могут отражать всю имеющуюся информацию, они могут отражать только ту информацию, которая важна для конкретного инвестиционного горизонта» — «Фрактальный анализ финансовых рынков», Э. Петерс.
В этой статье мы не будем подробно рассматривать понятие фрактальности, рассчитывая на то, что читатель уже имеет представление об этом методе анализа. Исчерпывающее описание его в применении к финансовым рынкам можно найти в работах Б. Мандельброта и Р. Л. Хадсона "(Не)послушные рынки. Фрактальная революция в финансах", Э. Петерса "Фрактальный анализ финансовых рынков", "Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка".
2. R/S-анализ и коэффициент Херста
2.1. Появление R/S-анализа
Ключевой параметр фрактального анализа — показатель Херста. Это мера, которую используют при анализе временных рядов. Чем больше задержка между двумя одинаковыми парами значений во временном ряду, тем меньше коэффициент Херста.
Этот важный показатель ввел Гарольд Эдвин Херст — выдающийся британский гидролог, который занимался проектом плотины на Ниле в Египте. Для строительства требовалось оценить приток воды и, соответственно, потребности в оттоке. Изначально считалось, что приток воды — величина случайная, стохастический процесс. Однако Херст изучил записи о разливах Нила за девять столетий и нашел в этом процессе закономерности. Это и стало отправной точкой в исследовании. Было обнаружено, что разливы больше среднего менялись еще большими разливами. После этого процесс менял свое направление, и разливы по уровню меньше среднего сменяли еще меньшие. Налицо наличие циклов с непериодичной продолжительностью.
Основой статистической модели Херста стала работа Альберта Эйнштейна о броуновском движении, которая по существу является моделью случайных блужданий частицы. Сущность теории в том, что расстояние, которое проходит частица, R, увеличивается пропорционально квадратному корню из времени T:
![]()
Перефразируем формулу: размах вариации, R, при большом
количестве испытаний равен корню из количества
испытаний, T. Именно эту формулу Херст взял за основу при доказательстве того, что разливы Нила — не случайность.
Для формирования своего метода гидролог использовал временной ряд X1..Xn значений разлива реки. Далее проводился следующий алгоритм, названный в последующем методом нормированного размаха или R/S-анализом:
- Расчет среднего значения, Xm, ряда X1..Xn
- Расчет стандартного отклонения ряда, S
- Нормализация ряда, путем вычитания из каждого значения среднего значения, Zr, где r=1..n
- Создание кумулятивного временного ряда Y1=Z1+Zr, где r=2..n
- Расчет размаха кумулятивного временного ряда R=max(Y1..Yn)-min(Y1..Yn)
- Деление размаха кумулятивного временного ряда на стандартное отклонение S.
Херст расширил уравнение Эйнштейна и привел его к более общей форме:
![]()
где с — константа.
В общем случае значение R/S изменяет масштаб по мере увеличения приращения времени, согласно значению степени зависимости, равной H, которая обычно и называется показателем Херста.
Гидролог принял показатель H за 0,5, если бы процесс разлива был случайным. В процессе наблюдений он обнаружил, что H=0.91! Получается, что нормированный размах изменяется быстрее, чем квадратный корень из времени, то есть система проходит большее расстояние, чем вероятностный процесс. Данный факт являлся предпосылкой момента, когда можно утверждать, что события прошлого оказывают существенное влияние на настоящее и будущее.
2.2. Применение теории к рынкам
Впоследствии была разработана методика вычисления коэффициента Херста в применении к финансовым и фондовым рынкам. Эта характеристика включает нормирование данных к нулевому среднему и единичному стандартному отклонению с целью компенсации инфляционной составляющей. Иными словами, мы снова имеем дело с R/S-анализом.
Как же интерпретируется коэффициент Херста на рынках?1. Если показатель Херста находится в промежутке между 0,5 и 1 и отличается от ожидаемого значения на два и более стандартных отклонения, то процесс характеризуется долговременной памятью. Иными словами, имеет место персистентность.
Это означает, что в пределах определенного периода времени последующие
показатели сильно зависят от предыдущих. Наглядные примеры персистентного временного
ряда — графики котировок наиболее устойчивых и авторитетных компаний. Пример — американские корпорации Apple, GE, Boeng и российские Роснефть,
Аэрофлот и ВТБ. Ниже приведены графики котировок этих компаний. Думаю, что каждый
практикующий инвестор узнал в этих картинках знакомую ситуацию «каждый новый
пик и впадина выше предыдущего».
Котировки акций Аэрофлота:
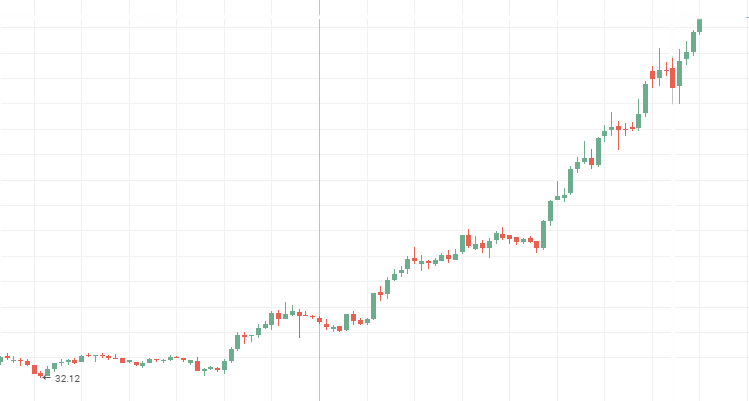
Котировки акций Роснефти:
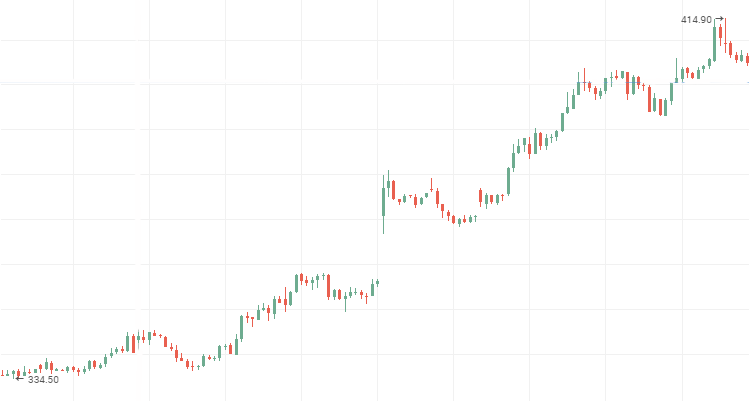
Котировки акций ВТБ, нисходящий персистентный временной ряд
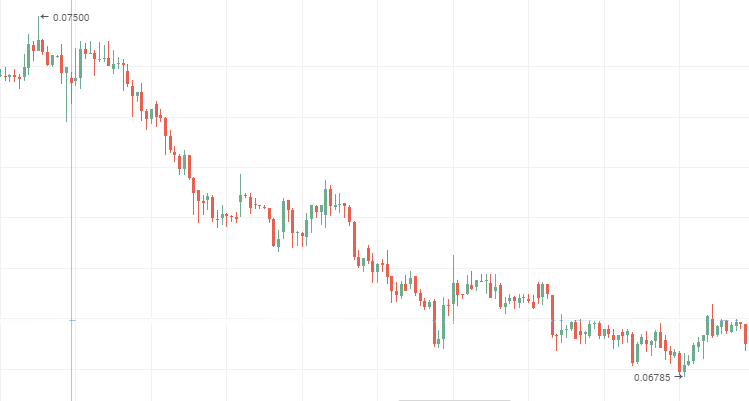
2. Показатель Херста, отличающийся от ожидаемого значения по абсолютной величине на два и более стандартных отклонения и принимающий значение из промежутка от 0 до 0,5, характеризует антиперсистентный временной ряд.
Система меняется быстрее, чем случайная, то есть ей присущи частые, но небольшие изменения. Антиперсистентный процесс являют собой графики котировок акций второго эшелона. В период ценового застоя такие графики демонстрируют и "голубые фишки". Ниже приведены графики цены на акции ПАО "Мечел", АВТОВАЗ, Ленэнерго, яркие примеры антиперсистентных временных рядов.
Привилегированные акции компании "Мечел":
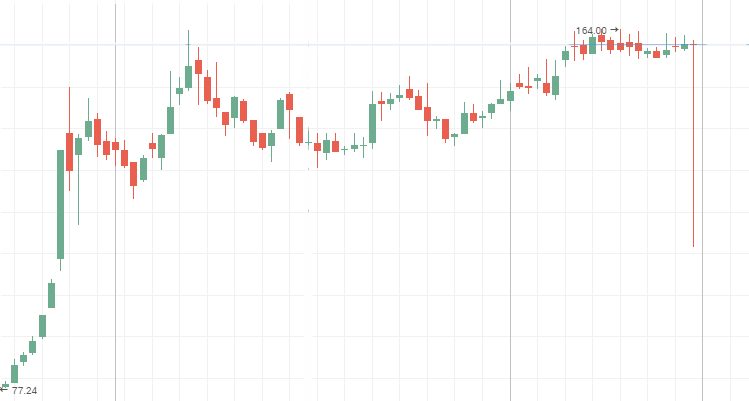
"Боковик" обыкновенных акций АВТОВАЗа:
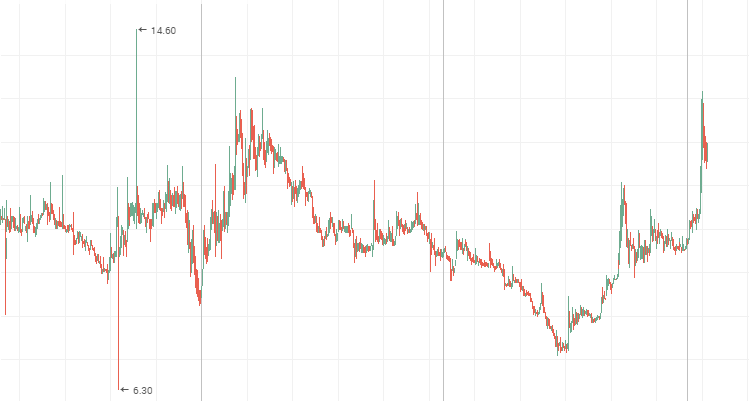
"Ленэнерго":
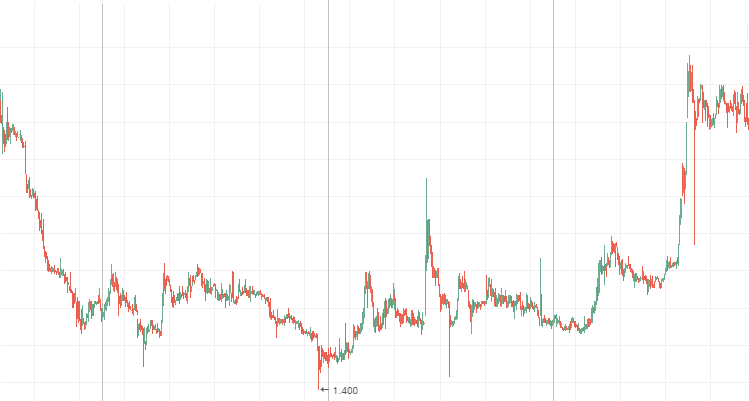
3. Если показатель Херста равен 0.5 или его величина отличается от ожидаемого значения менее, чем на два стандартных отклонения, то процесс считается случайным блужданием и вероятность наличия кратковременных или долговременных циклических зависимостей минимальна. Фактически это означает, что в торговле не стоит опираться на технический анализ, так как прошлые значения слабо влияют на настоящее. Здесь наилучшим решением станет фундаментальный анализ.
Примеры значений показателя Херста для инструментов фондового рынка — ценных бумаг различных корпораций, промышленных компаний, товаров — приведены в таблице ниже. Расчет проведен за последние 7 лет. Обратите внимание, что невысокие значения коэффициента у "голубых фишек" свидетельствуют о нахождении многих компаний в стадии консолидации во время финансового кризиса. Интересно, что многие ценные бумаги из Индекса акций второго эшелона показывают персистентный процесс, что говорит об их устойчивости к кризису.
| Название | Показатель Херста, H |
|---|---|
| Газпром | 0.552 |
| ВТБ | 0.577 |
| Магнит | 0.554 |
| МТС | 0.543 |
| Роснефть | 0.648 |
| Аэрофлот | 0.624 |
| Apple | 0.525 |
| GE | 0.533 |
| Boeing | 0.548 |
| Россети | 0.650 |
| Распадская | 0.656 |
| ТГК-1 | 0.641 |
| Таттелеком | 0.582 |
| Линэрго | 0.642 |
| Мечел | 0.635 |
| АВТОВАЗ | 0.574 |
| Бензин | 0.586 |
| Олово | 0.565 |
| Палладий | 0.564 |
| Натуральный газ | 0.560 |
| Никель | 0.580 |
3. Определение циклов и память во фрактальном анализе
Возникает вопрос: почему мы должны быть уверены, что наши результаты не являются случайными (тривиальными)? Отвечая на него, сперва мы изучим результаты RS-анализа, предполагая, что исследуемая система является случайной. То есть, проверим истинность нулевой гипотезы о том, что процесс является случайным блужданием и его структура независимая и нормально распределенная.
3.1. Расчет ожидаемого значения R/S-анализа
Введем понятие ожидаемого значения R/S-анализа.
Энис и Ллойд в 1976 году вывели уравнение, которое выражает необходимое нам ожидаемое значение:
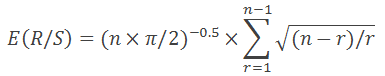
Где n — количество наблюдений, а r – целые числа от одного до n-1.
Как отмечается в книге «Фрактальный анализ финансовых рынков», приведенная выше формула справедлива только для значений n>20. Для n<20 следует использовать такую формулу: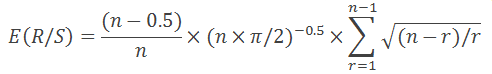
Все довольно просто:
- для каждого количества наблюдений считаем ожидаемое значение и вычерчиваем полученный график Log(E(R/S)) от Log(N) совместно с Log(R/S) от Log(N);
- рассчитываем ожидаемую дисперсию показателя Херста, по знакомой из статистической теории формуле
![]()
где H – показатель Херста;
N – число наблюдений в выборке;
3. проверяем значимость полученного коэффициента Херста путем оценки количества стандартных отклонений, на которые H превосходит E(H). Значимым считается результат, когда показатель значимости по модулю больше 2.
3.2. Определение циклов
Чтобы не быть голословными, разберем пример. Построим два графика — для RS-статистики и для ожидаемого значения E(R/S) — а затем сравним с динамикой рынка. Согласуются ли результаты расчетов с движением котировок?
Вспомним работы Петерса, который отметил, что наилучший способ понять, есть ли цикл, — это построение графика V-статистики в логарифмическом масштабе от логарифма числа наблюдений в подгруппе.
Оценить результат построения действительно просто:
- если график в логарифмическом масштабе по обеим осям представляет собой горизонтальную линию, то мы имеем дело с независимым вероятностным процессом;
- если график имеет положительный восходящий угол наклона, то мы имеем дело с персистентным процессом, под которым, повторюсь, подразумевается, что изменения масштаба R/S происходят быстрее, чем квадратный корень из времени;
- и наконец, если график показывает нисходящую динамику, то присутствует антиперсистентный процесс.
3.3. Память во фрактальном анализе и определение ее глубины
Чтобы еще больше понять сущность фрактального анализа, введем понятие памяти.
Выше уже упоминались такие словесные конструкции как долговременная и кратковременная память. Под памятью во фрактальном анализе понимается некоторый промежуток времени, в течение которого рынок помнит прошлое и учитывает его влияние на настоящих и будущих событиях. Этот промежуток времени называется глубиной памяти. В этом понятии в какой-то мере заключена вся сила и специфика фрактального анализа. Такая информация — ключевая для технического аналитика, который сомневается в значимости той или иной технической фигуры в прошлом.
Для определения глубины памяти не требуется какой-то особенной вычислительной мощности. Для этого достаточно простейшего визуального анализа графика логарифма V-статистики.
- Проведем линию тренда вдоль всех охватываемых точек графика.
- Удостоверимся в том, что кривая не горизонтальна.
- Определим пики кривой или участки, где функция достигала своих максимумов. Именно эти максимумы — первый «красный флажок», который предупреждает, что на графике с большой вероятностью присутствует цикл.
- Определим координату X графика в логарифмическом масштабе и преобразуем число в понятную для восприятия форму: Длина периода = exp^ (Длина периода в логарифмическом масштабе). Соответственно, если вы анализировали 12000 часовых данных пары GBPUSD и получили число 8.2 в логарифмическом масштабе, то цикл составляет exp^8.2=3772 часа или 157 дней.
- Любые истинные циклы должны сохраняться на том же промежутке времени, но с другим таймфреймом в качестве баз. Например, в п.4 мы исследовали 12000 часовых данных пары GBPUSD и предположили, что имеет место цикл длиной 157 дней. Переключаемся на четырехчасовой таймфрейм и проводим анализ уже, соответственно, 12000/4=3000 данных. Если цикл в 157 дней будет иметь место, то с большой вероятностью вы не прогадали. Если же нет, то не отчаивайтесь: возможно, вы сможете найти более короткие циклы памяти.
3.4. Фактические значения показателя Херста для валютных пар
Мы закончили изложение основных принципов теории фрактального анализа. Прежде чем перейти к непосредственной реализации RS-анализа с помощью средств языка программирования MQL5, я счел нужным привести еще некоторые иллюстрации.
В таблице ниже приведены значения показателя Херста для 11 валютных пар рынка FOREX на различных таймфреймах и количестве баров. Коэффициенты рассчитаны путем решения регрессии методом наименьших квадратов (МНК). Как видим, формально большинство валютных пар поддерживают персистентный процесс, хотя и встречаются антиперсистентные. Но насколько значим этот результат? Можно ли доверять этим цифрам? Об этом поговорим позже.
Таблица 1. Исследование показателя Херста для 2000 баров
| Символ | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.559 | 0.513 | 0.567 | 0.577 |
| EURCHF | 0.520 | 0.468 | 0.457 | 0.463 | 0.522 | 0.577 |
| EURJPY | 0.574 | 0.501 | 0.527 | 0.511 | 0.546 | 0.577 |
| EURGBP | 0.553 | 0.571 | 0.540 | 0.562 | 0.550 | 0.577 |
| EURRUB | недостаточно баров | 0.536 | 0.521 | 0.543 | 0.476 | 0.577 |
| USDJPY | 0.591 | 0.563 | 0.583 | 0.519 | 0.565 | 0.577 |
| USDCHF | недостаточно баров | 0.509 | 0.564 | 0.517 | 0.545 | 0.577 |
| USDCAD | 0.549 | 0.569 | 0.540 | 0.519 | 0.565 | 0.577 |
| USDRUB | 0.582 | 0.509 | 0.564 | 0.527 | 0.540 | 0.577 |
| AUDCHF | 0.522 | 0.478c | 0.504 | 0.506 | 0.509 | 0.577 |
| GBPCHF | 0.554 | 0.559 | 0.542 | 0.565 | 0.559 | 0.577 |
Таблица 2. Исследование показателя Херста для 400 баров
| Символ | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.513 | 0.604 | 0.617 | 0.578 |
| EURCHF | 0.471 | 0.460 | 0.522 | 0.603 | 0.533 | 0.578 |
| EURJPY | 0.545 | 0.494 | 0.562 | 0.556 | 0.570 | 0.578 |
| EURGBP | 0.620 | 0.589 | 0.601 | 0.597 | 0.635 | 0.578 |
| EURRUB | 0.580 | 0.551 | 0.478 | 0.526 | 0.542 | 0.578 |
| USDJPY | 0.601 | 0.610 | 0.568 | 0.583 | 0.593 | 0.578 |
| USDCHF | 0.505 | 0.555 | 0.501 | 0.585 | 0.650 | 0.578 |
| USDCAD | 0.590 | 0.537 | 0.590 | 0.587 | 0.631 | 0.578 |
| USDRUB | 0.563 | 0.483 | 0.465 | 0.531 | 0.502 | 0.578 |
| AUDCHF | 0.443 | 0.472 | 0.505 | 0.530 | 0.539 | 0.578 |
| GBPCHF | 0.568 | 0.582 | 0.616 | 0.615 | 0.636 | 0.578 |
Таблица 3. Результаты вычисления показателя Херста для таймфреймов 15М и 5М
| Символ | H (15M) | Значимость | H (5M) | Значимость | E(H) |
|---|---|---|---|---|---|
| EURUSD | 0.543 | не значим | 0.542 | не значим | 0.544 |
| EURCHF | 0.484 | значим | 0.480 | значим | 0.544 |
| EURJPY | 0.513 | не значим | 0.513 | не значим | 0.544 |
| EURGBP | 0.542 | не значим | 0.528 | не значим | 0.544 |
| EURRUB | 0.469 | значим | 0.495 | значим | 0.544 |
| USDJPY | 0.550 | не значим | 0.525 | не значим | 0.544 |
| USDCHF | 0.551 | не значим | 0.525 | не значим | 0.544 |
| USDCAD | 0.519 | не значим | 0.550 | не значим | 0.544 |
| USDRUB | 0.436 | значим | 0.485 | значим | 0.544 |
| AUDCHF | 0.518 | не значим | 0.499 | значим | 0.544 |
| GBPCHF | 0.533 | не значим | 0.520 | не значим | 0.544 |
В исследованиях Э. Петерса рекомендовано анализировать некоторый базовый таймфрейм и искать по нему временной ряд, обладающий циклическими зависимостями. Затем рекомендуется разбить проанализированный интервал времени на меньшее число баров путем изменения таймфрейма и "подгонкой" глубины истории. Отсюда вытекает следующее:
Если цикл присутствует на базовом таймфрейме, то его истинность, вероятно, будет доказана в случае, если такой же цикл будет найден при другом разбиении.
Используя различные комбинации доступных для исследования баров, можно отыскать непериодические циклы, длина которых окажет хорошую службу любому трейдеру, сомневающемуся в целесообразности использования прошлых сигналов технических индикаторов.
4. От теории к практике
Итак, мы получили начальные знания о фрактальном анализе, узнали о том, что такое коэффициент Херста и как интерпретировать его значения. Теперь на повестке вопрос программной реализации идеи средствами языка MQL5.
Техническое задание сформулируем так: необходимо составить программу, рассчитывающую по заданной валютной паре коэффициент Херста для 1000 баров истории.
Шаг 1. Создаем новый скрипт
В результате получаем "каркас", который будем заполнять информацией. Сразу же добавляем свойство #property script_show_inputs, так как нам будет необходимо выбирать валютную пару на входе.
//| New.mq5 |
//| Copyright 2016, Piskarev D.M. |
//| piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link "piskarev.dmitry25@gmail.com"
#property version "1.00"
#property script_show_inputs
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//---
}
//+------------------------------------------------------------------+
Шаг 2. Задаем массив цен закрытия и одновременно проверяем, доступны ли на текущий момент 1001 баров истории по выбранной валютной паре.
Почему 1001, хотя по ТЗ задано 1000 баров? Ответ: потому что будет создан массив логарифмических доходностей, для формирования которого необходимы данные предшествующего значения.
int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); //копируем цены закрытия выбранной пары в
//массив close[]
ArrayResize(close,1001); //задаем размер массиву
ArraySetAsSeries(close,true);
if(bars<1001) //создаем условие наличия 1001 бара истории
{
Comment("Too few bars are available! Try another timeframe.");
Sleep(10000); //задержка надписи в течение 10 секунд
Comment("");
return;
}
Шаг 3. Создаем массив логарифмических доходностей.
Подразумевается, что массив LogReturns уже объявлен и имеется строчка ArrayResize(LogReturns,1001)
LogReturns[i]=MathLog(close[i-1]/close[i]);
Шаг 4. Рассчитываем коэффициент Херста.
Итак, для корректного проведения анализа необходимо разделить исследуемое количество баров истории на подгруппы так, чтобы число элементов в каждой из них было не менее 10. Т.е. перед нами стоит задача поиска делителей числа 1000, значение которых превосходит десять. Таких делителей 11:
num1=10;
num2=20;
num3=25;
num4=40;
num5=50;
num6=100;
num7=125;
num8=200;
num9=250;
num10=500;
num11=1000;
Так как мы будем рассчитывать данные для RS-статистики 11 раз, то целесообразно написать пользовательскую функцию для этой цели. Параметрами функции будут конечный и начальный индекс подгруппы, для которой рассчитывается RS-статистика, а также количество исследуемых баров. Алгоритм, приведенный здесь, полностью аналогичен алгоритму, который был описан в начале статьи.
//| Функция расчета R/S |
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
{
Sum=0.0; //Начальное значение суммы равно нулю
DevSum=0.0; //Начальное значение суммы накопленных
//отклонений равно нулю
//--- Расчет суммы доходностей
for(int i=bottom; i<=top; i++)
Sum=Sum+LogReturns[i]; //Накопление суммы
//--- Расчет среднего
M=Sum/barscount;
//--- Расчет накопленных отклонений
for(int i=bottom; i<=top; i++)
{
DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
StdDevMas[i]=MathPow((LogReturns[i]-M),2);
DevSum=DevSum+StdDevMas[i]; //Составляющая для расчета отклонения
if(DevAccum[i]>MaxValue) //Если значение в массиве меньше некоторого
MaxValue=DevAccum[i]; //максимального, то присваиваем максимальному значению
//значение элемента массива DevAccum
if(DevAccum[i]<MinValue) //Логика идентична
MinValue=DevAccum[i];
}
//--- Расчет размаха R и отклонения S
R=MaxValue-MinValue; //Размах равен разности максимального и
MaxValue=0.0; MinValue=1000; //минимального значений
S1=MathSqrt(DevSum/barscount); //Расчет стандартного отклонения
//--- Расчет показателя R/S
if(S1!=0)RS=R/S1; //Исключаем ошибку деления на "ноль"
// else Alert("Zero divide!");
return(RS); //Возвращаем значение RS-статистики
}
Расчет произведем при помощи пары switch-case.
for(int A=1; A<=11; A++) //цикл позволяет нам сделать код довольно компактным
{ //к тому же мы сразу учитываем все возможные делители
switch(A)
{
case 1: // 100 групп по 10 элементов в каждой
{
ArrayResize(rs1,101);
RSsum=0.0;
for(int j=1; j<=100; j++)
{
rs1[j]=RSculc(10*j-9,10*j,10); //вызываем пользовательскую функцию RScuclc
RSsum=RSsum+rs1[j];
}
RS1=RSsum/100;
LogRS1=MathLog(RS1);
}
break;
case 2: // 50 групп по 20 элементов в каждой
{
ArrayResize(rs2,51);
RSsum=0.0;
for(int j=1; j<=50; j++)
{
rs2[j]=RSculc(20*j-19,20*j,20); //вызываем пользовательскую функцию RScuclc
RSsum=RSsum+rs2[j];
}
RS2=RSsum/50;
LogRS2=MathLog(RS2);
}
break;
...
...
...
case 9: // 125 and 16 groups
{
ArrayResize(rs9,5);
RSsum=0.0;
for(int j=1; j<=4; j++)
{
rs9[j]=RSculc(250*j-249,250*j,250);
RSsum=RSsum+rs9[j];
}
RS9=RSsum/4;
LogRS9=MathLog(RS9);
}
break;
case 10: // 125 and 16 groups
{
ArrayResize(rs10,3);
RSsum=0.0;
for(int j=1; j<=2; j++)
{
rs10[j]=RSculc(500*j-499,500*j,500);
RSsum=RSsum+rs10[j];
}
RS10=RSsum/2;
LogRS10=MathLog(RS10);
}
break;
case 11: //200 and 10 groups
{
RS11=RSculc(1,1000,1000);
LogRS11=MathLog(RS11);
}
break;
}
}
Шаг 5. Пользовательская функция расчета линейной регрессии методом наименьших квадратов (МНК).
Входные параметры — значения рассчитанных составляющих RS-статистики.
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
double Y7,double Y8,double Y9,double Y10,double Y11)
{
double SumY=0.0;
double SumX=0.0;
double SumYX=0.0;
double SumXX=0.0;
double b=0.0;
double N[]; //массив, в котором будут находиться логарифмы делителей
double n={10,20,25,40,50,100,125,200,250,500,1000} //массив делителей
//---Расчет коэффициентов N
for (int i=0; i<=10; i++)
{
N[i]=MathLog(n[i]);
SumX=SumX+N[i];
SumXX=SumXX+N[i]*N[i];
}
SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//---Расчет коэффициента Beta регрессии или искомого показателя Херста
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
return(b);
}
Шаг 6. Пользовательская функция расчета ожидаемых значений RS-статистики. Логика расчета объясняется в теоретической части.
//| Функция расчета ожидаемых значений E(R/S) |
//+----------------------------------------------------------------------+
double ERSculc(double m) //m - делители 1000
{
double e;
double nSum=0.0;
double part=0.0;
for(int i=1; i<=m-1; i++)
{
part=MathPow(((m-i)/i), 0.5);
nSum=nSum+part;
}
e=MathPow((m*pi/2),-0.5)*nSum;
return(e);
}
В конечном счете полный код программы может выглядеть следующим образом:
//| hurst_exponent.mq5 |
//| Copyright 2016, Piskarev D.M. |
//| piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link "piskarev.dmitry25@gmail.com"
#property version "1.00"
#property script_show_inputs
#property strict
input string symbol="EURUSD"; // Symbol
input ENUM_TIMEFRAMES timeframe=PERIOD_D1; // Timeframe
double LogReturns[],N[],
R,S1,DevAccum[],StdDevMas[];
int num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11;
double pi=3.14159265358979323846264338;
double MaxValue=0.0,MinValue=1000.0;
double DevSum,Sum,M,RS,RSsum,Dconv;
double RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11,
LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9,
LogRS10,LogRS11;
double rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[];
double E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11;
double H,betaE;
int bars=Bars(symbol,timeframe);
double D,StandDev;
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
double close[]; //Объявляем динамический массив цен закрытия
int copied=CopyClose(symbol,timeframe,0,1001,close); //Копируем цены закрытия выбранной пары в
//массив close[]
ArrayResize(close,1001); //Назначаем размер массива
ArraySetAsSeries(close,true);
if(bars<1001) //Создаем условие наличия 1001 бара истории
{
Comment("Too few bars are available! Try another timeframe.");
Sleep(10000); //Задержка надписи в течение 10 секунд
Comment("");
return;
}
//+------------------------------------------------------------------+
//| Подготовка массивов |
//+------------------------------------------------------------------+
ArrayResize(LogReturns,1001);
ArrayResize(DevAccum,1001);
ArrayResize(StdDevMas,1001);
//+------------------------------------------------------------------+
//| Массив логарифмических доходностей |
//+------------------------------------------------------------------+
for(int i=1;i<=1000;i++)
LogReturns[i]=MathLog(close[i-1]/close[i]);
//+------------------------------------------------------------------+
//| |
//| R/S-анализ |
//| |
//+------------------------------------------------------------------+
//--- Зададим количество элементов в каждой подгруппе
num1=10;
num2=20;
num3=25;
num4=40;
num5=50;
num6=100;
num7=125;
num8=200;
num9=250;
num10=500;
num11=1000;
//--- Расчет составных Log(R/S)
for(int A=1; A<=11; A++)
{
switch(A)
{
case 1:
{
ArrayResize(rs1,101);
RSsum=0.0;
for(int j=1; j<=100; j++)
{
rs1[j]=RSculc(10*j-9,10*j,10);
RSsum=RSsum+rs1[j];
}
RS1=RSsum/100;
LogRS1=MathLog(RS1);
}
break;
case 2:
{
ArrayResize(rs2,51);
RSsum=0.0;
for(int j=1; j<=50; j++)
{
rs2[j]=RSculc(20*j-19,20*j,20);
RSsum=RSsum+rs2[j];
}
RS2=RSsum/50;
LogRS2=MathLog(RS2);
}
break;
case 3:
{
ArrayResize(rs3,41);
RSsum=0.0;
for(int j=1; j<=40; j++)
{
rs3[j]=RSculc(25*j-24,25*j,25);
RSsum=RSsum+rs3[j];
}
RS3=RSsum/40;
LogRS3=MathLog(RS3);
}
break;
case 4:
{
ArrayResize(rs4,26);
RSsum=0.0;
for(int j=1; j<=25; j++)
{
rs4[j]=RSculc(40*j-39,40*j,40);
RSsum=RSsum+rs4[j];
}
RS4=RSsum/25;
LogRS4=MathLog(RS4);
}
break;
case 5:
{
ArrayResize(rs5,21);
RSsum=0.0;
for(int j=1; j<=20; j++)
{
rs5[j]=RSculc(50*j-49,50*j,50);
RSsum=RSsum+rs5[j];
}
RS5=RSsum/20;
LogRS5=MathLog(RS5);
}
break;
case 6:
{
ArrayResize(rs6,11);
RSsum=0.0;
for(int j=1; j<=10; j++)
{
rs6[j]=RSculc(100*j-99,100*j,100);
RSsum=RSsum+rs6[j];
}
RS6=RSsum/10;
LogRS6=MathLog(RS6);
}
break;
case 7:
{
ArrayResize(rs7,9);
RSsum=0.0;
for(int j=1; j<=8; j++)
{
rs7[j]=RSculc(125*j-124,125*j,125);
RSsum=RSsum+rs7[j];
}
RS7=RSsum/8;
LogRS7=MathLog(RS7);
}
break;
case 8:
{
ArrayResize(rs8,6);
RSsum=0.0;
for(int j=1; j<=5; j++)
{
rs8[j]=RSculc(200*j-199,200*j,200);
RSsum=RSsum+rs8[j];
}
RS8=RSsum/5;
LogRS8=MathLog(RS8);
}
break;
case 9:
{
ArrayResize(rs9,5);
RSsum=0.0;
for(int j=1; j<=4; j++)
{
rs9[j]=RSculc(250*j-249,250*j,250);
RSsum=RSsum+rs9[j];
}
RS9=RSsum/4;
LogRS9=MathLog(RS9);
}
break;
case 10:
{
ArrayResize(rs10,3);
RSsum=0.0;
for(int j=1; j<=2; j++)
{
rs10[j]=RSculc(500*j-499,500*j,500);
RSsum=RSsum+rs10[j];
}
RS10=RSsum/2;
LogRS10=MathLog(RS10);
}
break;
case 11:
{
RS11=RSculc(1,1000,1000);
LogRS11=MathLog(RS11);
}
break;
}
}
//+----------------------------------------------------------------------+
//| Расчет коэффициента Херста |
//+----------------------------------------------------------------------+
H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,
LogRS9,LogRS10,LogRS11);
//+----------------------------------------------------------------------+
//| Расчет ожидаемых значений log(E(R/S)) |
//+----------------------------------------------------------------------+
E1=MathLog(ERSculc(num1));
E2=MathLog(ERSculc(num2));
E3=MathLog(ERSculc(num3));
E4=MathLog(ERSculc(num4));
E5=MathLog(ERSculc(num5));
E6=MathLog(ERSculc(num6));
E7=MathLog(ERSculc(num7));
E8=MathLog(ERSculc(num8));
E9=MathLog(ERSculc(num9));
E10=MathLog(ERSculc(num10));
E11=MathLog(ERSculc(num11));
//+----------------------------------------------------------------------+
//| Расчет беты ожидаемых значений E(R/S) |
//+----------------------------------------------------------------------+
betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11);
Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
}
//+----------------------------------------------------------------------+
//| Функция расчета R/S |
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
{
Sum=0.0; //Начальное значение суммы равно нулю
DevSum=0.0; //Начальное значение суммы накопленных
//отклонений равно нулю
//--- Расчет суммы доходностей
for(int i=bottom; i<=top; i++)
Sum=Sum+LogReturns[i]; //Накопление суммы
//--- Расчет среднего
M=Sum/barscount;
//--- Расчет накопленных отклонений
for(int i=bottom; i<=top; i++)
{
DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
StdDevMas[i]=MathPow((LogReturns[i]-M),2);
DevSum=DevSum+StdDevMas[i]; //Составляющая для расчета отклонения
if(DevAccum[i]>MaxValue) //Если значение в массиве меньше некоторого
MaxValue=DevAccum[i]; //максимального, то присваиваем максимальному значению
//значение элемента массива DevAccum
if(DevAccum[i]<MinValue) //Логика идентична
MinValue=DevAccum[i];
}
//--- Расчет размаха R и отклонения S
R=MaxValue-MinValue; //Размах равен разности максимального и
MaxValue=0.0; MinValue=1000; //минимального значений
S1=MathSqrt(DevSum/barscount); //Расчет стандартного отклонения
//--- Расчет показателя R/S
if(S1!=0)RS=R/S1; //Исключаем ошибку деления на "ноль"
// else Alert("Zero divide!");
return(RS); //Возвращаем значение RS-статистики
}
//+----------------------------------------------------------------------+
//| Калькулятор регрессии |
//+----------------------------------------------------------------------+
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
double Y7,double Y8,double Y9,double Y10,double Y11)
{
double SumY=0.0;
double SumX=0.0;
double SumYX=0.0;
double SumXX=0.0;
double b=0.0; //массив, в котором будут лежать логарифмы делителей
double n[]={10,20,25,40,50,100,125,200,250,500,1000}; //массив делителей
//---Расчет коэффициентов N
ArrayResize(N,11);
for (int i=0; i<=10; i++)
{
N[i]=MathLog(n[i]);
SumX=SumX+N[i];
SumXX=SumXX+N[i]*N[i];
}
SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10];
//---Расчет коэффициента Beta регрессии или искомого показателя Херста
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
return(b);
}
//+----------------------------------------------------------------------+
//| Функция расчета ожидаемых значений E(R/S) |
//+----------------------------------------------------------------------+
double ERSculc(double m) //m - делители 1000
{
double e;
double nSum=0.0;
double part=0.0;
for(int i=1; i<=m-1; i++)
{
part=MathPow(((m-i)/i), 0.5);
nSum=nSum+part;
}
e=MathPow((m*pi/2),-0.5)*nSum;
return(e);
}
Разумеется, при желании вы сами сможете модернизировать код, реализовать в нем более широкий спектр рассчитываемых характеристик и создать удобный графический интерфейс.
В заключительной главе мы поговорим о существующих программных решениях.
5. Программные решения
Существует множество программных ресурсов, в которых уже реализован алгоритм R/S-анализа. Однако обычно реализация этого алгоритма сжата и оставляет большую часть аналитической работы пользователю. К таким примерам относится пакет Matlab.
Существует также утилита для терминала MetaTrader 5, доступная в Маркете, под названием Fractal Analysis, при помощи которой пользователь может проводить фрактальный анализ финансовых рынков. Давайте разберемся, как работать с этим анализатором.
5.1. Входные данные
Фактически из всего многообразия входных параметров нас будут интересовать только первые три, а именно Symbol, Number of bars и Timeframe.
Как видно из скриншота ниже, Fractal Analysis позволяет выбрать валютную пару, причем совершенно не имеет значения, в окне какого инструмента утилита была запущена: самое главное — указать символ в окне инициализации.
Выбираем интересующее количество баров определенного таймфрейма, который указывается пунктом ниже.
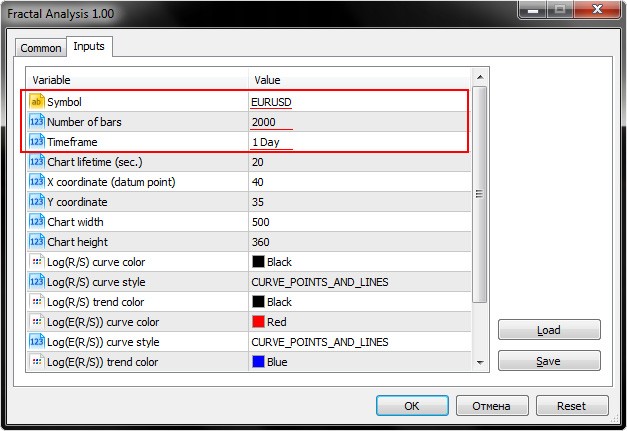
Также обратите внимание на параметр Chart lifetime, который задает количество секунд, в течение которых вы сможете работать с утилитой. В итоге после нажатия кнопки "ОК" в левом верхнем углу главного окна терминала MetaTrader 5 появится анализатор. Пример приведен на скриншоте ниже.
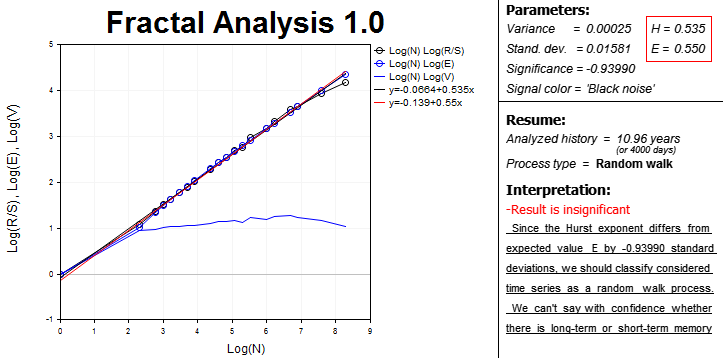
В конечном счете на экране появляются все необходимые для фрактального анализа данные и результаты, объединенные в блоки.
В левой части представлена область с графическими зависимостями в логарифмическом масштабе:
- R/S-статистики от числа наблюдений в выборке;
- ожидаемого значения R/S-статистики E(R/S) от числа наблюдений;
- V-статистики от числа наблюдений.
Это интерактивная область, которая подразумевает применение инструментария MetaTrader 5 для анализа графиков, так как иногда бывает довольно сложно отыскать длину цикла "на глаз".
Также представлены уравнения кривых и линий тренда, по наклону которых определяются числовые показатели Херста (H). Рассчитывается и ожидаемое значение показателя Херста (E). Эти уравнения находятся в соседнем правом блоке, и там же рассчитываются дисперсия и значимость анализа, цвет спектра сигнала.
Для удобства пользователя программа рассчитывает длину исследуемого периода в днях. Это необходимо понимать для оценки значимости исторических данных.
В строке Process type выводится характеристика временного ряда:
- персистентный;
- антиперсистентный;
- случайное блуждание.
И наконец, в блоке "Interpretation" выводится краткое резюме, которое будет полезно для аналитика, только еще начинающего знакомство с фрактальным анализом.
5.2. Пример работы
Определяем, какой инструмент и на каком временном интервале мы будем анализировать. Возьмем пару "новозеландский доллар и швейцарский франк" (NZDCHF) и посмотрим на последние котировки в часовом масштабе (H1).
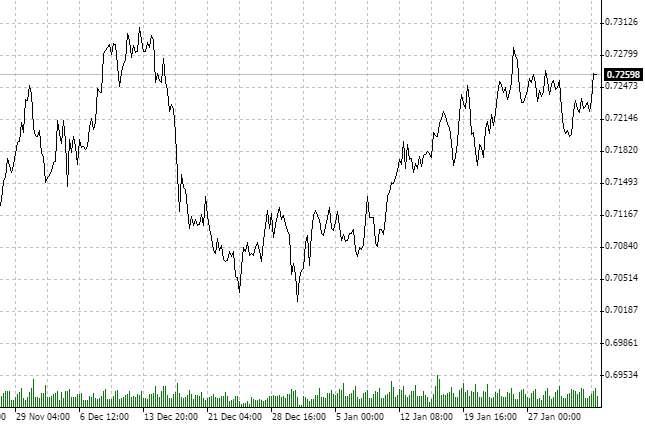
Обращаем внимание на то, что за последние приблизительно два месяца рынок находится в режиме консолидации. Опять же, нас НЕ интересуют другие инвестиционные горизонты. Вполне возможно, что график дневного таймфрейма показывал бы восходящий или нисходящий тренд. Мы выбрали 1H и определенное количество исторических данных.
Судя по всему, процесс антиперсистенттен. Давайте проверим это при помощи Fractal Analysis.
С 21.11 по 3.02 мы имеем 75-дневную историю. Переведем 75 дней в часы. Получаем 1800 часовых данных. Так как на входе утилиты нет такого количества баров, указываем ближайшее значение, то есть, 2000 анализируемых часовых периодов.
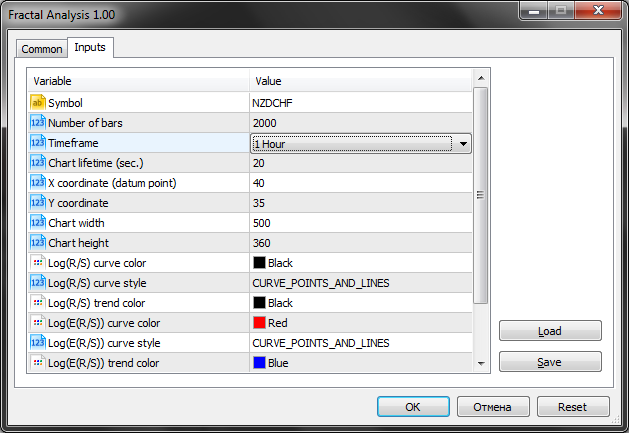
В результате получаем следующую картину:
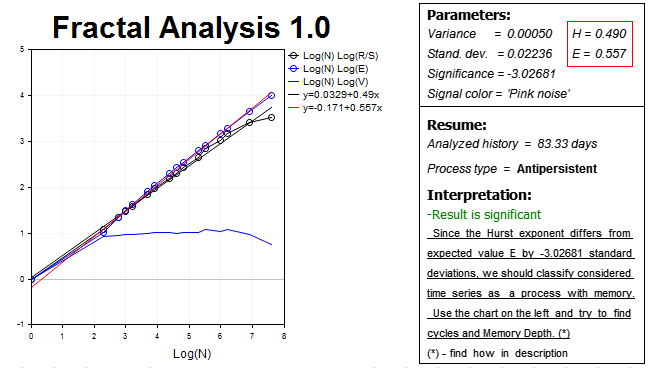
Как видите, наша гипотеза подтверждена, и рынок на этом горизонте демонстрирует антиперсистентный процесс, причем довольно значимый — значение показателя Херста H=0.490, это на практически три стандартных отклонения ниже ожидаемого значения E=0.557.
Давайте закрепим результат и возьмем чуть более старший таймфрейм, H2 и, соответственно, в два раза меньшее количество баров истории — 1000 значений. Результатом будет следующее:
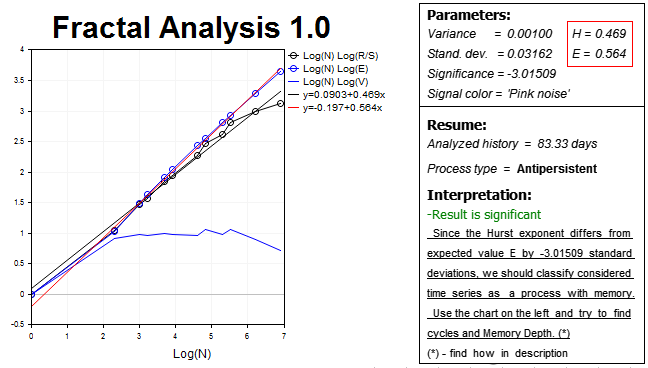
Мы снова видим антиперсистентность. Показатель Херста H=0.469, что более чем на три стандартных отклонения отстает от ожидаемого значения коэффициента E=0.564.
Теперь попытаемся найти циклы.
Вернемся к графику для H1 и попытаемся поймать момент отрыва кривой R/S от E(R/S). Этот момент характеризуется образованием вершины на графике V-статистики. Таким образом, теперь мы можем определить приблизительную величину цикла.
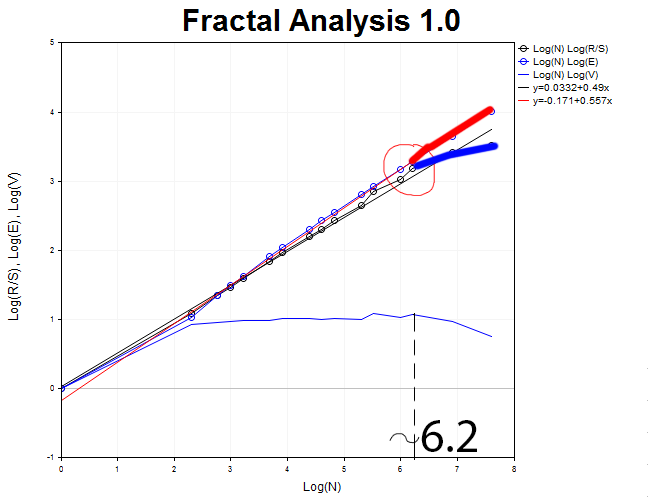
Она приблизительно равна N1 = 2.71828^6.2 = 493 часа, что эквивалентно двадцати одному дню.
Разумеется, по результатам одного эксперимента, нельзя с уверенностью говорить о достоверности результата. Как уже говорилось выше, нужно "играть" с таймфреймами и пытаться подбирать всевозможные комбинации "таймфрейм — число баров", чтобы удостовериться в истинности полученного результата.
Проведем графический анализ 1000 баров таймфрейма H2.
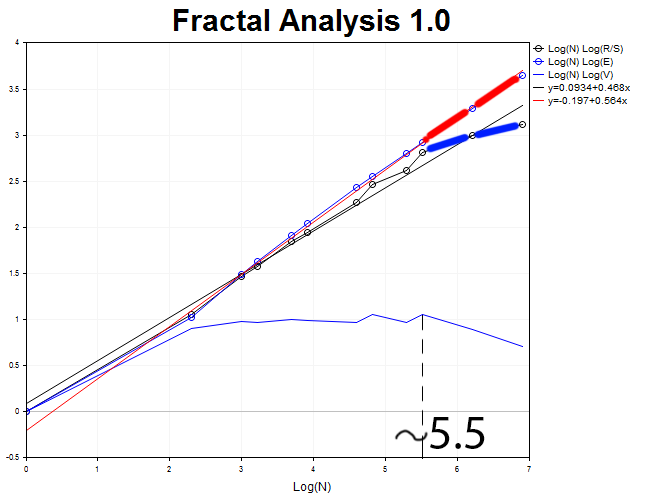
Длина цикла равна N2 = 2.71828^5.5 = 245 двухчасовых периодов, что эквивалентно приблизительно двадцати дням.
Проанализируем теперь 30-минутный таймфрейм и 4000 значений. Получаем антиперсистентный процесс с показателем Херста H = 0.492 и ожидаемым значением E=0.55, которое на целых 3,6 стандартных отклонений превосходит H.
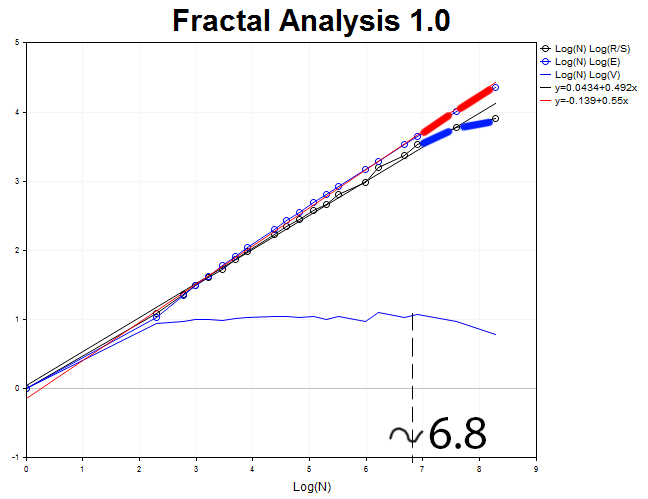
Длина цикла N3 = 2.71828^6.8 = 898 тридцатиминутных отрезков, или 18.7 дней.
Для обучающего примера будет достаточно трех испытаний. Найдем среднее значение полученных длин периода M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 или 20 дней.
В результате мы получаем период, в пределах которого техническим данным действительно можно доверять и строить на них торговую стратегию. В очередной раз повторюсь, что данный расчет и анализ приведены для инвестиционного горизонта длиной в два месяца. Это означает, что анализ теряет свою актуальность при переходе на внутридневную торговлю, так как там, вероятно, присутствуют свои сверхкраткосрочные циклические процессы, наличие или отсутствие которых нужно доказать. Если циклы не будут обнаружены, то значит, технический анализ потеряет релевантность и эффективность, и разумным решением будет перейти на новостную торговлю и "трейдинг на сентиментах" (на настроениях рынка).
Заключение
Фрактальный анализ — это некая синергия технического, фундаментального и статистического подхода к прогнозированию динамики рынка. Это универсальный способ обработки информации: R/S-анализ и показатель Херста успешно зарекомендовали себя в таких областях науки, как география, биология, физика, экономика. Фрактальный анализ можно применять для построения скоринговых или оценочных моделей, применяемых кредитными учреждениями для анализа платежеспособности заемщиков.
И в заключение повторю мысль, приведенную в начале статьи: для успешной торговли на финансовых рынках важно всегда знать чуть больше, чем другие инвесторы. Предвкушая ошибочное понимание изложенной информации, хочу предупредить читателя о том, что рынок имеет свойство "обманывать" аналитика. Поэтому всегда проверяйте наличие непериодического цикла на старших и младших таймфреймах. Если он не будет обнаруживаться на других таймфреймах — велика вероятность того, что цикл представляет собой лишь рыночный шум.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Визуализируй это! Графическая библиотека в MQL5 как аналог plot из R
Визуализируй это! Графическая библиотека в MQL5 как аналог plot из R
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
В реальной торговле применение коэф. Херста для детекции тренда работает еще хуже чем классическое пересечение машек. Причина классическая - большое запаздывание.
Однако идеи его применения все еще периодически возникают в алго-командах мат-ботанов, но чаще всего торговля заканчивается сливом, даже если в начале был случайных положительный результат. Показательным примером неуспешного применения торговли по usd на основе определения тренда по Херсту является стратегия w-surf от компании edgstone - первый год в плюс, все остальные - в минус (для просмотра реального перфоманса смотрите не рекламу на сайте компании, а погуглите w-surf + mfd).
Алексей, спасибо большое за конструктивный комментарий. Я продолжу изучение и исследование. Приму к сведению Ваше предложение.
Дмитрий,
Советую посмотреть этот фильм и почитать про этого человека.
https://forecaster-movie.com/en/the-movie/
Может быть вы будете следующим кто напишет эту программу. Свяжитесь со мной если у вас начнет получатся. Спасибо.
Уважаемый автор! За труд вам конечно спасибо, и показатель очень важный, НО... я так понимаю, что никто из отметившихся в комментах так и не пытался применять индикатор :D
Когда оказалось, что ваш индикатор не работает на малых таймфреймах, не работает с появлением новых баров (а значит его нельзя привязать к роботу и протестировать) и вычисляет отрицательные коэффициенты детерминации, я полез внутрь, чтобы это исправить и... забыл нематерные выражения приблизительно на неделю. Легкими путями вы ходить не любите. Там где нужны вещественные типы вы используете целые, вводите кучу ненужных переменных, бесполезные вычислительные этапы, оставляете кучу старых методов и отсылок, которые только путают и затрудняют понимание, много раз переворачиваете массивы данных из прямой индексации в обратную, создаете кучу ненужных объектов, передающих один и тот же набор переменных, а вместо стандартной в mql лаконичной системы учета предыдущих вычислений зачем-то придумываете свою, страшную и громоздкую...
Не проще ли было просто взять любой стандартный индикатор mql и на его основе вычислить все что вам нужно? Поверьте, разобраться в нем на порядок легче, чем в вашем коде...
Прикрепляю архив с исходниками, где все, что не работало, работает, и убрано все (или почти все) лишнее. Остается вопрос того, насколько медлительной будет эта конструкция при реальных тестах. Пока не проверял, но чувствую, придется и дальше исправлять...
Уважаемый автор! За труд вам конечно спасибо, и показатель очень важный, НО... я так понимаю, что никто из отметившихся в комментах так и не пытался применять индикатор :D
Когда оказалось, что ваш индикатор не работает на малых таймфреймах, не работает с появлением новых баров (а значит его нельзя привязать к роботу и протестировать) и вычисляет отрицательные коэффициенты детерминации, я полез внутрь, чтобы это исправить и... забыл нематерные выражения приблизительно на неделю. Легкими путями вы ходить не любите. Там где нужны вещественные типы вы используете целые, вводите кучу ненужных переменных, бесполезные вычислительные этапы, оставляете кучу старых методов и отсылок, которые только путают и затрудняют понимание, много раз переворачиваете массивы данных из прямой индексации в обратную, создаете кучу ненужных объектов, передающих один и тот же набор переменных, а вместо стандартной в mql лаконичной системы учета предыдущих вычислений зачем-то придумываете свою, страшную и громоздкую...
Не проще ли было просто взять любой стандартный индикатор mql и на его основе вычислить все что вам нужно? Поверьте, разобраться в нем на порядок легче, чем в вашем коде...
Прикрепляю архив с исходниками, где все, что не работало, работает, и убрано все (или почти все) лишнее. Остается вопрос того, насколько медлительной будет эта конструкция при реальных тестах. Пока не проверял, но чувствую, придется и дальше исправлять...
Спасибо за комментарий. Никто не говорил об оптимальности представленного кода. На момент написания статьи все проверялось и работало. Задача стояла рассказать, что концепция коэффициента Херста существует и ее можно применять. Спасибо за ваш код и желаю вам дальнейших успехов в его имплементации.
Дмитрий, добрый день!
хочу Вас тоже поблагодарить за проделанную работу и позвольте задать пару вопросов.
Исследованием фракталов занимаюсь достаточно давно, есть результаты. Первый код вычисления параметра Херста написал в 2017 в EXEL.
Сейчас меня интересует исследование некоторых хроник на МТ4 с помощью параметра Херста.
Мне будет необходимо задавать определенный интервал ( на чартах -дневных, 4х часовых и часовых), который соответствует границам циклического интервала, для того чтобы оценить персистентность последующего цикла, следующего за предыдущим. Какая есть возможность в настойках при выборе числа свечей ?
Т.е. меня будет интересовать параметр Херста только в одной точке- в границе перехода от одного цикла к другому, которые образуют фрактальную последовательность.
Обещаю Вас ознакомить с проведенным исследованием.
с уважением, Андрей