Статистические распределения в MQL5 - берем лучшее из R и делаем быстрее
Рассмотрим функции для работы с основными статистическими распределениями, реализованными в языке R.
Это распределения Коши, Вейбулла, нормальное, логнормальное, логистическое, экспоненциальное, равномерное, гамма-распределение, центральное и нецентральные распределения Бета, хи-квадрат, F-распределения Фишера, t-распределения Стьюдента, а также дискретные биномиальное и отрицательное биномиальные распределения, геометрическое, гипергеометрическое и распределение Пуассона. Кроме того, есть функции расчета теоретических моментов распределений, которые позволяют оценить степень соответствия реального распределения модельному.
Мы включили в стандартную библиотеку MQL5 большое количество математических функций из R. Причем добились их более быстрой работы от 3 до 7 раз по сравнению с исходными вариантами в языке R. Заодно обнаружили ошибки реализации некоторых функций в R.
Содержание
- Функции для расчета статистических характеристик элементов массива
- Функции для работы со статистическими распределениями
2.1. Нормальное распределение
- 2.1.1. MathProbabilityDensityNormal()
- 2.1.2. MathCumulativeDistributionNormal()
- 2.1.3. MathQuantileNormal()
- 2.1.4. MathRandomNormal()
- 2.1.5. MathMomentsNormal()
2.2. Логнормальное распределение
- 2.2.1. MathProbabilityDensityLognormal()
- 2.2.2. MathCumulativeDistributionLognormal()
- 2.2.3. MathQuantileLognormal()
- 2.2.4. MathRandomLognormal()
- 2.2.5. MathMomentsLognormal()
2.3. Бета-распределение
- 2.3.1. MathProbabilityDensityBeta()
- 2.3.2. MathCumulativeDistributionBeta()
- 2.3.3. MathQuantileBeta()
- 2.3.4. MathRandomBeta()
- 2.3.5. MathMomentsBeta()
2.4. Нецентральное бета-распределение
- 2.4.1. MathProbabilityDensityNoncentralBeta()
- 2.4.2. MathCumulativeDistributionNoncentralBeta()
- 2.4.3. MathQuantileNoncentralBeta()
- 2.4.4. MathRandomNoncentralBeta()
- 2.4.5. MathMomentsNoncentralBeta()
2.5. Гамма-распределение
- 2.5.1. MathProbabilityDensityGamma()
- 2.5.2. MathCumulativeDistributionGamma()
- 2.5.3. MathQuantileGamma()
- 2.5.4. MathRandomGamma()
- 2.5.5. MathMomentsGamma()
2.6. Распределение хи-квадрат
- 2.6.1. MathProbabilityDensityChiSquare()
- 2.6.2. MathCumulativeDistributionChiSquare()
- 2.6.3. MathQuantileChiSquare()
- 2.6.4. MathRandomChiSquare()
- 2.6.5. MathMomentsChiSquare()
2.7. Нецентральное распределение хи-квадрат
- 2.7.1. MathProbabilityDensityNoncentralChiSquare()
- 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
- 2.7.3. MathQuantileNoncentralChiSquare()
- 2.7.4. MathRandomNoncentralChiSquare()
- 2.7.5. MathMomentsNoncentralChiSquare()
2.8. Экспоненциальное распределение- 2.8.1. MathProbabilityDensityExponential()
- 2.8.2. MathCumulativeDistributionExponential()
- 2.8.3. MathQuantileExponential()
- 2.8.4. MathRandomExponential()
- 2.8.5. MathMomentsExponential()
2.9. F-распределение- 2.9.1. MathProbabilityDensityF()
- 2.9.2. MathCumulativeDistributionF()
- 2.9.3. MathQuantileF()
- 2.9.4. MathRandomF()
- 2.9.5. MathMomentsF()
2.10. Нецентральное F-распределение
- 2.10.1. MathProbabilityDensityNoncentralF()
- 2.10.2. MathCumulativeDistributionNoncentralF()
- 2.10.3. MathQuantileNoncentralF()
- 2.10.4. MathRandomNoncentralF()
- 2.10.5. MathMomentsNoncentralF()
2.11. Т-распределение
- 2.11.1. MathProbabilityDensityT()
- 2.11.2. MathCumulativeDistributionT()
- 2.11.3. MathQuantileT()
- 2.11.4. MathRandomT()
- 2.11.5. MathMomentsT()
2.12 Нецентральное T-распределение
- 2.12.1. MathProbabilityDensityNoncentralT()
- 2.12.2. MathCumulativeDistributionNoncentralT()
- 2.12.3. MathQuantileNoncentralT()
- 2.12.4. MathRandomNoncentralT()
- 2.12.5. MathMomentsNoncentralT()
2.13. Логистическое распределение
- 2.13.1. MathProbabilityDensityLogistic()
- 2.13.2. MathCumulativeDistributionLogistic()
- 2.13.3. MathQuantileLogistic()
- 2.13.4. MathRandomLogistic()
- 2.13.5. MathMomentsLogistic()
2.14. Распределение Коши
- 2.14.1. MathProbabilityDensityCauchy()
- 2.14.2. MathCumulativeDistributionCauchy()
- 2.14.3. MathQuantileCauchy()
- 2.14.4. MathRandomCauchy()
- 2.14.5. MathMomentsCauchy()
2.15. Равномерное распределение
- 2.15.1. MathProbabilityDensityUniform()
- 2.15.2. MathCumulativeDistributionUniform()
- 2.15.3. MathQuantileUniform()
- 2.15.4. MathRandomUniform()
- 2.15.5. MathMomentsUniform()
2.16. Распределение Вейбулла
- 2.16.1. MathProbabilityDensityWeibull()
- 2.16.2. MathCumulativeDistributionWeibull()
- 2.16.3. MathQuantileWeibull()
- 2.16.4. MathRandomWeibull()
- 2.16.5. MathMomentsWeibull()
2.17. Биномиальное распределение
- 2.17.1. MathProbabilityDensityBinomial()
- 2.17.2. MathCumulativeDistributionBinomial()
- 2.17.3. MathQuantileBinomial()
- 2.17.4. MathRandomBinomial()
- 2.17.5. MathMomentsBinomial()
2.18. Отрицательное биномиальное распределение
- 2.18.1. MathProbabilityDensityNegativeBinomial()
- 2.18.2. MathCumulativeDistributionNegativeBinomial()
- 2.18.3. MathQuantileNegativeBinomial()
- 2.18.4. MathRandomNegativeBinomial()
- 2.18.5. MathMomentsNegativeBinomial()
2.19. Геометрическое распределение
- 2.19.1. MathProbabilityDensityGeometric()
- 2.19.2. MathCumulativeDistributionGeometric()
- 2.19.3. MathQuantileGeometric()
- 2.19.4. MathRandomGeometric()
- 2.19.5. MathMomentsGeometric()
2.20. Гипергеометрическое распределение
- 2.20.1. MathProbabilityDensityHypergeometric()
- 2.20.2. MathCumulativeDistributionHypergeometric()
- 2.20.3. MathQuantileHypergeometric()
- 2.20.4. MathRandomHypergeometric()
- 2.20.5. MathMomentsHypergeometric()
2.21. Распределение Пуассона
- 2.21.1. MathProbabilityDensityPoisson()
- 2.21.2. MathCumulativeDistributionPoisson()
- 2.21.3. MathQuantilePoisson()
- 2.21.4. MathRandomPoisson()
- 2.21.5. MathMomentsPoisson()
- Таблицы соответствия статистическим функциям языка R
- Пример использования функций
- Сравнение скорости расчетов
- Обнаруженные ошибки расчетов в R
- Литература
Введение
Язык R — один из лучших инструментов статистической обработки и анализа данных.
Благодаря доступности и поддержке множества статистических распределений он получил широкое распространение при анализе и обработке различных данных. Использование аппарата теории вероятностей и математической статистики позволяет по-новому взглянуть на данные финансовых рынков и открывает новые возможности для создания торговых стратегий. С появлением статистической библиотеки эти возможности теперь доступны в языке MQL5.
Статистическая библиотека содержит функции для расчета статистических характеристик данных, а также функции для работы со статистическими распределениями.
В этой статье мы рассмотрим основные функции библиотеки и пример их практического использования.
1. Функции для расчета статистических характеристик элементов массива
Эта группа функций производит расчет статистических характеристик (среднее, дисперсия, коэффициент асимметрии, коэффициент эксцесса, медиана, среднеквадратичное и стандартные отклонения) элементов массива.
1.1. MathMean
Функция рассчитывает среднее значение (первый момент) элементов массива. В случае ошибки возвращает NaN (не число). Аналог mean() в R.
double MathMean( const double &array[] // [in] Массив с данными );
1.2. MathVariance
Функция рассчитывает дисперсию (второй момент) элементов массива. В случае ошибки возвращает NaN. Аналог var() в R.
double MathVariance( const double &array[] // [in] Массив с данными );
1.3. MathSkewness
Функция рассчитывает коэффициент асимметрии (третий момент) элементов массива. В случае ошибки возвращает NaN. Аналог skewness() в R (библиотека e1071).
double MathSkewness( const double &array[] // [in] Массив с данными );
1.4. MathKurtosis
Функция рассчитывает коэффициент эксцесса (четвертый момент) элементов массива. В случае ошибки возвращает NaN. Аналог kurtosis() в R (библиотека e1071).
double MathKurtosis( const double &array[] // [in] Массив с данными );
1.5. MathMoments
Функция рассчитывает первые 4 момента (среднее, дисперсия, коэффициент асимметрии, коэффициент эксцесса) элементов массива. Возвращает true, если моменты успешно рассчитаны, иначе false.
bool MathMoments( const double &array[], // [in] Массив с данными double &mean, // [out] Переменная для среднего значения (1 момент) double &variance, // [out] Переменная для дисперсии (2 момент) double &skewness, // [out] Переменная для коэффициента асимметрии (3 момент) double &kurtosis, // [out] Переменная для коэффициента эксцесса (4 момент) const int start=0, // [in] Начальный индекс для расчета const int count=WHOLE_ARRAY // [in] Количество элементов для расчета );
1.6. MathMedian
Функция рассчитывает медианное значение элементов массива. В случае ошибки возвращает NaN. Аналог median() в R.
double MathMedian( double &array[] // [in] Массив с данными );
1.7. MathStandardDeviation
Функция рассчитывает стандартное отклонение элементов массива. В случае ошибки возвращает NaN. Аналог sd() в R.
double MathStandardDeviation( const double &array[] // [in] Массив с данными );
1.8. MathAverageDeviation
Функция рассчитывает среднее отклонение элементов массива. В случае ошибки возвращает NaN. Аналог aad() в R.
double MathAverageDeviation( const double &array[] // [in] Массив с данными );
Во всех функциях, в которых производится расчет коэффициента эксцесса, используется коэффициент эксцесса относительно нормального распределения (excess kurtosis=kurtosis-3), т.е. коэффициент эксцесса нормального распределения равен нулю.
Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если вершина гладкая.
2. Статистические распределения
Для работы со статистическими распределениями в статистической библиотеке языка MQL5 есть 5 функций:
- Расчет плотности распределения (функции MathProbabilityDensityX());
- Расчет вероятностей (функции MathCumulativeDistributionX());
Функция распределения вероятностей равна вероятности попадания случайной величины в интервал (-inf; x]). - Расчет квантилей распределений (функции MathQuantileX());
Квантиль x распределения соответствует попаданию случайной величины в интервал (-inf, x] с вероятностью probability при заданных параметрах распределения. - Генерация случайных чисел с заданным распределением (функции MathRandomX());
- Расчет теоретических моментов распределений (функции MathMomentsX());
2.1. Нормальное распределение
2.1.1. MathProbabilityDensityNormal
Функция рассчитывает значение функции плотности вероятности нормального распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.double MathProbabilityDensityNormal( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean (математическое ожидание) const double sigma, // [in] Параметр распределения sigma (среднеквадратическое отклонение) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нормального распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNormal( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean (математическое ожидание) const double sigma, // [in] Параметр распределения sigma (среднеквадратическое отклонение) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значения функции плотности вероятности нормального распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dnorm() в R.
bool MathProbabilityDensityNormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean (математическое ожидание) const double sigma, // [in] Параметр распределения sigma (среднеквадратическое отклонение) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значения функции плотности вероятности нормального распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityNormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean (математическое ожидание) const double sigma, // [in] Параметр распределения sigma (среднеквадратическое отклонение) double &result[] // [out] Массив для значений функции плотности вероятности );
2.1.2. MathCumulativeDistributionNormal
Функция рассчитывает значение функции нормального распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Значение случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции нормального распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNormal( const double x, // [in] Значение случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение int &error_code // [out] Переменная для кода ошибки );Функция рассчитывает значение функции нормального распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pnorm() в R.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции нормального распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionNormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение double &result[] // [out] Массив для значений функции вероятности );
2.1.3. MathQuantileNormal
Для вероятности probability функция рассчитывает значение обратной функции нормального распределения с параметрами mu и sigma. В случае ошибки возвращает NaN.
double MathQuantileNormal( const double probability, // [in] Значение вероятности случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции нормального распределения с параметрами mu и sigma. В случае ошибки возвращает NaN.
double MathQuantileNormal( const double probability, // [in] Значение вероятности случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение int &error_code // [out] Переменная для кода ошибки );Для массива значений вероятности probability[] функция рассчитывает значения обратной функции нормального распределения с параметрами mu и sigma. В случае ошибки возвращает false. Аналог qnorm() в R.
bool MathQuantileNormal( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значения обратной функции нормального распределения с параметрами mu и sigma. В случае ошибки возвращает false.
bool MathQuantileNormal( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение double &result[] // [out] Массив со значениями квантилей );
2.1.4. MathRandomNormal
Функция генерирует псевдослучайную величину, распределенную по нормальному закону с параметрами mu и sigmа. В случае ошибки возвращает NaN.
double MathRandomNormal( const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по нормальному закону с параметрами mu и sigmа. В случае ошибки возвращает false. Аналог rnorm() в R.
bool MathRandomNormal( const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.1.5. MathMomentsNormal
Функция рассчитывает теоретические численные значения первых 4 моментов нормального распределения. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsNormal( const double mu, // [in] Математическое ожидание const double sigma, // [in] Среднеквадратическое отклонение double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.2. Логнормальное распределение
2.2.1. MathProbabilityDensityLognormal
Функция рассчитывает значение функции плотности вероятности логнормального распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Значение случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности логнормального распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityLognormal( const double x, // [in] Значение случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности логнормального распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает NaN. Аналог dlnorm() в R.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности логнормального распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityLognormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) double &result[] // [out] Массив для значений функции плотности вероятности );
2.2.2. MathCumulativeDistributionLognormal
Функция рассчитывает значение функции логнормального распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Значение случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции логнормального распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionLognormal( const double x, // [in] Значение случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции логнормального распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог plnorm() в R.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции логнормального распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionLognormal( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) double &result[] // [out] Массив для значений функции вероятности );
2.2.3. MathQuantileLognormal
Функция рассчитывает значение обратной функции логнормального распределения с параметрами mu и sigma для вероятности probability. В случае ошибки возвращает NaN.
double MathQuantileLognormal( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение обратной функции логнормального распределения с параметрами mu и sigma для вероятности probability. В случае ошибки возвращает NaN.
double MathQuantileLognormal( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значения обратной функции логнормального распределения с параметрами mu и sigma. В случае ошибки возвращает false. Аналог qlnorm() в R.
bool MathQuantileLognormal( const double &probability[], // [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значения обратной функции логнормального распределения с параметрами mu и sigma. В случае ошибки возвращает false.
bool MathQuantileLognormal( const double &probability[], // [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) double &result[] // [out] Массив со значениями квантилей );
2.2.4. MathRandomLognormal
Функция генерирует псевдослучайную величину, распределенную по логнормальному закону с параметрами mu и sigmа. В случае ошибки возвращает NaN.
double MathRandomLognormal( const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по логнормальному закону с параметрами mu и sigmа. В случае ошибки возвращает false. Аналог rlnorm() в R.
bool MathRandomLognormal( const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.2.5. MathMomentsLognormal
Функция рассчитывает теоретические численные значения первых 4 моментов логнормального распределения. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsLognormal( const double mu, // [in] Логарифм математического ожидания (log mean) const double sigma, // [in] Логарифм среднеквадратического отклонения (log standard deviation) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.3. Бета-распределение
2.3.1. MathProbabilityDensityBeta
Функция рассчитывает значение функции плотности вероятности бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dbeta() в R.
bool MathProbabilityDensityBeta( const double &x[], // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityBeta( const double &x[], // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) double &result[] // [out] Массив для значений функции плотности вероятности );
2.3.2. MathCumulativeDistributionlBeta
Функция рассчитывает значение функции распределения вероятностей бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool tail, // [in] Флаг расчета, если lower_tail=true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pbeta() в R.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) double &result[] // [out] Массив для значений функции вероятности );
2.3.3. MathQuantileBeta
Для вероятности probability функция рассчитывает значение обратной функции бета-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileBeta( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции бета-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileBeta( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значения обратной функции бета-распределения с параметрами a и b. В случае ошибки возвращает false. Аналог qbeta() в R.
bool MathQuantileBeta( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значения обратной функции бета-распределения с параметрами a и b. В случае ошибки возвращает false.
bool MathQuantileBeta( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) double &result[] // [out] Массив со значениями квантилей );
2.3.4. MathRandomBeta
Функция генерирует псевдослучайную величину, распределенную по закону бета-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathRandomBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону бета-распределения с параметрами a и b. В случае ошибки возвращает false. Аналог rbeta() в R.
bool MathRandomBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.3.5. MathMomentsBeta
Функция рассчитывает теоретические численные значения первых 4 моментов бета-распределения. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.4. Нецентральное бета-распределение
2.4.1. MathProbabilityDensityNoncentralBeta
Функция рассчитывает значение функции плотности вероятности нецентрального бета-распределения с параметрами a, b и lambda для случайной величины x. В случае ошибки возвращает NaN.double MathProbabilityDensityNoncentralBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального бета-распределения с параметрами a, b и lambda для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального бета-распределения с параметрами a, b и lambda для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dbeta() в R.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности нецентрального бета-распределения с параметрами a, b и lambda для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityNoncentralBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции плотности вероятности );
2.4.2. MathCumulativeDistributionNoncentralBeta
Функция рассчитывает значение функции распределения вероятностей нецентрального бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального бета-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralBeta( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pbeta() в R.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей нецентрального бета-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionNoncentralBeta( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции вероятности );
2.4.3. MathQuantileNoncentralBeta
Функция рассчитывает значение обратной функции распределения вероятностей нецентрального бета-распределения с параметрами a, b и lambda для вероятности появления значения случайной величины probability. В случае ошибки возвращает NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение обратной функции распределения вероятностей нецентрального бета-распределения с параметрами a, b и lambda для вероятности появления значения случайной величины probability. В случае ошибки возвращает NaN.
double MathQuantileNoncentralBeta( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей нецентрального бета-распределения с параметрами a, b и lambda. В случае ошибки возвращает false. Аналог qbeta() в R.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей нецентрального бета-распределения с параметрами a, b и lambda. В случае ошибки возвращает false.
bool MathQuantileNoncentralBeta( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности double &result[] // [out] Массив со значениями квантилей );
2.4.4. MathRandomNoncentralBeta
Функция генерирует псевдослучайную величину, распределенную по закону нецентрального бета-распределения с параметрами a, b и lambda. В случае ошибки возвращает NaN.
double MathRandomNoncentralBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону нецентрального бета-распределения с параметрами a, b и lambda. В случае ошибки возвращает false. Аналог rbeta() в R.
bool MathRandomNoncentralBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.4.5. MathMomentsNoncentralBeta
Функция рассчитывает теоретические численные значения первых 4 моментов нецентрального бета-распределения с параметрами a, b и lambda. Возвращает true, если расчет моментов произведен успешно, иначе false.
double MathMomentsNoncentralBeta( const double a, // [in] Первый параметр бета-распределения (shape1) const double b, // [in] Второй параметр бета-распределения (shape2) const double lambda, // [in] Параметр нецентральности double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.5. Гамма-распределение
2.5.1. MathProbabilityDensityGamma
Функция рассчитывает значение функции плотности вероятности гамма-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.double MathProbabilityDensityGamma( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности гамма-распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityGamma( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности гамма-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dgamma() в R.
bool MathProbabilityDensityGamma( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности гамма-распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityGamma( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) double &result[] // [out] Массив для значений функции плотности вероятности );
2.5.2. MathCumulativeDistributionGamma
Функция рассчитывает значение функции гамма-распределения вероятностей с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции гамма-распределения вероятностей с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionGamma( const double x, // [in] Значение случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции гамма-распределения вероятностей с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pgamma() в R.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции гамма-распределения вероятностей с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionGamma( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) double &result[] // [out] Массив для значений функции вероятности );
2.5.3. MathQuantileGamma
Для вероятности probability функция рассчитывает значение обратной функции гамма-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileGamma( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции гамма-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileGamma( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции гамма-распределения с параметрами a и b. В случае ошибки возвращает false. Аналог qgamma() в R.
bool MathQuantileGamma( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции гамма-распределения с параметрами a и b. В случае ошибки возвращает false.
bool MathQuantileGamma( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) double &result[] // [out] Массив со значениями квантилей );
2.5.4. MathRandomGamma
Функция генерирует псевдослучайную величину, распределенную по закону гамма-распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathRandomGamma( const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону гамма-распределения с параметрами a и b. В случае ошибки возвращает false. Аналог rgamma() в R.
bool MathRandomGamma( const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.5.5. MathMomentsGamma
Функция рассчитывает теоретические численные значения первых 4 моментов гамма-распределения с параметрами a и b. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsGamma( const double a, // [in] Первый параметр распределения (shape) const double b, // [in] Второй параметр распределения (scale) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.6. Распределение хи-квадрат
2.6.1. MathProbabilityDensityChiSquare
Функция рассчитывает значение функции плотности вероятности распределения хи-квадрат с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );Функция рассчитывает значение функции плотности вероятности распределения хи-квадрат с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности распределения хи-квадрат с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dchisq() в R.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности распределения хи-квадрат с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции плотности вероятности );
2.6.2. MathCumulativeDistributionChiSquare
Функция рассчитывает значение функции распределения вероятностей хи-квадрат с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей хи-квадрат с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей хи-квадрат с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pchisq() в R.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей хи-квадрат с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции вероятности );
2.6.3. MathQuantileChiSquare
Для вероятности probability функция рассчитывает значение обратной функции распределения вероятностей хи-квадрат. В случае ошибки возвращает NaN.
double MathQuantileChiSquare( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции распределения вероятностей хи-квадрат. В случае ошибки возвращает NaN.
double MathQuantileChiSquare( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей хи-квадрат. В случае ошибки возвращает false. Аналог qchisq() в R.
bool MathQuantileChiSquare( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей хи-квадрат. В случае ошибки возвращает false.
bool MathQuantileChiSquare( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив со значениями квантилей );
2.6.4. MathRandomChiSquare
Функция генерирует псевдослучайную величину, распределенную по закону распределения хи-квадрат с параметром nu. В случае ошибки возвращает NaN.
double MathRandomChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону распределения хи-квадрат с параметром nu. В случае ошибки возвращает false. Аналог rchisq() в R.
bool MathRandomChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.6.5. MathMomentsChiSquare
Функция рассчитывает теоретические численные значения первых 4 моментов распределения хи-квадрат с параметром nu. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.7. Нецентральное распределение хи-квадрат
2.7.1. MathProbabilityDensityNoncentralChiSquare
Функция рассчитывает значение функции плотности вероятности нецентрального распределения хи-квадрат с параметрами nu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального распределения хи-квадрат с параметрами nu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального распределения хи-квадрат с параметрами nu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dchisq() в R.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности нецентрального распределения хи-квадрат с параметрами nu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции плотности вероятности );
2.7.2. MathCumulativeDistributionNoncentralChiSquare
Функция рассчитывает значение функции распределения вероятностей нецентрального распределения хи-квадрат с параметрами nu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального распределения хи-квадрат с параметрами nu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralChiSquare( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального распределения хи-квадрат с параметрами nu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pchisq() в R.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей нецентрального распределения хи-квадрат с параметрами nu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции вероятности );
2.7.3. MathQuantileNoncentralChiSquare
Для вероятности probability функция рассчитывает значение обратной функции нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает NaN.
double MathQuantileNoncentralChiSquare( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает false. Аналог qchisq() в R.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает false.
bool MathQuantileNoncentralChiSquare( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив со значениями квантилей );
2.7.4. MathRandomNoncentralChiSquare
Функция генерирует псевдослучайную величину, распределенную по закону нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает NaN.
double MathRandomNoncentralChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону нецентрального распределения хи-квадрат с параметрами nu и sigma. В случае ошибки возвращает false. Аналог rchisq() в R.
bool MathRandomNoncentralChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.7.5. MathMomentsNoncentralChiSquare
Функция рассчитывает теоретические численные значения первых 4 моментов нецентрального распределения хи-квадрат с параметрами nu и sigma. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsNoncentralChiSquare( const double nu, // [in] Параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.8. Экспоненциальное распределение
2.8.1. MathProbabilityDensityExponential
Функция рассчитывает значение функции плотности вероятности экспоненциального распределения с параметром mu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityExponential( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности экспоненциального распределения с параметром mu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityExponential( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности экспоненциального распределения с параметром mu для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dexp() в R.
bool MathProbabilityDensityExponential( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности экспоненциального распределения с параметром mu для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityExponential( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) double &result[] // [out] Массив для значений функции плотности вероятности );
2.8.2. MathCumulativeDistributionExponential
Функция рассчитывает значение функции экспоненциального распределения вероятностей с параметром mu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции экспоненциального распределения вероятностей с параметром mu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionExponential( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции экспоненциального распределения вероятностей с параметром mu для случайной величины x. В случае ошибки возвращает false. Аналог pexp() в R.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции экспоненциального распределения вероятностей с параметром mu для случайной величины x. В случае ошибки возвращает false.
bool MathCumulativeDistributionExponential( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) double &result[] // [out] Массив для значений функции вероятности );
2.8.3. MathQuantileExponential
Для вероятности probability функция рассчитывает значение обратной функции экспоненциального распределения вероятностей с параметром mu. В случае ошибки возвращает NaN.
double MathQuantileExponential( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции экспоненциального распределения вероятностей с параметром mu. В случае ошибки возвращает NaN.
double MathQuantileExponential( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции экспоненциального распределения вероятностей с параметром mu. В случае ошибки возвращает false. Аналог qexp() в R.
bool MathQuantileExponential( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции экспоненциального распределения вероятностей с параметром mu. В случае ошибки возвращает false.
bool MathQuantileExponential( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Параметр распределения (математическое ожидание) double &result[] // [out] Массив со значениями квантилей );
2.8.4. MathRandomExponential
Функция генерирует псевдослучайную величину, распределенную по закону экспоненциального распределения с параметром mu. В случае ошибки возвращает NaN.
double MathRandomExponential( const double mu, // [in] Параметр распределения (математическое ожидание) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону экспоненциального распределения с параметром mu. В случае ошибки возвращает false. Аналог rexp() в R.
bool MathRandomExponential( const double mu, // [in] Параметр распределения (математическое ожидание) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.8.5. MathMomentsExponential
Функция рассчитывает теоретические численные значения первых 4 моментов экспоненциального распределения с параметром mu. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsExponential( const double mu, // [in] Параметр распределения (математическое ожидание) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.9. F-распределение
2.9.1. MathProbabilityDensityF
Функция рассчитывает значение функции плотности вероятности F-распределения Фишера с параметрами nu1 и nu2 для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности F-распределения Фишера с параметрами nu1 и nu2 для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности F-распределения Фишера с параметрами nu1 и nu2 для массива случайных величин x[]. В случае ошибки возвращает false. Аналог df() в R.
bool MathProbabilityDensityF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности F-распределения Фишера с параметрами nu1 и nu2 для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции плотности вероятности );
2.9.2. MathCumulativeDistributionF
Функция рассчитывает значение функции распределения вероятностей по закону F-распределения Фишера с параметрами nu1 и nu2 для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей по закону F-распределения Фишера с параметрами nu1 и nu2 для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей по закону F-распределения Фишера с параметрами nu1 и nu2 для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pf() в R.
bool MathCumulativeDistributionF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей по закону F-распределения Фишера с параметрами nu1 и nu2 для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции вероятности );
2.9.3. MathQuantileF
Для вероятности probability функция рассчитывает значение обратной функции F-распределения вероятностей с параметрами nu1 и nu2. В случае ошибки возвращает NaN.
double MathQuantileF( const double probability, // [in] Значение вероятности появления случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции F-распределения вероятностей с параметрами nu1 и nu2. В случае ошибки возвращает NaN.
double MathQuantileF( const double probability, // [in] Значение вероятности появления случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции F-распределения вероятностей с параметрами nu1 и nu2. В случае ошибки возвращает false. Аналог qf() в R.
bool MathQuantileF( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для вероятности probability функция рассчитывает значение обратной функции F-распределения вероятностей с параметрами nu1 и nu2. В случае ошибки возвращает false.
bool MathQuantileF( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) double &result[] // [out] Массив со значениями квантилей );
2.9.4. MathRandomF
Функция генерирует псевдослучайную величину, распределенную по закону F-распределения Фишера с параметрами nu1 и nu2. В случае ошибки возвращает NaN.
double MathRandomF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону F-распределения Фишера с параметрами nu1 и nu2. В случае ошибки возвращает false. Аналог rf() в R.
bool MathRandomF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.9.5. MathMomentsF
Функция рассчитывает теоретические численные значения первых 4 моментов F-распределения Фишера с параметрами nu1 и nu2. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.10. Нецентральное F- распределение
2.10.1. MathProbabilityDensityNoncentralF
Функция рассчитывает значение функции плотности вероятности нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог df() в R.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
double MathProbabilityDensityNoncentralF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции плотности вероятности );
2.10.2. MathCumulativeDistributionlNoncentralF
Функция рассчитывает значение функции распределения вероятностей нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralF( const double x, // [in] Значение случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает false. Аналог pf() в R.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma для случайной величины x. В случае ошибки возвращает NaN.
bool MathCumulativeDistributionNoncentralF( const double &x[], // [in] Массив со значениями случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции вероятности );
2.10.3. MathQuantileNoncentralF
Для вероятности probability функция рассчитывает значение обратной функции нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает NaN.
double MathQuantileNoncentralF( const double probability, // [in] Значение вероятности появления случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает NaN.
double MathQuantileNoncentralF( const double probability, // [in] Значение вероятности появления случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает false. Аналог qf() в R.
bool MathQuantileNoncentralF( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для вероятности probability функция рассчитывает значение обратной функции нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает false.
bool MathQuantileNoncentralF( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив со значениями квантилей );
2.10.4. MathRandomNoncentralF
Функция генерирует псевдослучайную величину, распределенную по закону нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает NaN.
double MathRandomNoncentralF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. В случае ошибки возвращает false. Аналог rf() в R.
bool MathRandomNoncentralF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &result[] // [out] Массив со значениями квантилей );
2.10.5. MathMomentsNoncentralF
Функция рассчитывает теоретические численные значения первых 4 моментов нецентрального F-распределения Фишера с параметрами nu1, nu2 и sigma. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsNoncentralF( const double nu1, // [in] Первый параметр распределения (число степеней свободы) const double nu2, // [in] Второй параметр распределения (число степеней свободы) const double sigma, // [in] Параметр нецентральности double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки )
2.11. Распределение T
2.11.1. MathProbabilityDensityT
Функция рассчитывает значение функции плотности вероятности T-распределения Стьюдента с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности T-распределения Стьюдента с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности T-распределения Стьюдента с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dt() в R.
bool MathProbabilityDensityT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности T-распределения Стьюдента с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции плотности вероятности );
2.11.2. MathCumulativeDistributionT
Функция рассчитывает значение функции распределения Стьюдента с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Стьюдента с параметром nu для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Стьюдента с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pt() в R.
bool MathCumulativeDistributionT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения Стьюдента с параметром nu для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив для значений функции вероятности );
2.11.3. MathQuantileT
Для вероятности probability функция рассчитывает значение обратной функции T-распределения Стьюдента с параметром nu. В случае ошибки возвращает NaN.
double MathQuantileT( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции T-распределения Стьюдента с параметром nu. В случае ошибки возвращает NaN.
double MathQuantileT( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции T-распределения Стьюдента с параметром nu. В случае ошибки возвращает false. Аналог qt() в R.
bool MathQuantileT( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции T-распределения Стьюдента с параметром nu. В случае ошибки возвращает false.
bool MathQuantileT( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) double &result[] // [out] Массив со значениями квантилей );
2.11.4. MathRandomT
Функция генерирует псевдослучайную величину, распределенную по закону T-распределения Стьюдента с параметром nu. В случае ошибки возвращает NaN.
double MathRandomT( const double nu, // [in] Параметр распределения (число степеней свободы) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону T-распределения Стьюдента с параметром nu. В случае ошибки возвращает false. Аналог rt() в R.
bool MathRandomT( const double nu, // [in] Параметр распределения (число степеней свободы) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.11.5. MathMomentsT
Функция рассчитывает теоретические численные значения первых 4 моментов T-распределения Стьюдента с параметром nu. Возвращает true, если расчет моментов произведен успешно, иначе false.
double MathMomentsT( const double nu, // [in] Параметр распределения (число степеней свободы) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.12. Нецентральное T-распределение
2.12.1. MathProbabilityDensityNoncentralT
Функция рассчитывает значение плотности вероятности нецентрального T-распределения Стьюдента с параметрами nu и delta для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального T-распределения Стьюдента с параметрами nu и delta для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNoncentralT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности нецентрального T-распределения Стьюдента с параметрами nu и delta для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dt() в R.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности нецентрального T-распределения Стьюдента с параметрами nu и delta для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityNoncentralT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции плотности вероятности );
2.12.2. MathCumulativeDistributionlNoncentralT
Функция рассчитывает значение функции распределения вероятностей нецентрального T-распределения с параметрами nu и delta для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального T-распределения с параметрами nu и delta для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNoncentralT( const double x, // [in] Значение случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей нецентрального T-распределения с параметрами nu и delta для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pt() в R.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения вероятностей нецентрального T-распределения с параметрами nu и delta для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionNoncentralT( const double &x[], // [in] Массив со значениями случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности double &result[] // [out] Массив для значений функции вероятности );
2.12.3. MathQuantileNoncentralT
Для вероятности probability функция рассчитывает значение обратной функции нецентрального T-распределения с параметрами nu и delta. В случае ошибки возвращает NaN.
double MathQuantileNoncentralT( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции нецентрального T-распределения с параметрами nu и delta. В случае ошибки возвращает NaN.
double MathQuantileNoncentralT( const double probability, // [in] Значение вероятности появления случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции нецентрального T-распределения с параметрами nu и delta. В случае ошибки возвращает false. Аналог qt() в R.
bool MathQuantileNoncentralT( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции нецентрального T-распределения с параметрами nu и delta. В случае ошибки возвращает false.
bool MathQuantileNoncentralT( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности double &result[] // [out] Массив со значениями квантилей );
2.12.4. MathRandomNoncentralT
Функция генерирует псевдослучайную величину, распределенную по закону нецентрального T-распределения Стьюдента с параметрами nu и delta. В случае ошибки возвращает NaN.
double MathRandomNoncentralT( const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону нецентрального T-распределения Стьюдента с параметрами nu и delta. В случае ошибки возвращает false. Аналог rt() в R.
bool MathRandomNoncentralT( const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.12.5. MathMomentsNoncentralT
Функция рассчитывает теоретические численные значения первых 4 моментов нецентрального T-распределения Стьюдента с параметрами nu и delta. Возвращает true, если расчет моментов произведен успешно, иначе false.
double MathMomentsNoncentralT( const double nu, // [in] Параметр распределения (число степеней свободы) const double delta, // [in] Параметр нецентральности double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.13. Логистическое распределение
2.13.1. MathProbabilityDensityLogistic
Функция рассчитывает значение функции плотности вероятности логистического распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности логистического распределения с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityLogistic( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности логистического распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dlogis() в R.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности логистического распределения с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityLogistic( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale double &result[] // [out] Массив для значений функции плотности вероятности );
2.13.2. MathCumulativeDistributionlLogistic
Функция рассчитывает значение функции логистического распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции логистического распределения вероятностей с параметрами mu и sigma для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionLogistic( const double x, // [in] Значение случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции логистического распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог plogis() в R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции логистического распределения вероятностей с параметрами mu и sigma для массива случайных величин x[]. В случае ошибки возвращает false. Аналог plogis() в R.
bool MathCumulativeDistributionLogistic( const double &x[], // [in] Массив со значениями случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale double &result[] // [out] Массив для значений функции вероятности );
2.13.3. MathQuantileLogistic
Для вероятности probability функция рассчитывает значение обратной функции логистического распределения с параметрами mu и sigma. В случае ошибки возвращает NaN.
double MathQuantileLogistic( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции логистического распределения с параметрами mu и sigma. В случае ошибки возвращает NaN.
double MathQuantileLogistic( const double probability, // [in] Значение вероятности появления случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции логистического распределения с параметрами mu и sigma. В случае ошибки возвращает false. Аналог qlogis() в R.
bool MathQuantileLogistic( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции логистического распределения с параметрами mu и sigma. В случае ошибки возвращает false.
bool MathQuantileLogistic( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale double &result[] // [out] Массив со значениями квантилей );
2.13.4. MathRandomLogistic
Функция генерирует псевдослучайную величину, распределенную по закону логистического распределения с параметрами mu и sigma. В случае ошибки возвращает NaN.
double MathRandomLogistic( const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону логистического распределения с параметрами mu и sigma. В случае ошибки возвращает false. Аналог rlogis() в R.
bool MathRandomLogistic( const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.13.5. MathMomentsLogistic
Функция рассчитывает теоретические численные значения первых 4 моментов логистического распределения с параметрами mu и sigma. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsLogistic( const double mu, // [in] Параметр распределения mean const double sigma, // [in] Параметр распределения scale double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.14. Распределение Коши
2.14.1. MathProbabilityDensityCauchy
Функция рассчитывает значение функции плотности вероятности распределения Коши с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности распределения Коши с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityCauchy( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности распределения Коши с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dcauchy() в R.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности распределения Коши с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityCauchy( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale double &result[] // [out] Массив для значений функции плотности вероятности );
2.14.2. MathCumulativeDistributionCauchy
Функция рассчитывает значение функции распределения вероятностей Коши с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей Коши с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionCauchy( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения вероятностей Коши с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pcauchy() в R.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции распределения вероятностей Коши с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionCauchy( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale double &result[] // [out] Массив для значений функции плотности вероятности );
2.14.3. MathQuantileCauchy
Для вероятности probability функция рассчитывает значение обратной функции распределения Коши с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileCauchy( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции распределения Коши с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileCauchy( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения Коши с параметрами a и b. В случае ошибки возвращает false. Аналог qcauchy() в R.
bool MathQuantileCauchy( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения Коши с параметрами a и b. В случае ошибки возвращает false.
bool MathQuantileCauchy( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale double &result[] // [out] Массив со значениями квантилей );
2.14.4. MathRandomCauchy
Функция генерирует псевдослучайную величину, распределенную по закону распределения Коши с параметрами a и b. В случае ошибки возвращает NaN.
double MathRandomCauchy( const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону распределения Коши с параметрами a и b. В случае ошибки возвращает false. Аналог rcauchy() в R.
double MathRandomCauchy( const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.14.5. MathMomentsCauchy
Функция рассчитывает теоретические численные значения первых 4 моментов распределения Коши. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsCauchy( const double a, // [in] Параметр распределения mean const double b, // [in] Параметр распределения scale double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.15. Равномерное распределение
2.15.1. MathProbabilityDensityUniform
Функция рассчитывает значение функции плотности вероятности равномерного распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityUniform( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности равномерного распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityUniform( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности равномерного распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dunif() в R.
bool MathProbabilityDensityUniform( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности равномерного распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityUniform( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) double &result[] // [out] Массив для значений функции плотности вероятности );
2.15.2. MathCumulativeDistributionUniform
Функция рассчитывает значение функции равномерного распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.double MathCumulativeDistributionUniform( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции равномерного распределения с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionUniform( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции равномерного распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог punif() в R.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции равномерного распределения с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionUniform( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) double &result[] // [out] Массив для значений функции плотности вероятности );
2.15.3. MathQuantileUniform
Для вероятности probability функция рассчитывает значение обратной функции равномерного распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileUniform( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции равномерного распределения с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileUniform( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции равномерного распределения с параметрами a и b. В случае ошибки возвращает false. Аналог qunif() в R.
bool MathQuantileUniform( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции равномерного распределения с параметрами a и b. В случае ошибки возвращает false.
bool MathQuantileUniform( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) double &result[] // [out] Массив со значениями квантилей );
2.15.4. MathRandomUniform
Функция генерирует псевдослучайную величину, распределенную по закону равномерного распределения, с параметрами a и b. В случае ошибки возвращает NaN.
double MathRandomUniform( const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону равномерного распределения, с параметрами a и b. В случае ошибки возвращает false. Аналог runif() в R.
bool MathRandomUniform( const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.15.5. MathMomentsUniform
Функция рассчитывает теоретические численные значения первых 4 моментов для равномерного распределения. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsUniform( const double a, // [in] Параметр распределения a (нижняя граница) const double b, // [in] Параметр распределения b (верхняя граница) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.16. Распределение Вейбулла
2.16.1. MathProbabilityDensityWeibull
Функция рассчитывает значение функции плотности вероятности распределения Вейбулла с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности распределения Вейбулла с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityWeibull( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции плотности вероятности распределения Вейбулла с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dweibull() в R.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции плотности вероятности распределения Вейбулла с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityWeibull( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) double &result[] // [out] Массив для значений функции плотности вероятности );
2.16.2. MathCumulativeDistributionWeibull
Функция рассчитывает значение функции распределения Вейбулла с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.double MathCumulativeDistributionWeibull( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Вейбулла с параметрами a и b для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionWeibull( const double x, // [in] Значение случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Вейбулла с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pweibull() в R.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции распределения Вейбулла с параметрами a и b для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionWeibull( const double &x[], // [in] Массив со значениями случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) double &result[] // [out] Массив для значений функции плотности вероятности );
2.16.3. MathQuantileWeibull
Для вероятности probability функция рассчитывает значение обратной функции распределения вероятностей Вейбулла с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileWeibull( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает значение обратной функции распределения вероятностей Вейбулла с параметрами a и b. В случае ошибки возвращает NaN.
double MathQuantileWeibull( const double probability, // [in] Значение вероятности появления случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей Вейбулла с параметрами a и b. В случае ошибки возвращает false. Аналог qweibull() в R.
bool MathQuantileWeibull( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает значение обратной функции распределения вероятностей Вейбулла с параметрами a и b. В случае ошибки возвращает false.
bool MathQuantileWeibull( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) double &result[] // [out] Массив со значениями квантилей );
2.16.4. MathRandomWeibull
Функция генерирует псевдослучайную величину, распределенную по закону распределения Вейбулла с параметрами a и b. В случае ошибки возвращает NaN.
double MathRandomWeibull( const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону распределения Вейбулла с параметрами a и b. В случае ошибки возвращает false. Аналог rweibull() в R.
bool MathRandomWeibull( const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.16.5. MathMomentsWeibull
Функция рассчитывает теоретические численные значения первых 4 моментов распределения Вейбулла. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsWeibull( const double a, // [in] Параметр распределения (shape) const double b, // [in] Параметр распределения (scale) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.17. Биномиальное распределение
2.17.1. MathProbabilityDensityBinomial
Функция рассчитывает значение функции вероятности (probability mass function) биномиального распределения с параметрами n и p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) биномиального распределения с параметрами n и p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) биномиального распределения с параметрами n и p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dbinom() в R.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Массив со значениями случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции вероятности (probability mass function) биномиального распределения с параметрами n и p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityBinomial( const double &x[], // [in] Массив со значениями случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) double &result[] // [out] Массив для значений функции плотности вероятности );
2.17.2. MathCumulativeDistributionBinomial
Функция рассчитывает значение функции распределения для биномиального закона с параметрами n и p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для биномиального закона с параметрами n и p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для биномиального закона с параметрами n и p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pbinom() в R.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Массив со значениями случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции распределения для биномиального закона с параметрами n и p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionBinomial( const double &x[], // [in] Массив со значениями случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) double &result[] // [out] Массив для значений функции плотности вероятности );
2.17.3. MathQuantileBinomial
Для вероятности probability функция рассчитывает обратное значение функции распределения для биномиального закона с параметрами n и p. В случае ошибки возвращает NaN.
double MathQuantileBinomial( const double probability, // [in] Значение вероятности появления случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает обратное значение функции распределения для биномиального закона с параметрами n и p. В случае ошибки возвращает NaN.
double MathQuantileBinomial( const double probability, // [in] Значение вероятности появления случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для биномиального закона с параметрами n и p. В случае ошибки возвращает false. Аналог qbinom() в R.
bool MathQuantileBinomial( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для биномиального закона с параметрами n и p. В случае ошибки возвращает false.
bool MathQuantileBinomial( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) double &result[] // [out] Массив со значениями квантилей );
2.17.4. MathRandomBinomial
Функция генерирует псевдослучайную величину, распределенную по закону биномиального распределения с параметрами n и p. В случае ошибки возвращает NaN.
double MathRandomBinomial( const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону биномиального распределения с параметрами n и p. В случае ошибки возвращает false. Аналог rbinom() в R.
bool MathRandomBinomial( const double n, // [in] Параметр распределения (количество испытаний) const double p, // [in] Параметр распределения (вероятность успеха для каждого испытания) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.17.5. MathMomentsBinomial
Функция рассчитывает теоретические численные значения первых 4 моментов биномиального распределения с параметрами n и p. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsBinomial( const double n, // [in] Количество испытаний const double p, // [in] Вероятность успеха каждого испытания double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.18. Отрицательное биномиальное распределение
2.18.1. MathProbabilityDensityNegativeBinomial
Функция рассчитывает значение функции вероятности (probability mass function) отрицательного биномиального распределения с параметрами r и p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) отрицательного биномиального распределения с параметрами r и p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityNegativeBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) отрицательного биномиального распределения с параметрами r и p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dnbinom() в R.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Массив со значениями случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции вероятности (probability mass function) отрицательного биномиального распределения с параметрами r и p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityNegativeBinomial( const double &x[], // [in] Массив со значениями случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха double &result[] // [out] Массив для значений функции плотности вероятности );
2.18.2. MathCumulativeDistributionNegativeBinomial
Функция рассчитывает значение функции распределения для отрицательного биномиального закона с параметрами r и p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для отрицательного биномиального закона с параметрами r и p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionNegativeBinomial( const double x, // [in] Значение случайной величины (целочисленное) const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для отрицательного биномиального закона с параметрами r и p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pnbinom() в R.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Массив со значениями случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения для отрицательного биномиального закона с параметрами r и p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionNegativeBinomial( const double &x[], // [in] Массив со значениями случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха double &result[] // [out] Массив для значений функции вероятности );
2.18.3. MathQuantileNegativeBinomial
Для вероятности probability функция рассчитывает обратное значение функции распределения для отрицательного биномиального закона с параметрами r и p. В случае ошибки возвращает NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Значение вероятности появления случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает обратное значение функции распределения для отрицательного биномиального закона с параметрами r и p. В случае ошибки возвращает NaN.
double MathQuantileNegativeBinomial( const double probability, // [in] Значение вероятности появления случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для отрицательного биномиального закона с параметрами r и p. В случае ошибки возвращает false. Аналог qnbinom() в R.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для отрицательного биномиального закона с параметрами r и p. В случае ошибки возвращает false.
bool MathQuantileNegativeBinomial( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха double &result[] // [out] Массив со значениями квантилей );
2.18.4. MathRandomNegativeBinomial
Функция генерирует псевдослучайную величину, распределенную по закону отрицательного биномиального распределения с параметрами r и p. В случае ошибки возвращает NaN.
double MathRandomNegativeBinomial( const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону отрицательного биномиального распределения с параметрами r и p. В случае ошибки возвращает false. Аналог rnbinom() в R.
bool MathRandomNegativeBinomial( const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.18.5. MathMomentsNegativeBinomial
Функция рассчитывает теоретические численные значения первых 4 моментов отрицательного биномиального распределения с параметрами r и p. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsNegativeBinomial( const double r, // [in] Количество успешных испытаний double p, // [in] Вероятность успеха double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.19. Геометрическое распределение
2.19.1. MathProbabilityDensityGeometric
Функция рассчитывает значение функции вероятности (probability mass function) геометрического распределения с параметром p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Значение случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) геометрического распределения с параметром p для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityGeometric( const double x, // [in] Значение случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) геометрического распределения с параметром p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dgeom() в R.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Массив со значениями случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции вероятности (probability mass function) геометрического распределения с параметром p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityGeometric( const double &x[], // [in] Массив со значениями случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) double &result[] // [out] Массив для значений функции плотности вероятности );
2.19.2. MathCumulativeDistributionGeometric
Функция рассчитывает значение функции распределения для геометрического закона с параметром p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Значение случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для геометрического закона с параметром p для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionGeometric( const double x, // [in] Значение случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для геометрического закона с параметром p для массива случайных величин x[]. В случае ошибки возвращает false. Аналог pgeom() в R.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Массив со значениями случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции распределения для геометрического закона с параметром p для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionGeometric( const double &x[], // [in] Массив со значениями случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) double &result[] // [out] Массив для значений функции плотности вероятности );
2.19.3. MathQuantileGeometric
Для вероятности probability функция рассчитывает обратное значение функции распределения для геометрического закона с параметром p. В случае ошибки возвращает NaN.
double MathQuantileGeometric( const double probability, // [in] Вероятность появления случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает обратное значение функции распределения для геометрического закона с параметром p. В случае ошибки возвращает NaN.
double MathQuantileGeometric( const double probability, // [in] Вероятность появления случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для геометрического закона с параметром p. В случае ошибки возвращает false. Аналог qgeom() в R.
bool MathQuantileGeometric( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для геометрического закона с параметром p. В случае ошибки возвращает false.
bool MathQuantileGeometric( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) double &result[] // [out] Массив со значениями квантилей );
2.19.4. MathRandomGeometric
Функция генерирует псевдослучайную величину, распределенную по закону геометрического распределения с параметром p. В случае ошибки возвращает NaN.
double MathRandomGeometric( const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону геометрического распределения с параметром p. В случае ошибки возвращает false. Аналог rgeom() в R.
bool MathRandomGeometric( const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.19.5. MathMomentsGeometric
Функция рассчитывает теоретические численные значения первых 4 моментов геометрического распределения с параметром p. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsGeometric( const double p, // [in] Параметр распределения (вероятность появления события в одном опыте) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.20. Гипергеометрическое распределение
2.20.1. MathProbabilityDensityHypergeometric
Функция рассчитывает значение функции вероятности (probability mass function) гипергеометрического распределения с параметрами m, k и n для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Значение случайной величины (целочисленное) const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) гипергеометрического распределения с параметрами m, k и n для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityHypergeometric( const double x, // [in] Значение случайной величины (целочисленное) const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) гипергеометрического распределения с параметрами m, k и n для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dhyper() в R.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Массив со значениями случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции вероятности (probability mass function) гипергеометрического распределения с параметрами m, k и n для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityHypergeometric( const double &x[], // [in] Массив со значениями случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) double &result[] // [out] Массив для значений функции вероятности );
2.20.2. MathCumulativeDistributionHypergeometric
Функция рассчитывает значение функции распределения для гипергеометрического закона с параметрами m, k и n для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Значение случайной величины (целочисленное) const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для гипергеометрического закона с параметрами m, k и n для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionHypergeometric( const double x, // [in] Значение случайной величины (целочисленное) const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения для гипергеометрического закона с параметрами m, k и n для массива случайных величин x[]. В случае ошибки возвращает false. Аналог phyper() в R.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Массив со значениями случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив для значений функции распределения );
Функция рассчитывает значение функции распределения для гипергеометрического закона с параметрами m, k и n для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionHypergeometric( const double &x[], // [in] Массив со значениями случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) double &result[] // [out] Массив для значений функции распределения );
2.20.3. MathQuantileHypergeometric
Для вероятности probability функция рассчитывает обратное значение функции распределения для гипергеометрического закона с параметрами m, k и n. В случае ошибки возвращает NaN.
double MathQuantileHypergeometric( const double probability, // [in] Значение вероятности появления случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает обратное значение функции распределения для гипергеометрического закона с параметрами m, k и n. В случае ошибки возвращает NaN.
double MathQuantileHypergeometric( const double probability, // [in] Значение вероятности появления случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для гипергеометрического закона с параметрами m, k и n. В случае ошибки возвращает false. Аналог qhyper() в R.
bool MathQuantileHypergeometric( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения для гипергеометрического закона с параметрами m, k и n. В случае ошибки возвращает false.
bool MathQuantileHypergeometric( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) double &result[] // [out] Массив со значениями квантилей );
2.20.4. MathRandomHypergeometric
Функция генерирует псевдослучайную величину, распределенную по закону гипергеометрического распределения с параметрами m, n и k. В случае ошибки возвращает NaN.
double MathRandomHypergeometric( const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону гипергеометрического распределения с параметрами m, n и k. В случае ошибки возвращает false. Аналог rhyper() в R.
bool MathRandomHypergeometric( const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) const int data_count, // [in] Количество необходимых данных double &result[] // [out] Массив со значениями псевдослучайных величин );
2.20.5. MathMomentsHypergeometric
Функция рассчитывает теоретические численные значения первых 4 моментов гипергеометрического распределения с параметрами m, n и k. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsHypergeometric( const double m, // [in] Общее количество объектов (целочисленное) const double k, // [in] Количество объектов с желаемой характеристикой (целочисленное) const double n, // [in] Количество взятых объектов (целочисленное) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
2.21. Распределение Пуассона
2.21.1. MathProbabilityDensityPoisson
Функция рассчитывает значение функции вероятности (probability mass function) распределения Пуассона с параметром lambda для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Значение случайной величины const double lambda, // [in] Параметр распределения (mean) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) распределения Пуассона с параметром lambda для случайной величины x. В случае ошибки возвращает NaN.
double MathProbabilityDensityPoisson( const double x, // [in] Значение случайной величины const double lambda, // [in] Параметр распределения (mean) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции вероятности (probability mass function) распределения Пуассона с параметром lambda для массива случайных величин x[]. В случае ошибки возвращает false. Аналог dpois() в R.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Массив со значениями случайной величины const double lambda, // [in] Параметр распределения (mean) const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то возвращается натуральный логарифм плотности вероятности double &result[] // [out] Массив для значений функции плотности вероятности );
Функция рассчитывает значение функции вероятности (probability mass function) распределения Пуассона с параметром lambda для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathProbabilityDensityPoisson( const double &x[], // [in] Массив со значениями случайной величины const double lambda, // [in] Параметр распределения (mean) double &result[] // [out] Массив для значений функции плотности вероятности );
2.21.2. MathCumulativeDistributionPoisson
Функция рассчитывает значение функции распределения Пуассона с параметром lambda для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Значение случайной величины const double lambda, // [in] Параметр распределения (mean) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Пуассона с параметром lambda для случайной величины x. В случае ошибки возвращает NaN.
double MathCumulativeDistributionPoisson( const double x, // [in] Значение случайной величины const double lambda, // [in] Параметр распределения (mean) int &error_code // [out] Переменная для кода ошибки );
Функция рассчитывает значение функции распределения Пуассона с параметром lambda для массива случайных величин x[]. В случае ошибки возвращает false. Аналог ppois() в R.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Массив со значениями случайной величины const double lambda, // [in] Параметр распределения (mean) const bool tail, // [in] Флаг расчета, если true, то рассчитывается вероятность того, что случайная величина не превысит x const bool log_mode, // [in] Флаг расчета логарифма значения, если log_mode=true, то рассчитывается натуральный логарифм вероятности double &result[] // [out] Массив для значений функции вероятности );
Функция рассчитывает значение функции распределения Пуассона с параметром lambda для массива случайных величин x[]. В случае ошибки возвращает false.
bool MathCumulativeDistributionPoisson( const double &x[], // [in] Массив со значениями случайной величины const double lambda, // [in] Параметр распределения (mean) double &result[] // [out] Массив для значений функции вероятности );
2.21.3. MathQuantilePoisson
Для вероятности probability функция рассчитывает обратное значение функции распределения Пуассона с параметром lambda. В случае ошибки возвращает NaN.
double MathQuantilePoisson( const double probability, // [in] Значение вероятности появления случайной величины const double lambda, // [in] Параметр распределения (mean) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) int &error_code // [out] Переменная для кода ошибки );
Для вероятности probability функция рассчитывает обратное значение функции распределения Пуассона с параметром lambda. В случае ошибки возвращает NaN.
double MathQuantilePoisson( const double probability, // [in] Значение вероятности появления случайной величины const double lambda, // [in] Параметр распределения (mean) int &error_code // [out] Переменная для кода ошибки );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения Пуассона с параметром lambda. В случае ошибки возвращает false. Аналог qpois() в R.
double MathQuantilePoisson( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double lambda, // [in] Параметр распределения (mean) const bool tail, // [in] Флаг расчета, если false, то расчет ведется для вероятности 1.0-probability const bool log_mode, // [in] Флаг расчета, если log_mode=true, то расчет ведется для вероятности Exp(probability) double &result[] // [out] Массив со значениями квантилей );
Для массива значений вероятности probability[] функция рассчитывает обратное значение функции распределения Пуассона с параметром lambda. В случае ошибки возвращает false.
double MathQuantilePoisson( const double &probability[],// [in] Массив со значениями вероятностей случайной величины const double lambda, // [in] Параметр распределения (mean) double &result[] // [out] Массив со значениями квантилей );
2.21.4. MathRandomPoisson
Функция генерирует псевдослучайную величину, распределенную по закону распределения Пуассона с параметром lambda. В случае ошибки возвращает NaN.
double MathRandomPoisson( const double lambda, // [in] Параметр распределения (mean) int &error_code // [out] Переменная для кода ошибки );
Функция генерирует псевдослучайные величины, распределенные по закону распределения Пуассона с параметром lambda. В случае ошибки возвращает false. Аналог rpois() в R.
double MathRandomPoisson( const double lambda, // [in] Параметр распределения (mean) int &error_code // [out] Переменная для кода ошибки );
2.21.5. MathMomentsPoisson
Функция рассчитывает теоретические численные значения первых 4 моментов распределения Пуассона с параметром lambda. Возвращает true, если расчет моментов произведен успешно, иначе false.
bool MathMomentsPoisson( const double lambda, // [in] Параметр распределения (mean) double &mean, // [out] Переменная для среднего значения double &variance, // [out] Переменная для дисперсии double &skewness, // [out] Переменная для коэффициента асимметрии double &kurtosis, // [out] Переменная для коэффициента эксцесса int &error_code // [out] Переменная для кода ошибки );
3. Таблица соответствия статистическим функциям языка R
Для удобства в табл. 1-2 приведены функции статистической библиотеки и соответствующие им функции языка R.
| № | Рассчитываемое значение | Функции MQL5 | Функция языка R |
|---|---|---|---|
| 1 | Среднее | MathMean | mean |
| 2 | Дисперсия | MathVariance | var |
| 3 | Коэффициент асимметрии | MathSkewness | skewness |
| 4 | Коэффициент эксцесса | MathKurtosis | kurtosis |
| 5 | Медианное значение | MathMedian | median |
| 6 | Стандартное отклонение | MathStandardDeviation | sd |
| 7 | Среднее отклонение | MathAverageDeviation | aad |
Табл. 1. Функции для расчета статистических характеристик данных массива
| № | Распределение | Функция плотности | Функции MQL5 | Функции языка R |
|---|---|---|---|---|
| 1 | Нормальное | 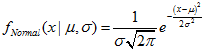 | MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal | dnorm pnorm qnorm rnorm |
| 2 | Бета | | MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta | dbeta pbeta qbeta rbeta |
| 3 | Биномиальное | | MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial | dbinom pbinom qbinom rbinom |
| 4 | Коши | 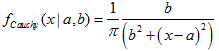 | MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy | dcauchy pcauchy qcauchy rcauchy |
| 5 | Хи-квадрат | 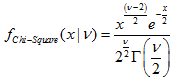 | MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare | dchisq pchisq qchisq rchisq |
| 6 | Экспоненциальное | | MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential | dexp pexp qexp rexp |
| 7 | F Фишера | 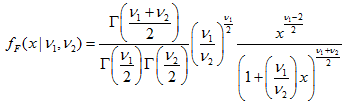 | MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF | df pf qf rf |
| 8 | Гамма | | MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma | dgamma pgamma qgamma rgamma |
| 9 | Геометрическое | | MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric | dgeom pgeom qgeom rgeom |
| 10 | Гипергеометрическое | 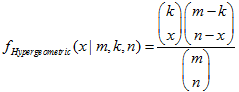 | MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric | dhyper phyper qhyper rhyper |
| 11 | Логистическое | 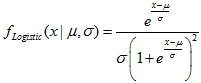 | MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic | dlogis plogis qlogis rlogis |
| 12 | Логнормальное | | MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal | dlnorm plnorm qlnorm rlnorm |
| 13 | Отрицательное биномиальное | | MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial | dnbinom pnbinom qnbinom rnbinom |
| 14 | Нецентральное бета | 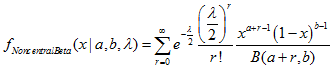 | MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta | dbeta pbeta qbeta rbeta |
| 15 | Нецентральное хи-квадрат | 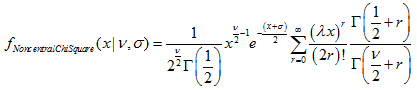 | MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare | dchisq pchisq qchisq rchisq |
| 16 | Нецентральное F | 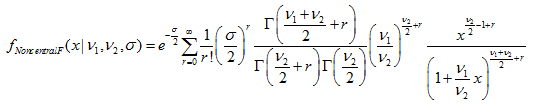 | MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF() | df pf qf rf |
| 17 | Нецентральное T Стьюдента | 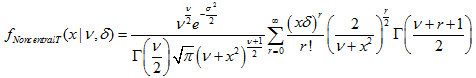 | MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT | dt pt qt rt |
| 18 | Пуассона | | MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson | dpois ppois qpois rpois |
| 19 | T Стьюдента | 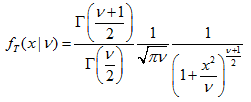 | MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT | dt pt qt rt |
| 20 | Равномерное | | MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform | dunif punif qunif runif |
| 21 | Вейбулла | 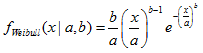 | MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull | dweibull pweibull qweibull rweibull |
Табл. 2. Функции для работы со статистическими распределениями
В статистической библиотеке MQL5 также есть функции для расчета математических функций на массивах, их список приведен в табл. 3.
| Описание | MQL5 | R |
|---|---|---|
| Формирует последовательность значений | bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[]) | seq() |
| Формирует повторяющуюся последовательность | bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[]) | rep() |
| Формирует массив с обратным порядком элементов | bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[]) | rev(x) |
| Сравнивает массивы и возвращает true, если совпадают все элементы | bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[]) | identical() |
| Формирует массив только с неповторяющимися значениями | bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[]) | unique() |
| Формирует целочисленный массив с перестановкой в соответствии с порядком элементов массива после сортировки | bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[]) | order() |
| Производит случайную выборку элементов массива. Аргумент replace=true позволяет осуществлять случайный отбор элементов с их возвратом в исходную совокупность. Массив probabilities[] задает вероятности, с которыми производится выборка элементов. | bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[]) | sample() |
| Возвращает сумму элементов массива | double MathSum(const double &array[]) | sum() |
| Возвращает произведение элементов массива | double MathProduct(const double &array[]) | prod() |
| Формирует массив с накопленной суммой | bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[]) | cumsum() |
| Формирует массив с накопленным произведением | bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[]) | cumprod() |
| Формирует массив с накопленными минимальными значениями | bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[]) | cummin() |
| Формирует массив с накопленными максимальными значениями | bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[]) | cummax() |
| Формирует массив с разностями элементов y[i]=x[i+lag]-x[i] | bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[]) | diff() |
| Возвращает минимальное значение элементов массива | double MathMin(const double &array[]) | min() |
| Возвращает максимальное значение элементов массива | double MathMax(const double &array[]) | max() |
| Рассчитывает минимальные и максимальные значения элементов массива | bool MathRange(const double &array[],double &min,double &max) | range() |
| Рассчитывает среднее значение элементов массива | double MathMean(const double &array[]) | mean() |
| Рассчитывает стандартное отклонение элементов массива | double MathStandardDeviation(const double &array[]) | sd() |
| Рассчитывает медианное значение элементов массива | double MathMedian(double &array[]) | median() |
| Рассчитывает ранги элементов массива | bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[]) | rank() |
| Рассчитывает коэффициенты корреляции Пирсона, Спирмена и Кендалла | bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau) | corr() |
| Рассчитывает выборочные квантили, соответствующие указанным вероятностям | bool MathQuantile(const double &array[],const double &probs[],double &quantile[]) | qunatile() |
| Рассчитывает Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum) для элементов массива | bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum) | fivenum() |
| Рассчитывает логарифмы элементов массива (натуральные и по заданному основанию) | bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base) | log() |
| Рассчитывает логарифмы элементов массива по основанию 2 | bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[]) | log2() |
| Рассчитывает логарифмы элементов массива по основанию 10 | bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[]) | log10() |
| Рассчитывает значение функции log(1+x) для элементов массива | bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[]) | log1p() |
| Рассчитывает значение функции exp(x) для элементов массива | bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[]) | exp() |
| Рассчитывает значение функции exp(x)-1 для элементов массива | bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[]) | expm1() |
| Рассчитывает значение функции sin(x) для элементов массива | bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[]) | sin() |
| Рассчитывает значение функции cos(x) для элементов массива | bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[]) | cos() |
| Рассчитывает значение функции tan(x) для элементов массива | bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[]) | tan() |
| Рассчитывает значение функции arcsin(x) для элементов массива | bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[]) | arcsin() |
| Рассчитывает значение функции arccos(x) для элементов массива | bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[]) | arccos() |
| Рассчитывает значение функции arctan(x) для элементов массива | bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[]) | arctan() |
| Рассчитывает значение функции arctan(y/x) для элементов массива | bool MathArctan2(const double &array1[], const double &array2[], double &result[]) | arctan2() |
| Рассчитывает значение функции sin(pi*x) для элементов массива | bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[]) | sinpi() |
| Рассчитывает значение функции cos(pi*x) для элементов массива | bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[]) | cospi() |
| Рассчитывает значение функции tan(pi*x) для элементов массива | bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[]) | tanpi() |
| Рассчитывает абсолютное значение элементов массива | bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[]) | abs() |
| Рассчитывает квадратный корень для элементов массива | bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[]) | sqrt() |
| Возвращает ближайшее сверху целое числовое значение для элементов массива | bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[]) | ceil() |
| Возвращает ближайшее снизу целое числовое значение для элементов массива | bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[]) | floor() |
| Рассчитывает целую часть элементов массива | bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[]) | trunc() |
| Рассчитывает округленное значение элементов массива | bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits) | round() |
| Для элементов массива рассчитывает значение, округленное до указанного количества знаков в мантиссе | bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits) | signinf() |
| Рассчитывает значение функции sinh(x) для элементов массива | bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[]) | sinh() |
| Рассчитывает значение функции cosh(x) для элементов массива | bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[]) | cosh() |
| Рассчитывает значение функции tanh(x) для элементов массива | bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[]) | tanh() |
| Рассчитывает значение функции arcsinh(x) для элементов массива | bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[]) | asinh() |
| Рассчитывает значение функции arccosh(x) для элементов массива | bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[]) | acosh() |
| Рассчитывает значение функции arctanh(x) для элементов массива | bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[]) | atanh() |
| Рассчитывает результат бинарной операции NOT для элементов массива | bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[]) | bitwNot() |
| Рассчитывает результат бинарной операции AND для заданных массивов | bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[]) | bitwAnd() |
| Рассчитывает результат бинарной операции OR для заданных массивов | bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[]) | bitwOr() |
| Рассчитывает результат бинарной операции XOR для заданных массивов | bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[]) | bitwXor() |
| Рассчитывает результат бинарной операции SHL для элементов массива | bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n) | bitwShiftL() |
| Рассчитывает результат бинарной операции SHR для элементов массива | bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n) | bitwShiftR() |
Табл. 3. Математические функции расчета значений на массивах
4. Пример использования функций
Рассмотрим практическое применение статистических функций на примере нормального распределения.
Пусть требуется решить задачи:
- Вычислить вероятность попадания случайной величины, распределенной по нормальному закону с параметрами mu и sigma, в интервал [mu-sigma,mu+sigma].
- Найти интервал значений случайной величины x, распределенной по нормальному закону с параметрами mu и sigma, симметричный относительно mu, соответствующий 95% доверительной вероятности.
- Сгенерировать 1000000 случайных чисел, распределенных по нормальному закону с параметрами mu и sigma, рассчитать гистограмму полученных значений, первые 4 момента и сравнить с теоретическими значениями.
Пример решения в скрипте NormalExample:
//+------------------------------------------------------------------+ //| NormalExample.mq5 | //| Copyright 2016, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //--- подключаем функции для расчета нормального распределения #include <Math\Stat\Normal.mqh> //+------------------------------------------------------------------+ //| CalculateHistogram | //+------------------------------------------------------------------+ void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv") { if(ArraySize(data)<=0) return; int n=ArraySize(data); //--- находим минимальное и максимальное значения данных в массиве data double minv,maxv,range; minv=data[0]; maxv=data[0]; for(int i=1; i<n; i++) { minv=MathMin(minv,data[i]); maxv=MathMax(maxv,data[i]); } //--- вычисляем диапазон range=maxv-minv; // Print("Min=",minv," Max=",maxv," range=",range," size=",n); if(range==0) return; //--- массивы для расчета гистограммы double x[]; double y[]; //--- задаем значения гистограммы ArrayResize(x,ncells); ArrayResize(y,ncells); for(int i=0; i<ncells; i++) { x[i]=minv+i*range/(ncells-1); y[i]=0; } //--- рассчитываем гистограмму for(int i=0; i<n; i++) { double v=(maxv-data[i])/range; int ind=int((v*(ncells-1))); y[ind]++; } //--- проверяем имя файла if(filename=="") return; //--- открываем файл для записи ResetLastError(); int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI); //--- записываем данные в файл if(filehandle!=INVALID_HANDLE) { for(int i=0; i<ncells; i++) { string str=StringFormat("%6.20f;%6.20f",x[i],y[i]); FileWrite(filehandle,str); } FileClose(filehandle); PrintFormat("Гистограмма сохранена в файл %s",filename); } else PrintFormat("Ошибка вызова FileOpen, код ошибки=%d",GetLastError()); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- 1. Рассчитаем вероятность попадания случайной величины, //--- распределенной по нормальному закону с параметрами mu и sigma, в интервал [mu-sigma,mu+sigma] //--- задаем параметры распределения double mu=5.0; double sigma=1.0; //--- задаем интервал double x1=mu-sigma; double x2=mu+sigma; //--- переменные для расчета вероятности double cdf1,cdf2,probability; //--- переменные для кода ошибки int error_code1,error_code2; //--- рассчитаем значения функции распределения cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1); cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2); //--- проверим код ошибок if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- рассчитаем вероятность probability=cdf2-cdf1; //--- выводим результат PrintFormat("x1=%5.8f, x2=%5.8f, Probability=%5.8f",x1,x2,probability); } //--- 2. Найдем интервал значений случайной величины x, распределенной по нормальному закону с параметрами mu и sigma, //--- симметричный относительно mu, соответствующий 95% доверительной вероятности. //--- задаем доверительную вероятность probability=0.95; //--- задаем вероятности на границах интервала double p1=(1.0-probability)*0.5; double p2=probability+(1.0-probability)*0.5; //--- вычислим границы интервала x1=MathQuantileNormal(p1,mu,sigma,error_code1); x2=MathQuantileNormal(p2,mu,sigma,error_code2); //--- проверим код ошибок if(error_code1==ERR_OK && error_code2==ERR_OK) { //--- выводим результат PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2); } //--- 3. Сгенерируем 1000000 случайных чисел, распределенных по нормальному закону с параметрами mu и sigma, //--- рассчитаем гистограмму полученных значений, первые 4 момента и сравним с теоретическими значениями //--- задаем количество значений и подготавливаем массив int data_count=1000000; double data[]; ArrayResize(data,data_count); //--- генерируем случайные значения и сохраняем их в массив for(int i=0; i<data_count; i++) { data[i]=MathRandomNormal(mu,sigma,error_code1); } //--- задаем индекс начального значения и количество данных для расчета int start=0; int count=data_count; //--- вычислим первые 4 момента сгенерированных значений double mean=MathMean(data,start,count); double variance=MathVariance(data,start,count); double skewness=MathSkewness(data,start,count); double kurtosis=MathKurtosis(data,start,count); //--- переменные для теоретических моментов double normal_mean=0; double normal_variance=0; double normal_skewness=0; double normal_kurtosis=0; //--- выводим значения рассчитанных моментов PrintFormat(" mean=%.10f, variance=%.10f skewness=%.10f kurtosis=%.10f",mean,variance,skewness,kurtosis); //--- рассчитываем теоретические значения моментов и сравниваем с полученными if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1)) { PrintFormat("Normal mean=%.10f, Normal variance=%.10f Normal skewness=%.10f Normal kurtosis=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis); PrintFormat("delta mean=%.4f, delta variance=%.4f delta skewness=%.4f delta kurtosis=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis); } //--- рассчитаем гистограмму распределения и сохраним в файл normal.csv int ncells=50; CalculateHistogram(data,ncells,"normal.csv"); }
Результат работы скрипта:
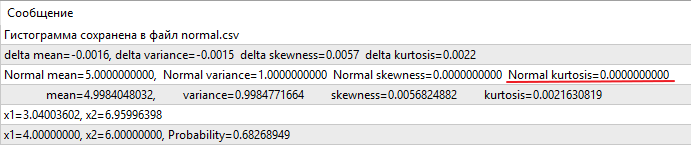
Рис 1. Результат работы скрипта TestNormal.mq5
Отметим, что при расчете значений параметра kurtosis используется excess kurtosis=kurtosis-3, т.е. для нормального распределения он равен 0.
Рассчитанная гистограмма сохраняется в файл normal.csv (рис. 2)
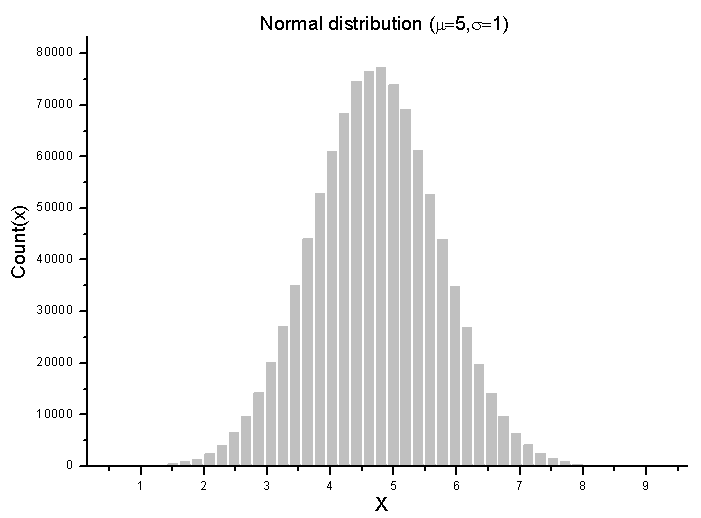
Рис. 2. Гистограмма распределения случайных чисел, сгенерированных по нормальному распределению с параметрами mu=5 и sigma=1
5. Сравнение скорости расчетов
Для сравнения скорости расчета статистических функций были подготовлены скрипты для измерения времени расчета функций плотности (pdf), функций вероятности (cdf), функций расчета квантилей и функций генерации псевдослучайных чисел.
Вычисления производились на массиве из 51 значения, для непрерывных распределений расчет значений функций производился в диапазоне от 0 до 1, для дискретных от 0 до 50. Измерение времени расчета статистических функций языка R производилось при помощи библиотеки microbenchmark. Время расчета функций на MQL5 рассчитывалось при помощи функции GetMicrosecondCount(). Скрипт расчета TestStatBenchmark.mq5 можно найти в папке каталог_данных_терминала\MQL5\Scripts\UnitTests\Stat. Скрипт для R и результаты измерения скорости расчетов приведены в Приложении.
Расчеты производились на Intel Core i7-4790, CPU 3.6 Ghz, 16 GB RAM, Windows 10 x64.
Результаты измерения времени расчетов (в микросекундах) представлены в табл. 3.
| № | Распределение | MQL5 время расчета PDF (мкс) | R время расчета PDF (мкс) | PDF R/MQL5 | MQL5 время расчета CDF (мкс) | R время расчета CDF (мкс) | CDF R/MQL5 | MQL5 время расчета квантилей (мкс) | R время расчета квантилей (мкс) | Quantile R/MQL5 | MQL5 время генерации случайных чисел (мкс) | R время генерации случайных чисел (мкс) | Random R/MQL5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Binomial | 4.39 | 11.663 | 2.657 | 13.65 | 25.316 | 1.855 | 50.18 | 66.845 | 1.332 | 318.73 | 1816.463 | 5.699 |
| 2 | Beta | 1.74 | 17.352 | 9.972 | 4.76 | 15.076 | 3.167 | 48.72 | 129.992 | 2.668 | 688.81 | 1723.45 | 2.502 |
| 3 | Gamma | 1.31 | 8.251 | 6.347 | 8.09 | 14.792 | 1.828 | 50.83 | 64.286 | 1.265 | 142.84 | 1281.707 | 8.973 |
| 4 | Cauchy | 0.45 | 1.423 | 3.162 | 1.33 | 15.078 | 11.34 | 1.37 | 2.845 | 2.077 | 224.19 | 588.517 | 2.625 |
| 5 | Exponential | 0.85 | 3.13 | 3.682 | 0.77 | 2.845 | 3.695 | 0.53 | 2.276 | 4.294 | 143.18 | 389.406 | 2.72 |
| 6 | Uniform | 0.42 | 2.561 | 6.098 | 0.45 | 1.423 | 3.162 | 0.18 | 2.846 | 15.81 | 40.3 | 247.467 | 6.141 |
| 7 | Geometric | 2.3 | 5.121 | 2.227 | 2.12 | 4.552 | 2.147 | 0.81 | 5.407 | 6.675 | 278 | 1078.045 | 3.879 |
| 8 | Hypergeometric | 1.85 | 11.095 | 5.997 | 0.9 | 8.819 | 9.799 | 0.75 | 9.957 | 13.28 | 302.55 | 880.356 | 2.91 |
| 9 | Logistic | 1.27 | 4.267 | 3.36 | 1.11 | 4.267 | 3.844 | 0.71 | 3.13 | 4.408 | 178.65 | 626.632 | 3.508 |
| 10 | Weibull | 2.99 | 5.69 | 1.903 | 2.74 | 4.268 | 1.558 | 2.64 | 6.828 | 2.586 | 536.37 | 1558.472 | 2.906 |
| 11 | Poisson | 2.91 | 5.974 | 2.053 | 6.26 | 8.534 | 1.363 | 3.43 | 13.085 | 3.815 | 153.59 | 303.219 | 1.974 |
| 12 | F | 3.86 | 10.241 | 2.653 | 9.94 | 22.472 | 2.261 | 65.47 | 135.396 | 2.068 | 1249.22 | 1801.955 | 1.442 |
| 13 | Chi Square | 2.47 | 5.974 | 2.419 | 7.71 | 13.37 | 1.734 | 44.11 | 61.725 | 1.399 | 210.24 | 1235.059 | 5.875 |
| 14 | Noncentral ChiSquare | 8.05 | 14.223 | 1.767 | 45.61 | 209.068 | 4.584 | 220.66 | 10342.96 | 46.873 | 744.45 | 1997.653 | 2.683 |
| 15 | Noncentral F | 19.1 | 28.446 | 1.489 | 14.67 | 46.935 | 3.199 | 212.21 | 2561.991 | 12.073 | 1848.9 | 2912.141 | 1.575 |
| 16 | Noncentral Beta | 16.3 | 26.739 | 1.64 | 10.48 | 43.237 | 4.126 | 153.66 | 2290.915 | 14.909 | 2686.82 | 2839.893 | 1.057 |
| 17 | Negative Binomial | 6.13 | 11.094 | 1.81 | 12.21 | 19.627 | 1.607 | 14.05 | 60.019 | 4.272 | 1130.39 | 1936.498 | 1.713 |
| 18 | Normal | 1.15 | 4.267 | 3.71 | 0.81 | 3.983 | 4.917 | 0.7 | 2.277 | 3.253 | 293.7 | 696.321 | 2.371 |
| 19 | Lognormal | 1.99 | 5.406 | 2.717 | 3.19 | 8.819 | 2.765 | 3.18 | 6.259 | 1.968 | 479.75 | 1269.761 | 2.647 |
| 20 | T | 2.32 | 11.663 | 5.027 | 8.01 | 19.059 | 2.379 | 50.23 | 58.596 | 1.167 | 951.58 | 1425.92 | 1.498 |
| 21 | Noncentral T | 38.47 | 86.757 | 2.255 | 27.75 | 39.823 | 1.435 | 1339.51 | 1930.524 | 1.441 | 1550.27 | 1699.84 | 1.096 |
| <PDF R/MQL5> | 3.474 | <CDF R/MQL5> | 3.465 | <Quantile R/MQL5> | 7.03 | <Random R/MQL5> | 3.13 |
Табл. 4. Время расчета статистических функций в R и MQL5 (в микросекундах)
Для R брались значения минимального времени, а для MQL5 брались средние значения (pdf_mean, cdf_mean, quantile_mean, random_mean).
Из табл. 3 видно, что даже при таких условиях расчет функций статистической библиотеки MQL5 производится в несколько раз быстрее R. В среднем MQL5 считает от 3 до 7 раз быстрее R даже с учетом того, что сравниваемые варианты функций R на самом деле написаны на C++.
На практике компилятор MQL5 языка оказался гораздо быстрее С++ реализаций функций в R, что показывает высокое качество наших разработок. При переносе программ из R на MQL5 можно получить серьезный прирост скорости и не нужно использовать сторонних DLL библиотек.
6. Обнаруженные ошибки расчетов в R
В процессе тестирования R была обнаружена ошибка расчета квантилей нецентрального t-распределения.
Например:
> n <- 10 > k <- seq(0,1,by=1/n) > nt_pdf<-dt(k, 10,8, log = FALSE) > nt_cdf<-pt(k, 10,8, log = FALSE) > nt_quantile<-qt(nt_cdf, 10,8, log = FALSE) > nt_pdf [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11 > nt_cdf [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12 > k [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 > nt_quantile [1] -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 [7] -1.340781e+154 7.000000e-01 8.000000e-01 9.000000e-01 1.000000e+00
Для расчета вероятности нецентрального T-распределения Стьюдента в языке R используется алгоритм AS 243, предложенный Lenth [6]. Достоинством этого метода является быстрый рекуррентный расчет членов бесконечного ряда с неполной бета-функций. Но в статье [7] было показано, что из-за ошибки оценки точности при суммировании членов ряда данный алгоритм приводит к ошибкам (таблица 2 в статье [7]), особенно для больших значений параметра нецентральности delta. Авторы статьи [7] предложили скорректированный алгоритм рекуррентного расчета вероятности нецентрального T-распределения.
У нас в статистической библиотеке MQL5 используется правильный алгоритм для расчета вероятностей из статьи [7] , что дает точные результаты.
Следует отметить, что в языке R способ определения плотностей для распределений Gamma, ChiSquare и Noncentral ChiSquare в точке x=0 приводит к бесконечным выражениям:
> dgamma(0,0.5,1) [1] Inf > dchisq(0,df=0.5,ncp=1) [1] Inf > dchisq(0,df=0.5,ncp=0) [1] Inf
Таким образом, в языке R в определении плотности вероятности в точке x=0 используются предельные значения. Несмотря на бесконечность в точке x=0, в данном случае при интегрировании расходимостей не возникает и интегралы от плотности
являются конечными.
При расчете вероятностей (например, для x=0.1) они совпадают со значениями Wolfram Alpha (Gamma, ChiSquare, NoncentralChiSquare).
> pgamma(0.1,0.5,1) [1] 0.3452792 > pchisq(0.1,df=0.5,ncp=0) [1] 0.5165553 > pchisq(0.1,df=0.5,ncp=1) [1] 0.3194965
В Wolfram Alpha (Mathematica) и Matlab используется другой способ определения плотности в точке x=0:
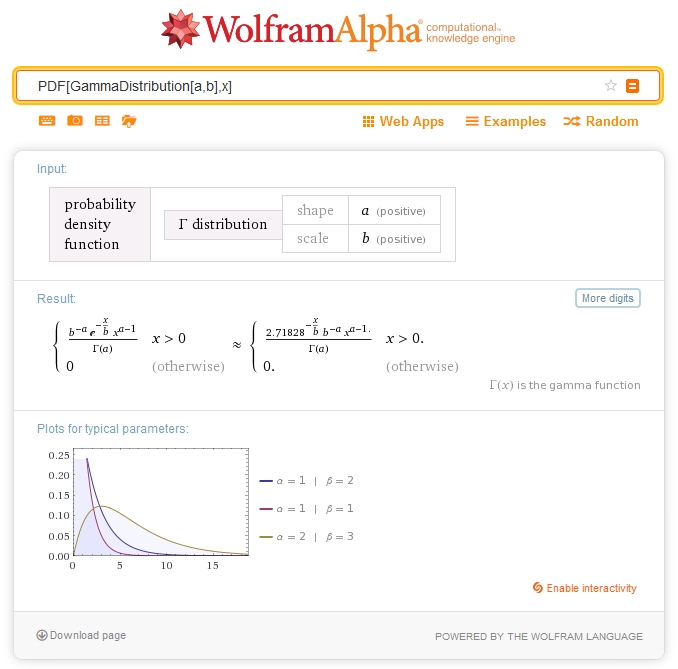
Рис. 3. Определение плотности вероятности распределения Gamma в Wolfram Alpha
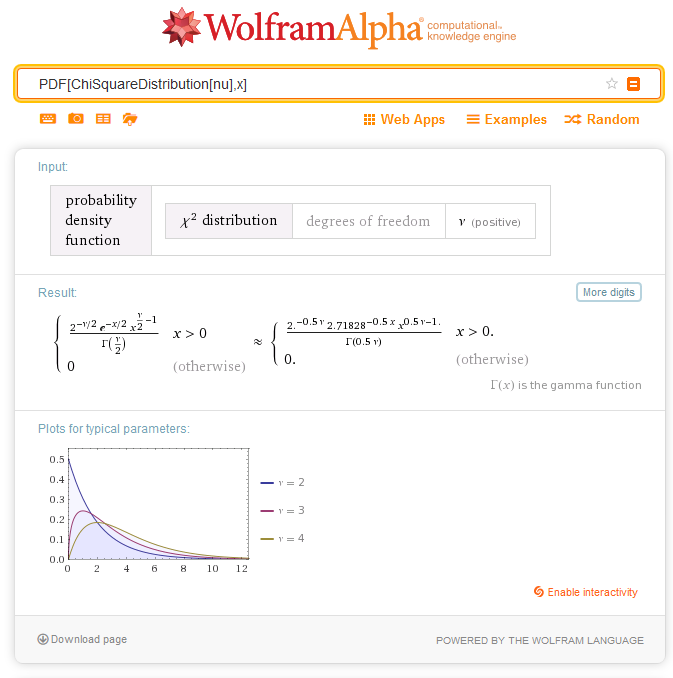
Рис. 4. Определение плотности вероятности распределения ChiSquare в Wolfram Alpha
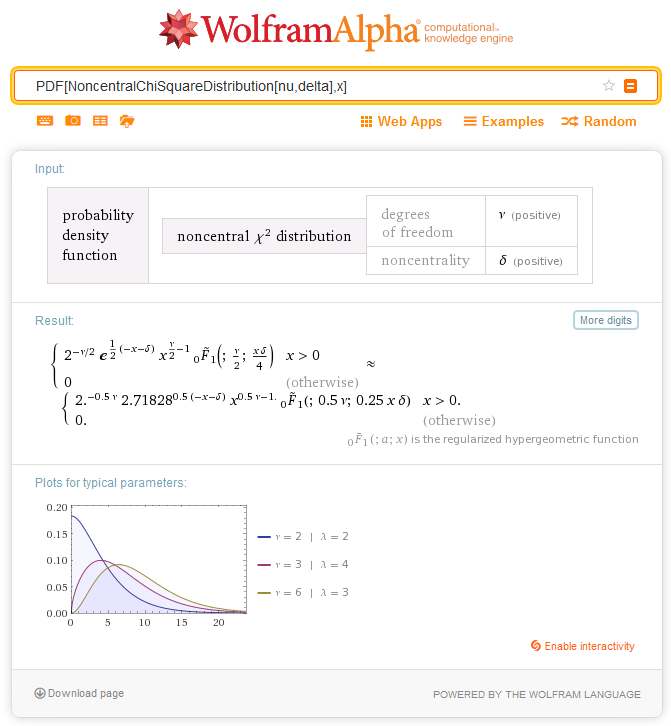
Рис. 5. Определение плотности вероятности распределения Noncentral ChiSquare в Wolfram Alpha
В статистической библиотеке языка MQL5 плотности данных распределений в точке x=0 считаются равными нулю по определению.
Чтобы быть уверенными в точности расчетов и дать возможность сторонним разработчикам проверить качество библиотеки, мы включили несколько unit test скриптов в поставку. Их можно найти в каталоге /Scripts/UnitTests/Stat.
Заключение
В статье рассмотрены основные функции статистической библиотеки языка MQL5.
Они позволяют производить расчет статистических характеристик данных и работать с основными статистическими распределениями, реализованными в языке R. Кроме того, в библиотеке также есть функции расчета теоретических моментов распределений, которые позволяют оценить степень соответствия реального распределения модельному.
Благодаря высокой производительности нового 64-битного компилятора языка MQL5 сложные математические расчеты производится в несколько раз быстрее, чем в языке R, что значительно упрощает проведение исследований.
Литература
- The R Project for Statistical Computing.
- Балакришнан Н., Джонсон Н.Л., Коц С. "Одномерные непрерывные распределения: часть 1." М.: БИНОМ. Лаборатория знаний, 2014.
- Балакришнан Н., Джонсон Н.Л., Коц С. "Одномерные непрерывные распределения: часть 2." М.: БИНОМ. Лаборатория знаний, 2014.
- Джонсон Н.Л., Коц С., Кемп А. "Одномерные дискретные распределения", М.: БИНОМ. Лаборатория знаний, 2014.
- Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
- Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics, vol. 38 (1989), 185–189.
- D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient", Computational Statistics & Data Analysis, 43, (2003), 249-267
Приложение. Результаты измерения времени расчета статистических функций
В приложении приведен скрипт для расчета времени вычисления статистических функций на языке R и результаты его работы, а также результаты выполнения скрипта TestStatBenchmark.mq5.
Скрипт на языке R:
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)
n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)
n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)
n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)
n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)
n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)
n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)
n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)
n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)
n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)
n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)
n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)
n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)
n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)
n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)
n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)
n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)
n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)
n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)
Результат:
R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes" Copyright (C) 2016 The R Foundation for Statistical Computing Platform: x86_64-w64-mingw32/x64 (64-bit) R is free software and comes with ABSOLUTELY NO WARRANTY. You are welcome to redistribute it under certain conditions. Type 'license()' or 'licence()' for distribution details. R is a collaborative project with many contributors. Type 'contributors()' for more information and 'citation()' on how to cite R or R packages in publications. Type 'demo()' for some demos, 'help()' for on-line help, or 'help.start()' for an HTML browser interface to help. Type 'q()' to quit R. [Workspace loaded from ~/Test/111/.RData] > library(microbenchmark) > n <- 50 > k <- seq(0,n,by=1) > binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE)) > binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE)) > binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE)) > binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6)) > print(binomial_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503 100 > print(binomial_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868 100 > print(binomial_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276 100 > print(binomial_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE)) > beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE)) > beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE)) > beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,)) > print(beta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797 100 > print(beta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379 100 > print(beta_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672 100 > print(beta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963 100 > > n <- 50 > k <- seq(0,1,by=1/n) > gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE)) > gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE)) > gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE)) > gamma_random <- microbenchmark(random<-rgamma(10000, 1,1)) > print(gamma_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684 9.104 9.389 122.312 100 > print(gamma_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099 100 > print(gamma_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988 100 > print(gamma_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204 100 > > n <- 50 > k <- seq(0,1,by=1/n) > cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE)) > cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE)) > cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE)) > cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1)) > print(cauchy_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431 1.709 2.278 67.415 100 > print(cauchy_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914 15.93 16.215 33.281 100 > print(cauchy_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044 3.131 3.415 56.606 100 > print(cauchy_random) Unit: microseconds expr min lq mean median uq max neval random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356 100 > > n <- 50 > k <- seq(0,1,by=1/n) > exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE)) > exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE)) > exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE)) > exponential_random <- microbenchmark(random<-rexp(10000, 2)) > print(exponential_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887 3.415 3.415 67.699 100 > print(exponential_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756 3.414 3.5565 58.597 100 > print(exponential_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659 100 > print(exponential_random) Unit: microseconds expr min lq mean median uq max neval random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE)) > uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE)) > uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE)) > uniform_random <- microbenchmark(random<-runif(10000, 0, 10)) > print(uniform_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734 3.13 3.131 66.277 100 > print(uniform_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635 1.992 1.993 53.477 100 > print(uniform_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561 3.415 3.6995 82.774 100 > print(uniform_random) Unit: microseconds expr min lq mean median uq max neval random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769 100 > > > n <- 50 > k <- seq(0,n,by=1) > geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE)) > geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE)) > geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE)) > geometric_random <- microbenchmark(random<-rgeom(10000, 0.3)) > print(geometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258 5.406 5.406 60.304 100 > print(geometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548 4.837 5.1215 46.081 100 > print(geometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107 5.975 6.259 71.681 100 > print(geometric_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267 100 > > n <- 50 > k <- seq(0,n,by=1) > hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE)) > hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE)) > hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE)) > hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11)) > print(hypergeometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548 100 > print(hypergeometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515 9.672 12.517 62.01 100 > print(hypergeometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618 10.81 11.948 64.286 100 > print(hypergeometric_random) Unit: microseconds expr min lq mean median uq max neval random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289 100 > > n <- 50 > k <- seq(0,1,by=1/n) > logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE)) > logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE)) > logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE)) > logistic_random <- microbenchmark(random<-rlogis(10000, 1,2)) > print(logistic_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354 4.553 4.837 53.477 100 > print(logistic_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056 4.837 4.837 96.428 100 > print(logistic_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742 3.415 3.699 56.036 100 > print(logistic_random) Unit: microseconds expr min lq mean median uq max neval random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191 100 > > n <- 50 > k <- seq(0,1,by=1/n) > weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE)) > weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE)) > weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE)) > weibull_random <- microbenchmark(random<-rweibull(10000, 5,1)) > print(weibull_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775 5.975 6.259 85.619 100 > print(weibull_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455 100 > print(weibull_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587 7.113 7.397 48.641 100 > print(weibull_random) Unit: milliseconds expr min lq mean median uq max neval random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603 100 > > n <- 50 > k <- seq(0,n,by=1) > poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE)) > poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE)) > poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE)) > poisson_random <- microbenchmark(random<-rpois(10000, 1)) > print(poisson_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316 6.544 6.828 54.046 100 > print(poisson_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846 9.104 9.388 64.286 100 > print(poisson_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438 13.37 13.654 61.157 100 > print(poisson_random) Unit: microseconds expr min lq mean median uq max neval random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477 100 > > n <- 50 > k <- seq(0,1,by=1/n) > f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE)) > f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE)) > f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE)) > f_random <- microbenchmark(random<-rf(10000, 10,20)) > print(f_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112 100 > print(f_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189 100 > print(f_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717 100 > print(f_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546 100 > > n <- 50 > k <- seq(0,1,by=1/n) > chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE)) > chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE)) > chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE)) > chisquare_random <- microbenchmark(random<-rchisq(10000, 2)) > print(chisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339 100 > print(chisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841 100 > print(chisquare_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553 100 > print(chisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE)) > nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE)) > nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE)) > nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1)) > print(nchisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548 100 > print(nchisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193 100 > print(nchisquare_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558 100 > print(nchisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE)) > nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE)) > nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE)) > nf_random <- microbenchmark(random<-rf(10000, 10,20,2)) > print(nf_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836 100 > print(nf_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953 100 > print(nf_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598 100 > print(nf_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE)) > nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE)) > nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE)) > nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1)) > print(nbeta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891 100 > print(nbeta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255 100 > print(nbeta_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764 100 > print(nbeta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789 100 > > n <- 50 > k <- seq(0,n,by=1) > nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE)) > nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE)) > nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE)) > nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5)) > print(nbinom_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508 100 > print(nbinom_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277 100 > print(nbinom_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028 100 > print(nbinom_random) Unit: milliseconds expr min lq mean median uq max neval random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061 100 > > n <- 50 > k <- seq(0,1,by=1/n) > normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE)) > normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE)) > normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE)) > normal_random <- microbenchmark(random<-rnorm(10000, 1,1)) > print(normal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927 4.553 4.837 75.663 100 > print(normal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911 4.553 4.979 50.632 100 > print(normal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042 2.845 2.846 45.227 100 > print(normal_random) Unit: microseconds expr min lq mean median uq max neval random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12 100 > > n <- 50 > k <- seq(0,1,by=1/n) > lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE)) > lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE)) > lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE)) > lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6)) > print(lognormal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638 5.975 6.259 50.917 100 > print(lognormal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681 100 > print(lognormal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277 6.544 6.828 58.881 100 > print(lognormal_random) Unit: milliseconds expr min lq mean median uq max neval random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395 100 > > n <- 50 > k <- seq(0,1,by=1/n) > t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE)) > t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE)) > t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE)) > t_random <- microbenchmark(random<-rt(10000, 8)) > print(t_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517 100 > print(t_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485 21.05 21.619 127.717 100 > print(t_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611 100 > print(t_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE)) > nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE)) > nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE)) > nt_random <- microbenchmark(random<-rt(10000, 10,1)) > print(nt_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276 100 > print(nt_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829 100 > print(nt_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987 100 > print(nt_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959 100
Результат выполнения скрипта TestStatBenchmark.mq5:
PP 0 13:06:15.252 TestStatBenchmark (EURUSD,H1)
KJ 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): pdf_mean=4.39, pdf_median=4.00, pdf_min=3.00, pdf_max=40.00, pdf_stddev=2.21, pdf_avgdev=0.95
MS 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): cdf_mean=13.65, cdf_median=12.00, cdf_min=11.00, cdf_max=54.00, cdf_stddev=4.09, cdf_avgdev=2.37
GF 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00, quantile_stddev=9.97, quantile_avgdev=7.41
QO 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): random_mean=318.73, random_median=312.00, random_min=284.00, random_max=478.00, random_stddev=28.74, random_avgdev=22.22
LP 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): pdf_mean=1.74, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.07, pdf_avgdev=0.53
EI 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): cdf_mean=4.76, cdf_median=4.00, cdf_min=3.00, cdf_max=68.00, cdf_stddev=3.07, cdf_avgdev=1.19
LM 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00, quantile_stddev=10.21, quantile_avgdev=6.96
QG 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): random_mean=688.81, random_median=680.00, random_min=625.00, random_max=976.00, random_stddev=43.92, random_avgdev=31.81
HE 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): pdf_mean=1.31, pdf_median=1.00, pdf_min=1.00, pdf_max=13.00, pdf_stddev=0.82, pdf_avgdev=0.47
GL 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): cdf_mean=8.09, cdf_median=7.00, cdf_min=7.00, cdf_max=92.00, cdf_stddev=3.67, cdf_avgdev=1.40
CF 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00, quantile_stddev=9.27, quantile_avgdev=6.72
GR 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): random_mean=142.84, random_median=132.00, random_min=128.00, random_max=260.00, random_stddev=19.73, random_avgdev=15.32
QD 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): pdf_mean=0.45, pdf_median=0.00, pdf_min=0.00, pdf_max=11.00, pdf_stddev=0.85, pdf_avgdev=0.54
QK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): cdf_mean=1.33, cdf_median=1.00, cdf_min=1.00, cdf_max=12.00, cdf_stddev=0.81, cdf_avgdev=0.48
MR 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00, quantile_stddev=0.89, quantile_avgdev=0.51
IK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): random_mean=224.19, random_median=215.00, random_min=200.00, random_max=352.00, random_stddev=26.86, random_avgdev=20.34
PQ 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): pdf_mean=0.85, pdf_median=1.00, pdf_min=0.00, pdf_max=18.00, pdf_stddev=1.40, pdf_avgdev=0.54
GK 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): cdf_mean=0.77, cdf_median=1.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.94, cdf_avgdev=0.47
HE 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.78, quantile_avgdev=0.54
HL 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): random_mean=143.18, random_median=130.00, random_min=128.00, random_max=272.00, random_stddev=21.58, random_avgdev=16.98
LK 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): pdf_mean=0.42, pdf_median=0.00, pdf_min=0.00, pdf_max=12.00, pdf_stddev=0.82, pdf_avgdev=0.52
CE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): cdf_mean=0.45, cdf_median=0.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.96, cdf_avgdev=0.55
LO 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00, quantile_stddev=0.38, quantile_avgdev=0.29
GE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): random_mean=40.30, random_median=36.00, random_min=35.00, random_max=83.00, random_stddev=7.61, random_avgdev=5.41
OP 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): pdf_mean=2.30, pdf_median=2.00, pdf_min=1.00, pdf_max=14.00, pdf_stddev=1.30, pdf_avgdev=0.52
DK 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): cdf_mean=2.12, cdf_median=2.00, cdf_min=1.00, cdf_max=18.00, cdf_stddev=1.69, cdf_avgdev=0.53
NE 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.68, quantile_avgdev=0.39
IL 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): random_mean=278.00, random_median=271.00, random_min=251.00, random_max=429.00, random_stddev=28.23, random_avgdev=21.62
PG 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): pdf_mean=1.85, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.07, pdf_avgdev=0.48
CM 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): cdf_mean=0.90, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=0.85, cdf_avgdev=0.32
NP 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.96, quantile_avgdev=0.48
FE 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): random_mean=302.55, random_median=295.00, random_min=272.00, random_max=466.00, random_stddev=30.20, random_avgdev=22.99
ML 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): pdf_mean=1.27, pdf_median=1.00, pdf_min=0.00, pdf_max=91.00, pdf_stddev=3.04, pdf_avgdev=0.56
DR 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): cdf_mean=1.11, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.34, cdf_avgdev=0.40
IH 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.79, quantile_avgdev=0.47
GL 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): random_mean=178.65, random_median=164.00, random_min=162.00, random_max=309.00, random_stddev=24.09, random_avgdev=17.94
MJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): pdf_mean=2.99, pdf_median=3.00, pdf_min=2.00, pdf_max=17.00, pdf_stddev=1.63, pdf_avgdev=0.57
GD 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): cdf_mean=2.74, cdf_median=3.00, cdf_min=2.00, cdf_max=19.00, cdf_stddev=1.23, cdf_avgdev=0.58
FO 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.64, quantile_avgdev=0.76
DJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): random_mean=536.37, random_median=526.00, random_min=483.00, random_max=759.00, random_stddev=46.99, random_avgdev=34.40
HR 0 13:06:18.485 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): pdf_mean=2.91, pdf_median=3.00, pdf_min=2.00, pdf_max=15.00, pdf_stddev=1.40, pdf_avgdev=0.58
IL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): cdf_mean=6.26, cdf_median=6.00, cdf_min=5.00, cdf_max=23.00, cdf_stddev=2.38, cdf_avgdev=1.07
HE 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00, quantile_stddev=1.48, quantile_avgdev=0.68
DL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): random_mean=153.59, random_median=144.00, random_min=138.00, random_max=265.00, random_stddev=18.57, random_avgdev=13.99
IH 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): pdf_mean=3.86, pdf_median=4.00, pdf_min=3.00, pdf_max=21.00, pdf_stddev=1.78, pdf_avgdev=0.76
GS 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): cdf_mean=9.94, cdf_median=9.00, cdf_min=7.00, cdf_max=36.00, cdf_stddev=3.82, cdf_avgdev=2.15
OI 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00, quantile_stddev=12.99, quantile_avgdev=9.64
DE 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): random_mean=1249.22, random_median=1213.00, random_min=1127.00, random_max=1968.00, random_stddev=117.69, random_avgdev=72.17
EL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): pdf_mean=2.47, pdf_median=2.00, pdf_min=2.00, pdf_max=13.00, pdf_stddev=1.32, pdf_avgdev=0.65
JK 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): cdf_mean=7.71, cdf_median=7.00, cdf_min=7.00, cdf_max=23.00, cdf_stddev=1.91, cdf_avgdev=0.88
KQ 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00, quantile_stddev=8.17, quantile_avgdev=5.38
CL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): random_mean=210.24, random_median=196.00, random_min=190.00, random_max=437.00, random_stddev=29.14, random_avgdev=21.00
HD 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): pdf_mean=8.05, pdf_median=8.00, pdf_min=7.00, pdf_max=24.00, pdf_stddev=2.41, pdf_avgdev=1.09
MR 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): cdf_mean=45.61, cdf_median=42.00, cdf_min=41.00, cdf_max=97.00, cdf_stddev=8.25, cdf_avgdev=5.70
FN 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00, quantile_stddev=24.71, quantile_avgdev=19.45
LI 0 13:06:21.099 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): random_mean=744.45, random_median=728.00, random_min=672.00, random_max=1082.00, random_stddev=62.42, random_avgdev=43.24
RE 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): pdf_mean=19.10, pdf_median=18.00, pdf_min=16.00, pdf_max=50.00, pdf_stddev=4.67, pdf_avgdev=2.64
FS 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): cdf_mean=14.67, cdf_median=13.00, cdf_min=12.00, cdf_max=39.00, cdf_stddev=3.94, cdf_avgdev=2.44
EN 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00, quantile_stddev=24.37, quantile_avgdev=19.30
EF 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): random_mean=1848.90, random_median=1819.00, random_min=1704.00, random_max=2556.00, random_stddev=118.75, random_avgdev=78.66
EN 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): pdf_mean=16.30, pdf_median=15.00, pdf_min=14.00, pdf_max=43.00, pdf_stddev=4.32, pdf_avgdev=2.43
EP 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): cdf_mean=10.48, cdf_median=10.00, cdf_min=8.00, cdf_max=32.00, cdf_stddev=3.02, cdf_avgdev=1.72
ME 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00, quantile_stddev=20.83, quantile_avgdev=16.16
QJ 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): random_mean=2686.82, random_median=2649.00, random_min=2457.00, random_max=3753.00, random_stddev=150.32, random_avgdev=98.23
OO 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): pdf_mean=6.13, pdf_median=6.00, pdf_min=5.00, pdf_max=24.00, pdf_stddev=2.38, pdf_avgdev=1.22
DG 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): cdf_mean=12.21, cdf_median=11.00, cdf_min=11.00, cdf_max=33.00, cdf_stddev=3.07, cdf_avgdev=1.58
LJ 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00, quantile_stddev=4.81, quantile_avgdev=2.28
EM 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): random_mean=1130.39, random_median=1108.00, random_min=1039.00, random_max=1454.00, random_stddev=69.41, random_avgdev=51.70
GP 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): pdf_mean=1.15, pdf_median=1.00, pdf_min=0.00, pdf_max=19.00, pdf_stddev=1.34, pdf_avgdev=0.45
OI 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): cdf_mean=0.81, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.16, cdf_avgdev=0.49
CN 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00, quantile_stddev=0.82, quantile_avgdev=0.49
EG 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): random_mean=293.70, random_median=281.00, random_min=256.00, random_max=537.00, random_stddev=43.28, random_avgdev=31.62
FD 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): pdf_mean=1.99, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.48, pdf_avgdev=0.48
PN 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): cdf_mean=3.19, cdf_median=3.00, cdf_min=2.00, cdf_max=17.00, cdf_stddev=1.61, cdf_avgdev=0.64
DH 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.77, quantile_avgdev=0.64
NR 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): random_mean=479.75, random_median=468.00, random_min=428.00, random_max=754.00, random_stddev=48.26, random_avgdev=34.30
FL 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): pdf_mean=2.32, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.29, pdf_avgdev=0.54
QE 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): cdf_mean=8.01, cdf_median=7.00, cdf_min=6.00, cdf_max=39.00, cdf_stddev=3.13, cdf_avgdev=1.73
MM 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00, quantile_stddev=10.28, quantile_avgdev=7.73
KG 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): random_mean=951.58, random_median=931.00, random_min=859.00, random_max=1439.00, random_stddev=78.14, random_avgdev=49.72
CQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): pdf_mean=38.47, pdf_median=35.00, pdf_min=32.00, pdf_max=164.00, pdf_stddev=9.66, pdf_avgdev=6.38
OO 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): cdf_mean=27.75, cdf_median=25.00, cdf_min=24.00, cdf_max=80.00, cdf_stddev=7.02, cdf_avgdev=4.63
PF 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00, quantile_stddev=128.18, quantile_avgdev=74.83
OR 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): random_mean=1550.27, random_median=1520.00, random_min=1418.00, random_max=2317.00, random_stddev=112.08, random_avgdev=73.74
LQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1)
GH 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) 21 of 21 passed
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
 Торговая система 'Turtle Soup' и её модификация 'Turtle Soup Plus One'
Торговая система 'Turtle Soup' и её модификация 'Turtle Soup Plus One'
 Нейросеть: Самооптимизирующийся советник
Нейросеть: Самооптимизирующийся советник
 Основы программирования на MQL5: Глобальные переменные терминала MetaTrader 5
Основы программирования на MQL5: Глобальные переменные терминала MetaTrader 5
 Основы программирования на MQL5: Файлы
Основы программирования на MQL5: Файлы
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Формула в Документации:
это аналог в Википедии:
Посмотрел код.
В функции MathRandomNoncentralBeta() есть такие строки:
В той же Википедии есть такое:
The noncentral beta distribution (Type I) is the distribution of the ratio
where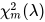 is a noncentral chi-squared random variable with degrees of freedom m and noncentrality parameter 𝜆 , and 𝜒 𝑛 2 is a central chi-squared random variable with degrees of freedom n, independent of 𝜒 𝑚 2 ( 𝜆 ) .
is a noncentral chi-squared random variable with degrees of freedom m and noncentrality parameter 𝜆 , and 𝜒 𝑛 2 is a central chi-squared random variable with degrees of freedom n, independent of 𝜒 𝑚 2 ( 𝜆 ) .
Т.е. берутся две случайные величины, где первая из нецентрального хи-квадрат распределения, а вторая - из центрального. Наверное код можно исправить на такой:
Изменённые графики в примере будут ниже.
Вот такие результаты.
Тоже не очень... Вообще работа с нецентральным бета-распределением скорее относится к классу нетривиальных задач. Из открытого кода удалось посмотреть Boost. И он будет посложнее чем тот, что сейчас есть в СБ.
В той же Википедии есть такое:
Т.е. берутся две случайные величины, где первая из нецентрального хи-квадрат распределения, а вторая - из центрального. Наверное код можно исправить на такой:
Изменённые графики в примере будут ниже.
Спасибо, Вы правы, нужно считать через эту формулу, однако там была еще другая ошибка, параметр нецентральности lambda нужно без множителя 2.
Тестовый скрипт:
Результат:
Проверил ещё функцию CFD для Noncentral Beta Distribution.
Какие-то сомнительные результаты:
В альтернативных источниках используется алгоритм ASA310:
К примеру некоторые из результатов в Wolfram Mathematica:
что более менее похоже на правду...