Матрицы и векторы в MQL5: функции активации

Введение

На тему обучения нейронных сетей уже опубликовано огромное количество книг и статей. И на нашем ресурсе MQL5.com участники сообщества также опубликовали множество материалов, в том числе несколько серий статей.

В данной публикации мы опишем только один из аспектов машинного обучения — функции активации. Мы покажем, что находится "под капотом".

Коротко

В искусственных нейронных сетях функция активации нейрона вычисляет значение выходного сигнала на основе значений входного сигнала или набора входных сигналов. Функция активации должна быть дифференцируемой на всём множестве значений. Это условие обеспечивает возможность обратного распространения ошибки при обучении нейронных сетей. Для обратного распространения ошибки должен быть вычислен градиент функции активации - вектор частных производных функции активации для каждого значения вектора входного сигнала. Считается, что нелинейные функции активации лучше для обучения. Хотя вполне линейная функция ReLU показала свою эффективность во многих моделях.

Иллюстрации

В качестве иллюстраций были подготовлены графики функции активации и их производных в монотонно возрастающей последовательности от -5 до 5. Был подготовлен скрипт, выводящий график функции на ценовом графике. Нажатием клавиши клавиши Page Down выводится диалог открытия файла для указания имени сохраняемой картинки.

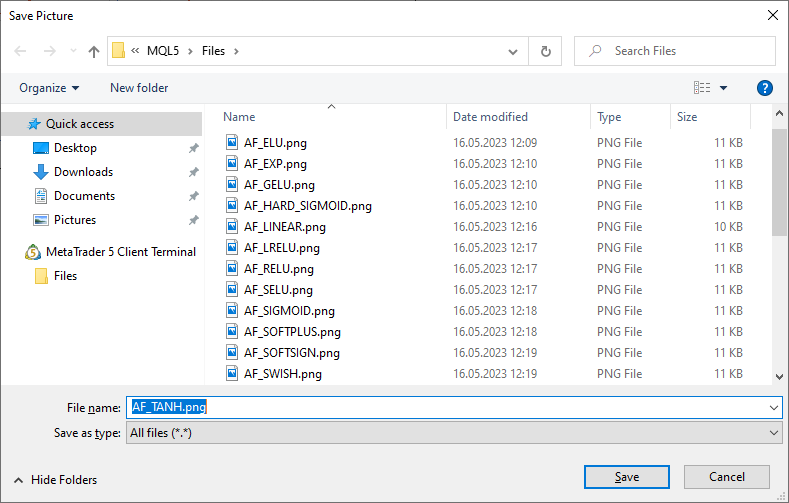
По клавише ESC производится завершение работы скрипта. Мы не приводим текст этого скрипта здесь - он приложен к статье. Аналогичный скрипт был написан автором статьи Нейронные сети обратного распространения ошибки на матрицах MQL5 — у него мы взяли идею выводить вместе с графиком функции активации ещё и график значений производных соответствующей функции активации.

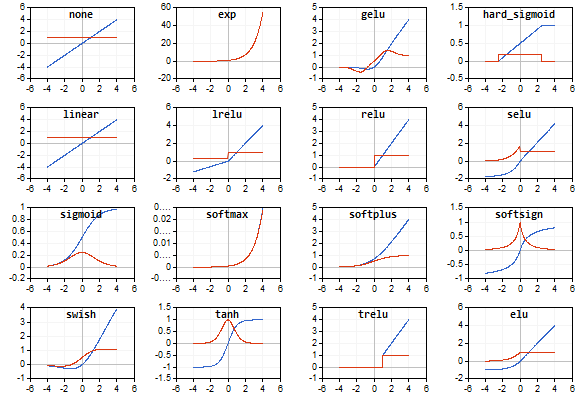
График функции активации отрисовывается линией синего цвета, график производных функции - красного.

Функция активации Exponential Linear Unit (ELU)

Вычисление функции

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Вычисление производной

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Эта функция предполагает дополнительный параметр alpha. Если он не указан, то его умолчательное значение равно 1.

   vector_a.Activation(vector_c,AF_ELU);      // вызов с умолчательным параметром

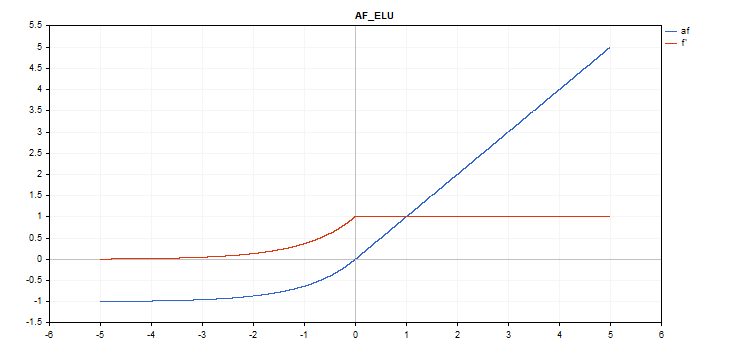
   vector_a.Activation(vector_c,AF_ELU,3.0);  // вызов с параметром alpha=3.0

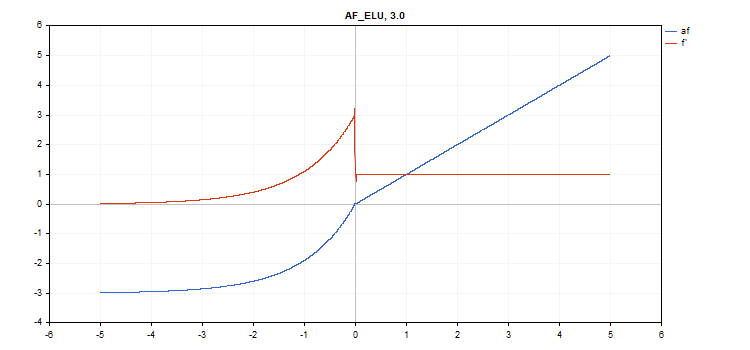
Функция активации Exponential

Вычисление функции

   f = exp(x);

Производной функции exp является эта же функция exp.

Как видно из формулы вычисления, у функции активации Exponential нет дополнительных параметров

vector_a.Activation(vector_c,AF_EXP);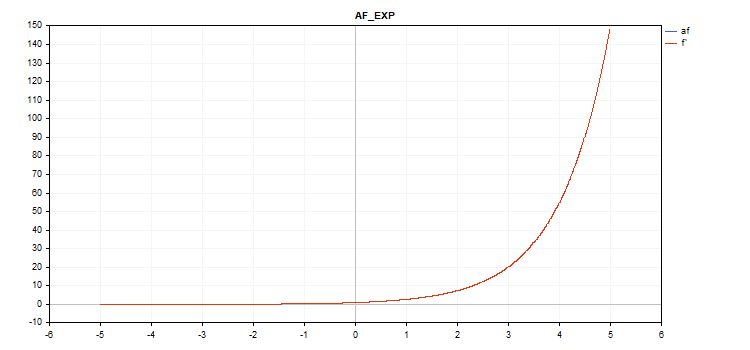

Функция активации Gaussian Error Linear Unit (GELU)

Вычисление функции

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Вычисление производной

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_GELU);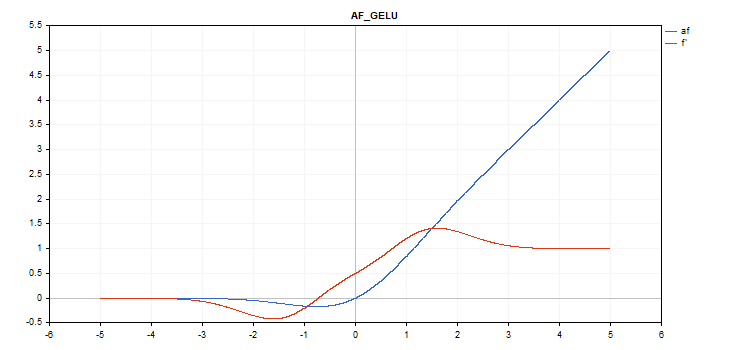

Функция активации Hard Sigmoid

Вычисление функции

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Вычисление производной

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

Дополнительных парметров нет.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);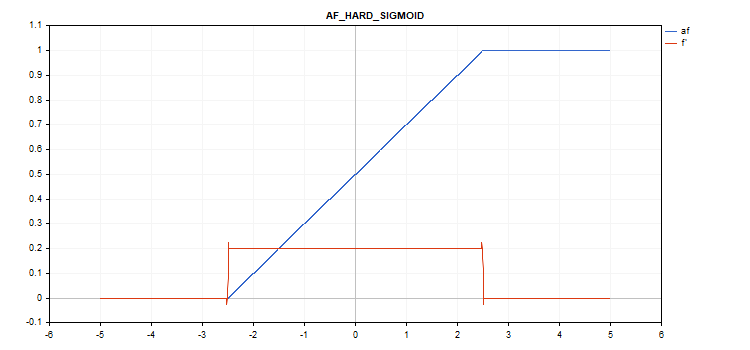

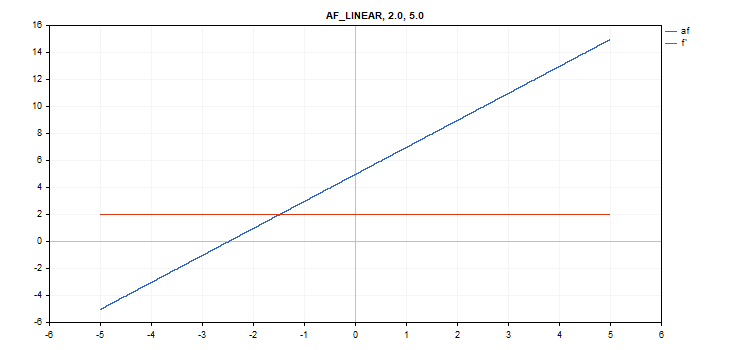
Функция активации Linear

Вычисление функции

   f = alpha*x + beta

Вычисление производной

   d = alpha

Дополнительные параметры alpha = 1.0 и beta = 0.0

vector_a.Activation(vector_c,AF_LINEAR);         // вызов с умолчательными параметрами

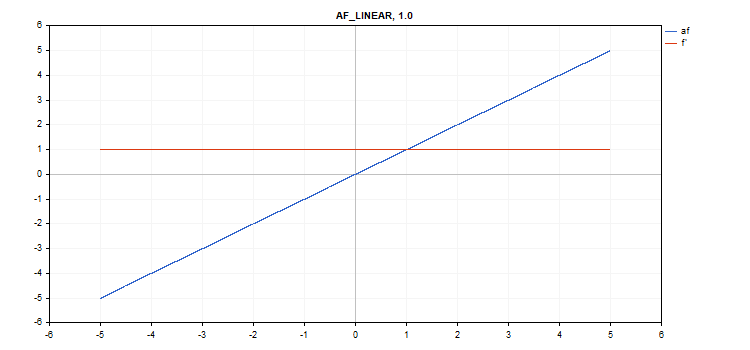
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // вызов с параметрами alpha=2.0 и beta=5.0

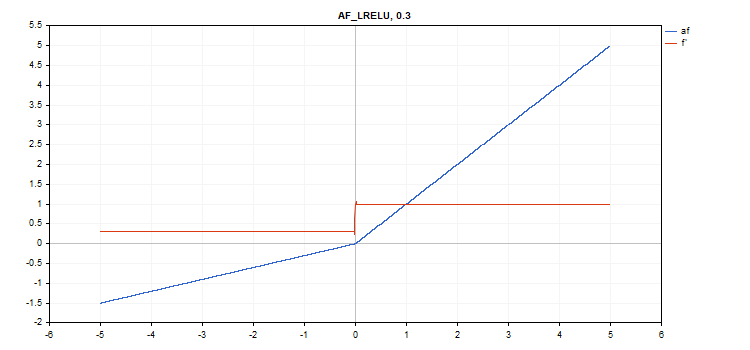
Функция активации Leaky Rectified Linear Unit (LReLU)

Вычисление функции

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Вычисление производной

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Эта функция предполагает дополнительный параметр alpha. Если он не указан, то его значение по умолчанию равно 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // вызов с умолчательным параметром

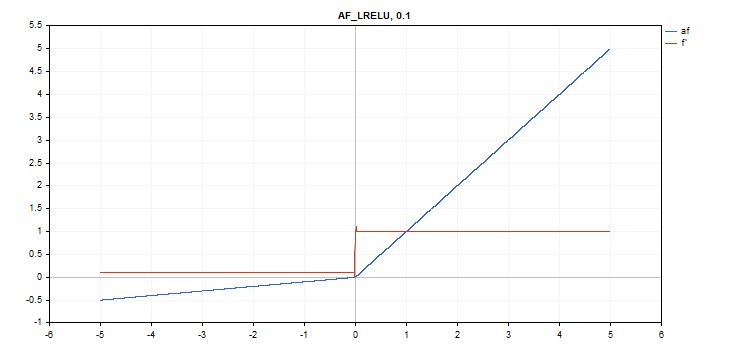
vector_a.Activation(vector_c,AF_LRELU,0.1);  // вызов с параметром alpha=0.1

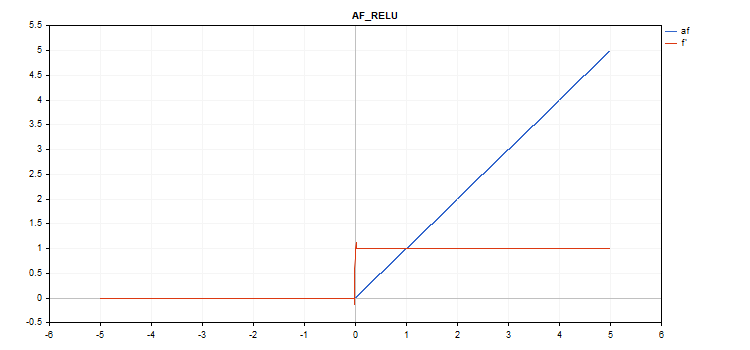
Функция активации Rectified Linear Unit (ReLU)

Вычисление функции

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Вычисление производной

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Дополнительные параметры alpha=0, max_value=0 и treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // вызов с умолчательными параметрами

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // вызов с параметрами alpha=2.0 и max_value=0.5

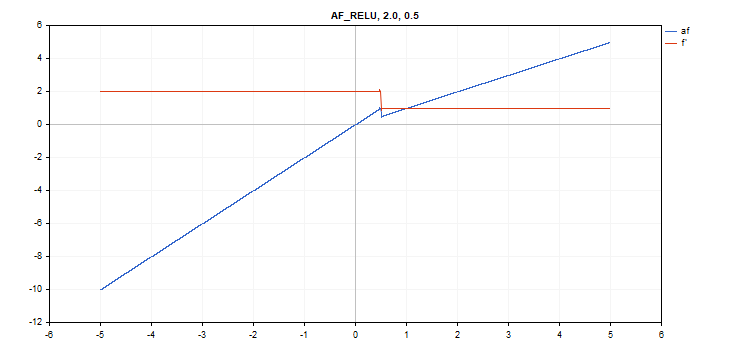
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // вызов с параметрами alpha=2.0, max_value=0.5 и treshold=1.0

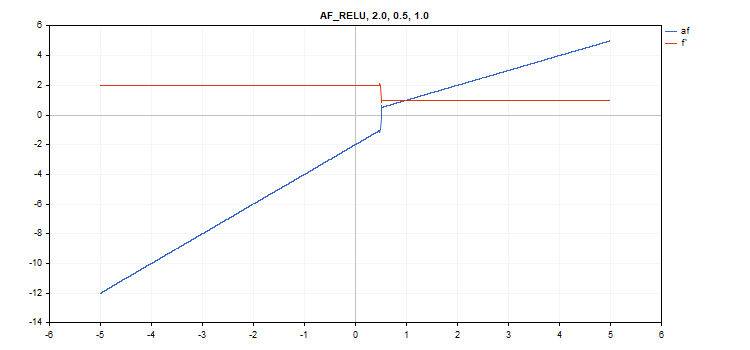
Функция активации Scaled Exponential Linear Unit (SELU)

Вычисление функции

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

где scale = 1.05070098, alpha = 1.67326324

Вычисление производной

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_SELU);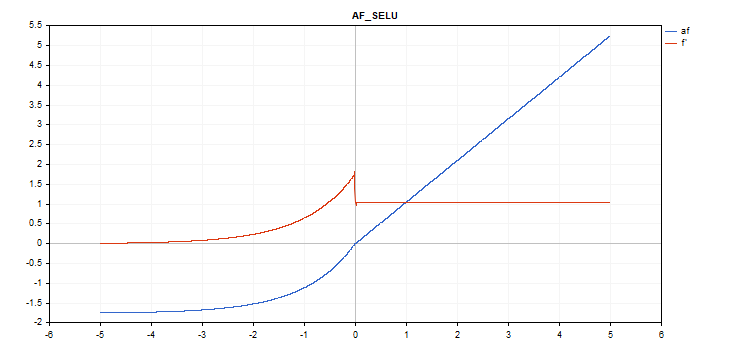

Функция активации Sigmoid

Вычисление функции

   f = 1 / (1 + exp(-x));

Вычисление производной

   d = exp(x) / pow(exp(x) + 1, 2);

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_SIGMOID);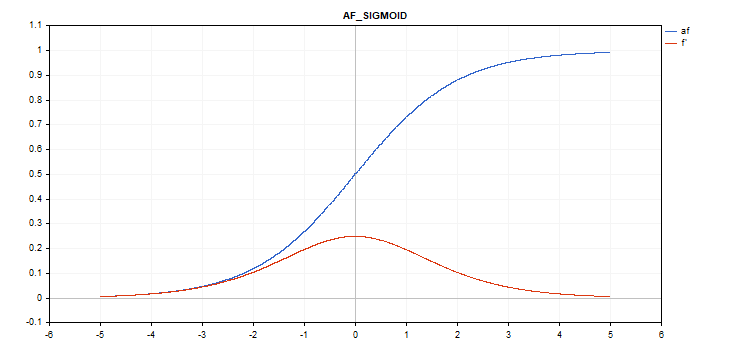

Функция активации Softplus

Вычисление функции

   f = log(exp(x) + 1);

Вычисление производной

   d = exp(x) / (exp(x) + 1);

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_SOFTPLUS);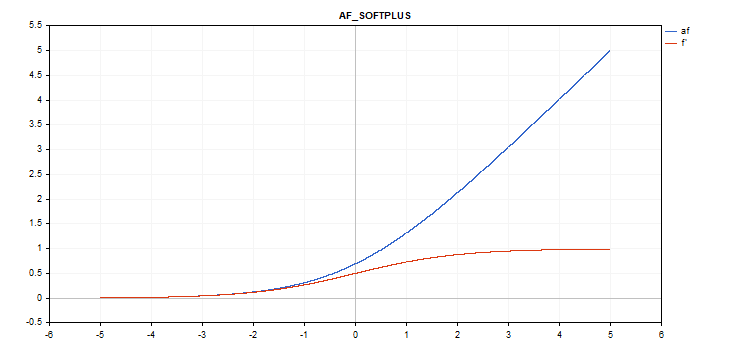

Функция активации Softsign

Вычисление функции

   f = x / (|x| + 1)

Вычисление производной

   d = 1 / (|x| + 1)^2

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_SOFTSIGN);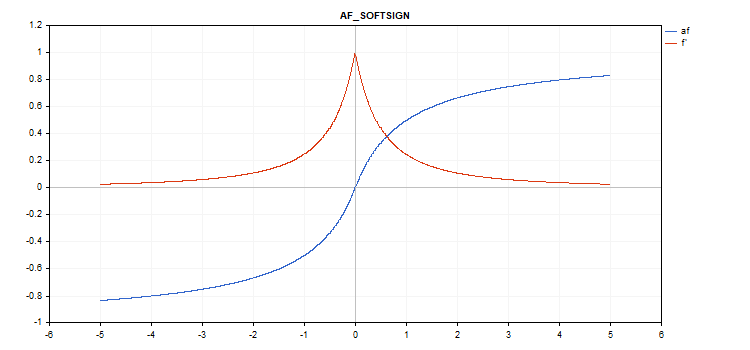

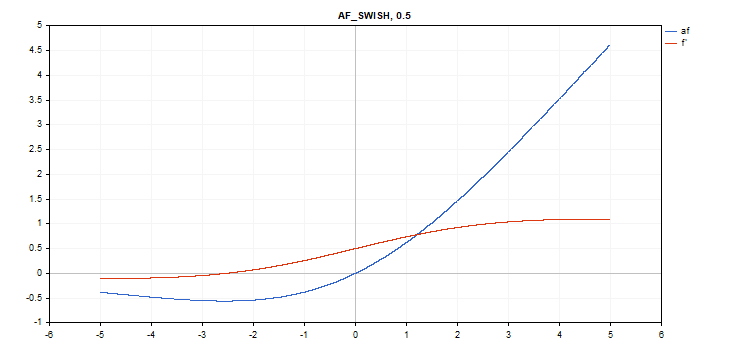
Функция активации Swish

Вычисление функции

   f = x / (1 + exp(-x*beta));

Вычисление призводной

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Дополнительный параметр beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // вызов с умолчательным параметром

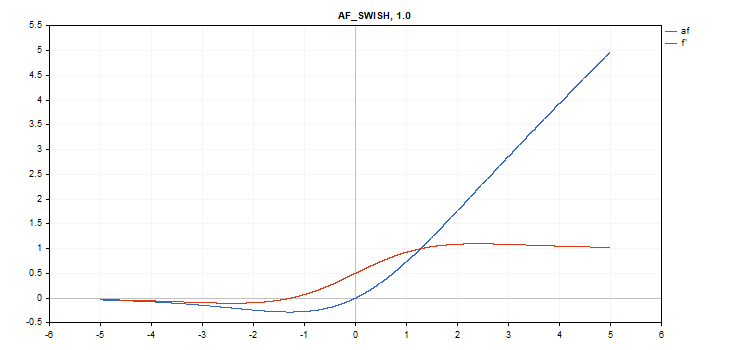
vector_a.Activation(vector_c,AF_SWISH,2.0);     // вызов с параметром beta = 2.0

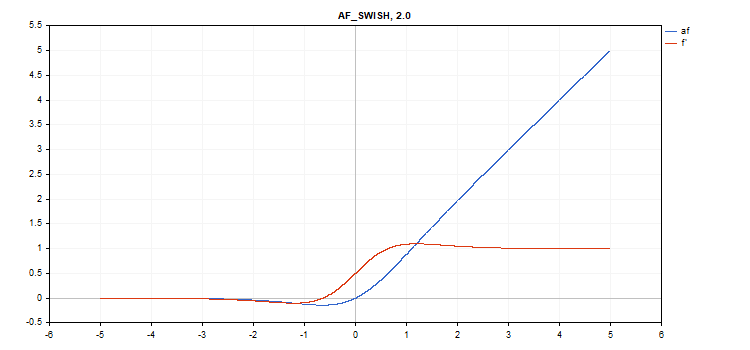
vector_a.Activation(vector_c,AF_SWISH,0.5);   // вызов с параметром beta=0.5

Функция активации Hyperbolic Tangent (TanH)

Вычисление функции

   f = tanh(x);

Вычисление производной

   d = 1 / pow(cosh(x),2);

Дополнительных параметров нет.

vector_a.Activation(vector_c,AF_TANH);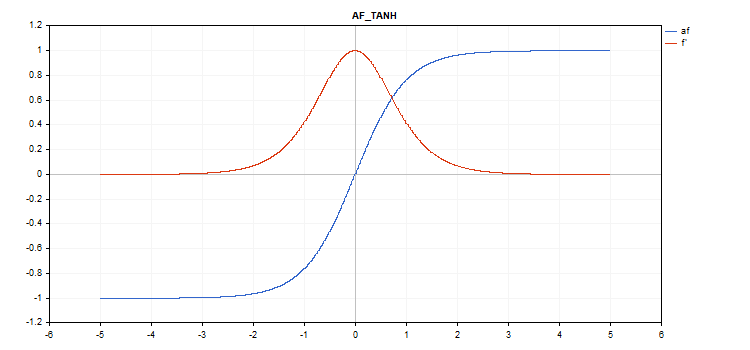

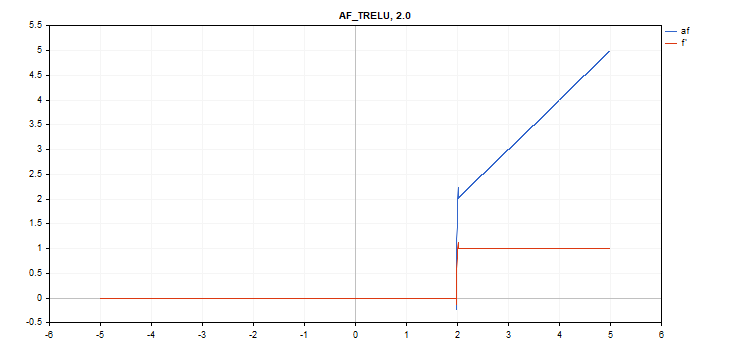
Функция активации Thresholded Rectifiedl Linear Unit (TReLU)

Вычисление функции

   if(x > theta)
      f = x;
   else
      f = 0;

Вычисление производной

   if(x > theta)
      d = 1;
   else
      d = 0;

Дополнительный параметр theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // вызов с умолчательным параметром

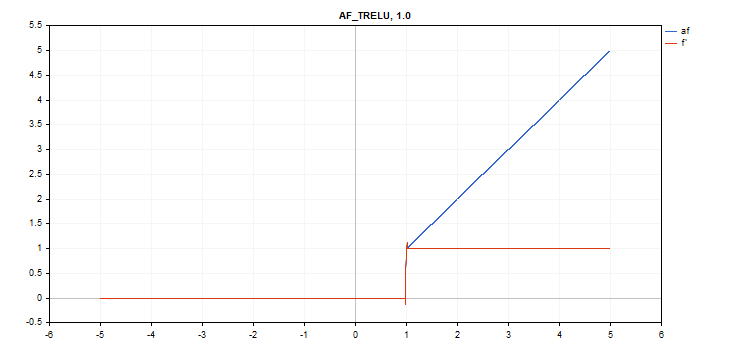
vector_a.Activation(vector_c,AF_TRELU,0.0);     // вызов с параметром theta = 0.0

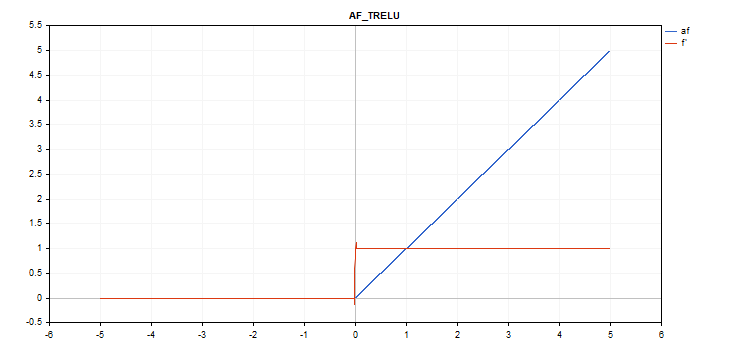
vector_a.Activation(vector_c,AF_TRELU,2.0);      // вызов с параметром theta = 2.0

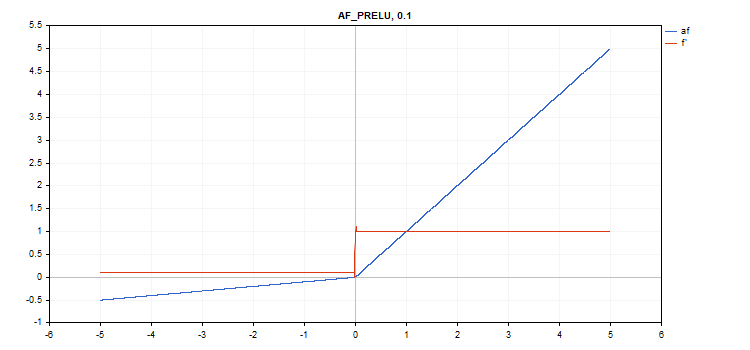
Функция активации Parametric Rectifiedl Linear Unit (PReLU)

Вычисление функции

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Вычисление производной

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

Дополнительный параметр - вектор коэффициентов alpha.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

Особая функция Softmax

Результат расчёта функции активации Softmax зависит не только от конкретного значения, но и от всех значений в векторе.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Вычисление производной

   d = f*(1 - f)

Таким образом, сумма всех активированных значений вектора равна 1. Поэтому функция активации Softmax очень часто используется для последнего слоя классификационных моделей.

График функции активации вектора со значениями от -5 до 5

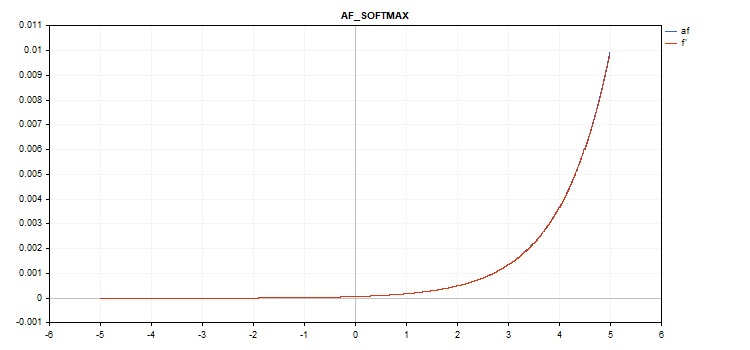
График функции активации вектора со значениями от -1 до 1

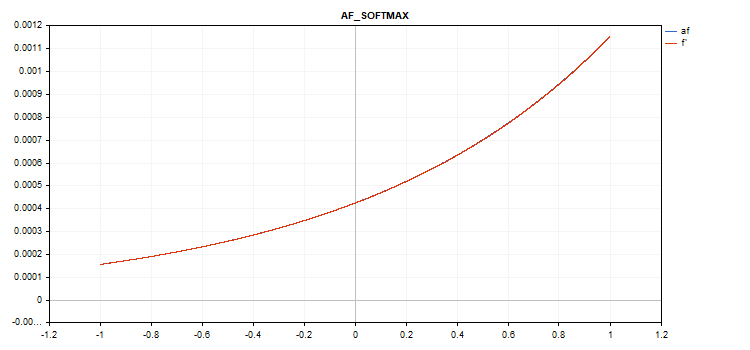
Если функция активации отсутствует (AF_NONE)

Если функция активации отсутствует, то значения из входного вектора передаются в выходной вектор без каких-либо преобразований. Фактически. это - функция активации Linear с параметрами alpha = 1 и beta = 0.

Заключение

В заключение предлагаем ознакомиться с исходными текстами функций активации и производных, которые содержатся в прикреплённом файле ActivationFunction.mqh.