Модель портфельного риска с использованием критерия Келли и моделирования по методу Монте-Карло

Введение

На протяжении десятилетий трейдеры использовали формулу критерия Келли для определения оптимальной доли капитала, которую можно направить на инвестиции или ставки, чтобы максимизировать долгосрочный рост при минимизации риска разорения. Однако слепое следование критерию Келли, основанному на результатах единственного бэк-тестирования, часто опасно для отдельных трейдеров, поскольку при реальной торговле торговое преимущество со временем тает, а прошлые результаты не являются предиктором будущих результатов. В настоящей статье я представлю реалистичный подход к применению критерия Келли для распределения рисков одного или нескольких советников в MetaTrader 5, основанный на результатах моделирования методом Монте-Карло с помощью Python.

Теория торговой модели с использованием кредитного плеча

Торговая модель с использованием кредитного плеча (Leverage Space Trading Model, LSTM) это теоретическая основа, используемая в основном в контексте финансовых рынков и управления активами. Она объединяет концепцию кредитного плеча, которая относится к использованию заемных средств для увеличения потенциальной прибыли, с более динамичным и пространственно ориентированным подходом к моделированию поведения рынка. 

LSTM использует критерий Келли для расчета процентного отношения портфеля к риску на сделку для единой стратегии

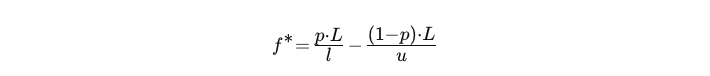
• L: коэффициент использования заёмных средств
• p: вероятность успеха
• u: коэффициент прибыли за счет заемных средств
• l: коэффициент убыточности с использованием заемных средств

Получив результат бэк-тестирования, можно получить значение переменной по следующим формулам.

Допустим, вы торгуете с кредитным плечом  2:1. Предположим следующее:

• Вероятность успешной сделки (p) = 0,6 (вероятность выигрыша 60%).
• Ожидаемая доходность (u) = 0,1 (10% прибыли без учета кредитного плеча, таким образом, при соотношении заемных средств 2:1 = 20% прибыли).
• Ожидаемая убыточность (l) = 0,05 (5% убытка без учета кредитного плеча, таким образом, при соотношении заемных средств 2:1 = 10% убытка).

Подставим в формулу Келли:

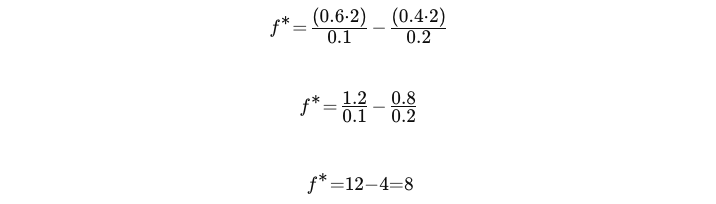
Таким образом, оптимальная доля вашего капитала, которой вы можете рискнуть в этой сделке, составит  8%  от вашего общего капитала.

Я полагаю, что после применения этой формулы к одному из ваших собственных советников вы неизбежно почувствуете дискомфорт, увидев, на какой риск вы пошли бы в каждой сделке. Действительно, эта формула предполагает, что ваши будущие результаты будут такими же хорошими, как и результаты бэк-тестирования, что нереально. Вот почему в этой отрасли люди обычно применяют дробную оценку своего риска по Келли, что означает, что они делят значение на некоторое целое число, чтобы уменьшить свой риск и оставить место для будущих неприятностей.

Теперь мы должны ответить: какую долю следует выбрать, чтобы трейдеры чувствовали себя комфортно, рискуя и при этом максимизируя ожидаемую прибыль на сделку?

Из книги The Leverage Space Trading Model Ральфа Винса (Ralph Vince), в ходе процесса стохастической оптимизации был сделан вывод о том, что функция ожидания доходности является выпуклой, независимо от размера. Это означает, что оптимальная ожидаемая доходность имеет единственное решение, и математическое ожидание непрерывно уменьшается по мере удаления значения f* от оптимального решения.

Это означает, что, поскольку торговля в реальном времени не так идеальна, как бэк-тестирование, мы ожидаем, что реальный f*, который максимизирует нашу прибыль, будет меньше, чем f*, рассчитанный по формуле Келли. Таким образом, все, что нам нужно сделать, это увеличить наш распределенный риск до максимально допустимого уровня, убедившись при этом, что он по-прежнему меньше, чем риск по Келли.

Обычно уровень толерантности трейдера измеряется максимальной просадкой, которую он может выдержать. Я предположу, что разумным уровнем допуска является максимальная просадка в 30% для остальной части статьи.

Применение риска с использованием кредитного плеча на MQL5

Чтобы применить риск с привлечением заемных средств в MQL5, сначала объявляем процент риска в качестве глобальной переменной. В этом случае у нас есть риск в размере 2% на сделку.

input double risk = 2.0;

Далее мы напишем функцию для расчета объема лота на основе стоп-лосса в текущей ценовой единице. Например, если стоп-лосс установлен по цене 0, точки стоп-лосса будут прямо соответствовать текущей цене, а результат сделки будет точно отражать движение базового актива.

//+------------------------------------------------------------------+
//| Calculate the corresponding lot size given the risk              |
//+------------------------------------------------------------------+
double calclots(double slpoints)
{
   double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

   double ticksize = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_SIZE);
   double tickvalue = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE);
   double lotstep = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP);

   double moneyperlotstep = slpoints / ticksize * tickvalue * lotstep;
   double lots = MathFloor(riskAmount / moneyperlotstep) * lotstep;
   lots = MathMin(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MAX));
   lots = MathMax(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MIN));
   return lots;
}

Приведенный выше код сначала определяет величину риска путем умножения баланса счета на процент риска.

Затем извлекает размер тика инструмента, значение тика и шаг лота, а также вычисляет денежную стоимость каждого шага лота на основе расстояния стоп-лосса.

Размер лота определяется путем деления суммы риска на сумму денег на каждый шаг лота и округления ее до ближайшего шага лота.

Наконец, прежде чем возвращать результат, он обеспечивает, что рассчитанный размер лота находится в пределах допустимых минимальных и максимальных объемов для данного инструмента.

Обратите внимание, что не каждая торговая стратегия предполагает фиксированный стоп-лосс и тейк-профит. Но в пространстве торговли с кредитным плечом мы предполагаем, что используем фиксированную точку стоп-лосса, потому что в соответствии с критерием Келли необходимо знать, насколько сильно мы хотим рискнуть, прежде чем заключать сделку.

Эта функция вызывается непосредственно перед выполнением каких-либо действий. Пример будет выглядеть следующим образом.

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy(double price) {
       double sl = price- slp*_Point;
       sl = NormalizeDouble(sl, _Digits);
       double lots = lotpoint;
       if (risk > 0) lots = calclots(slp*_Point);
       trade.BuyStop(lots,price,_Symbol,sl,0,ORDER_TIME_DAY,1);
       buypos = trade.ResultOrder();
       }

Обычно для стабильно прибыльного советника результат его бэк-тестирования должен быть похож на экспоненциальную функцию, подобную этой:

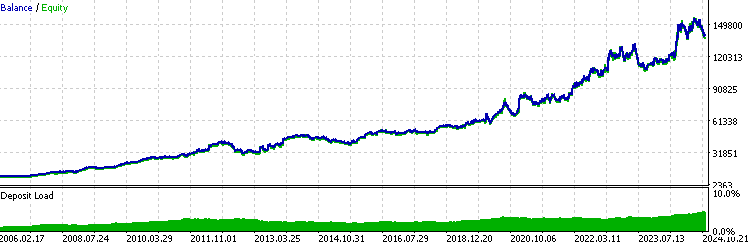
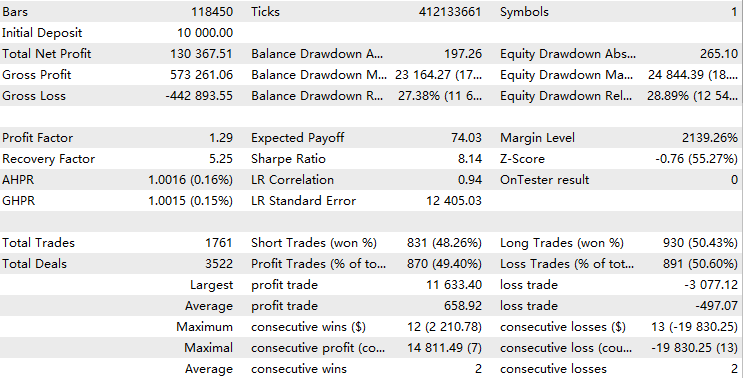
Вот несколько вещей, на которые следует обратить внимание при анализе статистики бэк-тестов при использовании этой модели торговли с кредитным плечом:

• Если ваш советник стабильно приносит прибыль, то последние результаты окажут большее влияние на общую эффективность бэк-тестирования, чем предыдущие. По сути, вы придаете больший вес важности недавних результатов.
• LR-Correlation бесполезен, поскольку график будет представлять собой экспоненциальную кривую.
• Коэффициент Шарпа становится нереалистичным, поскольку предполагает линейную зависимость между риском и доходностью. Кредитное плечо увеличивает как потенциальную доходность, так и риски, что приводит к искажению показателей эффективности с учетом рисков.

Если вы все еще хотите оценить вышеуказанные показатели, просто исправьте размер лота и проведите еще один тест.

Моделирование максимальной просадки по методу Монте-Карло

Мы рассматриваем кривую эквити как серию процентных изменений баланса нашего счета, а максимальную просадку можно рассматривать как сегмент этой серии с наименьшим совокупным процентом. Однократное бэк-тестирование представляет собой только один возможный вариант этой серии, что ограничивает ее статистическую надежность. Цель этого раздела - понять потенциальные просадки, с которыми можно столкнуться, а также выбрать 95-й процентиль в качестве ориентира для максимального допуска.

Моделирование по Монте-Карло можно использовать для моделирования возможной кривой эквити несколькими способами:

1. Случайная выборка доходности: Генерируя случайную доходность на основе исторических показателей или предполагаемых статистических распределений (например, нормальных), вы моделируете потенциальные кривые эквити, суммируя доходность с течением времени.

2. Бутстреппинг: Повторная выборка исторической доходности с заменой для создания нескольких имитируемых траекторий движения капитала, которые отражают изменчивость, наблюдавшуюся в прошлых показателях.

3. Перетасовка: Случайным образом изменяя порядок исторической доходности и используя перетасованные серии для создания различных траекторий движения капитала, можно использовать различные сценарии.

4. Корректировка рисков/доходности: Изменение входных параметров (например, волатильности или пределов просадки) на основе заданных критериев риска для получения реалистичных кривых эквити в различных рыночных условиях.

В настоящей статье мы сосредоточимся на методе перетасовки.

Во-первых, мы получаем отчет о сделке из результатов бэк-тестирования, щелкнув правой кнопкой мыши, как показано ниже.

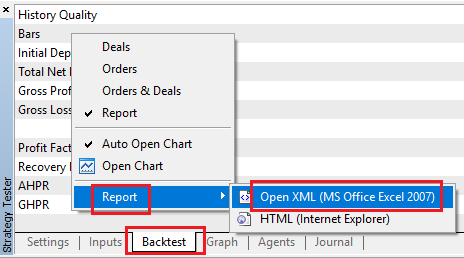
Затем мы открываем python и извлекаем полезные ряды, содержащие баланс счета и прибыль/убыток от каждой сделки, с помощью этого кода.

import pandas as pd
# Replace 'your_file.xlsx' with the path to your file
input_file = 'DBG-XAU.xlsx'
# Load the Excel file and skip the first {skiprows} rows
data = pd.read_excel(input_file, skiprows=10757)

# Select the 'profit' column (assumed to be 'Unnamed: 10') and filter rows as per your instructions
profit_data = data[['Profit','Balance']][1:-1] 
profit_data = profit_data[profit_data.index % 2 == 0]  # Filter for rows with odd indices
profit_data = profit_data.reset_index(drop=True)  # Reset index
# Convert to float, then apply the condition to set values to 1 if > 0, otherwise to 0
profit_data = profit_data.apply(pd.to_numeric, errors='coerce').fillna(0)  # Convert to float, replacing NaN with 0
# Save the processed data to a new CSV file with index
output_csv_path = 'processed-DBG-XAU.csv'
profit_data.to_csv(output_csv_path, index=True, header=['profit_loss','account_balance'])
print(f"Processed data saved to {output_csv_path}")

Ряды, которые нужно пропустить, - это в основном ряды выше этого индекса -1.

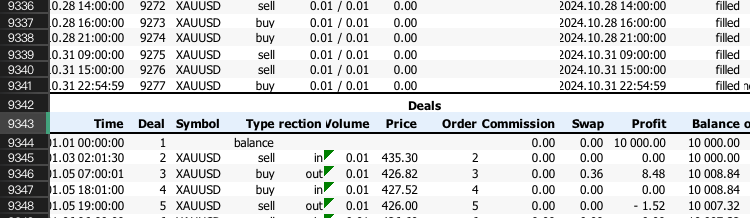
Затем нужно преобразовать прибыль в процентное изменение для каждой сделки, чтобы убедиться, что перетасованная серия приведет к одинаковому итоговому балансу. Это делается путем сдвига столбца баланса счета на один ряд и расчета прибыли или убытка в процентах от баланса перед каждой сделкой.

initial_balance = account_balance.iloc[0] - profit_loss.iloc[0]

# Calculate the account balance before each trade
account_balance_before_trade = account_balance.shift(1)
account_balance_before_trade.iloc[0] = initial_balance

# Compute the percentage change made to the account balance for each trade
percentage_change = profit_loss / account_balance_before_trade

# Fill any NaN values that might have occurred
percentage_change.fillna(0, inplace=True)

Наконец, мы моделируем 1000 случайных серий и выводим 10 лучших с наибольшей максимальной просадкой. Обратите внимание, что итоговое значение эквити должно быть одинаковым из-за коммутативного свойства умножения.  Умножение серии процентных изменений приведет к одному и тому же результату независимо от порядка, в котором значения были перетасованы.

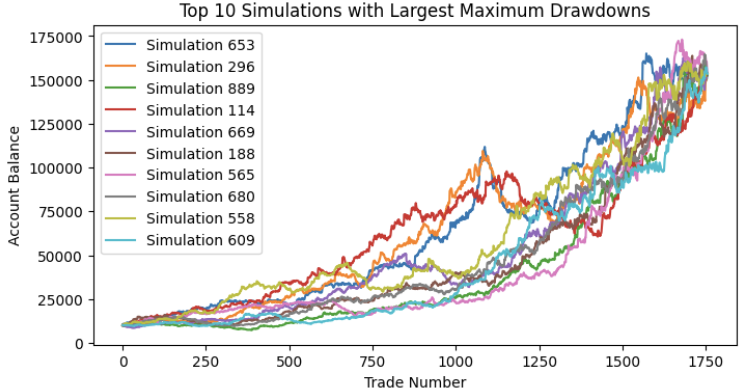
Распределение максимальной просадки должно быть похоже на нормальное распределение, и мы можем видеть здесь процентиль в 95% (около двух стандартных отклонений), здесь примерно 30% максимальная просадка.

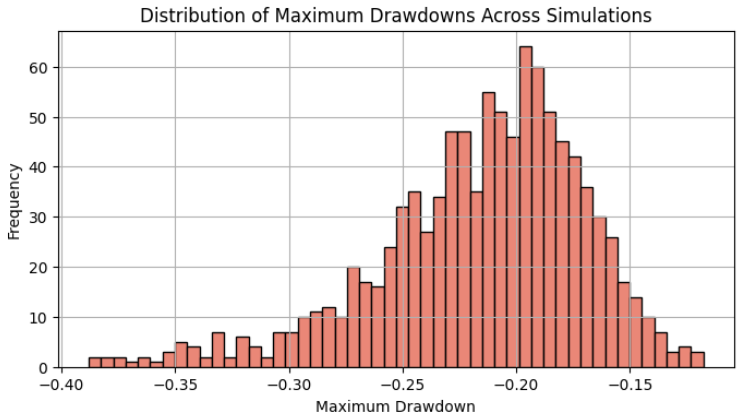
По нашим первоначальным бэк-тестам максимальная просадка составила всего 17%, что меньше среднего значения этого распределения. Если бы мы приняли это за максимальную просадку, которую ожидали, мы бы увеличили наш риск в 2 раза по сравнению с тем риском, на который мы готовы пойти сейчас, после получения результатов моделирования по методу Монте-Карло. Мы выбрали процентиль в 95%, потому что это общий результат, который, по мнению ученых, наиболее близок к реальным торговым показателям. Нам повезло, что процентиль в 95% точно соответствует нашему максимальному допуску в 30%, который был установлен в самом начале. Это означает, что если мы торгуем этим единственным советником в нашем портфеле, то риск в размере 2% на сделку максимизирует нашу прибыль, сохраняя при этом наши максимально допустимые пределы. Если результат отличается, следует повторять описанную выше процедуру до тех пор, пока не будет найдено оптимальное решение.

Критерий Келли для оптимизации портфеля

Если мы используем множество советников на одном счете, сначала необходимо выполнить описанную выше процедуру для каждого советника, чтобы определить его оптимальный риск. Затем мы применяем этот риск к выделенному капиталу для каждого советника в рамках общего портфеля. С точки зрения всего счета, сумма риска для каждого советника будет равна первоначальному риску, умноженному на выделенную долю.

Доля Келли, выделяемая каждому советнику, определяется его соотношением доходности с другими советниками и общей эффективностью при бэк-тестировании. Наша основная цель - обеспечить, чтобы советники максимально компенсировали просадку друг друга, что приведет к более плавной кривой эквити для всего портфеля. Важно отметить, что добавление большего количества советников и стратегий только увеличивает разнообразие портфеля, если они не связаны между собой; в противном случае это может увеличить общий риск, сродни увеличению риска одного советника.

В частности, мы рассчитываем долю распределения Келли для каждой стратегии на основе ожидаемой доходности и ковариационной матрицы доходности, используя следующие формулы:

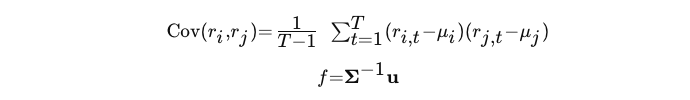
• r: доход EAi или EAj за время t
• μ: средний доход EAi или EAj
  
• f: Распределение Келли для каждого советника
• Σ−1: обратная ковариационная матрица
  
• u: вектор ожидаемой доходности для каждого советника

Чтобы извлечь значения для упомянутых выше переменных, необходимо провести бэк-тестирование по каждой стратегии и сохранить серию процентных значений доходности по каждой стратегии в одном фрейме данных. Затем, основываясь на частоте всех советников, мы выбираем подходящий временной интервал для записи, поскольку ковариация рассчитывается на основе корреляций доходностей за один и тот же период времени. Мы выполняем такие операции с помощью этого кода на python:

# Read returns for each strategy
    for file in strategy_files:
        try:
            data = pd.read_csv(file, index_col='Time')
            # Ensure 'Time' is parsed correctly as datetime
            data.index = pd.to_datetime(data.index, errors='coerce')
            
            # Drop rows where 'Time' or 'return' is invalid
            data.dropna(subset=['return'], inplace=True)
            
            # Aggregate duplicate time indices by mean (or could use 'sum', but here mean can ignore the trade frequency significance)
            data = data.groupby(data.index).agg({'return': 'mean'})
            
            # Append results
            returns_list.append(data['return'])
            strategy_names.append(file)
        except Exception as e:
            print(f"Error processing {file}: {e}")
            continue 
    # Check if any data was successfully loaded
    if not returns_list:
        print("No valid data found in files.")
        return  
    # Combine returns into a single DataFrame, aligning by date
    returns_df = pd.concat(returns_list, axis=1, keys=strategy_names) 
    # Uncomment the below line if u wanna drop rows with missing values across strategies
    #returns_df.dropna(inplace=True)
    #Uncomment the below line if u wanna just fill unaligned rows with 0( I think this is best for backtest that may have years differences)
    returns_df.fillna(0, inplace=True)

Убедитесь, что все результаты бэк-тестирования начинаются и заканчиваются в одно и то же время. Кроме того, выберем подходящий временной интервал для агрегирования результатов таким образом, чтобы ни в одном интервале не было чрезмерного количества сделок, а также, чтобы ни один интервал не был сделок вообще. Если временные интервалы слишком дискретны, то для точного вычисления ковариации может быть недостаточно точек данных в пределах одних и тех же временных диапазонов. В нашем случае выбираем интервал в один месяц и используем среднюю доходность за каждый месяц в качестве признака доходности.

Выполним расчеты:

    # Calculate expected returns (mean returns)
    expected_returns = returns_df.mean()
    
    # Calculate the covariance matrix of returns
    cov_matrix = returns_df.cov()
    
    # Compute the inverse of the covariance matrix
    try:
        inv_cov_matrix = np.linalg.inv(cov_matrix.values)
    except np.linalg.LinAlgError:
        # Use pseudo-inverse if covariance matrix is singular
        inv_cov_matrix = np.linalg.pinv(cov_matrix.values)
    
    # Calculate Kelly optimal fractions
    kelly_fractions = inv_cov_matrix @ expected_returns.values
    kelly_fractions = kelly_fractions / np.sum(kelly_fractions)

В конце концов, получаем примерно такой результат:

         Strategy  Kelly Fraction
0  A1-DBG-XAU.csv        0.211095
1   A1-DBG-SP.csv        0.682924
2   A1-DBG-EU.csv        0.105981

Мы можем напрямую внедрить этот риск в наш исходный MQL5-код, поскольку первоначальный расчет риска уже был основан на общем балансе счета. При изменении баланса счета выделенный капитал будет автоматически пересчитан и применен к следующей сделке.

double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

Например, чтобы применить рассчитанную долю Келли к нашему примеру советника, мы просто модифицируем эту часть исходного кода, и задача выполнена.

input double risk = 2.0*0.211095;

Я полностью осознаю, что мы могли бы в качестве альтернативы пересчитать риск, основываясь на изменении выделенного капитала для каждого советника, но предпочтительнее основывать расчет на всем портфеле по следующим причинам:

1. На мой взгляд, отслеживать изменения в различных распределенных капиталах непросто. Возможно, придется открыть несколько счетов или написать программу для обновления изменений после каждой сделки.
2. Критерий Келли используется для максимизации долгосрочного роста всего портфеля. Эффективность работы отдельных советников влияет на риск других советников, тем самым способствуя эффективному росту небольшого портфеля по мере его масштабирования.
3. Если мы будем основывать риск на изменении выделенного капитала для каждого советника, то у хорошо работающих советников с течением времени будет увеличиваться выделенный капитал, что приведет к увеличению подверженности этих советников риску. Это подрывает наше первоначальное намерение рассчитать распределение рисков на основе корреляций.

Однако наш подход обладает определенными ограничениями:

1. Риск для каждого советника колеблется с общей эффективностью портфеля, что затрудняет отслеживание эффективности отдельных советников. Весь портфель можно рассматривать как индекс, подобный S&P 500. Чтобы оценить индивидуальную эффективность, нужно было бы рассчитать процентное изменение, а не абсолютную прибыль.
2. Наш расчет распределения рисков не учитывает частоту сделок каждого советника. Это означает, что если у советников на одном и том же счете значительно различается частота совершения сделок, это может привести к неравномерной подверженности рискам, несмотря на распределение.

В целом, учитывая потенциал максимизации роста для индивидуальных трейдеров, этот подход стоит принять на вооружение.

Заключение

В настоящей статье мы представили критерий Келли в контексте торговой модели с использованием кредитного плеча и его применения к трейдингу. Затем мы предоставили код реализации на MQL5. После этого мы использовали моделирование Монте-Карло для определения оптимальной максимальной просадки на основе одного бэк-теста, который затем был применен для оценки риска для отдельных советников. Наконец, мы представили подход к распределению капитала для каждого советника, основанный на результатах их бэк-тестирования и корреляции.

Таблица файлов

Название	Применение
KellyMultiFactors.ipynb	Расчет доли Келли для распределения капитала
MonteCarloDrawdown.ipynb	Выполнение моделирования по методу Монте-Карло