
Нейросети в трейдинге: Модель адаптивной графовой диффузии (модуль внимания)
Введение
В предыдущей статье мы познакомились с фреймворком SAGDFN. Обсудили ключевые принципы его работы, расставили акценты на сильных сторонах. Но рынок — не музей архитектурных макетов. Здесь не прощают излишней задумчивости и безжизненных схем. Чтобы здание стояло, его надо строить — кирпич за кирпичом, при этом проверяя каждый уровень на прочность.
Фреймворк SAGDFN изначально задумывался, как ответ на одну из старейших и в то же время самых живых проблем финансовых рынков: избыточность данных и шум, маскирующий истинные сигналы. Классические методы анализа либо тонули в этом информационном потоке, либо пытались осушить его грубой фильтрацией. SAGDFN же предлагает иной путь — не просто фильтровать, а выбирать с умом. Авторы фреймворка предложили оставлять только тех соседей, которые действительно влияют на поведение системы. Это сродни старой торговой мудрости: слушай рынок, но умей отличать крики толпы от шёпота тех, кто знает путь.
Ключевая идея, вокруг которой строится вся архитектура, — это Significant Neighbors Sampling, динамическая система выборки значимых соседей. Представьте себе старый порт, куда каждую минуту приходят сотни кораблей с новостями со всех морей. Не каждый из них важен для твоего бизнеса: кто-то несёт лишь сплетни с чужих рынков, кто-то — груз, который завтра обесценится. Задача SAGDFN — впустить только тех, чьи паруса действительно тянут торговлю в нужном направлении. Для этого модель использует комбинацию детерминированной оценки важности и контролируемой случайности — своеобразного ветра перемен, который не даёт системе застыть в привычных связях и тем самым снижает риск переобучения.
Не менее значимым элементом стал и механизм α-Entmax — математический дирижёр распределения внимания. Он, в отличие от мягкого, но всепоглощающего SoftMax, не распыляет силы на всех, а разрежает распределение, оставляя сильные акценты там, где они действительно нужны. Это похоже на старинное умение купца — не распылять капитал на мелочи, а вкладывать в то, что принесёт наибольшую отдачу.
SAGDFN отличается ещё и сбалансированностью между локальным и глобальным контекстом. Он умеет, как опытный аналитик, смотреть на рынок вблизи — анализируя соседние данные, отдельные бары, локальные кластеры сделок. И в то же время держать в памяти общую картину: тренды, накопленные закономерности, структуру долгосрочных потоков. В этом отношении он выполняет функцию навигатора, который ведёт корабль по звёздам, но не забывает и про глубину под килем.
Архитектура фреймворка SAGDFNмодульна и расширяема, что особенно ценно в условиях постоянно меняющихся торговых условий. Здесь нет каменных стен, ограничивающих исследователя. Каждый блок — будь то выборка соседей, нормализация внимания или интеграция с внешними источниками данных — может быть доработан, оптимизирован или заменён.
Авторская визуализация фреймворка SAGDFN представлена ниже.
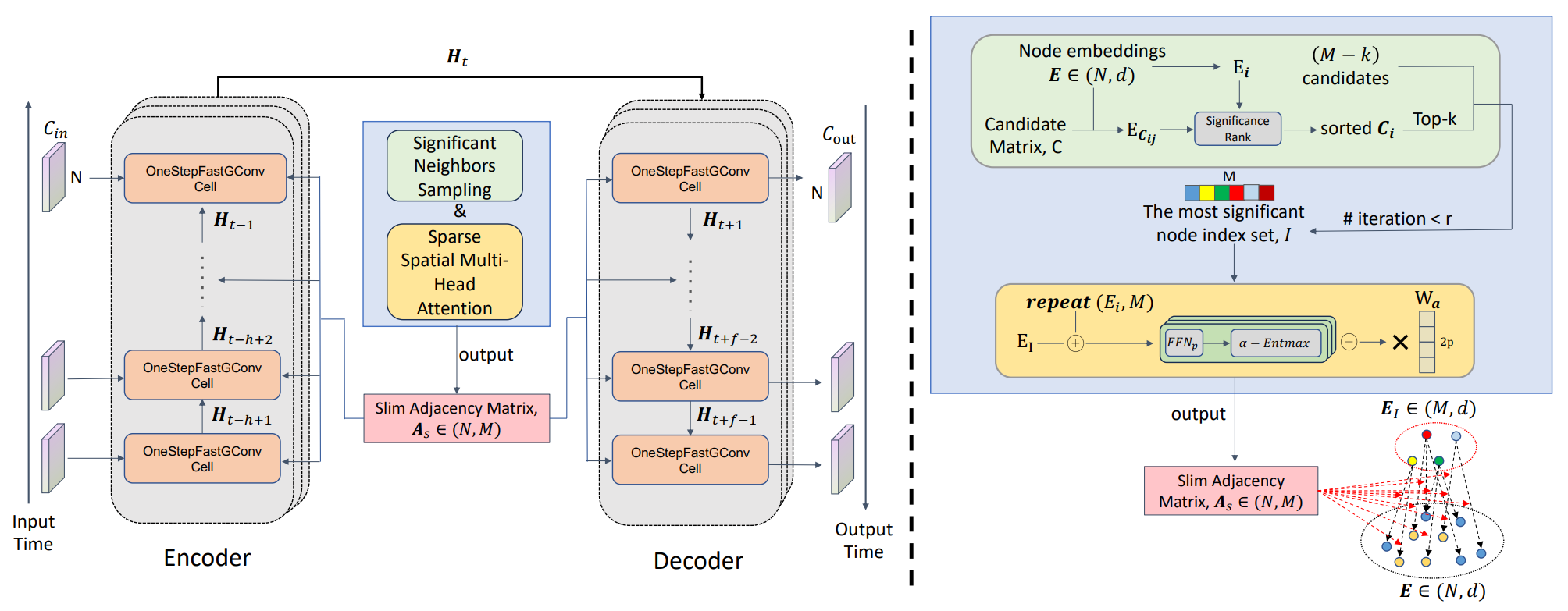
В практической части предыдущей статьи мы уже сделали первый серьёзный шаг — реализовали алгоритм модуля Significant Neighbors Sampling на стороне OpenCL-контекста, тем самым заложив фундамент всей конструкции. Мы научились извлекать из огромного массива данных именно те связи, которые имеют реальное значение, и передавать их в дальнейший вычислительный поток без избыточного шума. Это был не просто технический эксперимент, а ключевой этап формирования будущего торгового механизма: без отлаженного механизма выборки невозможно построить надёжную систему анализа.
Сегодня мы продолжаем нашу работу и переходим к следующему уровню интеграции собственного видения подходов, предложенных авторами фреймворка SAGDFN, средствами MQL5.
Обсуждение реализации
После успешной реализации алгоритмов модуля Significant Neighbors Sampling — механизма отбора наиболее значимых связей, наступает следующий логический этап — переход от подготовки данных к их более глубокому анализу и преобразованию. Сегодня мы начинаем работу с построения алгоритмов модуля Sparse Spatial Multi-Head Attention, который станет ключевым инструментом для извлечения структурных закономерностей из уже отобранных соседей.
Этот модуль — своего рода умное сито, способное не просто обработать информацию, а распределить внимание модели таким образом, чтобы она фокусировалась на действительно значимых пространственных связях, не теряя при этом глобального контекста. Он использует многоголовый механизм внимания, но в отличие от классического подхода, авторы фреймворка реализуют его в разреженном формате. Это позволяет существенно снизить вычислительную нагрузку без ущерба для качества анализа. Таким образом, каждый поток данных проходит не сквозь монолитную матрицу весов, а через более экономную, но при этом избирательно насыщенную сеть вниманий, где каждая голова внимания выполняет свою функцию фильтрации и акцентирования.
Прежде чем приступить к непосредственной реализации, важно очертить наше видение того, как будет построена наша реализация предлагаемых авторами фреймворка алгоритмов, и какие ключевые моменты заслуживают особого внимания. Авторы фреймворка предлагают достаточно интуитивный и наглядный подход. Для построения графа они попарно конкатенируют эмбеддинги каждого элемента с эмбеддингами его ближайших соседей, предварительно отобранных в модуле Significant Neighbors Sampling. Затем каждая такая пара проходит через компактную полносвязную модель, которая и формирует дальнейшее представление связей.
На первый взгляд, методика выглядит прозрачной и логичной, а процесс обработки — простым и прямолинейным. Однако, если рассматривать этот подход в контексте практической реализации, особенно на реальных торговых данных с высокой плотностью связей, становится очевидно, что за такой кажущейся простотой скрываются весьма серьёзные издержки. Попарная конкатенация эмбеддингов для каждого элемента и его соседей приводит к значительному росту объёмов данных, а значит, увеличивает и требования к оперативной памяти. Каждая пара фактически создаёт новый вектор, и чем больше таких пар, тем больше ресурсов требуется для их хранения и дальнейшей обработки.
Кроме того, использование полносвязной модели для каждой пары добавляет вычислительную нагрузку, поскольку каждая пара должна пройти индивидуальную обработку. Это приводит к увеличению времени выполнения и делает систему менее гибкой при работе с большими графами или в условиях ограниченных вычислительных мощностей. Таким образом, при всей визуальной ясности данного решения, оно может стать узким местом на пути к построению эффективной и масштабируемой системы.
Если присмотреться к исходному конструкту внимательнее, становится очевидно: авторы пропускают через одну и ту же маленькую полносвязную сеть все пары [ei ‖ ej]$, где ei — эмбеддинг узла, а ej — эмбеддинг одного из его отобранных соседей. Параметры этой сети общие для всех пар: это не множество разных моделей, а один и тот же набор весов, который переиспользуется снова и снова. Именно эта общность — наш рычаг для ускорения.
Полносвязный слой по своей сути — линейное преобразование плюс нелинейность. На этапе линейной части он умножает компоненты входного вектора на соответствующие веса и суммирует. Если вход — конкатенация [ei ‖ ej] ∈ R2d, а матрица весов первого слоя W ∈ Rh * 2d, то произведение распадается на сумму двух слагаемых.
![]()
где W1 и W2 ∈ Rh * d — левая и правая половины W.
Это простое алгебраическое наблюдение и открывает нам дорогу: вместо того чтобы по M раз прогонять каждый ei через один и тот же слой для всех его соседей, разумнее один раз посчитать проекцию каждого узла pi = W1 ei и отдельно проекцию соседа ki = W2 ei. Тогда любая пара (i,j) на линейной стадии получается мгновенно как pi + kj. Дальше — та же нелинейность и следующая линейная голова внимания, но уже без повторяющейся тяжёлой матрицы на конкатенации.
На практике это означает, что мы заранее умножаем исходный тензор эмбеддингов E на две матрицы весов, получая два тензора проекций. Эти операции выполняются один раз на батч и отлично векторизуются на GPU. После этого, для каждой пары узел—сосед нам остаётся только сложить соответствующие проекции. Выигрыш двоякий: каждое ei умножается на веса запроса W1 ровно один раз, независимо от того, сколько у него соседей, а каждое ej умножается на веса ключей W2 тоже один раз, даже если встречается в десятках чужих списков. Плотная часть работы перестаёт масштабироваться с M.
Если сосредоточиться на порядках сложности, становится заметно, как меняется профиль нагрузки. Наивная конкатенация заставляет выполнять N * M умножений матрица–вектор размерности h * 2d, что даёт O(NMhd) на первую линейную стадию. Перефакторизованный путь делает два умножения EW1 и EW2 за O(Nhd) каждое, а затем лишь N * M сложений h-мерных векторов и лёгкую голову, то есть O(NMh) без дорогостоящего множителя d. Когда d велик и M немал, разница ощущается буквально на стенке профайлера. В терминах памяти история похожая: вместо хранения N * M конкатенированных векторов длиной 2d мы держим два матрица-пула P и K по N * h и на лету формируем суммы для нужных пар. Давление на память спадает, а пропускная способность ALU используется эффективнее.
Эта же логика прекрасно стыкуется с нашей реализацией в MQL5 + OpenCL. Для формирования проекций можем воспользоваться обычным сверточным слоем с количеством фильтров равным 2h, который запускается один раз на проход, независимо от текущего набора соседей. Это важно, потому что список I может меняться от итерации к итерации, а пересчёт проекций всё равно остаётся стабильным и дешёвым. Далее для каждой пары (i,j) мы читаем строки Pi и Kj, суммируя поэлементно и применяем голову внимания. В местах, где раньше стояли матричные умножения на конкатенированные тензоры, теперь остаются аккуратные векторные суммирования и одна маленькая линейка — операции, идеально подходящие для широкой векторизации. Если поверх этого используется разреженная нормализация внимания, то она работает уже с полученными логитами и никак не ломает схему предварительных проекций.
Есть и приятный бонус в интерпретируемости. Матрица W1 начинает играть роль запросной проекции, а W2 — ключей. По их строкам и активациям видно, какие компоненты эмбеддинга активнее формируют внимание в конкретной голове. Для риск-менеджмента это мелочь, которая позволяет объяснить, почему модель смотрит на нефть, а не на облигации в данный момент, или почему валютная пара внезапно стала доминирующим соседом для технологических акций.
Ещё один важный аспект, который заслуживает отдельного внимания, связан с использованием функции α-Entmax. Её ключевая особенность заключается в способности мягко нормализовать исходные данные с возможностью регулирования уровня отсеивания малозначительных элементов. При α==1 данная функция эквивалентна классическому SoftMax, а при α==2 она приближается к Sparse-SoftMax, обеспечивая более агрессивное обнуление несущественных значений. Однако, несмотря на привлекательность этой идеи, необходимо учитывать, что алгоритм α-Entmax требует итеративного поиска параметра τ, что неизбежно увеличивает вычислительную сложность и время выполнения операции. В нашей реализации мы решили сделать акцент на эффективности и заменили данную функцию на Sparse-SoftMax. Такой выбор позволяет сохранить концепцию фреймворка, ориентированную на исключение малозначительных элементов из анализа, но при этом обеспечивает более высокую производительность и снижает затраты ресурсов на этапе вычислений.
В следующем шаге мы аккуратно вплетём эту схему в наш существующий конвейер. Линейная алгебра уже сделала за нас тяжёлую работу — осталось правильно разложить вычисления во времени и памяти, чтобы наша многоголовая оптика внимания фокусировалась быстро, чётко и без лишнего шума.
Дополнение OpenCL-программы
После того как мы обсудили архитектурные принципы модуля Sparse Spatial Multi-Head Attention, самое время перенести эту концепцию в практическую реализацию. На предыдущем этапе мы подчеркнули, что однократное умножение исходного тензора на матрицу параметров не только экономит ресурсы, но и позволяет сохранять все ключевые характеристики алгоритма, включая отбор наиболее значимых соседей. В контексте OpenCL это приобретает особое значение: здесь каждая операция и каждая локальная память оптимизируются для высокой производительности.
Мы начинаем с кернела прямого прохода SparseMHScores, который отвечает за вычисление весовых коэффициентов между центральными элементами и их наиболее значимыми соседями. Кернел построен так, чтобы обработка каждого элемента была максимально параллельной. И при этом сохраняется контроль за разреженностью весов.
__kernel void SparseMHScores(__global const float* data,
__global const float* indexes,
__global float* scores,
const float sparse ///< [0.0 .. 1.0) coefficient of sparse
)
{
const int main = (int)get_global_id(0);
const int slave = (int)get_local_id(1);
const int head = (int)get_global_id(2);
const int total_mains = (int)get_global_size(0);
const int total_slaves = (int)get_local_size(1);
const int total_heads = (int)get_global_size(2);
Сначала каждый глобальный поток получает индекс своего основного элемента main и локальный идентификатор соседа slave. Параллельно определяется текущая голова внимания head, что позволяет обрабатывать все головки одновременно и создавать многомерную карту корреляций. Далее создаётся локальный массив Temp, который используется для временного хранения промежуточных вычислений при нахождении максимальных и минимальных значений в блоке.
__local float Temp[LOCAL_ARRAY_SIZE];
Затем мы извлекаем значения логитов основного элемента и его соседа из массивов data. Функция IsNaNOrInf обеспечивает корректность последующих операций. Если значение некорректное (NaN или Inf), оно заменяется на 0.
float value = IsNaNOrInf(data[RCtoFlat(main, head, total_mains, 2 * total_heads, 0)], 0); int slave_id = (int)indexes[RCtoFlat(main, slave, total_mains, total_slaves, 0)]; if(slave_id < total_mains && slave_id >= 0) value += IsNaNOrInf( data[RCtoFlat(slave_id, head + total_heads, total_mains, 2 * total_heads, 0)], 0);
Обратите внимание, что предварительно мы получаем точный индекс соседа из буфера indexes. При этом особое внимание уделено проверке на допустимость полученного индекса. Если сосед выходит за границы или является отрицательным, он исключается из расчётов. Это обеспечивает корректность вычислений и предотвращает некорректное суммирование.
Далее реализована ключевая операция Sparse-Softmax. Сначала вычисляются локальные максимумы и минимумы с помощью функции LocalMax и LocalMin, что позволяет определить пороговое значение threshold. Этот порог контролирует отсеивание малозначимых элементов: значения, меньше порога, обнуляются, а значимые элементы проходят через экспоненту с нормализацией на сумму всех элементов в блоке.
const float max_value = LocalMax(value, 1, Temp); const float min_value = LocalMin(value, 1, Temp); const float threshold = (max_value - min_value) * sparse + min_value; value = (threshold <= value ? IsNaNOrInf(exp(value - max_value), 0) : 0); const float sum = LocalSum(value, 1, Temp); value = IsNaNOrInf(value / sum, 0); //--- scores[RCtoFlat(slave, head, total_slaves, total_heads, main)] = value; }
В результате получается разряженный, но информативный вектор весов, который отражает важность каждого соседа для текущего элемента. Вычисленные веса записываются в выходной массив scores. Функция RCtoFlat преобразует многоразмерные индексы в одномерные позиции. Такой подход обеспечивает согласованное хранение результатов и позволяет следующему этапу графовой свертки использовать их напрямую для агрегации информации.
В совокупности этот кернел реализует компактную, высокопроизводительную и параллельную обработку внимания, обеспечивая точное распределение весов между элементами и их значимыми соседями. Он сохраняет всю логику предложенного авторами SAGDFN подхода, но делает вычисления эффективными, масштабируемыми и пригодными для практического использования на больших временных рядах.
После того как мы детально разобрали прямой проход и поняли, как формируются разреженные веса внимания для каждой головы и каждого элемента, естественным шагом становится реализация обратного прохода.
Обратный проход необходим для корректного вычисления градиентов при обучении модели. Он отвечает за то, чтобы ошибки, полученные на выходе, аккуратно распространялись обратно к эмбеддингам и параметрам, участвующим в вычислении весов внимания. В контексте OpenCL это означает создание отдельного кернела, который будет повторять структуру прямого прохода, но с фокусом на корректное накопление градиентов и учёт разреженной структуры весов.
Однако здесь стоит подчеркнуть несколько важных моментов. Прежде всего, логит запроса участвует одновременно в вычислении всех коэффициентов внимания. Это означает, что в процессе обратного прохода он должен аккумулировать градиенты ошибки от всех связанных информационных потоков, обеспечивая корректное распространение сигналов ошибки по всей сети.
Во-вторых, для соседних элементов мы работаем со своеобразной разреженной матрицей, что накладывает определённые ограничения и особенности на построение алгоритма обратного прохода. Такая структура требует аккуратного учета того, какие элементы реально участвуют в вычислениях, чтобы градиенты распространялись только по активным связям, не расходуя ресурсы на пустые или незначимые позиции.
И конечно, нельзя забывать о специфике функции SoftMax: изменение одного элемента автоматически влияет на весь вектор, создавая взаимозависимость коэффициентов. В нашем случае, для элементов, которые не попали в выбранные соседи, мы принимаем нулевой вес. При этом градиент ошибки аккуратно распространяется по всей последовательности, обеспечивая корректное обновление параметров даже для тех элементов, которые фактически не участвовали в активных связях, сохраняя целостность и устойчивость процесса обратного распространения.
Для более плавного и глубокого понимания работы кернела обратного прохода следует сначала вернуться к логике, заложенной в модуле Sparse Spatial Multi-Head Attention. На этапе прямого прохода мы формировали разреженные оценки внимания для выбранных соседей, используя заранее вычисленные индексы и проекции узлов. Эти значения играют ключевую роль в распределении информации между узлами графа, и, соответственно, корректное распространение ошибки в обратном направлении критично для стабильного обучения модели.
Кернел SparseMHScoresGrad берёт на себя задачу аккуратно распределить градиенты ошибки на каждый элемент входного тензора, учитывая разреженность и особенности SoftMax. В частности, изменение одного логита влияет на все элементы вектора внимания, поэтому даже те соседи, которые не попали в финальный набор, должны получить корректный градиент. Это позволяет сохранить правильную структуру вычислений и не нарушить баланс распределения ошибки.
__kernel void SparseMHScoresGrad(__global float* data_gr, __global const float* indexes, __global const float* scores, __global const float* scores_gr ) { const int main = (int)get_global_id(0); const int slave = (int)get_local_id(1); const int head = (int)get_global_id(2); const int total_mains = (int)get_global_size(0); const int total_slaves = (int)get_local_size(1); const int total_heads = (int)get_global_size(2);
Каждому потоку кернела назначены три ключевых индекса:
- main — узел, для которого считается градиент,
- slave — локальный индекс соседа,
- head — голова внимания.
Буфер в локальной памяти Temp используется для временного хранения промежуточных значений градиентов в пределах локального блока потоков, а синхронизация через BarrierLoc обеспечивает согласованность данных при параллельной обработке.
__local float Temp[LOCAL_ARRAY_SIZE]; const uint ls = min((uint)total_slaves, (uint)LOCAL_ARRAY_SIZE);
В первом блоке вычислений градиенты формируются относительно анализируемого узла. Сначала извлекается коэффициент внимания для текущего соседа и его индекс slave_id.
//--- Calc grad by main { float value = IsNaNOrInf(scores[RCtoFlat(slave, head, total_slaves, total_heads, main)], 0); int slave_id = (int)indexes[RCtoFlat(main, slave, total_mains, total_slaves, 0)]; const float sc_gr = IsNaNOrInf( scores_gr[RCtoFlat(slave, head, total_slaves, total_heads, main)], 0);
Градиент grad вычисляется как разница между реальным весом и ожидаемым значением, умноженная на градиент ошибки коэффициента внимания sc_gr для текущей позиции.
float grad = 0; for(uint d = 0; d < total_slaves; d += ls) { if(slave >= d && slave < (d + ls)) Temp[slave - d] = IsNaNOrInf(sc_gr, 0); BarrierLoc; for(uint l = 0; l < min(ls, (uint)(total - d)); l++) grad += IsNaNOrInf(Temp[l] * ((float)((d + l) == slave && slave_id == main) - value), 0); BarrierLoc; }
Использование локальной агрегации через Temp и последующего суммирования LocalSum обеспечивает параллельное и эффективное суммирование, минимизируя задержки при работе с большими наборами данных.
grad = LocalSum(grad, 1, Temp); if(slave == 0) data_gr[RCtoFlat(main, head, total_mains, 2 * total_heads, 0)] = grad; }
Полученный результат сохраняется в глобальный буфер только одним потоком, исключая гонку.
Второй блок отвечает за вычисление градиентов относительно соседей. Здесь следует помнить, что гипотетически каждый сосед участвует при формировании соответствующего коэффициента внимания (пусть даже нулевого) для каждого узла. Поэтому мы принимаем значение main в качестве индекса анализируемого соседа и организовываем цикл перебора всех узлов.
//--- Calc grad by slave { float grad = 0; for(uint d = 0; d < total_mains; d++) { float value = IsNaNOrInf(scores[RCtoFlat(slave, head, total_slaves, total_heads, d)], 0); const float sc_gr = IsNaNOrInf( scores_gr[RCtoFlat(slave, head, total_slaves, total_heads, d)], 0); int slave_id = (int)indexes[RCtoFlat(d, slave, total_mains, total_slaves, 0)];
Каждый поток проверяет, соответствует ли текущий индекс узлу-соседу, и аккуратно добавляет его вклад в общий градиент. Локальные барьеры и суммирование через Temp гарантируют, что все потоки согласованно участвуют в процессе.
float gr = IsNaNOrInf(sc_gr * ((float)(slave_id == d) - value), 0); gr = LocalSum(gr, 1, Temp); if(slave == 0) grad += gr; } if(slave == 0) data_gr[RCtoFlat(main, head + total_heads, total_mains, 2 * total_heads, 0)] = IsNaNOrInf(grad, 0); } }
Результаты сохраняются в глобальный буфер data_gr для последующего обновления параметров модели. Такой подход позволяет корректно распространять ошибку даже в случае разреженной структуры внимания, где многие элементы имеют нулевой вес, при этом не нарушая целостности вычислений.
Дополнительно следует отметить, что данная реализация максимально использует параллельные возможности GPU. Каждый поток работает с независимым подмножеством данных, а локальная память и барьеры минимизируют конфликты и обеспечивают согласованность. Это особенно важно при обучении моделей на больших графах с тысячами узлов, где традиционное последовательное вычисление градиентов оказалось бы слишком медленным и ресурсозатратным.
В целом, кернел SparseMHScoresGrad демонстрирует, как можно эффективно реализовать обратное распространение ошибки для разреженного многоголового внимания, совмещая точность, сохранение разреженности и высокую вычислительную эффективность.
На этом мы можем подвести черту под этапом реализации на стороне OpenCL-программы. Весь процесс построения многоголового разреженного внимания, от прямого прохода с вычислением весов до аккуратного распределения градиентов в обратном проходе, полностью перенесён в параллельный контекст. Мы обеспечили корректное и эффективное взаимодействие между узлами и их соседями, сохранили разреженную структуру для экономии памяти и вычислительных ресурсов, а также гарантировали точность градиентов для дальнейшего обучения модели. Теперь алгоритм готов к интеграции с остальной частью MQL5-программы.
Объект многоголового внимания
На данном этапе мы переходим к интеграции всех ранее разработанных компонентов в единую структуру на стороне основной программы. Для этого создаем класс CNeuronSNSMHAttention, который наследует базовую функциональность сверточного слоя от CNeuronConvOCL и объединяет два ключевых модуля — Significant Neighbors Sampling и Sparse Spatial Multi-Head Attention. Этот класс становится своеобразным ядром вычислений, аккумулируя в себе процессы отбора значимых соседей, формирования проекций и вычисления весов внимания, что обеспечивает высокую когерентность и согласованность работы всей архитектуры.
class CNeuronSNSMHAttention : public CNeuronConvOCL { float fSparse; //--- CNeuronBaseOCL cNeighbors; CNeuronBaseOCL cRamdomCandidates; CNeuronConvOCL cProjection[2]; CNeuronBaseOCL cScores; //--- virtual bool SignificantNeighborsSampling(CNeuronBaseOCL *NeuronOCL); virtual bool SparseMHScores(void); virtual bool SparseMHScoresGrad(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSNSMHAttention(void) {}; ~CNeuronSNSMHAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint heads, uint m_units, float sparse, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSNSMHAttention; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Класс содержит несколько внутренних объектов, каждый из которых выполняет специализированную роль.
- cNeighbors и cRamdomCandidates отвечают за обработку кандидатов-соседей. Первый — за наиболее значимые, второй — за случайные, что позволяет сохранять разнообразие выборки и предотвращает локальные застревания модели на узких паттернах данных.
- Объекты cProjection обеспечивают формирование проекций исходных эмбеддингов в пространство запросов и ключей, что является основой для последующих вычислений многоголового внимания.
- cScores аккумулирует вычисленные коэффициентов внимания, превращая их в разреженную матрицу влияния, которая будет использоваться на этапе графовой свертки.
- Параметр fSparse задаёт коэффициент разреженности внимания, что позволяет управлять балансом между точностью прогнозирования и вычислительной нагрузкой, особенно при работе с большими временными рядами.
На этом этапе важно подчеркнуть, что все внутренние объекты класса CNeuronSNSMHAttention объявлены статично, что позволяет оставить конструктор и деструктор класса пустыми. Такая конструкция упрощает управление памятью и делает инициализацию слоя более предсказуемой. Основная настройка и развертывание архитектуры нейронного слоя осуществляется через метод Init, который аккуратно объединяет все элементы и задаёт их параметры.
bool CNeuronSNSMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint heads, uint m_units, float sparse, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!sparse >= 1 || sparse < 0) return false; fSparse = sparse; //--- if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, heads, heads, 1, units * m_units, 1, optimization_type, batch)) return false;
Алгоритм метода начинается с проверки корректности коэффициента разреженности sparse. Если значение не находится в допустимом диапазоне [0, 1), функция сразу возвращает false, предотвращая дальнейшие ошибки конфигурации. После этого параметр fSparse сохраняется для использования в вычислениях весов внимания.
Далее вызывается инициализация родительского класса, где задаются базовые параметры объекта.
Здесь стоит уточнить, что в данном случаем мы не ограничиваем функционал родительского класса только созданием базовых интерфейсов. Это полноценный объект нашей модели, который выполняет свертку многоголового внимания.
После базовой инициализации начинается поэтапная настройка внутренних объектов. Сначала инициализируется модуль cNeighbors, который отвечает за обработку наиболее значимых соседей.
int index = 0; if(!cNeighbors.Init(0, index, OpenCL, units * m_units, optimization, iBatch)) return false; CBufferFloat* temp = cNeighbors.getOutput(); if(!temp || !temp.Random(0, (float)(units - 1))) return false;
На начальном этапе заполняем буфер результатов объекта случайными значениями индексов соседей, обеспечивая разнообразие выборки.
Аналогичная последовательность выполняется для модуля cRamdomCandidates, который хранит случайные кандидаты для расширения выборки.
index++; if(!cRamdomCandidates.Init(0, index, OpenCL, units * m_units, optimization, iBatch)) return false; temp = cRamdomCandidates.getOutput(); if(!temp || !temp.Random(0, (float)(units - 1))) return false;
Такой подход обеспечивает гибридный механизм отбора соседей — комбинацию значимых и случайных элементов.
Затем инициализируются два объекта массива cProjection, которые формируют проекции исходных эмбеддингов в пространства запросов и ключей. Первому объекту присваивается функция активации SoftPlus, а второму — TANH. Это создаёт нелинейное преобразование и позволяет модели учитывать сложные взаимодействия между элементами.
index++; if(!cProjection[0].Init(index, 0, OpenCL, window, window, 2 * heads, units, 1, optimization, iBatch)) return false; cProjection[0].SetActivationFunction(SoftPlus); index++; if(!cProjection[1].Init(index, 0, OpenCL, 2 * heads, 2 * heads, 2 * heads, units, 1, optimization, iBatch)) return false; cProjection[0].SetActivationFunction(TANH); index++; if(!cScores.Init(0, index, OpenCL, units * m_units * heads, optimization, iBatch)) return false; //--- return true; }
В завершении инициализируется объект cScores, который аккумулирует разреженные веса внимания и формирует итоговую матрицу влияния, используемую в графовой свертке.
В целом, метод Init представляет собой тщательно продуманный процесс поэтапной инициализации, обеспечивающий корректную настройку всех компонентов слоя. Он гарантирует, что каждый объект получает необходимые размеры, функции активации и параметры для работы в единой архитектуре. Такой подход делает слой гибким и масштабируемым, позволяя адаптировать его под различные конфигурации данных, количество голов внимания и размеры выборки соседей, сохраняя при этом эффективность вычислений и высокую точность.
Метод feedForward аккуратно реализует прямой проход данных через объединённую архитектуру модуля, обеспечивая последовательное взаимодействие всех внутренних компонентов. Сначала вызывается метод SignificantNeighborsSampling, который формирует индексные массивы значимых соседей. Если по какой-либо причине этот шаг завершается неудачно, функция сразу возвращает false, предотвращая дальнейшие вычисления и сохраняя корректность состояния слоя.
bool CNeuronSNSMHAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!SignificantNeighborsSampling(NeuronOCL)) return false;
После успешного отбора соседей, в локальную переменную inputs сохраняется указатель на объект исходных данных NeuronOCL, который подаётся на последовательное прохождение через блоки проекций. Цикл проходит по каждому элементу массива cProjection. Для каждого элемента вызывается его собственный метод FeedForward, который выполняет линейные и нелинейные преобразования исходного тензора, формируя проекции запросов и ключей для последующей операции внимания.
CNeuronBaseOCL* inputs = NeuronOCL; for(uint i = 0; i < cProjection.Size(); i++) { if(!cProjection[i].FeedForward(inputs)) return false; inputs = cProjection[i].AsObject(); }
При этом, после обработки каждого блока, вход для следующего шага переназначается на выход предыдущего, обеспечивая непрерывный поток данных и аккуратное каскадное преобразование.
Следующий шаг — вызов метода SparseMHScores, который вычисляет разреженные коэффициенты внимания для всех пар узел–сосед с учётом коэффициента разрежения fSparse.
if(!SparseMHScores()) return false; if(!CNeuronConvOCL::feedForward(cScores.AsObject())) return false; //--- return true; }
Полученные значения аккумулируются и подаются на сверточный слой агрегации многоголового внимания, функционал которого выполняет родительский класс. Здесь выполняются итоговое преобразование, формируя окончательные выходные значения слоя.
Весь процесс построен так, чтобы обеспечить логичное и последовательное прохождение данных через ключевые этапы: сначала отбор значимых соседей, затем формирование проекций, вычисление разреженных коэффициентов внимания и агрегирование информации. Такой подход гарантирует высокую читаемость кода и позволяет легко интегрировать дополнительные преобразования или оптимизации без нарушения общей архитектуры. В конце метода возвращается true, сигнализируя о корректном завершении прямого прохода и готовности слоя к дальнейшей работе.
Метод calcInputGradients отвечает за аккуратное распределение градиента ошибки по всем внутренним компонентам слоя и исходным данным, обеспечивая корректный обратный проход для обучения модели. Сначала проверяется, что указатель на предыдущий слой prevLayer валиден. В случае его отсутствия, функция немедленно возвращает false, предотвращая некорректные вычисления.
bool CNeuronSNSMHAttention::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Далее вызывается одноименный метод родительского класса для распределения градиентов на уровне агрегирующего слоя cScores.
if(!CNeuronConvOCL::calcInputGradients(cScores.AsObject())) return false; if(!SparseMHScoresGrad()) return false;
После этого вызывается SparseMHScoresGrad, отвечающий за распределение градиентов через разреженные коэффициенты внимания, сформированные модулем Sparse Spatial Multi-Head Attention. Именно здесь учитываются особенности разреженной матрицы соседей, сохраняя принцип работы архитектуры.
Затем начинается цикл по массиву проекций cProjection в обратном порядке, начиная с последнего блока. Для каждой проекции определяется входной объект inputs: если это не первый блок, используется выход предыдущего блока, иначе — prevLayer.
int total=(int)cProjection.Size(); CNeuronBaseOCL* inputs = NULL; for(int i = total-1; i >=0; i--) { inputs = (i>0 ? cProjection[i-1].AsObject() : prevLayer); if(!inputs.CalcHiddenGradients(cProjection[i].AsObject())) return false; } //--- return true; }
Для каждого объекта вызывается метод CalcHiddenGradients, который рассчитывает локальные градиенты скрытых состояний, учитывая все накопленные градиенты от следующего уровня. Это обеспечивает последовательное и корректное распространение ошибки через все промежуточные слои, сохраняя согласованность весов и скрытых состояний.
Таким образом, calcInputGradients выполняет полный и структурированный обратный проход через объединённый модуль, аккуратно распределяя градиенты как по разреженным коэффициентам внимания, так и по всем слоям проекций, обеспечивая подготовку к последующему шагу оптимизации.
Метод updateInputWeights отвечает за последовательное обновление весовых параметров всех внутренних компонентов слоя после распределения градиентов ошибки. Он обеспечивает корректную оптимизацию модели на основе рассчитанных градиентов, аккуратно распределяя изменения по каждому элементу архитектуры.
bool CNeuronSNSMHAttention::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL* inputs = NeuronOCL; for(uint i = 0; i < cProjection.Size(); i++) { if(!cProjection[i].UpdateInputWeights(inputs)) return false; inputs = cProjection[i].AsObject(); }
Сначала метод объявляет локальный указатель на объект исходных данных inputs, который изначально указывает на внешний слой NeuronOCL. Далее запускается цикл по всем блокам проекций cProjection. Для каждого блока вызывается метод UpdateInputWeights, который применяет рассчитанные градиенты к весовым параметрам текущего блока. Если обновление весов на любом этапе не удалось, метод немедленно возвращает false, предотвращая неконсистентное состояние модели. После успешного обновления блока, указатель в inputs перенаправляется на выход текущей проекции, чтобы следующий блок корректно получил актуальные исходные данные.
По завершении цикла вызывается одноименный метод родительского класса, который обновляет веса агрегирующего слоя многоголового внимания, обеспечивая согласованность всех уровней модели. Этот шаг является критическим для поддержания корректной работы разреженных коэффициентов внимания и сохранения влияния каждого выбранного соседа в итоговой прогнозной функции.
if(!CNeuronConvOCL::updateInputWeights(cScores.AsObject())) return false; //--- return true; }
В завершение метод возвращает true, сигнализируя, что оптимизация весов выполнена успешно для всех внутренних компонентов модуля.
В совокупности объект CNeuronSNSMHAttention позволяет аккуратно объединить сложные алгоритмы отбора соседей и многоголового внимания в единой структуре, обеспечивая прозрачность, масштабируемость и гибкость.
Сегодняшняя работа была насыщенной и продуктивной. Мы глубоко погрузились в реализацию модулей Significant Neighbors Sampling и Sparse Spatial Multi-Head Attention. Проанализировали их архитектурные особенности и подробно разобрали механизмы прямого и обратного проходов, а также оптимизации весов. Настало время сделать небольшую паузу, чтобы дать усвоенной информации улечься и подготовить почву для следующего шага.
В следующей статье мы вернемся к начатой работе, аккуратно доведя её до логичного финала. И проведем тестирование построенной модели на исторических данных, оценим её устойчивость и точность прогнозов, а также продемонстрируем практическую применимость предложенного подхода на реальных финансовых временных рядах.
Заключение
В данной статье мы подробно рассмотрели практическую реализацию ключевых модулей фреймворка SAGDFN средствами MQL5 и OpenCL. Нами были проанализированы подходы к выбору значимых соседей через Significant Neighbors Sampling, построению разреженного многоголового внимания и эффективной организации прямого и обратного проходов в рамках единого нейронного слоя. Особое внимание было уделено оптимизации вычислений: мы показали, как повторное использование весовых параметров и переход к разреженной нормализации позволяют значительно снизить нагрузку на память и ускорить обработку данных.
В итоге, созданная архитектура обеспечивает одновременно высокую точность прогнозов и вычислительную эффективность, делая модель пригодной для работы с большим количеством временных рядов.
Ссылки
- SAGDFN: A Scalable Adaptive Graph Diffusion Forecasting Network for Multivariate Time Series Forecasting
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Форекс советник на нейросети N-BEATS Network
Форекс советник на нейросети N-BEATS Network
 Возможности Мастера MQL5, которые вам нужно знать (Часть 51): Обучение с подкреплением с помощью SAC
Возможности Мастера MQL5, которые вам нужно знать (Часть 51): Обучение с подкреплением с помощью SAC
 Возвратные стратегии дневной торговли RSI2 Ларри Коннорса
Возвратные стратегии дневной торговли RSI2 Ларри Коннорса
 От новичка до эксперта: Система автогеометрического анализа
От новичка до эксперта: Система автогеометрического анализа
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования