MetaTrader 5 / Торговые системы
preview
Нейросети в трейдинге: Адаптивная периодическая сегментация (Окончание)

Нейросети в трейдинге: Адаптивная периодическая сегментация (Окончание)

MetaTrader 5 — Торговые системы |
468 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Введение

В предыдущих работах мы шаг за шагом разобрали, как фреймворк LightGTS превращает временные ряды в музыкальные партитуры. Сначала в модуле Period Patching анализируемые данные автоматически разбиваются на полные циклы, определяемые через FFT. Затем каждый такой цикл проецируется в токен при помощи Flex Projection Layer, позволяющий гибко обрабатывать фрагменты разной длины. В Энкодере эти токены обогащаются Rotary Positional Encoding (RoPE) — компактным способом вплести фазовые сдвиги и относительные позиции — после чего классические Transformer‑блоки с многоголовым вниманием сливают локальные паттерны в единый контекст. Для генерации прогноза используется механизм Periodical Parallel Decoding, мгновенно создающий всю выходную последовательность без авторегрессии. Результат корректируется в модуле Flex‑resize, сберегающем периодическую согласованность.

Авторская визуализация фреймворка LightGTS

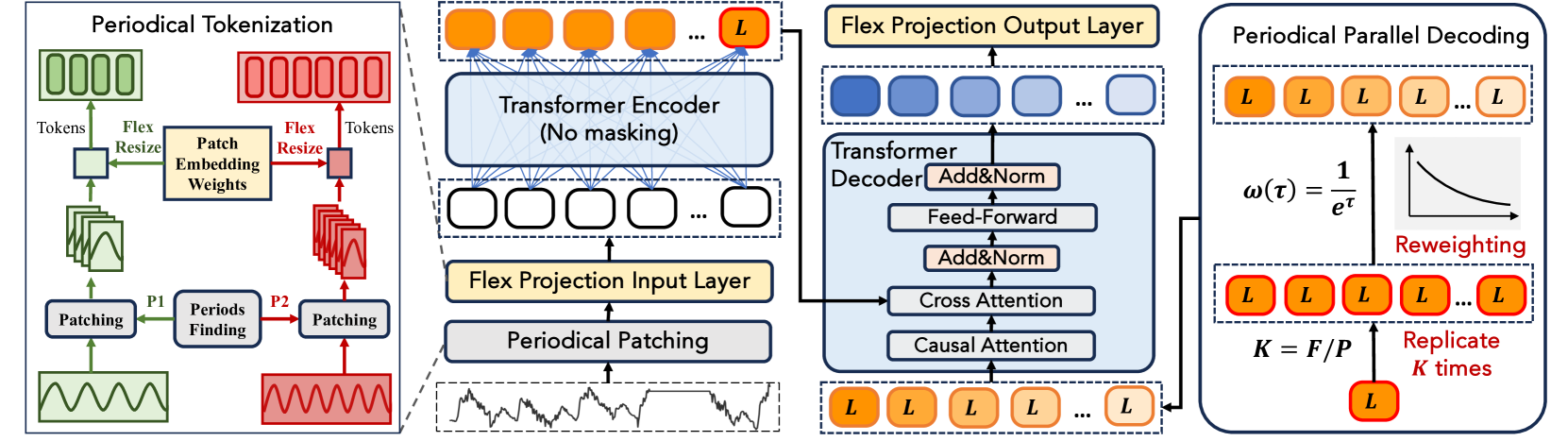
К этому моменту мы уже успешно воплотили в коде ключевые идеи LightGTS: научились автоматически нарезать временной ряд на периодические фрагменты через адаптивный патчинг и превращать каждый из них в информативный токен. Мы добавили свои штрихи к оригинальным алгоритмам, отточили логику гибкой проекции и получили готовые представления локальных циклов рынка. Сегодня мы сделаем следующий шаг вперёд на пути построения собственного видения подходов, предложенных авторами фреймворка LightGTS.

Механизм RoPE

После того как адаптивная свёртка выжала из сырого временного ряда концентрированный набор информативных токенов, настало время провести их через мощный фильтр Transformer‑блоков. В привычной архитектуре Encoder–Decoder к этим токенам просто добавляются векторы синусоидального или обучаемого позиционного кодирования, после чего они отправляются в механизм внимания. Авторы фреймворка LightGTS предлагают использовать куда более изящный и гибкий способ — Rotary Positional Encoding (RoPE). Вместо застывших векторов кодирования положения каждый токен вращается в эмбеддинговом пространстве.

Главная идея RoPE — ввести векторный сдвиг фазы, пропорциональный положению токена и его размерностям, не прибегая к дополнительным параметрам. Надо сказать, что данный приём был впервые представлен в работе "RoFormer: Enhanced Transformer with Rotary Position Embedding", где авторы показали, что вращение пар координат сущностей Query и Key с помощью матрицы вращения позволяет модели надёжно фиксировать относительные сдвиги во времени.

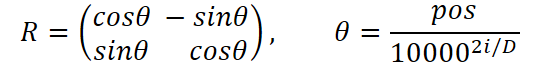
Метод легко обобщается на многомерные пространства путем деления размерности на пары значений. И здесь вытекает ограничение — размерность пространства должна быть парной.

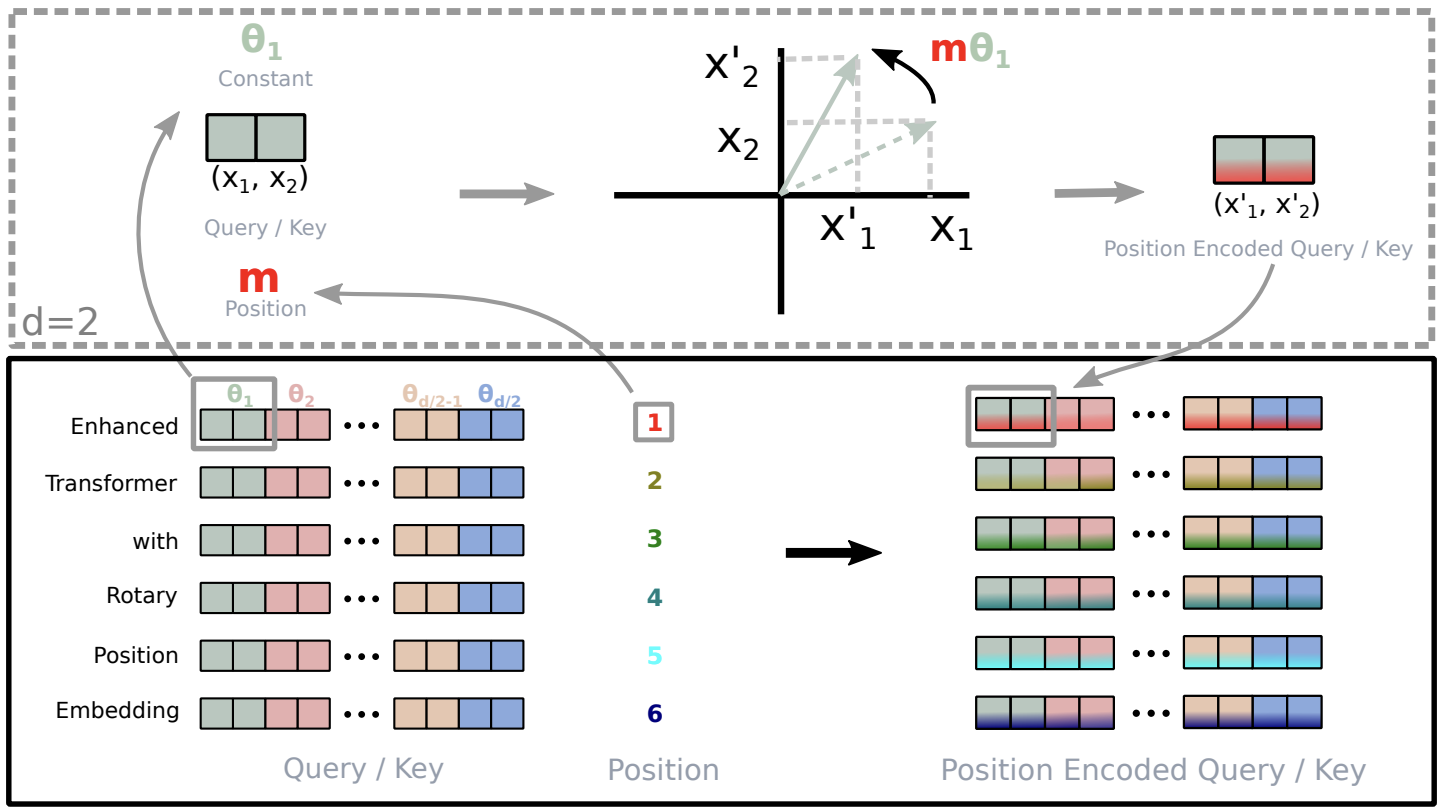
Благодаря такому вращению даже при переменном размере окон и динамичном шаге модель точно понимает, какие токены ближе во времени, а какие — дальше. В результате механизм Self‑Attention превращается в сверхчувствительный детектор временных закономерностей: он не просто сравнивает содержимое Query и Key, но и учитывает фазовые различия между токенами. Как итог, после нескольких слоёв многоголового внимания и Feed‑Forward токены выходят уже глубоко контекстуализированными.

Теперь, когда мы погрузились в математические и концептуальные основы Rotary Positional Encoding, пора спуститься в котёл реализации и посмотреть, как всё это перевести в код OpenCL-программы. У нас уже есть готовые токены — массив векторов, у каждого из которых по D измерений. Кроме того, мы заранее подготовим таблицы синусов и косинусов для каждой позиции. Наша задача — повернуть каждый вектор в эмбеддинговом пространстве так, чтобы фаза отражала временную метку, не теряя при этом общей скорости конвейера. Для этого мы создаём кернел RoPE, работающий в трёхмерном пространстве задач. Первое измерение отвечает за индекс пары координат внутри вектора. Его размерность равна половине длины вектора. Второе измерение указывает на длину последовательности (количество токенов). А третье — количество унитарных последовательностей.

Обратите внимание, что для удобства работы с парами значений мы используем векторный тип представления данных float2.

__kernel void RoPE(__global const float2* __attribute__((aligned(8))) inputs,
                   __global const float2* __attribute__((aligned(8))) position_emb,
                   __global float2* __attribute__((aligned(8))) outputs
                  )
  {
   const size_t id_d = get_global_id(0);     // dimension
   const size_t id_u = get_global_id(1);     // unit
   const size_t id_v = get_global_id(2);     // variable
   const size_t dimension = get_global_size(0);
   const size_t units = get_global_size(1);
   const size_t variables = get_global_size(2);

В теле кернела сначала идентифицируем координаты текущего потока операций в трёхмерном пространстве задач. Это необходимо для того, чтобы каждый поток точно знал, с каким именно фрагментом данных ему предстоит работать: какую пару координат вектора обрабатывать, к какому токену она относится и из какой переменной (или канала) поступает.

Как только координаты потока известны, следующим шагом становится вычисление смещений в плоских массивах OpenCL-буферов. Несмотря на многомерную структуру логики, все данные в OpenCL хранятся линейно, и потому нужно вручную рассчитать, где именно в памяти находится интересующий элемент.

   const int shift_in = (id_v * units + id_u) * dimension + id_d;
   const int shift_pos = id_u * dimension + id_d;
   const float2 inp = inputs[shift_in];
   const float2 pe = position_emb[shift_pos]; 

Чтобы свести к минимуму дорогие обращения к глобальной памяти, мы сразу же загружаем исходную пару координат и соответствующие синус/косинус-факторы в локальные векторные переменные — своеобразные регистр–драйверы кернела. Ведь каждое обращение к буферам глобальной памяти обходится значительно дороже, чем работа с уже локальными векторами. Это позволяет почти полностью исключить повторные выгрузки из глобальной памяти и удерживать горячие данные в регистрах или в локальной памяти GPU, что заметно ускоряет весь процесс вращения токенов и делает исполнение кернела максимально эффективным.

Когда все ингредиенты (исходные данные и значения sin/cos) под рукой, мы готовы приступить к главному действу — фазовому сдвигу. Именно он придаёт токенам чувство времени и обеспечивает корректную работу механизма внимания.

   float2 result = 0;
   result.s0 = inp.s0 * pe.s0 - inp.s1 * pe.s1;
   result.s1 = inp.s0 * pe.s1 + inp.s1 * pe.s0;
//---
   outputs[shift_in] = result;
  }

Здесь мы используем простые арифметические операции над локальными переменными: четыре умножения и два сложения на каждую пару значений. Благодаря предварительной загрузке данных, этот шаг выполняется почти моментально.

После этого подкрученную пару координат мы сразу записываем буфер результатов.

Вот и весь фокус: за счёт простого умножения на заранее подготовленные cos и sin мы наделяем каждый токен информацией о фазе и относительном времени, не прибавляя ни единого нового параметра. В результате этот кернел демонстрирует:

  • Максимальную параллельность — каждый поток операций работает независимо.
  • Нулевые накладные расходы на обучение — позиционное кодирование не содержит обучаемых параметров.
  • Идеальную интеграцию с последующими модулями внимания — эмбеддинги учитывают не только содержимое токенов, но и их фазовые различия.

Несмотря на то, что RoPE не вводит в модель ни единого обучаемого параметра, нам важно, чтобы градиенты могли корректно протекать сквозь этот слой, возвращаясь к исходным данным. Для этого мы создаем специальный кернел обратного прохода CalcHiddenGradRoPE, который выполняет обратный поворот векторов.

Идея проста: кернел прямого прохода умножал исходные данные (x, y) на поворотную матрицу. В обратном направлении нам нужно применить её транспонированную версию — то есть поворот на −θ, где cos(−θ)=cosθ, а sin(−θ)=−sinθ.

Алгоритм кернела обратного прохода практически идентичен, рассмотренному выше для прямого прохода. Используется то же пространство задач и аналогично определяются смещения в глобальных буферах данных. Небольшие отличие лишь в части вращения векторов. Да и исходными данными для выполнения операций являются градиенты ошибки на уровне результатов.

__kernel void CalcHiddenGradRoPE(__global float2* __attribute__((aligned(8))) inputs_gr,
                                 __global const float2* __attribute__((aligned(8))) position_emb,
                                 __global const float2* __attribute__((aligned(8))) outputs_gr
                                )
  {
   const size_t id_d = get_global_id(0);     // dimension
   const size_t id_u = get_global_id(1);     // unit
   const size_t id_v = get_global_id(2);     // variable
   const size_t dimension = get_global_size(0);
   const size_t units = get_global_size(1);
   const size_t variables = get_global_size(2);
//---
   const int shift_in = (id_v * units + id_u) * dimension + id_d;
   const int shift_pos = id_u * dimension + id_d;
   const float2 grad = outputs_gr[shift_in];
   const float2 pe = position_emb[shift_pos];
//---
   float2 grad_x;
   grad_x.s0 = grad.s0 * pe.s0 + grad.s1 * pe.s1;
   grad_x.s1 = grad.s1 * pe.s0 - grad.s0 * pe.s1;
//---
   inputs_gr[shift_in] = grad_x;
  }

Никаких условных переходов и сложных формул — всего четыре умножения и пара сложений. Благодаря этому градиенты RoPE‑слоя откручиваются так же быстро и экономно, как поворачивались токены на прямом проходе.

В результате CalcHiddenGradRoPE превращает слой RoPE в полноценного участника процесса обучения: мы можем включать его в любую глубину сети, и он вернёт градиенты во входные тензоры без потерь, сохраняя скорость и параллельность исполнения.

Теперь, когда наши OpenCL‑кернелы для Rotary Positional Encoding отлажены до блеска, самое время перенести эту мощь в MQL5‑мир и связать её с торговым роботом. У нас есть готовый механизм закручивания токенов на GPU — осталось лишь создать над ним лёгкую обёртку, которая вписалась бы в привычную структуру экспертов MQL5. Именно для этого мы создадим класс CNeuronRoPE, структура которого представлена ниже.

class CNeuronRoPE  :  public CNeuronPositionEncoder
  {
protected:
   uint              iWindow;
   uint              iVariables;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL)override;

public:
                     CNeuronRoPE(void) : iWindow(0), iVariables(0) {};
                    ~CNeuronRoPE(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint count, uint window, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override const {  return defNeuronRoPE; }
  };

В классе CNeuronRoPE всё устроено максимально просто: в нём есть только две переменные — iWindow, определяющая размерность вектора одного токена, и iVariables, задающая число каналов. Весь остальной тяжёлый функционал, связанный с буферами и проверкой параметров, унаследован от CNeuronPositionEncoder, поэтому конструктор и деструктор здесь пустуют. Основа работы всего слоя закладывается в методе Init.

bool CNeuronRoPE::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint count, uint window, uint variables,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(window % 2 > 0)
      return false;
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, count * window * variables, optimization_type, batch))
      return false;

В самом начале метода делаем простую, но крайне важную проверку: размерность каждого токена должна быть чётной, ведь RoPE оперирует парами координат. Без этого условного постулата дальше просто некуда двигаться — мы не сможем однозначно скрутить пары значений. И после успешного прохождения точки контроля передаем управление одноименному методу родительского класса, в котором уже организованы остальные точки контроля и алгоритм инициализации унаследованных интерфейсов.

Затем сохраняем параметры тензора исходных данных во внутренние переменные.

   iWindow = window;
   iVariables = variables;

И переходим к конструированию ключевой для RoPE матрицы эмбеддингов — двумерного массива, где в чётных столбцах будет cos(θ), а в нечётных — sin(θ).

В начале создаём матрицу pe необходимого размера. Это полотно, которое мы незамедлительно заполним значениями синусов и косинусов. Чтобы понять, как каждая колонка матрицы отзовётся на свой шаг временного ряда, мы на старте формируем вектор позиций: из единичного вектора делаем сумму префиксов и вычитаем единицу, получая [0, 1, 2, …, count–1]. Именно этот вектор говорит нам, какой именно шаг мы сейчас кодируем.

   matrix<float> pe = matrix<float>::Zeros(count, iWindow);
   vector<float> position = vector<float>::Ones(count);
   position = position.CumSum() - 1;

Далее наступает главный акт — мы пробегаемся по всем парам размерностей, ведь каждая пара координат токена требует своих собственных углов. Для каждой такой пары мы берём вектор позиций и делим его на растущий знаменатель, равный pow(10000, 2 * i / iWindow), чтобы понизить темп вращения старших размерностей и ускорить младших. В результате на выходе у нас получается массив углов — не простых чисел, а вектор θ для всех позиций.

   for(uint i = 0; i < iWindow / 2; i++)
     {
      vector<float> temp = position / MathPow(10000.0f, 2.0f * i / window);
      pe.Col(MathCos(temp), i * 2);
      pe.Col(MathSin(temp), i * 2 + 1);
     }

И вот в каждую чётную колонку матрицы pe мы записываем косинусы полученных углов, а в соседнюю, нечётную, — синусы. В итоге матрица превращается в настоящую фабрику, где каждая колонка снабжена своей парой значений [cos(θ), sin(θ)], готовых к тому, чтобы закрутить любой токен. Все эти вычисления выполняем один раз в CPU‑коде, чтобы затем передать GPU‑кернелам уже готовый набор функций.

Заполненную матрицу передаем в буфер данных и завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.

   PositionEncoder.BufferFree();
   if(!PositionEncoder.AssignArray(pe))
      return false;
   SetActivationFunction(None);
//---
   return PositionEncoder.BufferCreate(open_cl);
  }

Благодаря такому подходу наши OpenCL‑ядра получают на вход готовую таблицу синусов/косинусов и могут работать на полную мощность, не отвлекаясь на лишние математические операции.

В результате, вся стартовая настройка сосредоточена в одном методе: достаточно поменять параметры window или variables, и слой моментально адаптируется под новые условия. Такой подход гарантирует, что код остаётся строгим и понятным, а мы получаем полный контроль над поведением RoPE‑модуля.

Когда наступает этап прямого прохода, достаточно просто вызывать метод feedForward, передав в него указатель на объект исходных данных, уже заполненный токенами. Под капотом метод внимателен к деталям: он проверяет актуальность полученного указателя, ставит в очередь выполнения кернел RoPE с нужными размерами рабочей группы, ждёт его завершения и возвращает управление дальше. На выходе получаем буфер повёрнутых токенов, готовых к передаче в модуль внимания.

В процессе обучения на сцену выходит метод calcInputGradients. Этот метод запускает кернел CalcHiddenGradRoPE. Сама логика почти зеркальна прямому проходу: те же координаты, те же смещения, но вращение идёт в обратную сторону, чтобы вернуть градиент к исходному представлению. Итоговый результат аккуратно ложится в буфер градиентов по входу и беспрепятственно течёт дальше, к более ранним слоям модели.

Оба метода, по сути, являются обертками соответствующих кернелов и построены по уже знакомому Вам алгоритму. Поэтому мы не будем детально останавливаться на их рассмотрении в рамках данной статьи. С полным кодом представленного класса и всех его методов можно ознакомиться во вложении.

Теперь, когда токены прошли через фазовый фильтр RoPE, они готовы войти в сердце модели — модуль внимания. Фреймворк LightGTS по умолчанию строит свою логику вокруг классической схемы Энкодер–Декодер, и нам не придётся изобретать велосипед: все необходимые компоненты уже есть в нашей библиотеке. Достаточно передать повёрнутые токены в один из существующих модулей Self-Attention, где многоголовое внимание сработает на ура, связав локальные паттерны с глобальным контекстом временного ряда.

В оригинальной версии LightGTS авторы предлагают после Энкодера взять последний скрытый токен и размножить его ровно столько раз, сколько понадобится для покрытия заданного горизонта планирования, чтобы Декодер мог сразу сгенерировать всю выходную последовательность. Мы же сделали смелый шаг в сторону упрощения: репликация нам не нужна. Во‑первых, наша задача — не получить сверхточные цифры, а выжать из латентного представления всю ценную информацию для Агента, который будет строить торговые решения. Во‑вторых, мы запускаем расчёты на каждом новом баре, а это всегда короче, чем полный цикл периодичности рынка. Значит, нам вполне достаточно одного последнего токена для каждой унитарной последовательности.

Поэтому, минуя многократные копии, мы направляем этот последний эмбеддинг по основной магистрали в Декодер. Там он встречается с тем же многоголовым вниманием и Feed‑Forward, но уже без лишних повторов: модель опирается на чистое, концентрированное представление, содержащее всю актуальную информацию о последних движениях рынка. Такой подход экономит ресурсы, упрощает логику и позволяет Агенту действовать максимально оперативно — ведь каждый бар требует мгновенной реакции, а нам нужно не тысяча копий токена, а один мощный сигнал, готовый привести к прибыли.


Архитектура моделей

Наконец мы подходим к кульминации — моменту, когда все тщательно отлаженные модули собираются вместе в единую, слаженно работающую систему. В нашем MQL5‑проекте это происходит в функции CreateDescriptions, где мы шаг за шагом выстраиваем семь ветвей нейросети: Энкодер, 3 прогностических потока и три компонента Агента — Actor, Director и Critic.

bool CreateDescriptions(CArrayObj *&encoder,
                        CArrayObj *&forecast1,
                        CArrayObj *&forecast2,
                        CArrayObj *&forecast3,
                        CArrayObj *&actor,
                        CArrayObj *&director,
                        CArrayObj *&critic
                       )
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!forecast1)
     {
      forecast1 = new CArrayObj();
      if(!forecast1)
         return false;
     }
   if(!forecast2)
     {
      forecast2 = new CArrayObj();
      if(!forecast2)
         return false;
     }
   if(!forecast3)
     {
      forecast3 = new CArrayObj();
      if(!forecast3)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!director)
     {
      director = new CArrayObj();
      if(!director)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

Сначала мы проверяем корректность указателей на динамические массивы каждого из контейнеров. Если кто‑то из них ещё не создан, мы аккуратно выделяем память под новый динамический массив. Эти контейнеры станут скелетом, на который будут нанизываться описания нейронных слоёв нашей модели.

В Энкодере всё начинается с базового полносвязного слоя, куда поступают сырые исходные данные — последовательность исторических баров, каждый из которых описан набором признаков.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   uint prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormWithNoise;
   descr.count = prev_count;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Затем мы вводим пакетную нормализацию с добавлением шума, плавно выравнивающую распределение активаций. После чего переходим к первой операции над исходными данными, где извлекаются разности между соседними точками ряда. Это позволяет нам подчеркнуть динамику изменений.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatDiff;
   prev_count = descr.count = HistoryBars;
   descr.layers = BarDescr;
   descr.step = 1;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Следующий слой добавляет гармоники временных меток к исходным данным, превратив каждый бар не просто в набор ценовых и объёмных признаков, а в точку на временной шкале.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defMamba4CastEmbeding;
   prev_count = descr.count = HistoryBars;
   descr.window = 2 * BarDescr;
   uint prev_out = descr.window_out = NSkills;
     {
      uint temp[] = {PeriodSeconds(PERIOD_H1), PeriodSeconds(PERIOD_D1)};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = prev_count;
   prev_count = descr.window = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
   prev_out = descr.count;

А затем транспонируем результат, чтобы подготовить его к передаче в адаптивную свёртку CNeuronAdaptConv. На первый взгляд это может показаться обычной технической операцией, но именно здесь происходит ключевой переход: мы перестраиваем структуру данных так, чтобы каждая унитарная последовательность могла быть разбита на адаптивные патчи — компактные, локализованные отрезки временных рядов, содержащие локальные паттерны.

Это позволяет CNeuronAdaptConv гибко подстраиваться под характер исходных данных: одни патчи захватывают импульсные движения, другие — участки стабильности или колебаний. По сути, мы передаём модели не просто плоский массив значений, а структурированное представление с чётко заданной пространственно-временной иерархией. Благодаря этому Энкодер получает возможность сохранять как краткосрочный контекст, так и выявлять глубинные, скрытые закономерности в сложных временных рядах.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAdaptConv;
   descr.count = Segments;
   descr.window = 2*prev_out/Segments;
   descr.variables = prev_count;
   prev_out = descr.window_out = EmbeddingSize;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
   prev_count = descr.count;
   uint prev_var = descr.variables;

Следующим шагом идёт RoPE (Rotary Positional Embedding) — механизм, который на первый взгляд может показаться избыточным, учитывая, что временные метки уже были добавлены к исходным данным. Однако ключевое отличие здесь заключается в уровне применения.

Добавленные временные метки относятся к отдельным барам, то есть к сырым исходным данным. Они служат для того, чтобы зафиксировать абсолютные временные координаты каждого наблюдения до начала структурной обработки.

После этого данные проходят стадию патчинга, в результате которой каждая группа последовательных баров объединяется в сегменты. Этот сегмент затем преобразуется в один токен — агрегированное представление локального временного участка. И уже к полученным токенам применяется RoPE.

Таким образом, RoPE не кодирует позиции внутри патча — ведь на этом этапе они уже свернуты в одно представление. Вместо этого он встраивает информацию о положении самого патча в общей последовательности. Другими словами, RoPE позволяет модели понимать, в каком порядке идут патчи относительно друг друга, что критически важно для анализа глобальной структуры анализируемого временного ряда.

Такое позиционирование RoPE делает его идеальным дополнением: в паре с временными метками на уровне баров он обеспечивает иерархическую временную осведомлённость — от детальных значений на уровне баров до относительных позиций агрегированных блоков.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRoPE;
   descr.count = prev_count;
   descr.window = prev_out;
   descr.variables = prev_var;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

После применения RoPE мы снова выполняем транспонирование данных — на этот раз с прицелом на то, чтобы следующий модуль Multi-Head Self-Attention мог эффективно прочитать массив векторов токенов с учетом их хронологической последовательности. Это чисто технический, но важный шаг: внимание должно видеть данные в нужной форме, иначе мы получим лишь хаос, а не взвешенное сравнение токенов.

Далее в бой вступает Self-Attention, настроенное с параметрами 4 головы внимания и 3 последовательных слоя. Такая архитектура позволяет модели параллельно анализировать различные аспекты взаимосвязей между токенами — каждая голова фокусируется на своём признаковом подпространстве. Это словно 4 эксперта, каждый из которых по-своему оценивает важность связей между патчами.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeRCDOCL;
   descr.count = prev_var;
   descr.window = prev_count;
   descr.step = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronComplexMLMHAttentionOCL;
   descr.count = prev_count;
   descr.window = prev_out / 2 * prev_var;
   descr.window_out = descr.window / 4;
   descr.layers = 3;
   descr.step = 4;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     } 

Здесь стоит особо подчеркнуть: механизм RoPE — это не просто способ добавить порядковую информацию. Он выполняет вращение векторов токенов в комплексной плоскости, используя элементы комплексной математики. Такой подход позволяет явно учитывать относительное положение токенов, встраивая в эмбеддинги фазовые сдвиги.

Именно поэтому, в отличие от авторской реализации фреймворка LightGTS, где использовался обычный Self-Attention, мы сознательно применили комплексную версию модуля внимания CNeuronComplexMLMHAttentionOCL. Это обеспечивает математическую согласованность: если позиционное кодирование выполнено в комплексной области, то и слой внимания должен уметь оперировать с комплексными величинами.

В результате модель получает возможность не просто видеть взаимосвязи между токенами, но и учитывать их фазовое смещение, что критически важно при работе с периодическими и волнообразными структурами финансовых временных рядов. Три слоя внимания обеспечивают глубину обработки, позволяя моделировать как локальные, так и более отдалённые зависимости во временном ряду. Так формируется контекстуально насыщенное представление — своего рода сжатый обзор всей последовательности, подготовленный для следующих этапов модели.

В качестве Декодера мы используем модуль CNeuronTimeMoEAttention, который сочетает в себе мощь многоголового внимания и изящную механику разреженной смеси экспертов (MoE). Этот модуль специально разработан для эффективного анализа временных рядов и построения выразительных латентных представлений, что особенно важно в финансовых приложениях, где каждая деталь временной динамики имеет значение.

Важной инновацией становится замена классического блока FeedForward на блок разреженной смеси экспертов — CNeuronTimeMoESparseExperts. Такой подход позволяет гибко и эффективно распределять вычислительные ресурсы между разными специалистами, каждый из которых анализирует свою часть признаков, тем самым повышая качество обработки и снижая избыточность.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTimeMoEAttention;
   descr.window_out = EmbeddingSize;
     {
      uint temp[] = {prev_out, prev_out, 8, TopK};               //Window Main, Window Cross, Experts dimension, TopK
      if(ArrayCopy(descr.windows, temp) < ArraySize(temp))
         return false;
     }
     {
      uint temp[] = {prev_var, prev_var * prev_count, NExperts}; //Units Main, Units Cross, Experts
      if(ArrayCopy(descr.units, temp) < ArraySize(temp))
         return false;
     }
   descr.layers = 3;
   descr.step = 4;                                                // Attention heads
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }//---
   CLayerDescription *latent = descr; 

В результате работы Энкодера состояния окружающей среды мы получаем сжатое, но выразительное латентное представление анализируемых данных.

Это представление — не просто набор векторов. Это выверенное, насыщенное описание текущей рыночной ситуации, в котором сохранены все важнейшие особенности динамики, сезонности и краткосрочных аномалий. Энкодер словно впитывает в себя поведение рынка, фильтрует шум и концентрирует суть, передавая её в виде токенов компактного формата.

Эти токены не хранят в себе всю историю — вместо этого они аккумулируют смысл, агрегируют причинно-следственные связи, вычленяют наиболее важные факторы. И именно эти токены далее становятся универсальным источником знаний для всех остальных компонентов системы: блоков прогнозирования, модуля принятия решений (Actor) и оценщиков (Director и Critic).

Фактически, Энкодер в нашей архитектуре — это единственный канал смысловой компрессии, через который проходит вся историческая и текущая рыночная информация. Результат его работы можно сравнить с качественным снимком сложной сцены: сжатым, но в фокусе, насыщенным деталями, которые важны для дальнейшего анализа и принятия решений.

В процессе обучения, чтобы сформировать насыщенное и устойчивое латентное пространство, мы используем 3 параллельные прогностические модели, каждая из которых работает с разным горизонтом планирования. Такой подход позволяет нашему Энкодеру охватить как краткосрочные импульсы, так и долгосрочные рыночные тенденции, не теряя при этом обобщающей способности.

Каждая из этих моделей получает доступ к одному и тому же выходу Энкодера, но обучается на своём собственном таргете, соответствующем конкретному горизонту планирования. В процессе обратного распространения ошибки градиенты от всех трёх моделей агрегируются, что позволяет Энкодеру одновременно обучаться под многомерную задачу:

  • быть быстрым и точным в ближайшей перспективе;
  • сохранять устойчивость к рыночному шуму;
  • не терять стратегическую ориентацию.

Таким образом, уже на стадии обучения мы заставляем латентное пространство впитывать различные уровни рыночной логики, что в дальнейшем даёт серьёзное преимущество всем остальным компонентам системы. Состояние, сформированное таким Энкодером, одинаково хорошо подходит как для генерации торговых решений (Actor), так и для оценки их качества (Critic и Director).

Архитектура прогностических моделей была полностью перенесена из наших предыдущих работ без изменений. Поскольку она уже хорошо себя зарекомендовала в ряде задач, останавливаться на её деталях в рамках данной статьи не имеет смысла.

Однако архитектура Актёра (Actor) претерпела существенные улучшения, направленные на повышение адаптивности и экспрессивности политики. Обновлённая структура включает семь уровней, каждый из которых добавляет в модель специфические возможности. Вначале, как и ранее, используется базовый полносвязный слой, в который мы передаем информацию о текущем состоянии счета и открытых позициях.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = AccountDescr;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

За ним применяется пакетная нормализация для стабилизации обучения и выравнивания масштаба признаков, полученных из разных источников.

Слой многоголового кросс-внимания позволяет модели сопоставить текущее состояния счета с контекстом анализируемой рыночной ситуации, получаемым от Энкодера состояния окружающей среды.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronCrossDMHAttention;
     {
      uint temp[] = {AccountDescr,           // Inputs window
                    latent.windows[0]        // Cross window
                   };
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
     {
      uint temp[] = {1,                      // Inputs units
                    latent.units[0]          // Cross units
                   };
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.step = 4;                  // Heads
   descr.window_out = 8;
   descr.batch = 1e4;
   descr.layers = 2;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Благодаря двухслойной архитектуре внимания с четырьмя головами, модель может выбирать релевантные аспекты контекста для генерации действий.

Далее идет трехслойная MLP принятия решения. Здесь для каждого слоя используется своя функция активации. Гиперболический тангенс позволяет сжать токены в компактное непрерывное пространство с усиленной чувствительностью к границам.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = BatchSize;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Далее следует плавная нелинейность, которая сохраняет положительные значения. Это важно для генерации параметров действий.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SoftPlus;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

И формирует логиты для последующей выборки действий. Двойное количество выходов быть связано с параметризацией среднего и дисперсии в духе вероятностных политик.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Внедрение вариационного слоя позволяет стохастически порождать действия, сохраняя при этом контроль над распределением. Это повышает исследовательскую способность Агента.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Последний этап — свёртка, применяемая к уже сгенерированным действиям. Это позволяет усилить локальные зависимости между параметрами действиями и ввести мягкие вероятностные фильтры, преобразующие действие в диапазон [0, 1].

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

В целом, новая архитектура модуля Актёра демонстрирует более глубокое взаимодействие с контекстом, высокую вариативность поведения и способность учитывать исторические зависимости при принятии торговых решений.

Оценочные модели Режиссёра (Director) и Критика (Critic), как и прогнозные компоненты, были перенесены без каких-либо изменений из предыдущих работ. Эта часть архитектуры уже прошла проверку временем и хорошо зарекомендовала себя при обучении Агентов. Полная архитектура всех обучаемых компонентов представлена во вложении.


Тестирование

Процесс обучения модели был разделён на два этапа — это позволило выстроить систему последовательно, надёжно и без спешки.

Сначала мы провели офлайн-обучение. Для этого использовались 15 лет истории по паре EURUSD на таймфрейме M1. Такой объём данных охватывает огромное разнообразие рыночных ситуаций: от затяжных флэтов до стремительных трендов, от стабильных участков до периодов высокой волатильности. Модель получала уникальную возможность увидеть, как ведёт себя рынок в самых разных условиях. Энкодер учился распознавать закономерности, вычленять значимые паттерны и кодировать состояние рынка в компактный и насыщенный вектор признаков. Этот вектор становится основой для всех решений, которые Агент принимает в дальнейшем. Актёр в процессе обучения осваивал стратегию поведения, опираясь на сигналы обратной связи от Критика и Режиссёра — это позволяло формировать устойчивую и логичную модель поведения.

Затем мы перешли ко второму этапу — онлайн-настройке модели на исторических данных 2024 года. Здесь обучение переносилось в условия, приближённые к реальному времени: модель взаимодействовала с рынком в режиме свеча за свечой, сталкиваясь с рыночным шумом, случайными колебаниями и временными искажениями. Благодаря этому удавалось не просто дообучить модель, а адаптировать её поведение к живой динамике рынка, скорректировать стратегию и повысить устойчивость в условиях неопределённости.

После завершения обучения мы провели полноценное тестирование на новых данных — котировках за Январь–Март 2025 года. Все настройки были зафиксированы заранее и не менялись в процессе теста. Это гарантировало объективность и прозрачность оценки, исключая любые формы подгонки или вмешательства. Результаты теста приведены ниже.

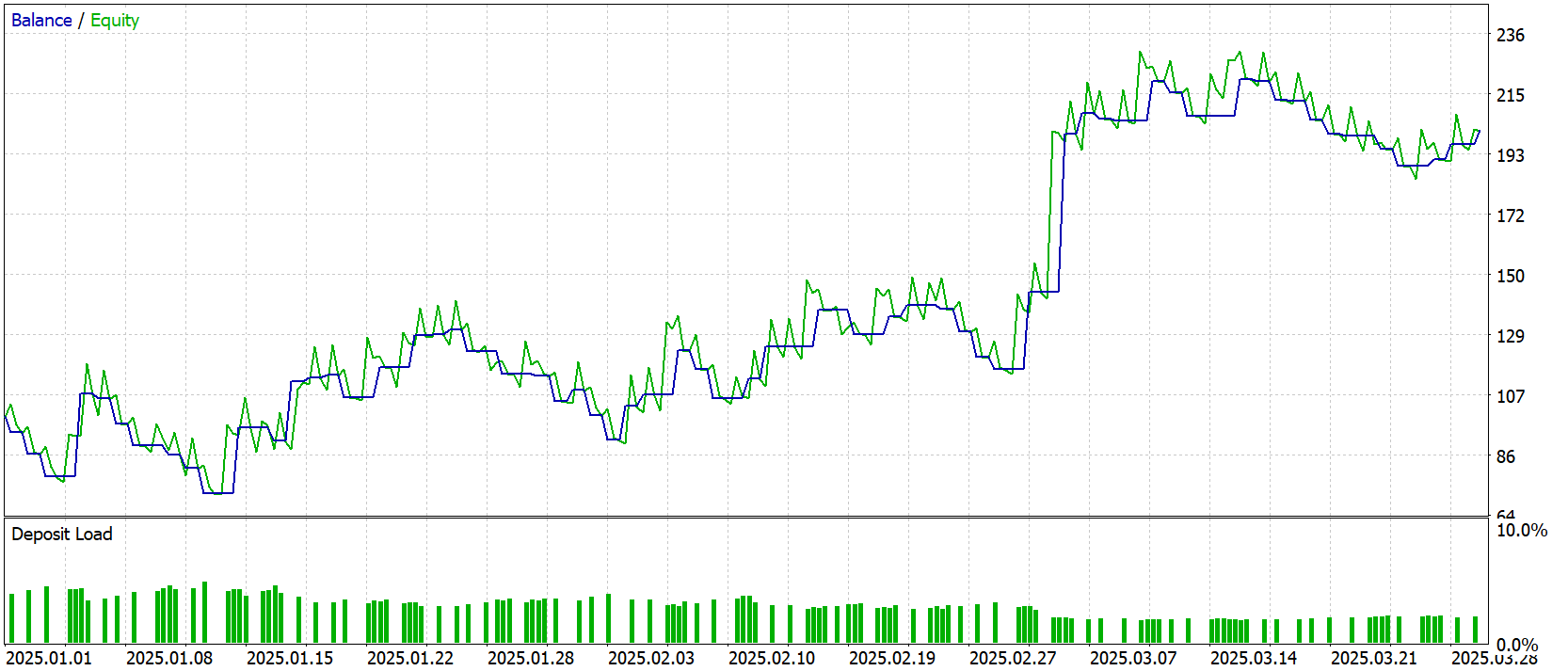
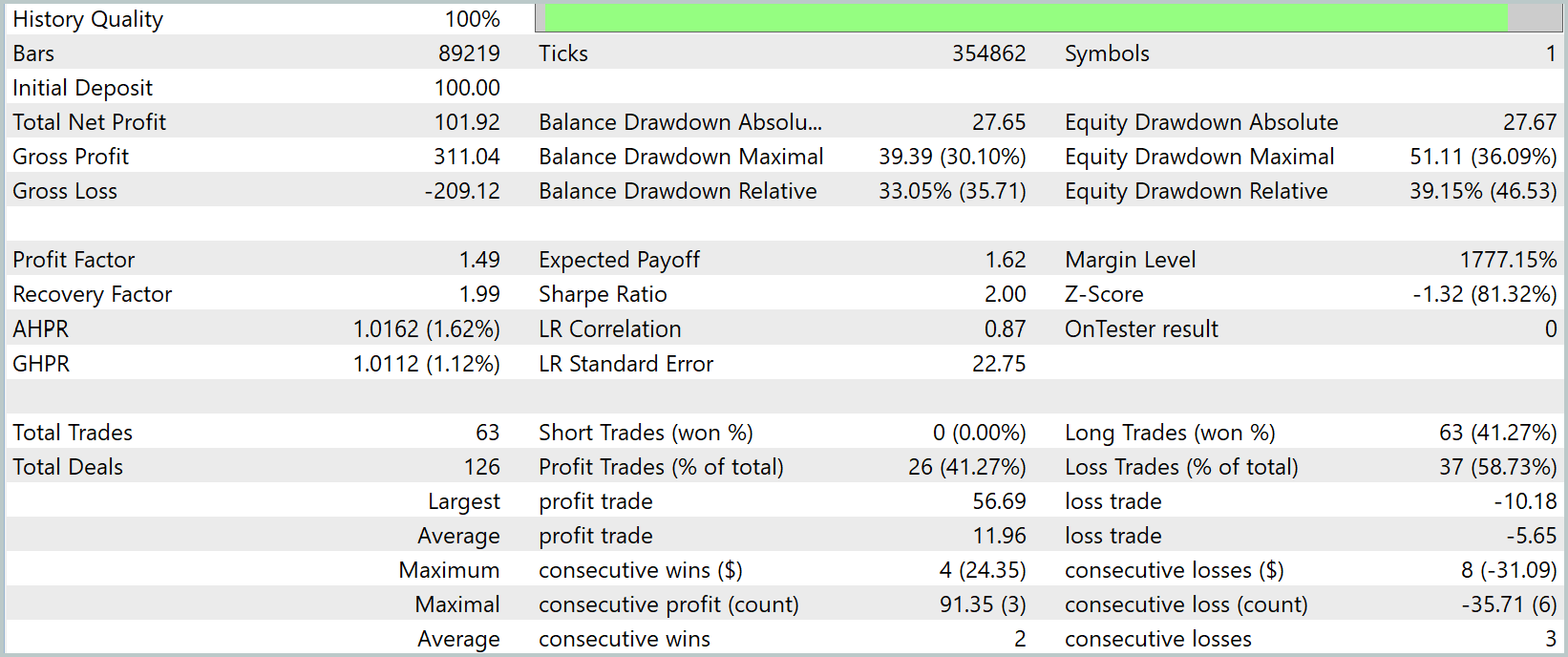
За три месяца тестирования на минутном графике (М1) наша модель показала впечатляющий рост капитала — с $100 до почти $202, однозначно удвоив депозит. При этом лишь около 41 % сделок оказались прибыльными, но средний выигрыш в $12 многократно перекрывал средний убыток в $5,6, что дало профит‑фактор 1,49. На Equity‑графике чётко видно резкие подъёмы после каждой просадки, а Recovery Factor почти в два балла подтверждает быстрый откат от максимальной просадки в 36 %.

Тем не менее при всём позитиве бросается в глаза один серьёзный уклон: модель стабильно входит только в длинные позиции, плывя за глобальным восходящим трендом. На минутном таймфрейме это проявляется особенно ярко — пока котировки растут, агент рубит профит, но при малейшем намёке на разворот он упускает возможность заработать на шорте.

Чтобы сделать стратегию действительно универсальной, нам ещё предстоит поработать над её оптимизацией.


Заключение

В ходе работы мы создали гибкую нейросетевую архитектуру: от адаптивного патчинга и RoPE до сложных модулей Time‑MoEAttention и Actor–Director–Critic. Система способна улавливать и краткосрочные импульсы, и долгосрочные тренды, а тройной прогноз на разных горизонтах делает её устойчивой к шумам рынка. Дальнейшая задача — оптимизировать стратегию под двустороннюю торговлю, добавив поддержку как лонговых, так и шортовых позиций, и отладить риск‑менеджмент для обоих направлений. Только пройдя этап масштабного тестирования и тонкой настройки под реальные данные, мы сможем получить по-настоящему конкурентоспособную систему автоматической торговли.


Ссылки


Программы, используемые в статье

# Имя Тип Описание
1 Study.mq5 Советник Советник офлайн обучения моделей
2 StudyOnline.mq5 Советник Советник онлайн обучения моделей
3 Test.mq5 Советник Советник для тестирования модели
4 Trajectory.mqh Библиотека класса Структура описания состояния системы и архитектуры моделей
5 NeuroNet.mqh Библиотека класса Библиотека классов для создания нейронной сети
6 NeuroNet.cl Библиотека Библиотека кода OpenCL-программы
Прикрепленные файлы |
Загрузить ZIP
MQL5.zip (2882.83 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Искусство ведения логов (Часть 1): Основные понятия и первые шаги в MQL5 Искусство ведения логов (Часть 1): Основные понятия и первые шаги в MQL5
Добро пожаловать в новое приключение! Данная статья открывает специальный цикл, в котором мы будем пошагово создавать библиотеку для манипуляций с журналами, предназначенную для тех, кто занимается разработкой на языке MQL5.
Торговая стратегия "Захват ликвидности" (Liquidity Grab) Торговая стратегия "Захват ликвидности" (Liquidity Grab)
Торговая стратегия захвата ликвидности является ключевым компонентом Концепции умных денег (Smart Money Concepts (SMC), которая направлена на выявление и использование действий институциональных игроков на рынке. Она предполагает нацеливание на области с высокой ликвидностью, такие как зоны поддержки или сопротивления, где крупные ордера могут спровоцировать движение цены до того, как рынок возобновит свой тренд. В настоящей статье подробно объясняется концепция захвата ликвидности и описывается процесс разработки советника по торговой стратегии захвата ликвидности на MQL5.
Реализация криптографического алгоритма SHA-256 с нуля на MQL5 Реализация криптографического алгоритма SHA-256 с нуля на MQL5
Создание интеграций с криптовалютными биржами без DLL-файлов долгое время было сложной задачей, но это решение обеспечивает полную основу для прямого подключения к рынку.
Алгоритм обратного поиска — Backtracking Search Algorithm (BSA) Алгоритм обратного поиска — Backtracking Search Algorithm (BSA)
Что если алгоритм оптимизации мог бы помнить свои прошлые путешествия и использовать эту память для поиска лучших решений? BSA делает именно это — балансируя между исследованием нового и возвращением к проверенному. В статье раскрываем секреты алгоритма. Простая идея, минимум параметров и стабильный результат.