Definição de sobrecompra e sobrevenda segundo a teoria do caos

Quando o caos se transforma em padrão

Imagine caminhar por uma floresta durante uma nevasca. Os flocos de neve parecem caóticos, seus movimentos imprevisíveis. Mas, se observar com mais atenção, você perceberá que eles se movem por fluxos invisíveis de ar, seguindo certas regularidades. Assim como esses flocos, os preços nos mercados financeiros dançam sua própria dança, que apenas aparenta ser aleatória.

A teoria do caos nos ensina uma verdade surpreendente: em sistemas que parecem totalmente imprevisíveis, escondem-se padrões e estruturas profundas. O meteorologista Edward Lorenz descobriu isso ao trabalhar com modelos meteorológicos e acidentalmente inserir dados arredondados em seu programa. Sua descoberta, mais tarde chamada de "efeito borboleta", mostrou que até pequenas variações nas condições iniciais podem levar a resultados completamente diferentes.

"Um sistema que possui um atrator estranho pode parecer totalmente aleatório, mas dentro dele há uma ordem oculta", dizia Lorenz. E da mesma forma que os sistemas climáticos possuem padrões invisíveis, os mercados financeiros seguem certas regularidades, apesar de sua aparente imprevisibilidade.

Atratores: os ímãs invisíveis do mercado

Imagine que você joga uma bola dentro de um quarto. Não importa a força ou a direção, no final ela acabará no chão. O chão, nesse caso, é o atrator, em outras palavras, o ponto de atração da bola.

Nos mercados financeiros, os atratores funcionam de forma semelhante. Em vez de uma força física, atuam forças econômicas que trazem os preços de volta a determinados níveis. Quando uma ação fica cara demais, os vendedores prevalecem; quando fica barata demais, predominam os compradores. Isso cria um efeito “elástico”, que constantemente puxa o mercado de volta a um ponto de equilíbrio.

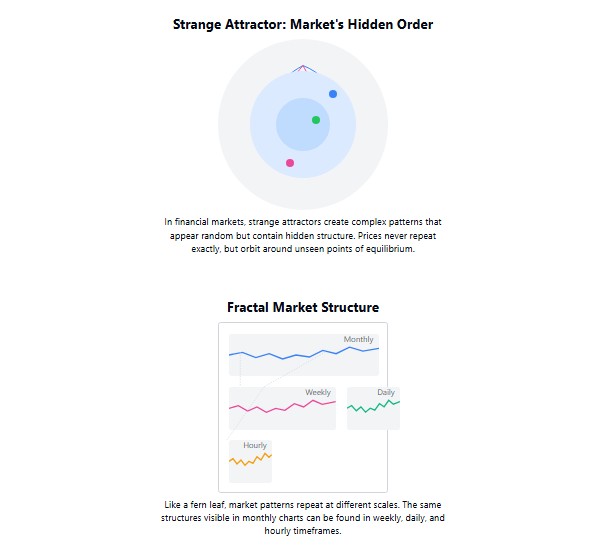
Mas, diferente de uma simples bola, os mercados possuem o que chamamos de “atratores estranhos”. Não são pontos fixos, e sim estruturas complexas para as quais o sistema tende, sem jamais repetir exatamente o mesmo estado. Como um riacho que deságua em um lago: a água sempre corre para ele, mas nunca pelo mesmo caminho.

Como compreender o padrão fractal do mercado

Benoît Mandelbrot, enquanto trabalhava na IBM na década de 1960, analisava as flutuações dos preços do algodão ao longo de um longo período. Ele notou algo surpreendente: os gráficos de preços pareciam idênticos, independentemente de observar os dados de um dia, de um mês ou de um ano. Essa descoberta marcou o início do desenvolvimento da geometria fractal, que é a ciência que estuda formas que se repetem em diferentes escalas.

Observe uma folha de samambaia: sua forma geral se repete em cada pequeno folíolo e, depois, em partes ainda menores. Os mercados funcionam de maneira semelhante. Os padrões que você vê em um gráfico de minutos frequentemente se repetem nos gráficos de horas, dias e até meses.

Essa auto-semelhança não é acidental. Ela reflete o fato de que os mercados não são apenas ruído aleatório, mas sistemas complexos com estrutura interna. E compreender essa estrutura nos dá a chave para prever movimentos futuros.

Retorno à média: o ritmo universal da natureza

No mundo financeiro existe um ditado: "As árvores não crescem até o céu". A história mostra que, após períodos de crescimento ou queda extremos, os mercados tendem a retornar ao seu valor médio de longo prazo.

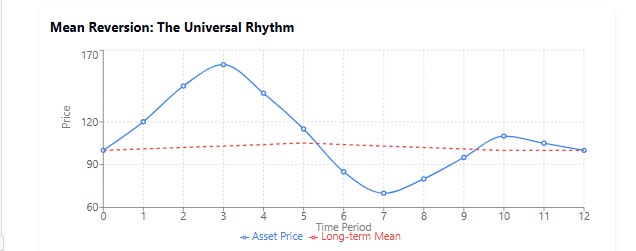
Esse fenômeno pode ser observado em toda a natureza. Imagine um pêndulo: quanto mais você o afasta, mais forte ele tende a retornar à posição central. Ou pense na temperatura do corpo humano: quando você tem febre, o organismo trabalha para trazê-la de volta ao nível normal de 36,6°C.

Nos mercados, esse efeito se manifesta o tempo todo. Ações que apresentam rentabilidade extraordinária em um período geralmente mostram resultados medianos no seguinte. Empresas que crescem mais rápido que o mercado por muito tempo quase inevitavelmente desaceleram. Como observou o lendário investidor Peter Lynch: "O retorno à média é a gravidade que nem mesmo uma grande empresa pode superar".

Mas o que torna o Sensory Neural Attractor revolucionário é sua capacidade de determinar não apenas uma média estática, mas um nível dinâmico para o qual o mercado tende no momento presente. É como ser capaz de prever exatamente onde o pêndulo vai parar se a força da gravidade mudar de repente.

Sensibilidade às condições iniciais: o efeito borboleta em Wall Street

"Será que o bater das asas de uma borboleta no Brasil pode causar um tornado no Texas?" — essa famosa pergunta de Lorenz ilustra um princípio fundamental da teoria do caos: a sensibilidade às condições iniciais.

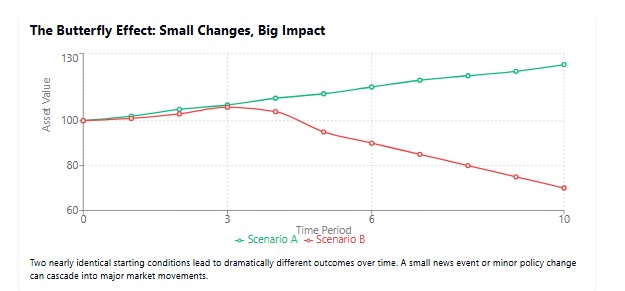
Nos mercados financeiros, observamos esses "efeitos borboleta" o tempo todo. Um simples tweet de um diretor executivo pode derrubar as ações de uma empresa. Uma decisão inesperada do Federal Reserve pode provocar uma correção global. Até mesmo rumores sobre problemas em um pequeno banco podem gerar pânico em todo o setor bancário, como vimos durante a crise de 2008.

Essa sensibilidade torna a previsão de longo prazo com precisão praticamente impossível. Como brincava Niels Bohr: "Prever é muito difícil, especialmente o futuro". No entanto, ao compreender a estrutura do sistema e identificar os atratores, podemos fazer previsões probabilísticas que oferecem vantagem.

Oscilador neural de atratores: domando o caos do mercado

Da teoria à prática: criando o indicador

Você já percebeu como o preço de um ativo, como se fosse guiado por uma força invisível, tende a retornar a determinado nível? Como após um forte rali surge uma correção abrupta, ou como depois de uma longa queda o preço inesperadamente começa a se recuperar? É como se algo invisível puxasse o preço de volta, impedindo-o de se mover para sempre em uma única direção. É exatamente essa força invisível que pretendemos capturar com nossa rede digital.

Enquanto outros traders continuam usando indicadores do século passado, nós embarcaremos em uma jornada mais profunda: a criação de um indicador que literalmente aprende a reconhecer o ritmo oculto do mercado. Nosso compasso nessa viagem será uma rede neural, e nosso mapa — a teoria dos atratores.

Arquitetura da rede neural: o cérebro do nosso indicador

Lembra daqueles filmes sobre hackers em que o protagonista cria uma superinteligência em poucos minutos de tela? Na prática, o processo é um pouco mais complexo, mas não a ponto de um trader-programador comum não conseguir fazê-lo.

Podemos imaginar nossa rede neural como um rastreador experiente que analisa pegadas na neve (os preços históricos) e tenta prever para onde está indo o animal (o mercado). A estrutura desse rastreador é bastante simples: uma camada de entrada, que coleta os dados; uma camada oculta, onde acontece a “mágica” do reconhecimento de padrões; e uma camada de saída, que gera a previsão.

É assim que se apresenta a inicialização do nosso centro neural:

void InitializeNetwork() {
   // Инициализация скрытого слоя
   ArrayResize(Network.hidden, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      ArrayResize(Network.hidden[i].weights, InputNeurons);
      // Инициализация весов случайными значениями в диапазоне [-0.5, 0.5]
      for(int j = 0; j < InputNeurons; j++) {
         Network.hidden[i].weights[j] = (MathRand() / 32767.0) - 0.5;
      }
      Network.hidden[i].bias = (MathRand() / 32767.0) - 0.5;
   }
   
   // Инициализация выходного нейрона
   ArrayResize(Network.output.weights, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      Network.output.weights[i] = (MathRand() / 32767.0) - 0.5;
   }
   Network.output.bias = (MathRand() / 32767.0) - 0.5;
}

Preste atenção nas linhas onde ocorre a inicialização dos pesos. É como ajustar a sensibilidade de um microscópio antes da análise. Começamos com valores aleatórios e, em seguida, o processo de aprendizado ajusta gradualmente esses “controles de precisão” para produzir uma imagem mais nítida.

Treinamento da rede: de iniciante a mestre

Imagine uma criança aprendendo a andar. No começo ela cai, depois dá alguns passos, cai de novo, mas aos poucos melhora suas habilidades. Da mesma forma, nossa rede aprende a “andar” pelos dados históricos, ajustando constantemente seus passos.

A parte essencial desse processo é a propagação para frente e a propagação reversa. Na propagação para frente, a rede faz a previsão; na propagação reversa, ela ajusta seus pesos com base no erro obtido.

double ForwardPass(double &inputs[]) {
   // Расчет выходов скрытого слоя
   for(int i = 0; i < HiddenNeurons; i++) {
      double sum = Network.hidden[i].bias;
      for(int j = 0; j < InputNeurons; j++) {
         sum += inputs[j] * Network.hidden[i].weights[j];
      }
      Network.hidden[i].output = Sigmoid(sum);
   }
   
   // Расчет выхода нейросети
   double sum = Network.output.bias;
   for(int i = 0; i < HiddenNeurons; i++) {
      sum += Network.hidden[i].output * Network.output.weights[i];
   }
   Network.output.output = Sigmoid(sum);
   
   return Network.output.output;
}

Se pudéssemos observar o interior dessa função em funcionamento, veríamos algo semelhante a impulsos elétricos percorrendo os neurônios do cérebro, a informação se desloca pela rede de conexões, sendo transformada e amplificada ao longo do caminho.

Função de ativação: acendendo os neurônios

Na versão atualizada do indicador, substituímos a clássica sigmoide pela tangente hiperbólica (tanh). Essa função opera no intervalo [-1, 1], o que a torna especialmente eficaz para modelar sistemas caóticos, nos quais tanto os valores positivos quanto os negativos têm importância.

double Tanh(double x) {
   return (MathExp(x) - MathExp(-x)) / (MathExp(x) + MathExp(-x));
}

A tangente hiperbólica apresenta uma inclinação mais acentuada na região central, permitindo que a rede aprenda mais rapidamente e capture com maior precisão mudanças bruscas nos dados. Isso é crucial em mercados caóticos, onde as transições entre estados podem ocorrer de forma repentina.

Normalização dos dados: falando a mesma língua

Antes de alimentar a rede neural com dados, é necessário normalizá-los, ou seja, trazê-los para uma mesma escala. É como traduzir um texto para um idioma que o interlocutor compreenda. Se você fala em russo e a outra pessoa entende apenas inglês, a comunicação simplesmente não acontece.

double NormalizePrice(double price) {
   double min = ArrayMin(PriceHistory);
   double max = ArrayMax(PriceHistory);
   return (price - min) / (max - min);
}

Essa função ajusta todas as cotações para o intervalo de 0 a 1, o que é ideal para alimentar nossa função de ativação sigmoide.

Cálculo do oscilador: o momento da verdade

Finalmente chegamos à parte mais interessante, o cálculo do valor do oscilador. Como fazemos isso? Essencialmente, comparamos o preço atual com o atrator previsto e expressamos o desvio em porcentagem.

// Рассчитываем значение осциллятора как отношение текущей цены к аттрактору
if(AttractorBuffer[i] > 0) {
   OscillatorBuffer[i] = (CurrentPriceBuffer[i] / AttractorBuffer[i] - 1.0) * 100.0;
} else {
   OscillatorBuffer[i] = 0; // Защита от деления на ноль
}

Essa fórmula simples nos mostra o quanto o preço atual se desviou de seu “nível natural”. Se o oscilador indicar +30%, o preço está “superaquecido” e pode logo retornar ao atrator. Se indicar -30%, o preço está “resfriado” e pode reagir com um movimento de alta.

Ajustando o indicador às suas necessidades

Lembra do velho ditado “Um tamanho serve para todos”? No trading isso raramente se aplica. Cada mercado, cada timeframe tem sua própria personalidade, seu próprio “humor”. E nosso indicador precisa se adaptar a essas nuances.

input int    InputNeurons = 10;     // Количество входных нейронов (исторические периоды)
input int    HiddenNeurons = 20;    // Количество нейронов в скрытом слое
input double LearningRate = 0.01;   // Скорость обучения
input int    TrainBars = 1000;      // Количество баров для обучения
input int    PredictionPeriod = 5;  // Период предсказания (в барах)
input bool   Smoothing = false;     // Применять сглаживание к осциллятору
input int    SmoothingPeriod = 3;   // Период сглаживания

Esses parâmetros são como os controles de um amplificador de som de alta qualidade. Quer um indicador mais sensível? Aumente o número de neurônios ou reduza o período de previsão. Está captando muito ruído? Ative o suavizamento.

Período de previsão: olhando para o futuro

Um dos parâmetros mais interessantes é o PredictionPeriod. Ele define o quão longe no futuro tentamos enxergar. Se você é um scalper que opera em gráficos de minuto, o valor 5 significa uma previsão para 5 minutos à frente. Se for um trader posicional que trabalha com gráficos diários, esse mesmo valor representa 5 dias.

Eu recomendo que você experimente esse parâmetro. Comece com valores pequenos e aumente-os gradualmente, observando como o comportamento do indicador muda. Assim como na verdadeira ciência, aqui não existem fórmulas prontas, há apenas prática e experimentação.

Expoente de Lyapunov: medindo a caoticidade do mercado

O componente central do nosso indicador aprimorado é o expoente de Lyapunov, uma medida da sensibilidade do sistema às condições iniciais. Esse parâmetro descreve matematicamente o famoso “efeito borboleta”, o fenômeno em que pequenas variações nas condições de partida levam a grandes divergências no longo prazo.

double CalculateLyapunovExponent(const double &close[], int bars) {
   double epsilon = 0.0001; // Малое возмущение
   double lyapunov = 0.0;
   int samples = MathMin(LyapunovPeriod, TrainBars/2);
   
   for(int i = 0; i < samples; i++) {
      int startIdx = MathRand() % (TrainBars - InputNeurons - PredictionPeriod);
      
      // Исходные входные данные
      double inputs1[];
      ArrayResize(inputs1, InputNeurons);
      for(int j = 0; j < InputNeurons; j++) {
         inputs1[j] = NormalizePrice(close[bars - TrainBars + startIdx + j]);
      }
      
      // Слегка возмущенные входные данные
      double inputs2[];
      ArrayResize(inputs2, InputNeurons);
      ArrayCopy(inputs2, inputs1);
      inputs2[MathRand() % InputNeurons] += epsilon;
      
      // Предсказания для обоих наборов данных
      double pred1 = ForwardPass(inputs1);
      double pred2 = ForwardPass(inputs2);
      
      // Расстояние между предсказаниями
      double distance = MathAbs(pred2 - pred1);
      
      // Показатель Ляпунова
      if(distance > 0) {
         lyapunov += MathLog(distance / epsilon);
      }
   }
   
   // Усредняем и нормализуем
   lyapunov = lyapunov / samples;
   
   // Ограничиваем значение для стабильности
   lyapunov = MathMax(-1.0, MathMin(1.0, lyapunov));
   
   return lyapunov;
}

Ruído fractal: adicionando estrutura natural

Um dos elementos mais inovadores do nosso indicador é a inclusão do ruído fractal, gerado pelo algoritmo de deslocamento do ponto médio (Midpoint Displacement). A geometria fractal, aplicada pela primeira vez aos mercados financeiros por Benoît Mandelbrot, permite modelar sua estrutura naturalmente auto-semelhante.

void GenerateFractalNoise(int size) {
   ArrayResize(FractalNoiseBuffer, size);
   
   // Начальные точки
   FractalNoiseBuffer[0] = 0;
   FractalNoiseBuffer[size-1] = 0;
   
   // Рекурсивное вычисление промежуточных точек
   MidpointDisplacement(FractalNoiseBuffer, 0, size-1, 1.0, FractalDimension);
   
   // Нормализация
   double min = ArrayMin(FractalNoiseBuffer, 0, size);
   double max = ArrayMax(FractalNoiseBuffer, 0, size);
   
   for(int i = 0; i < size; i++) {
      FractalNoiseBuffer[i] = 2.0 * (FractalNoiseBuffer[i] - min) / (max - min) - 1.0;
   }
}

Quanto maior o parâmetro de dimensão fractal (FractalDimension), mais “dentado” e caótico se torna o ruído, o que possibilita uma modelagem mais precisa de mercados com alta volatilidade.

Aplicação prática do indicador

Agora que entendemos como nosso indicador funciona, vamos discutir como aplicá-lo na prática. Assim como qualquer oscilador, o Neural Attractor Oscillator pode ser usado para identificar zonas de sobrecompra e sobrevenda do mercado.

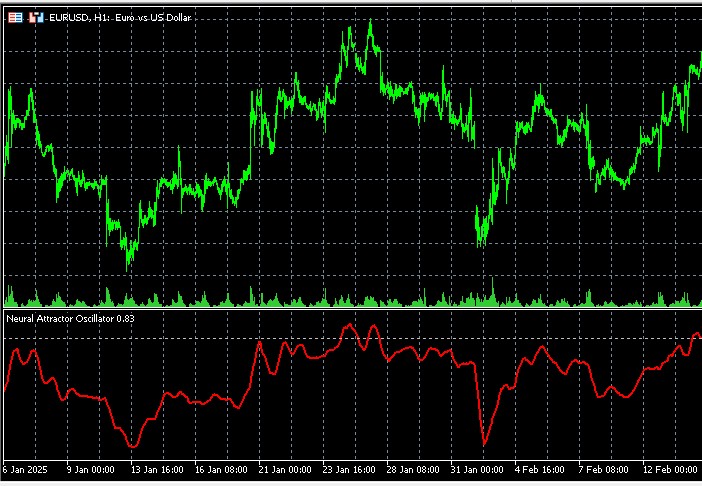
Imagine que você observa um pêndulo. Quando ele se afasta demais para a direita, você sabe que logo começará a se mover para a esquerda. Quando vai longe demais para a esquerda, em breve voltará para a direita. Nosso indicador funciona de maneira semelhante, mas, em vez de forças mecânicas trazendo o pêndulo de volta ao centro, aqui atuam forças de equilíbrio do próprio mercado.

Sinais de entrada considerando a caoticidade

1. Sinal de comprA: Quando o oscilador cai abaixo do limite inferior do atrator (que é dinamicamente ajustado conforme o valor do expoente de Lyapunov) e começa a subir, isso pode indicar um bom ponto para abrir uma posição de compra. É importante observar o valor atual do expoente de Lyapunov: quanto menor ele for, mais confiável é o sinal.
2. Sinal de venda: Quando o oscilador ultrapassa o limite superior do atrator e começa a cair, isso pode apontar para um bom momento de abrir uma posição de venda. Mais uma vez, um valor baixo do expoente de Lyapunov aumenta a confiabilidade do sinal.
3. DivergênciaS: Trata-se de um sinal especialmente valioso e preciso, observado quando há divergência entre os topos do indicador e os do preço.

Lembre-se de que, em períodos de alta caoticidade (alto valor do expoente de Lyapunov), mesmo sinais fortes se tornam menos confiáveis, e é prudente reduzir o tamanho da posição ou até mesmo evitar entrar no mercado.

Divergências no contexto da teoria do caos

O oscilador Chaos Attractor oferece uma nova perspectiva sobre as divergências clássicas. Quando o preço forma um novo extremo, mas o oscilador não o acompanha, isso pode indicar não apenas um enfraquecimento da tendência, mas uma mudança na própria estrutura do atrator, o ponto de equilíbrio para o qual o mercado tende.

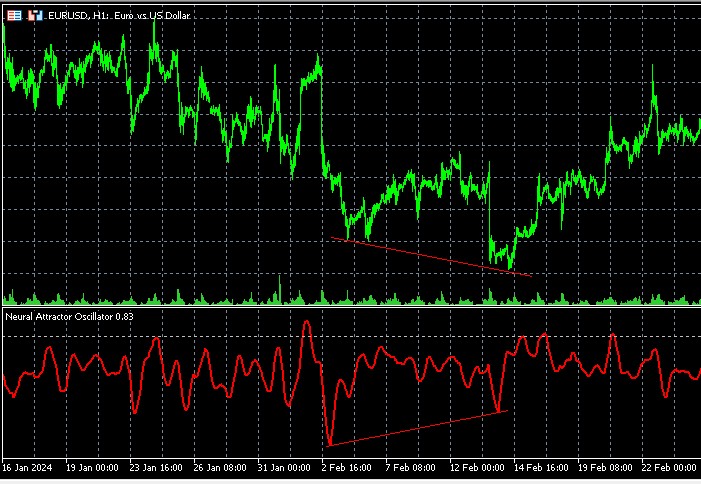
Sinais particularmente fortes surgem quando a divergência coincide com uma variação do expoente de Lyapunov. Por exemplo, uma transição de valores positivos para negativos pode sinalizar a formação de uma nova tendência estável após um período de comportamento caótico.

Otimização da rede com momento

Em nosso indicador aprimorado, aplicamos a técnica de otimização com momento, que acelera significativamente o processo de aprendizado e reduz a probabilidade de a rede ficar presa em mínimos locais:

// Обновление весов выходного слоя с моментом
for(int j = 0; j < HiddenNeurons; j++) {
    double delta = LearningRate * Network.output.error * Network.hidden[j].output;
    Network.output.momentum[j] = momentum * Network.output.momentum[j] + (1.0 - momentum) * delta;
    Network.output.weights[j] += Network.output.momentum[j];
}

O método do momento funciona como a “inércia” no mundo físico: se a rede vinha se movendo em uma determinada direção durante a otimização, ela continuará avançando nessa direção mesmo ao encontrar pequenos obstáculos (mínimos locais). Isso é especialmente útil em sistemas caóticos, onde a superfície da função de erro pode ser extremamente complexa.

Futuras melhorias

Embora nosso indicador já seja uma ferramenta poderosa, existem várias direções promissoras para o desenvolvimento da abordagem Chaos Attractor:

1. Redes neurais recorrentes: Substituir nossa rede neural feedforward por uma rede recorrente (LSTM ou GRU) pode aprimorar a capacidade do modelo de capturar dependências de longo prazo em sistemas caóticos.
2. Análise multifractal: A introdução de métodos de análise multifractal pode ajudar a identificar a estrutura da volatilidade em diferentes escalas temporais.
3. Análise da topologia dos atratores: Aplicar técnicas de topologia dinâmica pode permitir identificar e classificar atratores estranhos na dinâmica dos preços.
4. Algoritmos quânticos: No futuro, o uso de computação quântica poderá possibilitar a modelagem de sistemas caóticos complexos, representando um avanço revolucionário na previsão de movimentos de mercado.

E, claro, ainda abordaremos a criação de um EA (Expert Advisor) baseado nesse sistema. A seguir, temos um esboço inicial — uma prévia do expert em desenvolvimento:

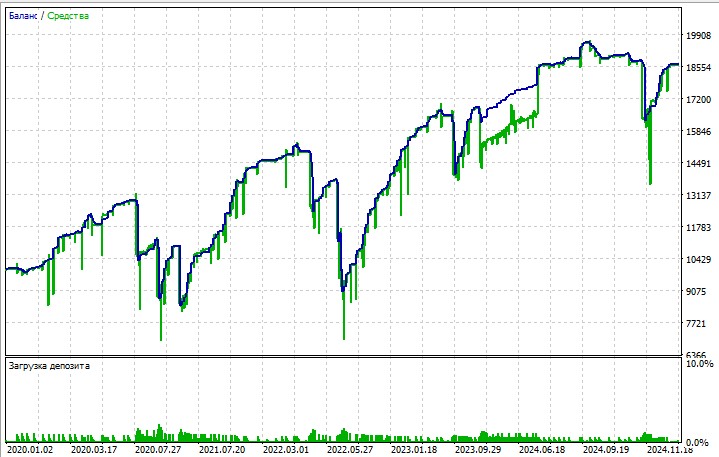
No geral, o sistema funciona de forma razoável: não é excepcional, mas também está longe de ser ruim.

Métodos flexíveis de suavização

Na versão atualizada do indicador, adicionamos a possibilidade de escolher entre diferentes métodos de suavização, o que permite ao trader ajustar a sensibilidade do indicador conforme as condições de mercado:

void ApplySmoothing(int rates_total, int prev_calculated, int period, ENUM_MA_METHOD method) {
   int start = prev_calculated == 0 ? InputNeurons + period : prev_calculated - 1;
   
   double temp[];
   ArrayResize(temp, rates_total);
   ArrayCopy(temp, OscillatorBuffer);
   
   for(int i = start; i < rates_total; i++) {
      switch(method) {
         case MODE_SMA: // Простое скользящее среднее
            {
               double sum = 0;
               for(int j = 0; j < period; j++) {
                  sum += temp[i - j];
               }
               OscillatorBuffer[i] = sum / period;
            }
            break;
            
         case MODE_EMA: // Экспоненциальное скользящее среднее
            {
               double alpha = 2.0 / (period + 1.0);
               OscillatorBuffer[i] = temp[i] * alpha + OscillatorBuffer[i-1] * (1.0 - alpha);
            }
            break;
            
         // ... другие методы ...
      }
   }
}

Para mercados caóticos com alto valor do expoente de Lyapunov, é melhor usar a EMA, que reage mais rapidamente às mudanças. Já para mercados mais previsíveis, com baixo valor do expoente de Lyapunov, a SMA pode oferecer sinais mais confiáveis, com menor quantidade de falsos alertas.

Considerações finais

Nós criamos não apenas mais um indicador técnico, mas um sistema completo de análise do caos de mercado. O Chaos Attractor Oscillator combina os mais recentes avanços da teoria do caos, da geometria fractal e das redes neurais, oferecendo ao trader uma ferramenta para navegar em condições de mercado complexas e imprevisíveis.

O valor especial desse indicador está em sua capacidade não só de gerar sinais de trade, mas também de avaliar a confiabilidade desses sinais por meio do expoente de Lyapunov. Isso permite que o trader adapte sua estratégia ao estado atual do mercado, sendo agressivo quando o sistema é previsível e cauteloso quando se torna caótico.

Na era do trading algorítmico e da inteligência artificial, vence quem consegue modelar melhor a natureza complexa do mercado. O Chaos Attractor Oscillator é um passo nessa direção, permitindo enxergar ordem onde outros veem apenas aleatoriedade.

Lembre-se: mesmo o indicador mais avançado não é uma fórmula mágica para o sucesso. O trading sempre exigirá disciplina, gestão de risco e compreensão do contexto de mercado. Mas, ao utilizar uma ferramenta que permite enxergar a própria natureza do caos de mercado, você ganha uma vantagem significativa no caminho para a rentabilidade consistente.

Boa sorte nas suas operações — e que os atratores do caos estejam com você!