Redes neurais em trading: Transformador hierárquico de duas torres (Hidformer)

Introdução

Modelos baseados em redes neurais tornaram-se especialmente requisitados na previsão financeira, graças à sua capacidade de levar em conta a estrutura temporal dos dados e identificar padrões ocultos. No entanto, abordagens tradicionais com redes neurais apresentam limitações, como alta complexidade computacional e baixa interpretabilidade dos resultados. Por isso, nos últimos anos, arquiteturas baseadas em mecanismos de atenção têm atraído a atenção dos pesquisadores, por possibilitarem uma análise mais precisa de séries temporais e dados financeiros.

As maiores inovações surgiram com modelos baseados na arquitetura Transformer e suas variações. No trabalho "Hidformer: Transformer-Style Neural Network in Stock Price Forecasting", é apresentada uma dessas modificações, chamada Hidformer. Este modelo foi criado especialmente para análise de séries temporais, com foco em melhorar a precisão das previsões através de mecanismos de atenção otimizados, identificação eficiente de dependências de longo prazo e adaptação às especificidades dos dados financeiros. A principal vantagem do Hidformer está na sua capacidade de considerar dependências temporais complexas, o que é um fator essencial na análise do mercado de ações, onde os preços dos ativos são influenciados por inúmeros fatores.

Os autores do framework propuseram um aprimoramento no tratamento das dependências temporais, a redução da complexidade computacional do modelo e o aumento da precisão das previsões. Isso torna o Hidformer uma ferramenta promissora para análise e previsão financeira.

Algoritmo Hidformer

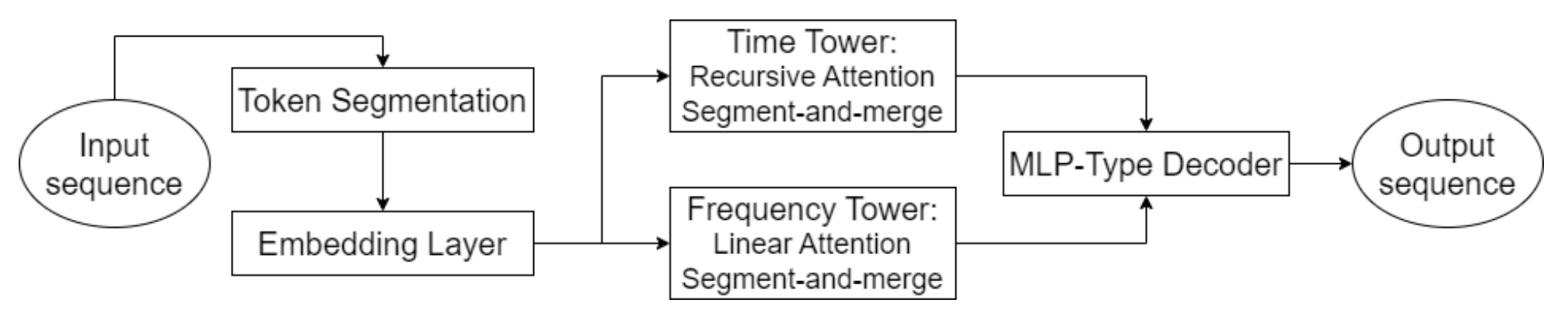
Uma das principais características do Hidformer é o processamento paralelo dos dados mediante dois codificadores. O primeiro analisa as características temporais, identificando tendências e padrões na escala do tempo. O segundo atua no domínio da frequência, permitindo detectar dependências mais profundas e eliminar o ruído de mercado. Essa abordagem possibilita a extração de padrões ocultos nos dados, o que é crítico na previsão de preços no mercado acionário, onde os sinais podem estar encobertos pelo ruído de mercado. Os dados brutos são divididos em subsequências, que são então combinadas em cada etapa do processamento, o que melhora a identificação de padrões relevantes.

Essa metodologia é especialmente útil para a análise de ativos voláteis, como ações de empresas de tecnologia ou criptomoedas, pois ajuda a separar as tendências fundamentais das oscilações de curto prazo. Em vez da atenção com múltiplas cabeças padrão usada na arquitetura Transformer, os autores do Hidformer propuseram o uso de um mecanismo de atenção recursiva no codificador temporal e um mecanismo de atenção linear para capturar dependências no espectro de frequência. Isso permitiu reduzir o consumo de recursos computacionais e aumentar a estabilidade das previsões, o que torna o modelo eficaz ao lidar com grandes volumes de dados de mercado.

O decodificador do modelo é baseado em um perceptron multicamada, o que permite prever toda a sequência de preços em um único passo. Como resultado, são eliminados erros que poderiam se acumular em previsões feitas etapa por etapa. Essa arquitetura é especialmente útil para previsões financeiras, pois reduz a probabilidade de acúmulo de imprecisões em previsões de longo prazo.

A visualização original do framework Hidformer é apresentada abaixo.

Implementação em MQL5

Após uma breve introdução aos aspectos teóricos do framework Hidformer, passamos agora à implementação da nossa própria visão das abordagens propostas usando MQL5. E começaremos nosso trabalho com a implementação dos algoritmos de atenção modificados.

Antes de tudo, vamos observar o algoritmo de atenção recursiva proposto. Originalmente, o algoritmo recurso recursivo de atenção foi criado para resolver tarefas de diálogo visual, já que ele permite encontrar o contexto correto de uma pergunta atual com base no histórico existente do diálogo anterior. É evidente que o processamento recursivo dos dados, em vez do cálculo paralelo da atenção com múltiplas cabeças, só tornará a tarefa mais difícil para nós. Por outro lado, a abordagem recursiva permite que a gente interrompa o processamento ao encontrar a primeira mensagem com contexto correspondente, sem precisar percorrer todo o histórico.

Esses raciocínios nos levam à construção de um algoritmo de atenção multiescalar. Já discutimos anteriormente diferentes algoritmos para capturar características locais e globais por meio da modificação da janela de atenção. Porém, os diferentes níveis de atenção eram utilizados em objetos distintos. Agora, proponho uma leve modificação no algoritmo de atenção com múltiplas cabeças já construído, atribuindo a cada cabeça sua própria janela de contexto. Mais ainda: propomos definir a janela de contexto não em torno do elemento analisado, mas a partir do início da sequência. Vale lembrar que, no início da sequência, armazenamos os dados mais recentes. Essa abordagem permitirá avaliar o histórico analisado justamente no contexto da situação atual do mercado.

Modificação da atenção no lado OpenCL

Para começar, vamos implementar as alterações descritas acima no lado do programa OpenCL. Para isso, criaremos um novo kernel chamado MultiScaleRelativeAttentionOut, do qual a maior parte do código será reutilizada a partir do kernel doador MHRelativeAttentionOut. A lista de parâmetros do kernel foi mantida sem alterações.

__kernel void MultiScaleRelativeAttentionOut(__global const float * q,        ///<[in] Matrix of Querys
                                             __global const float * k,        ///<[in] Matrix of Keys
                                             __global const float * v,        ///<[in] Matrix of Values
                                             __global const float * bk,       ///<[in] Matrix of Positional Bias Keys
                                             __global const float * bv,       ///<[in] Matrix of Positional Bias Values
                                             __global const float * gc,       ///<[in] Global content bias vector
                                             __global const float * gp,       ///<[in] Global positional bias vector
                                             __global float * score,          ///<[out] Matrix of Scores
                                             __global float * out,            ///<[out] Matrix of attention
                                             const int dimension              ///< Dimension of Key
                                            )
  {
//--- init
   const uint q_id = get_global_id(0);
   const uint k_id = get_local_id(1);
   const uint h = get_global_id(2);
   const uint qunits = get_global_size(0);
   const uint kunits = get_local_size(1);
   const uint heads = get_global_size(2);
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   const uint window = fmax((kunits + h) / (h + 1), fmin(3, kunits));
   float koef = sqrt((float)dimension);

No corpo do método, realizamos primeiro o trabalho preparatório. Aqui definimos todas as constantes necessárias, incluindo a janela de contexto.

Vale destacar que não criamos um buffer separado para transmitir tamanhos individuais de contexto para cada cabeça de atenção. Em vez disso, simplesmente dividimos o comprimento da sequência analisada pelo identificador da cabeça de atenção, incrementado em "1", já que os identificadores começam em "0". Dessa forma, a primeira cabeça de atenção analisa toda a sequência, e a partir daí ocorre uma redução proporcional do contexto analisado.

Em seguida, precisamos determinar os coeficientes de influência. Aqui, cada thread de operação calcula um coeficiente para o elemento correspondente. No entanto, as operações ocorrem apenas dentro da janela de contexto. Os demais elementos recebem automaticamente um coeficiente de influência igual a zero.

   __local float temp[LOCAL_ARRAY_SIZE];
//--- score
   float sc = 0;
   if(k_id < window)
     {
      for(int d = 0; d < dimension; d++)
        {
         float val_q = q[shift_q + d];
         float val_k = k[shift_kv + d];
         float val_bk = bk[shift_kv + d];
         sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + 
                                                                 gp[shift_q + d] * val_bk;
        }
      sc = sc / koef;
     }

Para melhorar a estabilidade no cálculo dos coeficientes, aplicamos um deslocamento para o intervalo de valores válidos. Para isso, encontramos o valor máximo entre os coeficientes calculados, desconsiderando aqueles que estão fora da janela de contexto.

//--- max value
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id < window)
         if(k_id >= cur_k && k_id < (cur_k + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc));
           }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < (window + 1) / 2)
         if(k_id < ls)
            temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count],
                                                                  temp[k_id]) : temp[k_id]);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Somente depois disso, determinamos o valor exponencial do coeficiente, subtraindo o valor máximo.

   if(k_id < window)
      sc = IsNaNOrInf(exp(fmax(sc - temp[0], -120)), 0);
   barrier(CLK_LOCAL_MEM_FENCE);

Contudo, é importante prestar atenção à realização das operações dentro dos limites da janela de contexto. Ao ajustar o valor máximo para "0", a exponencial máxima torna-se "1". Com isso, todos os demais coeficientes ficam no intervalo entre 0 e 1. Essa abordagem aumenta a estabilidade da função SoftMax. Mas devemos lembrar que os coeficientes fora da janela de contexto receberam automaticamente valor zero. Se calcularmos seu valor exponencial, eles obterão o maior coeficiente de influência, o que é altamente indesejável. Portanto, é essencial que esses coeficientes permaneçam em "0".

Depois disso, somamos os valores dos coeficientes obtidos dentro do grupo de trabalho.

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (uint)kunits);
   do
     {
      count = (count + 1) / 2;
      if(k_id < count && k_id < (window + 1) / 2)
         temp[k_id] += ((k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

E normalizamos cada coeficiente, dividindo-o pela soma obtida.

//--- score
   float sum = IsNaNOrInf(temp[0], 1);
   if(sum <= 1.2e-7f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Os valores normalizados são então armazenados no buffer de dados correspondente.

Agora, após obter os coeficientes normalizados de influência dos elementos individuais da sequência, podemos calcular o valor ajustado do elemento atual. Para isso, organizamos um laço no qual multiplicamos o Value pelos respectivos coeficientes de influência e somamos os valores resultantes.

//--- out
   int shift_local = k_id % ls;
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = IsNaNOrInf(sc * (val_v + val_bv), 0);
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = IsNaNOrInf(temp[0], 0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Os resultados dessas operações são armazenados no buffer de dados correspondente.

O uso dos coeficientes de influência nulos armazenados nos permite utilizar os recursos existentes para executar os algoritmos de propagação reversa. Com isso, encerramos o trabalho do lado do programa OpenCL. O código completo pode ser consultado no anexo.

Criação de objetos de atenção multiescalar

Em seguida, precisamos criar no lado do programa principal os objetos de atenção multiescalar. Aqui decidimos aproveitar ao máximo os recursos de herança de objetos. Simplesmente criamos os objetos Self-Attention e Cross-Attention com base nos métodos equivalentes já existentes, reescrevendo apenas o método de chamada do kernel criado anteriormente. A estrutura dos novos objetos está apresentada abaixo.

class CNeuronMultiScaleRelativeSelfAttention   :  public CNeuronRelativeSelfAttention
  {
protected:
   //---
   virtual bool      AttentionOut(void);

public:
                     CNeuronMultiScaleRelativeSelfAttention(void) {};
                    ~CNeuronMultiScaleRelativeSelfAttention(void) {};
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleRelativeSelfAttention; }
  };

class CNeuronMultiScaleRelativeCrossAttention   :  public CNeuronRelativeCrossAttention
  {
protected:
   virtual bool      AttentionOut(void);

public:
                     CNeuronMultiScaleRelativeCrossAttention(void) {};
                    ~CNeuronMultiScaleRelativeCrossAttention(void) {};
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleRelativeCrossAttention; }
  };

Para chamar o kernel, utilizamos o algoritmo clássico de enfileiramento para execução. Já discutimos métodos semelhantes muitas vezes. E acredito que você não terá dificuldade em compreendê-lo por conta própria. O código completo dos métodos mencionados está disponível no anexo.

Objeto de atenção recursiva

Os objetos de atenção multiescalar implementados acima nos permitem analisar os dados com diferentes janelas de contexto, mas isso ainda não representa a atenção recursiva proposta pelos autores do framework Hidformer. Realizamos apenas a parte preparatória.

Na próxima etapa do nosso trabalho, construiremos o objeto de atenção recursiva, que nos permitirá analisar os dados atuais no contexto do histórico previamente observado. Para isso, utilizaremos algumas práticas relacionadas à construção de módulos de memória. Em especial, vamos armazenar o contexto dos estados observados com uma profundidade histórica definida, o qual será usado para avaliar o estado atual. Implementaremos esse algoritmo no método CNeuronRecursiveAttention, cuja estrutura está apresentada abaixo.

class CNeuronRecursiveAttention  :  public CNeuronMultiScaleRelativeCrossAttention
  {
protected:
   CNeuronMultiScaleRelativeSelfAttention cSelfAttention;
   CNeuronTransposeOCL  cTransposeSA;
   CNeuronConvOCL       cConvolution;
   CNeuronEmbeddingOCL  cHistory;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
   override  { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                                        CBufferFloat *SecondGradient,
                                        ENUM_ACTIVATION SecondActivation = None)
   override  { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
   override  { return false; }

public:
                     CNeuronRecursiveAttention(void) {};
                    ~CNeuronRecursiveAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint history_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRecursiveAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como classe pai, neste caso, utilizaremos o objeto de atenção cruzada multiescalar implementado anteriormente.

No corpo do método, já vemos o conjunto familiar de métodos virtuais que serão reescritos, além de diversos objetos internos, cuja função será explorada durante a construção dos algoritmos de propagação para frente e propagação reversa.

Todos os objetos internos foram declarados como estáticos, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos herdados e declarados é realizada no método Init.

bool CNeuronRecursiveAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                        uint window, uint window_key, uint units_count,
                                                         uint heads, uint history_size,
                                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMultiScaleRelativeCrossAttention::Init(numOutputs, myIndex, open_cl, window,
                                               window_key, units_count, heads, window_key,
                                                  history_size, optimization_type, batch))
      return false;

Nos parâmetros do método, recebemos um conjunto de constantes que nos permite interpretar de forma inequívoca a arquitetura do objeto que está sendo criado. Aqui é importante destacar que, apesar de herdarmos da classe de atenção cruzada, nosso objeto trabalha com um único fluxo de dados brutos. O segundo fluxo de informações, necessário para o funcionamento correto dos métodos da classe pai, é formado dentro do próprio objeto. O tamanho da sequência analisada desse segundo fluxo é definido pela profundidade histórica do contexto salvo, ou seja, pelo parâmetro history_size.

No corpo do método, como já é tradição, chamamos imediatamente o método homônimo da classe pai, passando o conjunto necessário de parâmetros. Vale lembrar que o método da classe pai já contém os pontos de controle e a inicialização de todos os objetos herdados, incluindo as interfaces básicas.

Em seguida, passamos à inicialização dos novos objetos internos declarados. O primeiro da nossa lista é o objeto de Self-Attention multiescalar.

   int index = 0;
   if(!cSelfAttention.Init(0, index, OpenCL, iWindow, iWindowKey, iUnits, iHeads, 
                                                           optimization, iBatch))
      return false;

O uso deste objeto nos permite identificar os elementos dos dados brutos que exercem maior influência sobre o estado atual do ativo financeiro analisado.

Depois disso, é necessário adicionar o contexto do estado atual do ambiente à memória do nosso bloco de atenção recursiva. Ao fazer isso, queremos preservar o contexto de sequências unitárias individuais. Para isso, primeiramente transpomos os dados brutos.

   index++;
   if(!cTransposeSA.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

Em seguida, extraímos o contexto das sequências unitárias utilizando uma camada convolucional.

   index++;
   if(!cConvolution.Init(0, index, OpenCL, iUnits, iUnits, iWindowKey, 1, iWindow,
                                                            optimization, iBatch))
      return false;

Observe que, nos parâmetros da camada convolucional, especificamos um único elemento da sequência analisada, e informamos a quantidade de sequências unitárias no parâmetro referente ao número de variáveis independentes. Essa abordagem nos permite realizar uma análise completamente independente das sequências unitárias, já que cada uma contará com seu próprio conjunto de parâmetros treináveis para extração de contexto. Isso nos permite fazer uma análise mais profunda da sequência multimodal de entrada.

Em seguida, utilizamos uma camada de geração de incorporações (embedding) para registrar o contexto do estado analisado do ambiente e adicioná-lo à pilha de memória da sequência histórica.

   index++;
   uint windows[] = { iWindowKey * iWindow };
   if(!cHistory.Init(0, index, OpenCL, iUnitsKV, iWindowKey, windows))
      return false;
//---
   return true;
  }

Após a execução bem-sucedida de todas as operações, retornamos o resultado lógico do processamento ao programa chamador e encerramos o método.

Nosso próximo passo será a implementação do método de propagação para frente, feedForward, cujo algoritmo é bastante linear.

bool CNeuronRecursiveAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cSelfAttention.FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto de dados brutos, que contém a série temporal multimodal. Esse ponteiro é imediatamente repassado ao módulo Self-Attention, para análise das dependências na descrição atual do estado do ambiente. Os resultados da análise são transpostos para facilitar o processamento posterior.

   if(!cTransposeSA.FeedForward(cSelfAttention.AsObject()))
      return false;

E, extraímos o contexto das sequências unitárias utilizando uma camada convolucional.

   if(!cConvolution.FeedForward(cTransposeSA.AsObject()))
      return false;

Os dados preparados são enviados ao objeto de geração de incorporações, onde ocorre a extração do contexto do estado analisado e sua adição à pilha de memória.

   if(!cHistory.FeedForward(cConvolution.AsObject()))
      return false;

Agora, resta-nos enriquecer os resultados da análise feita anteriormente no bloco Self-Attention com o contexto da sequência histórica observada. Para isso, usamos o método homônimo da classe pai, passando a ele as informações necessárias.

   return CNeuronMultiScaleRelativeCrossAttention::feedForward(cSelfAttention.AsObject(),
                                                                   cHistory.getOutput());
  }

Aqui vale observar que, para analisar o estado atual no contexto dos estados previamente observados, utilizamos o objeto de atenção multiescalar criado anteriormente. Essa abordagem nos permite dar mais peso aos dados da história mais recente, diminuindo sua importância com o tempo. No entanto, continuamos com a possibilidade de extrair pontos-chave também das "profundezas da memória".

Ao final da execução do método, retornamos o resultado lógico das operações ao programa chamador.

Por trás da aparente simplicidade do método de propagação para frente, é fácil deixar passar o uso duplo dos resultados do objeto de Self-Attention multiescalar. Contudo, esse detalhe afeta diretamente o algoritmo de propagação reversa, que implementaremos no método calcInputGradients.

bool CNeuronRecursiveAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método de propagação reversa, recebemos um ponteiro para o mesmo objeto de dados brutos, mas agora precisamos transmitir a ele o gradiente de erro correspondente à sua influência no resultado da execução do modelo.

No corpo do método, verificamos de imediato a validade do ponteiro recebido, pois, caso contrário, não poderíamos transmitir dados para um objeto inexistente, e a execução de operações adicionais perderia totalmente o sentido. Portanto, prosseguimos com o método apenas se essa verificação for concluída com sucesso.

Como você já sabe, os fluxos de informação da propagação para frente e da propagação reversa são totalmente correspondentes, apenas com direções opostas. Encerramos o método de propagação para frente com a chamada ao método homônimo da classe pai. Assim, as operações da propagação reversa começam com a chamada ao método herdado. Ele irá distribuir o gradiente de erro recebido entre os dois fluxos de informação, de acordo com a influência de cada um no resultado final.

   if(!CNeuronMultiScaleRelativeCrossAttention::calcInputGradients(cSelfAttention.AsObject(),
                                                                        cHistory.getOutput(),
                                                                      cHistory.getGradient(),
                                                     (ENUM_ACTIVATION)cHistory.Activation()))
      return false;

Inicialmente, distribuímos o gradiente de erro do fluxo de informação auxiliar, que corresponde à memória do nosso objeto. Aqui, propagamos o erro até o nível da camada convolucional de extração de contexto das sequências unitárias.

   if(!cConvolution.calcHiddenGradients(cHistory.AsObject()))
      return false;

Em seguida, continuamos até a camada de transposição dos resultados do bloco Self-Attention.

   if(!cTransposeSA.calcHiddenGradients(cConvolution.AsObject()))
      return false;

Agora, precisamos transmitir o gradiente de erro até o nível da camada de Self-Attention multiescalar. No entanto, anteriormente já havíamos passado para ela o gradiente de erro do fluxo de informação principal, o qual precisamos preservar. Para isso, usamos a substituição de ponteiros para os buffers de dados. Primeiro, passamos ao objeto um ponteiro para um buffer livre, salvando previamente o que já estava sendo usado.

   CBufferFloat *temp = cSelfAttention.getGradient();
   if(!cSelfAttention.SetGradient(cTransposeSA.getPrevOutput(), false) ||
      !cSelfAttention.calcHiddenGradients(cTransposeSA.AsObject()) ||
      !SumAndNormilize(temp, cSelfAttention.getGradient(), temp, iWindow, false, 0, 0, 0, 1) ||
      !cSelfAttention.SetGradient(temp, false))
      return false;

Depois, propagamos o gradiente de erro e somamos os valores dos dois fluxos de informação. Em seguida, restauramos os ponteiros dos buffers de dados ao seu estado original.

Agora, resta apenas transmitir o gradiente de erro ao nível dos dados brutos.

   if(!NeuronOCL.calcHiddenGradients(cSelfAttention.AsObject()))
      return false;
//---
   return true;
  }

E ao final do método, retornamos o resultado lógico da execução das operações para o programa chamador.

O código completo deste objeto e de todos os seus métodos pode ser consultado no anexo.

Objeto de atenção linear

Além do objeto de atenção recursiva implementado, os autores do framework também propuseram o uso de atenção linear na torre de análise do espectro de frequência.

A atenção linear ("Linear Attention") é uma das formas de otimizar o mecanismo tradicional de atenção nos transformadores. Diferente do Self-Attention clássico, que utiliza operações matriciais totalmente conectadas com complexidade quadrática, a atenção linear reduz a complexidade computacional, tornando-a eficiente para o processamento de sequências longas.

Na atenção linear, introduz-se a decomposição das funções φ(Q) e φ(K), o que permite representar a atenção da seguinte maneira:

Vantagens da atenção linear

1. Complexidade linear: redução do custo computacional, permitindo o processamento de sequências longas.
2. Redução no consumo de memória: não há necessidade de armazenar a matriz completa de coeficientes de dependência Score, o que diminui o uso de memória.
3. Eficiência em tarefas online: a atenção linear é adequada para o processamento contínuo de dados, pois as atualizações ocorrem de forma incremental.
4. Flexibilidade na escolha das funções de kernel: o uso de diferentes funções φ(x) permite adaptar o mecanismo de atenção à natureza específica da tarefa.

A implementação do algoritmo de atenção linear está presente no objeto CNeuronLinerAttention, cuja estrutura é mostrada abaixo.

class CNeuronLinerAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindow;
   uint                 iWindowKey;
   uint                 iUnits;
   uint                 iVariables;
   //---
   CNeuronConvOCL       cQuery;
   CNeuronConvOCL       cKey;
   CNeuronTransposeVRCOCL  cKeyT;
   CNeuronBaseOCL       cKeyValue;
   CNeuronBaseOCL       cAttentionOut;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronLinerAttention(void) {};
                    ~CNeuronLinerAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronLinerAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Aqui, vemos o conjunto básico de métodos reescrevíveis e alguns objetos internos, que desempenham papel fundamental no algoritmo que estamos construindo. Exploraremos suas funcionalidades com mais detalhes ao longo da implementação dos métodos da nova classe.

Todos os métodos declarados são criados como estáticos, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos herdados e declarados é feita no método Init. Nos parâmetros deste método, recebemos um conjunto de variáveis que nos permite definir de forma inequívoca a arquitetura do objeto a ser criado.

bool CNeuronLinerAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint window_key, uint units_count,
                                 uint variables, ENUM_OPTIMIZATION optimization_type,
                                 uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables,
                                                                 optimization_type, batch))
      return false;

No corpo do método, chamamos imediatamente o método homônimo da classe pai. Neste caso, trata-se de uma camada totalmente conectada.

Em seguida, armazenamos os parâmetros-chave da arquitetura em variáveis internas. E passamos à inicialização dos objetos internos.

   iWindow = window;
   iWindowKey = fmax(window_key, 1);
   iUnits = units_count;
   iVariables = variables;

Primeiramente, inicializamos as camadas convolucionais de geração das entidades Query e Key. Na formação das queries, utilizamos a função de ativação sigmoide, que irá indicar a proporção de influência dos outros elementos sobre o objeto.

   int index = 0;
   if(!cQuery.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables,
                                                                optimization, iBatch))
      return false;
   cQuery.SetActivationFunction(SIGMOID);
   index++;
   if(!cKey.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables, 
                                                                optimization, iBatch))
      return false;
   cKey.SetActivationFunction(TANH);

Para as keys, usamos a tangente hiperbólica como função de ativação, o que nos permite determinar tanto a influência direta quanto a influência reversa do elemento correspondente.

Aqui também inicializamos o objeto de transposição da matriz Key.

   index++;
   if(!cKeyT.Init(0, index, OpenCL, iVariables, iUnits, iWindowKey, optimization, iBatch))
      return false;
   cKeyT.SetActivationFunction(TANH);

E o objeto responsável por armazenar o produto das matrizes Key e Value.

   index++;
   if(!cKeyValue.Init(0, index, OpenCL, iWindow * iWindowKey, optimization, iBatch))
      return false;
   cKeyValue.SetActivationFunction(None);

Vale destacar que não utilizamos uma camada de geração para a entidade Value. Em vez disso, planejamos utilizar diretamente os dados brutos.

Os resultados da atenção serão armazenados em um objeto interno criado especificamente para esse fim.

   index++;
   if(!cAttentionOut.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cAttentionOut.SetActivationFunction(None);

As interfaces da classe pai serão usadas para a criação das conexões residuais. Para isso, aplicamos a substituição do ponteiro para o buffer de gradientes de erro, o que permite evitar operações desnecessárias de cópia de dados.

   if(!SetGradient(cAttentionOut.getGradient(), true))
      return false;
//---
   return true;
  }

Antes de encerrar a execução, retornamos o resultado lógico das operações para o programa chamador.

Após finalizar a inicialização do objeto, passamos à construção do algoritmo de propagação para frente no método feedForward.

bool CNeuronLinerAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL))
      return false;
   if(!cKey.FeedForward(NeuronOCL) ||
      !cKeyT.FeedForward(cKey.AsObject()))
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto de sequência multidimensional dos dados brutos, que é utilizado diretamente para formar as entidades Query e Key.

Depois, determinamos a influência de cada elemento na sequência analisada, multiplicando a matriz transposta de Key pelos dados brutos.

   if(!MatMul(cKeyT.getOutput(), NeuronOCL.getOutput(), cKeyValue.getOutput(),
                                     iWindowKey, iUnits, iWindow, iVariables))
      return false;

Para obter os resultados da atenção linear, multiplicamos o tensor Query pelo resultado da operação anterior.

   if(!MatMul(cQuery.getOutput(), cKeyValue.getOutput(), cAttentionOut.getOutput(),
                                          iUnits, iWindowKey, iWindow, iVariables))
      return false;

Agora, resta adicionar as conexões residuais e normalizar os resultados da operação.

   if(!SumAndNormilize(NeuronOCL.getOutput(), cAttentionOut.getOutput(), Output,
                                                     iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Retornamos o resultado lógico da execução das operações ao programa chamador e encerramos o método.

Em seguida, precisamos organizar a distribuição dos gradientes de erro entre todos os objetos internos e os dados brutos, de acordo com sua influência no resultado final do modelo. Como de costume, essas operações são realizadas no método calcInputGradients, que recebe nos parâmetros um ponteiro para o objeto de dados brutos. Desta vez, ele será usado para registrar os resultados das operações.

bool CNeuronLinerAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

No corpo do método, verificamos imediatamente a validade do ponteiro recebido. Já discutimos anteriormente a importância crítica dessa verificação.

Graças à substituição dos ponteiros para os buffers de dados, o gradiente de erro recebido da próxima camada neural é automaticamente direcionado ao objeto interno de resultados da atenção linear. Em seguida, distribuímos esse gradiente entre os fluxos de informação.

   if(!MatMulGrad(cQuery.getOutput(), cQuery.getGradient(),
                  cKeyValue.getOutput(), cKeyValue.getGradient(),
                  cAttentionOut.getGradient(),
                  iUnits, iWindowKey, iWindow, iVariables))
      return false;
   if(!MatMulGrad(cKeyT.getOutput(), cKeyT.getGradient(),
                  NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(),
                  cKeyValue.getGradient(),
                  iWindowKey, iUnits, iWindow, iVariables))
      return false;

Aqui, vale destacar que devemos transmitir o gradiente de erro até o nível dos dados brutos por meio de quatro fluxos de informação:

• entidade Query;
• entidade Key;
• produto KeyValue;
• conexões residuais.

Na última operação, salvamos o gradiente de erro do produto KeyValue em um buffer livre. O gradiente do fluxo de conexões residuais é transferido integralmente a partir do nível dos resultados do objeto atual. Também é importante observar que esses gradientes ainda não foram ajustados pela derivada da função de ativação dos dados brutos. No entanto, ao distribuirmos o gradiente de erro através das camadas convolucionais de geração das entidades, ele é automaticamente corrigido com base na derivada da função de ativação. Para obter dados comparáveis entre todos os fluxos de informação, somamos os valores disponíveis e aplicamos a correção pela derivada da função de ativação do objeto de dados brutos. Os resultados são armazenados em um buffer de dados livre.

   if(!SumAndNormilize(Gradient, cAttentionOut.getPrevOutput(), cAttentionOut.getPrevOutput(),
                       iWindow, false, 0, 0, 0, 1))
      return false;
//---
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(),
                       cAttentionOut.getPrevOutput(), NeuronOCL.Activation()))
         return false;

Além disso, ajustamos os gradientes de erro dos demais fluxos de informação com base nas derivadas de suas respectivas funções de ativação.

   if(cKeyT.Activation() != None)
      if(!DeActivation(cKeyT.getOutput(), cKeyT.getGradient(),
                       cKeyT.getGradient(), cKeyT.Activation()))
         return false;
   if(cQuery.Activation() != None)
      if(!DeActivation(cQuery.getOutput(), cQuery.getGradient(),
                       cQuery.getGradient(), cQuery.Activation()))
         return false;

Depois, distribuímos o gradiente de erro pelo fluxo de informação da entidade Key e o somamos aos dados previamente acumulados.

   if(!cKey.calcHiddenGradients(cKeyT.AsObject()) ||
      !NeuronOCL.calcHiddenGradients(cKey.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(),
                       cAttentionOut.getPrevOutput(), iWindow, false, 0, 0, 0, 1))
      return false;

De forma semelhante, transmitimos o gradiente de erro pelo fluxo de informação da entidade Query, em seguida, repassamos o gradiente total acumulado ao objeto de dados brutos.

   if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(),
                       NeuronOCL.getGradient(), iWindow, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Ao final das operações do método, retornamos ao programa chamador o resultado lógico da execução.

Com isso, encerramos a análise dos algoritmos de construção dos métodos do objeto de atenção linear. O código completo desta classe e de todos os seus métodos pode ser consultado no anexo.

Trabalhamos intensamente e agora chegamos aos limites deste artigo. No entanto, nossa jornada ainda não terminou. Faremos uma breve pausa e continuaremos no próximo artigo, onde levaremos tudo a uma conclusão lógica.

Considerações finais

Exploramos o framework Hidformer, que demonstra eficácia na previsão de séries temporais, incluindo dados financeiros. Sua principal característica é o uso de um codificador de duas torres com análise separada dos dados brutos como sequência temporal e como suas características no domínio da frequência. Isso confere ao Hidformer grande flexibilidade e capacidade de adaptação a diferentes condições de mercado.

Na parte prática do artigo, implementamos alguns dos componentes propostos pelos autores do framework Hidformer. Mas nosso trabalho ainda não está concluído e será continuado em breve.

Links

• Hidformer: Transformer-Style Neural Network in Stock Price Forecasting
• Hidformer: Hierarchical dual-tower transformer using multi-scale mergence for long-term time series forecasting
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Atudy.mq5	Expert Advisor	EA para treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL