Neurônio biológico para previsão de séries temporais financeiras

O trading moderno está passando por uma verdadeira revolução. Redes neurais, algoritmos genéticos, aprendizado profundo — todas essas ferramentas apresentam resultados impressionantes, mas frequentemente sofrem de uma limitação importante: são excessivamente "mecanicistas" e incapazes de captar a natureza sutil das oscilações do mercado, que, essencialmente, são fruto do comportamento coletivo de participantes vivos do mercado.

Nesse contexto, o uso de modelos neurais biologicamente plausíveis se torna especialmente relevante. Em vez de criarmos construções matemáticas abstratas, recorremos ao computador mais avançado do (universo observável), o cérebro humano. Nosso grupo de pesquisa desenvolveu um sistema único baseado no modelo de Hodgkin-Huxley, que imita não apenas a funcionalidade, mas também a natureza física dos processos neurais.

O modelo de Hodgkin-Huxley, que recebeu o Prêmio Nobel, descreve o mecanismo de geração e propagação de impulsos nervosos em nível celular. Mas por que exatamente esse modelo pode ser a chave para entender os mercados financeiros? A resposta está em uma analogia surpreendente entre a propagação de impulsos nervosos no cérebro e a disseminação de informações nos mercados. Assim como os neurônios trocam sinais elétricos através de conexões sinápticas, os participantes do mercado trocam informações por meio das operações de trading.

A inovação da nossa abordagem está na adição de um componente semelhante ao plasma ao modelo clássico. Enxergamos a rede neural como um sistema dinâmico imerso em um "plasma" de informação de mercado, onde cada neurônio pode influenciar o comportamento de outros neurônios não apenas por conexões diretas, mas também através dos campos eletromagnéticos que gera. Isso permite ao sistema captar correlações e interdependências sutis que passam despercebidas pelos algoritmos tradicionais.

Neste artigo, analisaremos em detalhes a arquitetura do sistema, os princípios de seu funcionamento e os resultados da aplicação prática em diversos instrumentos financeiros. Mostraremos como uma abordagem inspirada biologicamente pode oferecer uma nova perspectiva para o problema de previsão de séries temporais financeiras e abrir novos horizontes no campo do trading algorítmico.

Modelo de Hodgkin-Huxley: quando a biologia encontra as finanças

Imagine um neurônio, uma célula surpreendente, capaz de processar e transmitir informação por meio de impulsos elétricos. Foi justamente essa unidade fundamental do cérebro que Alan Hodgkin e Andrew Huxley descreveram em seu trabalho revolucionário, pelo qual mais tarde receberam o Prêmio Nobel. O modelo deles se tornou um verdadeiro avanço na neurobiologia, e agora, imagine só, esse mesmo modelo pode nos ajudar a entender e prever os movimentos dos mercados financeiros.

No centro do modelo está a descrição matemática de como um neurônio gera impulsos elétricos. Assim como traders reagem à informação que chega do mercado, o neurônio responde aos sinais recebidos, criando seu próprio padrão único de atividade. Vamos dar uma olhada no código que descreve esse processo fascinante:

class HodgkinHuxleyNeuron:
    def __init__(self):
        self.V = -65.0  # Начальный потенциал покоя
        self.m = 0.05   # Активация натриевых каналов
        self.h = 0.6    # Инактивация натриевых каналов
        self.n = 0.32   # Активация калиевых каналов
        self.last_spike_time = float('-inf')

A dança dos íons: como o neurônio toma decisões

O aspecto mais surpreendente do modelo de Hodgkin-Huxley é a descrição de como os íons "dançam" através da membrana do neurônio. Sódio e potássio, dois atores-chave nesse balé molecular, movem-se por canais especiais, gerando um potencial elétrico. Muito parecido com o modo como fluxos de ordens criam o movimento de preço no mercado. Em nosso sistema de trading, usamos essa analogia, convertendo os dados de mercado em correntes iônicas:

def ion_currents(self, V):
    I_Na = self.g_Na * (self.m ** 3) * self.h * (V - self.E_Na)  # Натриевый ток
    I_K = self.g_K * (self.n ** 4) * (V - self.E_K)             # Калиевый ток
    I_L = self.g_L * (V - self.E_L)                             # Ток утечки
    return I_Na, I_K, I_L

Influência plasmática: uma nova visão sobre redes neurais

Fomos além do modelo clássico e adicionamos o conceito de um meio semelhante ao plasma. Imagine que os neurônios não estão apenas conectados por sinapses, mas imersos em uma "plasma de informação" do mercado. Cada spike de um neurônio cria uma onda de influência que se dissipa com o tempo, exatamente como uma notícia no mercado gradualmente perde sua influência sobre o preço:

def plasma_influence(self, current_time):
    time_since_spike = current_time - self.last_spike_time
    influence = self.plasma_strength * np.exp(-time_since_spike / self.plasma_decay)
    return influence * self.get_market_correlation()

Aprendizado ao longo do tempo: o mecanismo STDP

Talvez a parte mais empolgante do nosso sistema seja o mecanismo de aprendizado baseado na dependência temporal entre os spikes dos neurônios (STDP). Assim como um trader aprende com sua própria experiência, nossos neurônios ajustam a força de suas conexões com base em quão bem conseguiram prever os movimentos do mercado:

def update_synaptic_weights(self, pre_spike, post_spike, weight):
    delta_t = post_spike - pre_spike
    if delta_t > 0:
        return weight * (1 + self.A_plus * np.exp(-delta_t / self.tau_plus))
    else:
        return weight * (1 - self.A_minus * np.exp(delta_t / self.tau_minus))

Essa arquitetura inspirada na biologia permite ao nosso sistema não apenas processar os dados de mercado, mas "sentir" o mercado, como um trader experiente. Cada neurônio se torna um pequeno especialista em seu próprio aspecto da dinâmica de mercado, e o trabalho coletivo entre eles gera previsões surpreendentemente precisas.

Arquitetura do sistema: da biologia às decisões de trading

Imagine o cérebro de um trader analisando o mercado. Milhares de neurônios processam informações sobre preços, volumes, indicadores, notícias. Foi exatamente essa arquitetura natural que recriamos em nosso sistema, adicionando propriedades únicas de plasma e interações eletromagnéticas.

Olhos do sistema: estrutura dos dados de entrada

Assim como o cérebro humano recebe informações através dos sentidos, nosso sistema coleta e processa inúmeros sinais do mercado. Cada tick, cada movimento de preço é convertido em impulsos neurais. Veja o código de pré-processamento dos dados:

class MarketFeatures:
    def __init__(self, window_size=20):
        self.window_size = window_size
        self.scaler = StandardScaler()
        
    def add_price(self, price: float, ohlc_data: pd.DataFrame) -> Dict[str, float]:
        features = {}
        
        # Технические индикаторы
        features['sma_10'] = self._calculate_sma(ohlc_data['close'], window=10)
        features['ema_20'] = self._calculate_ema(ohlc_data['close'], window=20)
        features['rsi'] = self._calculate_rsi(ohlc_data['close'], window=14)
        
        # Объемные характеристики
        features['volume_sma'] = self._calculate_sma(ohlc_data['tick_volume'], window=10)
        
        # Временные паттерны
        features['hour'] = ohlc_data.index[-1].hour
        features['day_of_week'] = ohlc_data.index[-1].dayofweek
        
        return self.scaler.fit_transform(np.array(list(features.values())).reshape(1, -1))

Rede neural: ponte entre biologia e matemática

No centro do nosso sistema está uma arquitetura híbrida, que une redes neurais clássicas ao modelo biologicamente fiel de Hodgkin-Huxley. Cada neurônio aqui não é apenas uma função matemática, mas um pequeno sistema vivo:

class BioTradingModel(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(BioTradingModel, self).__init__()
        self.layers = nn.ModuleList([
            nn.Linear(input_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, output_size)
        ])
        
        # Биологические нейроны
        self.bio_neurons = [HodgkinHuxleyNeuron() for _ in range(hidden_size)]
        self.plasma_field = PlasmaField(hidden_size)

Campo plasmático: uma nova dimensão das interações neurais

A singularidade do nosso sistema está no meio semelhante ao plasma em que os neurônios estão imersos. Assim como campos eletromagnéticos atravessam o espaço, nossa "plasma" cria um nível adicional de interação entre os neurônios:

class PlasmaField:
    def __init__(self, size):
        self.field_strength = np.zeros(size)
        self.decay_rate = 0.95
        
    def update(self, neuron_activities):
        # Обновление поля на основе активности нейронов
        self.field_strength = self.field_strength * self.decay_rate
        self.field_strength += neuron_activities
        
    def get_influence(self, neuron_index):
        # Расчет влияния поля на конкретный нейрон
        return np.sum(self.field_strength * np.exp(-self.distance_matrix[neuron_index]))

Mecanismo de aprendizado: a dança dos neurônios e do plasma

O aprendizado em nosso sistema acontece em múltiplos níveis simultaneamente. A descida do gradiente clássico é combinada com o STDP biológico e a dinâmica plasmática:

def train_step(self, inputs, target):
    # Прямой проход
    predictions = self.forward(inputs)
    loss = self.criterion(predictions, target)
    
    # Обратное распространение
    self.optimizer.zero_grad()
    loss.backward()
    
    # Биологическое обучение
    for i, neuron in enumerate(self.bio_neurons):
        # STDP обновление
        neuron.update_weights(self.last_spike_times)
        
        # Плазменная модуляция
        plasma_influence = self.plasma_field.get_influence(i)
        neuron.modulate_weights(plasma_influence)
    
    self.optimizer.step()
    return loss.item()

Essa arquitetura multinível permite ao sistema captar não apenas padrões óbvios nos dados, mas também correlações sutis, quase imperceptíveis, entre diferentes aspectos da dinâmica do mercado. Cada componente do sistema desempenha seu papel único, e a sinergia entre eles cria algo maior do que a simples soma das partes, um verdadeiro cérebro artificial para análise dos mercados financeiros.

Indicadores técnicos: os órgãos sensoriais digitais do nosso sistema

Se imaginarmos nossa rede neural como o cérebro artificial de um trader, então os indicadores técnicos são seus órgãos sensoriais. Assim como um ser humano usa a visão, audição e tato para perceber o mundo, nosso sistema usa diversos indicadores para "sentir" o mercado em todas as suas nuances.

Indicadores básicos: a visão do sistema

Comecemos pelos indicadores mais fundamentais, as médias móveis. Elas são como a visão da nossa rede, permitindo distinguir a tendência principal no meio do ruído do mercado:

def calculate_moving_averages(self, prices):
    def sma(window):
        return np.convolve(prices, np.ones(window)/window, mode='valid')
    
    def ema(window):
        alpha = 2 / (window + 1)
        kernel = alpha * (1 - alpha)**np.arange(window)
        return np.convolve(prices, kernel[::-1], mode='valid')
    
    return {
        'sma_fast': sma(10),  # Быстрая SMA для краткосрочных трендов
        'sma_slow': sma(20),  # Медленная SMA для долгосрочных трендов
        'ema_fast': ema(10),  # Экспоненциальная MA для быстрой реакции
        'ema_slow': ema(20)   # Медленная EMA для фильтрации шума
    }

Osciladores: o tato dos impulsos do mercado

RSI, Momentum e Stochastic são os receptores táteis do nosso sistema. Eles permitem "sentir" a força do movimento dos preços e potenciais pontos de reversão:

def calculate_oscillators(self, data):
    def rsi(prices, period=14):
        delta = np.diff(prices)
        gain = np.where(delta > 0, delta, 0)
        loss = np.where(delta < 0, -delta, 0)
        
        avg_gain = np.mean(gain[:period])
        avg_loss = np.mean(loss[:period])
        
        for i in range(period, len(gain)):
            avg_gain = (avg_gain * 13 + gain[i]) / 14
            avg_loss = (avg_loss * 13 + loss[i]) / 14
            
        rs = avg_gain / avg_loss
        return 100 - (100 / (1 + rs))
    
    return {
        'rsi': rsi(data['close']),
        'momentum': data['close'] - np.roll(data['close'], 10),
        'stoch_k': self._calculate_stochastic_k(data)
    }

Volatilidade e volume: a audição do sistema

Os indicadores de volatilidade e volume funcionam como a audição do nosso sistema, pois eles captam o "ruído" do mercado e a força dos movimentos. As Bandas de Bollinger e o ATR ajudam a avaliar a amplitude das oscilações, enquanto os indicadores de volume indicam sua relevância:

def measure_market_dynamics(self, data):
    def bollinger_bands(prices, window=20):
        sma = np.mean(prices[-window:])
        std = np.std(prices[-window:])
        return {
            'upper': sma + 2 * std,
            'lower': sma - 2 * std,
            'width': 4 * std / sma  # Нормализованная ширина полос
        }
    
    def volume_profile(volumes, prices):
        return {
            'volume_ma': np.mean(volumes[-10:]),
            'volume_trend': np.corrcoef(volumes[-20:], prices[-20:])[0,1],
            'volume_oscillator': (np.mean(volumes[-5:]) / np.mean(volumes[-20:]) - 1) * 100
        }
    
    volatility = bollinger_bands(data['close'])
    volume = volume_profile(data['volume'], data['close'])
    return {**volatility, **volume}

Normalização: ajuste da sensibilidade

Assim como o cérebro humano adapta a sensibilidade dos sentidos às condições do ambiente, nosso sistema ajusta dinamicamente a escala dos dados de entrada. Isso é fundamental para o funcionamento estável da rede neural:

def normalize_features(self, features: dict) -> dict:
    class AdaptiveNormalizer:
        def __init__(self, window=100):
            self.window = window
            self.history = {}
            
        def update(self, feature_name, value):
            if feature_name not in self.history:
                self.history[feature_name] = []
            
            self.history[feature_name].append(value)
            if len(self.history[feature_name]) > self.window:
                self.history[feature_name].pop(0)
            
            mean = np.mean(self.history[feature_name])
            std = np.std(self.history[feature_name])
            return (value - mean) / (std + 1e-8)  # Избегаем деления на ноль
    
    normalizer = AdaptiveNormalizer()
    return {name: normalizer.update(name, value) 
            for name, value in features.items()}

Todos esses indicadores e características trabalham em conjunto, criando uma visão multidimensional da realidade do mercado. Assim como o cérebro humano integra informações de todos os sentidos, nosso sistema sintetiza os dados de todos os indicadores em uma representação única da situação de mercado. Isso permite que ela não apenas siga a tendência ou reaja a sinais isolados, mas desenvolva uma compreensão holística da dinâmica de mercado.

Resultados experimentais

Metodologia de testes

Durante a pesquisa, realizamos testes abrangentes do sistema com dados históricos do par de moedas EURUSD. O horizonte temporal foi de 5 anos, utilizando o timeframe diário D1. Seguindo os princípios clássicos de aprendizado de máquina, dividimos os dados em conjuntos de treino e teste na proporção de 80/20. Como resultado, foram utilizadas 1659 observações para treinamento e 415 para teste. O modelo passou por 20 iterações de aprendizado com diferentes inicializações de pesos, em busca da configuração ideal.

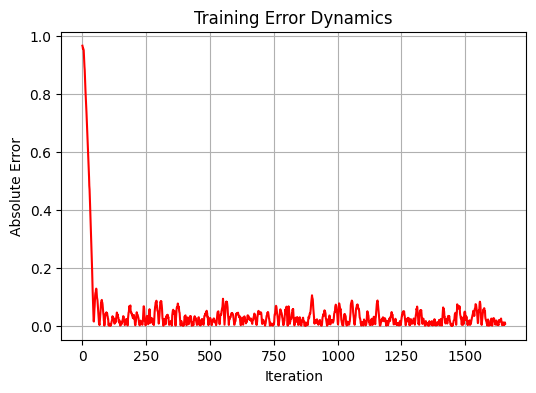
Análise de desempenho

Durante a análise dos resultados, observamos uma característica interessante no funcionamento do nosso modelo. Em vez de tentar prever oscilações de curto prazo nos preços, o sistema parece buscar um certo "preço justo" para o par de moedas. Essa observação é confirmada pela correlação relativamente alta no conjunto de treinamento, atingindo 0.583, com um erro quadrático médio de 0.012346. No entanto, no conjunto de teste, o desempenho do modelo cai consideravelmente — a correlação se torna negativa (-0.108), e o MSE aumenta mais de 90 vezes, alcançando 1.156584.

Comparação com abordagens tradicionais

Nosso modelo biologicamente inspirado apresenta um comportamento significativamente diferente em relação aos indicadores técnicos clássicos e redes neurais padrão. Suas previsões mostram uma volatilidade visivelmente maior. 

Veja abaixo o teste no conjunto de teste, com horizonte de previsão de 15 barras:

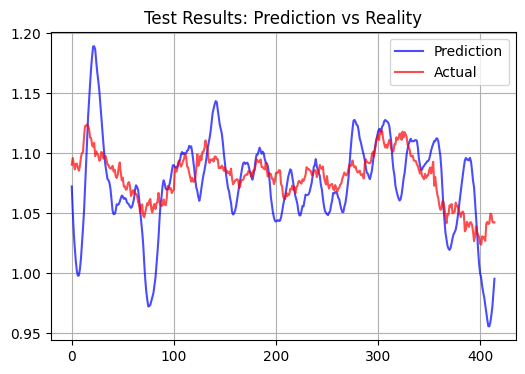
Métricas estatísticas de desempenho

O resultado mais revelador do desempenho da modelo foi o coeficiente de determinação (R²) extremamente baixo no conjunto de teste, que ficou em torno de 0.01. Curiosamente, no conjunto de treinamento, o modelo apresentou uma correlação relativamente alta, o que indica sua capacidade de capturar padrões de longo prazo nos dados. No entanto, as previsões do modelo frequentemente apresentam valores atípicos claramente visíveis. Se esses valores atípicos correspondem a movimentos de preço muito pequenos, e se isso é adequado para scalping, ainda precisa ser verificado.

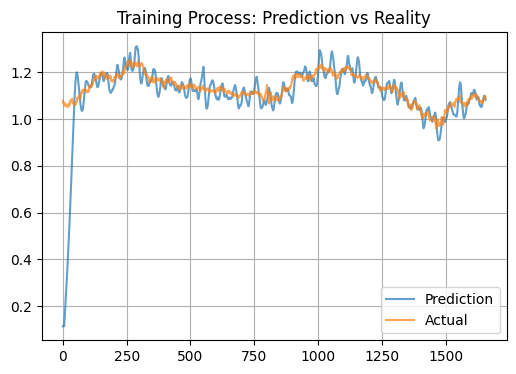
Características e aplicação prática

O comportamento observado do modelo pode ser explicado por sua natureza biológica. A rede neural com meio semelhante ao plasma parece atuar como um filtro poderoso, amplificando significativamente os sinais do mercado, o que resulta em previsões hipertrofiadas de incrementos. O mecanismo STDP (Plasticidade Dependente da Temporização dos Spikes), em teoria, deveria levar à formação de padrões estáveis de ativação, o que implicaria em previsões mais suavizadas e, portanto, deveríamos ter obtido um cenário diferente entre teste e realidade. Um fator adicional pode ser a grande quantidade de parâmetros de entrada representados pelos indicadores técnicos, gerando um efeito de superajuste.

Do ponto de vista prático, este modelo pode ser útil para determinar níveis de curto prazo de valor justo para um par de moedas. 

Considerações finais

Nossa pesquisa sobre uma rede neural biologicamente inspirada para previsão dos mercados financeiros levou a resultados inesperados, porém bastante intrigantes. Assim como o cérebro humano é capaz de sentir intuitivamente o "valor justo" de um ativo, nosso modelo, baseado nos princípios de funcionamento dos neurônios vivos, demonstrou uma notável habilidade para identificar níveis de preço fundamentados.

A introdução de um meio semelhante ao plasma na arquitetura da rede neural criou uma espécie de "inteligência coletiva", onde cada neurônio influencia o funcionamento do sistema não apenas por meio de conexões diretas, mas também por meio de interações eletromagnéticas de longo alcance. Esse mecanismo mostrou-se especialmente eficaz para filtrar o ruído do mercado e identificar tendências de longo prazo. 

Talvez haja aqui um significado mais profundo. Assim como os sistemas biológicos evoluíram para sobreviver no longo prazo, nossa rede neural, construída à sua imagem, também parece buscar padrões duradouros e fundamentados.

Bônus para quem leu até o fim

Também criei um indicador baseado nesse modelo. O indicador carrega o restante do sistema como um módulo e se abre nesta janelinha simples:

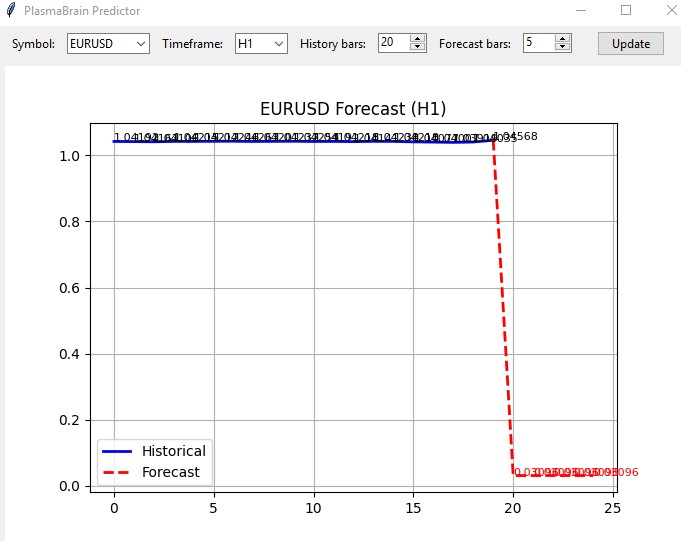
Ainda não testei ele ao vivo, mas levando em conta que todas as outras abordagens geralmente apontam para a mesma direção, talvez essa maquininha funcione como deveria?