Técnicas do MQL5 Wizard que você deve conhecer (Parte 45): Aprendizado por Reforço com Monte-Carlo

Introdução

Este artigo continua nossa análise sobre aprendizado por reforço considerando outro algoritmo, a saber o Monte-Carlo. Este algoritmo é muito semelhante e, de fato, pode ser considerado como englobando tanto o Q-Learning quanto o SARSA, já que pode ser tanto on-policy quanto off-policy. O que o diferencia, entretanto, é a ênfase em episódios. Estes simplesmente são uma forma de agrupar as atualizações do ciclo de aprendizado por reforço, que introduzimos neste artigo, de modo que a atualização dos Q-Values do Q-Map aconteça com menos frequência.

Com o algoritmo Monte Carlo, os Q-Values só são atualizados após a conclusão de um episódio. Um episódio é um lote de ciclos. Para este artigo, atribuímos esse número de ciclos ao parâmetro de entrada ‘m_episodes_size’, que é otimizável ou ajustável. O Monte Carlo é considerado bastante robusto à variabilidade do mercado porque consegue simular melhor uma ampla gama de cenários possíveis, permitindo que os traders determinem como diferentes estratégias se comportam sob várias condições. Essa variabilidade ajuda os traders a entender potenciais trade-offs, riscos e retornos, permitindo que tomem decisões mais informadas.

Essa vantagem, argumenta-se, decorre de sua “visão de desempenho de longo prazo”, que contrasta com métodos tradicionais que tendem a focar em resultados de curto prazo. O que isso significa é que as atualizações pouco frequentes realizadas pelas simulações de Monte Carlo — dado que só acontecem uma vez em um episódio — evitam o ruído de mercado no qual Q-Learning & SARSA inevitavelmente esbarram, já que executam suas atualizações com mais frequência. A avaliação do desempenho de longo prazo de estratégias de trading, medindo recompensas cumulativas ao longo do tempo, é portanto o que o Monte Carlo busca alcançar. Ao analisar múltiplos episódios, os traders podem obter insights sobre a lucratividade e a sustentabilidade geral de suas estratégias.

O algoritmo Monte Carlo calcula estimativas de valores de ação com base nos retornos médios de pares estado-ação ao longo de múltiplos ciclos dentro de um único episódio. Isso permite avaliar melhor quais ações (por exemplo, comprar ou vender) têm maior probabilidade de gerar resultados favoráveis com base no desempenho histórico. Essa atualização dos Q-Values decorre de o componente de recompensa desses Q-Values ser determinado da seguinte forma:

Onde:

• R t+1 , R t+2 ,…,R T são as recompensas recebidas em cada passo após o tempo t.
• γ /gamma é o fator de desconto (0 ≤ γ ≤ 1), que define em quanto as recompensas futuras são “descontadas” (isto é, valem menos do que recompensas imediatas).
• T representa o passo de tempo no qual o episódio termina (estado terminal ou tamanho do episódio em ciclos).

Essas considerações de recompensa abrangentes, implícitas na atualização dos Q-Values mencionada acima, tendem a tornar o Monte Carlo mais adaptável, como já aludido. Essa adaptabilidade inerente permite que os traders ajustem suas estratégias com base nas condições de mercado em evolução. Essa adaptabilidade é crucial nos mercados financeiros, onde as tendências podem mudar rapidamente e o desempenho passado nem sempre prevê resultados futuros. No último artigo de aprendizado por reforço que tratou do SARSA, vimos o aprendizado por reforço como um modelo independente treinado para prever a ação do preço e não apenas como assistente no treinamento de outros modelos de machine learning, como tradicionalmente seria o caso se o considerássemos como uma 3^ª forma de treinamento, além do supervisionado e não supervisionado. Seguimos abordagem semelhante para este artigo.

As estratégias, portanto, que seriam adaptáveis sob Monte Carlo seriam em muitos aspectos determinadas pela escolha do Q-Map e dos estados. No último artigo, como o algoritmo de aprendizado por reforço também era o principal modelo de previsão para o Expert Advisor, por meio de uma classe de sinal personalizada, usamos 3 estados de ambiente cruzados entre um horizonte de curto prazo e um de longo prazo para criar uma grade/matriz de 9 opções. O que esses estados capturaram foi simplesmente alta, lateralidade e baixa, sendo relativamente simples/cru. No entanto, há potencial para torná-lo mais elaborado e sensível aos mercados, não apenas aumentando suas dimensões gerais, mas também adicionando mais fatores para considerar. Quando isso é combinado ao Monte Carlo, a adaptabilidade será ampliada.

Recapitulação sobre Aprendizado por Reforço (RL) em Trading

O aprendizado por reforço (RL) é projetado para operar em ambientes dinâmicos, como os mercados financeiros, onde interage continuamente com seu “entorno” tomando ações (como comprar, vender, manter) com base em seu estado atual (onde esses estados são definidos por preços de mercado, indicadores etc.). Cada ação tomada pelo agente influencia o estado do ambiente, levando a novas observações e potenciais recompensas.

Exemplos adicionais de conjuntos de estados que podem ser adotados pelos traders para seus Q-Maps podem incluir Estados Baseados em Indicadores Técnicos. Estes podem incluir Médias Móveis, onde se a MM de curto prazo estiver acima da MM de longo prazo, isso representa um estado de Alta, enquanto a MM de curto prazo abaixo da de longo prazo implicaria um estado de Baixa, e a igualdade representaria um estado Neutro.

Como combinamos perspectivas de curto e longo prazo em um único eixo, isso significa que agora temos a oportunidade de introduzir outro eixo que cubra diferentes métricas além das leituras de indicadores de MM. Outra leitura de indicador que poderia ser usada para isso é o Índice de Força Relativa (RSI). Com ele, consideraríamos os estados de Sobrecompra (RSI > 70), que poderia ser potencialmente um sinal de venda, e o estado de Sobrevenda (RSI < 30), que poderia ser um sinal de compra, além de um estado transitório adicional que não oferece sinal.

Ou ainda dentro dos estados baseados em indicadores, poderíamos observar as Bandas de Bollinger, onde o preço próximo ou acima da banda superior poderia ser um estado de baixa, enquanto o preço na banda inferior ou abaixo dela poderia ser um estado de alta, com novamente um 3^º estado neutro implícito para qualquer outra posição.

Além dos estados de indicadores técnicos, a volatilidade do mercado também poderia representar um eixo alternativo para a matriz de estados do ambiente. Com isso, a medição seria baseada em indicadores como o desvio padrão do preço ou o ATR e, embora se possa usar três estados possíveis de alta, baixa e moderada volatilidade, muitas outras gradações poderiam ser adicionadas para tornar o algoritmo mais sensível ao mercado. Essa configuração de estados (ou eixo) ajudaria a guiar o agente sobre quando negociar de forma agressiva ou conservadora. Estados baseados em volume também podem ser considerados para ações, com gradação semelhante.

Além das tendências de baixa e alta na ação do preço que usamos nos artigos anteriores e estamos considerando para este também, padrões de ação de preço mais específicos como rompimentos de níveis de suporte/resistência poderiam ser adotados. Alternativamente, poderia ser para padrões de ombro-cabeça-ombro, tanto para sinais de alta quanto de baixa, com qualquer outro padrão sendo um falso rompimento. O reconhecimento desses padrões na ação de preço recente permitiria que o agente antecipasse continuidade ou reversão.

Outro eixo possível para os estados do Q-Map poderia ser os estados baseados em tempo. Lembre-se de que esse eixo seria então combinado com outro eixo, como a ação do preço mencionada ou indicadores técnicos, de modo que se pudesse inferir qual ação do preço é mais confiável em cada período de tempo. Possíveis estados de tempo podem incluir abertura/fechamento do mercado, sessões de negociação ou até dias da semana. Estados baseados em sentimento são outro eixo que poderia compor a matriz de estados do ambiente. A mensuração desses sentimentos dependeria de leituras do calendário de notícias econômicas para um indicador específico, dada a variedade disponível. A gradação desses estados deve variar de positivo a neutro a negativo, com estados intermediários adicionáveis dependendo da granularidade desejada. Incorporar estados de sentimento, particularmente com esses métodos, poderia ajudar o agente a responder a eventos externos que afetam o mercado.

Similar e alternativo a isso seriam os estados baseados em eventos econômicos. Porém, algo diferente desses dois que também poderia ser considerado são os estados baseados em portfólio. Essa categoria é muito aplicável fora do forex e apresenta diversos potenciais eixos. Primeiro estão os níveis de exposição, onde o portfólio é classificado pela exposição relativa, por exemplo, de ações a títulos. A gradação poderia variar de 90-10 em uma ponta até 10-90 na outra ponta, respectivamente. Tal eixo pode ser combinado com tempo ou qualquer outra métrica relacionada, de modo que o desempenho do portfólio (alinhado às recompensas do agente) possa guiar o processo de atualização dos Q-Values.

Outra opção nos estados baseados em portfólio é o nível de risco. Isso poderia considerar percentuais de alocação de capital para cada investimento, com graduações de um valor pequeno < 0,5% até um limite de, digamos, 10%. Novamente, a comparação ou combinação disso com outra métrica específica de portfólio e uma otimização sobre um conjunto de dados adequado deve fornecer um Q-Map que guie quais níveis de risco usar em cada situação. Outra alternativa poderia ser estados de drawdown e, em resumo, esses estados baseados em portfólio permitiriam ao agente considerar o contexto financeiro mais amplo e não apenas sinais de mercado isolados.

Eu também poderia mencionar estados de macro-tendência; os princípios são semelhantes, mas mais importante é que os exemplos compartilhados aqui não são exaustivos. A escolha dos estados do ambiente pode ser decisiva para definir a estratégia e, portanto, entregar sua vantagem competitiva dependendo de quão única ela é, bem como do esforço empregado não apenas em testá-la, mas também em validá-la de forma cruzada.

Além dos estados do ambiente, os sinais de recompensa após cada ação fornecem ao agente feedback na forma que indica o sucesso ou fracasso de sua ação. As recompensas podem ser quantificadas em termos de lucro/prejuízo (como temos aplicado até agora), retornos ajustados ao risco ou qualquer outro indicador de desempenho relevante que possa guiar o agente em direção a ações mais favoráveis. Lembre-se: as recompensas são um componente chave na atualização dos Q-Values do Q-Map.

O RL é talvez mais conhecido por equilibrar exploração vs. exploração ao fazer previsões. Na prática, o agente frequentemente emprega estratégias de exploração para descobrir novas ações que possam gerar melhores recompensas, enquanto alternadamente explora ações conhecidas que já se mostraram bem-sucedidas. O equilíbrio entre exploração e exploração, controlado por um parâmetro de entrada epsilon, é crucial para que o agente evite ótimos locais e continue melhorando sua tomada de decisão ao longo do tempo.

Por tentativa e erro, portanto, já que a abordagem epsilon-greedy na seleção de ações adequadas incorpora seleção aleatória, o agente aprende com suas experiências no ambiente e ajusta sua política de seleção de ações com base em resultados passados. A cada experiência, a compreensão do agente sobre quais ações levam a recompensas positivas melhora, permitindo que ele faça melhores escolhas em situações semelhantes no futuro.

Essa melhoria se deve aos valores do Q-Map do agente ou à política. O mapa representa uma estratégia que associa estados a ações e atualiza continuamente as ações de cada estado com base nas recompensas observadas. A melhoria da política é guiada por algoritmos de aprendizado por reforço que visam maximizar recompensas cumulativas ao longo do tempo.

Esses são os aspectos básicos que analisamos nos últimos três artigos sobre RL; no entanto, ainda há conceitos mais inovadores dentro de RL. Um deles é a estimativa de função de valor, onde o agente frequentemente estima a função de valor, que pode prever o retorno esperado de um determinado estado ou par estado-ação. Ao aproximar a função de valor, o agente pode avaliar os potenciais benefícios de longo prazo de diferentes ações, facilitando assim melhores decisões.

Atribuição Temporal de Crédito é outro conceito, onde o agente conecta ações tomadas no passado com recompensas recebidas no futuro. Essa abordagem, em teoria, permite ao agente compreender como suas ações passadas afetam os resultados futuros, o que pode levar a um melhor planejamento ou ao estabelecimento preventivo de certas políticas que substituem o pareamento padrão ação-estado.

Outro conceito é o de taxas de aprendizado adaptativas, tema que consideramos neste artigo anterior quando tratamos de Perceptrons Multicamadas. Estas também podem ser aplicadas como alpha ao realizar atualizações dos Q-Values. O agente pode empregá-las ajustando com base na incerteza dos valores estado-ação, permitindo atualizações mais agressivas quando o agente está incerto e mais conservadoras à medida que ganha confiança. Essa adaptabilidade pode ajudar o agente a aprender de forma eficiente em condições de mercado variáveis.

Outras ideias relevantes relacionadas ao RL incluem Generalização entre Estados para melhorar a eficiência e Desenvolvimento de Estratégias de Longo Prazo que olham além das recompensas imediatas.

O Algoritmo de Monte Carlo

A abordagem de aprendizado adotada pelos métodos de Monte Carlo é diferente dos algoritmos de RL anteriores que consideramos, pois aprende a partir de episódios completos de experiência, esperando até o final de um episódio para “aprender”, mas adotando uma visão holística sobre múltiplos pontos de recompensa recebidos no intervalo. Isso, portanto, exige a necessidade de ter valores de recompensa armazenados ao longo de múltiplos tempos, de modo que, quando o episódio for concluído, todos os valores de recompensa passados estejam acessíveis. Implementamos isso em MQL5 da seguinte forma, dentro da função get output de nossa classe de sinal personalizada:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

O Q-Learning, por contraste, usa um método de aprendizado por diferença temporal (TD) que atualiza as estimativas de valor após cada ação tomada (ou após cada ciclo), utilizando bootstrapping a partir dos valores estado-ação subsequentes. Isso é semelhante ao SARSA, mas aqui as atualizações das estimativas de valor são feitas usando a ação tomada no próximo estado, fornecendo uma abordagem on-policy.

O mecanismo de atualização de Monte Carlo baseia-se no retorno médio observado após tomar ações a partir de um estado ao longo de múltiplos ciclos dentro de um episódio. Cada par estado-ação é atualizado apenas quando o episódio é concluído, de modo a refletir o verdadeiro retorno de longo prazo. O valor de recompensa usado nessa atualização é, portanto, uma soma ponderada, como mostrado na fórmula já compartilhada acima, bem como no código MQL5 na função get output acima.

O Q-Learning, no entanto, usa a recompensa futura máxima do próximo estado (off-policy) para fazer atualizações no valor da ação do estado atual, o que pode levar a um aprendizado mais agressivo, pois considera o melhor resultado possível em cada passo do ciclo dentro de um episódio. Da mesma forma, o SARSA atualiza o valor com base na ação realmente tomada no próximo estado (on-policy), incorporando a política atual do agente ao processo de aprendizado, o que pode levar a atualizações ligeiramente mais conservadoras do que o Q-Learning, mas ainda mais agressivas do que o Monte Carlo.

Como regra, o Monte Carlo depende da exploração completa do ambiente por meio de múltiplos ciclos em um episódio para aprender ações ótimas, permitindo uma amostragem abrangente dos pares estado-ação antes de realizar atualizações. Isso ocorre via uma abordagem ε-greedy, que introduzimos em nosso artigo introdutório sobre Q-Learning, na qual as atualizações eram influenciadas por ações não tomadas pelo agente.

O SARSA também é ε-greedy em sua abordagem de balancear exploração e exploração; porém, ele atualiza valores com base na ação de fato tomada no próximo estado, tornando-o mais responsivo à política atual do agente e às escolhas de exploração. A diferença do Monte Carlo em relação a esses dois, além de realizar atualizações apenas uma vez por episódio, é que ele pode ser tanto on-policy quanto off-policy. Para isso, nossa classe de sinal personalizada para Monte Carlo possui um parâmetro de entrada m_on_policy, que é booleano e, como o nome sugere, orienta se ele está sendo usado em estado on ou off policy.

A interface da classe para essa classe de sinal personalizada é apresentada abaixo:

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

A convergência do Monte Carlo tende a ser mais lenta, pois requer episódios completos para atualizações, o que pode não ser necessariamente eficiente em ambientes com episódios longos ou recompensas esparsas. Isso contrasta com o algoritmo Q-Learning que, em grande parte, converge mais rápido devido à sua natureza de bootstrapping; contudo, tende a ser instável, já que pode oscilar ou divergir em ambientes com recompensas não estacionárias ou alta variância. O SARSA é considerado mais estável do que o Q-Learning em certas situações, pois leva em conta a política real do agente durante as atualizações, o que tende a resultar em curvas de aprendizado mais suaves.

Quando se trata de eficiência de amostragem, o Monte Carlo é tipicamente menos eficiente, devido à necessidade de episódios completos para obter atualizações, o que pode ser uma grande desvantagem em ambientes com um grande espaço de estados e ações. O Q-Learning, por outro lado, é mais eficiente em amostragem, pois atualiza valores a cada passo, permitindo modificações mais rápidas com base no feedback imediato. De fato, é possivelmente ainda mais eficiente do que o SARSA, já que este pode exigir mais amostras do que o Q-Learning por ser sensível à política atual e à estratégia de exploração utilizada.

O Monte Carlo é bem adequado para ambientes em que os episódios podem ser definidos com clareza e os retornos de longo prazo tendem a ser mais cruciais do que surtos de curto prazo, como em simulações de trading. Isso claramente o posiciona como uma estratégia chave para “traders” de valor ou de longo prazo. O Q-Learning é eficaz em ambientes com uma estrutura de recompensas clara e transições de estado bem definidas, tornando-o ideal para tarefas como day trading. Enquanto isso, o SARSA é benéfico em situações em que o aprendizado precisa refletir de perto a política do agente, como em ambientes dinâmicos ou parcialmente observáveis, nos quais a adaptação é crucial — por exemplo, swing trading.

Implementando Monte Carlo em uma Classe de Sinal Personalizada

Implementamos nosso sinal personalizado que usa RL de Monte Carlo como o modelo raiz e gerador de sinais. As etapas principais para realizar isso já foram compartilhadas acima com a interface da classe e a função get output. Abaixo estão as funções de condição de compra (long) e venda (short):

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

O código-fonte completo desta implementação está anexado ao final, e orientações sobre como usá-lo para montar um Expert Advisor via wizard podem ser encontradas aqui e aqui. O processo de decisão de Markov é inerente ao uso de Q-Maps; ainda assim, há um parâmetro de entrada que oferece a opção de usar ponderação de Markov ao realizar atualizações de Q-Value. Além disso, podemos otimizar se usamos ou não on-policy, o tamanho do epsilon — nosso parâmetro que orienta o quanto exploramos vs. exploramos — e o número de ciclos em um episódio. Realizamos execuções de otimização no par GBP USD para o ano de 2022 no timeframe de uma hora. Abaixo estão nossos resultados:

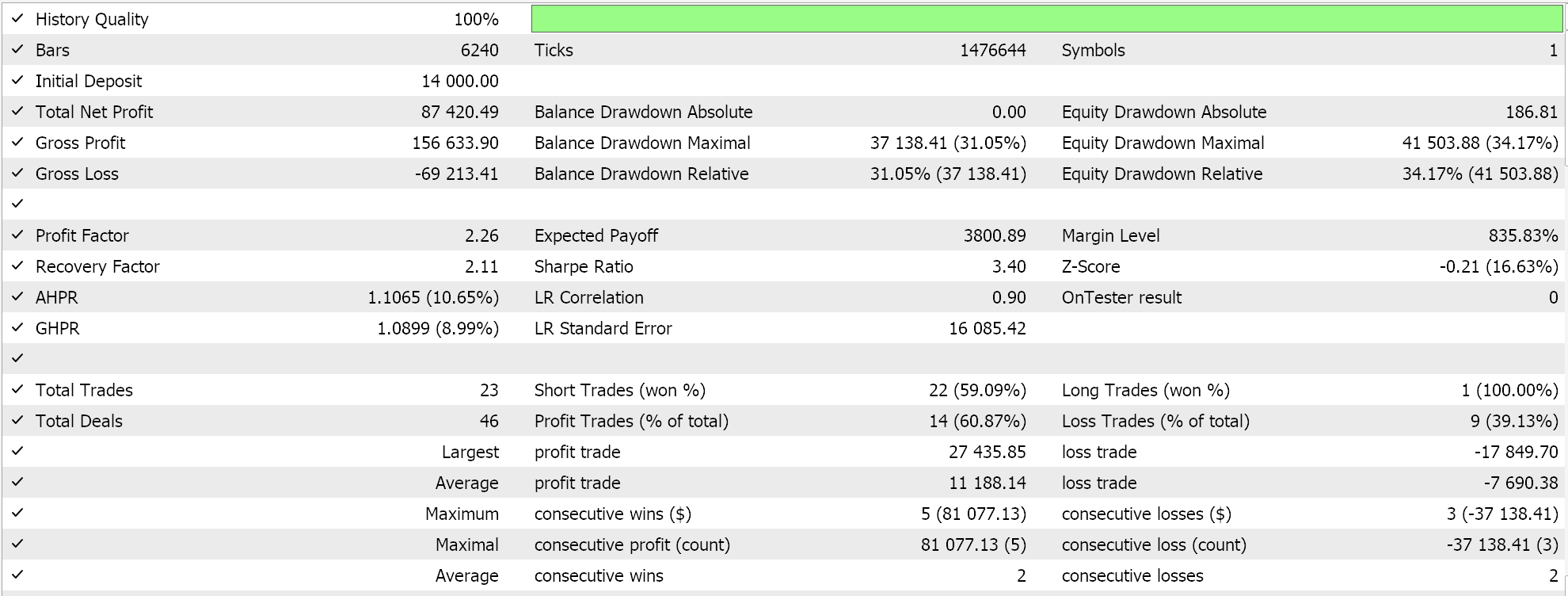
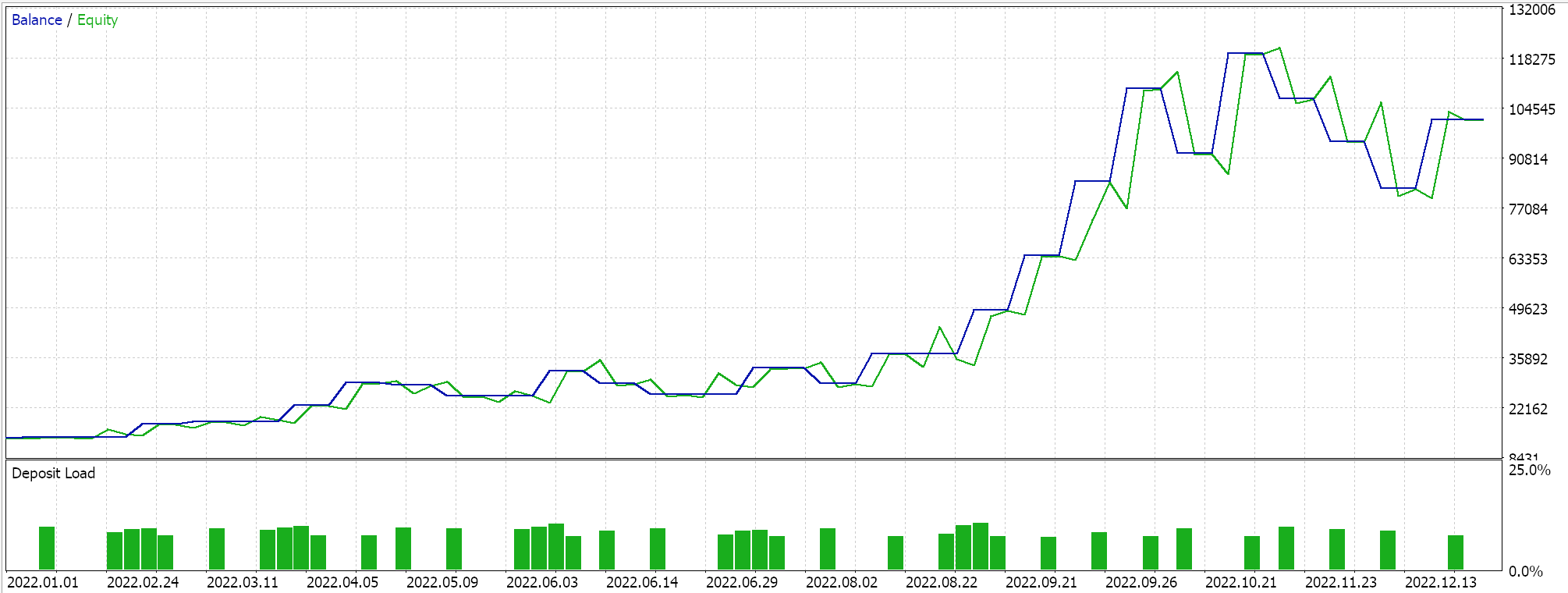
Conclusão e Considerações Adicionais

Em resumo, analisamos o algoritmo de Monte Carlo do Aprendizado por Reforço, que incorpora muitos recursos do Q-Learning e do SARSA — dois algoritmos que cobrimos anteriormente aqui e aqui, respectivamente — e apresenta uma forma ainda mais dinâmica e adaptável de aprendizado, mantendo o foco em traços e atributos de longo prazo de seu ambiente. Além de usar uma matriz de ambiente mais personalizada, como destacado em algumas alternativas listadas neste artigo, uma escala de ações alternativa, com mais de 3 opções, também pode ser explorada.

Há ainda considerações adicionais ao implementar Monte Carlo (MC) que merecem menção. O MC equilibra o trade-off entre viés e variância na forma como o valor de recompensa de atualização é calculado. Em casos em que o número de ciclos em um episódio é pequeno, tende a haver alto viés e baixa variância, enquanto episódios mais longos, com alta contagem de ciclos, tendem a apresentar o oposto. Portanto, dependendo dos objetivos, isso é algo a considerar ao desenvolver o Q-Map, porque um alto viés tenderá a tornar o modelo mais adaptável à ação de curto prazo, enquanto alta variância se alinhará melhor com a intenção do algoritmo de capturar traços e atributos de longo prazo.

A exploração mais granular do espaço estado-ação, proporcionada por múltiplas recompensas em diferentes pontos no tempo ao usar múltiplos retornos de n passos, significa que, ao variar horizontes de retornos possíveis (o que, em nossa classe de sinal personalizada, foi controlado pelo parâmetro de entrada m_episode_cycles), podemos ajustar finamente a força do sinal para estratégias de trading. Essa granularidade leva a decisões mais nuançadas ao determinar pontos de entrada e saída, permitindo otimizar ambos e ajustar o timing e a intensidade de seus sinais.