Redes neurais em trading: Modelos híbridos de sequências de grafos (Conclusão)

Introdução

No artigo anterior, analisamos os aspectos teóricos do GSM++, um framework unificado de sequências de grafos GSM++, que representa um método inovador de processamento de dados, combinando os benefícios de diferentes soluções arquitetônicas. O GSM++ é composto por três etapas principais: tokenização do grafo, codificação local dos nós e codificação global das dependências. Essa estrutura permite maior eficiência no trabalho com dados representados na forma de grafos, aprimorando as capacidades analíticas para a resolução de tarefas complexas no setor financeiro e em outras áreas relacionadas à análise de séries temporais e de dados estruturados.

Um dos elementos mais importantes do sistema é a tokenização hierárquica de grafos, que permite transformar dados complexos em uma representação sequencial compacta. A metodologia de tokenização utilizada no GSM++ preserva as características topológicas e temporais dos dados brutos, aumentando significativamente a precisão na extração de características. Além disso, essa abordagem ajuda a reduzir os custos computacionais na análise de grandes volumes de dados, garantindo um equilíbrio entre a velocidade de processamento da informação e a profundidade da análise. Dependendo da tarefa, o nível de detalhamento da análise pode ser ajustado, o que torna a metodologia universal e flexível.

A codificação local dos nós desempenha um papel importante, sendo responsável pelo processamento da informação no nível dos elementos individuais do grafo. Nos métodos tradicionais de análise, frequentemente surge o problema da redundância de informações, o que aumenta a carga computacional e complica a identificação de padrões. Entretanto, o uso de mecanismos adaptativos de codificação permite destacar as características mais relevantes dos nós e transmiti-las de maneira eficiente para os níveis seguintes de análise. Isso possibilita reduzir o volume de informações irrelevantes e melhorar a capacidade do modelo de identificar relações locais entre os nós. Outra vantagem da codificação local é sua capacidade de se adaptar dinamicamente às mudanças nos dados brutos, o que é especialmente importante em condições de instabilidade dos mercados financeiros, em que mudanças bruscas podem afetar significativamente a precisão das previsões.

A melhoria adicional das capacidades analíticas é alcançada com o uso de um codificador híbrido, que combina os recursos dos modelos recorrentes e dos transformadores. Essa abordagem permite aproveitar as vantagens de ambos os métodos: os mecanismos recorrentes garantem um processamento eficiente de séries temporais, considerando a sequência dos eventos, enquanto os transformadores, que utilizam o mecanismo Self-Attention, identificam de maneira eficaz relações complexas nos dados, independentemente de sua ordem. Essa combinação torna o modelo não apenas mais preciso, mas também mais resistente às mudanças na dinâmica do mercado. Além disso, o codificador híbrido consegue se adaptar a diferentes cenários, ajustando o equilíbrio entre a precisão da previsão e a eficiência computacional conforme os requisitos de cada tarefa específica.

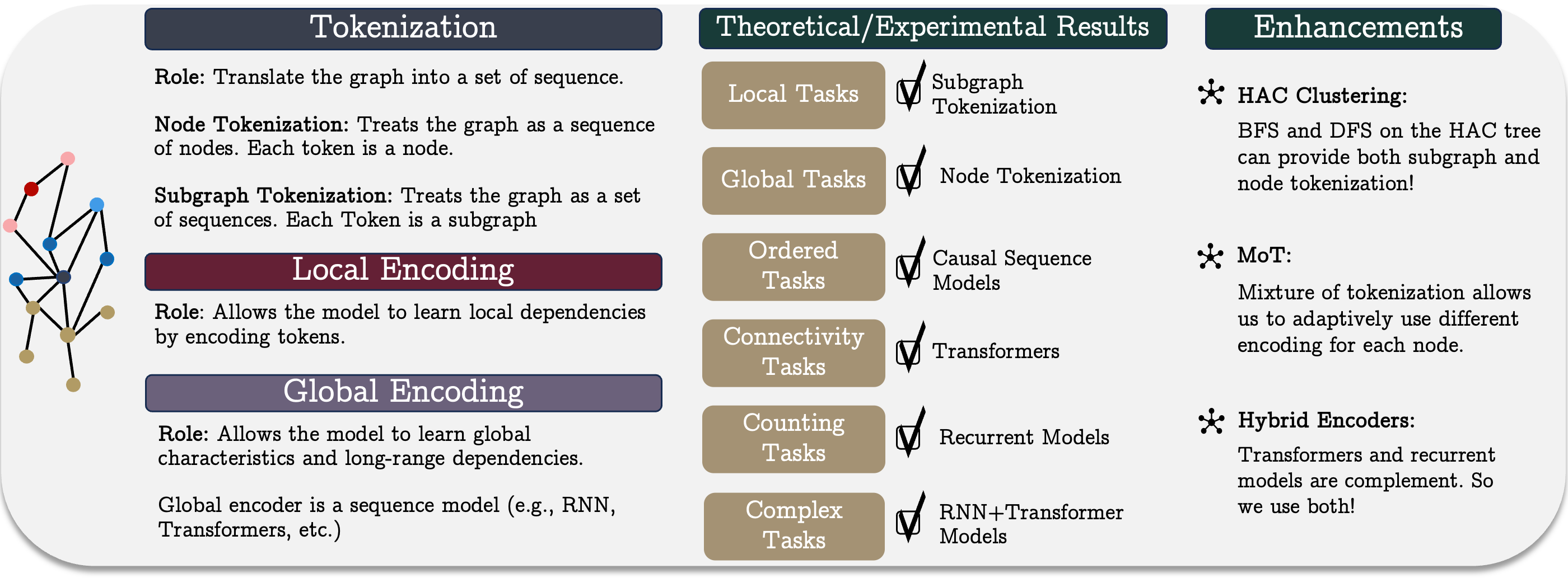
Na parte prática do artigo anterior, iniciamos a implementação de uma visão própria dos métodos propostos pelos autores do framework GSM++, utilizando MQL5. Devido à alta variabilidade dos dados financeiros, optamos por não utilizar a clusterização hierárquica baseada em similaridade (HAC), sugerida pelos autores do framework. Em seu lugar, usamos um módulo de tokenização mista treinável, que aumenta significativamente a flexibilidade e a adaptabilidade do modelo ao trabalhar com dados reais de mercado.

O algoritmo de tokenização mista implementado (Mixture of Tokenization — MoT) prevê o uso de quatro tipos diferentes de tokens para cada barra, para que seja possível realizar uma análise mais detalhada da informação de mercado. Neste experimento, utilizamos as seguintes abordagens para a codificação dos dados brutos:

• Tokenização de nós — cada barra é considerada como um elemento separado de análise, o que permite avaliar suas características individuais e identificar os principais parâmetros que influenciam o desenvolvimento posterior dos eventos.
• Tokenização de arestas — inclui a análise das interdependências entre barras vizinhas, revelando correlações e tendências de curto prazo que podem ser úteis para a previsão de mudanças rápidas.
• Tokenização de subgrafos — analisa grupos de barras, permitindo identificar estruturas mais complexas e padrões estáveis que possuem importância significativa para previsões estratégicas.
• Tokenização de subgrafos de sequências unitárias individuais — garante uma análise profunda das sequências unitárias e de suas interdependências, sendo especialmente relevante na identificação de padrões ocultos nos dados.

A unificação desses tokens é feita com o mecanismo Attention Pooling, do framework R-MAT. Tal método permite que o modelo se concentre nas características mais relevantes e descarte os dados menos importantes, melhorando significativamente o processo de tomada de decisão. A principal vantagem do Attention Pooling está em sua capacidade de processar estruturas de dados complexas de maneira eficiente, destacando os atributos mais relevantes e minimizando a influência do ruído.

Para implementar a abordagem proposta, foi criado o objeto CNeuronMoT, que herda a funcionalidade básica do CNeuronMHAttentionPooling e garante a aplicação eficiente do algoritmo Attention Pooling. Essa abordagem modular aumenta a adaptabilidade do modelo, possibilita um processamento mais eficaz dos dados de mercado e melhora a qualidade da análise e da previsão dos movimentos de preços, o que torna esse recurso valioso para o trading algorítmico.

A próxima etapa do processamento de dados é a codificação local dos nós. Em nossa implementação, decidimos utilizar o módulo previamente desenvolvido de suavização adaptativa de características. O método de suavização adaptativa de características dos nós (Node-Adaptive Feature Smoothing — NAFS) permite a formação de representações vetoriais mais informativas dos nós, considerando tanto as características estruturais do grafo quanto as particularidades de cada nó. Esse método parte da premissa de que diferentes nós podem exigir diferentes graus de suavização. Isso torna possível o processamento adaptativo de cada nó de acordo com o seu contexto. O NAFS utiliza uma abordagem combinada, aplicando suavização de ordem baixa e alta, o que permite considerar de maneira eficiente as interdependências locais e globais no grafo.

No NAFS, é utilizado um método de ensemble para unificar as características. Essa abordagem aumenta a resistência do modelo ao ruído e torna o processo de codificação mais confiável. Entre as vantagens do uso do módulo NAFS, estão:

• Filtragem flexível dos dados, permitindo destacar as características mais relevantes e eliminar componentes de ruído.
• Otimização dos custos computacionais, especialmente importante na análise de grandes grafos e dados de mercado de alta frequência.
• Adaptabilidade às condições em mudança, graças à possibilidade de ajuste dinâmico dos parâmetros de suavização.
• Aumento da precisão do modelo, garantido pela combinação equilibrada de análise detalhada e alta capacidade de generalização dos algoritmos.

O elemento final e essencial do GSM++ é o codificador híbrido. Os autores do framework propõem combiná-lo com o módulo Mamba e o Transformer. Em nossa implementação, seguimos a mesma ideia. No entanto, fomos além: substituímos o Mamba pelo Chimera, e o Transformer pelo Hidformer.

O Chimera utiliza modelos bidimensionais de espaço de estados (2D-SSM), o que permite modelar de maneira eficiente as dependências ao longo do eixo temporal e de uma dimensão adicional relacionada à topologia do grafo. Essa abordagem amplia significativamente as possibilidades de análise das complexas interdependências de mercado. As vantagens do Chimera incluem:

• O codificador bidimensional de dependências contribui para uma melhor identificação de padrões ocultos do mercado e para o aumento da precisão das previsões;
• Maior expressividade do modelo, proporcionando uma análise mais profunda das relações não lineares complexas entre ativos;
• A adaptabilidade às mudanças dinâmicas do mercado permite que o modelo se ajuste rapidamente às condições em transformação.

O Hidformer tem uma arquitetura de duas torres e, ao contrário do Transformer clássico, divide o processamento dos dados brutos em dois fluxos: um codificador analisa as dependências temporais, enquanto o outro analisa os componentes de frequência dos dados de mercado. Essa solução permite modelar a dinâmica dos processos de mercado com mais precisão. As principais vantagens do Hidformer são:

• A separação da análise em componentes temporais e de frequência garante previsões mais precisas da dinâmica do mercado;
• O uso de atenção recursiva no codificador temporal e de atenção linear no codificador de frequência reduz a complexidade computacional e aumenta a eficiência do processamento.

Dessa forma, a utilização do Chimera e do Hidformer no GSM++ pode potencialmente proporcionar alta precisão no codificador de dependências, minimizar o impacto do ruído de mercado e aumentar a confiabilidade das previsões analíticas.

Ajuste do módulo SSM

É importante lembrar que, durante os testes do modelo construído com o framework Chimera, notamos que a manutenção de posições levava tempo demais. Na época, levantamos a hipótese de que o modelo capturasse apenas tendências de longo prazo, ignorando as de curto prazo. Para tentar corrigir essa limitação, decidimos modernizar o objeto previamente implementado e adicionar a ele um objeto interno adicional do modelo bidimensional de espaço de estados. Os algoritmos atualizados foram implementados no objeto CNeuronChimeraPlus, cuja estrutura é apresentada a seguir.

class CNeuronChimeraPlus    :  public CNeuronChimera
  {
protected:
   CNeuron2DSSMOCL    cSSMPlus;
   CLayer             cDiscretizationPlus;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronChimeraPlus(void) {};
                    ~CNeuronChimeraPlus(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override  const   {  return defNeuronChimeraPlus; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como pode ser observado na estrutura apresentada do novo objeto, não reescrevemos totalmente o objeto CNeuronChimera já criado. Pelo contrário, utilizamos esse objeto como classe pai, o que nos permitiu herdar toda a funcionalidade previamente implementada. No entanto, a adição do novo terceiro módulo 2D-SSM e do respectivo bloco de projeção de dados exige a redefinição do conjunto usual de métodos virtuais. A inicialização dos objetos recém-declarados e herdados é realizada no método Init, cuja estrutura de parâmetros foi totalmente herdada do método equivalente da classe pai.

bool CNeuronChimeraPlus::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                              uint window_in, uint window_out, uint units_in, uint units_out,
                              ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronChimera::Init(numOutputs, myIndex, open_cl, window_in, window_out, units_in,
                                                      units_out, optimization_type, batch))
      return false;

No corpo do método, a primeira ação é chamar o método homônimo da classe pai, no qual os pontos de controle dos valores recebidos e os algoritmos de inicialização dos objetos herdados já estão implementados.

Após a execução bem-sucedida das operações do método da classe pai, passamos para a etapa de inicialização dos objetos recém-declarados, que são responsáveis por garantir a funcionalidade expandida do modelo. Um dos componentes-chave adicionados nesta etapa é o módulo adicional do modelo bidimensional de espaço de estados (2D-SSM).

É importante ressaltar que, no método da classe pai, dois módulos 2D-SSM já foram inicializados, cada um com uma função específica. Um deles atua em dimensões específicas dos resultados, garantindo o codificador padrão das dependências espaciais, enquanto o segundo utiliza um espaço de características expandido, o que permite abranger interdependências mais complexas e multiníveis entre os elementos da análise.

Para aumentar a capacidade de generalização do modelo e melhorar a precisão no processamento dos dados de mercado, o módulo adicional 2D-SSM funcionará, diferentemente dos já existentes, em um espaço de características definido, mas com projeção expandida no eixo temporal. Essa arquitetura cria condições para uma análise mais precisa das séries temporais e dos dados de mercado distribuídos espacialmente.

   int index = 0;
   if(!cSSMPlus.Init(0, index, OpenCL, window_in, window_out, units_in, 2 * units_out, optimization, iBatch))
      return false;

Em seguida, precisamos realizar a projeção dos resultados no subespaço definido. E aqui é importante observar que não podemos realizar imediatamente a projeção pelo eixo temporal. Portanto, será necessário montar uma pequena sequência interna de objetos.

Primeiro, preparamos um array dinâmico e variáveis locais para registrar os ponteiros dos objetos que serão criados.

   CNeuronTransposeOCL *transp = NULL;
   CNeuronConvOCL      *conv = NULL;
   cDiscretizationPlus.Clear();
   cDiscretizationPlus.SetOpenCL(OpenCL);

O primeiro objeto a ser criado é o de transposição de dados, que permitirá ajustar os dados para a forma necessária.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, 2 * units_out, window_out, optimization, iBatch) ||
      !cDiscretizationPlus.Add(transp))
     {
      delete transp;
      return false;
     }

Em seguida, adicionamos uma camada convolucional de projeção dos dados na dimensão temporal definida.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, 2 * units_out, 2 * units_out, units_out, window_out, 1, optimization, iBatch) ||
      !cDiscretizationPlus.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Depois, retornamos os dados à sua representação original por meio de mais um objeto de transposição.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_out, units_out, optimization, iBatch) ||
      !cDiscretizationPlus.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Com isso, finaliza-se o processo de inicialização dos objetos internos e encerramos o método, retornando previamente o resultado lógico da execução das operações ao programa chamador.

A próxima etapa do nosso trabalho é a construção do método de propagação para frente (feedForward). Aqui é importante observar que a normalização dos dados é realizada na saída do método equivalente da classe pai. Como você sabe, essa operação altera a distribuição dos dados. A soma desses dados com os resultados não normalizados do fluxo de informação adicional pode resultar em um desvio imprevisível em direção a uma das ramificações. Para evitar esse problema, reescrevemos completamente o método de propagação para frente.

bool CNeuronChimeraPlus::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   for(uint i = 0; i < caSSM.Size(); i++)
     {
      if(!caSSM[i].FeedForward(NeuronOCL))
         return false;
     }
   if(!cSSMPlus.FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método recebemos um ponteiro para o objeto dos dados brutos, que transmitimos imediatamente para os métodos homônimos dos modelos internos de espaço de estados. Os modelos internos de espaço de estados geram resultados em três projeções distintas.

Em seguida, com a ajuda dos objetos internos de discretização, trazemos os resultados das operações dos modelos de espaço de estados para uma forma comparável.

   if(!cDiscretization.FeedForward(caSSM[1].AsObject()))
      return false;
   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *current = NULL;
   for(int i = 0; i < cDiscretizationPlus.Total(); i++)
     {
      current = cDiscretizationPlus[i];
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

Além disso, obtemos a projeção dos dados brutos pela ramificação das conexões residuais.

   inp = NeuronOCL;
   for(int i = 0; i < cResidual.Total(); i++)
     {
      current = cResidual[i];
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

Por fim, somamos os dados dos quatro fluxos de informação. Nesse processo, a normalização dos valores é realizada apenas na fase final.

   inp = cDiscretizationPlus[-1];
   if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) ||
      !SumAndNormilize(Output, inp.getOutput(), Output, 1, false, 0, 0, 0, 1) ||
      !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

O resultado lógico da execução das operações é retornado ao programa chamador e finalizamos o método.

A próxima etapa do nosso trabalho é a construção dos algoritmos de propagação reversa. Como de costume, eles são implementados em dois métodos: calcInputGradients e updateInputWeights. No primeiro, são realizadas as operações de distribuição do gradiente de erro entre os objetos participantes do processo. O segundo é destinado ao ajuste dos parâmetros treináveis dos modelos. Nesta etapa, diferentemente do método de propagação para frente, podemos utilizar a funcionalidade da classe pai.

Nos parâmetros do método de distribuição do gradiente do erro, recebemos um ponteiro para o mesmo objeto dos dados brutos, mas desta vez devemos transmitir a ele os valores do gradiente do erro, na proporção da influência dos dados brutos sobre o resultado do modelo.

bool CNeuronChimeraPlus::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronChimera::calcInputGradients(NeuronOCL))
      return false;

Mas, diferentemente da abordagem usual, não verificamos a validade do ponteiro recebido, apenas o transmitimos diretamente para o método homônimo da classe pai. Lá, já estão implementados os pontos de controle necessários e o algoritmo de distribuição do gradiente do erro entre os três fluxos de informação herdados (dois 2D-SSM e a ramificação das conexões residuais).

Agora, só nos resta transmitir o gradiente do erro pela ramificação adicionada. Para isso, primeiro ajustamos o gradiente do erro recebido dos objetos subsequentes em relação à derivada da função de ativação da última camada do modelo de discretização adicionado.

   CNeuronBaseOCL *current = cDiscretizationPlus[-1];
   if(!current ||
      !DeActivation(current.getOutput(), current.getGradient(), Gradient, current.Activation()))
      return false;

E então passamos os valores obtidos pelo bloco de discretização no sentido inverso. Para isso, organizamos um laço de iteração reversa dos elementos, com chamadas sequenciais dos métodos homônimos dos respectivos objetos.

   for(int i = cDiscretizationPlus.Total() - 2; i >= 0; i--)
     {
      current = cDiscretizationPlus[i];
      if(!current ||
         !current.calcHiddenGradients(cDiscretizationPlus[i + 1]))
         return false;
     }

Em seguida, conduzimos o gradiente do erro através do modelo bidimensional de espaço de estados.

   if(!cSSMPlus.calcHiddenGradients(current.AsObject()))
      return false;

Resta apenas transmitir o gradiente do erro para o nível dos dados brutos. Mas aqui é necessário considerar que no buffer do objeto de dados brutos já foi armazenado o gradiente do erro transmitido pelos três fluxos de informação herdados. Para preservar esses dados, realizamos a substituição do ponteiro para o buffer de gradientes de erro do objeto de dados brutos.

   current = cResidual[0];
   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(current.getGradient(), false) ||
      !NeuronOCL.calcHiddenGradients(cSSMPlus.AsObject()) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(temp, false))
      return false;
//---
   return true;
  }

Depois, transmitimos o gradiente do erro do modelo bidimensional de espaço de estados para o nível dos dados brutos. Somamos os valores obtidos aos que já haviam sido acumulados e retornamos os ponteiros dos buffers de dados ao estado original.

Resta apenas retornar o resultado lógico da execução das operações ao programa chamador e encerrar o método.

Com isso, concluímos a análise dos algoritmos do módulo Chimera expandido. O código completo da classe CNeuronChimeraPlus e de todos os seus métodos pode ser consultado no anexo.

Construção do decodificador híbrido

Após a construção do módulo Chimera modernizado, passamos ao desenvolvimento do codificador híbrido. Como foi dito anteriormente, em nossa implementação ele contém o módulo Chimera e o bloco Hidformer. E aqui é importante lembrar que o objeto Hidformer recebe na entrada os dados do estado analisado do sistema e, na saída, gera o tensor de ações do agente. Nesse contexto, nosso novo objeto talvez seja mais corretamente chamado de decodificador híbrido. A estrutura do objeto é apresentada a seguir.

class CNeuronHypridDecoder :  public CNeuronHidformer
  {
protected:
   CNeuronChimeraPlus   cChimera;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronHypridDecoder(void){};
                    ~CNeuronHypridDecoder(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint stack_size, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronHypridDecoder; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como se pode ver, na estrutura apresentada, é declarado apenas um objeto interno: o módulo Chimera modificado, cujos algoritmos foram descritos anteriormente. O objeto CNeuronHidformer é utilizado como classe pai, o que permite evitar a duplicação desnecessária de funcionalidades e aplicar, de maneira eficiente, métodos e estruturas já implementados, sem a necessidade de se criar uma instância adicional dentro do objeto. No entanto, ainda precisamos redefinir o conjunto usual de métodos virtuais.

O objeto interno é declarado de forma estática, o que significa que o construtor e o destrutor da nova classe permanecem vazios. A inicialização dos objetos declarados e herdados é realizada no método Init.

bool CNeuronHypridDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                uint window, uint window_key, uint units_count,
                                uint heads, uint layers, uint stack_size, uint nactions,
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronHidformer::Init(numOutputs, myIndex, open_cl, window_key, window_key, nactions,
                             heads, layers, stack_size, nactions, optimization_type, batch))
      return false;

Nos parâmetros do método de inicialização, recebemos um conjunto de constantes que determinam, de forma inequívoca, a arquitetura do objeto a ser criado. A estrutura dos parâmetros é totalmente herdada do método homônimo da classe pai. No entanto, ao chamarmos o método da classe pai, não passamos os valores recebidos exatamente da mesma forma. Isso ocorre porque, ao invés de transmitir os dados brutos recebidos do programa externo, planejamos transmitir os resultados do objeto interno Chimera. Consequentemente, também no processo de inicialização dos objetos herdados da classe pai, devemos indicar as dimensões dos resultados do módulo interno como dados recebidos de entrada. Nesse caso, a dimensionalidade das características é definida pelo valor especificado do vetor de estado interno. Já o comprimento da sequência é igual ao espaço de ações do agente. Em outras palavras, na saída do módulo Chimera, esperamos obter um tensor de estado latente, no qual cada linha representa um token de um elemento individual das ações do agente.

Após a execução bem-sucedida das operações do método da classe pai, chamamos o método homônimo do módulo Chimera, especificando as dimensões dos dados de entrada e o tensor de resultados desejado.

   if(!cChimera.Init(0, 0, OpenCL, window, window_key, units_count, nactions, optimization, iBatch))
      return false;
//---
   return true;
  }

Retornamos o resultado lógico da execução das operações e finalizamos o método.

Creio que você tenha notado que o algoritmo do método de inicialização do objeto é bastante simples. O mesmo vale para os demais métodos. Por exemplo, o método de propagação para frente feedForward, como de costume, recebe nos parâmetros um ponteiro para o objeto de dados brutos, que é imediatamente transmitido ao método homônimo do módulo Chimera.

bool CNeuronHypridDecoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cChimera.FeedForward(NeuronOCL))
      return false;
   return CNeuronHidformer::feedForward(cChimera.AsObject());
  }

Os valores obtidos são então transmitidos ao método homônimo da classe pai. E o resultado lógico da execução das operações é retornado ao programa chamador. Em seguida, finalizamos o método.

Quanto aos demais métodos desta classe, sugiro que você os analise por conta própria. O código completo deles pode ser facilmente encontrado no anexo.

Arquitetura do modelo

Concluído o trabalho de construção dos blocos individuais do framework GSM++, passamos à criação da arquitetura completa do modelo. Neste caso, treinamos apenas um modelo — o Ator. A descrição da arquitetura do modelo é apresentada no método CreateDescriptions.

bool CreateDescriptions(CArrayObj *&actor)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }

Nos parâmetros do método recebemos um ponteiro para um array dinâmico destinado ao registro da sequência de objetos que descrevem a arquitetura do modelo. E imediatamente verificamos a validade do ponteiro recebido. Se necessário, criamos uma nova instância do objeto.

Em seguida, criamos a descrição da camada de dados brutos. Aqui, como de costume, utilizamos uma camada totalmente conectada de tamanho suficiente.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Na entrada do modelo planejamos alimentar os dados brutos recebidos do terminal. E o pré-processamento inicial desses dados é realizado diretamente pelos recursos do modelo. Para essa etapa inicial é utilizada uma camada de normalização em lote, que traz os valores dispersos dos dados brutos para uma forma comparável.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, vem o módulo de tokenização mista.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMoT;
   descr.window = BarDescr;
   descr.count = HistoryBars;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Depois utilizamos o módulo S3, que aprende o método ótimo de permutação dos tokens. Ele permite encontrar a melhor ordem dos elementos levando em conta suas interdependências e sua relevância na estrutura geral dos dados.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Os resultados do processamento dos dados são transmitidos ao codificador local dos nós, cuja função é desempenhada pelo módulo NAFS.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronNAFS;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

O tensor de ações do Agente é gerado no módulo do decodificador híbrido, cujos algoritmos de funcionamento foram descritos anteriormente.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronHypridDecoder;
//--- Windows
     {
      int temp[] = {BarDescr, 120, NActions};      //Window, Stack Size, N Actions
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = HistoryBars;
   descr.window_out = 32;
   descr.step = 4;                                  // Heads
   descr.layers = 3;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

É importante destacar que a arquitetura do Agente que desenvolvemos está voltada exclusivamente para a análise dos estados do ambiente. No entanto, isso não é suficiente para uma avaliação completa e precisa dos riscos, pois o modelo não leva em consideração os ativos disponíveis e sua influência nas decisões tomadas.

Para resolver esse problema, na etapa seguinte complementamos a arquitetura com o bloco de gerenciamento de risco, que foi aproveitado de modelos analisados anteriormente.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMacroHFTvsRiskManager;
//--- Windows
     {
      int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = 10;
   descr.window_out = 16;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Após criar a descrição da arquitetura do modelo, retornamos o resultado lógico da execução das operações ao programa chamador e finalizamos o método.

O código completo do método de descrição da arquitetura do modelo está apresentado no anexo. Lá também você encontrará o código dos programas de treinamento e teste do modelo, que foram transferidos de trabalhos anteriores. Recomendo analisá-los de forma independente. 

Testes

Realizamos um trabalho extenso para implementar nossa própria visão dos métodos propostos pelos autores do framework GSM++. Chegamos, então, a uma das etapas mais importantes, quando verificamos se as soluções implementadas são eficazes com dados históricos reais.

É importante ressaltar que as últimas camadas neurais do Agente repetem, em grande medida, a arquitetura utilizada em nossa implementação do framework Hidformer. Aplicamos uma estrutura idêntica do módulo de gerenciamento de risco e, na saída do decodificador híbrido, utilizamos o objeto CNeuronHidformer. Essa semelhança arquitetural torna pertinente a comparação do desempenho do novo modelo com o Hidformer.

Para garantir a correção da comparação, ambos os modelos foram treinados na mesma amostra, formada anteriormente para o treinamento do Hidformer. Lembrando que:

• A amostra de treinamento inclui dados históricos do par de moedas EURUSD no timeframe M1 durante todo o ano de 2024.
• Os parâmetros de todos os indicadores analisados permanecem no padrão, sem otimização adicional, o que elimina a influência de fatores externos.
• O teste do modelo treinado é realizado em dados históricos de janeiro de 2025, mantendo todos os demais parâmetros inalterados para garantir a objetividade da comparação.

Os resultados do teste são apresentados abaixo.

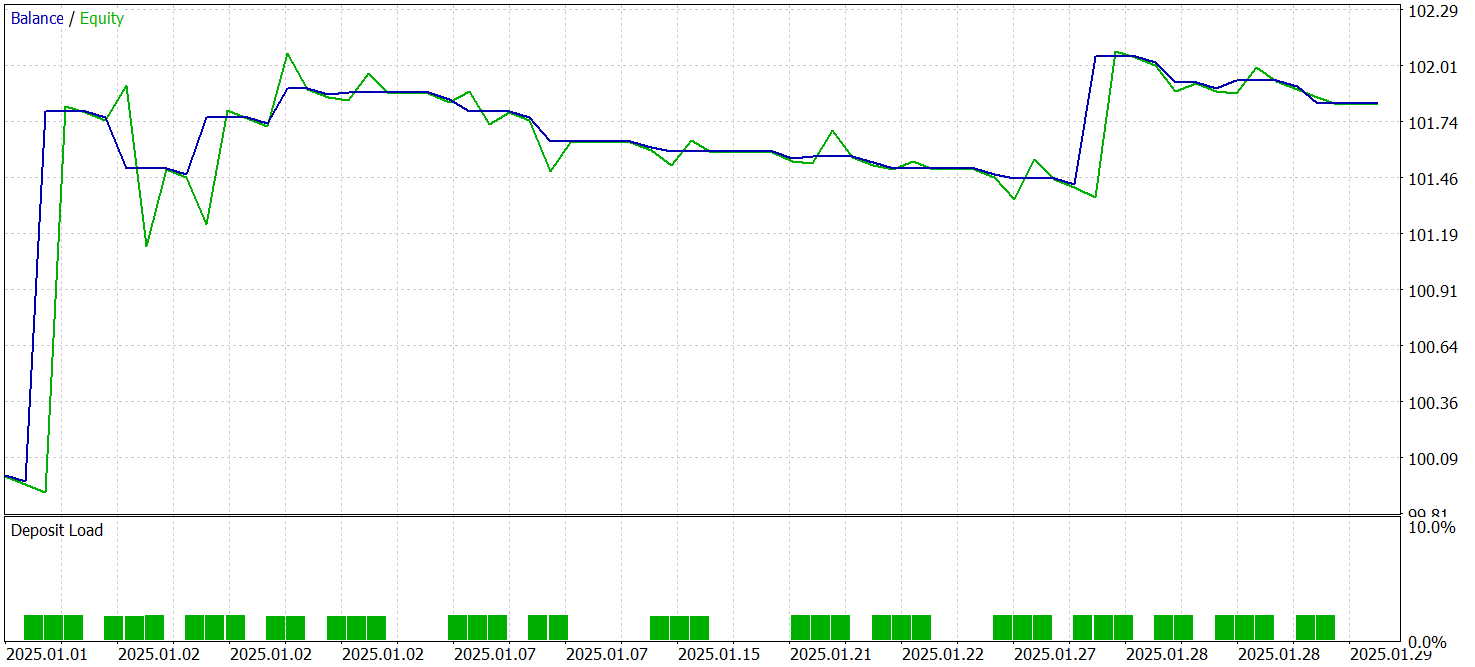
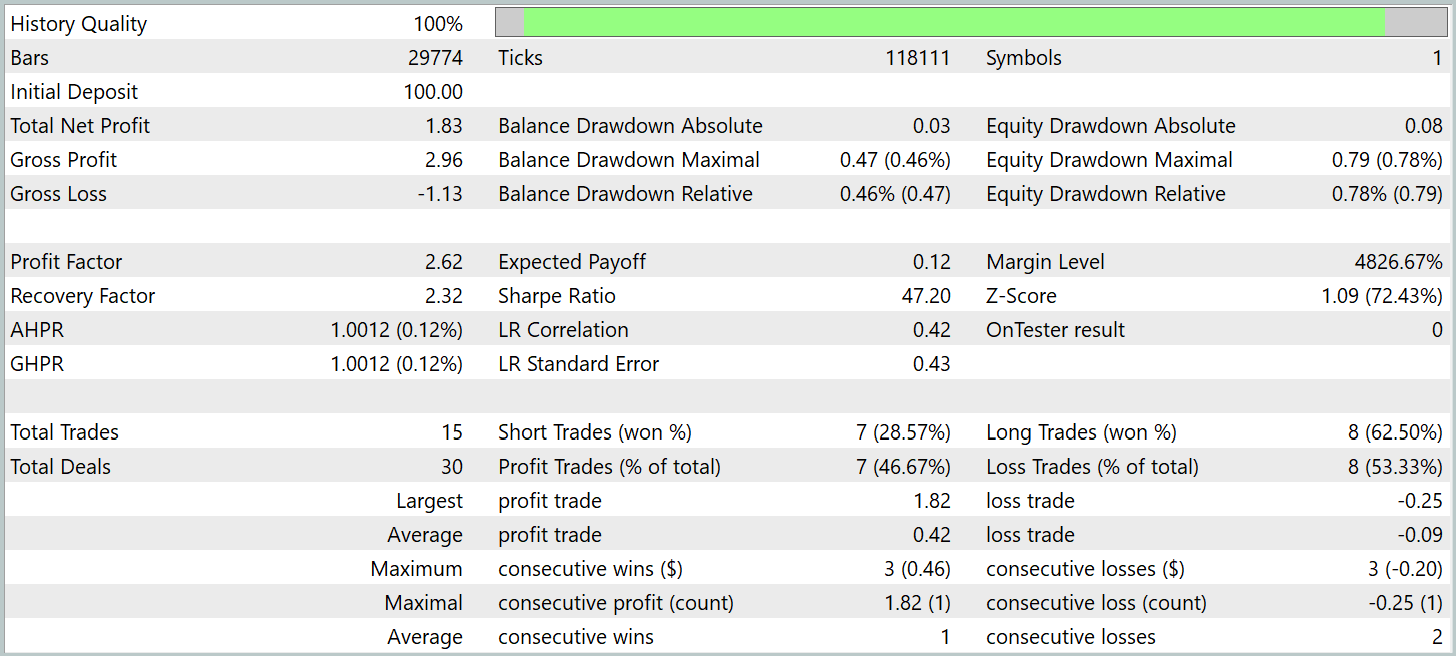
Durante o período de teste, o modelo realizou 15 operações de trading, o que é relativamente pouco para uma negociação de alta frequência no timeframe M1. Esse número é até inferior ao demonstrado pelo modelo básico (Hidformer). Apenas 7 delas foram encerradas com lucro, representando 46,67%. E esse índice também é menor do que o básico, de 62,07%. Aqui observamos uma redução na precisão das posições curtas. No entanto, foi notado um leve decréscimo no tamanho das posições perdedoras em comparação ao crescimento relativo do mesmo indicador nas operações lucrativas.

Enquanto no modelo básico a relação entre as médias das posições lucrativas e perdedoras era de 1,6, no novo modelo esse valor ultrapassa 4. Isso permitiu quase dobrar o lucro total no período de teste, acompanhado de um crescimento proporcional do profit factor. Esse fato pode indicar que a estratégia implementada na nova arquitetura dá ênfase à minimização das perdas e ao aumento dos ganhos nas posições bem-sucedidas. No longo prazo, isso potencialmente poderá garantir resultados financeiros mais estáveis. No entanto, o curto período de teste e o baixo número de operações realizadas não nos permitem avaliar a eficácia do modelo em intervalos de tempo prolongados.

Considerações finais

Conhecemos o método unificado de processamento de sequências de grafos GSM++, que combina abordagens avançadas de análise de dados de mercado. A principal vantagem desse framework está em sua representação híbrida de dados, que inclui tokenização hierárquica, codificação local dos nós e codificação global das dependências. Essa abordagem multinível permite a extração eficiente de padrões relevantes e a formação de embeddings altamente informativos, o que é crítico para as tarefas de previsão de séries temporais financeiras.

Na parte prática, apresentamos a implementação de nossa visão dos métodos propostos utilizando MQL5. É importante destacar que há diferenças significativas entre as soluções implementadas e os métodos sugeridos pelos autores do framework. Portanto, todos os resultados obtidos durante os testes referem-se exclusivamente à solução implementada por nós.

O modelo treinado demonstrou capacidade de gerar lucro com dados fora da amostra de treinamento. No entanto, não nos volumes desejados. Isso nos permite falar sobre o potencial dos métodos implementados, mas ainda é necessário realizar trabalhos adicionais de treinamento do modelo com uma amostra mais representativa e submetê-lo a testes mais abrangentes. Além disso, é necessário buscar um conjunto mais otimizado de indicadores analisados e seus parâmetros. Afinal, o modelo procura padrões nos dados de treinamento; ele não os cria.

Referências

• Best of Both Worlds: Advantages of Hybrid Graph Sequence Models
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programas OpenCL