Funções de ativação de neurônios durante o aprendizado: chave para uma convergência rápida?

Introdução

No artigo anterior, analisamos as propriedades de uma rede neural MLP simples como aproximador (aprendizado por reforço) dentro de um EA (Expert Advisor). Na ocasião, não demos atenção especial às propriedades das funções de ativação e utilizamos a popular sigmoide do tangente hiperbólico. Também em um dos artigos discutimos as possibilidades do conhecido e amplamente aplicado algoritmo ADAM, porém modificado por mim em um método populacional independente de otimização global chamado ADAMm.

Neste artigo, aprofundaremos as capacidades da rede neural como interpoladora de dados (aprendizado supervisionado), com ênfase nas propriedades das funções de ativação dos neurônios. Usaremos o algoritmo de otimização ADAM incorporado à rede neural (como normalmente é feito no uso de redes neurais) e conduziremos estudos sobre a influência da função de ativação e sua derivada na velocidade de convergência do algoritmo de otimização.

Imagine um rio com muitos afluentes. Em condições normais, a água flui livremente, formando um padrão complexo de correntes e redemoinhos. Mas o que acontece se começarmos a construir um sistema de eclusas e represas? Conseguiremos controlar o fluxo da água, direcioná-lo para o caminho desejado e regular a força da corrente. A função de ativação em redes neurais cumpre papel semelhante: ela decide qual sinal deve ser transmitido adiante, qual deve ser retido ou enfraquecido. Sem ela, uma rede neural seria apenas um conjunto de transformações lineares.

A função de ativação traz dinâmica ao funcionamento da rede neural, permitindo capturar sutilezas nos dados. Por exemplo, em tarefas de reconhecimento facial, a função de ativação ajuda a rede a perceber detalhes mínimos, como a curvatura das sobrancelhas ou o formato do queixo. A escolha adequada da função de ativação afeta diretamente como a rede neural lida com diferentes tarefas. Algumas funções são mais eficazes nas fases iniciais do aprendizado, fornecendo sinais claros e compreensíveis. Outras permitem que a rede capte padrões mais sutis em estágios avançados. E há aquelas que eliminam tudo o que é desnecessário, preservando apenas o essencial.

Se não conhecermos as propriedades das funções de ativação, podemos nos deparar com problemas. A rede neural pode começar a "tropeçar" em tarefas simples ou "ignorar" detalhes importantes. A principal tarefa das funções de ativação é introduzir não linearidade na rede neural e normalizar os valores de saída.

O objetivo deste artigo é identificar os problemas associados ao uso de diferentes funções de ativação e seu impacto na precisão com que a rede neural atravessa os pontos dos exemplos (interpolação) durante a minimização do erro. Também vamos investigar se as funções de ativação realmente influenciam a velocidade de convergência ou se isso é uma característica do algoritmo de otimização utilizado. Como referência, aplicaremos o ADAMm populacional modificado, que utiliza elementos de estocasticidade, e realizaremos testes com o ADAM incorporado no MLP (uso clássico). Este último, intuitivamente, deveria ter vantagem, pois tem acesso direto ao gradiente da superfície da função de fitness graças à derivada da função de ativação. Já o ADAMm populacional estocástico não tem acesso à derivada e não tem nenhuma noção da superfície do problema de otimização. Vamos observar o que resulta disso e tirar conclusões.

Este artigo tem caráter investigativo e a narrativa segue a ordem de realização do experimento.

Implementação de rede neural MLP com ADAM incorporado

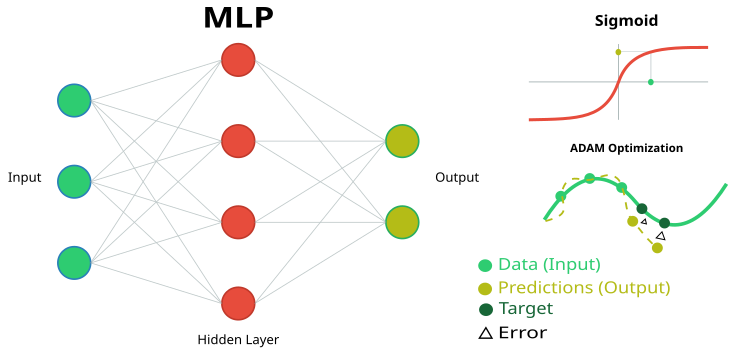
Figura 1. Esquema da rede neural MLP e seu treinamento

Para realizar esta pesquisa, precisamos de um código simples e transparente de uma rede neural MLP, sem utilizar cálculos matriciais especializados e integrados à linguagem MQL5. Isso nos permitirá entender claramente o que está acontecendo na lógica da rede neural e também compreender de que dependem determinados resultados.

Vamos implementar um perceptron multicamadas (MLP) com o algoritmo de otimização ADAM (Estimativa de Momento Adaptativo) incorporado. A classe e sua estrutura representam parte da implementação da rede neural, na qual são definidos os principais componentes: neurônios, camadas de neurônios e pesos.

1. A classe "C_Neuro" representa um neurônio, que é a unidade básica da rede neural.

• C_Neuron() — construtor, inicializa os valores das propriedades "m" e "v" com zeros. Esses valores são usados pelo algoritmo de otimização.
• out — valor de saída do neurônio após a aplicação da função de ativação.
• delta — delta do erro, usada para calcular o gradiente durante o aprendizado.
• bias — valor de viés, adicionado às entradas do neurônio.
• m e v — usados para armazenar o primeiro e o segundo momentos do viés, utilizados pelo método de otimização ADAM.

2. A estrutura "S_NeuronLayer" representa uma camada de neurônios. "C_Neuron n []" — vetor de neurônios na camada da rede neural.

Para armazenar os pesos entre os neurônios, utilizamos uma abordagem orientada a objetos em vez de simples matrizes bidimensionais. A base é a classe "C_Weight", que armazena não apenas o valor do peso da conexão, mas também os parâmetros para otimização — o primeiro e o segundo momentos, usados no algoritmo ADAM. A estrutura de dados é organizada de forma hierárquica: "S_WeightsLayer" contém um vetor de estruturas "S_WeightsLayerR", que por sua vez contêm vetores de objetos "C_Weight". Isso permite acessar facilmente qualquer peso da rede por meio de uma cadeia clara de índices.

Por exemplo, para acessar o peso da conexão entre o primeiro neurônio da camada zero e o segundo neurônio da próxima camada, usamos a seguinte notação: wL [0].nOnL [1].nOnR [2].w. Aqui, o primeiro índice indica o par de camadas vizinhas; o segundo, o neurônio na camada da esquerda; o terceiro, o neurônio na camada da direita.

//——————————————————————————————————————————————————————————————————————————————
// Класс нейрона
class C_Neuron
{
  public:
  C_Neuron ()
  {
    m = 0.0;
    v = 0.0;
  }
  double out;   // Выход нейрона после функции активации
  double delta; // Дельта ошибки
  double bias;  // Смещение
  double m;     // Первый момент смещения
  double v;     // Второй момент смещения
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Структура слоя нейронов
struct S_NeuronLayer
{
    C_Neuron n []; // нейроны в слое
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Класс веса
class C_Weight
{
  public:
  C_Weight ()
  {
    w = 0.0;
    m = 0.0;
    v = 0.0;
  }

  double w; // Вес
  double m; // Первый момент
  double v; // Второй момент
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов справа
struct S_WeightsLayerR
{
    C_Weight nOnR [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов слева
struct S_WeightsLayer
{
    S_WeightsLayerR nOnL [];
};
//——————————————————————————————————————————————————————————————————————————————

A classe "C_MLPa" do perceptron multicamadas (MLP) implementa as principais funcionalidades da rede neural, incluindo a propagação para frente e o treinamento por meio da propagação reversa do erro utilizando o algoritmo de otimização ADAM. Vamos entender o que ela é capaz de fazer:

Estrutura da rede:

• A rede é composta por camadas sequenciais: camada de entrada -> camadas ocultas -> camada de saída.
• Cada neurônio em uma camada está conectado a todos os neurônios da camada seguinte (rede totalmente conectada).

Funcionalidades principais:

• Init — método que cria a rede com a configuração especificada.
• ImportWeights e ExportWeights — carregamento e salvamento dos pesos da rede.
• ForwProp — propagação para frente: obtém a resposta da rede para os dados de entrada.
• BackProp — treinamento da rede baseado na propagação reversa do erro.

Parâmetros de aprendizado (algoritmo ADAM):

• alpha (0.001) — define a velocidade de aprendizado da rede.
• beta1 (0.9) e beta2 (0.999) — parâmetros que ajudam a rede a aprender de forma estável.
• epsilon (1e-8) — número pequeno para evitar divisão por zero.

Componentes internos:

• BackProp — armazena as informações sobre o tamanho de cada camada (layersSize).
• Contém todos os neurônios (nL) e os pesos entre eles (wL).
• Faz a contagem da quantidade de pesos (wC) e do número de camadas (nLC).
• actFunc — utiliza a função de ativação escolhida.
  

Em essência, essa classe é o "cérebro" da rede neural, que sabe receber dados de entrada, processá-los através do sistema de neurônios e pesos, fornecer o resultado e aprender com seus erros, melhorando gradualmente a precisão de suas previsões.

//+----------------------------------------------------------------------------+
//| Класс многослойного персептрона (MLP)                                      |
//| Реализует прямой проход по полносвязной нейронной сети и обучение методом  |
//| обратного распространения ошибки алгоритмом оптимизации ADAM               |
//| Архитектура: Lin -> L1 -> L2 -> ... Ln -> Lout                             |
//+----------------------------------------------------------------------------+
class C_MLPa
{
  public: //--------------------------------------------------------------------
  ~C_MLPa ()
  {
    delete actFunc;
  }
  C_MLPa ()
  {
    alpha   = 0.001;   // Скорость обучения
    beta1   = 0.9;     // Коэффициент затухания для первого момента
    beta2   = 0.999;   // Коэффициент затухания для второго момента
    epsilon = 1e-8;    // Малая константа для численной стабильности
  }

  // Инициализация сети с заданной конфигурацией, Возвращает общее количество весов в сети или 0 в случае ошибки
  int    Init          (int &layerConfig [], int actFuncType, int seed);
  bool   ImportWeights (double &weights []);  // Импорт весов
  bool   ExportWeights (double &weights []);  // Экспорт весов

  // Прямой проход по сети
  void   ForwProp (double &inLayer  [],  // входные значения
                   double &outLayer []); // значения выходного слоя

  // Обратное распространение ошибки с оптимизацией алгоритмом ADAM
  void   BackProp (double &errors []);

  // Получить общее количество весов в сети
  int    GetWcount () { return wC; }

  // Параметры оптимизации ADAM
  double alpha;          // Скорость обучения
  double beta1;          // Коэффициент затухания для первого момента
  double beta2;          // Коэффициент затухания для второго момента
  double epsilon;        // Малая константа для численной стабильности

  int layersSize    [];  // Размер каждого слоя (количество нейронов)
  S_NeuronLayer  nL [];  // Слои нейронов,                    пример обращения: nLayers [].n [].a
  S_WeightsLayer wL [];  // Слои весов между слоями нейронов, пример обращения: wLayers [].nOnLeft [].nOnRight [].w

  private: //-------------------------------------------------------------------
  int            wC;       // Общее количество весов в сети (включая смещения)
  int            nLC;      // Общее количество слоев нейронов (включая входной и выходной)
  int            wLC;      // Общее количество слоев весов (между слоями нейронов)
  int            t;        // Счетчик итераций
  C_Base_ActFunc *actFunc; // Функции активации и их производные
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" inicializa a estrutura do perceptron multicamadas, definindo a quantidade de neurônios em cada camada, escolhendo a função de ativação e gerando os pesos iniciais para os neurônios. Ele verifica se a configuração da rede está correta e retorna a quantidade total de pesos necessários ou 0 em caso de erro.

Parâmetros:

• layerConfig [] — vetor que contém a quantidade de neurônios em cada camada da rede.
• actFuncType — tipo da função de ativação que será usada na rede neural (por exemplo, sigmoide etc.).
• seed — semente para inicializar o gerador de números aleatórios, permitindo resultados reproduzíveis na inicialização dos pesos.

Lógica de funcionamento:

1. O método determina a quantidade de camadas com base no vetor passado "layerConfig".
2. Verifica se o número de camadas é pelo menos 2 e se cada camada contém uma quantidade positiva de neurônios. Em caso de erro, exibe uma mensagem e interrompe a execução.
3. Copia os tamanhos das camadas para o vetor "layersSize" e inicializa os vetores para armazenar os neurônios e os pesos.
4. Calcula o total de pesos necessários para conectar os neurônios entre as camadas.
5. Inicializa os pesos utilizando o método de Xavier, o que, teoricamente, ajuda a evitar problemas de desaparecimento ou explosão dos gradientes.
6. Com base no tipo de função de ativação fornecido, cria o objeto correspondente da função de ativação.
7. Inicializa o contador de iterações com zero, usado no algoritmo ADAM.
   

//+----------------------------------------------------------------------------+
//| Инициализация сети                                                         |
//| layerConfig - массив с количеством нейронов в каждом слое                  |
//| Возвращает общее количество необходимых весов или 0 при ошибке             |
//+----------------------------------------------------------------------------+
int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed)
{
  nLC = ArraySize (layerConfig);

  if (nLC < 2)
  {
    Print ("Ошибка конфигурации сети! Меньше 2 слоев!");
    return 0;
  }

  // Проверка конфигурации
  for (int i = 0; i < nLC; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Ошибка конфигурации сети! Слой №" + string (i + 1) + " содержит 0 нейронов!");
      return 0;
    }
  }

  wLC = nLC - 1;
  ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY);

  // Инициализация слоев нейронов
  ArrayResize (nL, nLC);
  for (int i = 0; i < nLC; i++)
  {
    ArrayResize (nL [i].n, layersSize [i]);
  }

  // Инициализация слоев весов
  ArrayResize (wL, wLC);
  for (int w = 0; w < wLC; w++)
  {
    ArrayResize (wL [w].nOnL, layersSize [w]);
    for (int n = 0; n < layersSize [w]; n++)
    {
      ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]);
    }
  }

  // Подсчет общего количества весов
  wC = 0;
  for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1];

  // Инициализация весов
  double weights [];  ArrayResize (weights, wC);

  srand (seed);
  
  //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂)))
  double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1]));
  for (int i = 0; i < wC; i++)
  {
    weights [i] = (2.0 * n) * (rand () / 32767.0) - n;
  }

  ImportWeights (weights);

  switch (actFuncType)
  {
    case eActACON:      actFunc = new C_ActACON      (); break;
    case eActAlgSigm:   actFunc = new C_ActAlgSigm   (); break;
    case eActBentIdent: actFunc = new C_ActBentIdent (); break;
    case eActRatSigm:   actFunc = new C_ActRatSigm   (); break;
    case eActSiLU:      actFunc = new C_ActSiLU      (); break;
    case eActSoftPlus:  actFunc = new C_ActSoftPlus  (); break;
    default:            actFunc = new C_ActTanh      (); break;
  }

  t = 0;
  return wC;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos agora analisar dois métodos: "ImportWeights" e "ExportWeights". Esses métodos servem para importar e exportar os pesos e viéses do perceptron multicamadas. "ImportWeights" é responsável por importar os pesos e viéses do vetor "weights" para a estrutura da rede neural.

Primeiramente, o método verifica se o tamanho do vetor "weights" passado é igual ao número de pesos armazenado na variável "wC". Se os tamanhos forem diferentes, o método retorna "false", indicando erro.

A variável "wCNT" é usada para rastrear o índice atual no vetor "weights".
Laços sobre camadas e neurônios:

• O laço externo percorre cada camada, a partir da segunda (índice 1), pois a primeira camada é a camada de entrada e não possui nem pesos nem viéses.
• O laço interno percorre cada neurônio na camada atual.
• Para cada neurônio, é atribuído o valor de viés "bias" a partir do vetor "weights", e o contador "wCNT" é incrementado.
• O laço aninhado percorre todos os neurônios da camada anterior, definindo os pesos que conectam os neurônios da camada atual aos neurônios da camada anterior.

"ExportWeights" — método responsável por exportar os pesos e viéses da estrutura da rede neural para o vetor "weights". A lógica do método é semelhante à do método "ImportWeights". Ambos os métodos permitem salvar os pesos e viéses externamente em relação à classe da rede, usar a rede treinada futuramente e também permitem empregar algoritmos de otimização externos, como os populacionais.

//+----------------------------------------------------------------------------+
//| Импорт весов и смещений сети                                               |
//+----------------------------------------------------------------------------+
bool C_MLPa::ImportWeights (double &weights [])
{
  if (ArraySize (weights) != wC) return false;

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      nL [ln].n [n].bias = weights [wCNT++];

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++];
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

//+----------------------------------------------------------------------------+
//| Экспорт весов и смещений сети                                              |
//+----------------------------------------------------------------------------+
bool C_MLPa::ExportWeights (double &weights [])
{
  ArrayResize (weights, wC);

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      weights [wCNT++] = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w;
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "ForwProp" (propagação para frente) executa o cálculo sequencial dos valores de todos os layers do perceptron multicamadas, indo da camada de entrada até a de saída. Ele recebe os valores de entrada, os processa através das camadas ocultas e gera os valores de saída. Parâmetros:

• inLayer [] — vetor de valores de entrada para a rede neural (na figura 1 em verde).
• outLayer [] — vetor no qual serão armazenados os valores da camada de saída após o processamento (na figura 1 em amarelo).
  

O método inicializa os valores de ativação dos neurônios da camada de entrada, copiando os dados do vetor "inLayer" para os respectivos neurônios.

Processamento das camadas ocultas e de saída:

• O laço externo percorre todas as camadas, começando da segunda (índice 1), pois a primeira é a camada de entrada.
• O laço interno percorre cada neurônio da camada atual.
• Para cada neurônio, é calculada a soma ponderada das entradas:
• Inicia-se somando o valor de viés (bias) do neurônio.
• O laço aninhado percorre todos os neurônios da camada anterior, somando a "val" o produto entre o valor de saída do neurônio anterior e o peso correspondente.
• Após calcular a soma, aplica-se a função de ativação ao valor "val", e o resultado é armazenado como valor de saída do neurônio da camada atual.

Depois de processar todas as camadas, o método copia os valores de saída da última camada (camada de saída) para o vetor "outLayer".

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

O método "BackProp" implementa a propagação reversa do erro no perceptron multicamadas. Ele atualiza os pesos e viéses de todas as camadas, do final para o início, utilizando o algoritmo de otimização ADAM. Lógica de funcionamento:

A variável "t" é incrementada em uma unidade para acompanhar o número de iterações e é usada na fórmula da lógica do ADAM.

Cálculo das deltas para todas as camadas:

• O laço externo percorre as camadas em ordem reversa, começando da camada de saída até a de entrada.
• O laço interno percorre os neurônios da camada atual.
• Se a camada atual for a de saída, a delta (delta) é calculada como o produto do erro (errors [nCurr]) pela derivada da função de ativação aplicada ao neurônio de saída.
• Para as camadas ocultas, a delta é calculada como a soma dos produtos das deltas da próxima camada pelos pesos correspondentes.
• Depois disso, a delta é ajustada levando em conta a derivada da função de ativação, e o resultado é armazenado em nL [ln].n [nCurr].delta.

Atualização dos viéses com uso do ADAM:

• O laço externo percorre todas as camadas, a partir da segunda.
• Para cada neurônio da camada atual, os momentos do viés "m" e "v" são atualizados com os parâmetros "beta1" e "beta2".
• Em seguida, realiza-se a correção dos momentos do viés "m_hat" e "v_hat".
• Por fim, o viés é atualizado utilizando os momentos corrigidos.

Atualização dos pesos com uso do ADAM:

• O laço externo percorre todas as camadas de pesos.
• Os laços internos percorrem os neurônios da camada atual e da próxima camada.
• Para cada peso, calcula-se o gradiente, que então é usado para atualizar os momentos "m" e "v".
• Depois da correção dos momentos dos pesos "m_hat" e "v_hat", os pesos são atualizados com base nos momentos corrigidos.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Código de bancada para desenhar funções de ativação

A bancada serve para testar a correta operação de diferentes funções de ativação utilizadas em redes neurais, além de permitir exibi-las graficamente. As imagens geradas são utilizadas mais adiante no artigo para avaliação visual do seu formato. O código é bastante simples, não sendo necessário descrevê-lo em detalhes.

#include <Graphics\Graphic.mqh>
#include <Math\AOs\NeuroNets\MLPa.mqh>

#define SIZE_X 750
#define SIZE_Y 200

//--- input parameters
input E_Act ACT = eActTanh;
input int   CNT = 10000;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  ObjectDelete (ChartID (), "Test");
  double activ [];
  double deriv [];

  //----------------------------------------------------------------------------
  C_Base_ActFunc *act;
  switch (ACT)
  {
    default:            act = new C_ActTanh      (); break;
    case eActAlgSigm:   act = new C_ActAlgSigm   (); break;
    case eActRatSigm:   act = new C_ActRatSigm   (); break;
    
    case eActSoftPlus:  act = new C_ActSoftPlus  (); break;
    case eActBentIdent: act = new C_ActBentIdent (); break;
    case eActSiLU:      act = new C_ActSiLU      (); break;
    
    case eActACON:      act = new C_ActACON      (); break;
    case eActSnake:     act = new C_ActSnake     (); break;
    case eActSERF:      act = new C_ActSERF      (); break;
  }
  
  //----------------------------------------------------------------------------
  ActFuncTest (act, activ, deriv, CNT, -10, 10);
  
  //----------------------------------------------------------------------------
  CGraphic gr_test;
  gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20);
  gr_test.YAxis ().Name (act.GetFuncName () + ": Value");
  gr_test.YAxis ().NameSize (13);
  gr_test.HistorySymbolSize (10);
  gr_test.CurveAdd (activ, ColorToARGB (clrRed,  255), CURVE_LINES, "activ");
  gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv");
  gr_test.CurvePlotAll ();
  gr_test.Redraw (true);
  gr_test.Update ();
  
  //----------------------------------------------------------------------------
  delete act;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max)
{
  Print (act.GetFuncName (), " [", min, "; ", max, "]");
  Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max));
  Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max));

  ArrayResize (arrayAct, testCount);
  ArrayResize (arrayDer, testCount);
  double x    = 0.0;
  double step = (max - min) / testCount;
  
  for (int i = 0; i < testCount; i++)
  {
    x = min + step * i;

    arrayAct [i] = act.Activ (x);
    arrayDer [i] = act.Deriv (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Código das classes de funções de ativação

Há diversas funções de ativação de neurônios aplicadas em diferentes tarefas com redes neurais. Procurei selecionar funções que incluíssem tanto o bem conhecido tangente hiperbólico quanto funções menos populares, como a função de ativação Snake, excluindo da análise funções muito semelhantes em aparência e comportamento. Podemos dividi-las, de forma geral, em três grupos:

1. Funções sigmoides,
2. Interruptores não lineares,
3. Funções de tipo periódico.

Vamos implementar a classe base "C_Base_ActFunc" para funções de ativação de neurônios. Ela contém duas funções virtuais: "Activ", que calcula a ativação, e "Deriv", que calcula a derivada. O método "GetFuncName()" retorna o nome da função de ativação, armazenado na célula protegida "funcName". A classe é projetada para ser herdada por outras, a fim de criar implementações específicas de funções de ativação. Com um objeto de função de ativação, conseguimos acelerar os cálculos ao evitar o uso repetido de "if" e "switch".

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  virtual double Activ (double inp) = 0; // Виртуальная функция активации
  virtual double Deriv (double inp) = 0; // Виртуальная функция производной
  string         GetFuncName () {return funcName;}
  protected:
  string funcName;
};
//——————————————————————————————————————————————————————————————————————————————

A classe "C_ActTanh" implementa a função de ativação do tangente hiperbólico e sua derivada, herdando da classe base "C_Base_ActFunc". No construtor da classe, o nome da função de ativação é definido na variável "funcName" como "ActTanh". O método de ativação:

• Activ (double x) calcula o valor da função de ativação do tangente hiperbólico pela fórmula: f(x) = 2 / (1 + exp(−2 ⋅ x)) − 1. Essa fórmula transforma o valor de entrada "x" no intervalo de -1 a 1.

O método da derivada:

• Deriv(double x) calcula a derivada da função de ativação. A derivada do tangente hiperbólico é expressa como: f′(x) = 1 − (f(x))², onde f(x) é o valor da função de ativação calculado para o "x" atual. A derivada mostra quão rapidamente a função muda em relação ao valor de entrada.

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh () {funcName = "ActTanh";}

  double Activ (double x)
  {
    return 2.0 / (1.0 + exp (-2 * (x))) - 1.0;
  }

  double Deriv (double x)
  {
    //1 - (f(x))^2
    double fx = Activ (x);
    return 1.0 - fx * fx;
  }
};
//——————————————————————————————————————————————————————————————————————————————

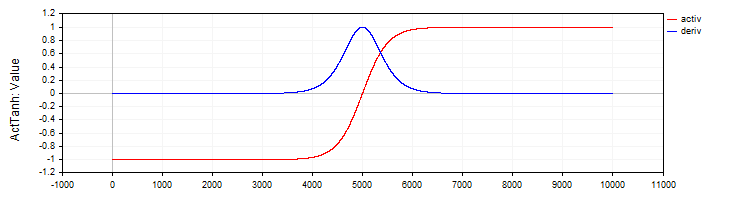
Figura 2. Tangente hiperbólico e sua derivada

A classe "C_ActAlgSigm", de forma semelhante à classe "C_ActTanh", implementa a sigmoide algébrica como função de ativação, com métodos para cálculo da ativação e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// Алгебраическая сигмоида
class C_ActAlgSigm : public C_Base_ActFunc
{
  public:
  C_ActAlgSigm () {funcName = "ActAlgSigm";}

  double Activ (double x)
  {
    return x / sqrt (1.0 + x * x);
  }

  double Deriv (double x)
  {
    // (1 / sqrt (1 + x * x))^3
    double d = 1.0 / sqrt (1.0 + x * x);
    return d * d * d;
  }
};
//——————————————————————————————————————————————————————————————————————————————

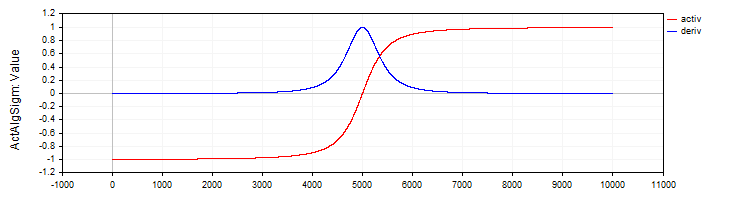
Figura 3. Sigmoide algébrica e sua derivada

A classe "C_ActRatSigm" implementa a sigmoide racional com métodos de ativação e derivada.

//——————————————————————————————————————————————————————————————————————————————
// Рациональная сигмоида
class C_ActRatSigm : public C_Base_ActFunc
{
  public:
  C_ActRatSigm () {funcName = "ActRatSigm";}

  double Activ (double x)
  {
    return x / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    //1 / (1 + abs (x))^2
    double d = 1.0 + fabs (x);
    return 1.0 / (d * d);
  }
};
//——————————————————————————————————————————————————————————————————————————————

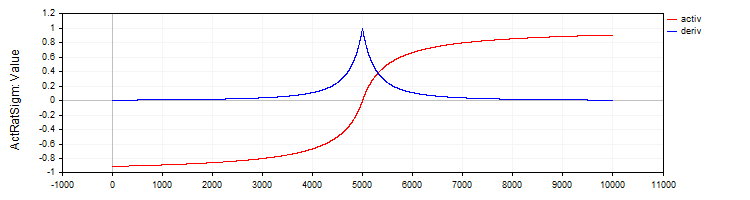
Figura 4. Sigmoide racional e sua derivada

A classe "C_ActSoftPlus" implementa a função de ativação "Softplus" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// Softplus
class C_ActSoftPlus : public C_Base_ActFunc
{
  public:
  C_ActSoftPlus () {funcName = "ActSoftPlus";}

  double Activ (double x)
  {
    return log (1.0 + exp (x));
  }

  double Deriv (double x)
  {
    return 1.0 / (1.0 + exp (-x));
  }
};
//——————————————————————————————————————————————————————————————————————————————

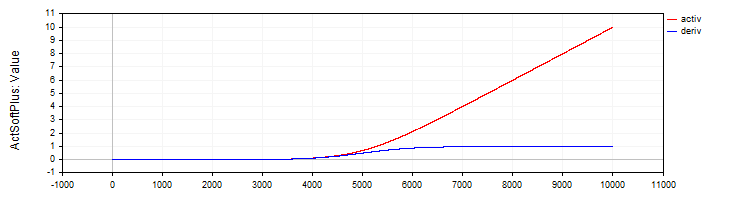
Figura 5. Função "Softplus" e sua derivada

A classe "C_ActBentIdent" implementa a função de ativação "Bent Identity" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// Bent Identity
class C_ActBentIdent : public C_Base_ActFunc
{
  public:
  C_ActBentIdent () {funcName = "ActBentIdent";}

  double Activ (double x)
  {
    return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x;
  }

  double Deriv (double x)
  {
    return x / (2.0 * sqrt (x * x + 1.0)) + 1.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

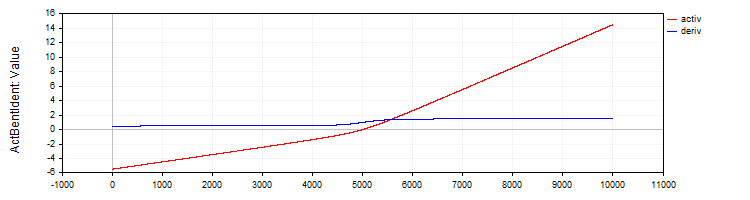
Figura 6. Função "Bent Identity" e sua derivada

A classe "C_ActSiLU" fornece a implementação da função de ativação "SiLU" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// SiLU (Swish)
class C_ActSiLU : public C_Base_ActFunc
{
  public:
  C_ActSiLU () {funcName = "ActSiLU";}

  double Activ (double x)
  {
    return x / (1.0 + exp (-x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 0.5;

    // f(x) + (f(x)*(1 - f(x)))/ x
    double fx = Activ (x);
    return fx + (fx * (1.0 - fx)) / x;
  }
};
//——————————————————————————————————————————————————————————————————————————————

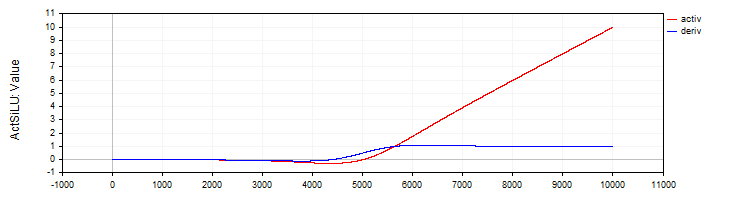
Figura 7. Função "SiLU" e sua derivada

A classe "C_ActACON" implementa a função de ativação "ACON" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// ACON
class C_ActACON : public C_Base_ActFunc
{
  public:
  C_ActACON () {funcName = "ActACON";}

  double Activ (double x)
  {
    return (x * cos (x) + sin (x)) / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 2.0;

    //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)]
    double sinX   = sin  (x);
    double cosX   = cos  (x);
    double fabsX  = fabs (x);
    double fabsXp = fabsX + 1.0;

    // Разделяем формулу на две части
    double part1 = (2.0 * cosX - x * sinX) / fabsXp;
    double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp);
    return part1 + part2;
  }
};
//——————————————————————————————————————————————————————————————————————————————

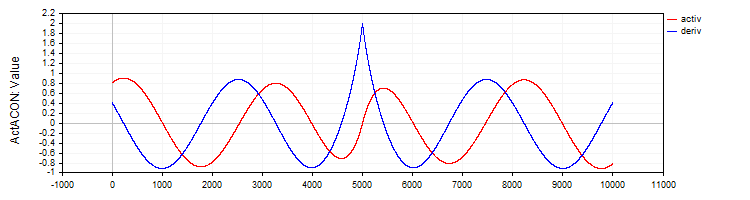
Figura 8. Função "ACON" e sua derivada

A classe "C_ActSERF" implementa a função de ativação "SERF" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// SERF (Функция сигмоидально-взвешенного экспоненциального выпрямления)
class C_ActSERF : public C_Base_ActFunc
{
  public:
  C_ActSERF ()
  {
    alpha    = 0.5;
    funcName = "ActSERF";
  }

  double Activ (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));

    if (x >= 0) return sigmoid * x;
    else return sigmoid * (exp (x) - 1.0);
  }

  double Deriv (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));
    double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid);
    double e = exp (x);
    if (x >= 0) return sigmoid + x * sigmoidDeriv;
    else return sigmoid * e + (e - 1.0) * sigmoidDeriv;
  }

  private:
  double alpha;
};
//——————————————————————————————————————————————————————————————————————————————

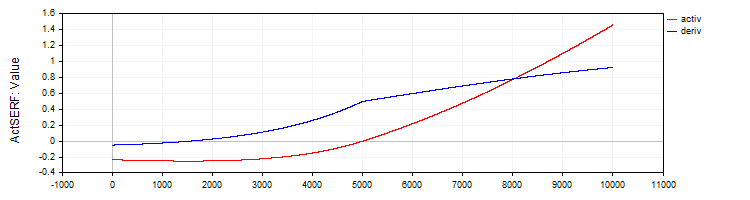
Figura 9. Função "SERF" e sua derivada

A classe "C_ActSNAKE" implementa a função de ativação "SNAKE" e sua derivada.

//——————————————————————————————————————————————————————————————————————————————
// Snake (Периодическая активационная функция)
class C_ActSnake : public C_Base_ActFunc
{
  public:
  C_ActSnake ()
  {
    frequency = 1;
    funcName  = "ActSnake";
  }

  double Activ (double x)
  {
    double sinx = sin (frequency * x);
    return x + sinx * sinx;
  }

  double Deriv (double x)
  {
    double fx = frequency * x;
    return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency;
  }

  private:
  double frequency;
};
//——————————————————————————————————————————————————————————————————————————————

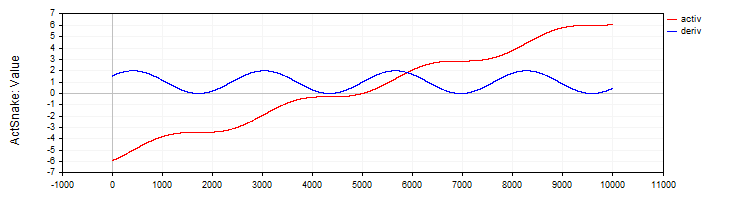
Figura 10. Função "SNAKE" e sua derivada

Teste das funções de ativação

Agora chegou o momento de analisar como ocorre o treinamento da rede MLP com diferentes funções de ativação. A complexidade que a função de ativação impõe ao algoritmo de otimização pode ser claramente ilustrada com a configuração MLP 1-1-1, utilizando apenas um exemplo de treinamento (um valor de entrada e um valor-alvo).

À primeira vista, isso pode parecer contraintuitivo: por que uma tarefa tão simples seria interessante? A resposta está em um ponto metodológico importante: o uso de um único ponto de dado permite isolar e investigar exclusivamente a complexidade da função de ativação e seu impacto no processo de otimização. Quando usamos um grande conjunto de dados, o processo de aprendizado é influenciado por muitos fatores: a distribuição dos dados, as interdependências entre os exemplos e o modo como esses fatores se manifestam ao passar pela função de ativação. Ao utilizar apenas um ponto, eliminamos todos esses fatores externos e podemos focar exclusivamente em quão difícil é para o algoritmo de otimização lidar com determinada função de ativação.

A questão é que uma rede neural passando por um único ponto de uma função interpolada pode ter infinitas combinações de pesos. Isso pode parecer inacreditável, mas é o que resulta da equação "in * w + b = out", onde in é a entrada da rede, w é o peso, b é o viés e out é a saída da rede para a configuração 1-1.

Não há problemas com essa configuração inicial, porém eles surgem ao se adicionar mais uma camada, ou seja, na configuração 1-1-1. Nesse caso, mesmo a tarefa mais simples se torna não trivial para o algoritmo de otimização, pois o espaço de busca da solução se torna significativamente mais complexo: agora é necessário encontrar a combinação correta de pesos através de uma camada intermediária com sua função de ativação. É justamente essa complexidade que nos permite avaliar quão eficazes são os diferentes algoritmos de otimização na tarefa de ajustar os pesos ao trabalhar com várias funções de ativação.

Abaixo estão apresentadas tabelas com os resultados obtidos pelos algoritmos ADAM em sua implementação clássica e pelo ADAMm populacional. Para ambos os algoritmos, foram realizadas 10.000 iterações, sendo que, no caso do algoritmo populacional, foi considerada a presença da população, mas o número total de cálculos da rede neural permaneceu o mesmo. As impressões indicam a semente do gerador de números pseudorrandômicos (para permitir a reprodução de execuções problemáticas do aprendizado), a iteração na qual foi obtido o melhor resultado e o resultado da época atual, em múltiplos de 1000.

A inicialização dos pesos foi feita com números aleatórios pelo método de Xavier para o ADAM, e com números aleatórios no intervalo [-10; 10] para o ADAMm. Foram realizados vários testes com sementes diferentes, e os piores resultados foram selecionados. O processo de ajuste dos pesos era encerrado ao atingir o número máximo de iterações ou ao reduzir o erro abaixo de 0.000001.

Tabela de resultados para funções de ativação sigmoides:

Tanh	AlgSigm	RatSigm
MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 4 -----Integrated ADAM----- 0: 0.1878131682539310, 0: 0.18781316825393096 0: 0.1878131682539310, 1000: 0.22880505258129305 0: 0.1878131682539310, 2000: 0.2395439537933131 0: 0.1878131682539310, 3000: 0.24376284285887292 0: 0.1878131682539310, 4000: 0.24584964230029535 0: 0.1878131682539310, 5000: 0.2470364071634453 0: 0.1878131682539310, 6000: 0.24777681648987268 0: 0.1878131682539310, 7000: 0.2482702131676117 0: 0.1878131682539310, 8000: 0.24861563983949608 0: 0.1878131682539310, 9000: 0.2488669473265396 Best result iteration: 0, Err: 0.187813 -----Population-based ADAMm----- 0: 0.2481251241755712 1000: 0.0000009070157679 Best result iteration: 1000, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 4 -----Integrated ADAM----- 0: 0.0354471509280691, 0: 0.03544715092806905 0: 0.0354471509280691, 1000: 0.10064226929576263 0: 0.0354471509280691, 2000: 0.13866170841306655 0: 0.0354471509280691, 3000: 0.16067944018111643 0: 0.0354471509280691, 4000: 0.17502946224977484 0: 0.0354471509280691, 5000: 0.18520767592761297 0: 0.0354471509280691, 6000: 0.19285431843628092 0: 0.0354471509280691, 7000: 0.1988366186290051 0: 0.0354471509280691, 8000: 0.20365853142896836 0: 0.0354471509280691, 9000: 0.20763502064394074 Best result iteration: 0, Err: 0.035447 -----Population-based ADAMm----- 0: 0.1928944265733889 Best result iteration: 688, Err: 0.000000

Таблица результатов для функций активации типа SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 131.77685264891647 0: 0.5380138004155748, 2000: 1996.1250363225556 0: 0.5380138004155748, 3000: 8050.259717531171 0: 0.5380138004155748, 4000: 20321.169969814575 0: 0.5380138004155748, 5000: 40601.21872791767 0: 0.5380138004155748, 6000: 70655.44591598355 0: 0.5380138004155748, 7000: 112311.81150857621 0: 0.5380138004155748, 8000: 167489.98562842538 0: 0.5380138004155748, 9000: 238207.27978678182 Best result iteration: 0, Err: 0.538014 -----Population-based ADAMm----- 0: 18.4801637203493884 778: 0.0000022070092175 Best result iteration: 1176, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 185.646717568436 0: 15.1221330593320857, 2000: 1003.1026112225994 0: 15.1221330593320857, 3000: 2955.8393027057205 0: 15.1221330593320857, 4000: 6429.902382962495 0: 15.1221330593320857, 5000: 11774.781156010686 0: 15.1221330593320857, 6000: 19342.379583340015 0: 15.1221330593320857, 7000: 29501.355075464813 0: 15.1221330593320857, 8000: 42640.534930000824 0: 15.1221330593320857, 9000: 59168.850722337185 Best result iteration: 0, Err: 15.122133 -----Population-based ADAMm----- 0: 7818.0964949082390376 Best result iteration: 15, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 2 -----Integrated ADAM----- 0: 0.0021199944516222, 0: 0.0021199944516222444 0: 0.0021199944516222, 1000: 4.924850697388685 0: 0.0021199944516222, 2000: 14.827133542234415 0: 0.0021199944516222, 3000: 28.814259008218087 0: 0.0021199944516222, 4000: 45.93517121925276 0: 0.0021199944516222, 5000: 65.82077308420028 0: 0.0021199944516222, 6000: 88.26782602934948 0: 0.0021199944516222, 7000: 113.15535264604428 0: 0.0021199944516222, 8000: 140.41067538093935 0: 0.0021199944516222, 9000: 169.9878269747845 Best result iteration: 0, Err: 0.002120 -----Population-based ADAMm----- 0: 17.2288020548757288 1000: 0.0000030959186317 Best result iteration: 1150, Err: 0.000001

Таблица результатов для периодических функций активации:

ACON	SERF	Snake
MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 481, Err: 0.000000	MLP config: 1|1|1, Weights: 4, Activation func: eActSERF, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001

Agora já podemos tirar conclusões preliminares sobre a complexidade das funções de ativação para o ADAM clássico baseado em gradiente e o ADAMm populacional. Embora o ADAM tradicional possua acesso direto ao gradiente da função de ativação, ou seja, literalmente conhece a direção da descida mais rápida, ele não conseguiu resolver essa tarefa aparentemente simples. Pelos resultados, a função mais fácil para o ADAM foi a ACON — com ela ele conseguiu minimizar o erro de forma consistente. Já funções como a SiLU mostraram-se problemáticas: com elas o erro não só não diminuía, mas crescia rapidamente. É evidente que, como não foram impostas condições de limite para os pesos e viéses no ADAM, ao escolher a direção errada ele aumentava os valores dos pesos. Os pesos se espalhavam livremente em todas as direções, sem qualquer restrição, literalmente levados por um vento direcionado gerado pela derivada da função de ativação.

O problema só se agrava quando se utilizam mais neurônios nas camadas, pois cada neurônio recebe como entrada a soma dos produtos das saídas dos neurônios da camada anterior pelos pesos correspondentes. Assim, a soma pode se tornar tão grande que se torna impossível calcular corretamente a função exponencial.

Como podemos ver, para o ADAMm populacional, nenhuma das funções de ativação representa um problema. Ele converge de forma estável em todas elas, e apenas em alguns casos o número de iterações ultrapassou ligeiramente as 1000.

Aprimoramento das classes de funções de ativação, MLP e ADAM

Para corrigir o problema dos pesos se espalhando na rede neural, vamos fazer alterações nas classes das funções de ativação. Isso permitirá controlar os limites das funções correspondentes e evitar o acúmulo de somas excessivamente grandes ao serem alimentadas no neurônio, além de limitar os próprios valores dos pesos e viéses.

Adicionaremos ao classe base os métodos "GetBoundUp" e "GetBoundLo", que fornecem acesso aos limites superiores e inferiores das funções de ativação correspondentes, permitindo que outras classes ou funções obtenham informações sobre os valores permitidos.

Abaixo está o código da classe base e da classe do tangente hiperbólico com as modificações feitas (o restante do código permanece inalterado). As outras classes de funções de ativação foram implementadas da mesma forma, com seus próprios limites específicos.

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  double         GetBoundUp  () { return boundUp;}
  double         GetBoundLo  () { return boundLo;}
  protected:
  double boundUp;  // верхняя граница входного диапазона
  double boundLo;  // нижняя граница входного диапазона
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh ()
  {
    boundUp  =  6.0;
    boundLo  = -6.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Agora adicionaremos no código do método de propagação para frente da MLP uma verificação dos valores da soma antes de aplicá-la à função de ativação do neurônio, para garantir que ela não ultrapasse os limites definidos. Não faz sentido acumular somas acima desses limites, além de isso permitir a parada antecipada do cálculo da soma nas configurações de redes com muitos neurônios por camada, o que pode acelerar significativamente o processamento.

Verificação do limite superior: neste trecho do código, verifica-se se o valor atual da soma ultrapassa o limite superior definido. Se o valor for maior que esse limite, ele é ajustado para esse limite e a execução do laço é interrompida. Da mesma forma, a verificação do limite inferior é realizada.

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;

        if (val >  actFunc.GetBoundUp ())
        {
          val =  actFunc.GetBoundUp ();
          break;
        }
        if (val < actFunc.GetBoundLo ())
        {
          val = actFunc.GetBoundLo ();
          break;
        }
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

Agora adicionaremos o código de verificação dos limites no método de propagação reversa do erro. Nessa adição, é implementada a lógica de reflexão dos valores dos viéses e pesos a partir dos limites estabelecidos para o limite oposto. Isso é necessário para garantir que os valores não ultrapassem os intervalos permitidos, evitando aumentos ou reduções descontrolados dos pesos e viéses.

Simplesmente cortar os valores nos limites resultaria em estagnação do aprendizado, já que o peso ficaria preso na borda e a alteração deixaria de ser possível. Para evitar esse tipo de situação, foi implementada a reflexão e não o corte dos valores. Isso assegura uma "revitalização" ou uma espécie de "sacudida" durante o ajuste dos pesos e viéses.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя
  double bias;      // смещение

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
      bias = nL [ln].n [nCurr].bias;

      if (bias < actFunc.GetBoundLo ())
      {
        nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias);  // отражаем от нижней границы
      }
      else
        if (bias > actFunc.GetBoundUp ())
        {
          nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ());  // отражаем от верхней границы
        }
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
        w = wL [lw].nOnL [nCurr].nOnR [nNext].w;

        if (w < actFunc.GetBoundLo ())
        {
          wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w);  // отражаем от нижней границы
        }
        else
          if (w > actFunc.GetBoundUp ())
          {
            wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ());  // отражаем от верхней границы
          }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora vamos repetir os mesmos testes realizados anteriormente e observar os resultados obtidos. Desta vez, não há explosão de pesos nem crescimento descontrolado do erro ao longo do treinamento.

Tabela de resultados para funções de ativação sigmoides:

Tanh	AlgSigm	RatSigm
MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 2 -----Integrated ADAM----- 0: 0.0095411465043040, 0: 0.009541146504303972 0: 0.0095411465043040, 1000: 0.20977102640908893 0: 0.0095411465043040, 2000: 0.23464558094398064 0: 0.0095411465043040, 3000: 0.23657904914082925 0: 0.0095411465043040, 4000: 0.17812555648593617 0: 0.0095411465043040, 5000: 2.1749975763135927 0: 0.0095411465043040, 6000: 2.2093668968051166 0: 0.0095411465043040, 7000: 2.1657244506071813 0: 0.0095411465043040, 8000: 1.9330415523200173 0: 0.0095411465043040, 9000: 0.10441382194622865 Best result iteration: 0, Err: 0.009541 -----Population-based ADAMm----- 0: 0.2201830630768654 Best result iteration: 750, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 1 -----Integrated ADAM----- 0: 1.2866075458561122, 0: 1.2866075458561121 1000: 0.2796061866784148, 1000: 0.2796061866784148 2000: 0.0450819127087337, 2000: 0.04508191270873367 3000: 0.0200306843648248, 3000: 0.020030684364824806 4000: 0.0098744349153286, 4000: 0.009874434915328582 5000: 0.0049448920462547, 5000: 0.00494489204625467 6000: 0.0024344513388710, 6000: 0.00243445133887102 7000: 0.0011602603038120, 7000: 0.0011602603038120354 8000: 0.0005316894732581, 8000: 0.0005316894732581081 9000: 0.0002339388712666, 9000: 0.00023393887126662818 Best result iteration: 9999, Err: 0.000099 -----Population-based ADAMm----- 0: 1.8418367346938778 Best result iteration: 645, Err: 0.000000

Таблица результатов для функций активации типа SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 12.377378915308087 0: 0.5380138004155748, 2000: 12.377378915308087 3000: 0.1996421769021168, 3000: 0.19964217690211675 4000: 0.1985425345613517, 4000: 0.19854253456135168 5000: 0.1966512639256550, 5000: 0.19665126392565502 6000: 0.1933509943676914, 6000: 0.1933509943676914 7000: 0.1874142582090466, 7000: 0.18741425820904659 8000: 0.1762132792048514, 8000: 0.17621327920485136 9000: 0.1538331138702293, 9000: 0.15383311387022927 Best result iteration: 9999, Err: 0.109364 -----Population-based ADAMm----- 0: 12.3773789153080873 Best result iteration: 677, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 25.619316876852988 1922: 8.6344718719116980, 2000: 8.634471871911698 1922: 8.6344718719116980, 3000: 8.634471871911698 1922: 8.6344718719116980, 4000: 8.634471871911698 1922: 8.6344718719116980, 5000: 8.634471871911698 1922: 8.6344718719116980, 6000: 8.634471871911698 6652: 4.3033564303197833, 7000: 8.634471871911698 6652: 4.3033564303197833, 8000: 8.634471871911698 6652: 4.3033564303197833, 9000: 7.11489380279475 Best result iteration: 9999, Err: 3.589207 -----Population-based ADAMm----- 0: 25.6193168768529880 Best result iteration: 15, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 4 -----Integrated ADAM----- 0: 0.6585816582701970, 0: 0.658581658270197 0: 0.6585816582701970, 1000: 5.142928362480306 1393: 0.3271208998291733, 2000: 0.32712089982917325 1393: 0.3271208998291733, 3000: 0.32712089982917325 1393: 0.3271208998291733, 4000: 0.4029355474095988 5000: 0.0114993205601383, 5000: 0.011499320560138332 6000: 0.0003946998191595, 6000: 0.00039469981915948605 7000: 0.0000686308316624, 7000: 0.00006863083166239227 8000: 0.0000176901182322, 8000: 0.000017690118232197302 9000: 0.0000053723044223, 9000: 0.000005372304422295116 Best result iteration: 9999, Err: 0.000002 -----Population-based ADAMm----- 0: 19.9499415647445524 1000: 0.0000057228950379 Best result iteration: 1051, Err: 0.000000

Таблица результатов для периодических функций активации:

ACON	SERF	Snake
MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 300, Err: 0.000000	MLP config: 1|1|1, Weights: 4, Activation func: eActSERF, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001

Considerações finais

Vamos então resumir nossa pesquisa. Relembrando o objetivo do experimento: pegamos dois algoritmos de otimização baseados na mesma lógica, mas que operam de formas fundamentalmente diferentes. O primeiro (ADAM clássico) é um otimizador embutido, que atua de dentro da rede neural, com acesso direto às funções de ativação e à estrutura interna — como um navegador com um mapa detalhado do terreno. O segundo (ADAMm populacional) é um otimizador externo, que trabalha com a rede neural como uma "caixa-preta", sem qualquer informação sobre sua estrutura interna ou a natureza da tarefa — como um viajante que encontra o caminho guiando-se apenas pelas estrelas e pelo rumo geral.

Utilizamos a mesma rede neural para ambos os algoritmos como objeto de estudo. Isso é importante, pois nos permite localizar precisamente a origem de possíveis problemas: se surgirem dificuldades com determinadas funções de ativação, podemos afirmar com segurança que não se trata de uma limitação da rede em si, mas sim de como o algoritmo de otimização interage com essas funções.

Essa tipo de configuração experimental nos dá uma visão clara de como diferentes funções de ativação se comportam dentro de abordagens distintas de otimização. É importante destacar que não abordamos deliberadamente a capacidade de generalização da rede nem de sua atuação com dados novos. Nosso foco é estudar exclusivamente a interação entre funções de ativação e algoritmos de otimização, sua compatibilidade e a eficácia dessa interação.

Essa abordagem nos permite obter uma visão clara de como diferentes estratégias de otimização lidam com várias funções de ativação, sem interferência de fatores externos. E os resultados do experimento mostram claramente que, às vezes, um otimizador externo "cego" pode ser mais eficiente que um algoritmo que possui total conhecimento da estrutura da rede.

Em todas as funções de ativação, o ADAMm externo apresentou convergência rápida e estável, o que nos leva a concluir que as propriedades da função de ativação não têm peso significativo para ele. Por outro lado, o ADAM embutido clássico enfrentou sérios obstáculos.

Agora vamos analisar o comportamento do ADAM embutido com cada uma das funções de ativação e resumir nas seguintes conclusões:

1. Funções problemáticas (travam ou apresentam convergência lenta):

• TanH (tangente hiperbólico)
• AlgSigm (sigmoide algébrica)
• SERF (retificação exponencial ponderada sigmoidal)
• Snake (função periódica)

2. Casos de sucesso (convergência):

• RatSigm (sigmoide racional), a melhor entre as sigmoides
  
• SoftPlus
• BentIdent (identidade dobrada)
  
• SiLU (Swish), a melhor do segundo grupo
  
• ACON (função adaptativa), a melhor entre as periódicas
  

3. Padrões observados:

Funções sigmoides clássicas (TanH, AlgSigm) apresentaram problemas de estagnação. Já as funções adaptativas mais modernas (ACON, SiLU) demonstraram melhor convergência. Entre as funções periódicas, ACON convergiu bem, enquanto Snake travou.

Dessa forma, o estudo apresentado desenvolve uma abordagem abrangente para a otimização de redes neurais, combinando o controle dos pesos, os limites das funções de ativação e o processo de aprendizado em um sistema unificado e interligado. A principal inovação foi a introdução dos métodos GetBoundUp e GetBoundLo, que permitem a cada função de ativação definir seus próprios limites, os quais são usados para o controle dos pesos da rede. Esse mecanismo é complementado por um sistema de interrupção antecipada da soma ao atingir os limites, o que não só evita cálculos desnecessários, especialmente em redes grandes, mas também garante o controle dos valores antes da aplicação da função de ativação.

Um elemento particularmente importante foi o mecanismo de reflexão dos pesos que, ao contrário do corte ou normalização tradicional, previne a estagnação do aprendizado por meio de uma espécie de "sacudida" nos pesos ao atingirem os limites. Essa solução mantém a possibilidade de ajuste dos pesos mesmo em situações críticas, garantindo a continuidade do processo de aprendizado. A integração sistemática de todos esses componentes cria um mecanismo eficaz para evitar o espalhamento dos pesos sem comprometer a flexibilidade do aprendizado, o que é especialmente relevante ao lidar com diferentes funções de ativação. Essa abordagem abrangente não apenas resolve o problema do controle de pesos, como também abre novas perspectivas para a compreensão da interação entre os diversos componentes da rede neural durante o treinamento.

A pesquisa realizada não sugere que o ADAM seja inútil para o treinamento de redes neurais, mas sim chama atenção para sua sensibilidade a determinadas funções de ativação. É possível que, para redes neurais de grande porte, ele ainda não tenha alternativa (ou que suas versões modernas baseadas em métodos de descida do gradiente sejam indispensáveis). Esse pode ser o próximo tema a ser abordado: a eficácia do ADAM (como representante dos algoritmos modernos de otimização por propagação reversa) no contexto de redes neurais de larga escala, bem como o estudo do impacto da escolha das funções de ativação na capacidade de generalização da rede e na estabilidade do seu desempenho com novos dados.

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	C_AO.mqh	Arquivo incluído	Classe pai dos algoritmos de otimização populacionais
2	C_AO_enum.mqh	Arquivo incluído	Enumeração dos algoritmos de otimização populacionais
3	MLPa.mqh	Script	Rede neural MLP com ADAM
4	Tests and Drawing act func.mq5	Script	Script para visualização gráfica das funções de ativação
5	Test act func in training.mq5	Script	Script de treinamento do MLP com ADAM e ADAMm