Redes neurais em trading: Modelos com uso de transformação wavelet e atenção multitarefa

Introdução

Prever o retorno dos ativos é um tema amplamente estudado no setor financeiro. O desafio da previsão de retorno surge por diversas razões. Primeiro, os múltiplos fatores que influenciam os retornos dos ativos e a baixa relação sinal/ruído em matrizes esparsas de alta dimensão dificultam a extração de informações relevantes usando modelos econométricos tradicionais. Segundo, as relações funcionais entre características preditoras e os retornos dos ativos são pouco claras, o que dificulta a captura de estruturas não lineares entre eles.

Nos últimos anos, o aprendizado profundo se tornou uma ferramenta essencial em investimentos quantitativos, especialmente na melhoria de estratégias multifatoriais, que são a base para entender o movimento de preços dos ativos financeiros. Ao automatizar a extração de características e capturar relações não lineares nos dados do mercado financeiro, os algoritmos de aprendizado profundo identificam padrões complexos de forma eficaz, aumentando assim a precisão das previsões. A comunidade global de pesquisa reconhece o potencial das redes neurais profundas, como as redes neurais recorrentes (RNN) e as redes neurais convolucionais (CNN), para prever preços de ações e contratos futuros. No entanto, o uso de modelos de aprendizado profundo como RNN e CNN, embora amplamente difundido, raramente explora redes neurais mais profundas que extraem e estruturam informações relevantes e de mercado sobre sequências, o que indica espaço para avanços no uso do aprendizado profundo nos mercados de ações.

Hoje apresentamos o framework Multitask-Stockformer, descrito no artigo "Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks". Apesar da semelhança no nome com o framework anteriormente destrinchado StockFormer, os frameworks não têm relação entre si. Com exceção, claro, do objetivo: gerar uma carteira lucrativa de ações para atuar no mercado acionário.

O framework Multitask-Stockformer constrói um modelo de previsão de ações multitarefa baseado em transformação wavelet e modelos de Self-Attention.

Algoritmo Multitask-Stockformer

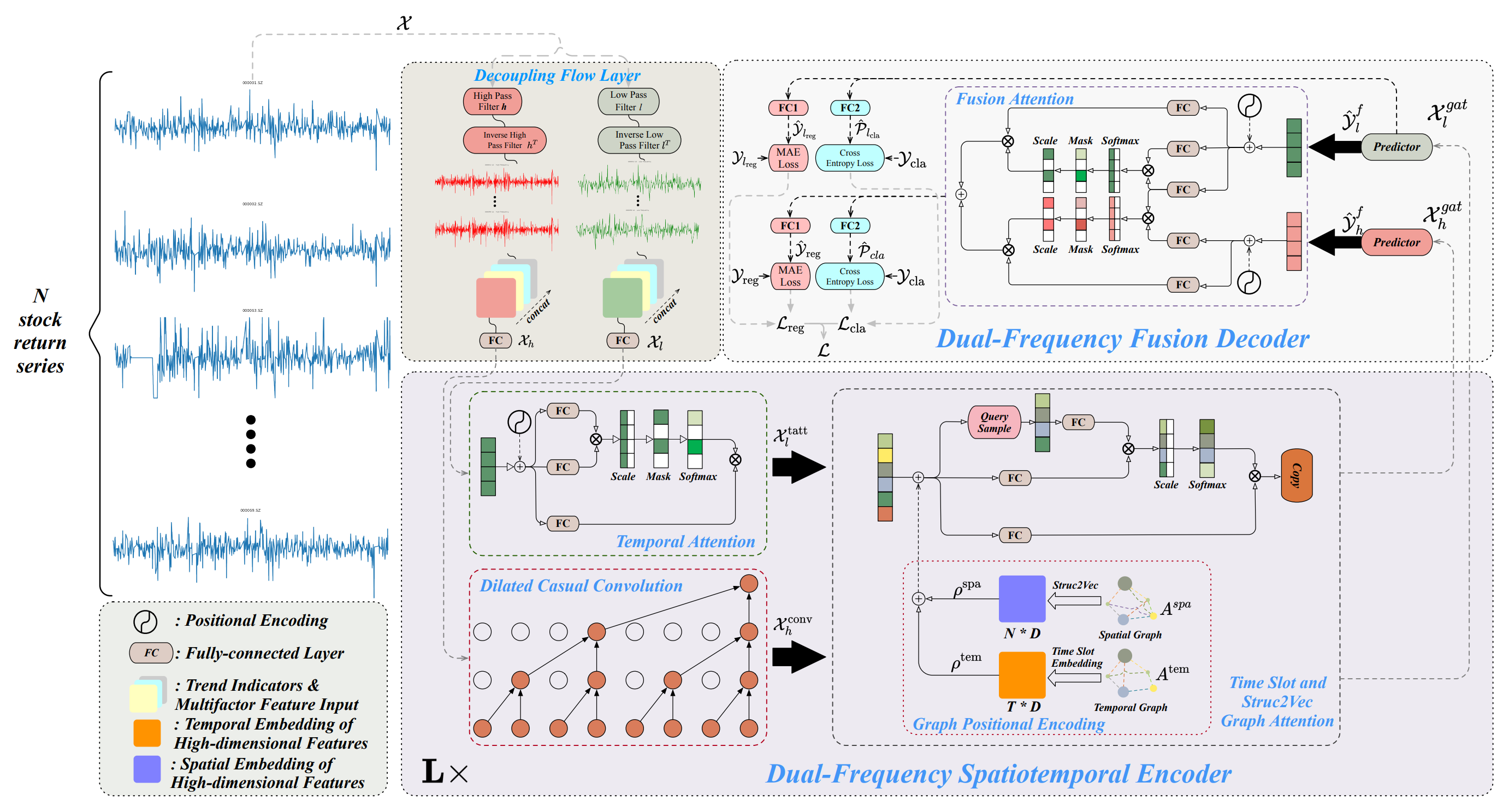
A arquitetura do framework Multitask-Stockformer é dividida em 3 blocos: módulo de divisão de fluxo, codificador espaço-temporal de dupla frequência e decodificador de dupla frequência. Os dados históricos analisados dos ativos 𝒳 ∈ RT1×N×362 são processados no módulo de divisão de fluxo. Neste estágio, o tensor da série de retorno dos ativos é dividido em componentes de alta e baixa frequência por meio da transformação wavelet discreta. Nesse processo, o rótulo de tendência e os coeficientes preço-volume permanecem inalterados. Em seguida, esses componentes são combinados com as partes não modificadas do sinal na última dimensão.

A componente de baixa frequência reflete as tendências de longo prazo, enquanto a de alta frequência captura as flutuações de curto prazo e eventos bruscos. Elas são representadas como 𝒳l, 𝒳h ∈ RT1×N×362, respectivamente. Em seguida, 𝒳h e 𝒳l são linearmente transformadas por uma camada totalmente conectada para a dimensão RT1×N×D. Neste caso, T1 indica a profundidade do histórico analisado.

O codificador espaço-temporal de dupla frequência é projetado para representar esses diferentes padrões de séries temporais: os objetos de baixa frequência são alimentados no módulo de atenção temporal (denotado como tatt), enquanto as características de alta frequência são processadas por uma camada convolucional causal estendida (denotada como conv). Esses componentes são então inseridos em redes neurais de atenção baseadas em grafos (denotadas como gat). A interação com a informação dos grafos permite ao modelo capturar relações e dependências complexas entre ativos e tempo. Neste módulo, o grafo espacial Aspa e o grafo temporal Atem são transformados por meio de uma camada totalmente conectada e operações de translação de tensores em incorporações multidimensionais, denotadas como ρspa, ρtem ∈ RT1×N×D, que são então combinadas com 𝒳l,tatt, 𝒳h,conv por meio de soma e operações de atenção em grafos para gerar 𝒳l,gat, 𝒳h,gat ∈ RT1×N×D. O codificador espaço-temporal de dupla frequência é composto por L camadas, destinadas a representar de forma eficaz padrões espaço-temporais em duas escalas para ondas de baixa e alta frequência. Por fim, no decodificador de dupla frequência, os preditores geram 𝒴l,f, 𝒴h,f ∈ RT2×N×D, que são agregados com o uso de interações Fusion Attention para obter a representação oculta dos padrões temporais em múltiplas escalas. Com camadas totalmente conectadas separadas (camada de regressão FC1 e camada de classificação FC2) são gerados os resultados multitarefa, incluindo previsões de retorno das ações (resultado de regressão, denotado como reg) e probabilidades de previsão de tendência das ações (resultado de classificação, denotado como cla).

Além disso, são exibidos os valores da regressão e da probabilidade de previsão de tendência para a componente de baixa frequência, o que permite melhorar o aprendizado do sinal de baixa frequência.

A visualização original do framework Multitask-Stockformer é apresentada abaixo.

Implementação com MQL5

Acima foi apresentada apenas uma descrição resumida do framework Multitask-Stockformer. O framework é bastante complexo. E acredito que será mais eficiente explorar os algoritmos individualmente durante sua implementação. E começaremos pelo módulo de divisão de fluxo dos dados brutos.

Módulo de decomposição de sinal

Para dividir o sinal analisado em componentes de baixa e alta frequência, os autores do framework propõem o uso da transformação wavelet discreta. Diferente da decomposição de Fourier, a transformação wavelet consegue capturar não apenas a componente de frequência, mas também a estrutura do sinal. Isso a torna mais vantajosa para a análise dos mercados financeiros, nos quais não só a frequência, mas também a ordem dos sinais é importante.

Anteriormente já utilizamos a transformação wavelet discreta ao construir o framework FEDformer, mas naquela ocasião isolamos apenas a componente de baixa frequência. Agora, no entanto, também precisamos da componente de alta frequência. Mesmo assim, podemos aproveitar os desenvolvimentos já existentes.

A transformação wavelet discreta é, essencialmente, uma operação de convolução com uma wavelet específica usada como filtro. Isso nos permite utilizar os algoritmos da camada convolucional como base funcional. No entanto, é importante considerar que no processo de transformação utilizamos wavelets estáticas, cujos parâmetros não são ajustados durante o treinamento. Portanto, devemos desativar o mecanismo de otimização dos parâmetros do nosso objeto.

Com essas premissas apresentadas, criamos um novo objeto para extrair as componentes de alta e baixa frequência do sinal por meio da transformação wavelet discreta CNeuronLegendreWaveletsHL.

class CNeuronLegendreWaveletsHL :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronLegendreWaveletsHL(void) {};
                    ~CNeuronLegendreWaveletsHL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          uint filters, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWaveletsHL;   }
   //---
   virtual uint      GetFilters(void)  const {return (iWindowOut / 2); }
   virtual uint      GetVariables(void)  const {return (iVariables); }
   virtual uint      GetUnits(void)  const {return (Neurons() / (iVariables * iWindowOut)); }
  };

Como já foi dito, a transformação wavelet discreta é uma convolução com um filtro-wavelet. Isso nos permite aproveitar totalmente o funcional do método da classe-mãe da camada convolucional para construir o algoritmo. Basta reescrever o método de inicialização, definindo os dados dos wavelets no lugar de parâmetros aleatórios de filtro.

No entanto, os filtros-wavelet utilizados são estáticos. Por isso, sobrescrevemos o método de otimização de parâmetros updateInputWeights com um placeholder neutro.

A inicialização do novo objeto é realizada no método Init. Como de costume, os parâmetros desse método são recebidos de um programa externo e consistem em constantes que permitem identificar claramente a arquitetura do objeto criado. Neste caso, são:

• window — tamanho da janela analisada;
• step — passo da janela analisada;
• units_count — número de operações de convolução para uma sequência unitarizada;
• filters — número de filtros utilizados;
• variables — número de sequências unitarizadas na série temporal multimodal analisada. 

bool CNeuronLegendreWaveletsHL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                     uint window, uint step, uint units_count, 
                                     uint filters, uint variables, 
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 2 * filters, 
                                  units_count, variables, optimization_type, batch))
      return false;

No corpo do método, os parâmetros recebidos são imediatamente passados ao método homônimo da classe-mãe. No entanto, é importante observar que, ao chamar o método da classe-mãe, dobramos a quantidade de filtros. Isso ocorre porque precisamos criar filtros separados para extrair as componentes de alta e baixa frequência.

Após a execução bem-sucedida do método da classe-mãe, limpamos o buffer de parâmetros de convolução preenchendo-o com zeros e definimos a constante de deslocamento no buffer entre os elementos dos filtros de baixa e alta frequência.

   WeightsConv.BufferInit(WeightsConv.Total(), 0);
   const uint shift_hight = (iWindow + 1) * filters;

Em seguida, organizamos um sistema de laços aninhados para gerar a quantidade necessária de filtros. Aqui, utilizamos a recursividade na geração das wavelets de Legendre. E preenchemos progressivamente a matriz de filtros com wavelets de ordem superior.

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(2.0 * i - 1.0) / iWindow;
      for(uint f = 1; f <= filters; f++)
        {
         float value = 0;
         switch(f)
           {
            case 1:
               value = k;
               break;
            case 2:
               value = (3 * k * k - 1) / 2;
               break;
            default:
               value = ((2 * f - 1) * k * WeightsConv.At(shift - (iWindow + 1)) - 
                       (f - 1) * WeightsConv.At(shift - 2 * (iWindow + 1))) / f;
               break;
           }

Para cada elemento da janela analisada, criamos um laço aninhado de geração dos elementos do filtro. Nele, primeiro geramos o elemento correspondente do filtro de baixa frequência.

Depois, organizamos mais um laço aninhado, onde espalhamos o elemento gerado nos filtros de todas as variáveis independentes da sequência multimodal. E, nesse mesmo ponto, adicionamos o elemento do filtro de alta frequência, formado com base no respectivo elemento do filtro de baixa frequência.

         for(uint v = 0; v < iVariables; v++)
           {
            uint shift_var = 2 * shift_hight * v;
            if(!WeightsConv.Update(shift + shift_var, value))
               return false;
            if(!WeightsConv.Update(shift + shift_var + shift_hight, 
                                    MathPow(-1.0f, float(i))*value))
               return false;
           }

A seguir, ajustamos o deslocamento até o próximo elemento do filtro e passamos para a próxima iteração do sistema de laços.

         shift += iWindow + 1;
        }
     }

O restante do algoritmo deste método de inicialização do objeto é diferente de tudo que vimos até aqui. Até agora, não havíamos utilizado fragmentos de programas em OpenCL durante a inicialização de objetos. Mas este método será uma exceção. Aqui, normalizamos os filtros wavelet gerados.

   if(!!OpenCL)
     {
      if(!WeightsConv.BufferWrite())
         return false;
      uint global_work_size[] = {iWindowOut * iVariables};
      uint global_work_offset[] = {0};
      OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, WeightsConv.GetIndex());
      OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)iWindow + 1);
      if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
         return false;
        }
     }
//---
   return true;
  }

Após a normalização bem-sucedida dos parâmetros, finalizamos a execução do método retornando o resultado lógico da operação ao programa chamador.

O código completo deste objeto e de todos os seus métodos está disponível no anexo.

Vale destacar que a funcionalidade do módulo de decomposição dos dados analisados é um pouco mais ampla do que apenas a transformação wavelet discreta, embora esta seja a parte principal. Planejamos utilizar o objeto na implementação de nossos modelos, nos quais a entrada será um tensor bidimensional de uma sequência temporal multimodal com a dimensão {Bar, Indicator Value}. Mas, para que nosso objeto de transformação wavelet discreta funcione corretamente, é necessário transpor esses dados. Claro que essa operação pode ser feita antes de alimentar o objeto com os dados brutos. Mas nosso objetivo é criar objetos que sejam o mais fáceis possível de usar. Por isso, vamos criar um objeto para o módulo de decomposição de fluxo com funcionalidade ligeiramente ampliada: CNeuronDecouplingFlow. E, como classe-mãe, usaremos o objeto de transformação wavelet discreta que criamos anteriormente.

class CNeuronDecouplingFlow   :  public   CNeuronLegendreWaveletsHL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDecouplingFlow(void) {};
                    ~CNeuronDecouplingFlow(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          uint filters, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDecouplingFlow;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

No corpo do novo objeto, adicionamos uma camada de transposição preliminar dos dados e alteramos a interpretação do parâmetro externo do método de inicialização units_count. Tornamos esse parâmetro mais amigável para o usuário, tratando-o como o comprimento da sequência analisada. Assim, o parâmetro units_count representa a profundidade do histórico analisado (número de barras), e variables — o número de parâmetros analisados (indicadores).

Vamos analisar a implementação dessa abordagem no método de inicialização Init. No corpo do método, primeiro recalculamos o número de operações de convolução para uma sequência unitarizada, com base no tamanho da sequência original, na janela de convolução e em seu passo. Somente após esse ajuste, chamamos o método homônimo da classe-mãe, passando os parâmetros corrigidos.

bool CNeuronDecouplingFlow::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint units_count,
                                 uint filters, uint variables,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint units_out = (units_count - window + step) / step;
   if(!CNeuronLegendreWaveletsHL::Init(numOutputs, myIndex, open_cl, window, step, units_out, 
                                                filters, variables, optimization_type, batch))
      return false;

Depois da execução bem-sucedida do método da classe-mãe, inicializamos a camada de transposição dos dados brutos.

   if(!cTranspose.Init(0, 0, OpenCL, units_count, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

E finalizamos o método retornando à aplicação chamadora o resultado lógico da execução das operações.

O algoritmo dos métodos de propagação para frente e propagação reversa é bastante simples. Por exemplo, para realizar a propagação para frente, primeiro transpomos os dados brutos e então alimentamos o tensor resultante no método homônimo da classe-mãe.

bool CNeuronDecouplingFlow::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!CNeuronLegendreWaveletsHL::feedForward(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Portanto, não nos deteremos nesses métodos aqui. O código completo deste objeto e de todos os seus métodos pode ser consultado no anexo.

Para finalizar a análise do módulo de decomposição de sinal, é necessário comentar os resultados que ele gera. A questão é que a estrutura de operações que criamos não permite que a camada neural de saída produza dois tensores separadamente. Por esse motivo, optamos por agrupar os resultados dos filtros de baixa e alta frequência em um único tensor de dados. Consequentemente, na saída do módulo de decomposição de sinal, obtemos uma estrutura semelhante a um tensor 4D no formato {Variables, Units, [Low, High], Filters}. O processo de separação do tensor em diferentes fluxos de processamento de dados está planejado para ser realizado no codificador espaço-temporal de dupla frequência.

Após a construção do módulo de decomposição dos dados brutos, iniciamos a implementação dos métodos do codificador espaço-temporal de dupla frequência, composto por três componentes principais: atenção temporal, convolução causal estendida e slot temporal com redes neurais de atenção em grafos Struc2Vec.

Vale destacar que os autores do framework Multitask-Stockformer organizam dois fluxos independentes para as componentes de baixa e alta frequência. Além disso, esses fluxos possuem arquiteturas distintas, o que permite focar em tendências e componentes sazonais.

A componente de baixa frequência é enviada ao bloco de atenção espaço-temporal, que capta tendências de longo prazo de baixa frequência ao considerar as relações globais das sequências.

Enquanto isso, a parte de alta frequência do sinal é processada por uma camada convolucional causal estendida. Essa abordagem permite focar em padrões locais, modelando com eficácia as componentes de alta frequência e eventos bruscos.

Espera-se que essa estratégia de modelagem dupla aumente a precisão na previsão de sequências financeiras complexas.

Como bloco de atenção espaço-temporal, podemos reutilizar um dos objetos já existentes construídos com a arquitetura do codificador Transformer. No entanto, ainda precisaremos desenvolver o algoritmo para a camada convolucional causal.

Camada convolucional causal

A convolução causal estendida proposta pelos autores do framework é um tipo específico de convolução unidimensional que percorre os dados brutos pulando valores em um determinado intervalo, conforme ilustrado na figura acima. Teoricamente, dada uma sequência unidimensional x ∈ RT e um filtro f ∈ RJ, a operação de convolução causal estendida no instante temporal t é definida como:

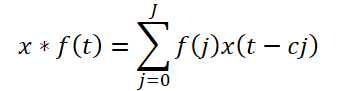
Aqui, c é o fator de dilatação. A convolução causal estendida aplicada à componente de alta frequência é expressa como:

Vale observar que na implementação proposta é adicionado mais um hiperparâmetro — o fator de dilatação. Além disso, esse fator é fixo. Mas será que a distância entre os elementos dependentes se mantém constante em toda a sequência analisada? A situação se complica com o uso de um único coeficiente para diferentes sequências unitarizadas.

Na nossa implementação, decidimos modificar um pouco a arquitetura do módulo causal estendido. Em vez de saltos fixos, propomos utilizar o algoritmo Segment, Shuffle, Stitch (S3). E, logo após, aplicar uma camada convolucional comum.

O S3 permite configurar uma permutação treinável de segmentos nos dados brutos. Com isso, deixamos de lado os saltos fixos de valores no tensor de entrada e deixamos a cargo do modelo aprender as dependências entre os elementos das sequências analisadas. A criação de um stack com vários desses blocos permite identificar e capturar de forma adaptativa as dependências da componente de alta frequência.

Essa abordagem será implementada no objeto CNeuronDilatedCasualConv. Acredito que fica claro que o algoritmo descrito acima é linear. Portanto, como classe-mãe, utilizamos a CNeuronRMAT, que já oferece a funcionalidade principal e as interfaces para implementar algoritmos lineares. A estrutura do novo objeto está apresentada abaixo.

class CNeuronDilatedCasualConv   :  public CNeuronRMAT
  {
public:
                     CNeuronDilatedCasualConv(void) {};
                    ~CNeuronDilatedCasualConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint dimension,
                          uint units_count, uint variables, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDilatedCasualConv; }
  };

Como é possível perceber, ao escolher a classe-mãe “correta”, podemos nos limitar a definir a arquitetura do objeto no método de inicialização. Todo o restante da funcionalidade já está implementado nos métodos herdados da classe-mãe.

Nos parâmetros do método Init, recebemos como de costume um conjunto de constantes que nos permite definir a arquitetura do objeto criado:

• window — tamanho da janela analisada;
• step — passo da janela analisada;
• dimension — dimensionalidade do vetor de cada elemento da sequência;
• units_count — número de elementos na sequência;
• variables — número de elementos analisados na sequência multimodal;
• layers — número de camadas de convolução.

Aqui, é importante destacar alguns aspectos específicos sobre o uso dessas variáveis. Mas antes, vamos relembrar a dimensionalidade do tensor dos dados brutos analisados. Como mencionado anteriormente, do módulo de decomposição do sinal analisado obtemos um tensor 4D no formato {Variables, Units, [Low, High], Filters}. Após a decomposição do tensor em componentes de alta e baixa frequência no terceiro eixo, obtemos apenas um valor, o que na prática torna o tensor tridimensional: {Variables, Units, Filters}.

Lembrando que, no contexto do OpenCL, trabalhamos com buffers unidimensionais de dados. A decomposição do buffer em dimensões é simbólica, mas implica uma sequência de valores compatível.

Tendo clareza sobre a dimensionalidade do tensor de entrada, conseguimos relacionar corretamente os parâmetros recebidos do programa externo. É evidente que o parâmetro variables corresponde à primeira dimensão Variables. O parâmetro units_count indica o comprimento da sequência analisada, que corresponde à segunda dimensão Units. E dimension determina a última dimensão Filters. Esses parâmetros especificam o tamanho bruto do tensor de dados de entrada.

Além disso, o tamanho da janela (window) e seu passo (step) são indicados em unidades da segunda dimensão Units. Ou seja, se indicarmos um tamanho de janela igual a 2 (window = 2), serão utilizados 2*dimension elementos do buffer de entrada para cada operação de convolução.

Voltando ao algoritmo do método de inicialização do objeto.

bool CNeuronDilatedCasualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint step, uint dimension, uint units_count,
                                    uint variables, uint layers,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 1, optimization_type, batch))
      return false;

Como de costume, no corpo do método, chamamos primeiro o método homônimo da classe-mãe, que organiza os controles necessários e a inicialização dos objetos herdados. E aqui surgem dois pontos importantes. Primeiro: a estrutura da classe-mãe CNeuronRMAT difere bastante da que precisamos. Portanto, em vez de chamar o método da classe imediatamente acima, chamamos o método da camada totalmente conectada base. Como você deve lembrar, essa camada é a base para todas as camadas neurais da nossa biblioteca.

O segundo ponto: durante a convolução, o tamanho do tensor de saída muda. E no momento da chamada ainda não temos o tamanho final, necessário para informar as dimensões das interfaces base. Por isso, inicializamos essas interfaces com uma dimensão de saída fictícia, contendo apenas um elemento.

Em seguida, limpamos o array dinâmico de ponteiros para os objetos internos e preparamos as variáveis auxiliares.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   uint units = units_count;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3 *s3 = NULL;

Após concluir essa etapa de preparação, passamos à construção da arquitetura do objeto. Para isso, organizamos um laço com número de iterações igual à quantidade de camadas internas.

   for(uint i = 0; i < layers; i++)
     {
      s3 = new CNeuronS3();
      if(!s3 ||
         !s3.Init(0, i*2, OpenCL, dimension, dimension*units*variables, optimization, iBatch) ||
         !cLayers.Add(s3))
        {
         if(!!s3)
            delete s3;
         return false;
        }
      s3.SetActivationFunction(None);

No corpo do laço, primeiro inicializamos o objeto S3. É importante observar que este objeto funciona apenas com tensores unidimensionais. Por isso, para evitar “quebras” no vetor que representa cada elemento da sequência, o tamanho do segmento precisa ser múltiplo da dimensionalidade desse vetor. Neste caso, definimos que ambos sejam iguais. Além disso, o comprimento da sequência corresponde ao tamanho total do tensor, considerando todas as variáveis analisadas.

Após a inicialização bem-sucedida do objeto, adicionamos seu ponteiro ao nosso array dinâmico de objetos internos. E desativamos a função de ativação.

Em seguida, iniciamos o processo de inicialização da camada convolucional. Antes de começar, calculamos a quantidade de operações de convolução para a camada que será criada. E salvamos o valor obtido em uma variável local. Esse valor é justamente o que utilizamos na etapa anterior para definir a dimensão da sequência analisada. Portanto, na próxima iteração do laço, criaremos o objeto S3 com o tamanho atualizado.

      conv = new CNeuronConvOCL();
      units = MathMax((units - window + step) / step, 1);
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window * dimension, step * dimension, dimension,
                                                   units, variables, optimization, iBatch) ||
         !cLayers.Add(conv))
        {
         if(!!conv)
            delete conv;
         return false;
        }
      conv.SetActivationFunction(GELU);
     }

A camada convolucional que utilizamos, ao contrário do objeto S3, pode operar com base nas sequências unitárias. Isso nos permite não apenas aplicar a convolução a cada série temporal unitarizada separadamente, como também usar filtros distintos para cada sequência. O que torna sua análise totalmente independente.

Na saída da camada convolucional, utilizamos a função de ativação GELU no lugar da ReLU sugerida pelos autores do framework.

Adicionamos o ponteiro do objeto inicializado ao nosso array dinâmico e seguimos para a próxima iteração do laço para criar a camada seguinte.

Após a inicialização bem-sucedida de todas as camadas internas do objeto, chamamos novamente o método de inicialização da camada totalmente conectada base, agora para criar buffers corretos para as interfaces externas, especificando a dimensão da última camada interna do bloco.

  if(!CNeuronBaseOCL::Init(numOutputs, myIndex, OpenCL, conv.Neurons(), optimization_type, batch))
      return false;

E, por fim, substituímos os ponteiros dos buffers das interfaces externas pelos buffers da última camada interna.

   if(!SetGradient(conv.getGradient(), true) ||
      !SetOutput(conv.getOutput(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Copiamos o ponteiro da função de ativação, retornamos o resultado lógico da operação ao programa chamador e finalizamos o método.

Como você notou, nesta arquitetura utilizamos objetos internos que trabalham com tensores de diferentes dimensões. Primeiro, a camada S3 reorganiza os elementos dentro de todo o buffer de dados, sem considerar as sequências unitárias. Nesse formato, é perfeitamente possível que elementos sejam “embaralhados” entre diferentes sequências. Por um lado, isso remove qualquer restrição à reorganização dentro dos limites de uma sequência específica. Por outro, a sequência de reorganização é aprendida com base no conjunto de dados de treinamento. E se o modelo identificar dependências entre elementos de diferentes sequências, isso pode aumentar sua eficácia. Será bastante interessante observar os resultados após o treinamento.

O volume deste artigo está chegando ao seu limite, mas nosso trabalho não termina aqui. Continuaremos na próxima publicação da nossa série.

Considerações finais

Neste trabalho, exploramos o framework Multitask-Stockformer —, um modelo inovador de seleção de ações que combina transformação wavelet com módulos multitarefa de Self-Attention. O uso da transformação wavelet permite identificar características temporais e de frequência nos dados de mercado, enquanto os mecanismos de Self-Attention possibilitam a modelagem precisa das interações complexas entre os fatores analisados.

Na parte prática, implementamos nossa própria visão de alguns blocos do framework proposto usando MQL5. E na próxima publicação finalizaremos a implementação do framework analisado. Além disso, avaliaremos a eficácia dos métodos desenvolvidos em dados históricos reais.

Links

• Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos usando o método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste de modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL