Neuronale Netze leicht gemacht (Teil 90): Frequenzinterpolation von Zeitreihen (FITS)
Einführung
Die Zeitreihenanalyse spielt eine wichtige Rolle bei Managemententscheidungen auf den Finanzmärkten. Zeitreihendaten im Finanzwesen sind oft komplex und dynamisch, und ihre Verarbeitung erfordert effiziente Methoden.
Im Rahmen der fortgeschrittenen Forschung auf dem Gebiet der Zeitreihenanalyse werden ausgefeilte Modelle und Methoden entwickelt. Diese Modelle sind jedoch häufig sehr rechenintensiv, sodass sie für den Einsatz unter dynamischen Finanzmarktbedingungen weniger geeignet sind. Das heißt, sie können kaum angewendet werden, wenn der Zeitpunkt einer Entscheidung entscheidend ist.
Darüber hinaus werden heutzutage immer mehr Verwaltungsentscheidungen über mobile Geräte getroffen, die ebenfalls nur über begrenzte Ressourcen verfügen. Diese Tatsache stellt zusätzliche Anforderungen an die Modelle, die für solche Entscheidungen verwendet werden.
In diesem Zusammenhang kann die Darstellung von Zeitreihen im Frequenzbereich eine effizientere und kompaktere Darstellung der beobachteten Muster ermöglichen. So können beispielsweise Spektraldaten und Frequenzanalysen mit hoher Amplitude helfen, wichtige Merkmale zu identifizieren.
In den vorangegangenen Artikeln haben wir die Methode FEDformer besprochen, die den Frequenzbereich nutzt, um Muster in einer Zeitreihe zu finden. Der bei dieser Methode verwendete Transformator kann jedoch kaum als leichtes Modell bezeichnet werden. Anstelle komplexer Modelle, die einen hohen Rechenaufwand erfordern, schlägt der Artikel „FITS: Modeling Time Series with 10k Parameters“ eine Methode zur Frequenzinterpolation von Zeitreihen (Frequency Interpolation Time Series - FITS) vor. Es ist eine kompakte und effiziente Lösung für die Zeitreihenanalyse und -prognose. FITS nutzt die Interpolation im Frequenzbereich, um das Fenster des analysierten Zeitabschnitts zu erweitern, und ermöglicht so die effiziente Extraktion von zeitlichen Merkmalen ohne großen Rechenaufwand.
Die Autoren von FITS heben die folgenden Vorteile ihrer Methode hervor:
- FITS ist ein leichtgewichtiges Modell mit einer geringen Anzahl von Parametern, was es zu einer idealen Wahl für den Einsatz auf Geräten mit begrenzten Ressourcen macht.
- FITS verwendet ein komplexes neuronales Netz, um Informationen über die Amplitude und Phase des Signals zu sammeln, was die Effizienz der Zeitreihendatenanalyse verbessert.
1. FITS-Algorithmus
Die Zeitreihenanalyse im Frequenzbereich ermöglicht die Zerlegung des Signals in eine lineare Kombination sinusförmiger Komponenten ohne Datenverlust. Jede dieser Komponenten hat eine eigene Frequenz, Anfangsphase und Amplitude. Während die Vorhersage einer Zeitreihe eine schwierige Aufgabe sein kann, ist die Vorhersage einzelner sinusförmiger Komponenten relativ einfach, da lediglich die Phase der Sinuswelle auf der Grundlage der Zeitverschiebung angepasst werden muss. Die auf diese Weise verschobenen Sinuswellen werden linear kombiniert, um vorhergesagte Werte der analysierten Zeitreihen zu erhalten.
Dieser Ansatz ermöglicht es uns, die Frequenzmerkmale des analysierten Zeitreihenfensters effektiv zu erhalten. Außerdem wird die semantische Reihenfolge zwischen dem Zeitfenster und dem Prognosehorizont beibehalten.
Die Vorhersage der einzelnen Sinuskomponenten im Zeitbereich kann jedoch recht arbeitsintensiv sein. Um dieses Problem zu lösen, schlagen die Autoren der Methode FITS die Verwendung eines komplexen Frequenzbereichs vor, der eine kompaktere und informativere Datendarstellung ermöglicht.
Die schnelle Fourier-Transformation (FFT) transformiert diskrete Zeitreihensignale effizient vom Zeitbereich in den komplexen Frequenzbereich. In der Fourier-Analyse wird der komplexe Frequenzbereich durch eine Sequenz dargestellt, in der jede Frequenzkomponente durch eine komplexe Zahl gekennzeichnet ist. Diese komplexe Zahl spiegelt die Amplitude und Phase der Komponente wider und liefert eine vollständige Beschreibung. Die Amplitude einer Frequenzkomponente stellt die Größe bzw. Stärke dieser Komponente im Originalsignal im Zeitbereich dar. Im Gegensatz dazu gibt die Phase die Zeitverschiebung oder Verzögerung an, die durch diese Komponente verursacht wird. Mathematisch gesehen kann eine komplexe Zahl, die mit einer Frequenzkomponente verbunden ist, als komplexes Exponentialelement mit einer bestimmten Amplitude und Phase dargestellt werden:
![]()
wobei X(f) eine komplexe Zahl ist, die mit einer Frequenzkomponente bei der Frequenz f verbunden ist,
|X(f)| ist die Amplitude der Komponente,
θ(f) ist die Phase der Komponente.
In der komplexen Ebene kann das Exponentialelement als Vektor mit einer Länge gleich der Amplitude und einem Winkel gleich der Phase dargestellt werden:
![]()
Somit bietet eine komplexe Zahl im Frequenzbereich eine prägnante und elegante Möglichkeit, die Amplitude und Phase jeder Frequenzkomponente in der Fourier-Transformation darzustellen.
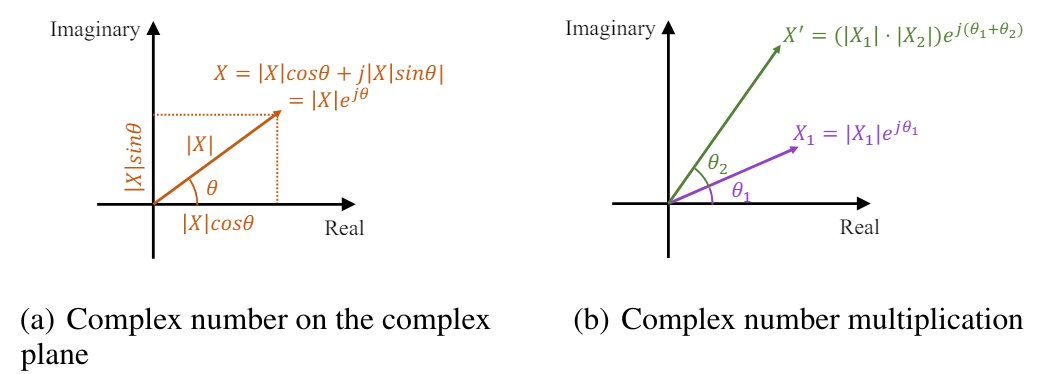
Die Zeitverschiebung eines Signals entspricht der Phasenverschiebung im Frequenzbereich. Im Bereich der komplexen Frequenzen kann eine solche Phasenverschiebung als Multiplikation eines Einheitselements eines komplexen Exponentials mit der entsprechenden Phase ausgedrückt werden. Das verschobene Signal hat immer noch eine Amplitude von |X(f)|, und die Phase zeigt eine lineare Verschiebung in der Zeit.
Die Amplitudenskalierung und die Phasenverschiebung können also gleichzeitig als Multiplikation komplexer Zahlen ausgedrückt werden.
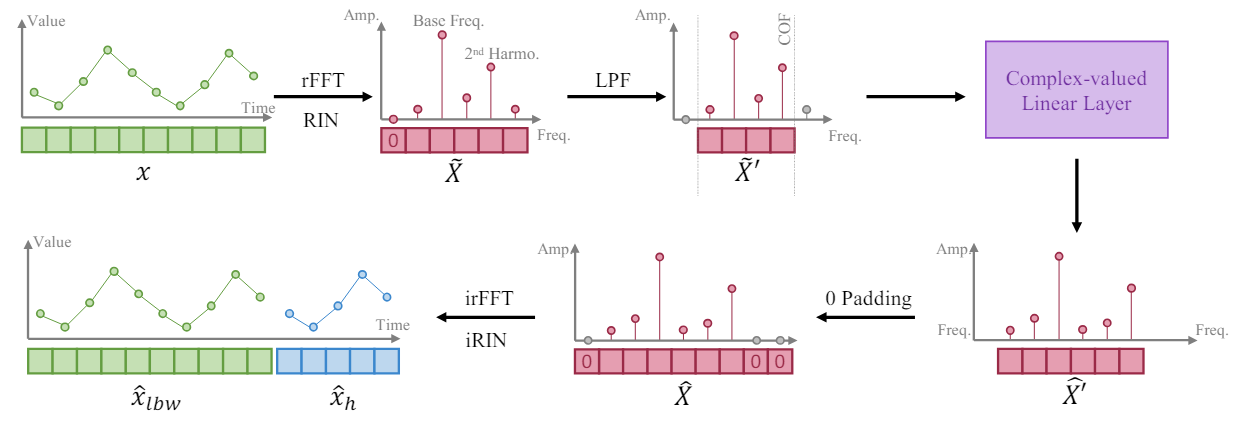
Ausgehend von der Tatsache, dass eine längere Zeitreihe eine höhere Frequenzauflösung in ihrer Frequenzdarstellung bietet, trainieren die Autoren der Methode FITS das Modell, um ein Zeitreihensegment durch Interpolation der Frequenzdarstellung des analysierten Fensters der Eingabedaten zu erweitern. Sie schlagen vor, eine einzige komplexe lineare Schicht zu verwenden, um eine solche Interpolation zu trainieren. Dadurch kann das Modell die Amplitudenskalierung und Phasenverschiebung als Multiplikation komplexer Zahlen während des Interpolationsprozesses lernen. Beim FITS-Algorithmus wird die schnelle Fourier-Transformation verwendet, um Zeitreihensegmente in den komplexen Frequenzbereich zu projizieren. Nach der Interpolation wird die Frequenzdarstellung mit Hilfe der inversen FFT auf die Zeitdarstellung zurückprojiziert.
Der Mittelwert solcher Segmente führt jedoch zu einer sehr großen Null-Frequenz-Komponente in der komplexen Frequenzdarstellung. Um dieses Problem zu lösen, wird das empfangene Signal einer reversiblen Normalisierung unterzogen (RevIN) unterzogen, wodurch wir eine Instanz mit Mittelwert Null erhalten.
Darüber hinaus ergänzen die Autoren der Methode FITS mit einem Tiefpassfilter (LPF), um die Größe des Modells zu reduzieren. Der Tiefpassfilter entfernt effektiv hochfrequente Komponenten oberhalb einer bestimmten Grenzfrequenz und verdichtet die Modelldarstellung, während wichtige Zeitreiheninformationen erhalten bleiben.
Obwohl FITS im Frequenzbereich arbeitet, wird es im Zeitbereich unter Verwendung von Standardverlustfunktionen wie dem mittleren quadratischen Fehler (MSE) nach der inversen schnellen Fourier-Transformation trainiert. Dies bietet einen vielseitigen Ansatz, der an eine Vielzahl von Zeitreihenproblemen angepasst werden kann.
Bei Prognoseaufgaben erzeugt FITS zusammen mit dem Planungshorizont ein retrospektives Analysefenster. Dies ermöglicht die Kontrolle über die Vorhersage und die rückwirkende Analyse, wobei das Modell dazu angehalten wird, das rückwirkende Analysefenster genau zu rekonstruieren. Die in dem zitierten Artikel durchgeführte Analyse zeigt, dass eine Kombination aus Rückblick und Prognoseüberwachung in bestimmten Szenarien zu einer besseren Leistung führen kann.
Für Rekonstruktionsaufgaben nimmt FITS eine Teilabtastung des ursprünglichen Zeitreihensegments auf der Grundlage einer bestimmten Unterteilungsrate vor. Anschließend wird eine Frequenzinterpolation durchgeführt, um das verkleinerte Segment wieder in seine ursprüngliche Form zu rekonstruieren. Daher wird eine direkte Kontrolle mit Hilfe von Verlusten angewandt, um eine genaue Signalrekonstruktion zu gewährleisten.
Um die Länge des Tensors vom Modellergebnis zu kontrollieren, führen die Autoren der Methode eine Interpolationsrate ein, die als 𝜂 bezeichnet wird und das Verhältnis zwischen der erforderlichen Größe des Modellergebnis-Tensors und der entsprechenden Größe des ursprünglichen Datentensors darstellt.
Es ist bemerkenswert, dass bei der Anwendung eines Tiefpassfilters (LPF) die Größe des Eingangsdatentensensors unserer komplexen Schicht der Grenzfrequenz (COF) des LPF entspricht. Nach Durchführung der Frequenzinterpolation wird die komplexe Frequenzdarstellung mit Nullen auf die erforderliche Größe des Ergebnissensors aufgefüllt. Vor der Anwendung der umgekehrten FFT führen sie eine zusätzliche Null als Komponente der Nullfrequenzdarstellung ein.
Der Hauptzweck der Einbeziehung des LPF in FITS ist die Komprimierung des Modellvolumens unter Beibehaltung wichtiger Informationen. LPF erreicht dies, indem Frequenzkomponenten oberhalb einer bestimmten Grenzfrequenz (COF) verworfen werden, was zu einer übersichtlicheren Darstellung im Frequenzbereich führt. LPF bewahrt relevante Informationen in den Zeitreihen, während Komponenten, die die Lernfähigkeit des Modells übersteigen, verworfen werden. Dadurch wird sichergestellt, dass ein erheblicher Teil des aussagekräftigen Inhalts der eingegebenen Zeitreihen erhalten bleibt. Die von den Autoren der Methode durchgeführten Experimente zeigen, dass das gefilterte Signal nur minimale Verzerrungen aufweist, selbst wenn nur ein Viertel der ursprünglichen Darstellung im Frequenzbereich erhalten bleibt. Außerdem enthalten die mit LPF gefilterten Hochfrequenzkomponenten in der Regel Rauschen, das für eine effektive Zeitreihenmodellierung irrelevant ist.
Die schwierige Aufgabe besteht hier darin, eine geeignete Grenzfrequenz (COF) zu wählen. Um dieses Problem zu lösen, schlagen die Autoren von FITS eine Methode vor, die auf dem Oberwellengehalt der dominanten Frequenz basiert. Oberschwingungen, die ganzzahlige Vielfache der dominanten Frequenz sind, spielen eine wichtige Rolle bei der Gestaltung der Wellenform eines Zeitreihensignals. Durch den Vergleich der Grenzfrequenz mit diesen Oberschwingungen bleiben die entsprechenden Frequenzkomponenten erhalten, die mit der Struktur und Periodizität des Signals zusammenhängen. Dieser Ansatz nutzt die inhärente Beziehung zwischen den Frequenzen, um aussagekräftige Informationen zu extrahieren und gleichzeitig Rauschen und unnötige hochfrequente Komponenten zu unterdrücken.
Die ursprüngliche Visualisierung des Autors von FITS wird im Folgenden vorgestellt.
2. Implementierung in MQL5
Wir haben uns mit den theoretischen Aspekten der Methode FITS beschäftigt. Nun können wir uns der praktischen Umsetzung der vorgeschlagenen Ansätze mit MQL5 zuwenden.
Wie üblich werden wir die vorgeschlagenen Ansätze verwenden, aber unsere Implementierung wird sich aufgrund der Besonderheiten des von uns zu lösenden Problems von der Vision des Autors für den Algorithmus unterscheiden.
2.1 FFT-Implementierung
Aus der theoretischen Beschreibung der oben vorgestellten Methode geht hervor, dass sie auf der direkten und inversen schnellen Fourier-Zerlegung beruht. Mit Hilfe der schnellen Fourier-Zerlegung übersetzen wir das analysierte Signal zunächst in den Frequenzbereich und führen die vorhergesagte Sequenz dann in die Zeitreihendarstellung zurück. In diesem Fall können wir zwei Hauptvorteile der schnellen Fourier-Transformation erkennen:
- Schnelligkeit der Vorgänge im Vergleich zu anderen vergleichbaren Umwandlungen
- Die Fähigkeit, die inverse Transformation durch die direkte Transformation auszudrücken
An dieser Stelle ist anzumerken, dass wir im Rahmen unserer Aufgabenstellung eine Implementierung von FFT für eine multivariate Zeitreihe benötigen. In der Praxis ist es FFT, die auf jede unitäre Zeitreihe in unserer multivariaten Sequenz angewendet wird.
Die meisten mathematischen Operationen in unseren Implementierungen werden auf OpenCL übertragen. So können wir die Ausführung einer großen Anzahl ähnlicher Operationen mit unabhängigen Daten auf mehrere parallele Threads verteilen. Dadurch wird die für die Ausführung von Vorgängen erforderliche Zeit verkürzt. Wir werden also eine schnelle Fourier-Zerlegungsoperationen auf der OpenCL-Seite durchführen. In jedem der parallelen Threads führen wir die Zerlegung einer separaten unitären Zeitreihe durch.
Wir werden den Algorithmus zur Durchführung von Operationen in Form eines FFT-Kerns formalisieren. In den Kernel-Parametern werden wir Zeiger auf 4 Daten-Arrays übergeben. Hier verwenden wir zwei Arrays für die Eingabedaten und die Ergebnisse der Operationen. Ein Feld enthält den reellen Teil des komplexen Werts (die Signalamplitude), das zweite den Imaginärteil (die Phase).
Bitte beachten Sie jedoch, dass wir nicht immer den Imaginärteil des Signals in den Kernel einspeisen werden. Bei der Zerlegung der Eingangszeitreihen beispielsweise fehlt dieser Teil. In dieser Situation ist die Lösung ganz einfach: Wir ersetzen die fehlenden Daten durch Nullwerte. Um keinen separaten, mit Nullwerten gefüllten Puffer zu übergeben, werden wir in den Kernel-Parametern das Flag input_complex setzen.
Der zweite Punkt ist, dass der Cooley-Tukey-Algorithmus, den wir für die FFT verwenden, nur für Sequenzen funktioniert, deren Länge eine Potenz von 2 ist. Diese Bedingung führt zu erheblichen Einschränkungen. Diese Einschränkung betrifft jedoch die Aufbereitung des analysierten Signals. Die Methode funktioniert gut, wenn wir die fehlenden Elemente der Folge mit Nullwerten füllen. Um auch hier unnötiges Kopieren von Daten zur Neuformatierung der Zeitreihen zu vermeiden, fügen wir den Kernel-Parametern zwei Variablen hinzu: input_window und output_window. In der ersten Variable wird die tatsächliche Länge der analysierten Sequenz angegeben, in der zweiten die Größe des Ergebnisvektors der Zerlegung, die eine Potenz von 2 ist. In diesem Fall handelt es sich um die Größen einer unitären Folge.
Ein weiterer Parameter, reverse, gibt die Richtung der Operation an: direkte oder inverse Transformation.
__kernel void FFT(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im, const int input_window, const int input_complex, const int output_window, const int reverse ) { size_t variable = get_global_id(0);
Im Kernelkörper definieren wir zunächst einen Thread-Identifikator, der uns auf die zu analysierende Unitary Sequence verweist. Hier werden auch Verschiebungen in Datenpuffern und andere notwendige Konstanten definiert.
const ulong N = output_window; const ulong N2 = N / 2; const ulong inp_shift = input_window * variable; const ulong out_shift = output_window * variable;
Im nächsten Schritt werden die Eingabedaten in einer bestimmten Reihenfolge neu sortiert, wodurch der FFT-Algorithmus ein wenig optimiert werden kann.
uint target = 0; for(uint position = 0; position < N; position++) { if(target > position) { outputs_re[out_shift + position] = (target < input_window ? inputs_re[inp_shift + target] : 0); outputs_im[out_shift + position] = ((target < input_window && input_complex) ? inputs_im[inp_shift + target] : 0); outputs_re[out_shift + target] = inputs_re[inp_shift + position]; outputs_im[out_shift + target] = (input_complex ? inputs_im[inp_shift + position] : 0); } else { outputs_re[out_shift + position] = inputs_re[inp_shift + position]; outputs_im[out_shift + position] = (input_complex ? inputs_im[inp_shift + position] : 0); } unsigned int mask = N; while(target & (mask >>= 1)) target &= ~mask; target |= mask; }
Danach folgt die direkte Umwandlung der Daten, die in einem System von verschachtelten Zyklen erfolgt. In der äußeren Schleife bilden wir FFT-Iterationen für Segmente der Länge 2, 4, 8, ... n.
float real = 0, imag = 0; for(int len = 2; len <= (int)N; len <<= 1) { float w_real = (float)cos(2 * M_PI_F / len); float w_imag = (float)sin(2 * M_PI_F / len);
Im Hauptteil der Schleife definieren wir einen Multiplikator für das Argument Rotation pro 1 Punkt der Schleifenlänge und organisieren eine verschachtelte Schleife für die Iteration über die Blöcke der analysierten Sequenz.
for(int i = 0; i < (int)N; i += len) { float cur_w_real = 1; float cur_w_imag = 0;
Hier deklarieren wir die Variablen der aktuellen Phasendrehung und organisieren eine weitere verschachtelte Schleife über die Elemente im Block.
for(int j = 0; j < len / 2; j++) { real = cur_w_real * outputs_re[out_shift + i + j + len / 2] - cur_w_imag * outputs_im[out_shift + i + j + len / 2]; imag = cur_w_imag * outputs_re[out_shift + i + j + len / 2] + cur_w_real * outputs_im[out_shift + i + j + len / 2]; outputs_re[out_shift + i + j + len / 2] = outputs_re[out_shift + i + j] - real; outputs_im[out_shift + i + j + len / 2] = outputs_im[out_shift + i + j] - imag; outputs_re[out_shift + i + j] += real; outputs_im[out_shift + i + j] += imag; real = cur_w_real * w_real - cur_w_imag * w_imag; cur_w_imag = cur_w_imag * w_real + cur_w_real * w_imag; cur_w_real = real; } } }
Im Schleifenkörper ändern wir zunächst die zu analysierenden Elemente und dann den Wert der aktuellen Phasenvariablen für die nächste Iteration.
Bitte beachten Sie, dass die Änderung von Pufferelementen „an Ort und Stelle“ durchgeführt wird, ohne dass zusätzlicher Speicher zugewiesen wird.
Nachdem die Iterationen des Schleifensystems abgeschlossen sind, überprüfen wir den Wert des Flags reverse. Wenn wir die umgekehrte Transformation durchführen, werden die Daten im Ergebnispuffer neu sortiert. In diesem Fall werden die erhaltenen Werte durch die Anzahl der Elemente in der Sequenz geteilt.
if(reverse) { outputs_re[0] /= N; outputs_im[0] /= N; outputs_re[N2] /= N; outputs_im[N2] /= N; for(int i = 1; i < N2; i++) { real = outputs_re[i] / N; imag = outputs_im[i] / N; outputs_re[i] = outputs_re[N - i] / N; outputs_im[i] = outputs_im[N - i] / N; outputs_re[N - i] = real; outputs_im[N - i] = imag; } } }
2.2 Kombination von reellen und imaginären Teil der prognostizierten Verteilung
Der oben vorgestellte Kernel ermöglicht die Durchführung direkter und inverser schneller Fourier-Zerlegungen, was unseren Bedürfnissen durchaus entspricht. Aber es gibt noch einen weiteren Punkt in der FITS-Methode, der beachtet werden sollte. Die Autoren der Methode verwenden ein komplexes neuronales Netz zur Interpolation von Daten. Für eine ausführliche Einführung in komplexe neuronale Netze empfehle ich die Lektüre des Artikels „A Survey of Complex-Valued Neural Networks“. In dieser Implementierung werden wir bestehende Klassen von neuronalen Schichten verwenden, die den reellen und den imaginären Teil getrennt interpolieren und dann nach der folgenden Formel kombinieren:
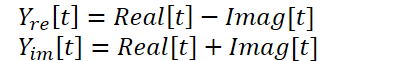
Um diese Operationen durchzuführen, erstellen wir den Kernel ComplexLayer. Der Kernel-Algorithmus ist recht einfach. Wir identifizieren einfach einen Thread in zwei Dimensionen, der auf eine Zeile und eine Spalte von Matrizen verweist. Wir bestimmen die Verschiebungen in den Datenpuffern und führen einfache mathematische Operationen durch.
__kernel void ComplexLayer(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im ) { size_t i = get_global_id(0); size_t j = get_global_id(1); size_t total_i = get_global_size(0); size_t total_j = get_global_size(1); uint shift = i * total_j + j; //--- outputs_re[shift] = inputs_re[shift] - inputs_im[shift]; outputs_im[shift] = inputs_im[shift] + inputs_re[shift]; }
Der Backpropagation-Kernel von ComplexLayerGradient wird auf ähnliche Weise konstruiert. Sie können diesen Code anhand der beigefügten Dateien studieren.
Damit sind unsere Operationen auf der Programmseite von OpenCL abgeschlossen.
2.3 Erstellen einer FITS-Methodenklasse
Nachdem wir die Arbeit mit den OpenCL abgeschlossen haben, gehen wir zum Hauptprogramm über, wo wir die Klasse CNeuronFITSOCL erstellen, um die von den Autoren der FITS-Methode vorgeschlagenen Ansätze zu implementieren. Die neue Klasse wird von der Neuronenschicht-Basisklasse CNeuronBaseOCL abgeleitet. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronFITSOCL : public CNeuronBaseOCL { protected: //--- uint iWindow; uint iWindowOut; uint iCount; uint iFFTin; uint iIFFTin; //--- CNeuronBaseOCL cInputsRe; CNeuronBaseOCL cInputsIm; CNeuronBaseOCL cFFTRe; CNeuronBaseOCL cFFTIm; CNeuronDropoutOCL cDropRe; CNeuronDropoutOCL cDropIm; CNeuronConvOCL cInsideRe1; CNeuronConvOCL cInsideIm1; CNeuronConvOCL cInsideRe2; CNeuronConvOCL cInsideIm2; CNeuronBaseOCL cComplexRe; CNeuronBaseOCL cComplexIm; CNeuronBaseOCL cIFFTRe; CNeuronBaseOCL cIFFTIm; CBufferFloat cClear; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool ComplexLayerOut(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); virtual bool ComplexLayerGradient(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFITSOCL(void) {}; ~CNeuronFITSOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFITSOCL; } virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
Die Struktur der neuen Klasse enthält eine ganze Reihe von Deklarationen interner neuronaler Schichtobjekte. Dies erscheint angesichts der erwarteten Einfachheit des Modells seltsam. Bitte beachten Sie jedoch, dass wir nur die Parameter von 4 verschachtelten neuronalen Schichten trainieren, die für die Dateninterpolation zuständig sind (cInsideRe* und cInsideIm*). Andere Objekte dienen als Zwischenpuffer für Daten. Wir werden ihren Zweck bei der Umsetzung der Methoden berücksichtigen.
Achten Sie auch darauf, dass wir zwei CNeuronDropoutOCL-Schichten haben. In dieser Implementierung werde ich keine LFP verwenden, bei der eine bestimmte Grenzfrequenz festgelegt wird. Hier erinnerte ich mich an die Experimente der Autoren der FEDformer-Methode, die über die Effizienz der Abtastung eines Satzes von Frequenzmerkmalen sprechen. Deshalb habe ich beschlossen, eine Dropout-Ebene zu verwenden, um eine bestimmte Anzahl von zufälligen Frequenzmerkmalen auf Null zu setzen.
Wir deklarieren alle internen Objekte als statisch und können daher den Konstruktor und Destruktor der Klasse leer lassen. Objekte und alle lokalen Variablen werden in der Init-Methode initialisiert. Wie üblich geben wir in den Methodenparametern Variablen an, die eine eindeutige Bestimmung der gewünschten Struktur des Objekts ermöglichen. Hier haben wir die Fenstergrößen der unitären Eingangs- und Ausgangsdatenfolge (window und window_out), die Anzahl der unitären Zeitreihen (count) und den Anteil der genullten Frequenzmerkmale (dropout). Beachten Sie, dass wir eine einheitliche Schicht aufbauen und die Größe der Fenster sowohl der Quelldaten als auch der Ergebnisse eine beliebige positive Zahl sein kann, ohne dass die Anforderungen des FFT-Algorithmus berücksichtigt werden müssen. Wie wir gesehen haben, erfordert der angegebene Algorithmus eine Eingabegröße, die einer der Potenzen von 2 entspricht.
bool CNeuronFITSOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch) { if(window <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false;
Im Hauptteil der Methode führen wir zunächst einen kleinen Kontrollblock aus, in dem wir die Größe des Eingabefensters überprüfen (muss eine positive Zahl sein) und die gleichnamige Methode der Elternklasse aufrufen. Wie Sie wissen, implementiert die Methode der Elternklasse zusätzliche Steuerelemente und die Initialisierung der geerbten Objekte.
Nach erfolgreicher Übergabe des Kontrollblocks speichern wir die erhaltenen Parameter in lokalen Variablen.
//--- Save constants
iWindow = window;
iWindowOut = window_out;
iCount = count;
activation=None;
Wir bestimmen die Größen der Tensoren für die direkte und die inverse FFT in Form der nächstliegenden großen Potenzen von 2 zu den entsprechenden erhaltenen Parametern.
//--- Calculate FFT and iFFT size int power = int(MathLog(iWindow) / M_LN2); if(MathPow(2, power) != iWindow) power++; iFFTin = uint(MathPow(2, power)); power = int(MathLog(iWindowOut) / M_LN2); if(MathPow(2, power) != iWindowOut) power++; iIFFTin = uint(MathPow(2, power));
Dann folgt der Block zur Initialisierung der verschachtelten Objekte. cInputs*-Objekte werden als Eingangsdatenpuffer für die direkte FFT verwendet. Ihre Größe ist gleich dem Produkt aus der Größe der unitären Sequenz am Eingang des jeweiligen Blocks und der Anzahl der analysierten Sequenzen.
if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
Die Objekte zur Aufzeichnung der Ergebnisse der direkten Fourier-Zerlegung cFFT* haben eine ähnliche Größe.
if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
Als Nächstes deklarieren wir Dropout-Objekte. Ihre Größe ist gleich groß wie die vorherigen.
if(!cDropRe.Init(0, 4, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false; if(!cDropIm.Init(0, 5, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false;
Für die Sequenzinterpolation wird ein MLP mit einer versteckten Schicht und tanh-Aktivierung zwischen den Schichten verwendet. Am Ausgang des Blocks erhalten wir Daten, die den Anforderungen des inversen FFT-Blocks entsprechen.
if(!cInsideRe1.Init(0, 6, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe1.SetActivationFunction(TANH); if(!cInsideIm1.Init(0, 7, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm1.SetActivationFunction(TANH); if(!cInsideRe2.Init(0, 8, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe2.SetActivationFunction(None); if(!cInsideIm2.Init(0, 9, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm2.SetActivationFunction(None);
Wir werden die Interpolationsergebnisse in cComplex*-Objekten zusammenfassen.
if(!cComplexRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Nach der FITS-Methode werden die interpolierten Sequenzen einer inversen Fourier-Zerlegung unterzogen, bei der die Frequenzmerkmale in eine Zeitreihe umgewandelt werden. Wir werden die Ergebnisse dieser Operation in cIFFT-Objekte schreiben.
if(!cIFFTRe.Init(0, 12, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 13, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Zusätzlich werden wir einen Hilfspuffer mit Nullwerten deklarieren, den wir zur Ergänzung der fehlenden Werte verwenden werden.
if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Nachdem alle verschachtelten Objekte erfolgreich initialisiert wurden, schließen wir die Methode ab.
Der nächste Schritt ist die Implementierung der Klassenfunktionalität. Bevor wir jedoch direkt zu den Feedforward- und Backpropagation-Methoden übergehen, müssen wir einige vorbereitende Arbeiten durchführen, um die Funktionalität für die Platzierung der oben erstellten Kernel in der Ausführungswarteschlange zu implementieren. Solche Kernel haben ähnliche Algorithmen. Im Rahmen dieses Artikels werden wir nur die Methode zum Aufruf des Fast-Fourier-Transformationskerns CNeuronFITSOCL::FFT betrachten.
bool CNeuronFITSOCL::FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false) { uint global_work_offset[1] = {0}; uint global_work_size[1] = {iCount};
In den Methodenparametern übergeben wir Zeiger auf 4 benötigte Datenpuffer (2 für Eingabedaten und 2 für Ergebnisse) und ein Flag für die Operationsrichtung.
Im Hauptteil der Methode definieren wir den Aufgabenbereich. Wir verwenden hier einen eindimensionalen Problemraum in der Anzahl der zu analysierenden Sequenzen.
Dann übergeben wir die Parameter an den Kernel. Zunächst übergeben wir Zeiger auf die Quelldatenpuffer.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_re, inp_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_im, (!!inp_im ? inp_im.GetIndex() : inp_re.GetIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Beachten Sie, dass wir die Möglichkeit zulassen, den Kernel ohne einen Puffer für den Imaginärteil des Signals zu starten. Wie Sie sich erinnern, haben wir hierfür das Flag input_complex im Kernel verwendet. Wenn jedoch nicht alle erforderlichen Parameter an den Kernel übergeben werden, wird ein Laufzeitfehler auftreten. Da es keinen imaginären Teil des Puffers gibt, geben wir einen Zeiger auf den reellen Teil des Puffers des Signals an und setzen das entsprechende Flag auf false.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_complex, int(!!inp_im))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Dann übergeben wir Zeiger auf die Ergebnispuffer.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_re, out_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_im, out_im.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Wir übergeben auch die Größen der Eingabe- und Ausgabefenster. Letzteres ist eine Potenz von 2. Bitte beachten Sie, dass wir die Fenstergrößen berechnen, anstatt sie aus Konstanten zu übernehmen. Das liegt daran, dass wir diese Methode sowohl für direkte als auch für inverse Fourier-Transformationen verwenden werden, die mit unterschiedlichen Puffern und dementsprechend mit unterschiedlichen Eingangs- und Ausgangsfenstern durchgeführt werden.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_window, (int)(inp_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_output_window, (int)(out_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Als letzten Parameter übergeben wir ein Flag, das angibt, ob der Algorithmus für die inverse Transformation verwendet werden soll.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_reverse, int(reverse))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Den Kernel stellen wir in die Ausführungswarteschlange.
if(!OpenCL.Execute(def_k_FFT, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
In jeder Phase kontrollieren wir den Ablauf der Operationen und geben den logischen Wert der durchgeführten Operationen an den Aufrufer zurück.
Die Methoden CNeuronFITSOCL::ComplexLayerOut und CNeuronFITSOCL::ComplexLayerGradient, in denen die gleichnamigen Kernel aufgerufen werden, sind nach einem ähnlichen Prinzip aufgebaut. Sie finden sie in der Anlage.
Nach Abschluss der vorbereitenden Arbeiten gehen wir zur Konstruktion des Algorithmus‘ des Vorwärtsdurchgangs über, der in der Methode CNeuronFITSOCL::feedForward beschrieben wird.
In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, die die Eingabedaten übergibt. Im Hauptteil der Methode wird der empfangene Zeiger sofort überprüft.
bool CNeuronFITSOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Das FITS-System erfordert eine vorläufige Normalisierung der Daten. Wir gehen davon aus, dass die Datennormalisierung in den vorangehenden neuronalen Schichten durchgeführt wird und lassen diesen Schritt in dieser Klasse aus.
Wir übersetzen die erhaltenen Daten in den Frequenzbereich mit einer direkten schnellen Fourier-Transformation. Dazu rufen wir die entsprechende Methode auf (ihr Algorithmus ist oben dargestellt).
//--- FFT if(!FFT(NeuronOCL.getOutput(), NULL, cFFTRe.getOutput(), cFFTIm.getOutput(), false)) return false;
Wir klaffen die resultierenden Frequenzcharakteristiken mit Hilfe von Dropout-Schichten.
//--- DropOut if(!cDropRe.FeedForward(cFFTRe.AsObject())) return false; if(!cDropIm.FeedForward(cFFTIm.AsObject())) return false;
Danach interpolieren wir die Frequenzmerkmale mit der Größe der vorhergesagten Werte
//--- Complex Layer if(!cInsideRe1.FeedForward(cDropRe.AsObject())) return false; if(!cInsideRe2.FeedForward(cInsideRe1.AsObject())) return false; if(!cInsideIm1.FeedForward(cDropIm.AsObject())) return false; if(!cInsideIm2.FeedForward(cInsideIm1.AsObject())) return false;
und kombinieren die getrennten Interpolationen von reellen und den imaginären Teil des Signals.
if(!ComplexLayerOut(cInsideRe2.getOutput(), cInsideIm2.getOutput(), cComplexRe.getOutput(), cComplexIm.getOutput())) return false;
Das Ausgangssignal wird durch inverse Dekomposition in den zeitlichen Bereich zurückgeführt.
//--- iFFT if(!FFT(cComplexRe.getOutput(), cComplexIm.getOutput(), cIFFTRe.getOutput(), cIFFTIm.getOutput(), true)) return false;
Bitte beachten Sie, dass die resultierende Prognosereihe die Größe der Sequenz, die wir an die nachfolgende neuronale Schicht weitergeben müssen, überschreiten kann. Daher wählen wir den gewünschten Block aus dem reellen Teil des Signals aus.
//--- To Output if(!DeConcat(Output, cIFFTRe.getGradient(), cIFFTRe.getOutput(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false; //--- return true; }
Vergessen wir nicht, die Ergebnisse bei jedem Schritt zu kontrollieren. Nachdem alle Iterationen abgeschlossen sind, geben wir das logische Ergebnis der durchgeführten Operationen an den Aufrufer zurück.
Nach der Implementierung des Vorwärtsdurchgangs gehen wir zur Konstruktion der Backpropagation-Methoden über. Die Methode CNeuronFITSOCL::calcInputGradients überträgt den Fehlergradienten auf alle internen Objekte und die vorherige Schicht entsprechend ihrem Einfluss auf das Endergebnis.
bool CNeuronFITSOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorherigen Schicht, an das wir den Fehlergradienten übergeben müssen. Und im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers.
Der Fehlergradient, den wir von der nächsten Ebene erhalten haben, ist bereits im Gradientenpuffer gespeichert. Sie enthält jedoch nur den reellen Teil des Signals und nur bis zu einer bestimmten Vorhersagetiefe. Wir benötigen den Fehlergradienten sowohl für den reellen und auch für den imaginären Teil im Horizont des Gesamtsignals aus der inversen Transformation. Um solche Daten zu generieren, gehen wir von zwei Annahmen aus:
- Am Ausgang des Blocks für die inverse Fourier-Transformation während des Vorwärtsdurchgangs erwarten wir diskrete Zeitreihenwerte. In diesem Fall entspricht der reellen Teil des Signals der gewünschten Zeitreihe, und der Imaginärteil ist gleich (oder nahe bei) „0“. Daher ist der Fehler des Imaginärteils gleich seinem Wert mit umgekehrtem Vorzeichen.
- Da wir keine Informationen über die Korrektheit der Prognosewerte jenseits des gegebenen Planungshorizonts haben, vernachlässigen wir mögliche Abweichungen einfach und setzen den Fehler für sie auf „0“.
//--- Copy Gradients if(!SumAndNormilize(cIFFTIm.getOutput(), GetPointer(cClear), cIFFTIm.getGradient(), 1, false, 0, 0, 0, -1)) return false;
if(!Concat(Gradient, GetPointer(cClear), cIFFTRe.getGradient(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false;
Beachten Sie auch, dass der Fehlergradient in Form einer Zeitreihe dargestellt wird. Die Prognose wurde jedoch im Frequenzbereich erstellt. Daher müssen wir den Fehlergradienten auch in den Frequenzbereich übersetzen. Bei diesem Vorgang verwenden wir die schnelle Fourier-Transformation.
//--- FFT if(!FFT(cIFFTRe.getGradient(), cIFFTIm.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient(), false)) return false;
Wir verteilen die Frequenzmerkmale auf 2 MLPs mit reellen und den imaginären Teil.
//--- Complex Layer if(!ComplexLayerGradient(cInsideRe2.getGradient(), cInsideIm2.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient())) return false;
Dann verteilen wir den Fehlergradienten durch die MLP.
if(!cInsideRe1.calcHiddenGradients(cInsideRe2.AsObject())) return false; if(!cInsideIm1.calcHiddenGradients(cInsideIm2.AsObject())) return false; if(!cDropRe.calcHiddenGradients(cInsideRe1.AsObject())) return false; if(!cDropIm.calcHiddenGradients(cInsideIm1.AsObject())) return false;
Über die Dropout-Schicht wird der Fehlergradient an den Ausgang des Blocks für die direkte Fourier-Transformation weitergeleitet.
//--- Dropout if(!cFFTRe.calcHiddenGradients(cDropRe.AsObject())) return false; if(!cFFTIm.calcHiddenGradients(cDropIm.AsObject())) return false;
Nun müssen wir den Fehlergradienten aus dem Frequenzbereich in eine Zeitreihe umwandeln. Diese Operation wird mit Hilfe der inversen Transformation durchgeführt.
//--- IFFT if(!FFT(cFFTRe.getGradient(), cFFTIm.getGradient(), cInputsRe.getGradient(), cInputsIm.getGradient(), true)) return false;
Und schließlich geben wir nur den notwendigen Teil des tatsächlichen Fehlergradienten an die vorherige Schicht weiter.
//--- To Input Layer if(!DeConcat(NeuronOCL.getGradient(), cFFTIm.getGradient(), cFFTRe.getGradient(), iWindow, iFFTin - iWindow, iCount)) return false; //--- return true; }
Wie immer kontrollieren wir die Ausführung aller Operationen im Methodenkörper und geben am Ende einen logischen Wert für die Korrektheit der Operation an den Aufrufer zurück.
Dem Prozess der Fehlergradientenfortpflanzung folgt die Aktualisierung der Modellparameter. Dieser Prozess ist in der Methode CNeuronFITSOCL::updateInputWeights implementiert. Wie bereits erwähnt, enthalten von den vielen in der Klasse deklarierten Objekten nur die MLP-Schichten Lernparameter. Daher werden wir die Parameter dieser Ebenen in der folgenden Methode anpassen.
bool CNeuronFITSOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cInsideRe1.UpdateInputWeights(cDropRe.AsObject())) return false; if(!cInsideIm1.UpdateInputWeights(cDropIm.AsObject())) return false; if(!cInsideRe2.UpdateInputWeights(cInsideRe1.AsObject())) return false; if(!cInsideIm2.UpdateInputWeights(cInsideIm1.AsObject())) return false; //--- return true; }
Bei der Arbeit mit Datei-Operationsmethoden müssen wir auch die Tatsache berücksichtigen, dass wir eine große Anzahl von internen Objekten haben, die keine trainierbaren Parameter enthalten. Es macht keinen Sinn, relativ große Mengen an Informationen zu speichern, die keinen Wert haben. Deshalb rufen wir in der Datenspeicherungsmethode CNeuronFITSOCL::Save zunächst die gleichnamige Methode der Elternklasse auf.
bool CNeuronFITSOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
Danach speichern wir die Architekturkonstanten.
//--- Save constants if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iWindowOut)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iIFFTin)) < INT_VALUE) return false;
Und speichern Sie MLP-Objekte.
//--- Save objects if(!cInsideRe1.Save(file_handle)) return false; if(!cInsideIm1.Save(file_handle)) return false; if(!cInsideRe2.Save(file_handle)) return false; if(!cInsideIm2.Save(file_handle)) return false;
Fügen wir weitere Dropout-Blockobjekte hinzu.
if(!cDropRe.Save(file_handle)) return false; if(!cDropIm.Save(file_handle)) return false; //--- return true; }
Das war's. Die übrigen Objekte enthalten nur Datenpuffer, deren Informationen nur innerhalb eines Vorwärts-Rückwärts-Durchlaufs relevant sind. Deshalb speichern wir sie nicht und sparen so Speicherplatz. Aber alles hat seinen Preis: Wir müssen den Algorithmus der Datenlademethode CNeuronFITSOCL::Load verkomplizieren.
bool CNeuronFITSOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Bei dieser Methode spiegeln wir zunächst die Methode der Datenspeicherung:
- Rufen Sie die Methode der übergeordneten Klasse mit demselben Namen auf.
- Konstanten laden. Kontrolle des Erreichens des Endes der Datendatei.
//--- Load constants if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iWindowOut = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iIFFTin = uint(FileReadInteger(file_handle)); activation=None;
- Lesen Sie die MLP- und Dropout-Parameter ab.
//--- Load objects if(!LoadInsideLayer(file_handle, cInsideRe1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideRe2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropRe.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropIm.AsObject())) return false;
Nun müssen wir die fehlenden Objekte initialisieren. Hier wiederholen wir einen Teil des Codes aus der Initialisierungsmethode der Klasse.
//--- Init objects if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cComplexRe.Init(0, 8, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 9, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Damit ist unsere Arbeit zur Beschreibung der Methoden unserer neuen Klasse CNeuronFITSOCL und ihrer Algorithmen abgeschlossen. Den vollständigen Code dieser Klasse und alle ihre Methoden finden Sie im Anhang. Der Anhang enthält auch alle in diesem Artikel verwendeten Programme. Betrachten wir nun die Architektur des Modelltrainings.
2.4 Modellarchitektur
Die FITS-Methode wurde für die Zeitreihenanalyse und -prognose vorgeschlagen. Sie haben vielleicht schon geahnt, dass wir die vorgeschlagenen Ansätze im Environmental State Encoder verwenden werden. Seine Architektur wird in der Methode CreateEncoderDescriptions beschrieben.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
In den Methodenparametern erhalten wir einen Zeiger auf ein dynamisches Array-Objekt, um die Architektur des erstellten Modells zu speichern. Und im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers. Falls erforderlich, erstellen wir eine neue Instanz des dynamischen Array-Objekts.
Wie immer füttern wir das Modell mit „rohen“ Daten, die den aktuellen Zustand der Umwelt beschreiben.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die Daten werden in der Batch-Normalisierungsschicht vorverarbeitet. Dies bringt die Daten in eine vergleichbare Form und erhöht die Stabilität des Modelltrainingsprozesses.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Unsere Eingabedaten sind eine multivariate Zeitreihe. Jeder Datenblock enthält verschiedene Parameter, die eine Kerze der historischen Daten beschreiben. Um jedoch unitäre Sequenzen in unserem Datensatz zu analysieren, müssen wir den resultierenden Tensor transponieren.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
In diesem Stadium können die vorbereitenden Arbeiten als abgeschlossen betrachtet werden, und wir können zur Analyse und Vorhersage von unitären Zeitreihen übergehen. Wir implementieren diesen Prozess in dem Objekt unserer neuen Klasse.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFITSOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.activation = None; descr.window_out = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Im Hauptteil unserer Klasse haben wir fast die gesamte vorgeschlagene FITS-Methode implementiert. Am Ausgang der neuronalen Schicht erhalten wir Vorhersagewerte. Wir müssen also nur den Tensor der vorhergesagten Werte in die Dimension der erwarteten Ergebnisse transponieren.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Wir müssen auch die zuvor entfernten Parameter der statistischen Verteilung der Eingabedaten hinzufügen.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Wie Sie sehen können, ist das Modell für die Analyse und Vorhersage der nachfolgenden Zustände der Umwelt recht kurz, wie von den Autoren der FITS-Methode versprochen. Gleichzeitig hatten die von uns vorgenommenen Änderungen an der Modellarchitektur keinerlei Auswirkungen auf den Umfang oder das Format der Eingabedaten. Wir haben auch das Format der Modellausgabe nicht verändert. Daher können wir die zuvor erstellten Modellarchitekturen von Akteur und Kritiker ohne Änderungen verwenden. Darüber hinaus können wir für die Interaktion mit der Umgebung und die Modellschulung bereits erstellte EAs sowie zuvor gesammelte Schulungsdatensätze verwenden. Das Einzige, was wir ändern müssen, ist der Zeiger auf die latente Repräsentationsschicht des Umgebungszustands.
#define LatentLayer 3
Und im Anhang finden Sie den vollständigen Code aller hier verwendeten Programme. Es ist Zeit für einen Test.
3. Tests
Wir haben uns mit der FITS-Methode vertraut gemacht und ernsthaft an der Implementierung der vorgeschlagenen Ansätze mit MQL5 gearbeitet. Nun ist es an der Zeit, die Ergebnisse unserer Arbeit anhand echter historischer Daten zu testen. Wie zuvor werden wir die Modelle anhand historischer EURUSD-Daten mit dem Zeitrahmen H1 trainieren und testen. Um die Modelle zu trainieren, verwenden wir historische Daten für das gesamte Jahr 2023. Um das trainierte Modell zu testen, verwenden wir Daten vom Januar 2024.
Der Prozess der Modelltraining wurde im vorherigen Artikel beschrieben. Zunächst trainieren wir den Environment State Encoder, um die nachfolgenden Zustände vorherzusagen. Dann trainieren wir iterativ die Verhaltenspolitik des Akteurs, um eine maximale Rentabilität zu erreichen.
Wie erwartet, erwies sich das Modell Encoder als recht leicht. Der Lernprozess ist relativ schnell und reibungslos. Trotz seiner geringen Größe zeigt das Modell eine vergleichbare Leistung wie das im vorherigen Artikel besprochene FEDformer-Modell. Es ist erwähnenswert, dass die Größe des Modells fast 84 Mal kleiner ist.

Die Trainingsphase des Akteurs war jedoch enttäuschend. Das Modell ist nur in bestimmten historischen Abschnitten in der Lage, Rentabilität zu demonstrieren. Die nachstehenden Saldenkurven, die über den Testbereich hinausgehen, ist ein recht schnelles Wachstum in den ersten zehn Tagen des Monats zu erkennen. Aber das zweite Jahrzehnt ist verlustreich mit seltenen gewinnbringenden Geschäften. Das dritte Jahrzehnt nähert sich der Parität zwischen gewinnbringenden und verlustreichen Geschäften.

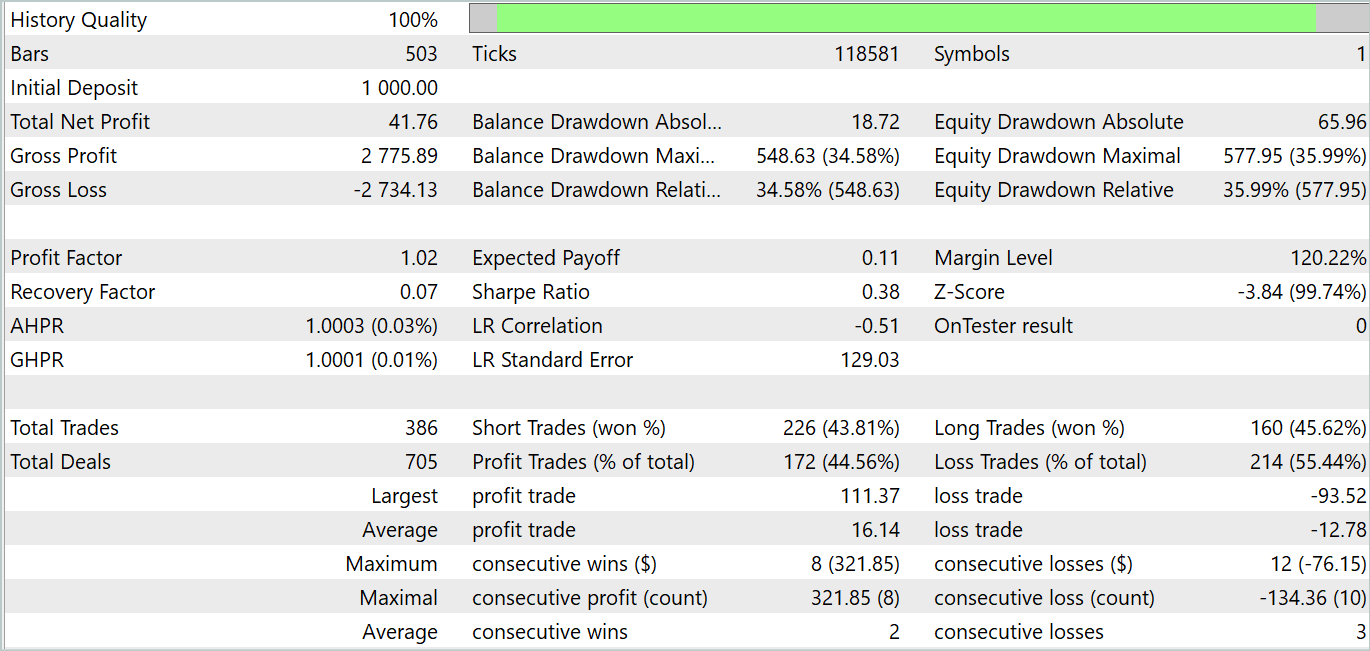
Insgesamt haben wir in diesem Monat ein kleines Einkommen erzielt. Hier ist festzustellen, dass die Größe der größten und durchschnittlich gewinnbringenden Geschäfte die entsprechende Verlustmetrik übersteigt. Die Anzahl der gewinnbringenden Geschäfte ist jedoch weniger als die Hälfte, was die Überlegenheit des durchschnittlich gewinnbringenden Geschäfts zunichte macht.
An dieser Stelle kann festgehalten werden, dass die Testergebnisse teilweise die Schlussfolgerungen der Autoren der Methode FEDformer zum Teil bestätigen: Da die Eingabedaten keine eindeutige Periodizität aufweisen, ist DFT nicht in der Lage, den Zeitpunkt zu bestimmen, an dem sich der Trend ändert.
Schlussfolgerung
In diesem Artikel haben wir eine neue FITS-Methode für die Zeitreihenanalyse und -prognose erörtert. Das Hauptmerkmal dieser Methode ist die Analyse und Vorhersage von Zeitreihen im Bereich der Frequenzmerkmale. Da die Methode den Algorithmus der direkten und inversen schnellen Fourier-Transformation verwendet, können wir mit bekannten diskreten Zeitreihen am Eingang und Ausgang des Modells arbeiten. Dank dieser Eigenschaft kann die vorgeschlagene leichtgewichtige Architektur in vielen Bereichen eingesetzt werden, in denen Zeitreihenanalysen und -vorhersagen verwendet werden.
Im praktischen Teil dieses Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben die Modelle anhand echter historischer Daten trainiert und getestet. Leider brachten die Tests nicht das gewünschte Ergebnis. Ich möchte jedoch darauf aufmerksam machen, dass die vorgestellten Ergebnisse nur für die vorgestellte Implementierung der vorgeschlagenen Ansätze relevant sind. Die Ergebnisse könnten anders ausfallen, wenn wir den Algorithmus des Originalautors verwenden würden.
Referenzen
- FITS: Modeling Time Series with 10k Parameters
- A Survey of Complex-Valued Neural Networks
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14913
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Algorithmus für die künstliche, kooperative Suche (Artificial Cooperative Search, ACS)
Algorithmus für die künstliche, kooperative Suche (Artificial Cooperative Search, ACS)
 Nachrichtenhandel leicht gemacht (Teil 2): Risikomanagement
Nachrichtenhandel leicht gemacht (Teil 2): Risikomanagement
 Beispiel für stochastische Optimierung und optimale Kontrolle
Beispiel für stochastische Optimierung und optimale Kontrolle
 Visualisierung der Geschäfte auf dem Chart (Teil 1): Auswahl eines Zeitraums für die Analyse
Visualisierung der Geschäfte auf dem Chart (Teil 1): Auswahl eines Zeitraums für die Analyse
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.