Beispiel für stochastische Optimierung und optimale Kontrolle

Einführung in die stochastische Modellierung und Kontrolloptimierung

Stochastische Modellierung und Kontrolloptimierung sind mathematische Methoden, die helfen, Probleme unter Unsicherheit zu lösen. Sie werden im Finanzwesen, im Ingenieurwesen, in der künstlichen Intelligenz und in vielen anderen Bereichen eingesetzt.

Die stochastische Modellierung wird verwendet, um Systeme mit Zufallselementen zu beschreiben, wie z. B. Kursbewegungen an der Börse oder eine Warteschlange in einem Restaurant. Sie basiert auf Zufallsvariablen, Wahrscheinlichkeitsverteilungen und stochastischen Prozessen. Methoden wie Monte Carlo und Markov-Ketten können diese Prozesse modellieren und ihr Verhalten vorhersagen.

Die Steuerungsoptimierung hilft Ihnen, bessere Lösungen für die Steuerung von Systemen zu finden. Sie wird eingesetzt, um verschiedene Prozesse zu automatisieren und zu verbessern, vom Autofahren bis zum Betrieb von Chemieanlagen. Zu den grundlegenden Methoden gehören lineare quadratische Regler, modellprädiktive Steuerung und Verstärkungslernen. Die stochastische Kontrolloptimierung kombiniert beide Ansätze und wird auf Probleme angewandt, bei denen Entscheidungen in Ermangelung vollständiger Informationen über die Zukunft getroffen werden müssen, z. B. bei Investitionen oder im Lieferkettenmanagement.

Diese Methoden ermöglichen es uns, unsichere Systeme zu modellieren und fundierte Entscheidungen in komplexen Umgebungen zu treffen, was sie zu wichtigen Instrumenten in der modernen Welt macht.

EA

Der SMOC-Advisor (Smart Money Optimal Control) verwendet eine Kombination aus technischen Indikatoren, mathematischen Modellen und Risikomanagementmethoden, um Handelsentscheidungen auf dem Forex-Markt zu treffen - ein einfaches Beispiel, das seine Fähigkeiten demonstriert.

Hauptmerkmale:

1. Prädiktives Management-Modell: Der EA verwendet einen optimalen Verwaltungsalgorithmus, um zukünftige Kursbewegungen vorherzusagen und Handelsentscheidungen zu treffen.
2. Adaptive Parameter: Das System passt den Prognosehorizont und die Losgröße in Abhängigkeit von der Marktvolatilität und dem Kontoverlust an.
3. Mehrere technische Indikatoren: Enthält einfache gleitende Durchschnitte (SMA), parabolische SAR, Relative Strength Index (RSI) und Average True Range (ATR) für Trend- und Volatilitätsanalysen.
4. Dynamischer Stop Loss und Take Profit: Der EA berechnet und aktualisiert SL- und TP-Levels basierend auf der Marktvolatilität.
5. Risikomanagement: Enthält Funktionen zur Anpassung der Positionsgröße auf der Grundlage von Kontostand und Drawdown.

Mögliche Anwendungsbereiche:

• Mittel- und langfristige Handelsstrategien
• Märkte mit ausgeprägten Trends
• Portfolios, die ein komplexes Risikomanagement erfordern

Vorteile:

1. Adaptiver Ansatz: Das System passt sich an die sich ändernden Marktbedingungen an, was seine Widerstandsfähigkeit erhöhen kann.
2. Komplexe Analyse: Durch die Kombination mehrerer Indikatoren und mathematischer Modelle soll sie verschiedene Aspekte des Marktverhaltens widerspiegeln.
3. Risikoberücksichtigung: Der Berater bietet Schutz gegen Drawdowns und eine dynamische Bestimmung der Positionsgröße.
4. Ausführliche Protokollierung: Zur Leistungsanalyse und Fehlersuche wird eine Protokolldatei geführt.

Nachteile

1. Komplexität: Komplexe Algorithmen können dazu führen, dass das System schwer zu verstehen und zu optimieren ist.
2. Sehr rechenintensiv: Berechnungen zur optimalen Steuerung können rechenintensiv sein, was ihre Verwendung auf weniger leistungsfähigen Systemen einschränken kann.
3. Potenzielle Überanpassung: Bei einer großen Anzahl von Parametern und Indikatoren besteht die Gefahr der Überanpassung an historische Daten.
4. Marktannahme: Die Wirksamkeit der Strategie beruht auf der Annahme, dass das Kursverhalten der Vergangenheit künftige Bewegungen vorhersagen kann, was auf den Finanzmärkten nicht immer der Fall ist.

Hauptmerkmale des SMOC-Beraters

Modellprädiktive Steuerung (MPC): Der EA verwendet einen optimalen Kontrollalgorithmus, um zukünftige Kursbewegungen vorherzusagen und Handelsentscheidungen zu treffen. Dies wird durch die Funktion OptimalControl() realisiert.

//+------------------------------------------------------------------+
//| Function for optimal control using Model Predictive Control      |
//+------------------------------------------------------------------+
int OptimalControl( double currentPrice)
  {
   int predictionHorizon = CalculateAdaptiveHorizon();
   double mu = EstimateDrift();
   double sigma = EstimateVolatility();
   double baseThreshold = 0.001 ;
   double decisionThreshold = baseThreshold * ( 1 + ( 1 - successRate));
   double dt = 1.0 / 1440.0 ;

   double bestExpectedReturn = - DBL_MAX ;
   int bestDecision = 0 ;
   double bestU1 = 0 , bestU2 = 0 ;

// Optimize the search space
   double u1Start = 0.01 , u1End = 0.99 , u1Step = 0.01 ;
   double u2Start = 0.01 , u2End = 0.99 , u2Step = 0.01 ;

// Calculate historical average price
   int lookbackPeriod = 20 ; // You can adjust this
   double historicalPrices[];
   ArraySetAsSeries (historicalPrices, true );
   CopyClose ( Symbol (), PERIOD_CURRENT , 0 , lookbackPeriod, historicalPrices);
   double avgHistoricalPrice = ArraySum(historicalPrices) / lookbackPeriod;

   for ( double u1 = u1Start; u1 <= u1End; u1 += u1Step)
     {
       for ( double u2 = u2Start; u2 <= u2End; u2 += u2Step)
        {
         double expectedReturn = CalculateExpectedReturn(currentPrice, mu, sigma, dt, predictionHorizon, u1, u2);

         // Compare with historical average
         if (currentPrice > avgHistoricalPrice)
           {
            expectedReturn *= - 1 ; // Invert expected return to favor selling when price is high
           }

         if (expectedReturn > bestExpectedReturn)
           {
            bestExpectedReturn = expectedReturn;
            bestU1 = u1;
            bestU2 = u2;
           }
        }
     }

   LogMessage( StringFormat ( "OptimalControl - Best u1: %f, Best u2: %f, Best Expected Return: %f, Decision Threshold %f" ,
                           bestU1, bestU2, bestExpectedReturn, decisionThreshold));

   if (bestExpectedReturn > decisionThreshold)
       return 1 ; // Buy
   if (bestExpectedReturn < decisionThreshold)
       return - 1 ; // Sell
   return 0 ; // Hold
  }

Dabei wird die Model Predictive Control (MPC) eingesetzt, um optimale Handelsentscheidungen zu treffen. Die Funktion OptimalControl ist das Herzstück dieses Algorithmus, der auf der Grundlage der aktuellen Marktbedingungen und -prognosen bestimmt, ob gekauft, verkauft oder gehalten werden soll.

Die Funktion OptimalControl nimmt den aktuellen Kurs als Eingabe und gibt eine ganze Zahl zurück, die die Handelsentscheidung darstellt:

• 1 für Kaufen
• -1 für Verkaufen
• 0 für Halten

Wichtige Komponenten

1. Adaptiver Vorhersagehorizont: Die Funktion berechnet einen adaptiven Prognosehorizont, sodass der Algorithmus die Prognosespanne je nach Marktbedingungen anpassen kann.
2. Bewertung der Marktparameter: Bewertet die wichtigsten Marktparameter:
   • Drift (μ): Erwartete Rendite eines Vermögenswerts
   • Volatilität (σ): die Änderungsrate des Preises eines Vermögenswerts.
3. Entscheidungsschwelle: Der dynamische Schwellenwert wird auf der Grundlage des Basisschwellenwerts und der Erfolgsquote des Algorithmus berechnet. Dadurch wird die Empfindlichkeit des Algorithmus an Marktveränderungen angepasst.
4. Optimierungsprozess: Die Funktion nutzt die Gittersuche, um zwei Regelparameter (u1 und u2) in einem definierten Suchraum zu optimieren.
5. Historischer Vergleich der Preise: Der aktuelle Kurs wird mit dem historischen Durchschnitt verglichen, um die Strategie anzupassen, je nachdem, ob der aktuelle Kurs relativ hoch oder niedrig ist.
6. Berechnung der erwarteten Rendite: Für jede Kombination von Kontrollparametern wird die erwartete Rendite mit einer separaten Funktion berechnet (in diesem Codeausschnitt nicht gezeigt).
7. Entscheidungsfindung: Auf der Grundlage der besten erwarteten Rendite und der Entscheidungsschwelle wird entschieden, ob der Vermögenswert gekauft, verkauft oder gehalten werden soll.

Ausführliche Überprüfung

1. Die Funktion beginnt mit der Initialisierung von Variablen und der Berechnung der erforderlichen Parameter.
2. Anschließend wird eine verschachtelte Schleife zur Ermittlung der optimalen Steuerungsparameter (u1 und u2) eingeleitet.
3. Für jede Kombination von u1 und u2 wird die erwartete Rendite berechnet.
4. Liegt der aktuelle Kurs über dem historischen Durchschnitt, kehrt er die erwartete Rendite um. Dies führt zu einer Tendenz, bei hohen Preisen zu verkaufen und bei niedrigen Preisen zu kaufen.
5. Er verfolgt die beste erwartete Rendite und die entsprechenden Benchmarks.
6. Nach der Optimierung werden die besten Parameter und die erwartete Rentabilität aufgezeichnet.
7. Schließlich vergleicht er die beste erwartete Rendite mit dem Schwellenwert für eine Handelsentscheidung.

Wichtige Ideen

• Der Algorithmus passt sich mit Hilfe eines adaptiven Horizonts und einer dynamischen Schwelle an die Marktbedingungen an.
• Dabei geht es sowohl um kurzfristige Optimierung (mit dem MPC-Ansatz) als auch um das langfristige Verständnis von Trends (mit Hilfe historischer Preisvergleiche).
• Die Verwendung der Gittersuche für die Optimierung ermöglicht eine gründliche Erkundung des Parameterraums, was zu robusteren Entscheidungen führen kann.

Mögliche Verbesserungen

1. Die Gittersuche kann durch einen effizienteren Optimierungsalgorithmus ersetzt werden, um die Leistung zu verbessern.
2. Der Vergleich historischer Preise kann komplexer gestaltet werden, etwa durch Einbeziehung mehrerer Zeiträume.
3. Risikomanagementfunktionen können hinzugefügt werden, um ein Gleichgewicht zwischen Renditeoptimierung und Risikominimierung herzustellen.

 /+------------------------------------------------------------------+
//| Calculate expected return for given parameters                   |
//+------------------------------------------------------------------+
double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)
  {
   double tempPrice = currentPrice;
   double totalReturn = 0 ;

   for ( int i = 0 ; i < horizon; i++)
     {
       double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);
       double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);
      totalReturn += nextPrice - tempPrice;
      tempPrice = nextPrice;
     }

   return totalReturn / horizon;
  }

Sie ist eine entscheidende Komponente in Finanzmodellen und algorithmischen Handelssystemen. Diese Funktion schätzt die erwartete Rendite eines Vermögenswerts über einen bestimmten Zeithorizont anhand eines stochastischen Prozesses, der als geometrische Brownsche Bewegung (GBM) bekannt ist.

 double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)

Parameter

1. currentPrice : Aktueller Preis des Vermögenswerts
2. mu : Driftparameter (erwartete Rendite)
3. sigma: Volatilitätsparameter
4. dt: Zeitschritt (in der Regel 1/Anzahl der Schritte pro Jahr)
5. Horizon: Die Anzahl der zu simulierenden Zeitschritte.
6. u1, u2: Zufallszahlen, die zur Erzeugung normalverteilter Zufallsvariablen verwendet werden.

Überblick über die Funktionen

Diese Funktion modelliert den Kursverlauf eines Vermögenswerts anhand des geometrischen Brownschen Bewegungsmodells, das in der Finanzmathematik zur Modellierung von Aktienkursen weit verbreitet ist. Anschließend wird die durchschnittliche Rendite entlang des modellierten Pfads berechnet.

Ausführliche Erklärung

1. Initialisierung:
   • tempPreis wird mit dem aktuellen Preis initialisiert.
   • totalReturn wird auf 0 gesetzt, um die Erträge zu kumulieren.
2. Simulationsschleife: Die Funktion tritt in eine Schleife ein, die den Horizont mal durchläuft. In jeder Iteration: Erzeugen einer zufälligen, normalverteileten Variable:

 double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);

Diese Zeile implementiert die Box-Muller-Transformation zur Erzeugung einer standardnormalen Zufallsvariablen. Dies ist eine Schlüsselkomponente bei der Modellierung eines Random Walk bei Vermögenspreisen.

Berechnen des nächsten Preises:

 double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);

Diese Zeile setzt die Formel für die geometrische Brownsche Bewegung um:

• (mu - 0,5 * sigma * sigma) * dt ist die Driftkomponente
• sigma * MathSqrt(dt) * Z ist die zufällige Schockkomponente

Kumulierte Rendite:

totalReturn += nextPrice - tempPrice;

Die Funktion berechnet und kumuliert den Ertrag für jeden Schritt.

Preis-Update:

tempPrice = nextPrice;

Der aktuelle Preis wird bei der nächsten Iteration aktualisiert.

Berechnen Sie den Durchschnittsertrag:

 return totalReturn / horizon;

Die Funktion liefert die durchschnittliche Rendite über den simulierten Horizont.

Bedeutung für die Finanzmodellierung

1. Risikobewertung: Durch die Simulation mehrerer Preispfade hilft diese Funktion, die mit einem Vermögenswert verbundenen potenziellen Risiken zu bewerten.
2. Preisgestaltung für Optionen: Diese Art der Modellierung ist grundlegend für Optionspreismodelle, insbesondere für Monte-Carlo-Methoden.
3. Optimierung des Portfolios: Erwartete Renditen sind wichtige Inputs für Algorithmen zur Portfoliooptimierung.
4. Handelsstrategien: Algorithmische Handelsstrategien verwenden häufig die erwarteten Erträge, um Kauf-/Verkaufsentscheidungen zu treffen.

Beschränkungen und Überlegungen

1. Modell-Annahmen: Das GBM-Modell geht davon aus, dass die Renditen normalverteilt und unabhängig sind, was auf realen Märkten nicht immer der Fall sein muss.
2. Schätzung der Parameter: Die Genauigkeit der Funktion hängt weitgehend von der richtigen Schätzung von mu und sigma ab.
3. Einzelne Simulation: Diese Funktion führt eine einzelne Simulation durch. In der Praxis werden oft mehrere Simulationen durchgeführt, um eine zuverlässigere Schätzung zu erhalten.
4. Zeithorizont: Die Wahl des Horizonts und von dt kann die Ergebnisse erheblich beeinflussen und sollte je nach Anwendungsfall sorgfältig ausgewählt werden.

Diese Funktion ist ein grundlegender Baustein in der quantitativen Finanzwirtschaft, da sie eine Möglichkeit bietet, künftige Erträge auf der Grundlage aktueller Marktparameter zu schätzen. Seine Implementierung in Handelsalgorithmen ermöglicht eine datengesteuerte Entscheidungsfindung in komplexen Finanzumgebungen.

Adaptive Parameter: Das System passt seinen Prognosehorizont und die Losgröße auf der Grundlage der Marktvolatilität und des Kontoverlusts an. Dies wird durch Funktionen wie CalculateAdaptiveHorizon() und AdjustLotSizeForDrawdown() erreicht.

//+------------------------------------------------------------------+
//| Calculate adaptive horizon                                       |
//+------------------------------------------------------------------+
int CalculateAdaptiveHorizon()
  {
   double currentVolatility = EstimateVolatility();
   int baseHorizon = 5 ;
   return MathMax (baseHorizon, MathMin ( 20 , ( int )(baseHorizon * ( 1 + currentVolatility))));
  }

 // Función para ajustar el tamaño del lote basado en drawdown
double AdjustLotSizeForDrawdown()
  {
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   double drawdown = (maxBalance - currentEquity) / maxBalance;

   double baseLotSize = CalculateDynamicLotSize();

   if (drawdown > 0.1 ) // 10% drawdown
     {
       return baseLotSize * 0.5 ; // Reducir el tamaño del lote a la mitad
     }
   else
       if (consecutiveLosses > 3 )
        {
         return baseLotSize * 0.75 ; // Reducir el tamaño del lote en un 25%
        }

   return baseLotSize;
  }

Dies ist eine wichtige Komponente des Risikomanagements im Handel. Mit dieser Funktion wird die Größe des Handelsloses auf der Grundlage des aktuellen Kontoverlustes und der Anzahl der aufeinanderfolgenden Verluste angepasst.

Überblick über die Funktionen

Die Funktion AdjustLotSizeForDrawdown dient der dynamischen Anpassung der Handelslosgröße, um Risiken unter volatilen Marktbedingungen zu steuern. Dabei werden zwei Hauptfaktoren berücksichtigt:

1. Aktueller Drawdown des Handelskontos
2. Anzahl der aufeinanderfolgenden Debakel

Wichtige Komponenten

1. Statische Variablen:
   • consecutiveLosses: Verfolgt die Anzahl der aufeinanderfolgenden Verlustgeschäfte
   • maxBalance: hält den maximalen Saldo des Kontos aufrecht
2. Informationen zum Konto:
   • currentBalance: Aktueller Saldo des Handelskontos
   • currentEquity: Aktuelles Kapital des Handelskontos
3. Berechnung des Drawdowns: Der Drawdown wird als prozentualer Rückgang vom maximalen Saldo (balance) bis zum aktuellen Kapital (equity) berechnet.
4. Basislosgröße: Die Funktion ruft CalculateDynamicLotSize() auf (in diesem Ausschnitt nicht gezeigt), um die Basislosgröße zu bestimmen.
5. Anpassung der Losgröße: Die Funktion passt die Losgröße auf der Grundlage von zwei Bedingungen an:
• Wenn der Drawdown mehr als 10% beträgt
• Wenn es mehr als 3 aufeinanderfolgende Verluste (consecutiveLosses) gab

Ausführliche Erklärung

Aktualisierung des Höchstbetrags:

 if (currentBalance > maxBalance)
   maxBalance = currentBalance;

Auf diese Weise können Sie den maximal erreichten Saldo verfolgen, was für die Berechnung des Drawdowns entscheidend ist.

Berechnung des Drawdowns:

 double drawdown = (maxBalance - currentEquity) / maxBalance;

Damit wird der aktuelle Drawdown als Prozentsatz des maximalen Saldos berechnet.

Ermittlung der Basislosgröße:

 double baseLotSize = CalculateDynamicLotSize();

Dabei wird eine separate Funktion zur Berechnung der ursprünglichen Losgröße aufgerufen.

Anpassung für hohe Drawdowns:

 if (drawdown > 0.1 ) // 10% drawdown
  {
   return baseLotSize * 0.5 ; // Reduce lot size by half
  }

Wenn der Drawdown 10 % überschreitet, reduziert die Funktion die Losgröße um die Hälfte, um das Risiko zu verringern.

Konsekutive Verlustanpassung:

 else if (consecutiveLosses > 3 )
  {
   return baseLotSize * 0.75 ; // Reduce lot size by 25%
  }

Bei mehr als 3 aufeinanderfolgenden Verlusten reduziert die Funktion die Losgröße um 25%.

Rückgabe Standardwert: Wenn keine der Bedingungen erfüllt ist, gibt die Funktion die Basislosgröße ohne Anpassung zurück.

Bedeutung für das Risikomanagement:

1. Schutz vor einem Drawdown: Durch die Verringerung der Losgrößen bei starken Rückgängen trägt diese Funktion dazu bei, das Konto vor weiteren Verlusten unter ungünstigen Marktbedingungen zu schützen.
2. Bewältigung von Pechsträhnen: Die Anpassung an aufeinanderfolgende Verluste hilft, die Auswirkungen von Pechsträhnen zu mildern, die psychologisch und finanziell verheerend sein können.
3. Dynamische Risikoanpassung: Mit dieser Funktion können Sie Ihre Risiken dynamisch verwalten, indem Sie sich an die aktuellen Marktbedingungen und Handelsergebnisse anpassen.

Überlegungen und mögliche Verbesserungen

1. Schrittweise Anpassung: Die Funktion kann modifiziert werden, um eine schrittweise Anpassung der Losgrößen auf der Grundlage verschiedener Drawdown-Niveaus zu implementieren.
2. Mechanismus zur Wiederherstellung: Ein zusätzlicher Mechanismus kann hinzugefügt werden, um die Losgrößen schrittweise zu erhöhen, wenn sich das Konto von einem Drawdown erholt.
3. Maximale Losgröße: Die Einführung einer Obergrenze für die Losgröße kann eine zusätzliche Ebene des Risikomanagements darstellen.
4. Gewinnverfolgung: Die Funktion kann erweitert werden, um aufeinanderfolgende Gewinne zu verfolgen und möglicherweise die Losgrößen in günstigen Zeiten zu erhöhen.

Diese Funktion ist ein wichtiger Aspekt des Risikomanagements in Handelssystemen, da sie dazu beiträgt, das Kapital unter schwierigen Marktbedingungen zu erhalten und die Auswirkungen von Verlustphasen abzumildern.

Mehrere technische Indikatoren: Der Advisor enthält mehrere technische Indikatoren für die Analyse:

• Einfache gleitende Durchschnitte (SMA)
• Parabolic SAR
• Relative Strength Index (RSI)
• Average True Range (ATR)

 // Initialize indicator handles
   smaHandle = iMA ( Symbol (), PERIOD_CURRENT , 50 , 0 , MODE_SMA , PRICE_CLOSE );
   psarHandle = iSAR ( Symbol (), PERIOD_CURRENT , 0.02 , 0.2 );
   rsiHandle = iRSI ( Symbol (), PERIOD_CURRENT , 14 , PRICE_CLOSE );
   atrHandle = iATR ( Symbol (), PERIOD_CURRENT , 14 );

Dynamischer Stop Loss und Take Profit: Der EA berechnet und aktualisiert SL- und TP-Levels auf der Grundlage der Marktvolatilität mithilfe der Funktionen CalculateDynamicSL() und CalculateDynamicTP().

 double CalculateDynamicSL( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

   return NormalizeDouble (dynamicSL, _Digits );
  }


double CalculateDynamicTP( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

   return NormalizeDouble (dynamicTP, _Digits );
  }

Diese Funktion berechnet dynamische Stop-Loss- (SL) und Take-Profit-Niveaus (TP) auf der Grundlage der aktuellen Marktvolatilität, was das Risikomanagement verbessert und die Handelsergebnisse potenziell erhöht.

Berichte über Merkmale

Beide Funktionen verwenden den Indikator Average True Range (ATR), um die Marktvolatilität zu messen und die SL- und TP-Level entsprechend anzupassen. Dabei wird berücksichtigt, ob es sich um eine Kauf- (1) oder Verkaufsentscheidung (-1) handelt.

 double CalculateDynamicSL( double price, int decision)

Diese Funktion berechnet ein dynamisches Stop-Loss-Niveau auf der Grundlage des aktuellen Kurses, der Handelsrichtung und der Marktvolatilität.

 double CalculateDynamicTP( double price, int decision)

Diese Funktion berechnet ein dynamisches Take-Profit-Niveau auf der Grundlage des aktuellen Kurses, der Handelsrichtung und der Marktvolatilität.

Wichtige Komponenten

1. ATR-Indikator: Beide Funktionen verwenden den ATR-Indikator zur Messung der Marktvolatilität.
2. Preis: Der aktuelle Marktpreis des Vermögenswerts.
3. Lösung: Eine ganze Zahl (1 für Kaufen, -1 für Verkaufen), die die Richtung des Handels angibt.
4. Multiplikator: Die Globalvariable multi wird verwendet, um die Auswirkungen der Volatilität zu berücksichtigen.

Ausführliche Erklärung

Funktion CalculateDynamicSL

ATR-Wert abrufen :

 double atrValue[];
if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
{
   LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
   return 0.0 ;
}
double volatility = atrValue[ 0 ];

Dieser Code ruft den letzten ATR-Wert ab, der die Marktvolatilität widerspiegelt.

Dynamisches SL berechnen :

 double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

Bei einem Kaufgeschäft (Lösung == 1) setzt er SL unter den aktuellen Kurs.

Bei einem Verkauf wird der SL über den aktuellen Kurs gesetzt.

Der Abstand wird als ein Vielfaches der ATR berechnet und mit Hilfe der Multi-Variablen und eines Faktors angepasst (1,2 für Käufe, 0,8 für Verkäufe, ich habe dies getan, um den Unterschied im Artikel zu zeigen).

Normalisieren und zurückkehren:

 return NormalizeDouble (dynamicSL, _Digits );

Der SL-Wert wird auf die entsprechende Anzahl von Dezimalstellen für das gehandelte Instrument normalisiert.

Die Funktion CalculateDynamicTP

ATR-Wert abrufen: Dieser Teil ist identisch mit der SL-Funktion.

Berechnen des dynamischen TPs:

 double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

Bei einer Kauftransaktion wird der TP oberhalb des aktuellen Kurses festgelegt.

Bei einem Verkaufsgeschäft wird der TP unter dem aktuellen Kurs festgelegt.

Der Abstand wird als ein Vielfaches vom ATR berechnet, angepasst durch die Variable multi und einen Faktor (1,8 für Käufe, 2,2 für Verkäufe, ich habe dies getan, um den Unterschied zu zeigen; Sie können verwenden, was Sie brauchen).

Normalisieren und zurückgeben: ähnlich wie die SL-Funktion.

Bedeutung für den Handel

1. Volatilitätsbasiertes Risikomanagement: Durch die Verwendung von ATR passen diese Funktionen die SL- und TP-Levels an die aktuellen Marktbedingungen an und ermöglichen ein angemesseneres Risikomanagement.
2. Asymmetrisches Risiko-Ertrags-Verhältnis: Die TP-Levels sind weiter vom Einstiegskurs entfernt als die SL-Levels, wodurch sich ein günstiges Risiko-Ertrags-Verhältnis ergeben kann.
3. Dynamische Anpassung: Wenn sich die Marktvolatilität ändert, passen diese Funktionen automatisch die SL- und TP-Niveaus für neue Trades an.

Überlegungen und mögliche Verbesserungen

1. Fehlerbehandlung: Beide Funktionen verfügen über eine grundlegende Fehlerbehandlung für das Abrufen von ATR, die jedoch erweitert werden kann.
2. Einstellung: Multiplikatoren (1,2, 0,8, 1,8, 2,2) können zur einfacheren Einstellung in Parameter umgewandelt werden.
3. Mindestabstand: Die Einführung eines Mindestabstands für SL und TP kann Probleme bei extrem niedriger Volatilität verhindern.
4. Maximale Entfernung: Ebenso kann ein maximaler Abstand eingegeben werden, um das Risiko unter sehr instabilen Bedingungen zu begrenzen.

Diese Funktionen stellen einen Ansatz für die Festlegung von SL- und TP-Levels dar, der sich an die Marktbedingungen anpasst, um die Handelsergebnisse zu verbessern und gleichzeitig das Risiko effektiv zu steuern.

Risikomanagement: Enthält Funktionen zur Anpassung der Positionsgröße auf der Grundlage von Kontostand und Drawdown, implementiert in AdjustLotSizeForDrawdown() und CalculateDynamicLotSize().

 // Function to adjust the lot size based on drawdown
double AdjustLotSizeForDrawdown()
{
   // Static variables to keep track of consecutive losses and maximum balance
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   // Get current account balance and equity
   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   // Update the maximum balance if current balance is higher
   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   // Calculate the current drawdown as a percentage
   double drawdown = (maxBalance - currentEquity) / maxBalance;

   // Calculate the base lot size using a separate function
   double baseLotSize = CalculateDynamicLotSize();

   // If drawdown is greater than 10%, reduce lot size by half
   if (drawdown > 0.1 ) // 10% drawdown
   {
       return baseLotSize * 0.5 ; // Reduce lot size by half
   }
   else if (consecutiveLosses > 3 )
   {
       return baseLotSize * 0.75 ; // Reduce lot size by 25% after 3 consecutive losses
   }

   // Return the base lot size if no adjustments are needed
   return baseLotSize;
}

Die Funktion AdjustLotSizeForDrawdown() dient der dynamischen Anpassung der Handelslotgröße auf der Grundlage des Kontoverlustes und der jüngsten Performance. Nachfolgend finden Sie eine Aufschlüsselung der wichtigsten Funktionen:

1. Es verwendet statische Variablen, um die aufeinanderfolgenden Verluste und das erreichte maximale Gleichgewicht zu verfolgen.
2. Er berechnet die aktuelle Inanspruchnahme, indem er den maximalen Saldo mit dem aktuellen Eigenkapital vergleicht.
3. Die Funktion setzt zwei Risikomanagementstrategien um:
   • Wenn der Drawdown 10 % übersteigt, wird die Losgröße halbiert.
   • Bei mehr als 3 aufeinanderfolgenden Verlusten wird die Losgröße um 25% reduziert.
4. Die Basislosgröße wird mit einer anderen Funktion namens CalculateDynamicLotSize() berechnet, die in diesem Ausschnitt nicht gezeigt wird.
5. Wenn keine der Risikobedingungen erfüllt ist, gibt die Funktion die Basislosgröße ohne Anpassung zurück.

Dieser Ansatz hilft, Ihr Handelskonto in Zeiten schlechter Performance oder hoher Volatilität zu schützen, indem er die Auswirkungen reduziert. Es handelt sich um eine einfache, aber effektive Methode zur Umsetzung der adaptiven Positionsgrößenbestimmung im algorithmischen Handel.

 // Function to dynamically calculate the lot size
double CalculateDynamicLotSize()
{
   // Get current account balance and equity
   double accountBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double equity = AccountInfoDouble ( ACCOUNT_EQUITY );
   double riskPercentage = 0.01 ; // 1% risk per trade

   // Use the lower value between balance and equity to be conservative
   double baseAmount = MathMin (accountBalance, equity);

   // Calculate the value of a pip for the current symbol
   double tickSize = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_SIZE );
   double tickValue = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_VALUE );
   double pipValue = (tickValue / tickSize) * 10 ; // Assuming a pip is 10 ticks

   // Calculate lot size based on desired risk
   double riskAmount = baseAmount * riskPercentage;
   double stopLossPips = 50 ; // Adjust according to your strategy

   double lotSize1 = NormalizeDouble (riskAmount / (stopLossPips * pipValue), 2 );

   // Ensure the lotSize is within the allowed limits
   double minLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MIN );
   double maxLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MAX );
   double lotSize2 = MathMax (minLot, MathMin (maxLot, lotSize1));

   return lotSize2;
}

Die Funktion CalculateDynamicLotSize() dient zur Berechnung der geeigneten Losgröße für den Handel auf der Grundlage Ihres Kontostands, Ihrer Risikotoleranz und der aktuellen Marktbedingungen. Nachfolgend finden Sie eine Aufschlüsselung der wichtigsten Funktionen:

1. Sie extrahiert den Leistungsbilanzsaldo und das Eigenkapital, wobei der niedrigere der beiden Werte für einen konservativeren Ansatz verwendet wird.
2. Die Funktion verwendet einen festen Prozentsatz des Risikos pro Handel, der in diesem Fall auf 1 % festgelegt ist.
3. Er berechnet den Pip-Wert für das aktuelle Handelssymbol, wobei davon ausgegangen wird, dass ein Pip 10 Ticks entspricht.
4. Die Chargengröße wird dann auf der Grundlage berechnet:
   • Risikobetrag (1% des Grundbetrags)
   • Vordefinierter Stop-Loss in Pips (in diesem Beispiel ist er auf 50 Pips eingestellt)
   • Berechneter Wert der Position
5. Die Funktion stellt sicher, dass die berechnete Losgröße innerhalb der für das Handelssymbol zulässigen minimalen und maximalen Losgröße liegt.
6. Die endgültige Losgröße wird zurückgegeben, normalisiert auf zwei Dezimalstellen.

Dieser dynamische Ansatz für die Losgröße trägt dazu bei, dass unabhängig von der Kontogröße und den Marktbedingungen ein gleichbleibendes Risikoniveau bei den Geschäften aufrechterhalten wird. Sie ist ein wichtiger Bestandteil einer Risikomanagementstrategie und arbeitet mit der Funktion AdjustLotSizeForDrawdown() zusammen, die wir bereits besprochen haben.

Die Kombination dieser beiden Funktionen bietet ein robustes Risikomanagementsystem, das:

1. Anpassung der Positionsgrößen auf der Grundlage von Kontoperformance und Drawdown
2. Behält einen konstanten Prozentsatz des Risikos pro Handel bei
3. Passt sich an wechselnde Kontostände und Marktbedingungen an

Dieser Ansatz kann Händlern helfen, Disziplin zu wahren und ihr Kapital sowohl unter günstigen als auch unter schwierigen Marktbedingungen zu schützen.

Wichtige Merkmale:

1. OptimalControl(double currentPrice): Dies ist die zentrale Entscheidungsfunktion von EA. Er verwendet Model Predictive Control, um zu entscheiden, ob gekauft, verkauft oder gehalten werden soll. Er berechnet die erwartete Rendite über den Prognosehorizont und vergleicht sie mit der Entscheidungsschwelle.
2. CalculateExpectedReturn(...): Diese Funktion berechnet die erwartete Rendite für einen bestimmten Satz von Parametern, die in der OptimalControl-Funktion verwendet werden.
3. ManageOpenOrder(int decision): Verwaltet bestehende offene Aufträge und entscheidet anhand der Anzahl der offenen Takte, ob sie geschlossen werden sollen oder ob die aktuelle Entscheidung mit einer offenen Position kollidiert.
4. ExecuteTrade(int decision): Führt einen neuen Handel auf der Grundlage der OptimalControl-Entscheidung aus und setzt dabei die entsprechenden Stop-Loss- und Take-Profit-Levels.
5. UpdateSLTP(ulong ticket, int decision): Aktualisiert die Stop-Loss- und Take-Profit-Niveaus für eine bestehende Position auf der Grundlage der aktuellen Marktbedingungen.
6. EstimateDrift() und EstimateVolatility(): Diese Funktionen schätzen die Preisdrift und die Volatilität, die bei der Berechnung der optimalen Steuerung verwendet werden.
7. IsTrendFavorable(int Entscheidung) und IsLongTermTrendFavorable(int Entscheidung): Diese Funktionen prüfen anhand von gleitenden Durchschnitten und RSI, ob der aktuelle Markttrend mit der Handelsentscheidung übereinstimmt.
8. AdjustLotSizeForDrawdown() und CalculateDynamicLotSize(): Diese Funktionen passen das Handelsvolumen auf der Grundlage des aktuellen Drawdowns und des Kontostands an und implementieren ein dynamisches Risikomanagement.
9. LogMessage(string message): Protokolliert wichtige Ereignisse und Entscheidungen in einer Datei zur späteren Analyse und Fehlersuche.

Ergebnisse

Zeitrahmen 1 Tag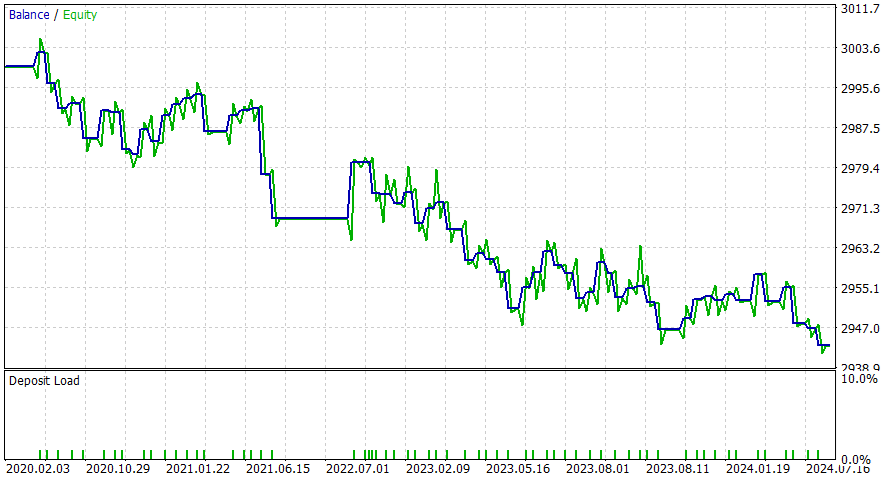

Zeitrahmen 1 Stunde

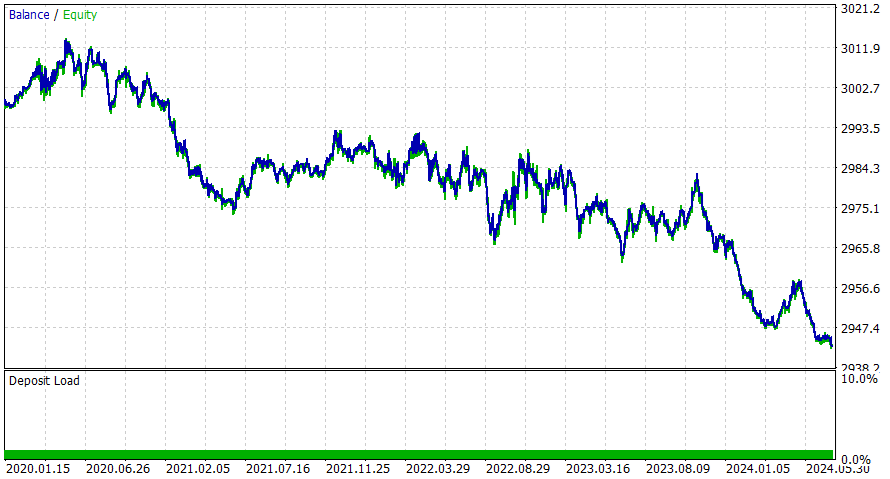
Zeitrahmen 4 Stunden

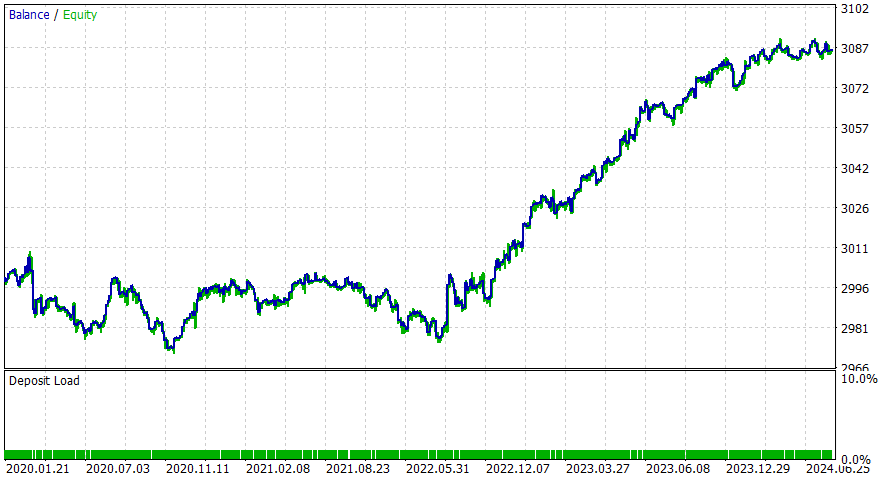
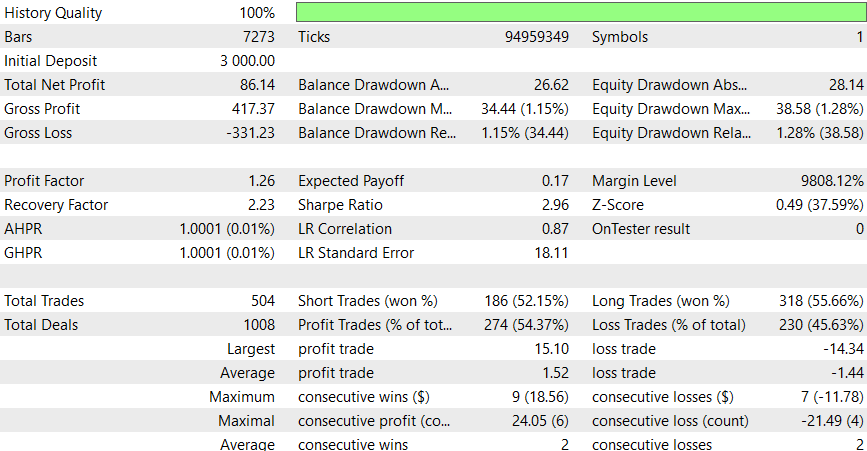
Zeitrahmen 6 Stunden

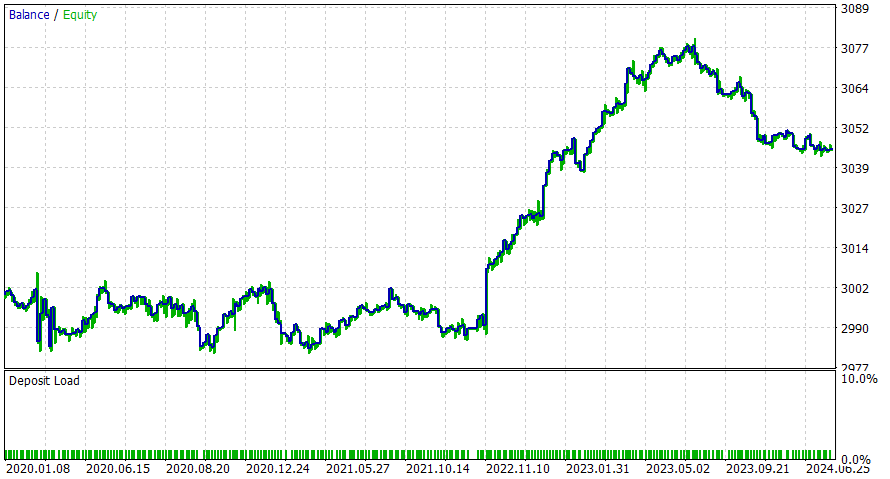
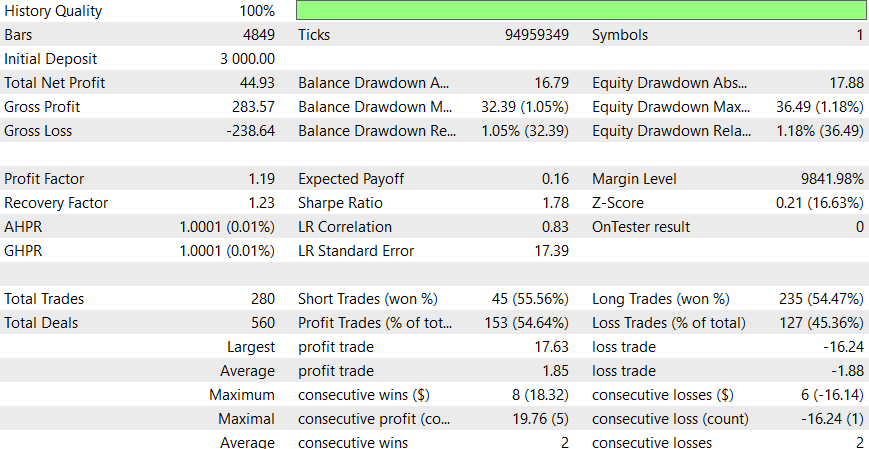
Dieser EA scheint besser mit einem Intraday-Zeitrahmen zu funktionieren, aber ich bin sicher, dass Sie bessere Ergebnisse erzielen können, indem Sie SL hinzufügen oder die potenziellen Verbesserungen berücksichtigen.

Schlussfolgerung

Der SMOC Expert Advisor ist eine vereinfachte Version eines anspruchsvollen Ansatzes für den automatisierten Handel mit stochastischer Modellierung und Steuerungsoptimierung. Durch die Kombination verschiedener Analysemethoden, einschließlich gleitender Durchschnitte, RSI, ATR und nutzerdefinierter optimaler Kontrollalgorithmen, zielt es darauf ab, fundierte Handelsentscheidungen zu treffen. Der adaptive Charakter des Systems mit Merkmalen wie dynamischer Losgröße und Drawdown-basierter Risikoanpassung zeigt, dass der Schwerpunkt auf der langfristigen Nachhaltigkeit liegt. Wie bei jedem Handelssystem sind jedoch gründliche Backtesting- und Vorwärtstests von entscheidender Bedeutung, um die Leistung und Zuverlässigkeit des Systems in der Praxis zu beurteilen.

Zum Abschied: Dies ist nur ein einfaches Beispiel eines fortgeschrittenen Beraters.