MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
头脑风暴优化算法（第二部分）： 多模态

头脑风暴优化算法（第二部分）： 多模态

MetaTrader 5 — 示例 | 31 十月 2024, 09:06
275 0
Andrey Dik
Andrey Dik

内容

1.
2. 算法实现
3. 测试结果


1. 概述

在文章的第一部分中，我们深入探讨了以头脑风暴优化（BSO）算法为核心的优化方式，揭示了这一受头脑风暴启发的创新方法的基本原理。在研究其逻辑结构的同时，我们还深入讨论了聚类方法，包括K-Means和K-Means++。BSO是一种优化方法，它在群体活动中融入了观点的产生和评估阶段。该算法与聚类方法相结合，为优化领域做出了贡献。聚类使我们能够识别出相似的数据元素组，这有助于BSO找到最优解。变异方法使算法能够绕过解决方案搜索空间中的障碍，并寻找通往最优解的更高效路径。

现在是时候实践该算法了！在第二部分中，我们将深入探讨算法的实际实现，讨论多模态性，测试算法，并总结归纳得出结论。


2. 算法实现

让我们简要概述一下BSO算法逻辑中的关键点：

  1. 聚类。
  2. 集群转移。
  3. 从聚类中选择观点：聚类质心或聚类中的观点。
  4. 合并所选观点。
  5. 对前一阶段获得的观点进行变异。
  6. 为第2、3和4阶段选择观点。将新想法放入父代种群并进行排序。

接下来，我们描述BSO算法的代码。

让我们来实现S_BSO_Agent智能体算法的结构。该结构用于描述BSO算法中的每个智能体。

1. 该结构包含以下字段：

  • c[] - 用于存储智能体坐标的数组。
  • f - 用于存储智能体得分（适应度）的变量。
  • label - 用于存储集群成员标签的变量。

2. Init - S_BSO_Agent结构方法，用于初始化结构字段。它接受一个名为“coords”的整数参数，该参数用于通过ArrayResize函数调整“c”坐标数组的大小。
3. f = -DBL_MAX - 将“f”变量的初始值设置为双精度数的最小可能值，即负无穷大。
4. label = -1 - 将“label”变量的初始值设置为-1，这意味着该智能体不属于任何聚类。

这段代码表示BSO优化算法中智能体的基本数据结构，并在创建新智能体时完成字段的初始化。

//——————————————————————————————————————————————————————————————————————————————
struct S_BSO_Agent
{
    double c     []; //coordinates
    double f;        //fitness
    int    label;    //cluster membership label

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      f     = -DBL_MAX;
      label = -1;
    }
};
//——————————————————————————————————————————————————————————————————————————————

在之前的文章中，我们已经详细讨论了K-Means和K-Means++聚类算法，因此在这里不再赘述。

接下来，让我们描述C_AO_BSO类代码，该类是C_AO种群算法基类的继承者，包含以下字段和方法：

1. 公共字段:

  • ao_name - 优化算法名称。
  • ao_desc - 优化算法描述。
  • ao_link - 关于优化算法的文章链接。
  • popSize - 种群大小。
  • parentPopSize - 父代规模。
  • clustersNumb - 聚类的数量。
  • p_Replace - 替换概率。
  • p_One - 单选概率。
  • p_One_center - 在所选集群中选择一个中心或个体的概率。
  • p_Two_center - 在所选集群中选择两个中心或两个个体的概率。
  • k_Mutation - 变异率。
  • distribCoeff - 分配比。
  • agent - 智能体数组。
  • parents - 父类数组。
  • clusters - 集群数组。
  • km - KMeans类对象。

2. 可用的选项有：

  • SetParams - 算法参数设置方法。
  • Init - 算法初始化方法。该方法需要最小和最大搜索范围、搜索步长和迭代次数。
  • Moving - 智能体移动方法。
  • Revision - 智能体修改方法。

3. 私有字段：

  • parentsTemp - 临时父类数组。
  • epochs - 最多阶段数。
  • epochsNow - 当前阶段。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_BSO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BSO () { }
  C_AO_BSO ()
  {
    ao_name = "BSO";
    ao_desc = "Brain Storm Optimization";
    ao_link = "https://www.mql5.com/en/articles/14622";

    popSize        = 25;   //population size

    parentPopSize  = 50;   //parent population size;
    clustersNumb   = 5;    //number of clusters
    p_Replace      = 0.1;  //replace probability
    p_One          = 0.5;  //probability of choosing one
    p_One_center   = 0.3;  //probability of choosing one center
    p_Two_center   = 0.2;  //probability of choosing two centers
    k_Mutation     = 20.0; //mutation coefficient
    distribCoeff   = 1.0;  //distribution coefficient

    ArrayResize (params, 9);

    params [0].name = "popSize";       params [0].val  = popSize;

    params [1].name = "parentPopSize"; params [1].val  = parentPopSize;
    params [2].name = "clustersNumb";  params [2].val  = clustersNumb;
    params [3].name = "p_Replace";     params [3].val  = p_Replace;
    params [4].name = "p_One";         params [4].val  = p_One;
    params [5].name = "p_One_center";  params [5].val  = p_One_center;
    params [6].name = "p_Two_center";  params [6].val  = p_Two_center;
    params [7].name = "k_Mutation";    params [7].val  = k_Mutation;
    params [8].name = "distribCoeff";  params [8].val  = distribCoeff;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    parentPopSize = (int)params [1].val;
    clustersNumb  = (int)params [2].val;
    p_Replace     = params      [3].val;
    p_One         = params      [4].val;
    p_One_center  = params      [5].val;
    p_Two_center  = params      [6].val;
    k_Mutation    = params      [7].val;
    distribCoeff  = params      [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    parentPopSize; //parent population size;
  int    clustersNumb;  //number of clusters
  double p_Replace;     //replace probability
  double p_One;         //probability of choosing one
  double p_One_center;  //probability of choosing one center
  double p_Two_center;  //probability of choosing two centers
  double k_Mutation;    //mutation coefficient
  double distribCoeff;  //distribution coefficient

  S_BSO_Agent  agent   [];
  S_BSO_Agent  parents [];

  S_Clusters   clusters [];
  S_BSO_KMeans km;

  private: //-------------------------------------------------------------------
  S_BSO_Agent  parentsTemp [];
  int          epochs;
  int          epochsNow;
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSO类的Init方法通过执行以下操作来初始化优化算法：

  • 检查初始化。首先，使用搜索范围和步长参数调用StandardInit方法。如果StandardInit返回'false'，则初始化被中止，并且Init方法返回'false'。
  • 智能体初始化。“agent”数组被调整为“popSize”（种群大小）。对于每个智能体，都使用定义坐标数量的“coords”参数调用Init方法。
  • 聚类初始化。“clusters”数组的大小被调整为“clustersNumb”（最大聚类数），并且为每个聚类调用Init方法。
  • 父代初始化。“parents”和“parentsTemp”数组被调整为“parentPopSize + popSize”（父代种群大小加子代种群大小），并且为每个父代调用Init方法。数组的大小应该能够容纳后续的排序操作中的父代和子代种群。
  • 设置迭代次数。“epochs”（总迭代次数）和“epochsNow”（当前迭代次数）的值分别根据传递的参数“epochsP”和“0”进行设置。

成功完成所有初始化步骤后，则该方法返回“true”。为算法执行给定迭代次数的优化操作做好准备。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BSO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (clusters, clustersNumb);
  for (int i = 0; i < clustersNumb; i++) clusters [i].Init (coords);

  ArrayResize (parents,     parentPopSize + popSize);
  ArrayResize (parentsTemp, parentPopSize + popSize);

  for (int i = 0; i < parentPopSize + popSize; i++)
  {
    parents     [i].Init (coords);
    parentsTemp [i].Init (coords);
  }

  epochs    = epochsP;
  epochsNow = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSO类的Moving方法用于在优化过程中移动智能体。该方法执行以下操作：

  1. 当前迭代次数（“epochsNow++”）的值会增加。
  2. 如果“revision”为'false'，则智能体的坐标会在指定的范围内被初始化为随机值。然后，该方法终止。
  3. 如果“revision”值不是'false'，则使用方程和概率为每个智能体计算新的坐标。
  4. 通过各种数学计算、随机数和概率确定智能体的新坐标。
  5. 根据条件和概率计算得出新坐标。
  6. 使用SeInDiSp方法来设置新坐标，并根据搜索范围和步骤调整值。
  7. 新观点如下：如果满足条件“u.RNDprobab () < p_Replace”，则替换选定的聚类中心（聚类中心偏移）。
  8. 如果满足条件“u.RNDprobab () < p_One”，则从一个聚类中选择一个观点。
  9. 如果不满足条件“u.RNDprobab () < p_One”，则从两个聚类中选择观点。
  10. 智能体坐标发生变异。
  11. 保存新智能体坐标。

该方法负责根据当前阶段和概率在BSO优化算法中更新智能体的坐标。让我们用颜色区分，描述不同智能体行为模型的相应代码部分：

  • 产生新观点。随着每个新阶段的到来，根据“p_Replace”比例，智能体更加彻底地探索已发现的全局解附近的邻域，试图接近全局最优解并移动质心。
  • 探索单个簇的邻域。考虑到“p_One”比例，智能体探索一个随机选择的簇的邻域。因此，智能体在种群中所在的所有区域的探索仍在继续。
  • 从两个簇中选择观点。如果不满足“u.RNDprobab() < p_One”条件，则从两个簇中随机选择一个簇的观点。
  • 变异。智能体的坐标会发生变异，这确保了种群的多样性，并有助于避免过早收敛到局部最优解。
  • 保存智能体。在所有操作完成后，新的智能体坐标会被保存，以供下一次迭代使用。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Moving ()
{
  epochsNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  //----------------------------------------------------------------------------
  int    cIndx_1    = 0;  //index in the list of non-empty clusters
  int    iIndx_1    = 0;  //index in the list of ideas in the cluster
  int    cIndx_2    = 0;  //index in the list of non-empty clusters
  int    iIndx_2    = 0;  //index in the list of ideas in the cluster
  double min        = 0.0;
  double max        = 0.0;
  double dist       = 0.0;
  double val        = 0.0;
  double X1         = 0.0;
  double X2         = 0.0;
  int    clListSize = 0;
  int    clustList [];
  ArrayResize (clustList, 0, clustersNumb);

  //----------------------------------------------------------------------------
  //let's make a list of non-empty clusters
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    if (clusters [cl].count > 0)
    {
      clListSize++;
      ArrayResize (clustList, clListSize);
      clustList [clListSize - 1] = cl;
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    //==========================================================================
    //generating a new idea that replaces the selected cluster center (cluster center offset)
    if (u.RNDprobab () < p_Replace)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      for (int c = 0; c < coords; c++)
      {
        val = clusters [clustList [cIndx_1]].centroid [c];

        dist = (rangeMax [c] - rangeMin [c]) * 0.8;

        min = val - dist; if (min < rangeMin [c]) min = rangeMin [c];
        max = val + dist; if (max > rangeMax [c]) max = rangeMax [c];

        val = u.GaussDistribution (val, min, max, 3);
        val = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        clusters [clustList [cIndx_1]].centroid [c] = val;
      }
    }

    //==========================================================================
    //an idea from one cluster is selected
    if (u.RNDprobab () < p_One)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_One_center) //select cluster center
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = clusters [clustList [cIndx_1]].centroid [c];
        }
      }
      //------------------------------------------------------------------------
      else                               //random idea from the cluster
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);

        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
        }
      }
    }
    //==========================================================================
    //select ideas from two clusters
    else
    {
      if (clListSize == 1)
      {
        cIndx_1 = 0;
        cIndx_2 = 0;
      }
      else
      {
        if (clListSize == 2)
        {
          cIndx_1 = 0;
          cIndx_2 = 1;
        }
        else
        {
          cIndx_1 = u.RNDminusOne (clListSize);

          do
          {
            cIndx_2 = u.RNDminusOne (clListSize);
          }
          while (cIndx_1 == cIndx_2);
        }
      }

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_Two_center) //two cluster centers selected
      {
        for (int c = 0; c < coords; c++)
        {
          X1 = clusters [clustList [cIndx_1]].centroid [c];
          X2 = clusters [clustList [cIndx_2]].centroid [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
      //------------------------------------------------------------------------
      else //two ideas from two selected clusters
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);
        iIndx_2 = u.RNDminusOne (clusters [clustList [cIndx_2]].count);

        for (int c = 0; c < coords; c++)
        {
          X1 = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
          X2 = parents [clusters [clustList [cIndx_2]].ideasList [iIndx_2]].c [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
    }

    //==========================================================================
    //Mutation
    for (int c = 0; c < coords; c++)
    {
      int x = (int)u.Scale (epochsNow, 1, epochs, 1, 200);

      double ξ = (1.0 / (1.0 + exp (-((100 - x) / k_Mutation))));// * u.RNDprobab ();

      double dist = (rangeMax [c] - rangeMin [c]) * distribCoeff * ξ;
      double min = a [i].c [c] - dist; if (min < rangeMin [c]) min = rangeMin [c];
      double max = a [i].c [c] + dist; if (max > rangeMax [c]) max = rangeMax [c];

      val = a [i].c [c];

      a [i].c [c] = u.GaussDistribution (val, min, max, 8);
    }

    //Save the agent-----------------------------------------------------------
    for (int c = 0; c < coords; c++)
    {
      val = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a     [i].c [c] = val;
      agent [i].c [c] = val;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSO类的Revision方法的主要任务是更新全局解决方案并构建解决方案集群。该方法执行以下操作：

  1. 获取适应度。从种群中的每个智能体中提取一个适应度值，并将其保存在智能体结构的相应字段中。
  2. 将新观点引入种群。将优化过程中产生的新观点（智能体）添加到父代种群中。
  3. 对父代种群进行排序。根据适应度对父代种群进行排序。仅允许最优解决方案参与下一阶段的新观点的诞生。
  4. 检查最佳解决方案。如果父代种群中最佳智能体的适应度超过了当前最优解决方案，则更新最优解决方案及其坐标。
  5. 执行聚类。如果是第一次迭代，则使用父代种群和聚类初始化k-means算法。然后启动k-means算法对父代种群进行聚类。
  6. 将最佳聚类解决方案作为聚类中心。对于每个聚类，检查它是否包含智能体（聚类可能为空）。如果包含，则检查父代种群中的每个智能体是否属于该聚类。如果智能体的适应度超过当前聚类的适应度，则更新聚类的适应度和其质心（质心参与新观点的诞生）。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Revision ()
{
  //get fitness--------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;
  }

  //pass new ideas to the population--------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = agent [i - parentPopSize];
  }

  //sort out the parent population----------------------------------------
  u.Sorting (parents, parentsTemp, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }

  //perform clustering-----------------------------------------------------
  if (!revision)
  {
    km.KMeansInit (parents, parentPopSize, clusters);
    revision = true;
  }

  km.KMeansInit (parents, parentPopSize, clusters);
  km.KMeans     (parents, parentPopSize, clusters);

  //Assign the best cluster solution as the cluster center--------------------------
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    clusters [cl].f = -DBL_MAX;

    if (clusters [cl].count > 0)
    {
      for (int p = 0; p < parentPopSize; p++)
      {
        if (parents [p].label == cl)
        {
          if (parents [p].f > clusters [cl].f)
          {
            clusters [cl].f = parents [p].f;
            ArrayCopy (clusters [cl].centroid, parents [p].c, 0, 0, WHOLE_ARRAY);
          }
        }
      }
    }
  }
}//——————————————————————————————————————————————————————————————————————————————

关于多模态性，BSO算法最初是作为解决多模态问题的优化方法而引入的。然而，测试结果表明，该算法对显著局部极值的探索不够充分，许多局部极值被忽略。我当前的实现可能不是最优解决方案。因此，我决定在K-Means聚类的背景下更加关注智能体的适应性。这需要对聚类算法进行一些改进。

您可能还记得，在优化算法的框架中，多模态性意味着待优化的函数有多个最优点或峰值。这样的函数可能包含多个局部最优解，这些局部最优解在适应度函数值方面可能接近全局最优解，或者在所解决问题的框架内具有重要意义。聚类有助于突出搜索空间中具有不同模态性特征的不同区域。

那么，我们尝试增强个体适应度，测试对聚类的影响。让我们在新的FitnessDistance函数中封装计算个体之间距离的功能。该函数将增加一个额外的参数“alpha”，它作为平衡距离和适应度之间重要性的比率。

FitnessDistance函数会计算单个个体与聚类质心之间的距离，同时考虑他们的距离以及适应度函数之间的差异。通过计算距离与个体适应度函数与质心之差绝对值之间的加权和来完成。“alpha”权重决定了距离对比适应度函数差异的相对重要性。

//——————————————————————————————————————————————————————————————————————————————
double FitnessDistance (S_BSO_Agent &data, S_Cluster &clust, double alpha)
{
  double distance = VectorDistance (data.c, clust.centroid);
  double fitness_diff = fabs (data.f - clust.f);
  return alpha * distance + (1 - alpha) * fitness_diff;
}
//——————————————————————————————————————————————————————————————————————————————

KMeans方法补充了“alpha”参数： 

void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [], double alpha)

让我们修改KMeans方法中负责更新质心（centroids）的代码部分，以便每个聚类对其个体具有最大的适应度值。

// Update the centroids
double sum_c [];
ArrayResize (sum_c, ArraySize (data [0].c));
double sum_f = 0.0;

for (int cl = 0; cl < nClusters; cl++)
{
  ArrayInitialize (sum_c, 0.0);

  clust [cl].count = 0;
  ArrayResize (clust [cl].ideasList, 0);
  sum_f = -DBL_MAX;

  for (int d = 0; d < dataSizeClust; d++)
  {
    if (data [d].label == cl)
    {
      for (int k = 0; k < ArraySize (data [d].c); k++)
      {
        sum_c [k] += data [d].c [k];
      }

      if (data [d].f > sum_f) sum_f = data [d].f;

      clust [cl].count++;
      ArrayResize (clust [cl].ideasList, clust [cl].count);
      clust [cl].ideasList [clust [cl].count - 1] = d;
    }
  }

  if (clust [cl].count > 0)
  {
    for (int k = 0; k < ArraySize (sum_c); k++)
    {
      clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
    }
  }
}

更改后允许在聚类过程中考虑适应度函数，但这些更改并未显著改进适应度函数中个体模式的分配，也未对结果产生影响。这可能是由于在聚类过程中使用适应度函数并不总是有效的，至少在BSO的实现中是这样的。

如果K-Means和K-Means++未能提供所需结果，我们可以尝试其他聚类方法：

1. 基于密度的噪声应用空间聚类（DBSCAN） - 该聚类方法基于密度而非距离。它将特征空间中彼此接近且具有足够数量邻居的点组合在一起。DBSCAN是最常用的聚类算法之一。

2. 层次聚类 - 构建了一个聚类层次结构，其中每个聚类都与其两个最接近的聚类相关联。层次聚类可以是凝聚的（自下而上）或分裂的（自上而下）。

3. 高斯混合模型（GMM） - 这个统计模型假设所有观测数据都是由几个未知参数的高斯分布的混合生成的。每个聚类都对应这些分布中的一个。

4. 谱聚类 - 使用相似矩阵的特征向量来降低数据的维度，然后在低维空间中进行聚类。

在这个领域有很多聚类方法值得尝试并做进一步研究。如果您愿意自行实验，可以在附带的代码中用任何其他方法替换K-Means方法。


3. 测试结果

BSO算法结果：

BSO|Brain Storm Optimization|25.0|50.0|5.0|0.1|0.5|0.3|0.2|20.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9301770731803266
25 Hilly's; Func runs: 10000; result: 0.5801719580773876
500 Hilly's; Func runs: 10000; result: 0.30916005647304245
=============================
5 Forest's; Func runs: 10000; result: 0.929981802038364
25 Forest's; Func runs: 10000; result: 0.5907047167619348
500 Forest's; Func runs: 10000; result: 0.2477599978259004
=============================
5 Megacity's; Func runs: 10000; result: 0.5246153846153847
25 Megacity's; Func runs: 10000; result: 0.2784615384615384
500 Megacity's; Func runs: 10000; result: 0.1253384615384627
=============================
总分：4.51637 (50.18%)

在测试函数上对算法进行测试的结果（所有得分为4.51637，对应于最大可能值的50.18%）表明，使用上述第一行指定的参数可以获得相当好的结果。函数结果值范围从1000个优化参数对应的0.125，提升到10个参数对应的0.93，这表明算法在寻找最优解方面相当成功。

我想特别指出，在可视化方面解的聚类效果如何。这一过程在参数最多的函数上尤其明显，因为从最初的混乱状态开始，随着每次迭代的完成，聚类的特征部分开始变得越来越清晰。

Hilly值

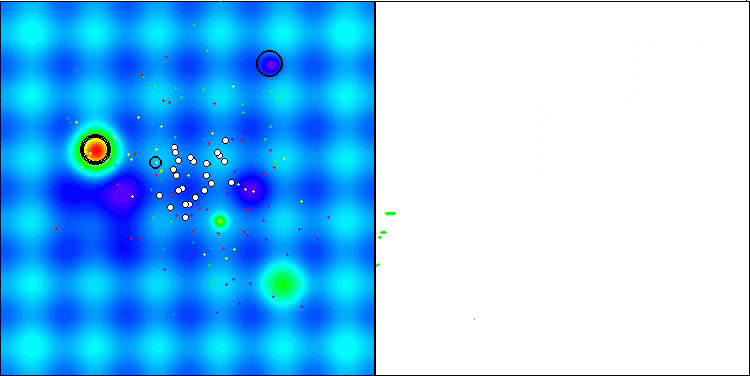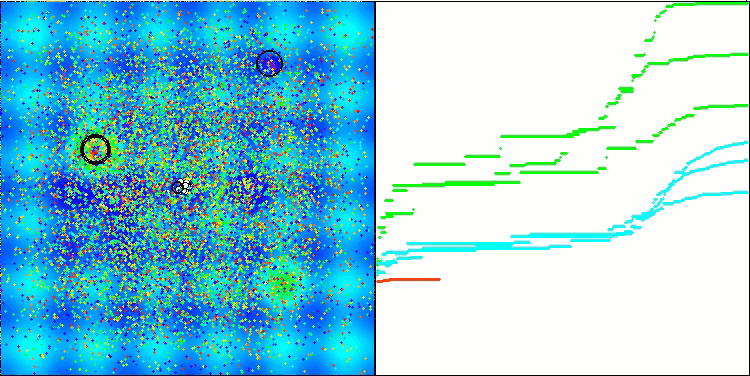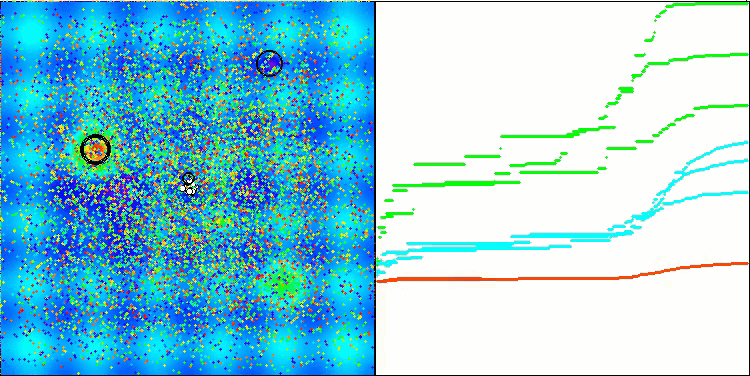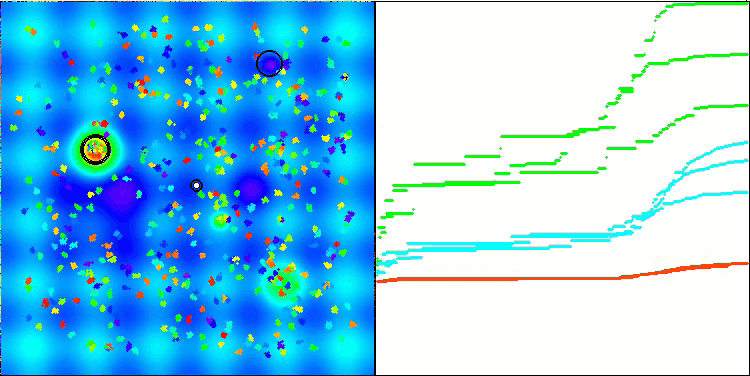
  BSO在 Hilly 测试函数上。

Forest值

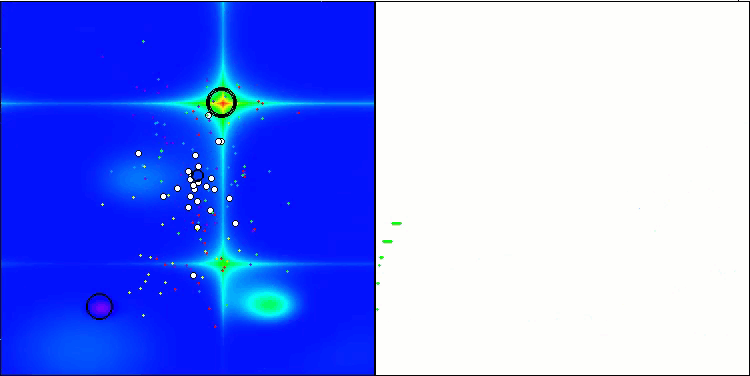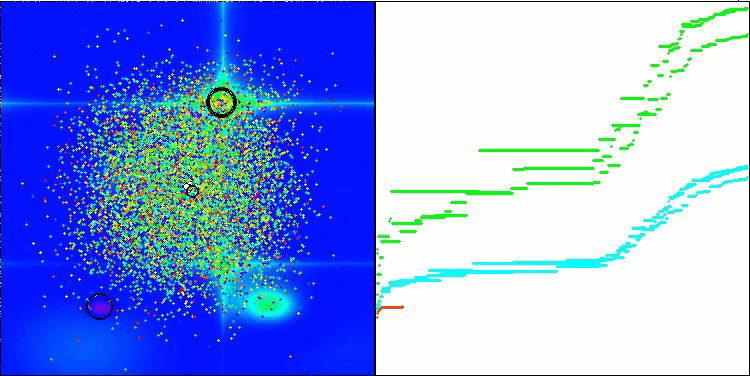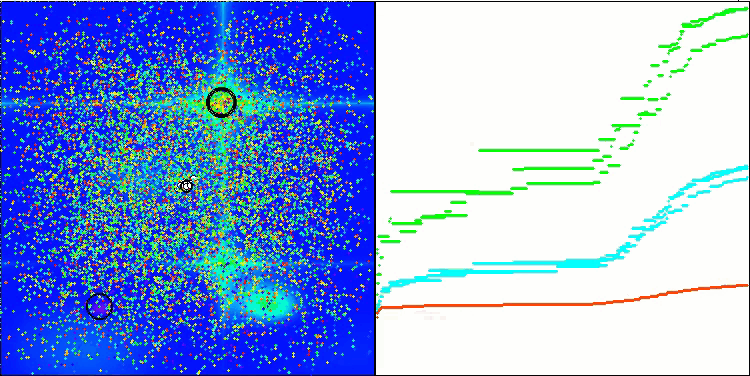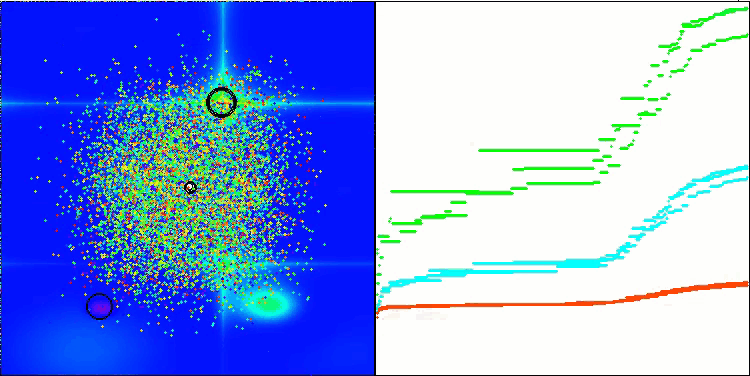
  BSO在 Forest 测试函数上。

Megacity

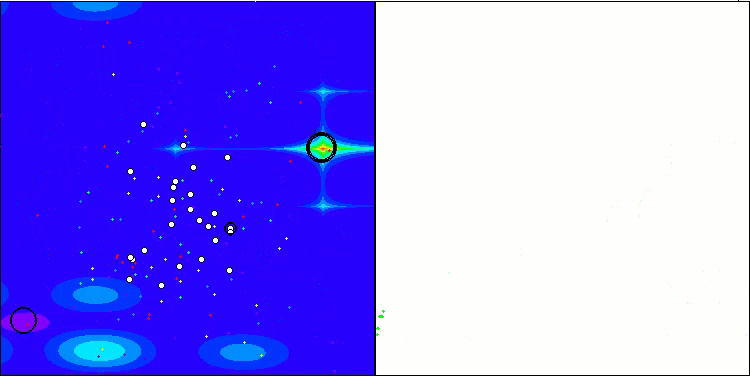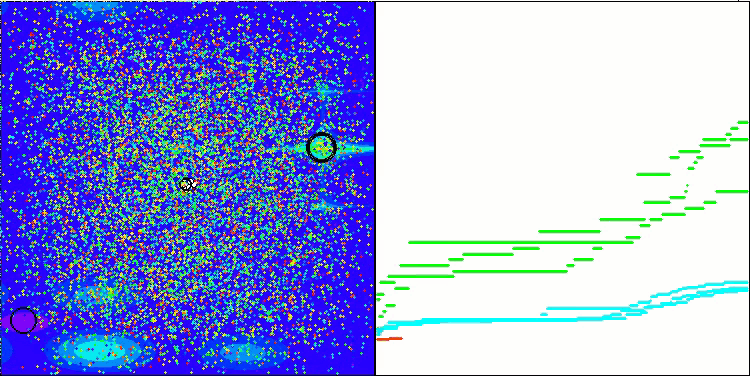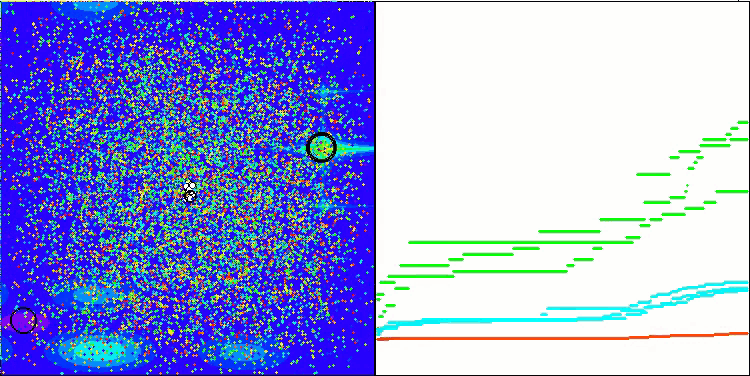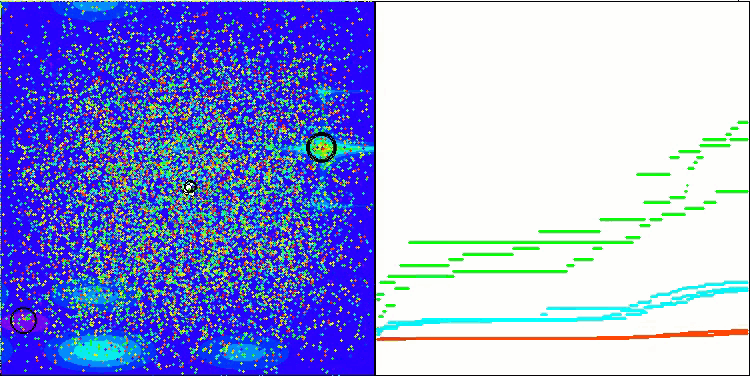
  BSO在 Megacity 测试函数上。

我对这个算法抱有很高的期望值，并希望看到它能登上排行榜的榜首。毕竟，这是我第一次将聚类方法与变异方法相结合使用，本来期望能够展现出独特的结果。当我看到该算法只是排在排行榜靠前的位置，但并没有进入领先者的行列时，我略微有些失望。BSO在具有1000个参数的Forest和Megacity函数上展示了出色的结果，这些结果让其完全有资格成为排行榜的领先者。

然而，尽管BSO总体上表现良好，在排名中也名列前茅，但要实现最大效率，还需要对参数进行有效调整。许多可调参数，包括收敛速度、种群大小、变异方法和观点评估，都会影响算法的性能。

#
AO
说明
Hilly值
Hilly最终值
Forest值
Forest最终值
Megacity (离散)
Megacity最终值
最终结果
最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA 二进制遗传算法 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O) 进化策略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 模拟退火算法 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA 鸟群算法 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 BSO 头脑风暴优化 0.91301 0.56222 0.30047 1.77570 0.97162 0.57162 0.23449 1,77772 0.60462 0.27138 0.12011 0.99611 4.550 50.55
12 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
13 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
14 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
15 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
16 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
17 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
18 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
19 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
20 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
21 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
22 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
23 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
24 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
25 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
26 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
27 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
28 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
29 Boids 虚拟生物算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
30 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
31 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
32 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
33 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
34 GWO 灰狼优化算法 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
35 CSS 人工电场算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
36 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


总结

BSO算法具有多项优势，包括灵活性、探索与开发之间的平衡性以及对各种优化问题的适应性。

然而，该算法的效率高度依赖于外部参数设置（外部参数的数量是BSO的主要缺点），因此有必要对每个特定任务进行仔细的研究和实验，以确定达到最佳设置。

我鼓励所有优化爱好者参与实验，共同探索该算法在解决实际问题方面的能力。如果有人发现了更有趣的结果或更好的外部参数，欢迎在文章的评论中分享。

标签

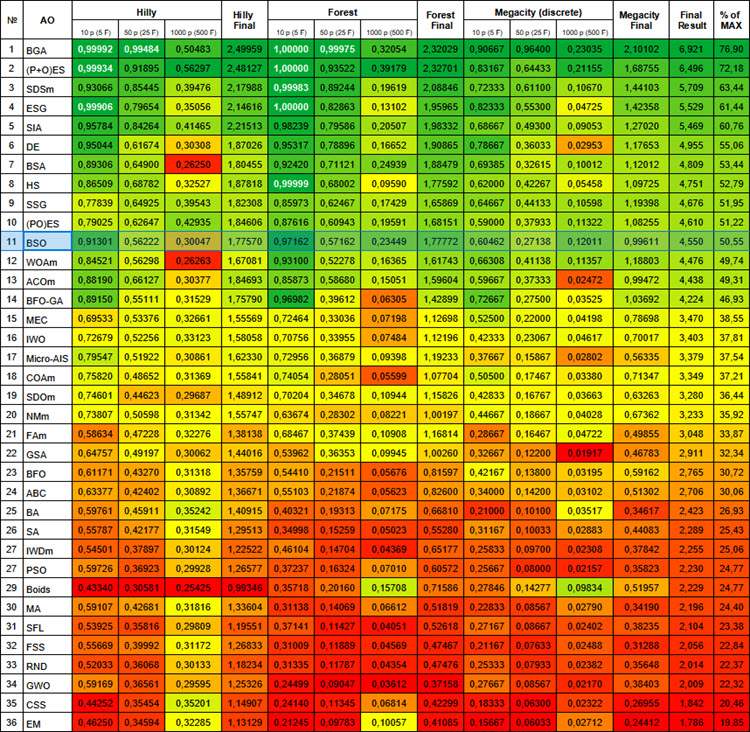
Figure 1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

图表

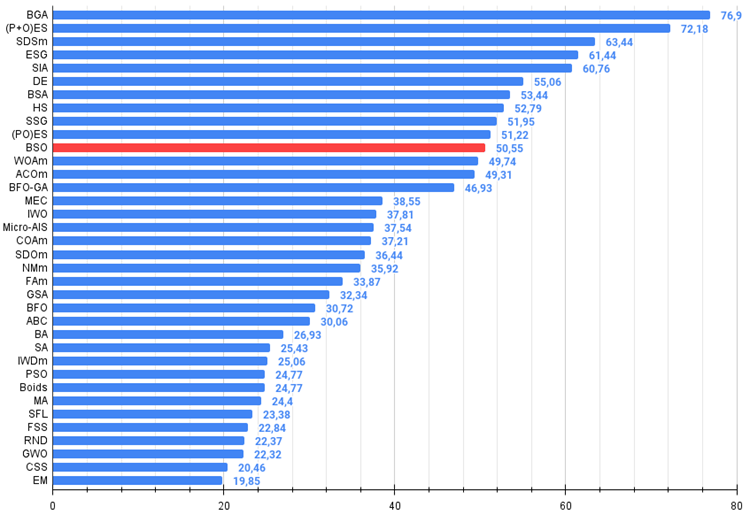
Figure 2. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）。

BSO的优缺点：

优势：

  1. 在尖锐森林函数和高维离散模型问题上取得了良好的结果。

缺点：

  1. 大量的外部参数。
  2. 复杂的架构和实现。
  3. 对计算资源的高负载。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14622

附加的文件 |
下载ZIP
BSO.zip (28.18 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
MQL5 中的高级变量和数据类型 MQL5 中的高级变量和数据类型
不仅在 MQL5 编程中，在任何编程语言中，变量和数据类型都是非常重要的主题。MQL5 变量和数据类型可分为简单类型和高级类型。在这篇文章中，我们将识别并学习高级类型，因为我们在前一篇文章中已经提到过简单类型。
构建一个用于实现带约束条件的自定义最大值的通用优化公式（GOF） 构建一个用于实现带约束条件的自定义最大值的通用优化公式（GOF）
在这篇文章中，我们将介绍一种在MetaTrader 5终端的设置选项卡中选择“自定义最大值”时，实现具有多个目标和约束的优化问题的方法。举例来说，优化问题可以是：最大化利润因子、净利润和恢复因子，同时满足以下条件：回撤小于10%，连续亏损次数少于5次，每周交易次数多于5次。
克服集成ONNX（Open Neural Network Exchange ）的挑战 克服集成ONNX（Open Neural Network Exchange ）的挑战
ONNX是集成不同平台间复杂AI代码的强大工具，尽管它非常出色，但要想充分发挥其作用，就必须解决一些伴随而来的挑战。在本文中，我们将讨论您可能会遇到的一些常见问题，以及如何处理这些问题。
矩阵分解基础知识 矩阵分解基础知识
由于这里的目标是教学，我们将尽可能简单地进行。也就是说，我们将只实现所需的功能：矩阵乘法。今天您将看到，这足以模拟矩阵标量乘法。许多人在使用矩阵分解实现代码时遇到的最大困难是：与标量分解不同，在标量分解中，几乎所有情况下因子的顺序都不会改变结果，但使用矩阵时情况并非如此。