MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
矩阵分解基础知识

矩阵分解基础知识

MetaTrader 5 — 示例 | 30 十月 2024, 10:40
553 0
Daniel Jose
Daniel Jose

概述

欢迎大家阅读我的新文章，其中包含的是教育内容。

本文将讨论矩阵计算。亲爱的读者，不要急于拒绝阅读这篇文章，以为我们会谈论一些纯粹的数学和过于复杂的东西。与许多人的想法相反，优秀的程序员并不是编写只有自己才能理解的巨型程序的人，也不是用时髦的编程语言编写代码的人。一个真正优秀的程序员明白，计算机只不过是一台计算机器，我们可以告诉它应该如何执行计算。无论我们创建的是什么，它都是一个不包含任何数学代码的简单文本编辑器。但这只是一种幻觉。即使是文本编辑器，其代码中也包含相当多的数学运算，特别是如果它内置了拼写检查器。

基本上，在编程中，如果你喜欢称之为因式分解或计算，有两种方法可以执行。第一种方法是以标量形式计算，即使用语言提供的函数编写如下公式：


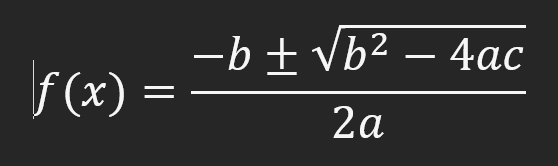
这个公式人人都会，可以计算二次函数的根。它可以很容易地用任何编程语言编写，使用该语言中可用的函数和资源。但还有另一种计算方法：矩阵或向量，有些人更喜欢这样称呼它。在本文中，我们称之为 "矩阵"，因为我们将使用矩阵来表示事物。这种分解方式是这样的：


一些刚刚开始学习编程的爱好者不知道如何用代码写出这些内容。他们最终将矩阵表示法转换为标量表示法，以获得相同的结果。

问题不在于它是对还是错。如果得到的结果是正确的，那就没有多大关系。在这种情况下，该矩阵显示某物围绕给定点旋转。在这篇文章中，亲爱的读者们，我想向你们展示如何使用 MQL5 或任何其他语言，直接在代码中编写这个矩阵形式，而不必将其转换为标量形式。很多人认为这很难做到。事实上，一切都比想象中简单得多。因此，请跟随本文学习如何做到这一点。


为什么使用矩阵而不是标量形式？

在了解如何编写代码之前，让我们先弄清楚如何选择一种或另一种方法来实现分解。

显然，如果我们搜索有关编程语言的信息，肯定会遇到标量形式的代码编写方法，但为什么呢？原因是使用矩阵形式在编写代码时比较混乱。要理解这一点，请尝试将上图所示矩阵或任何其他矩阵写成代码行。你会发现这有些尴尬。代码看起来很奇怪，没有多大意义。以标量形式，代码将更容易理解。这就是为什么你永远不会看到有人以矩阵形式编写因式分解代码。

然而，一些因式分解以矩阵形式编写比以标量形式编写要容易得多。例如，如果您需要处理大量可以轻松表示为多维数组的数据。要理解这一点，让我们先想想矢量图像。我们使用矢量而不是逐像素绘制屏幕。这使我们能够使用矩阵以极其简单的方式旋转、缩放、执行剪切变形和其他操作。换句话说，就是编写使用矩阵的计算代码。同样的转换可以以标量形式执行，但使用矩阵会简单得多。

如果矢量图形看起来不够复杂，我们可以考虑三维对象。也许现在你明白为什么矩阵分解如此有趣了。

在三维对象中，使用矩阵执行任何变换都要容易得多。以标量方式做同样的事情是非常困难和耗时的。这是可能的，但太难了，令人沮丧。想想是否需要使用类似文章开头给出的公式对三维物体进行正投影。实现这样的功能将是一场噩梦。然而，在创建使用矩阵的代码时，三维对象的复杂性并不重要：制作正交投影非常简单。

这就是视频卡和三维建模程序所使用的。事实上，它们在计算中使用矩阵，即使你没有注意到。那么，在编写因式分解代码时，什么时候应该使用一种形式，什么时候应该使用另一种形式呢？这取决于您的经验和知识。没有硬性规定强迫你使用一种或另一种方法。不过，重要的是要知道如何对这两种方法进行编程，以使一切尽可能快速、简单和高效。

由于标量形式被广泛使用，并且是按字面意思编程的，因此我们在此只关注如何编写矩阵形式的代码。为了使其更简单易懂，我们将把它分解成具体的主题。我们现在就开始吧。


标量方法

在这里，你会看到一些简单明了的东西。请记住，本文仅用于教学目的。它不是用来编制任何特定程序的。

首先，让我们在 MQL5 中创建一个小程序。我们将介绍的内容也适用于您想使用的任何其他语言。这完全取决于你对语言的掌握程度。我们将从下面一段非常简单的代码开始。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. int OnInit()
11. {
12.     
13.     int px, py;
14.     
15.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
16.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
17. 
18.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
19.     canvas.Erase(ColorToARGB(clrWhite, 255));
20.         
21.     canvas.Update(true);
22.     
23.     return INIT_SUCCEEDED;
24. }
25. //+------------------------------------------------------------------+
26. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
27. {
28.     return rates_total;
29. }
30. //+------------------------------------------------------------------+
31. void OnDeinit(const int reason)
32. {
33.     canvas.Destroy();
34. }
35. //+------------------------------------------------------------------+

如您所见，该代码是一个指标。我们可以使用任何其他指标，但该指标将更有趣，原因有几个：我们可以用它实现一些东西，它允许我们拦截来自 MetaTrader 5 的某些调用。

这段代码非常简单，几乎什么都没有做。它只是将图表窗口更改为白色或您想要使用的任何颜色。请注意，为了尽可能简化生成的代码，在第六行中我们使用了 MQL5 标准库。在这一行中，我告诉编译器应添加 Canvas.mqh 头文件，该文件在安装 MetaTrader 5 时默认创建。这将大大简化我们在本文中要介绍的内容。然后，在第8行，我们声明一个全局变量，以便我们可以访问 CCanvas 类。既然我们谈论的是 "类"，我们就必须以特定的方式来使用它。一个重要的细节：我通常喜欢用类作为指针。但是，由于许多人可能对我为什么这样做或那样做有疑问，为了尽可能简化事情，我将使用每个人通常使用的类，即作为一个允许我们引用某物的简单变量。

因此，在第 15 行和第 16 行中，我们固定了放置指标的图表窗口的大小。请注意，我们并没有为其创建窗口。这是在第 3 行中指出的。由于指标根本不跟踪任何东西，我们避免了编译器警告消息。为此，我们使用第 4 行。如果我们在子窗口中应用该指标，第 15 行和第 16 行显示的信息将有所不同。

在第 18 行，我们告诉 Canvas 类，我们想创建一个区域，在那里我们想绘制一些东西。此区域从左上角（第二个和第三个参数）延伸到左下角（接下来的两个参数）。第一个参数是 CCanvas 类创建的对象名称。最后一个参数指定将在该区域中使用哪种组合进行绘制。有关这些绘图模式的更多详细信息，请参阅文档。我们将使用以 alpha 作为颜色的模型，这意味着我们可以为所选区域内绘制的所有内容创建透明度。

下一步是清理该区域。这在第 19 行完成，紧接着，在第 21 行，指出存储器中的信息应显示在屏幕上。重要的是要明白，我们使用 CCanvas 放置在区域中的信息不会在创建信息的同时出现在屏幕上。所有绘图都是先在内存中完成的。在执行第 21 行之前，它们不会显示在屏幕上。这一切都很简单。现在我们已经掌握了基础知识，让我们看看我们将在屏幕上绘制什么。代码如下所示。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle)
13. {
14.     int ax[] = {0, 150, 100, 150},
15.         ay[] = {0, -75,   0,  75};
16.     int dx[ax.Size()], dy[ax.Size()];
17.     
18.     for (int c = 0; c < (int)ax.Size(); c++)
19.     {
20.         dx[c] = (int)((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
21.         dy[c] = (int)((ax[c] * (-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
22.     }
23. 
24.     canvas.FillPolygon(dx, dy, ColorToARGB(clrBlue, 255));
25.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
26. }
27. //+------------------------------------------------------------------+
28. int OnInit()
29. {    
30.     int px, py;
31.     
32.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
33.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
34. 
35.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
36.     canvas.Erase(ColorToARGB(clrWhite, 255));
37.         
38.     Arrow(px / 2, py / 2, 60);
39. 
40.     canvas.Update(true);
41.     
42.     return INIT_SUCCEEDED;
43. }
44. //+------------------------------------------------------------------+
45. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
46. {
47.     return rates_total;
48. }
49. //+------------------------------------------------------------------+
50. void OnDeinit(const int reason)
51. {
52.     canvas.Destroy();
53. }
54. //+------------------------------------------------------------------+

请注意，这里我们对文章开头给出的公式进行了标量转换，使用的是矩阵表示法。换句话说，我们将旋转对象。但这个对象是什么呢？要理解这一点，请看下图。这就是我们在 MetaTrader 5 中运行代码时将看到的结果。


我们旋转的对象是箭头。但看看这段代码，你能看到箭头是在哪里绘制的吗？请看第 38 行，我们调用了 ARROW 函数。ARROW 在第 12 行。很明显，箭头一定在第 12 行函数的某个地方，但在哪里呢？箭头的定义见第 14 和 15 行。请注意，我们有两个数组来绘制这个箭头。在这里，我们以一种非常简单的方式绘制它。现在，最有趣的部分开始了。

箭头是用绝对方式定义的。也就是说，我们可以按照现实世界的表现方式绘制，但也可以虚拟地表现。您可以使用浮点数值来代替整数数值。因此，将绘制箭头的数值乘以任意标量，就可以确定箭头的大小。不过，为了避免使情况复杂化，我们在这里没有这样做。我想把它说得尽可能简单，以便亲爱的读者们了解如何实现矩阵分解。

第 16 行中的某些内容可能会让许多人感到困惑。但这样写的原因很容易理解。由于我们事先不知道将使用多少点来绘制对象，并且我们需要一个中间数组在第 24 行中绘制它，因此我们需要以某种方式告诉应用程序为我们分配内存。使用第 16 行中的形式，我们告诉编译器，它应该分配与绘制点所需的空间一样多的空间。也就是说，我们使用了一个动态数组，但它是静态分配的。如果我们不使用这种编写代码的方式，我们将不得不创建与 Arrow 函数中相同的代码，如下面的代码所示进行组装。

11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle)
13. {
14.     int ax[] = {0, 150, 100, 150},
15.         ay[] = {0, -75,   0,  75};
16.     int dx[], dy[];
17.     
18.     ArrayResize(dx, ax.Size());
19.     ArrayResize(dy, ax.Size());
20.     
21.     for (int c = 0; c < (int)ax.Size(); c++)
22.     {
23.         dx[c] = (int)((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
24.         dy[c] = (int)((ax[c] * (-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
25.     }
26. 
27.     canvas.FillPolygon(dx, dy, ColorToARGB(clrBlue, 255));
28.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
29. 
30.     ArrayFree(dx);
31.     ArrayFree(dy);
32. }
33. //+------------------------------------------------------------------+

请注意，在第 16 行，我们现在有了一个动态数组指示。这种类型的数组定义了执行期间将使用的空间。我们需要做出以下更改。在代码的第 18 行和第 19 行，我们必须分配必要的空间，以便程序在执行过程中不会异常终止。此外，在这段代码中，我们必须将第 30 行和第 31 行中分配的内存归还给操作系统，这被认为是一种良好的编程做法。许多程序员倾向于不归还已分配的资源，但这使得应用程序消耗资源：应用程序不释放资源，并且这使得管理变得困难。但是，除了您可以看到代码片段和主代码之间的细微差别外，其他一切工作原理都是一样的。

现在让我们回到主代码。第 18 行的循环将遍历我们要旋转的形状中的所有点。

现在请关注一些有趣的事情。我们旋转形状并将其移动到某个位置。具体来说，我们将其移动到 X 、Y 点，在本例中就是屏幕的中心点。请看第 38 行，我们在这里定义了位置和旋转角度，即 60 度。

由于所有三角函数都默认使用弧度值，而不是度数值，因此我们需要将度数转换成弧度。这正是第 10 行的定义所做的事情。这样，我们就能更自然地说出形状应该旋转多少，而不是用弧度来表示数值，因为弧度在很多情况下会让人很困惑。

因此，对于数组中的每个点，我们都要应用下图所示的公式。


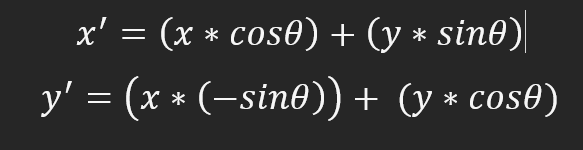
图像将逆时针旋转，使零度对应时钟上的九点钟位置。更清楚地说，90 度是 6 小时，180 度是 3 小时，270 度是 12 小时。记住是逆时针旋转。要改变这种行为，就需要更改计算方法。事实上，一切都很简单，没有任何复杂之处。要计算顺时针旋转的速率，需要将公式改为下面的公式。


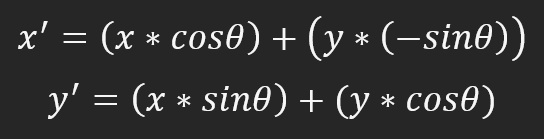
一切都非常简单。在这个例子中，三点钟方向是零度角，六点钟方向是 90 度角，九点钟方向是 180 度角，十二点钟方向是 270 度角。虽然看起来我们只是将角度值从 0 改为 180 度，但我们做了更多事情：旋转方向从逆时针改为顺时针。

但这不是我想展示的。这只是一个有趣的问题。要真正解释我想展示的内容，首先让我们以大家通常使用的形式展示一切。正是因为在许多情况下，这样做更简单、更容易。然而，这并不是我们在任何情况下都能轻易采用的。

现在我们不再详细讨论这个问题，因为文章的重点不在于此，而在于建模矩阵计算。让我们看看程序员通常是如何解决这些问题的。最简单的方法就是将我们感兴趣的事物转化为虚拟单位。我们首先执行所有计算，然后将结果转换为图形测量单位。使用虚拟单位创建时，我们将使用浮点数值，通常是 double 类型，而不是整数。所以我们之前看到的代码看起来像这样：

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
13. {
14.     double ax[] = {0.0,  1.5, 1.0, 1.5},
15.            ay[] = {0.0, -.75, 0.0, .75};
16.     int dx[ax.Size()], dy[ax.Size()];
17.     
18.     for (int c = 0; c < (int)ax.Size(); c++)
19.     {
20.         ax[c] *= size;
21.         ay[c] *= size;
22.         dx[c] = (int) ((ax[c] * cos(_ToRadians(angle))) + (ay[c] * sin(_ToRadians(angle)))) + x;
23.         dy[c] = (int) ((ax[c] *(-sin(_ToRadians(angle)))) + (ay[c] * cos(_ToRadians(angle)))) + y;
24.     }
25. 
26.     canvas.FillPolygon(dx, dy, ColorToARGB(clrGreen, 255));
27.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
28. }
29. //+------------------------------------------------------------------+
30. int OnInit()
31. {    
32.     int px, py;
33.     
34.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
35.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
36. 
37.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.         
40.     Arrow(px / 2, py / 2, 60);
41. 
42.     canvas.Update(true);
43.     
44.     return INIT_SUCCEEDED;
45. }
46. //+------------------------------------------------------------------+
47. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
48. {
49.     return rates_total;
50. }
51. //+------------------------------------------------------------------+
52. void OnDeinit(const int reason)
53. {
54.     canvas.Destroy();
55. }
56. //+------------------------------------------------------------------+

几乎没有什么变化，除了我们现在可以放大创建的对象。这在第 20 和 21 行完成。对象在第 14 和 15 行创建的。所有代码几乎保持不变。然而，这个简单的更改可以帮助将应用程序移植到其他场景。例如，如果用户改变了图表的尺寸，可以只更改第 12 行中的尺寸参数，使对象保持一定的比例。

但我仍然不明白这将如何帮助我使用矩阵。如果我能这样做，为什么要把它复杂化？好吧，让我们看看用矩阵做这样的事情是否真的更难。为此，我们将启动一个新主题。


现在使用矩阵分解

由于本文的目的是读者教学，我将尽量简单明了。因此，我们只实现了演示我们所需的材料所必需的部分，即这种特殊情况下的矩阵乘法。但是，亲爱的读者们，你们会看到，即使仅凭这一点，也足以执行矩阵标量乘法。许多人在使用矩阵分解实现代码时遇到的最大困难是：与标量分解不同，在标量分解中，几乎所有情况下因子的顺序都不会改变结果，但使用矩阵时情况并非如此。如果使用矩阵，与上一主题相同的代码会是什么样子？下面是使用矩阵进行分解的代码。
01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

我们尽可能简化代码，不做任何特殊修改，以便亲爱的读者们能够理解。通常，当我使用矩阵计算编写因式分解时，我的做法有点不同，但我们将在以后的文章中讨论这个问题，因为一些细节需要解释。所以，我必须进一步解释这些细节，虽然这看起来很简单，但如果你不妥善处理，你会发现自己陷入了一个无底洞。但这个疯狂的代码到底是做什么用的呢？它的功能与上一主题相同，只是在这里我们使用矩阵乘法来执行相同的计算。你可能会觉得这段代码很复杂，其实不然，它比前一段代码要简单得多。如果了解了如何将一个矩阵乘以另一个矩阵，一切就简单多了。然而，乘法运算并没有像预期的那样发生。换句话说，如果我们需要修改代码，它不会让我们做一些事情。但是，正如我已经说过的，这个版本仅供演示之用。正确的选项将在下一篇文章中介绍。然而，即使以一种有点奇怪的方式执行，因子分解也会给出预期的结果。

在使用之前，您应该了解这一细节。但是，如果你已经对矩阵分解的工作原理有了一定的了解，后面的内容就会容易理解得多。请注意，第 12 行是执行矩阵分解的代码。很简单。基本上，我们将第一个矩阵乘以第二个矩阵，然后将结果放入第三个矩阵。由于乘法是用一个矩阵的列乘以另一矩阵的行，因此因子分解相当容易。这里需要遵循一些规则，例如，一个矩阵中的行数必须等于另一个矩阵中的列数。这是有关矩阵的基本数学知识，如果不知道如何进行或为什么要这样做，请先试着理解一下。我们在矩阵 A 中放置列，在矩阵 B 中放置行。在我们的示例中，我们得到的结果就像下面看到的一样。

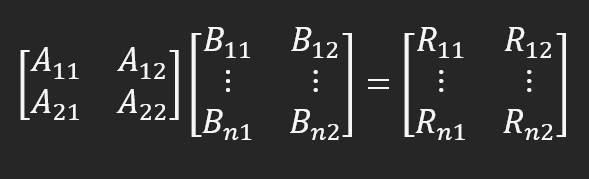
我知道，乍一看这一切可能会让人感到非常困惑，但其实一切都很简单。元素 A 的矩阵必须乘以元素 B 的矩阵，这样就得到了元素 R 的矩阵：
R11 = (A11 x B11) + (A12 x B12); R12 = (A21 x B11) + (A22 x B12) R21 = (A11 x B21) + (A12 x B22); R22 = (A21 x B21) + (A22 x B22) R31 = (A11 x B31) + (A12 x B32); R32 = (A21 x B31) + (A22 x B32)
以此类推。需要注意的是，如果计算是标量计算，就会出现这种情况。这正是第 12 行程序所要做的。我认为，重要的是，我们在构建计算时要有更大的自由度。要理解这一点，让我们看一下第 21 行的函数，箭头就是在这里构建和呈现的。这里定义了 5 个矩阵。我们可以少用一些。我们先把话说清楚。在未来，我们可能会考虑如何以一种更直观、更容易理解的方式对其进行建模，但即使在这种模型中，它仍然很容易理解。在第 23 行和第 33 行之间，我们绘制矩阵，它们将用于计算。现在，在第 35 行，我们声明将在屏幕上用来表示箭头的元素。在第 37 行和第 40 行之间，我们进行了必要的计算。现在请注意：我们要做的事情非常有趣。无论是从实用角度还是从因子分解的自由度角度来看，都是如此。在第 37 行，我们首先用矩阵 M_1 乘以矩阵 M_2，然后将结果输入矩阵 M_3。这个乘法的结果是什么？图像进行了旋转。不过，我们还不能将其显示在屏幕上，因为模型中仍然使用了 M_2 矩阵中的比例。要以正确的比例表示图像，还需要进行一次计算。但首先，在第 38 行，我们要清除矩阵 M_1 的内容，紧接着在第 39 行，我们要指定如何改变图像的比例。目前我们有一些新的选择，但我们只关注缩放。在第 40 行，我们将已经旋转过的对象数据乘以一个新的矩阵，该矩阵已经包含了要使用的所需比例。如下图所示。

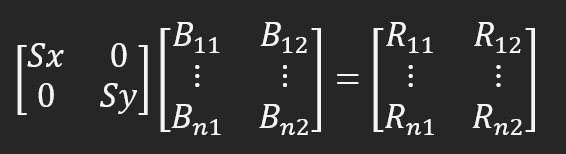
这里，Sx 是沿 X 轴的新尺寸，Sy 是沿 Y 轴的新尺寸。由于我们将这两个值都设置为 "Size"，因此所发生的变化就如同放大对象一样。这就是为什么我说我们可以做得更多。由于 FillPolygon 函数不知道如何处理这种矩阵结构，因此我们需要分割数据，以便 FillPolygon 可以为我们绘制箭头。我们在第 48 行设置了一个 for 循环，结果与上一个主题相同。


最后的探讨

在这篇文章中，我介绍了一种相当简单的矩阵计算方法。我试图呈现一些有趣的东西，同时找到一种最简单的方法来解释这个计算是如何完成的。然而，本文所考虑的矩阵模型并不是最适合执行所有可能类型因子分解的模型。因此，我很快将发表一篇新文章，其中我将讨论一种更适合表示矩阵的模型。我还将给出一个解释，以便您可以使用这种新的数据分解方法。我们很快在下一篇文章中再见。


本文由MetaQuotes Ltd译自葡萄牙语
原文地址： https://www.mql5.com/pt/articles/13646

附加的文件 |
下载ZIP
App1.mq5 (1.87 KB)
App2.mq5 (1.97 KB)
App3.mq5 (2.62 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
构建一个用于实现带约束条件的自定义最大值的通用优化公式（GOF） 构建一个用于实现带约束条件的自定义最大值的通用优化公式（GOF）
在这篇文章中，我们将介绍一种在MetaTrader 5终端的设置选项卡中选择“自定义最大值”时，实现具有多个目标和约束的优化问题的方法。举例来说，优化问题可以是：最大化利润因子、净利润和恢复因子，同时满足以下条件：回撤小于10%，连续亏损次数少于5次，每周交易次数多于5次。
头脑风暴优化算法（第一部分）：聚类 头脑风暴优化算法（第一部分）：聚类
在本文中，我们将探讨一种受自然现象“头脑风暴”启发的新型优化方法——头脑风暴优化（Brain Storm Optimization，简称BSO）。我们还将讨论BSO方法所应用的一种解决多模态优化问题的新方法。该方法能够在无需预先确定子种群数量的情况下，找到多个最优解。此外，我们还会考虑K-Means和K-Means++聚类方法。
头脑风暴优化算法（第二部分）： 多模态 头脑风暴优化算法（第二部分）： 多模态
在文章的第二部分，我们将继续讨论BSO算法的实际应用，对测试函数进行测试，并将BSO的效率与其他优化方法进行比较。
非平稳过程和伪回归 非平稳过程和伪回归
本文基于蒙特卡洛模拟，展示了回归分析非平稳过程时产生的伪回归现象。